Viscoelastic Properties of the Aortic Valve Interstitial Cell

Abstract

There has been growing interest in the mechanobiological function of the aortic valve interstitial cell (AVIC), due to its role in valve tissue homeostasis and remodeling. In a recent study we determined the relation between diastolic loading of the AV leaflet and the resulting AVIC deformation, which was found to be substantial. However, due to the rapid loading time of the AV leaflets during closure (~0.05 s), time-dependent effects may play a role in AVIC deformation during physiological function. In the present study, we explored AVIC viscoelastic behavior using the micropipette aspiration technique. We then modeled the resulting time-length data over the 100 sec test period using a standard linear solid (SLS) model which included Boltzmann superposition. To quantify the degree of creep and stress relaxation during physiological timescales, simulations of micropipette aspiration were preformed with a valve loading time of 0.05 s and a full valve closure time of 0.3 s. The 0.05 s loading simulations suggest that, during valve closure, AVICs act elastically. During diastole, simulations revealed creep (4.65%) and stress relaxation (4.39%) over the 0.3 s physiological timescale. Simulations also indicated that if Boltzmann superposition was not used in parameter estimation, as in much of the micropipette literature, creep and stress relaxation predicted values were nearly doubled (7.92% and 7.35%, respectively). We conclude that while AVIC viscoelastic effects are negligible during valve closure, they likely contribute to the deformation time-history of AVIC deformation during diastole.

INTRODUCTION

The aortic valve (AV) lies at the entrance to the aorta and functionally serves to facilitate unidirectional flow of blood from the left ventricle to aorta. The primary deformation mode of the AV leaflets are large in-plane deformations induced by high in-plane stresses (250–400 kPa), resulting from ~80 mmHg transvalvular pressure that occurs across the closed AV. While the primary biomechanical function of the AV is at the organ system scale, its constituent tissues are maintained by the population of interstitial cells (AVICs) found within the AV leaflet tissues. We have recently determined that AVICs undergo very large deformations during AV closure [1] that occur over a time scale ~0.05 s [2], so that AVICs apparently undergo very high strain rates.

Recent work has examined the mechanical stimuli-dependent biosynthetic and contractile response of valvular interstitial cells [3–5]. We recently observed that valve interstitial cells from the aortic and mitral valves were significantly stiffer (p<0.001) than those from the pulmonary and tricuspid valves [4]. Differences in stiffness were found to be a result of higher cytoskeletal protein content in the left side interstitial cells compared to their right side counterparts. Moreover, the increased left side interstitial cell cytoskeletal protein content has been shown to be correlated with increased type I collagen synthesis rates, possibly in order to maintain structural tissue competence. This finding suggested that the left side heart valve interstitial cells (aortic and mitral) appear to functionally adapted to the significantly tissue stresses imposed on them as compared to the right side heart valve interstitial cells.

In these studies, many idealized assumptions have been made regarding the mechanical properties of the AVIC and their relation to the underlying cytoskeleton [3, 4], cell-ECM connectivity [5, 6], and the in-vivo deformations during the cardiac cycle [1]. For example, in our previous study of AVIC mechanical properties [4], viscoelastic effects were ignored and only the equilibrium stiffness E∞ was reported after viscoelastic creep had apparently dissipated (>100 s). Irrespective of the specific question or application, all studies universally assumed that AVICs behave elastically. Thus, due to the highly dynamic biomechanical environment in which AVICs reside, we sought to quantify AVIC viscoelastic properties using the micropipette aspiration technique. We then performed simulations of loading during valve closure as well as creep and stress relaxation simulations over diastolic time scales to estimate if viscoelastic effects play a significant role in AVIC deformation.

METHODS

AVIC isolation

Ovine AV leaflets were harvested from a young lamb upon sacrifice. The leaflets were dissected, surfaces scrapped with a razor blade to remove the endothelial cells, then minced into ~1 mm² pieces, and digested with 0.2% collagenase A (Sigma, St. Louis, MO) in DMEM for 30 min with gentle rotation (10 rev/min). Following digestion, the cell-tissue solution was strained with a 0.5 ⍰m cell strainer. The population was plated in complete media (DMEM, 10% FBS, 1% penicillin/streptomycin, and 0.5% fungizone, all from Gibco) for 8 days, frozen in 10% DMSO, and shipped. Upon arrival the AVICs were replated in complete media and cultured for 2 days to assess survival during shipping by attachment to the culture dish and proliferation.

Micropipette aspiration of AVICs

The micropipette aspiration system and setup used here has been described previously [4, 7]. Briefly, AVICs were trypsinized, pelleted (1500 rpm, 5 min), and resuspended in media prior to testing. 80⍰~L of cell suspended media was aspirated and placed in a chamber that allows entry of a micropipette from the side [8]. Capillary tubes (A-M Systems, Inc., Carlborg, WA) were fabricated into micropipettes with a pipette puller (David Kopf Instruments, Tujunga, CA) and then fractured with a microforge to achieve an inner diameter of 7–9⍰m. Pressures were applied to the surface of an AVIC through the micropipette via a custom-built water reservoir with an in-line pressure transducer having a resolution of 1 Pa (Model no. DP15–28, Validyne Engineering Corp., Northridge, CA). While pressure was applied, digital images of the cell aspiration, applied pressure, and time were recorded to a DVD-R with a CCD camera (COHU, San Diego, CA) through a bright-field microscope (Diaphot 300, Nikon Inc., Melville, NY), using a 40× oil immersion objective and a 10× wide field eyepiece (Edmund Scientific Co., Barrington, NJ). 11 AVICs were tested by applying a tare pressure of ~50 Pa for 60 s, then a single step pressure was applied for a final pressure of ~500 Pa. Aspiration length was recorded until the cell had reached equilibrium and no more displacement was detectable (~100 s).

Viscoelastic models of AVIC deformation

In much of the micropipette aspiration literature a standard linear solid (SLS) model is typically utilized under the assumption of instantaneously applied aspiration pressure [7]. However, the loading time for micropipette aspiration is finite, with the pressure ramped from zero to maximum over several seconds. We thus utilized Boltzmann superposition [9] to account for aspiration length creep during loading in the SLS model

$$\mathrm{L}\left(\mathrm{t}\right)={\int }_0^{\mathrm{t}}\frac{\varphi \mathrm{a}}{\pi {\mathrm{k}}_1}\left[1-\frac{{\mathrm{k}}_2}{{\mathrm{k}}_1+{\mathrm{k}}_2}{\mathrm{e}}^{\frac{-\mathrm{t}}{{\tau }_{\epsilon }}}\right]\frac{\text{dP}}{\mathrm{d}\tau }\mathrm{d}\tau ,{\tau }_{\epsilon }=\frac{\mu ({\mathrm{k}}_1+{\mathrm{k}}_2)}{{\mathrm{k}}_1{\mathrm{k}}_2}$$ (1)

where ϕ is defined as the wall function (a dimensionless parameter calculated from the ratio of the pipette inner radius to the wall thickness) and is set to 2.1, a is the micropipette inner radius, dP is instantaneous differential step pressure, L(t) is the measured aspiration length at time t, and k₁, k₂, and μ are the SLS model parameters. We refer to this model as the Boltzmann SLS (BSLS) model throughout for clarification. The traditionally used SLS model simply employs a ⍰P term and assumes application of a Heaviside step function such that the applied pressure is achieved at t>0.

Parameter values were determined by fitting each L(t) experimental response with the BSLS and SLS models using the Levenberg Marquardt algorithm [10] (MathCad, PTC, inc.) with initial parameter assigned as follow: k₁ = 100 Pa, k₂ = 100 Pa, and μ = 1000 Pa-s. Essentially, the algorithm provides a numerical solution to the problem of minimizing a nonlinear function over a space of parameters of the function. The Levenberg Marquardt algorithm interpolates between the Gauss-Newton algorithm and the method of gradient descent. From the parameters, the instantaneous stiffness E₀=3/2(k₁₊k₂) and equilibrium stiffness (E∞=3/2 k₁) were determined.

Simulations of AVIC deformation under physiologic loading rates

With k₁, k₂, and μ parameters determined for both the BSLS and SLS models for each AVIC tested, the following simulations were performed. First, we estimated the AVIC aspiration length response a linear pressure ramp applied from 0 to 500 Pa, using time scales from a physiologic loading rate for full AV closure of 0.05 s [11] to 5.0 sec; the upper limit representing approximately twice the time used in ex-vivo native and engineered heart valve tissue cultures studies [12–14]. Next, we explored the potential effects of AVIC viscoelasticity when the AV is closed and the fully loaded by simulating creep and relaxation over a typical diastolic time period of 0.3 s. SLS and BSLS model equations were given a prescribed combination of time and either length or pressure, and the corresponding length or pressure response computed. For creep, simulations proceeded from using the 0.5 s loading period to 500 Pa aspiration pressure, which was then held for an additional 0.3 s. Similarly, stress relaxation was simulated by applying a linear aspiration length ramp to the level achieved for that particular AVIC while loading in the micropipette aspiration experiments mentioned above in 0.05 s, then held for an additional 0.3 s. All simulations were performed using MathCAD (PTC, inc.) with the BSLS model integral solved using Romberg numerical integration, and performed using BSLS and SLS model parameter values from each AVIC tested. Results from the simulations were compiled and reported as mean ± standard error (SEM).

RESULTS

AVIC time-dependent response to micropipette aspiration

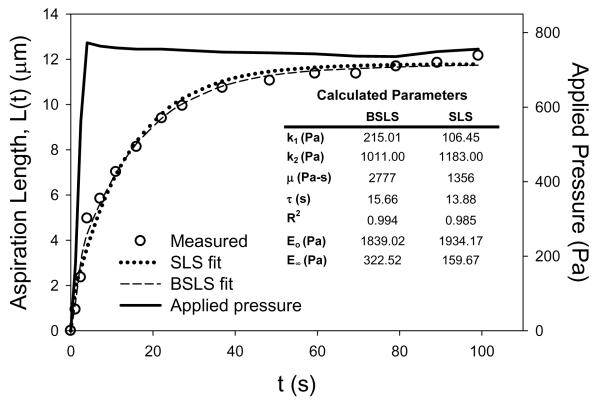
The average applied pressure to the AVICs during the micropipette aspiration tests was 519 ± 36 Pa with an average ramp time to apply the pressure of 2.48 ± 0.31 s. The reason for this ~2.5 s ramp pressure to achieve a steady but expedient single pressure ramp to ~500 Pa, which resulted in an AVIC response to micropipette aspiration similar to other cells. This included a large initial change in aspiration length which began to plateau at ~60 s (Figure 1). Both model parameter values (Table 1) were typical of cells measured previously [7].

Figure 1.

Representative response of an AVIC under micropipette aspiration (circles) with both the BSLS and SLS model fits. Applied pressure history is plotted on the right y-axis. Inset table shows determined parameters from both models for the representative AVIC (n=1) that was used.

Merryman et al., AVIC Viscoelasticity, 2007

Table 1.

Calculated parameters from BSLS and SLS models.

n=11 AVICs	BSLS model		SLS model
	AVG	± SEM	AVG	± SEM
k1 (Pa)	188.32	49.36	119.83	20.16
k2 (Pa)	613.88	130.52	650.65	92.68
μ (Pa-s)	3479.09	563.24	2591.18	368.13
τ (s)	37.04	7.02	31.08	5.31
R2	0.980	0.003	0.967	0.004
Eo (Pa)	1203.29	262.11	1155.73	149.08
E∞ (Pa)	282.48	74.05	179.75	30.25

AVIC loading simulations

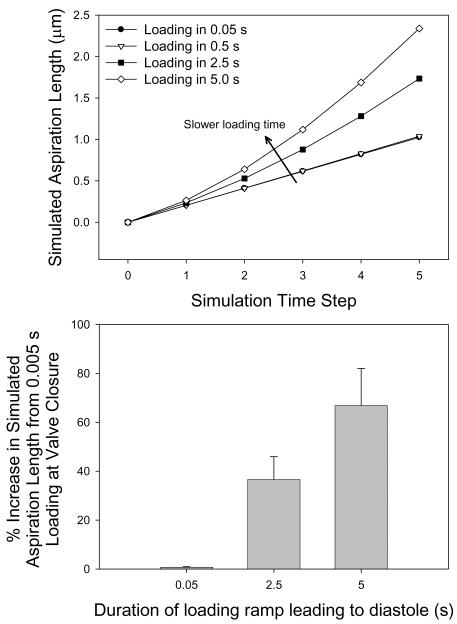
To explore the rate dependent influence of viscous effects during AV closure, we simulated aspiration length-time responses for 0.05, 0.5, 2.5, and 5.0 s loading times using BSLS and SLS model parameters. For near physiological loading rates we observed little viscous effects (Figure 2). At 0.5 s, there were negligible viscous effects (0.74 ± 0.21% increase) versus 0.05 s loading (Figure 2-b). However, at 2.5 and 5.0 s the viscous effects were very pronounced (36.59 ± 9.35% and 66.84 ± 15.20% increases, respectively) compared to the 0.05 s loading case.

Figure 2.

(a) Viscous effects due to varying simulation loading times for a single AVIC at 0.05, 0.5, 2.5 and 5.0 s. (b) % increase in simulated aspiration length at the end of the applied pressure ramp versus 0.05 s. As loading time increase, viscous effects are more pronounced. While below 0.5 s viscous effects appear to be negligible, it is interesting to note that over 2.5 ms, the time needed to apply pressure during the micropipette aspiration experiment, viscous effects are %40 greater than when applying the load in 0.05 s.

Merryman et al., AVIC Viscoelasticity, 2007

Creep and stress relaxation simulations

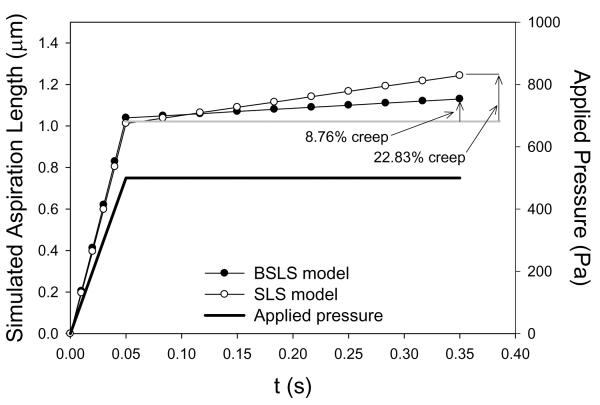
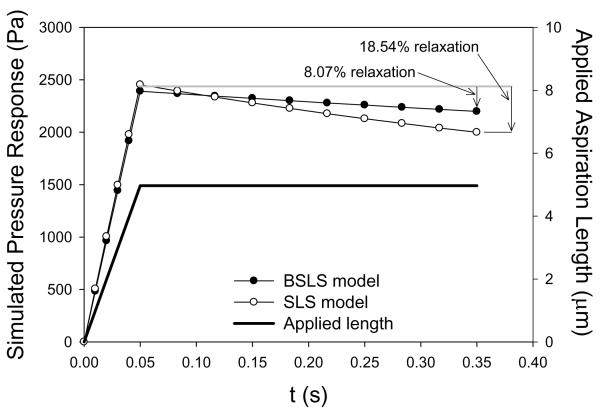
Using the BSLS and SLS models, the representative creep and stress relaxation simulations, respectively, are shown for the same cell (Figures 3 and 4). For the BSLS model, average creep during diastole was 4.65 ± 1.34%, and similarly, the average stress relaxation during diastole was 4.39 ± 1.12% (Table 2). For the SLS model, average creep during diastole was 7.92 ± 1.88%, and similarly, the average stress relaxation during diastole was 7.35 ± 1.51% (Table 2). These basic simulations suggest that over diastolic loading timescales viscous-dependent deformations can occur in AVICs.

Figure 3.

Representative creep simulation response for an AVIC loaded to 500 Pa in 0.05 s and held for 0.3 s using both the BSLS and SLS models.

Merryman et al., AVIC Viscoelasticity, 2007

Figure 4.

Representative stress relaxation simulation response for an AVIC aspirated to 2.3 ⍰m in 0.05 s and held for an additional 0.3 s using both the BSLS and SLS models. Note that 4.96 ⍰m was the actual aspiration length occurring for that AVIC during the micropipette aspiration experiments.

Merryman et al., AVIC Viscoelasticity, 2007

Table 2.

Micropipette aspiration simulations of stress relaxation and creep using the parameters from Table 1.

Creep Simulations
n=11	BSLS Simulation			SLS Simulation
	L0.05s (μm)	L0.35s (μm)	% creep	L0.05s (μm)	L0.35s (μm)	% creep
AVG±SEM	2.68	2.77	4.65	2.07	2.21	7.92
	0.58	0.59	1.34	0.31	0.31	1.88

Stress Relaxation Simulations
n=11	BSLS Simulation			SLS Simulation
	P0.05s (Pa)	P0.35s (Pa)	% relaxation	P0.05s (Pa)	P0.35s (Pa)	% relaxation
AVG±SEM	1112.91	1035.18	4.39	1085.45	985.45	7.35
	273.82	233.96	1.12	154.01	117.92	1.51

For both simulations, a loading time of 0.5 s was used, followed by a 0.3 s period where either L or P were held constant for stress relaxation and creep simulations, respectively.

DISCUSSION

Physiologic relevance of AVIC viscoelasticity

In the present study, AVIC viscoelastic behavior over physiological timescales was simulated using micropipette aspiration, a well established technique for the study of cell biomechanics. Our goal was to examine the potential for viscoelastic contributions to in-vivo deformation during AV loading, as well as changes during diastole when the AV is closed. A SLS model incorporating Boltzmann superposition (BSLS) was used, as the rapid loading times (0.05 s) that occur in the valve could not be attained with the micropipette aspiration testing system. As the AVIC in-vivo deformations have only begun to be explored [1], we used micropipette aspiration tests to emulate AVIC in-vivo responses. Physiologic loading, creep, and stress relaxation simulations were performed as bounds on possible in-vivo AVIC behavior.

Interestingly, we observed that under physiologic loading time scales there were negligible effects of viscoelasticity on AVIC deformation (Figure 2). Not surprisingly, this result suggests that the 0.05 s loading times are sufficient fast that no cellular strain rate effects occur. Interpretation of these results suggests an elastic response of the AVIC during physiologic loading times. Yet, under a diastolic time frame of ~0.3 s, model simulations for creep and stress relaxation suggest that some degree of time-dependent deformation can occur (Figures 3 and 4). Thus, our simulation results suggest that, while not large, AVIC time-dependent deformations may occur when the V is closed. Moreover, the small differences between 0.05 s and 0.5 s loading times support extended bioreactor studies examining AVIC mechanobiology where cyclic loads are applied at 1 Hz.

Mechanotransduction describes the molecular mechanism by which cells respond to changes in their physical environment by translating mechanical stimuli into biochemical signals. We have shown that AVIC cell nuclear deformations correlate well with overall cellular deformations [15]. It has been proposed that the nucleus itself acts as a mechanosensor, with changes in nuclear shape causing conformational changes in chromatin structure and organization and directly affecting transcriptional regulation [16]. Moreover, studies of on nuclear shape and structure have revealed strong correlations between shape change and cellular phenotype. Thus, even though the nucleus is 2–10 time stiffer than the surrounding cytoskeleton, extracellular matrix forces and strain result in clearly detectable nuclear deformations. As previously stated, AVICs undergo very large deformations during AV closure [1] and undergo very high strain rates [2]. Thus, knowledge of how AVIC deform, and presumably their nuclei, during the cardiac cycle is clearly central to understanding their responses to extracellular matrix forces and pathological states

Use of Boltzmann superposition for micropipette aspiration analysis

While the use of Boltzmann superposition is routine in viscoelastic modeling [9] and utilized in most biomechanical testing modalities, it is surprisingly absent in most micropipette aspiration studies. Rather, the SLS model is commonly used, where ΔP is the applied aspiration pressure. The commonly used SLS model [7] ignores any creep that occurs during application of the pressure (~2.5 s in this study), which we believed to be important for study of the AVICs. The use of the SLS model in this case resulted in decreased parameter values for k₁ and μ and increased parameter value for k₂ versus the SLS (Table 1). These changes in model parameters predictably produced substantial differences in predicted creep and relaxation responses (Figures 3 and 4). While not large for valvular timescales, these results suggest that for AVIC mechanical studies one needs to be cognizant of time-dependent effects that occur during the experiment. Clearly, implementation of the correct model could prove beneficial for those dealing with highly viscoelastic cellular studies.

Use of micropipette aspiration in the study of time dependent AVIC properties

We have reported the stiffness of ovine AVICs as measured by micropipette aspiration [4] and porcine AVICs measured with atomic force microscopy (AFM) [3]. The primary differences between AFM and micropipette aspiration testing arise from scale, depending on the type of AFM probe tip that is used. With a sharp tip, the AFM probes a very small, localized region surrounding the contact region of the AFM tip. Micropipette aspiration, on the other hand, provides mechanical properties that are averaged over the micropipette tip area, which is generally several square microns [17]. Thus, AFM indentation using a microsphere tip that is several microns in diameter provides measurements over a similar area [18]

It has been reported that, using micropipette aspiration, the viscoelastic properties of the ovine AVIC are primarily influenced by the actin cytoskeleton [17]. From a biomechanical perspective, it can be argued that testing AVIC cells in an attached and spread configuration gives a more physiologic representation of the mechanical properties of the cell than micropipette aspiration as the cells are generally attached to an underlying substrate such that the cytoskeleton is anchored at focal adhesions. This configuration is in contrast to testing with micropipette aspiration where the cell is in suspension and does not form focal contacts, in the absence of a substrate. Nonetheless, previous studies have shown that these techniques provide similar cellular mechanical properties if the area of the testing site is comparable [18].

While appropriate for the functional questions raised in this study, the linear viscoelastic model for AVIC loaded in under micropipette aspiration is only a first step. More advanced descriptions of the time dependent behavior of cells exist [20]. For example, Trepat et al. [21] report that in response to transient stretch (such as those that occur in AVICs) the cytoskeleton fluidizes in such a way to as to define a universal response class. These findings support the idea that the cell interior is a crowded chemical space/fragile soft material which yield remarkably simple phenomenological laws. Specifically, over a wide range of conditions, the abilities of a cell to fluidize suddenly in response to stretch and to resolidify subsequently seem to be insensitive to molecular details, but only on the proximity of the cell to a solid-like state before deformation. Thus, conventional descriptions of cell deformation, such as viscoelasticity used here, will need to be updated to account for these cellular dynamic events.

Regardless of the specific testing modality and physical model of the cell, the biomechanical environment of the AVIC remains ill defined. Current evidence suggests that AVICs are tightly attached to the surrounding ECM [5, 19] and are subjected to substantial compression [1]. While the micropipette simulations utilized in this study clearly do not emulate the AVIC in-vivo environment, they do provide useful insight into the intrinsic mechanical properties of the cells and the potential for time-dependent effects.

Conclusions

The viscoelastic properties of AVICs were measured for the first time using micropipette aspiration. Simulations using the micropipette aspiration loading configuration suggest the loading time for the AVIC is sufficiently fast that viscous effects are negligible. However, during diastole when the AV tissue is subjected to its largest planar stresses, viscoelastic effects may contribute to AVIC deformations. These results will provide new insight into mechanobiological studies of the AVIC, wherein the AV mechanical environment is being emulated.