Skip to main content
PMC home page
Medical Physics logoLink to Medical Physics
. 2013 Mar 11;40(4):041901. doi: 10.1118/1.4793724

Respiratory triggered 4D cone-beam computed tomography: A novel method to reduce imaging dose

Benjamin J Cooper 1, Ricky T O’Brien 2, Salim Balik 3, Geoffrey D Hugo 3, Paul J Keall 4,a)
PMCID: PMC3612115  PMID: 23556895

Abstract

Purpose: A novel method called respiratory triggered 4D cone-beam computed tomography (RT 4D CBCT) is described whereby imaging dose can be reduced without degrading image quality. RT 4D CBCT utilizes a respiratory signal to trigger projections such that only a single projection is assigned to a given respiratory bin for each breathing cycle. In contrast, commercial 4D CBCT does not actively use the respiratory signal to minimize image dose.

Methods: To compare RT 4D CBCT with conventional 4D CBCT, 3600 CBCT projections of a thorax phantom were gathered and reconstructed to generate a ground truth CBCT dataset. Simulation pairs of conventional 4D CBCT acquisitions and RT 4D CBCT acquisitions were developed assuming a sinusoidal respiratory signal which governs the selection of projections from the pool of 3600 original projections. The RT 4D CBCT acquisition triggers a single projection when the respiratory signal enters a desired acquisition bin; the conventional acquisition does not use a respiratory trigger and projections are acquired at a constant frequency. Acquisition parameters studied were breathing period, acquisition time, and imager frequency. The performance of RT 4D CBCT using phase based and displacement based sorting was also studied. Image quality was quantified by calculating difference images of the test dataset from the ground truth dataset. Imaging dose was calculated by counting projections.

Results: Using phase based sorting RT 4D CBCT results in 47% less imaging dose on average compared to conventional 4D CBCT. Image quality differences were less than 4% at worst. Using displacement based sorting RT 4D CBCT results in 57% less imaging dose on average, than conventional 4D CBCT methods; however, image quality was 26% worse with RT 4D CBCT.

Conclusions: Simulation studies have shown that RT 4D CBCT reduces imaging dose while maintaining comparable image quality for phase based 4D CBCT; image quality is degraded for displacement based RT 4D CBCT in its current implementation.

Keywords: 4D cone-beam computed tomography, imaging dose, respiratory motion, respiratory triggered

INTRODUCTION

Image guidance is a useful tool to reduce patient setup errors1 in external beam radiation therapy and a steady rise in the use of image guidance has been reported.2 An orthogonal pair of megavoltage or kilovoltage images just prior to a patient receiving radiotherapy can be utilized to correct for spatial discrepancy between the bony anatomy in the current state and a reference state, usually a set of digitally reconstructed radiographs from the planning CT dataset. Both megavoltage and kilovoltage imaging play important roles within the array of image guidance techniques3 and accordingly, there is a sliding scale of imaging dose to the patient depending on the level of complexity of the image guidance technique.4, 5

The advent of kilovoltage cone-beam computed tomography (3D CBCT) (Refs. 6 and 7) has provided the ability to discern soft tissue anatomy and thus a more detailed picture of interfraction and intrafraction organ motion and thereby an ability to detect and correct for more complex target positioning problems.

Due to the rotational speed limitations of kV imaging systems on linear accelerator gantries, conventional 3D CBCT acquisition gives rise to motion blurring8, 9 of moving organs, particularly those organs in the proximity of the diaphragm (lungs, liver, kidney, etc.). This has been the motivation for the development of 4D CBCT which attempts to address the problem of respiration induced organ motion blurring by correlating the acquired projections with the respiratory signal.10, 11, 12 4D CBCT raises a problem of undersampling causing artifacts and some approaches employ slow gantry or multiple gantry rotations to increase projections13 to address undersampling which potentially increases imaging dose. The use of daily image guidance using CBCT at treatment time in external beam radiation therapy has been shown to improve geometric accuracy in locally advanced lung cancer;14 however, there is a trade-off between increasing imaging dose, both from the frequency and type of daily imaging, and the improvement in accuracy. Increased imaging from IGRT raises clinical concern and has motivated the development of novel iterative CBCT reconstruction algorithms which can use fewer projections leading to a 36-72 times reduction in imaging dose compared to a widely used head and neck scanning protocol.15 The purpose of this work is to introduce and investigate a novel method called “respiratory triggered 4D CBCT” with the goal to reduce imaging dose. ICRP 73 poses the question, “Are there any reasonable steps I can take to improve protection?”16 More recently, the “Image Wisely” and “Image Gently” campaigns have been established to address public concern of radiation in medical procedures for both the adult and pediatric populations. The stated objectives are “lowering the amount of radiation used in medically necessary imaging studies and eliminating unnecessary procedures” (http://www.imagewisely.org/About-Us - retrieved 2012-08-28) and “to change practice by increasing awareness of the opportunities to promote radiation protection in the imaging of children” (http://www.pedrad.org/associations/5364/ig/ - retrieved 2012-08-28), respectively. We will show that the proposed method can reduce imaging dose to the patient thus making a positive impact for these campaigns.

METHODS AND MATERIALS

In order to generate a phase-based 4D CBCT dataset from a linear accelerator imaging system, it is necessary to subdivide the acquired projection images into bins according to when the projection occurs during the patient's respiratory cycle. In phase based 4D CBCT, the respiratory cycle is typically subdivided into 6–10 time windows or bins. A side effect of the subdivision into bins is that the angular distribution of the projections in any given bin exhibits clustering. During reconstruction using FDK based algorithms, streaking artifacts have been reported due to this clustering effect.17 To illustrate, in Fig. 1 we consider the angular distribution of the projections sorted into respiratory bin 1 over three respiratory cycles. During the first respiratory cycle, a number of consecutive projections separated by a small angle δθ will be sorted into bin 1. Time passes and acquired projections get sorted into the other bins (not shown). When the second respiratory cycle starts, the projections are again sorted into bin 1 but there is now a large angular gap Δθ between the first and second cluster of projections.

Figure 1.

Figure 1

Open in a new tab

Angular distribution of projections for bin 1 showing projection clustering. δθ is the angle between consecutive projections in bin 1; Δθ is the angular span travelled by the gantry in one respiratory cycle.

In this work, there were two arms of simulation studies undertaken:

  1. a conventional 4D CBCT acquisition method with no respiratory signal feedback, referred to as “conventional 4D CBCT” throughout this paper where the imaging frequency is constant during acquisition representing current clinical systems;

  2. the novel respiratory triggered 4D CBCT acquisition method, referred to as “RT 4D CBCT” where imaging frequency is variable and triggered based on the respiratory signal.

It should be noted that the RT 4D CBCT method requires an independent respiratory signal that is not derived from the imaging system acquiring the 4D CBCT. For simplicity, the respiratory signal is assumed to be a sine wave as studied in Ref. 18. Figure 2 illustrates the difference between a conventional 4D CBCT method [Figs. 2a, 2b] and the proposed respiratory triggered 4D CBCT method [Figs. 2c, 2d].

Figure 2.

Figure 2

Open in a new tab

Conventional 4D CBCT acquisition method [(a) and (b)] compared to RT 4D CBCT acquisition method [(c) and (d)]. Part (a) shows two 4 s respiratory cycles with a sinusoidal respiratory signal (lower) and a pulse train for the imaging system acquiring projections (upper). “Bin 1” is highlighted as the vertical shaded box. Part (b) shows the corresponding gantry angles for the clustered projections in “Bin 1” over three respiratory cycles. Part (c) is analogous to (a) except that the pulse train is only triggered once per respiratory phase bin in RT 4D CBCT and (d) shows the corresponding gantry angles for a single projection per respiratory phase bin.

Conventional 4D CBCT

Figure 2a shows the sine wave respiratory signal over two cycles. The larger spacing vertical lines represent the subdivision of a cycle into 10 phase bins. The shaded vertical rectangles depict “Bin 1.” Above the respiratory signal is a graphical depiction of the imaging system triggering at a constant rate of 5.5 Hz (densely spaced vertical bars). Note that the triggering frequency is fixed and has no feedback from the respiratory signal. Considering just the first bin in the cycle, the corresponding projection angles over three respiratory cycles are shown on the polar graph in Fig. 2b. For clarity, the polar graph is scaled: one degree on the figure represents 0.1 degrees of gantry rotation.

Respiratory triggered 4D CBCT

Figure 2c shows how the imaging system triggering frequency is now controlled such that only one projection is triggered and acquired per phase bin per cycle illustrated by only one imaging system pulse per bin per cycle [vertical bars in Fig. 2c]. A reduction in the total number of projections is evident. The corresponding projection angles for the RT 4D CBCT method are shown on the polar graph in Fig. 2d. Although Fig. 2 illustrates the RT 4D CBCT method for respiratory phase type bin sorting, the method can also be applied to respiratory displacement type bin sorting. Both respiratory phase and displacement type bin sorting will be discussed but the focus is on phase type bin sorting as this approach has been implemented commercially (Elekta, Kungstensgatan 18, SE-103 93 Stockholm).

Materials

A stationary thorax phantom was imaged using a linac based kV imaging system with the following parameters:

  • 3600 projections;

  • 200° span of gantry rotation;

  • Full fan bowtie filter.

The set of projection images serves two purposes: (1) to generate a “ground truth” reconstruction CBCT dataset using a commercial FDK reconstruction package (COBRA, Exxim Computing Corporation, 3825 Hopyard Road, Suite 220, Pleasanton, CA 94588) for image comparison analyses and (2) to provide a large pool of projections from which the simulation program can select for the various simulation studies. Using 3600 projections essentially eliminates the introduction of angular sampling error during the simulation experiments. The largest possible sampling error is less than 0.028º using 3600 projections over a 200º span. This mode of projection acquisition is only available in a nonclinical mode of the linac's imaging system.

Phase based projection sorting experiment

A set of 4D CBCT simulation studies were performed to investigate the imaging dose and image quality using a conventional respiratory phase based 4D CBCT method and the RT 4D CBCT method. Acquisition time, breathing period, and imager frequency (frame rate) were varied. Acquisition time is varied by varying gantry speed over a fixed 200º span for acquisition. The parameter values for each simulation are summarized in Table 1. Simulation 1 represents the image acquisition parameters from a commercially available 4D CBCT system along with a rounded patient population mean breathing period of 4.0 s, based on the report by George et al.18 To account for variations in breathing period, simulations were performed with 2.1 and 6.7 s representing the measured patient population for the 5th and 95th percentiles for free breathing.18 For the acquisition time and imager frequency parameters, the variations are multiples of the representative commercial 4D CBCT acquisition parameters (simulations 2 and 5, Table 1).

Table 1.

Parameter values for phase based sorting simulation studies. Bold type indicates the parameter varying.

Simulation Acquisition Breathing Imager
number time (s) period (s) frequency (Hz)
1 240 4.0 5.5
2 120 4.0 5.5
3 240 2.1 5.5
4 240 6.7 5.5
5 240 4.0 10.0
Open in a new tab

Displacement based projection sorting experiment

A further set of simulations was performed to investigate the imaging dose and image quality of the conventional 4D CBCT and the RT 4D CBCT using displacement based projection sorting rather than phase based sorting. We investigate changes in dose and image quality between displacement bins for all 10 bins. In this set, the acquisition parameters are fixed: acquisition time = 240 s; breathing period = 4 s; imager frequency = 5.5 Hz. Work by Abdelnour et al. gives a good general description of phase and amplitude (displacement) based projection sorting.19

Simulations

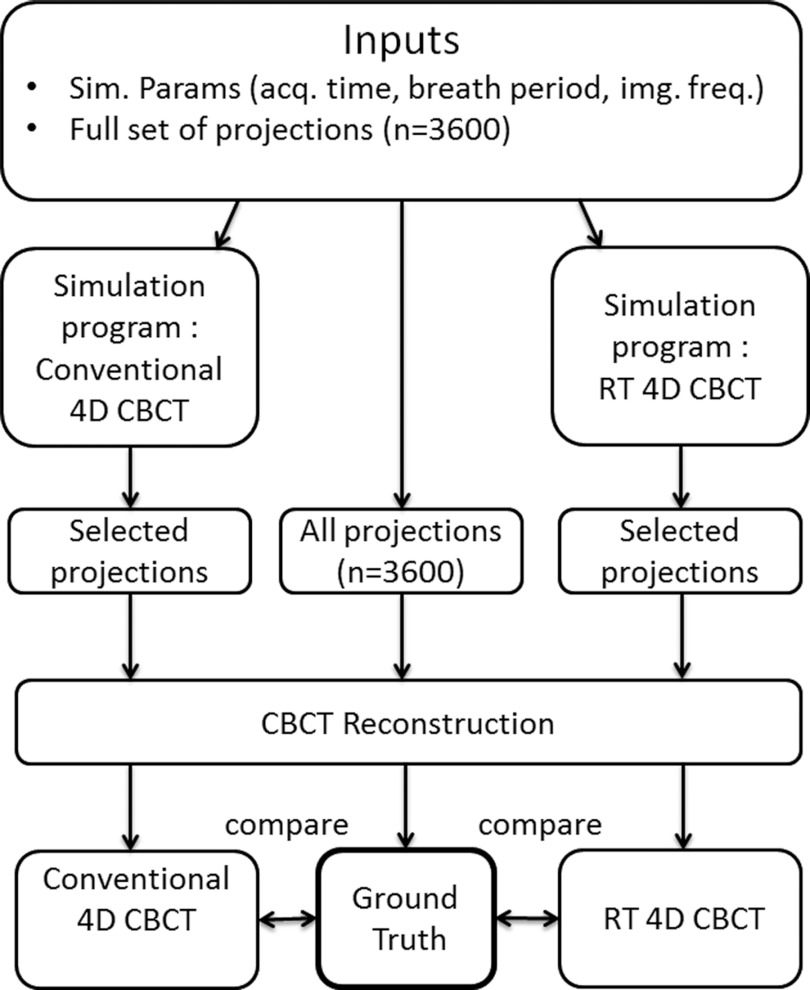
Using all 3600 projections as input to the cone-beam reconstructor program Cobra, a “ground truth” CT dataset was generated giving 160 CT slices (256 × 256 pixels/slice) spaced 1 mm apart. The same reconstruction parameters were used to generate the conventional 4D CBCT datasets and the RT 4D CBCT datasets. Figure 3 shows the work flow for the conventional 4D CBCT, the RT 4D CBCT, and the “ground truth” simulations.

Figure 3.

Figure 3

Open in a new tab

Flow diagram showing schema for simulation experiments showing conventional 4D CBCT (left), ground truth (middle), and RT 4D CBCT (right). The ground truth (middle) is a CBCT reconstruction of all 3600 projections and is compared to the reconstructions from the conventional 4D CBCT (left) and the RT 4D CBCT (right).

Analysis

ImageJ (ImageJ version 1.46q, http://rsbweb.nih.gov/ij/) was used to calculate difference images. A difference image is defined to be the scalar difference between corresponding pairs of pixels in a pair of images of the same dimensions. An ImageJ macro was developed to calculate slice by slice difference images for all slices thus quantifying the overall average pixel difference values for:

  1. ground truth and the conventional 4D CBCT;

  2. ground truth and the respiratory triggered 4D CBCT methods.

The overall average pixel difference is defined as follows. The average pixel difference (diffs) is the average value for the difference image and is given for a single slice as

diff s=∑a,b=1N| pix a− pix b|N,

where pixa and pixb are pixel values from image (a) and image (b); and N is the total number of pixels in the difference image. The overall average pixel difference is defined as

Overall average pixel difference =∑i=1S diff s,iS,

where S is the number of image slices in the dataset. The overall average pixel difference for each dataset is used as the metric for image quality. A higher value means that the test dataset is worse quality in the sense that it is farther from the ground truth.

Imaging dose was assessed assuming one projection equals one dose unit. Kim et al.5 reported a measured dose of 7.68 mGy per 677 projections for a low dose thorax imaging CBCT protocol. Using this for an indicative imaging dose for the simulation studies gives approximately 11.3 μGy per projection. The number of projections resulting from the conventional 4D CBCT and the RT 4D CBCT simulations was counted to compare imaging dose.

RESULTS

Phase based projection sorting

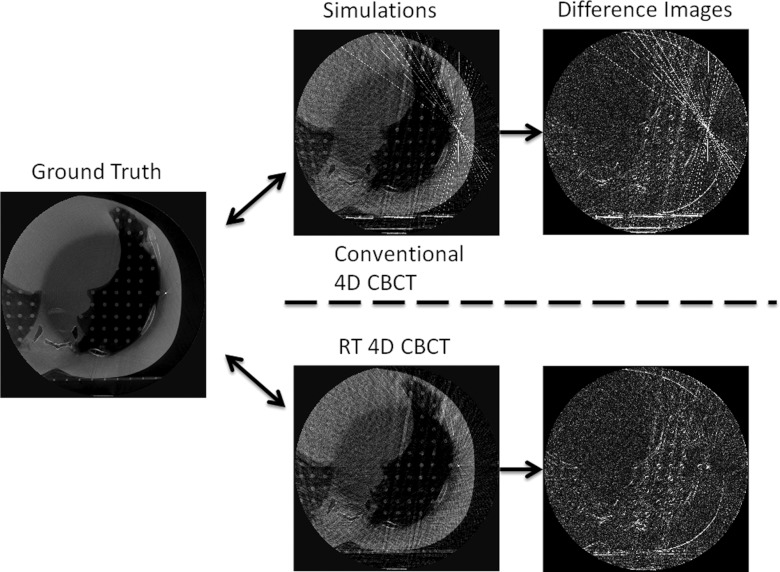
The reconstruction images for simulation 1 (Table 1) are shown in Fig. 4. Ground truth and simulation reconstructions and the resulting scalar difference images are shown left to right; top row is conventional 4D CBCT and bottom row is RT 4D CBCT.

Figure 4.

Figure 4

Open in a new tab

The ground truth image (left) is compared to both the conventional 4D CBCT (top middle) and RT 4D CBCT images (bottom middle) using phase type projection sorting. The corresponding difference images are shown (right). Window and level settings are consistent for both conventional 4D CBCT and RT 4D CBCT.

The average pixel value differences for all simulations are shown in column pairs for both the conventional 4D CBCT and the RT 4D CBCT methods (left and right columns, respectively) in Fig. 5a. One interpretation of the average pixel differences is a measure of how much the image (or set of images) under examination has been degraded from the ground truth image set. The corresponding comparisons in imaging dose are shown in Fig. 5b. The simulations are grouped into three parameter groups corresponding to the three groups in Table 1.

Figure 5.

Figure 5

Open in a new tab

Comparison of average pixel value difference [Fig. 5a] and imaging dose [Fig. 5b] for conventional 4D CBCT (left columns) and RT 4D CBCT (right columns) from the Ground Truth 4D CBCT dataset. In each group of three, the first left/right column pair is a repeat of the result from simulation 1 (Table 1) which represents reference acquisition parameters from a commercial 4D CBCT system and an average breathing period. The latter column pairs in each parameter group show variations of that particular parameter group (acquisition time, breathing period, and imager frequency).

Displacement based projection sorting

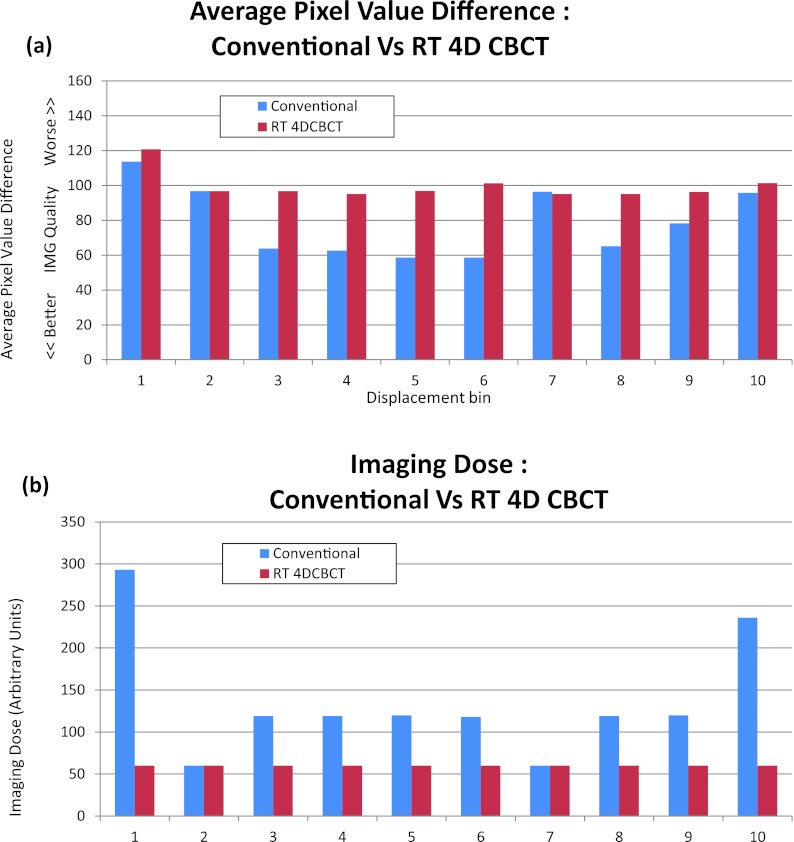
The average pixel value differences and imaging dose differences for the effects of displacement type bin sorting using conventional and RT 4D CBCT methods are shown in Figs. 6a, 6b, respectively.

Figure 6.

Figure 6

Open in a new tab

(a) Comparison of average pixel value differences for conventional 4D CBCT and RT 4D CBCT from the Ground Truth 4D CBCT dataset for all 10 displacement bins. (b) The corresponding imaging dose for all 10 displacement bins.

DISCUSSION

A new method, RT 4D CBCT, has been developed that substantially reduces imaging dose without degrading image quality for 4D CBCT that employs projection sorting by phase. Conceptually, the method is simple: take the patient respiratory signal and use this to trigger image acquisition. Qualitatively, Fig. 4 shows that there is not much difference between the conventional 4D CBCT images and the RT 4D CBCT images, apart from a notable star artifact that is more prominent around a fiducial marker in the conventional 4D CBCT images. For all three of the parameter groups, acquisition time, breathing period, and imager frequency, there are only small differences in image quality between conventional 4D CBCT and RT 4D CBCT. Conventional 4D CBCT shows a strong correlation between increased imaging dose as imaging frequency is increased with no clear improvement in imaging quality. Yet despite the comparable image quality, there is a marked saving in imaging dose with the RT 4D CBCT method showing roughly half or less the relative dose (and number of projections needed) compared to the 4D CBCT method with the exception of simulation 3 (2.1 s breathing period). A possible explanation for this result goes as follows. In Fig. 1 the projection sampling scheme for bin 1 is shown. There are essentially two sampling frequencies that are present-–a higher sampling frequency for all the projections within a single cluster (1/δθ) and a lower sampling frequency between clusters (1/Δθ). Having two different sampling frequencies violates the assumption of equally spaced samples (projections) in the formulation of the FDK cone-beam reconstruction algorithm.20 This, in turn, leads to streaking and star artifacts in the reconstructed images, especially as observed around highly attenuating material such as bone and fiducial markers. Another interpretation is that if δθ is very small, this implies only a very subtle change in the contents of those clustered projections. As there is very little “new” spatial information within a group of clustered projections, the high signal pixels in the projection (bone, fiducial markers, and highly attenuating material) tend to be reinforced along the ray line giving rise to streaks and star artifacts. The reason for this is that there are missing projections in the span (Δθ, Fig. 1) and so the high signal pixels are not “balanced out” in the back projection process. In contrast, a conventional (nonbinned) 3D CBCT case has a complete set of projections in the span (Δθ) and so streaking artifact is absent. The RT 4D CBCT method effectively removes the clustering effect thus removing the (1/δθ) sampling frequency component and leaving only the (1/Δθ) sampling frequency. As the angular sampling frequency becomes sparser, as might be the case for long period breathers (6.7 s), then the reconstructed images are further degraded because projection data sufficiency is not met. As RT 4D CBCT is a subset of the conventional method, both methods would suffer from a sparser angular sampling frequency.

For those patients where it might be indicated to use frequent CBCT image guidance for improved geometrical accuracy, as suggested by Higgins et al.,14 any saving in imaging dose with minimal impact on image quality is desirable. RT 4D CBCT employing a phase based binning scheme offers a benefit in this situation. Other authors have shown that reducing tube current and longer CBCT acquisitions can improve 4D CBCT image quality.13 Another approach to reducing imaging dose is through the use of iterative algorithms. The RT 4D CBCT method described in this paper could be coupled with non-FDK based reconstruction algorithms, like the GPU-based approach described,15 to further optimize the use of imaging dose.

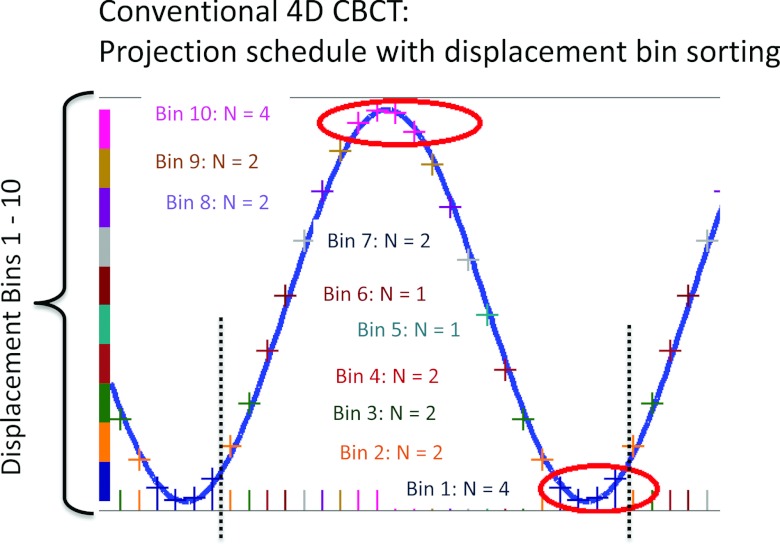
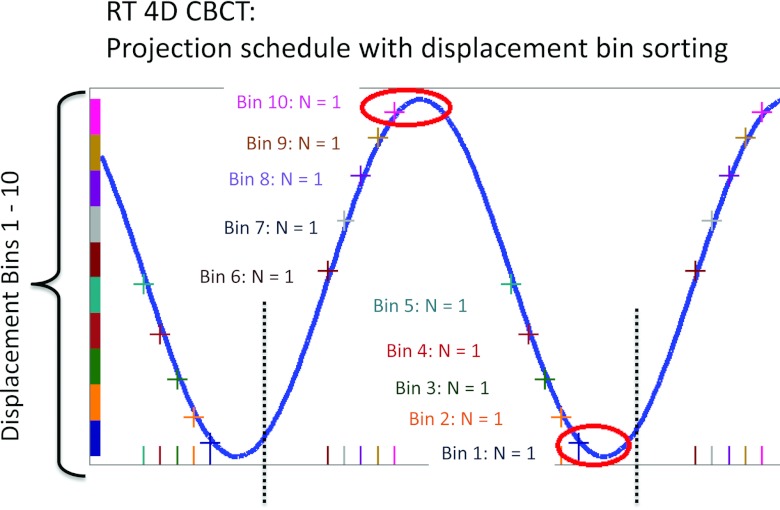
Figure 6 shows the average pixel difference and imaging dose, respectively, for each bin using a displacement based sorting method for both the conventional 4D CBCT and RT 4D CBCT. The conventional 4D CBCT exhibits marked variability in image quality across the ten bins with poorer image quality at the extremes (bins 1 and 10). Additionally, the imaging dose at these bins is highest. The reason for this is illustrated in Fig. 7. Both bins 1 and 10 show multiple projection acquisitions which cause the worst clustering effect. For the remaining bins, the clustering effect is greatly reduced and in some cases (bins 2 and 7, Fig. 6; bins 5 and 6, Fig. 7) it just so happens that only one projection per respiratory cycle is acquired. Here, the image quality and imaging dose for conventional 4D CBCT and RT 4D CBCT converge. The RT 4D CBCT image quality is fairly consistent across all ten bins. For bins 1, 2, 7, and 10, the average pixel difference is roughly in agreement (within 6 %) between conventional 4D CBCT and RT 4D CBCT. The imaging dose for bins 2 and 7 is correspondingly identical between conventional 4D CBCT and RT 4D CBCT; however, bins 1 and 10 suffer from clustering in conventional 4D CBCT and have a much higher dose than the RT 4D CBCT counterparts. The remaining bins show better image quality for conventional 4D CBCT but with correspondingly higher dose. By virtue of only one projection being allowed in the RT 4D CBCT, the imaging dose is consistent across all bins. This is illustrated in Fig. 8.

Figure 7.

Figure 7

Open in a new tab

Projection schedule for conventional 4D CBCT with displacement bin sorting over one respiratory cycle indicated with dashed vertical lines. Cross marks on the respiratory signal (sine wave) show how many projections will be sorted into displacement bins 1 through 10. Bins 1 and 10 exhibit the worst clustering effect.

Figure 8.

Figure 8

Open in a new tab

Projection schedule for RT 4D CBCT with displacement bin sorting over one respiratory cycle indicated with dashed vertical lines. Cross marks on the respiratory signal (sine wave) show how only one projection will be sorted into displacement bins 1 through 10. One projection per bin per cycle guarantees no clustering.

Why do bins 2 and 7 have the same imaging dose for both conventional 4D CBCT and RT 4D CBCT? This is explained by a chance happening that only one projection per respiratory cycle was sorted into bins 2 and 7 for this simulation. In fact, this is actually what the RT 4D CBCT algorithm does for all bins. Depending on the interplay between imager frequency, breathing period, and acquisition time, it is also possible that no projections will be sorted into some displacement bins for one or more respiratory cycles. These “misses” will in turn lead to potentially unusable images for the affected displacement bins. The likelihood of projection “misses” would be exacerbated by irregular breathing. These problems are not solved by RT 4D CBCT at present because it is a subset of the conventional 4D CBCT acquisition. Further work is currently being pursued to overcome these problems. Controlling the imaging frequency according to an input respiratory signal creates another degree of freedom in how 4D CBCT can be acquired. Extending this idea, it is possible to trigger projections on the rising and falling part of the respiratory motion, instead of just once per bin per cycle which has been the focus of this work. This could offer better image quality for displacement type projection sorting, particularly for the most rapidly moving part of the respiratory motion. For example, projections could be triggered on the rise and fall of the respiratory signal for displacement bins 4, 5, 6, and 7, in Fig. 8. The imaging dose will of course increase, however. A more general approach to solve this optimization problem is currently being developed.

There are several limitations in this study. The choice of using a stationary phantom was to study the effects of projection clustering and the interplay of the acquisition time, breathing period, and imager frequency in isolation from the possible introduction of interference from a phantom undergoing respiratory motion. Additionally, a stationary phantom allows for a “ground truth” dataset for comparative analysis using difference images. It is expected that phantom motion will contribute to temporal blurring and reduce the image quality.21 It is well known that breathing is anything but regular, in general. In this study we assume a sine wave for the respiratory signal with a reproducible period of 4 s. The sinusoidal model was chosen for simplicity and has been shown to be a reasonable model for respiratory motion which can exhibit moderate correlation to measured breathing signals.18 A known challenge for both conventional and RT 4D CBCT is the ability to maintain regular/constant angle spacing between projections in the presence of an irregular respiratory signal. Irregular breathing is not dealt with in the current study in order to answer the question, “is there any benefit from the RT 4D CBCT method?” without the potentially confounding effects of irregular breathing. However, a practical implementation of RT 4D CBCT would have to address irregular breathing. A possible solution would be to detect irregularity through monitoring the breathing signal in near real time. If the gradient of the signal falls outside a reasonable threshold, the acquisition is paused. After breathing stabilizes, perhaps over the next few breathing cycles, the acquisition resumes. Other investigators have successfully implemented a beam “hold off” for projections during kV CBCT.22 Pausing and restarting the linac gantry motion is achievable although considerations of inertia would probably require the gantry to rewind and resume acquisition at the right angular position and the right phase bin of the breathing trace. On a Varian linac, it is possible to stop and restart a conventional CBCT manually. Pausing and resuming gantry motion would need to be automated in the proposed RT 4D CBCT scheme. These simulation studies rely on the regularity of the respiratory period as it gives the ability to trigger a projection at a correspondingly regular angle between projections.

CONCLUSION

A novel 4D CBCT acquisition method has been described and compared to a conventional 4D CBCT system. Imaging dose and image quality have been quantified for respiratory phase and displacement based projection sorting. The proposed RT 4D CBCT system simulations under phase based projection sorting showed that the imaging dose is roughly halved, regardless of acquisition time; imaging dose and image quality decrease with longer breathing periods; imaging dose remains constant despite increasing imager frequency. The proposed respiratory signal triggered 4D CBCT system can give comparable image quality to the conventional 4D CBCT system using fewer projections and thus less dose, simply by triggering the projection acquisitions according to an input respiratory signal. In principle, the RT 4D CBCT system could be implemented on existing linac systems through utilizing a respiratory signal to trigger projection acquisitions during 4D CBCT and eliminating projection clustering and thereby reducing imaging dose.

ACKNOWLEGDMENTS

The authors acknowledge Douglas J. Vile who helped with collecting experimental data. The authors acknowledge funding support from the Australian National Health and Medical Research Council (NHMRC) Project Grant, an NHMRC Australia Fellowship, and a US NIH/NCI Grant No. P01CA116602. Thanks to Julie Baz for reviewing and improving the clarity of the paper. A patent application (PCT/US2012/048693) has been lodged which is related to this work.

References

  1. Pisani L., Lockman D., Jaffray D., Yan D., Martinez A., and Wong J., “Setup error in radiotherapy: On-line correction using electronic kilovoltage and megavoltage radiographs,” Int. J. Radiat. Oncol., Biol., Phys. 47, 825–839 (2000). 10.1016/S0360-3016(00)00476-4 [DOI] [PubMed] [Google Scholar]
  2. Simpson D. R., Lawson J. D., Nath S. K., Rose B. S., Mundt A. J., and Mell L. K., “A survey of image-guided radiation therapy use in the United States,” Cancer 116, 3953–3960 (2010). 10.1002/cncr.25129 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Dawson L. A. and Jaffray D. A., “Advances in image-guided radiation therapy,” J. Clin. Oncol. 25, 938–946 (2007). 10.1200/JCO.2006.09.9515 [DOI] [PubMed] [Google Scholar]
  4. Islam M. K., Purdie T. G., Norrlinger B. D., Alasti H., Moseley D. J., Sharpe M. B., Siewerdsen J. H., and Jaffray D. A., “Patient dose from kilovoltage cone beam computed tomography imaging in radiation therapy,” Med. Phys. 33, 1573–1583 (2006). 10.1118/1.2198169 [DOI] [PubMed] [Google Scholar]
  5. Kim S., Yoo S., Yin F.-F., Samei E., and Yoshizumi T., “Kilovoltage cone-beam CT: Comparative dose and image quality evaluations in partial and full-angle scan protocols,” Med. Phys. 37, 3648–3660 (2010). 10.1118/1.3438478 [DOI] [PubMed] [Google Scholar]
  6. Jaffray D. A., Drake D. G., Moreau M., Martinez A. A., and Wong J. W., “A radiographic and tomographic imaging system integrated into a medical linear accelerator for localization of bone and soft-tissue targets,” Int. J. Radiat. Oncol., Biol., Phys. 45, 773–789 (1999). 10.1016/S0360-3016(99)00118-2 [DOI] [PubMed] [Google Scholar]
  7. Jaffray D., Siewerdsen J. H., Wong J., and Martinez A., “Flat-panel cone-beam computed tomography for image-guided radiation therapy,” Int. J. Radiat. Oncol., Biol., Phys. 53, 1337–1349 (2002). 10.1016/S0360-3016(02)02884-5 [DOI] [PubMed] [Google Scholar]
  8. Li T., Xing L., Munro P., McGuinness C., Chao M., Yang Y., Loo B., and Koong A., “Four-dimensional cone-beam computed tomography using an on-board imager,” Med. Phys. 33, 3825–3834 (2006). 10.1118/1.2349692 [DOI] [PubMed] [Google Scholar]
  9. Brehm M., Berkus T., Oehlhafen M., Kunz P., and Kachelriess M., “Motion-compensated 4D cone-beam computed tomography,” IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), 3986–3993 (2011).
  10. Dietrich L., Jetter S., Tucking T., Nill S., and Oelfke U., “Linac-integrated 4D cone beam CT: First experimental results,” Phys. Med. Biol. 51, 2939–2952 (2006). 10.1088/0031-9155/51/11/017 [DOI] [PubMed] [Google Scholar]
  11. Sonke J.-J., Zijp L., Remeijer P., and van Herk M., “Respiratory correlated cone beam CT,” Med. Phys. 32, 1176–1187 (2005). 10.1118/1.1869074 [DOI] [PubMed] [Google Scholar]
  12. Li T., Schreibmann E., Yang Y., and Xing L., “Motion correction for improved target localization with on-board cone-beam computed tomography,” Phys. Med. Biol. 51, 253–267 (2006). 10.1088/0031-9155/51/2/005 [DOI] [PubMed] [Google Scholar]
  13. Li T. and Xing L., “Optimizing 4D cone-beam CT acquisition protocol for external beam radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. 67, 1211–1219 (2007). 10.1016/j.ijrobp.2006.10.024 [DOI] [PubMed] [Google Scholar]
  14. Higgins J., Bezjak A., Hope A., Panzarella T., Li W., Cho J. B., Craig T., Brade A., Sun A., and Bissonnette J. P., “Effect of image-guidance frequency on geometric accuracy and setup margins in radiotherapy for locally advanced lung cancer,” Int. J. Radiat. Oncol., Biol., Phys. 80, 1330–1337 (2011). 10.1016/j.ijrobp.2010.04.006 [DOI] [PubMed] [Google Scholar]
  15. Jia X., Lou Y., Li R., Song W. Y., and Jiang S. B., “GPU-based fast cone beam CT reconstruction from undersampled and noisy projection data via total variation,” Med. Phys. 37, 1757–1760 (2010). 10.1118/1.3371691 [DOI] [PubMed] [Google Scholar]
  16. Smith H., “Radiological protection and safety in medicine,” Ann. ICRP 26, 1–47 (1996). 10.1016/S0146-6453(00)89195-2 [DOI] [PubMed] [Google Scholar]
  17. Leng S., Zambelli J., Tolakanahalli R., Nett B., Munro P., Star-Lack J., Paliwal B., and Chen G.-H., “Streaking artifacts reduction in four-dimensional cone-beam computed tomography,” Med. Phys. 35, 4649–4659 (2008). 10.1118/1.2977736 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. George R., Vedam S. S., Chung T. D., Ramakrishnan V., and Keall P. J., “The application of the sinusoidal model to lung cancer patient respiratory motion,” Med. Phys. 32, 2850–2862 (2005). 10.1118/1.2001220 [DOI] [PubMed] [Google Scholar]
  19. Abdelnour A. F., Nehmeh S. A., Pan T., Humm J. L., Vernon P., Schöder H., Rosenzweig K. E., Mageras G. S., Yorke E., Larson S. M., and Erdi Y. E., “Phase and amplitude binning for 4D-CT imaging,” Phys. Med. Biol. 52, 3515–3529 (2007). 10.1088/0031-9155/52/12/012 [DOI] [PubMed] [Google Scholar]
  20. Feldkamp L. A., Davis L. C., and Kress J. W., “Practical cone-beam algorithm,” J. Opt. Soc. Am. A 1, 612–619 (1984). 10.1364/JOSAA.1.000612 [DOI] [Google Scholar]
  21. Lu J., Guerrero T. M., Munro P., Jeung A., Chi P.-C. M., Balter P., Zhu X. R., Mohan R., and Pan T., “Four-dimensional cone beam CT with adaptive gantry rotation and adaptive data sampling,” Med. Phys. 34, 3520 (2007). 10.1118/1.2767145 [DOI] [PubMed] [Google Scholar]
  22. van Herk M., Ploeger L., and Sonke J. J., “A novel method for megavoltage scatter correction in cone-beam CT acquired concurrent with rotational irradiation,” Radiother. Oncol. 100, 365–369 (2011). 10.1016/j.radonc.2011.08.019 [DOI] [PubMed] [Google Scholar]

Articles from Medical Physics are provided here courtesy of American Association of Physicists in Medicine

RESOURCES