Abstract
Negative outcomes, whether self-identified or resulting from feedback, cause a short-latency negative deflection in the event-related-potential (ERP) waveform over medial frontal electrode sites. This brain response is considered a type of “error related negativity” representing a coarse evaluation of performance; within monetary gambling tasks, it has been postulated to signal the valence of the chosen outcome. Yet, under such feedback circumstances, other information besides experienced valence may be critical for the adaptive control of behavior. Here, we used a gambling task in which subjects chose between two options that could vary in both outcome valence (gain or loss) and outcome magnitude (larger or smaller). We measured changes in brain ERP responses associated with the presentation of the outcomes. We found, as shown in prior studies, that valence of the chosen outcome has an early effect upon frontal ERPs, peaking at ~250 ms. However, our results demonstrated that the early ERP responses to outcome feedback were driven not just by valence, but by the combination of valence and magnitude for both chosen and unchosen options. Beginning even earlier, at around 150 ms, responses to high-consequence outcomes showed a greater, more centrally distributed, positive potential than those involving low-consequence outcomes, independent of valence. Furthermore, the amplitude of these early effects was significantly modulated by the sequence of outcomes in previous trials. These results indicate that early evaluation of feedback goes beyond simple identification of valence – it involves the consideration of multiple factors, including outcome magnitude, context of unchosen options, and prior history.
Introduction
A prerequisite for adaptive control of behavior is the ability to determine – as quickly as possible – whether choices result in positive or negative outcomes. Studies using electrophysiological methods, particularly the recording of scalp event-related potentials (ERPs), have revealed that the human brain is able to differentiate positive and negative outcomes within a few hundred milliseconds of their occurrence, following both self-identified mistakes and error feedback (Gehring, Coles, Meyer, & Donchin, 1995; Holroyd & Coles, 2002; Miltner, Braun, & Coles, 1997; Nieuwenhuis, Holroyd, Mol, & Coles, 2004; Ruchsow, Grothe, Spitzer, & Kiefer, 2002). In all cases, there is an increase in the negativity of the ERP response at medial frontal electrodes, typically peaking at around 100ms after self-generated behavioral responses that are in error and at around 250ms after explicit external feedback. The scalp distributions of the early negative ERP effects suggest an anterior cingulate cortex (ACC) generator (Dehaene, Posner, & Tucker, 1994; Gehring & Willoughby, 2002; Hajcak, Holroyd, Moser, & Simons, 2005; Miltner, Braun, & Coles, 1997), consistent with theoretical perspectives (Bush, Luu, & Posner, 2000; Paus, 2001) and research studies (Kerns et al., 2004; MacDonald, Cohen, Stenger, & Carter, 2000; Menon, Adleman, White, Glover, & Reiss, 2001; Botvinick et. al, 2001) that argue for the significance of medial frontal cortex in the regulation of cognitive control.
Less well understood, however, are the aspects of feedback that influence these early brain responses. Some research emphasizes the role of rapid feedback in reinforcement learning, noting that ACC activity is elicited when an error processing mechanism first detects that a choice has resulted in an undesirable and unexpected event (Holroyd & Coles, 2002). This perspective has typically been used to explain the resulting change in scalp-related potential observed after the presentation of positive and negative feedback, known as the feedback error-related negativity (feedback ERN). Alternatively, early feedback effects may reflect competing influences from conflicting information. This interpretation has been offered to explain the response error-related negativity (response ERN) elicited when subjects make an error in a speeded reaction-time task, signaling their self-identification of the mistake (Falkenstein, Hohnsbein, Hoormann, & Blanke, 1990; Gehring & Fencsik, 2001; Gehring, Goss, Coles, & Meyer, 1993). Although both may involve the ACC, the feedback and response ERNs have different scalp topographies, with the topography of the feedback ERN being more anterior and more right lateralized (Gehring & Willoughby, 2004), suggesting that the two error responses are at least partly generated by different sets of neural sources.
A novel example of rapid brain signals that participate in outcome evaluation was identified by Gehring and Willoughby (2002), who used a monetary gambling paradigm. They found that ERP amplitude within 200-300 ms of feedback delivery depended on whether the gamble resulted in a gain or a loss. The observed difference in ERP activity between gains and losses was labeled the medial frontal negativity (MFN) and was localized, like other forms of the ERN, to an ACC generator. The amplitude of the MFN was attributed to a pure valence effect: there was a greater negative response when the chosen gamble resulted in a loss than in a gain, regardless of its magnitude and regardless of whether the indicated outcome showed that the unchosen choice in the gamble would have been incorrect (Masaki, Takeuchi, Gehring, Takasawa, & Yamazaki, 2006; Yeung & Sanfey, 2004). A subsequent study revealed, however, that an ERN could be elicited if the task emphasized whether a response was correct or incorrect – that is, whether it was the better of two choices (Nieuwenhuis, Yeung, Holroyd, Schurger, & Cohen, 2004). This suggested that the MFN may reflect a special case of the ERN: a coarse error-detection mechanism that serves as an “early warning system” to identify something that is amiss in the environment without ascertaining exactly what is awry.
Under this last perspective, there is no a priori reason why rapid ERP responses like the MFN or ERN should be specific to the valence of outcome of the chosen stimulus. Behavioral economics studies have demonstrated that the interpretation of a given outcome depends, in many cases, on how that outcome is framed or on its relative value compared to other outcomes that could be obtained (Tversky & Kahneman, 1981). The MFN could reflect the activity of a system that quickly assesses not just gains and losses but the motivational significance of a wide range of events (Bush, Luu, & Posner, 2000; Taylor et al., 2006), both to recognize consequential choices (e.g., for reinforcement learning) and to engage or disengage cognitive control mechanisms (e.g., conflict detection and corresponding adjustment). These slower mechanisms, potentially represented by ERP responses in later time windows such as the P300 (Yeung & Sanfey, 2004), may determine more precisely what went wrong (e.g., calculations of higher-level evaluations like regret and satisfaction) so corrections can be put in place (Taylor et.al, 2006; Gehring & Fencsik, 2001).
Thus we hypothesized that the rapid ERP response to monetary gains and losses depends on multiple factors, including the valence and magnitude of both chosen and unchosen options, proportionally to their influence on the overall utility of choice outcomes. We used a version of the simple gamble-selection paradigm devised by Gehring and Willoughby (2002) to elicit an electrophysiological response to choice outcomes. We had four aims. First, we wanted to replicate the basic valence-related MFN effect, both in its time course and its topography. Second, to characterize contributors to rapid ERP responses, we compared models for ERP amplitude that include not just the valence of the obtained outcome – the key parameter identified in prior studies – but also both the valence and magnitude of both the chosen and unchosen gambles. Third, we additionally examined longer-latency (e.g., 300-600ms) loss-related ERP responses, under the hypothesis that there is a progression from an initial coarse evaluation for motivational significance that is followed by more specific evaluations of particular stimulus properties. Finally, we investigated to what extent prior trial history – which presumably affects the motivational significance of the current outcomes – might blunt or eliminate entirely the differential ERP responses to different outcomes.
Materials and Methods
Subjects
Twenty subjects (10 female) between the ages of 19 and 38 (mean = 23y) participated in the experiment. Participants received $10 per hour plus a bonus amount based on their earnings in the task, resulting in final payments ranging from $33 to $60. All were right-handed, had normal or corrected-to-normal visual acuity, and had normal color vision. The study protocol was approved by the Duke University Health System Institutional Review Board, and written informed consent was obtained from all subjects.
Apparatus and procedure
We used a monetary gambling task (Figure 1a) adapted from that of Gehring and Willoughby (2002). Each trial began with the presentation of a white fixation cross. Then two white squares simultaneously appeared for one second, disappeared for one second, and then each reappeared containing either the numeral 5 or 25. These numbers indicated the value, in cents, that could be gained or lost if that square were chosen. The values in the two squares were independent: each had equal chances of being 5 or 25, so the two squares could contain different numbers or the same number.
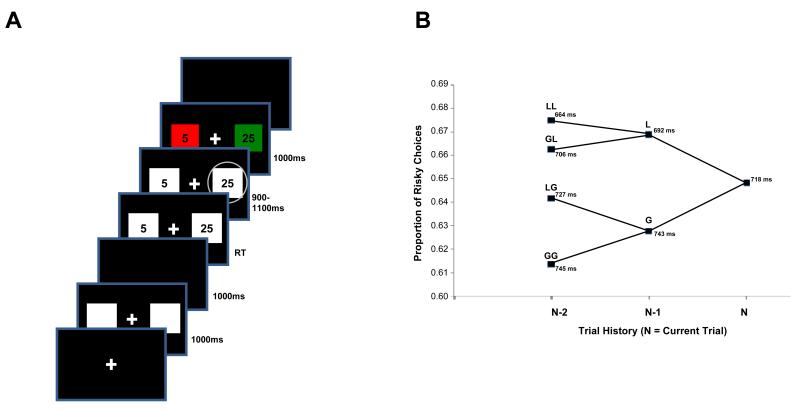
Figure 1. Experimental task and behavioral data.
(A) Subjects participated in a monetary decision-making task adapted from Gehring and Willoughby (2002). Each trial began with the presentation of two squares, which thereafter disappeared and then reappeared with numbers inside. The numbers indicated the amount, in cents, that could be wagered by choosing that square. Following the subject’s response and a variable interval, each square changed color to indicate whether it was associated with a monetary gain or loss. Note that the squares’ outcomes were independent: both could be gains, both could be losses, or one could be a gain and the other a loss. (B) When subjects were faced with a choice between a smaller-magnitude (i.e., 5¢) and a larger-magnitude (i.e., 25¢) alternative, their choices tended to be risk seeking (65%). The proportion of risk-seeking choices increased further when the previous trials were losses, compared to when they were gains. Response time (shown adjacent to each node) also became systematically faster as choices became riskier. The prior-history nodes use the notation “N-2, N-1”; e.g., “GL” indicates a gain, then a loss, then the current trial.
Once participants chose a square, a white circle immediately appeared around the selected option, before the stimuli again disappeared, leaving only the fixation cross in the center. For clarity, we hereafter refer to trials in which the two squares had different values as “free” choices (because participants were free to choose between two possible reward levels) and trials in which the two squares had the same value as “forced” choices (because in these cases the subjects were forced to choose a particular value). In addition, choices of a square worth 25¢ will be termed “risky”, since that option is associated with higher outcome variance, whereas choices of a square worth 5¢ will be termed “safe”. Thus, these two factors combine to form four basic trial types: free-risky, free-safe, forced-risky, and forced-safe.
After a variable delay (stimulus-onset asynchrony of 900-1100 ms), the squares were then presented simultaneously for 1 second with the same numerals as before, but now colored either red or green (to indicate valence of outcome). For half of the subjects, green squares indicated monetary gains and red squares indicated monetary losses, while the reverse mapping was used for the remaining subjects. On each trial, the subject saw the outcomes of both the chosen and unchosen square, but only the amount from the chosen square was added or subtracted from their earnings for that run. Information about the total amount earned was only provided between runs. Each run was approximately 220s in duration.
The experimental session consisted of 20 runs of 32 trials each, separated by short breaks. The participants were instructed to indicate their choices on each trial by pressing the left or right button with their right hand, for the left and right squares respectively, and to keep their eyes on the fixation cross. The compensation procedure was similar to that of Gehring and Willoughby (2002). When a run resulted in a net gain, poker chips were given to the participant to represent the money earned (i.e., gains minus losses within that run). When a run resulted in a net loss, however, no poker chips were taken away. Thus, the bonus amount earned by subjects was equal to the sum of the money won on the trial blocks resulting in net gains. These procedures were used to increase the participants’ motivation to attend to the gains and losses.
Data acquisition
Scalp potentials were recorded continuously from 64 electrodes in a customized elastic cap (Electro-Cap International) spanning much of the surface of the scalp. Electrodes in the 64-channel cap are labeled in reference to the 10-20 electrode location system. Scalp and mastoid electrode impedances were kept below 5 and 2 kilo-ohms respectively. Scalp sites and the left mastoid were recorded in relation to a reference electrode at the right mastoid. Fixation and eye movements were monitored with both electrooculogram (EOG) recordings and a zoom-lens video camera. Electrodes located over the left and right canthus were used to monitor horizontal eye position. The electrode over the right outer canthus was referenced to the left outer canthus, which in turn was referenced to the right mastoid. Electrodes beneath the two eyes, referenced to Fp1 or Fp2, were used to detect eyeblinks. Both the electroencephalographic and electrooculographic signals were amplified online by a Neuroscan amplifier with a bandpass filter of 0.01-100 Hz and gain of 1000, and were digitized at a rate of 500 Hz per channel.
ERP Analysis
Artifact rejection was performed off-line to remove ERP epochs contaminated by eye movements, eye blinks, excessive muscle activity, or drift. We used standard event-averaging techniques to extract the mean time courses of activity for each subject, at each electrode, for each combination of stimulus, choice, and outcome. All reported analyses describe ERP epochs that are time-locked to the onset of the outcome screen. Frequencies in the averaged ERP waveforms were low-pass filtered using a nine-point moving average filter, which heavily attenuates activity at and above 57 Hz at our 500-Hz digitization rate. The resulting ERP waveforms were then re-referenced to the algebraic average of the left and right mastoids. We report the time-locked average waveforms associated with the individual conditions for the outcome event (i.e., Figure 2, left panel) and topographic plots of activation associated with the differences between conditions (i.e., Figure 2, right panel; Figure 4).
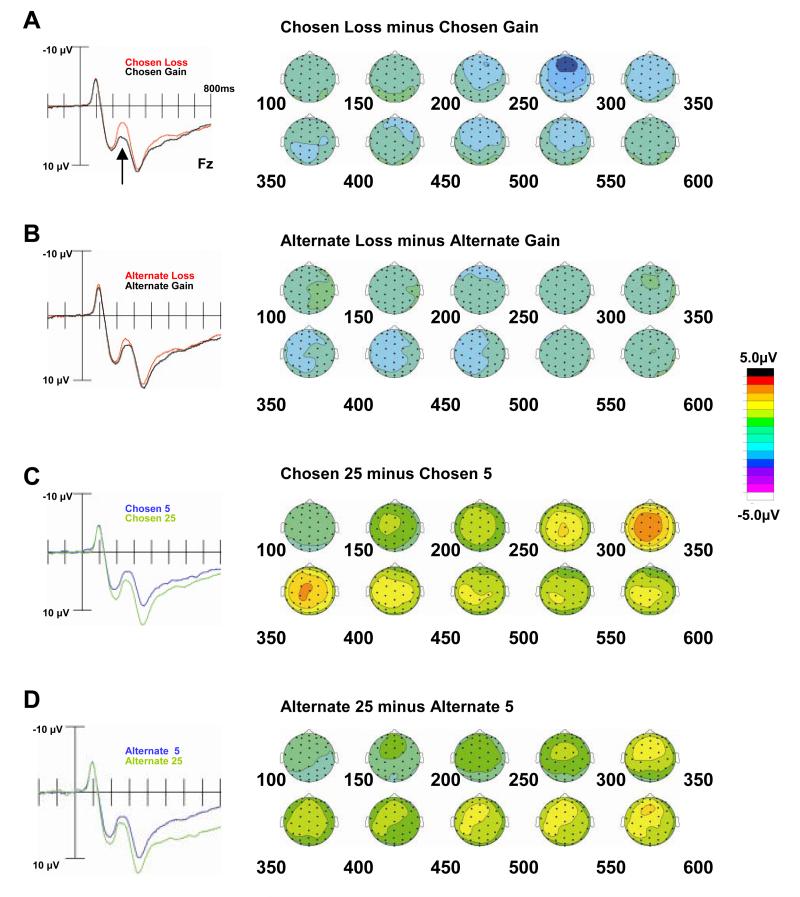
Figure 2. Effects of valence and magnitude upon early ERP responses.
The electrophysiological responses evoked by the revelation of the outcomes of the chosen and unchosen gambles are shown (time courses at left, topographic maps over intervals from 100ms-600ms at right). Note that negative is plotted up in all ERP graphs. (A) When the chosen gamble resulted in a loss, compared to a gain, the ERP response was more negative during the 200-300ms time window (indicated by arrow). This valence effect, which was maximal over frontocentral electrodes (shown at right), replicates prior reports of the Medial Frontal Negativity, or MFN. (B) There was a smaller, but still significant effect of the valence of the unchosen gamble – collapsing over chosen gains and losses – during the same time window. Furthermore, the magnitude of the chosen (C) and unchosen (D) gambles also contributed significantly to the observed ERP response at early latencies. However, the magnitude effects began earlier, were more sustained in time, and were more posteriorly distributed, compared to the valence effects. All ERP waveforms are taken from Fz.
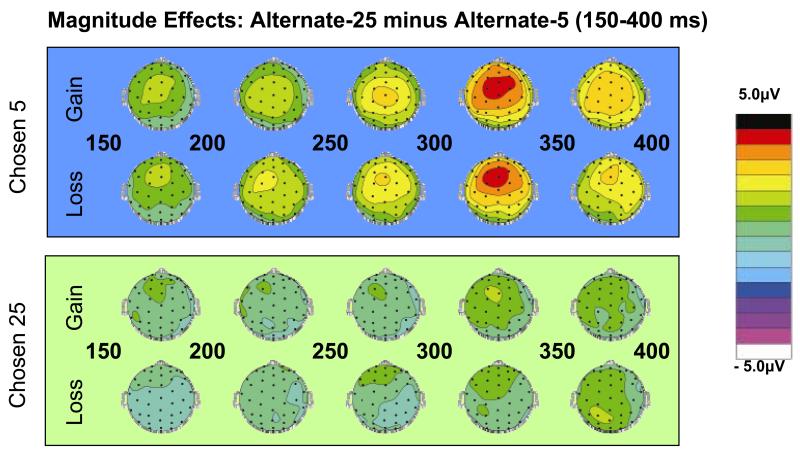
Figure 4. Influence of alternative gambles on the early ERP response.
To investigate how and under what circumstances the alternative outcome was processed, we generated topographic plots that contrasted large and small alternative gambles. (A) When the subjects chose the smaller option (i.e., 5¢), the potential difference over frontal regions was much more positive when the alternative was of large magnitude (i.e., 25¢) then when it was small (i.e., 5¢). This difference was present by about 150ms following the revelation of the gamble outcomes and was evident for both loss trials and for gain trials. (B) When subjects chose the larger option (i.e., 25¢), there was no differential effect of the amplitude of the unchosen outcome.
We additionally examined the modulatory effects of valence and magnitude upon the ERP responses. Each of the chosen and unchosen options could have one of four outcomes: +25¢, +5¢, −5¢, or −25¢. The 4*4 factorial combination of these factors resulted in a total of 16 possible trial types that could be encountered over the course of the experiment.
We next constructed a set of simple models that might account for the relative changes in ERP amplitude across these trial types. In the simple valence-chosen model, each trial type was categorized as 1 if the chosen outcome resulted in a loss or 2 if the chosen outcome resulted in a gain. This model replicates previous analyses of the MFN. In the magnitude-chosen model, trials where the subject chose a 5¢ option were categorized as 1, and trials where the subject chose a 25¢ option were categorized as 2. We also examined valence-unchosen and magnitude-unchosen models, which categorized trials similarly by the contents of the unchosen option. Finally, we examined models that combined these factors (e.g., additive effects of both magnitude and valence and/or chosen and unchosen options).
We then examined how well each of these models predicted relative differences in ERP amplitude during the 200-300ms MFN-latency window, at the electrode location where there was maximal effect of valence (Fz). Reported are the correlations between mean ERP amplitude (across all subjects) for each of the 16 trial types and the predictions of each model. The significance of these across-subject correlations were evaluated through random-effect analyses, using the similar within-subject correlations as the first-level input. We used this analysis to replicate the finding that variance in the early ERP amplitude at frontal electrodes could be predicted by valence of the chosen outcome, while also evaluating whether other factors made a significant and unique contribution to these early ERP responses.
Results
Choice Behavior
On one-half of the trials, subjects were faced with a choice between two different potential outcomes: 25¢ and 5¢. The proportion of risky choices (i.e., choosing the 25¢ option when given the choice between 25¢ and 5¢) ranged from 0.31 to 0.97 (mean ± SD, 0.65 ±0.16) across subjects. Thus, subjects in our sample were slightly risk-seeking, as frequently found when small rewards are used (Prelec & Loewenstein, 1991; Weber & Chapman, 2005). Given that subjects could not lose money if a run resulted in a net loss – as adopted from Gehring and Willoughby (2002) – this tendency toward risk-seeking behavior is adaptive, because increased variance results in valuable increased gains but also inconsequential increased losses. We note that because whether a given choice resulted in a gain or loss on each trial was determined by a random process, there was no strategy participants could use to win more often, and thus winning probabilities were similar (around 50%) for all subjects.
The proportion of risky choices also varied as a function of preceding outcome valence (see Figure 1b). Participants’ choices were more risky following a loss (mean ± SD: 0.67 ± 0.15) than following a gain [mean ± SD: 0.63 ± 0.17; t(19)=2.47, p=0.02], as found in previous studies utilizing this sort of paradigm (Gehring & Willoughby, 2002; Masaki, Takeuchi, Gehring, Takasawa, & Yamazaki, 2006). In addition, participants were most risk-seeking after a loss of 25¢ (mean ± SD: 0.68 ± 0.15) and least risk-seeking after a gain of 25¢ (mean ± SD: 0.61 ±0.22; t(19)=2.27, p=0.03). To further examine the effects of previous outcome on risk-seeking behavior, we calculated the mean probability of a risky choice following various sequences of two and three successive outcomes. In each case, participants made a greater proportion of risky choices following successive losses than successive gains [two trials back, GG vs. LL: t(19)=2.52, p=0.02; three trials back, GGG vs. LLL: t(19)=2.23, p=0.04].
To corroborate the effects of previous outcome on risk-taking behavior, we also calculated response time for selecting one of the squares, following various sequences of outcomes (mean ± SD, 718 ± 166 ms). Subjects were faster to respond after a loss (mean ± SD, 692 ± 158 ms) than after a gain [mean ± SD, 743 ± 172; t(19) = 3.35, p = 0.003). This difference increased when comparing response times after two losses to those after two gains [t(19) = 3.35, p = 0.003), but did not increase further when comparing response times after three previous losses to those after three previous gains [t(19) = 2.00, p = 0.06]. With regard to losses specifically, subjects were quicker to make a selection following two losses than they were following one loss [t(19) = 3.66, p = 0.002].
The Early ERP Response to Outcome: Valence and Magnitude
We examined differences in the ERP response associated not only with the valence of the chosen outcome (as reported in previous studies), but also with the valence of the unchosen outcome and with the magnitudes of both the chosen and unchosen outcomes.
As shown in Figure 2a, the mean ERP response during the time interval 200-300ms after the outcome screen was significantly more negative when the chosen option resulted in a loss than when it resulted in a gain (at Fz: F(1,19) = 18.5, p = 0.0004), with maximal difference observed around 250ms. This effect of the valence of the chosen option was largest at frontal electrode sites, particularly at Fz, and was slightly right-lateralized, replicating previous reports of the MFN (Gehring & Willoughby, 2002; Gehring & Willoughby, 2004; Niewenhuis, Yeung, Holroyd, Schurger, & Cohen, 2004; Masaki, Takeuchi, Gehring, Takasawa, & Yamazaki, 2006). Thus, for the remainder of this manuscript, when we refer to the MFN, we are referring to the mean amplitude of the difference wave between gain and loss trials at Fz, during the interval 200-300 ms after the outcome is revealed.
The difference between losses and gains (MFN effect) on a given trial was influenced by the outcomes of the preceding trials (Figure 3), becoming smaller when the prior outcome was a loss compared to when the prior outcome was a gain [F(1,19) = 6.18, p = 0.02]. Moreover, when the previous two trials were both losses, the difference between gains and losses was even smaller [F(1,19) = 4.68, p = 0.04], especially on forced-safe trials (which had similar ERP responses). Furthermore, the difference, as measured at Fz in this same latency range, between gains and losses was greatest when subjects chose the 25¢ option, either under free or forced conditions (chose 25¢ over 5¢: 1.80 μV; 25¢, 25¢: 1.83 μV) and was smallest when subjects chose the 5¢ option, particularly when this involved making a safe choice by choosing 5¢ over 25¢ (0.16 μV). Thus, the previously reported loss-versus-gain MFN effect – which we replicate when aggregating across all trials – was enhanced under some trial histories and nearly absent on others.
Figure 3. Effects of prior trial history on the valence effect (MFN).
The mean difference between gains and losses (MFN) was reduced following losses, decreasing to less than half of its mean amplitude when a trial followed two prior losses.
Given these data suggesting that the MFN-latency ERP amplitude was modulated by factors other than valence of the chosen option, our analyses hereafter focus on these other factors and use the mean ERP response in each condition (not the difference between gains and loss outcomes) as the dependent measure. As illustrated by Figure 2b, the mean ERP response during the 200-300ms window was also significantly modulated by the valence of the unchosen option [F(1,19) = 6.63, p = 0.0186], such that the ERP response was more negative for unchosen losses than unchosen gains. This indicates that the valence of the unchosen option affects ERP amplitude in the same direction – but with a smaller effect – as the valence of the chosen option.
While there were clear effects of valence, the raw ERP waveforms indicated that there were also early effects of the magnitude of the chosen option. The ERP response was significantly more negative from 200-300ms when the subject chose a 5¢ option, compared to choices of a 25¢ option [F(1,19) = 23.1, p = 0.0001; Figure 2c]. Examination of the time course of this magnitude effect, however, indicated that it began earlier than the loss-gain MFN, starting at about 150ms after the outcome was revealed, and persisted longer than the valence effect. In addition, the topographic maps of this magnitude effect showed a more posterior distribution than that of the loss-gain MFN, with greatest effects over central rather than frontal scalp sites.
Furthermore, during this 200-300ms interval, there was also a significant effect of the magnitude of the unchosen option, with a more negative early ERP response when the unchosen option was 5¢ compared to 25¢ [F(1,19) = 12.97, p = 0.0019; Figure 2d]. We investigated to what extent this effect was conditional on the subject’s choice by examining topographic plots of the difference between ERP responses to 25¢ and 5¢ alternative outcomes, given each of the four possible outcomes of the chosen stimulus. We found substantial effects of the magnitude of the alternative option only when the subject chose the 5¢ option (Figure 4), regardless of whether the chosen stimulus resulted in a loss or gain. This may reflect the possible relevance of the alternative option in those trials for inducing regret or satisfaction, a possibility considered further in the Discussion.
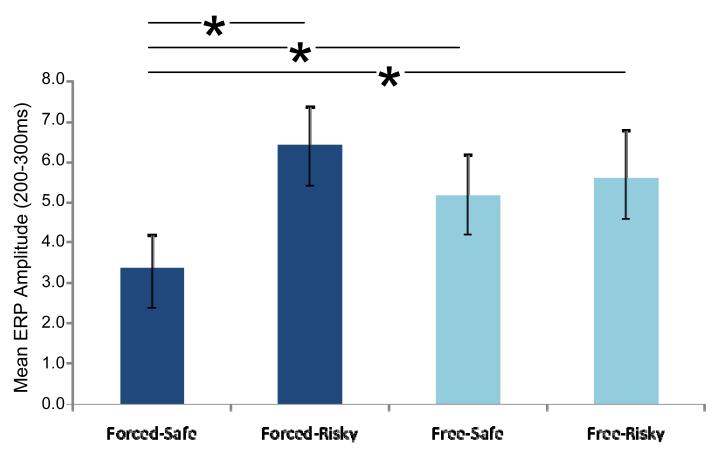
These effects of magnitude were also evident when comparing specific decision types. When collapsing across losses and gains, the greatest ERP amplitude was to the forced-risky trials (6.40 μV), with next greatest to the free-risky and free-safe trials (5.59 μV and 5.17 μV, respectively), and the smallest to the forced-safe trials (3.36 μV; Figure 5). All pairwisecomparisons between forced-safe and other trial types were significant at p < 0.05. These results indicated that valence of the obtained outcome was not the only factor influencing early ERP responses, and thus our following analyses sought to compare different models for predicting relative ERP amplitude among conditions.
Figure 5. Effects of trial type upon early ERP responses.
There were significant effects of the type of decision, when controlling for outcome valence, upon the ERP responses observed to the revelation of the outcome. The most-positive ERP amplitude was observed to Forced-Risky trials (e.g., 25¢ - 25¢), with the least-positive ERP amplitude found for Forced-Safe trials (e.g., 5¢ - 5¢). Trials where the subjects had freely chosen between one risky and one safe gamble were of intermediate ERP amplitude. Bars indicate pairs of conditions that were significantly different at p < 0.05.
The Early ERP Response to Outcome: Comparison of Models
We compared models that predicted the relative ERP amplitude across trial types during the MFN latency range of 200-300 ms as a function of magnitude and/or valence of the outcomes of the chosen and/or unchosen options (see Methods for details). As expected from the prior literature, a model that uses only the valence of the chosen outcome (typically cited as the primary determinant of the MFN) had a reasonably good correlation with the observed data [r = 0.57, t(14) = 2.60, p = 0.02; see Figure 6a]. Even so, substantial variance remained to be explained. A similar model that used only the magnitude of the chosen outcome had nearly identical performance [r = 0.55, t(14) = 2.46, p = 0.03], indicating that both factors had similar explanatory power. Furthermore, both the valence and magnitude of the unchosen outcome made a significant contribution to the ERP response during this time window.
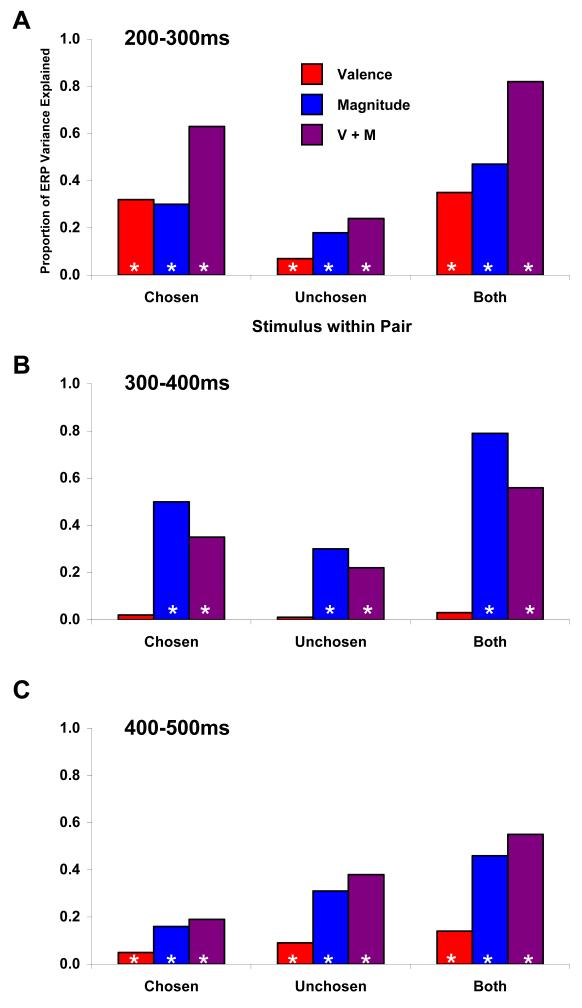
Figure 6. Variance in ERP amplitude explained by valence and/or magnitude during different latency windows.
(A) During the time window associated with the MFN (200-300ms), the valence of the chosen outcome explains a significant proportion of the total variance in ERP amplitude (~30%, red bar at left) across the 16 possible trial types (see text for details). However, significant contributions are also made by the magnitude of the chosen outcome and by both the valence and magnitude of the unchosen outcomes. A model which linearly combines both factors for both outcomes explains more than 80% of the ERP variance across trial types. (B) In contrast, from 300-400ms only magnitude information, particularly from the chosen outcome, makes a significant contribution to ERP amplitude. (C) Later in processing, from 400-500ms, both valence and magnitude again make significant contributions, but with the greatest contribution coming from the magnitude of the unchosen outcome. Stars indicate factors with significant contributions at p < 0.05.
We next examined models that combined valence and magnitude. Most notably, the best model for ERP amplitude during the 200-300ms time window was a simple addition of both the valence and the magnitude for both the chosen and unchosen outcomes [r = 0.90, t(14) = 7.72, p < 0.0001]. This model explained more than 82% of the variance in amplitude of the ERP waveform during that interval, providing compelling evidence that the rapid ERP response depended on more than just the valence of the observed outcome. Other factors, including at least the magnitude of the reward and the characteristics of the unchosen outcome, were also significant contributors.
Later ERP Responses to Outcome
We also repeated our comparison of models for later time windows. Unlike for the 200-300ms window, the mean ERP amplitude during the 300-400ms window was best predicted by a model that used only the magnitude of the chosen and unchosen outcomes (Figure 6b). This model had very high correlations with the ERP responses recorded at both Fz and Pz, a posterior midline site where P300 amplitude is typically maximal. For both electrodes, most of the variance was explained by the magnitude of the chosen outcome [Fz: r = 0.71, t(14) = 3.77, p = 0.002; Pz: r = 0.85, t(14) = 6.04, p < 0.001], with a smaller (but still significant) component associated with the magnitude of the unchosen outcome at Fz (r = 0.55, t(14) = 2.46, p = 0.027). Virtually none of the variance during this time window could be explained by the valence of either the chosen or alternative outcome (for both Fz and Pz, each p > 0.2).
Interestingly, ERP amplitude at Fz for this 300-400 ms window increased as a function of the absolute magnitude of difference between the chosen and alternative outcomes [ANOVA with four levels of difference: F(1,19) = 9.73, p < 0.01]. Though greater negative differences between chosen and alternative outcomes might be presumed to induce greater regret, and greater positive differences might be presumed to induce greater satisfaction, the similarity in the ERP amplitudes associated with both types of differences suggests such a regret-to-satisfaction continuum is unlikely. The response in this interval was also modulated by the outcome of the preceding trial. The responses to gains at Fz were more positive following a gain than following a loss [F(1,19) = 7.64, p = 0.01].
The valence effect reappeared at an even later window: 400-600 ms after feedback. Within this interval, the ERP response at Fz was significantly more negative for losses than for gains [F(1,19) = 14.1, p = 0.001]. Additionally, during the 400-600ms time period, the unchosen option, particularly its magnitude, had a greater effect upon ERP amplitude than did the chosen option (Figure 6c). The valence and magnitude of the alternative outcome explained 38% of the variance between 400-500 ms and 41% of the variance between 500-600ms. Furthermore, from 500-600ms, only 7% of the variance in ERP amplitude across trial types could be explained by the magnitude of the chosen outcome, while 53% of the variance could be explained by the magnitude of the alternative outcome.
Discussion
There has undoubtedly been significant selection pressure for cognitive mechanisms that support rapid estimates of stimulus utility. Prior studies have demonstrated brain activity that might support some aspects of such estimates, most notably a short-latency (200-300 ms) electrophysiological response in the medial frontal lobe that indicates the valence of an obtained outcome (Gehring & Willoughby, 2002; Holroyd & Coles, 2002; Miltner, Braun, & Coles, 1997; Yeung & Sanfey, 2004). Our results, though consistent with these earlier findings, suggest an additional consideration: the rapid neural response is neither unique to valence, nor to information from the chosen (i.e., obtained) outcome and should not simply be defined as the gain minus loss difference of the chosen outcome, as in previous studies. Instead, both valence and magnitude, of both the chosen and unchosen outcomes, influence neural processing at an early stage. Valence information is manifest at distinct time windows: between 200-300 ms and 400-600 ms, at least. In addition, magnitude information is processed earlier than valence information (beginning around 150 ms after the outcome screen) and continues to modulate the ERP response for more than several hundred milliseconds subsequently.
Amplitude of Early ERP Activity Depends on More Than Valence
Outcome valence is relevant in a wide variety of situations, from error monitoring in simple motor tasks to decision making involving monetary gambles. Yet, an outcome can be of negative valence or an action can be an error while still being of minimal consequence. Both outcome valence and outcome magnitude predict the need for cognitive control to guide learning and behavior. Examples of the effects of magnitude are evident in the ERP waveforms themselves (e.g., in Figure 5, where there are difference between trial types with and without a 25¢ outcome). Magnitude effects upon ERP amplitude began at 150 ms, earlier than the typical latency of the valence-defined MFN (200-300 ms), and persisted for several hundred milliseconds afterwards. Because the scalp topography suggests that magnitude effects have a different, somewhat more posterior distribution than the effects of valence, these results should not be interpreted to mean that there is necessarily a single error signal that provides information about both magnitude and valence. Indeed, our results suggest that there may be separate contributions of valence and magnitude that have different timing and topography. During the classic MFN latency of 200-300 ms, these separate effects – i.e., the temporally focal loss-gain MFN effect and the longer-duration magnitude effect -- appear to overlap -- such that the activity over fronto-central scalp during this time range is a function of both valence and magnitude.
Furthermore, our results indicate that these early ERP responses to outcome feedback depend upon the characteristics of the unchosen stimulus as well. Prior studies have suggested that the ERP response between 200-300 ms was unaffected by the status of the alternative choice (Gehring & Willoughby, 2002; Yeung & Sanfey, 2004). In addition, previous theories have posited that the feedback ERN, of which the loss-related MFN may be a special case, reflected scalar errors that indicate outcome valence but not vector errors that also include correctness (Mars, De Bruijn, Hulstijn, Miltner, & Coles, 2004). Yet, unchosen options contextualize the psychological valence of an outcome, just like the magnitude of a chosen option would; getting a small monetary gain could cause regret if one had passed up the option that resulted in a much larger reward. Consequently, early error signals could vary according to the extent to which the chosen outcome differs from the most desirable outcome (Bernstein, Scheffers, & Coles, 1995; Falkenstein, Hohnsbein, & Hoormann, 1996).
Along these lines, prior studies have shown that the amplitude of early error or valence signals can be altered by task properties that change the motivational value of outcomes. Instructions that emphasize speed over accuracy, which may devalue the significance of error trials, have been shown to decrease the size of the response-related ERN (Falkenstein, Hohnsbein, & Hoormann, 1995; Gehring, Goss, Coles, & Meyer, 1993). Errors that cause monetary losses have been found in fMRI studies to evoke more ACC activation than errors that do not lead to monetary loss (Taylor et al., 2006). Furthermore, subjects who score highly on tests of negative emotionality personality traits, and who were initially distressed by errors, lose motivation and exhibit decreased ERN amplitude over the course of an experiment (Luu, Collins, & Tucker, 2000). We observed a similar effect of prior losses: increases in the number of losses on previous trials were accompanied by decreases both in response time and in the ERP difference between losses and gains on the current trial. This effect was present following one loss and was even more prominent following two losses. Note that because all outcomes in the current task were determined randomly, the observed modulation of MFN amplitude might reflect similar modulations of control systems based on short-term predictions of event outcomes (Huettel, Mack, & McCarthy, 2002; Squires, Wickens, Squires, & Donchin, 1976).
Sustained Effects of Outcome Magnitude upon ERP Signals
The rapid MFN response is not the only aspect of the ERP signal that represents an evaluation of outcome. Later responses, such as the P300, also have been found to vary in accordance with feedback. When measured during gambling tasks, for example, P300 amplitude increases both with increasing outcome magnitude and when the alternative outcome is larger than the obtained outcome or is a gain (Yeung & Sanfey, 2004). Although positive and negative feedback evoke similar P300 responses if both occur with equal probability (Campbell, Courchesne, Picton, & Squires, 1979; Yeung & Sanfey, 2004), subjective beliefs about probability may result in differential P300 responses to positive and negative feedback, even though each form of feedback may be equally likely (Hajcak, Holroyd, Moser, & Simons, 2005).
To explain why the P300 appears to be sensitive to valence under some circumstances but not others, Yeung and Sanfey (2004) speculated that the P300 may be influenced by emotional consequences of decisions (e.g., regret) but not by reward value itself. Supporting this perspective, in an fMRI study in which regret was induced by revealing the outcome of the unchosen option in a gambling task, increased regret was associated with enhanced activity in the ACC (Coricelli et al., 2005). However, we found that outcomes leading to regret and outcomes leading to satisfaction evoked similar P300 amplitudes, when controlling for the amount of difference between the chosen and alternative outcomes. Thus the P300, when quantified as the mean amplitude between 300-400 ms, seems to reflect a reward magnitude effect (i.e., the difference between the chosen and alternative outcomes) and not a psychological valence effect measurable along a satisfaction-to-regret continuum. Instead, emotional appraisal of the outcome may not occur until 400 ms, when the ERP response to losses again becomes more negative than the ERP responses to gains.
Conclusions
In sum, we found that rapid ERP responses to a monetary reward depend on more than the valence of that reward – they also depend on its magnitude. The effects of reward magnitude were observed at even shorter latency than the effects of valence. Furthermore, the variance in relative ERP amplitude during the MFN window (200-300ms) was explained best by including, as predictors, both the magnitude and the valence of both the chosen and unchosen outcomes. Together, these results support the idea that early discrepancy signals, evident in activity from sources in the medial frontal cortex and more posteriorly, detect not just errors but motivationally salient events, more broadly. These early signals presumably encode the urgency or severity of the problem (Gehring, Himle, & Nisenson, 2000), whereupon they engage other, slower mechanisms (Taylor et al., 2006), that could be reflected in later ERP responses. Future studies should examine more precisely the specific neural systems underlying valence and magnitude effects, including the extent to which they can be spatially distinguished in the brain.
Acknowledgments
We thank Tineke Grent-’t-Jong, Chien-Te Wu, and Kenneth Roberts for assistance in data collection and analysis, and McKell Carter, Kevin LaBar, James Morris, O’Dhaniel Mullette-Gillman, David Smith, and Bethany Weber for comments on the manuscript. Support was provided by NIMH R01-70685 (S.A.H.) and NIMH R01-60415 (M.G.W.).
References
- Bernstein PS, Scheffers MK, Coles MG. “Where did I go wrong?” A psychophysiological analysis of error detection. Journal of Experimental Psychology. Human Perception and Performance. 1995;21(6):1312–1322. doi: 10.1037//0096-1523.21.6.1312. [DOI] [PubMed] [Google Scholar]
- Bush G, Luu P, Posner MI. Cognitive and emotional influences in anterior cingulate cortex. Trends Cogn Sci. 2000;4(6):215–222. doi: 10.1016/s1364-6613(00)01483-2. [DOI] [PubMed] [Google Scholar]
- Campbell KB, Courchesne E, Picton TW, Squires KC. Evoked potential correlates of human information processing. Biol Psychol. 1979;8(1):45–68. doi: 10.1016/0301-0511(79)90004-8. [DOI] [PubMed] [Google Scholar]
- Coricelli G, Critchey HD, Joffily M, O’Doherty JP, Sirigu A, Dolan R. j. Regret and its avoidance: a neuroimaging study of choice behavior. Nature Neuroscience. 2005;8:1255–1262. doi: 10.1038/nn1514. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Posner MI, Tucker DM. Localization of a neural system for error detection and compensation. Psychological Science. 1994;5(5):303–305. [Google Scholar]
- Falkenstein M, Hohnsbein J, Hoormann J. Event-related potential correlates of errors in reaction tasks. In: Karmos G, Molnar M, Csepe V, Czigler I, Desmedt JE, editors. Perspectives of event-related potentials research. Elsevier; Amsterdam: 1995. pp. 287–296. [PubMed] [Google Scholar]
- Falkenstein M, Hohnsbein J, Hoormann J. Differential processing of motor errors. In: Ogura C, Koga Y, Shimokochi M, editors. Recent Advances in Event-Related Potential Research. Elsevier; Amsterdam: 1996. pp. 579–585. [Google Scholar]
- Falkenstein M, Hohnsbein J, Hoormann J, Blanke L. Effects of errors in choice reaction tasks on the ERP under focused and divided attention. In: Brunia CHM, Gaillard AWK, Kok A, editors. Psychophysiological brain research. Tilburg University Press; Tilburg, The Netherlands: 1990. pp. 192–195. [Google Scholar]
- Gehring WJ, Coles MG, Meyer DE, Donchin E. A brain potential manifestation of error-related processing. Electroencephalogr Clin Neurophysiol Suppl. 1995;44:261–272. [PubMed] [Google Scholar]
- Gehring WJ, Fencsik DE. Functions of the medial frontal cortex in the processing of conflict and errors. The Journal of Neuroscience. 2001;21:9430–9437. doi: 10.1523/JNEUROSCI.21-23-09430.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gehring WJ, Goss B, Coles MGH, Meyer DE. A neural system for error detection and compensation. Psychological Science. 1993;4:385–390. [Google Scholar]
- Gehring WJ, Himle JA, Nisenson LG. Action monitoring dysfunction in obsessive-compulsive disorder. Psychological Science. 2000;11:1–6. doi: 10.1111/1467-9280.00206. [DOI] [PubMed] [Google Scholar]
- Gehring WJ, Willoughby AR. The medial frontal cortex and the rapid processing of monetary gains and losses. Science. 2002;295(5563):2279–2282. doi: 10.1126/science.1066893. [DOI] [PubMed] [Google Scholar]
- Gehring WJ, Willoughby AR. Are all medial frontal negativities created equal? Toward a richer empirical basis for theories of action monitoring. In: Ullsperger M, Falkenstein M, editors. Errors, Conflicts, and the Brain. Current Opinions on Performance Monitoring. Max Planck Institute of Cognitive Neuroscience; Leipzig: 2004. pp. 14–20. [Google Scholar]
- Hajcak G, Holroyd CB, Moser JS, Simons RF. Brain potentials associated with expected and unexpected good and bad outcomes. Psychophysiology. 2005;42(2):161–170. doi: 10.1111/j.1469-8986.2005.00278.x. [DOI] [PubMed] [Google Scholar]
- Holroyd CB, Coles MG. The neural basis of human error processing: reinforcement learning, dopamine, and the error-related negativity. Psychol Rev. 2002;109(4):679–709. doi: 10.1037/0033-295X.109.4.679. [DOI] [PubMed] [Google Scholar]
- Huettel SA, Mack PB, McCarthy G. Perceiving patterns in random series: Dynamic processing of sequence in prefrontal cortex. Nature Neuroscience. 2002;5(5):485–490. doi: 10.1038/nn841. [DOI] [PubMed] [Google Scholar]
- Kerns JG, Cohen JD, MacDonald AW, 3rd, Cho RY, Stenger VA, Carter CS. Anterior cingulate conflict monitoring and adjustments in control. Science. 2004;303(5660):1023–1026. doi: 10.1126/science.1089910. [DOI] [PubMed] [Google Scholar]
- Luu P, Collins P, Tucker DM. Mood, personality, and self-monitoring: negative affect and emotionality in relation to frontal lobe mechanisms of error monitoring. Journal of Experimental Psychology. General. 2000;129(1):43–60. doi: 10.1037//0096-3445.129.1.43. [DOI] [PubMed] [Google Scholar]
- MacDonald AW, Cohen JD, Stenger VA, Carter CS. Dissociating the role of the dorsolateral prefrontal and anterior cingulate cortex in cognitive control. Science. 2000;288(5472):1835–1838. doi: 10.1126/science.288.5472.1835. [DOI] [PubMed] [Google Scholar]
- Mars RB, De Bruijn ERA, Hulstijn W, Miltner WHR, Coles MGH. What if I told you: “You were wrong”? Brain potentials and behavioral adjustments elicited by feedback in a time-estimation task. In: Ullsperger M, Falkenstein M, editors. Errors, Conflicts, and the Brain. Current Opinions on Performance Monitoring. Max Planck Institute of Cognitive Neuroscience; Leipzig: 2004. pp. 129–134. [Google Scholar]
- Masaki H, Takeuchi S, Gehring WJ, Takasawa N, Yamazaki K. Affective-motivational influences on feedback-related ERPs in a gambling task. Brain Res. 2006;1105(1):110–121. doi: 10.1016/j.brainres.2006.01.022. [DOI] [PubMed] [Google Scholar]
- Miltner WHR, Braun CH, Coles MGH. Event-related brain potentials following incorrect feedback in a time-estimation task: evidence for a ‘generic’ neural system for error-detection. Journal of Cognitive Neuroscience. 1997;9:788–798. doi: 10.1162/jocn.1997.9.6.788. [DOI] [PubMed] [Google Scholar]
- Nieuwenhuis S, Holroyd CB, Mol N, Coles MG. Reinforcement-related brain potentials from medial frontal cortex: origins and functional significance. Neurosci Biobehav Rev. 2004;28(4):441–448. doi: 10.1016/j.neubiorev.2004.05.003. [DOI] [PubMed] [Google Scholar]
- Nieuwenhuis S, Yeung N, Holroyd CB, Schurger A, Cohen JD. Sensitivity of Electrophysiological Activity from Medial Frontal Cortex to Utilitarian and Performance Feedback. Cerebral Cortex. 2004;14:741–747. doi: 10.1093/cercor/bhh034. [DOI] [PubMed] [Google Scholar]
- Paus T. Primate anterior cingulate cortex: where motor control, drive and cognition interface. Nature Reviews Neuroscience. 2001;2(6):417–424. doi: 10.1038/35077500. [DOI] [PubMed] [Google Scholar]
- Prelec D, Loewenstein G. Decision making over time and under uncertainty: A common approach. Management Science. 1991;37:770–786. [Google Scholar]
- Ruchsow M, Grothe J, Spitzer M, Kiefer M. Human anterior cingulate cortex is activated by negative feedback: evidence from event-related potentials in a guessing task. Neurosci Lett. 2002;325(3):203–206. doi: 10.1016/s0304-3940(02)00288-4. [DOI] [PubMed] [Google Scholar]
- Squires KC, Wickens C, Squires NK, Donchin E. The effect of stimulus sequence on the waveform of the cortical event-related potential. Science. 1976;193:1142–1145. doi: 10.1126/science.959831. [DOI] [PubMed] [Google Scholar]
- Taylor SF, Martis B, Fitzgerald KD, Welsh RC, Abelson JL, Liberzon I, et al. Medial frontal cortex activity and loss-related responses to errors. Journal of Neuroscience. 2006;26(15):4063–4070. doi: 10.1523/JNEUROSCI.4709-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tversky A, Kahneman D. The framing of decisions and the psychology of choice. Science. 1981;211(4481):453–458. doi: 10.1126/science.7455683. [DOI] [PubMed] [Google Scholar]
- Weber BJ, Chapman GB. Playing for peanuts: Why is risk seeking more common for low-stakes gambles? Organizational Behavior and Human Decision Processes. 2005;97:31–46. [Google Scholar]
- Yeung N, Sanfey AG. Independent coding of reward magnitude and valence in the human brain. Journal of Neuroscience. 2004;24(28):6258–6264. doi: 10.1523/JNEUROSCI.4537-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]