Modeling Sleep Propensity when Sleep is Severely Restricted

We have read with interest the recent article by Paech et al.¹ in this journal. The authors have performed an important study with the aim to disentangle homeostatic and circadian influences on sleep under conditions of high sleep pressure, induced by severe sleep restriction with only 4.7 h of sleep per 28-hour sleep-wake cycle of a forced desynchrony protocol.^1,2 Their results show a strong homeostatic sleep drive, an attenuated circa-dian modulation in different sleep variables and most important, a loss of circadian modulation of sleep efficiency, which was found to be above 90% at any circadian phase. The latter result differs clearly from results of studies which had measured sleep efficiency in either forced desynchrony protocols with a 1:2 sleep-wake ratio^3,4 or ultra-short sleep-wake cycles for 24 hours.⁵ In all these studies sleep efficiency displayed an explicit circadian modulation, with less sleep in the so-called forbidden zone of sleep⁵ or wake maintenance zone,⁶ which corresponds to the rising limb of core body temperature, near its circadian crest. Lavie et al.⁵ observed a pronounced circadian modulation of sleep efficiency, sparing the wake maintenance zone, even after a preceding night without sleep.

While the forced desynchrony protocol has shown to be successful in earlier studies to separate homeostatic and circa-dian influences on sleep parameters,^3,4 obviously this was not the case under conditions of high sleep pressure in the present study. The authors suggest that the strong homeostatic drive was overriding the circadian component under the conditions of severe sleep restriction, cumulating over eight consecutive sleep-wake cycles. As a consequence sleep efficiency was very high at all circadian phases, without circadian modulation. Paech at al. concluded “that the two-process model for sleep regulation may best describe the individual and interactive effects of the homeostatic and circadian processes on sleep structure and consolidation in the absence of sleep restriction” (p. 944) and suggested that “…this model may be most applicable to non-restricted sleep opportunities.” (p. 947). This is obviously a critical point since the authors have used the two-process model as conceptual framework for their study. They aimed to sort out the homeostatic and circadian influences on sleep at different phases of the circadian process, measured as core body temperature which, as expected, preserved a strong circadian modulation in their study. The results led the authors to assume “that when homeostatic sleep pressure reaches a critical level, the effect of the circadian process on sleep propensity is masked.”²

If, however, a model of sleep regulation does not allow representation of the interaction of its main constituents under conditions of severe sleep restriction, as Peach et al. consider, this would indicate an unexpected and serious limitation of the scope of application of the model. We have used the Paech et al. data, as published, for simulation with a variant of the two-process model, which we have proposed earlier.⁹ Our model takes over the concept of two major processes regulating sleep, including the homeostatic component S, derived from slow wave EEG activity, while it deviates from the two-process model in two ways. First, we define the circadian component as R, which is derived from REM sleep latency, a sleep variable with known circadian variation,^10,11 instead of a circadian threshold process in the original model. We consider S and R as two essential sleep drives, the interaction of which determines sleep propensity (SP) as a continuous output variable. In addition, we suggest that this interaction is multiplicative, i.e., SP = S × R. Contrary to the two-process model, which assumes an additive interaction between a threshold process C and a quantitative variable S, our model uses two quantitative sleep variables having a multiplicative interaction to model SP.

In the case of sleep restriction, where S will increase, as shown by many studies including that of Paech et al.,¹ nothing was known on the reaction of REM latency under the combined conditions of forced desynchrony and sleep restriction before the study of Paech and colleagues.^1,2 Their study is the first to measure REM latency under high sleep pressure at various circadian phases. Under these conditions the circadian variation of REM latency is sharply attenuated.

Using data of normal sleepers without sleep restriction¹¹ and those with severe sleep restriction¹ as anchor points, we would predict a dose-related increase of SP with increasing sleep restriction. As a consequence SP will reach maximum values with severe and prolonged sleep restriction or deprivation. Figure 1 displays a simulation of this with the S × R model. It depicts the situation without sleep restriction (solid symbols) and in addition, the last part of the forced desynchrony protocol¹ (open symbols), where the prolonged sleep restriction will show the most severe effects. In the situation without sleep restriction, the SP curve (Figure 1, solid diamonds) shows a minimum at the end of night sleep at 8:00, followed by an increase in the early afternoon, which corresponds to the nap zone or post-lunch dip. Later, SP reaches a second minimum at 20:00, corresponding to the wake maintenance zone and thereafter the curve increases steeply until sleep onset at midnight. In this situation, multiplying the two sleep drives S and R always results in a bimodal SP curve: the nighttime peak is reached when S is high and R is increasing, while the smaller post-noon peak appears when R is still high and S is increasing (see Bes et al.⁹).

Figure 1.

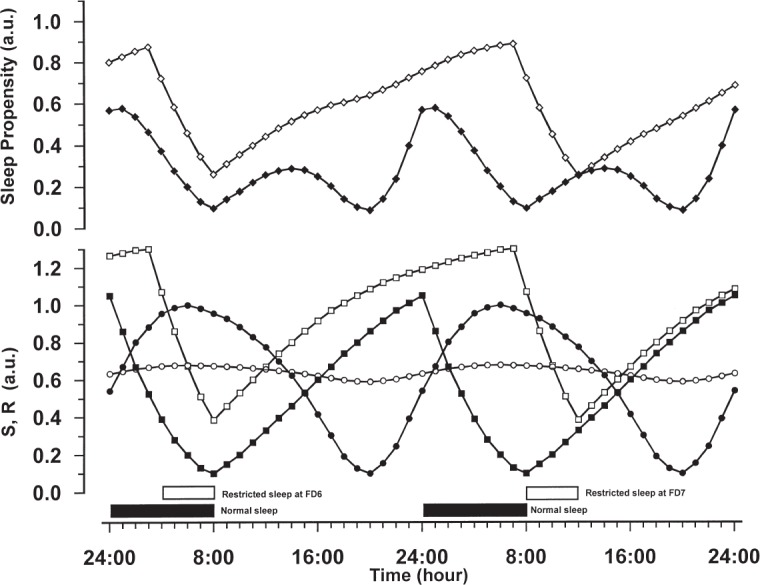
The time courses for the homeostatic sleep drive S (rectangles) and the circadian sleep drive R (circles) are represented in the lower panel. The sleep propensity function SP (diamonds) is displayed in the upper panel and was computed by multiplying the values of S and R at each point in time. The scale of the model functions is relative, running in arbitrary units, with 0 indicating a low intensity and 1 a high intensity. For further details about the model functions we refer to Bes.⁹ Sleep periods are indicated by the horizontal bars. Solid symbols refer to data of normal sleepers without sleep restriction, open symbols to data of sleepers under conditions of forced desynchrony with severe sleep restriction. FD6 and FD7 indicate the last two sleep episodes of the forced desynchrony protocol of Paech.¹ The different time courses of the model functions are described in the text.

Under the conditions of forced desynchrony with severe sleep restriction the outcome is dramatically different. We fitted the original R-curve^9,11 (Figure 1, solid circles) to the REM latency data as given in Figure 2 of Paech et al.¹ The resulting flattened time course has a moderate intensity and hardly shows any circadian modulation (Figure 1, open circles). To estimate the time course of S across the whole experimental procedure we assumed that the original S curve^9,11 (Figure 1, solid squares) optimally represents the adaptation part of the protocol of Paech et al. Using these data as a point of departure, we calculated the further time course of S by letting it decrease during sleep and increase during wakefulness, as determined by the sleep and wake times of the protocol, while assuming saturating exponential functions for increase and decrease.^9,12 The resulting time course shows that the overall level of S increases after the start of the forced desynchrony (FD) part at FD0, reaching a steady balance in waxing and waning from FD2 onwards. The part around FD6 and FD7 is shown in Figure 1 (open squares) and is representative for this balance. The multiplicative combination of a flattened time course of R and an elevated time course of S has drastic effects on the time course of SP (Figure 1, open diamonds). SP values at any time are higher than the baseline values and the time course is nearly exclusively dominated by the homeostatic properties of S. The SP values indicate neither a nap-zone nor a wake maintenance zone. Furthermore, from FD2 onwards the time courses of SP are almost identical for every sleep episode; they all have the same high level at the beginning of sleep and the same lower level at the end of sleep. As these sleep episodes are scheduled at different circadian times, the SP values thus demonstrate a lack of circadian variability. The simulated time course of SP fits the observations by Paech at al., in particular those about the high sleep efficiency and high amounts of total sleep time in the scheduled sleep episodes and the lack of circadian modulation.

An interesting point is that REM latency looses its circadian characteristic under severe sleep restriction, while this is not the case for core body temperature, as Paech et al. have clearly shown. Whatever the cause may be, these are the main reasons why the original two-process model falls short in giving an optimal description of the observations by Paech et al. The preserved circadian modulation in core body temperature suggests that the circadian threshold process C is unaffected by the experimental conditions and, by consequence, the lack of circadian modulation in sleep propensity can not be described accurately by the original model. Furthermore, as REM sleep has no meaning in the original two-process model, the loss of circadian modulation of REM latency has no relevance in that model. In contrast to this, the flattening of sleep drive R in response to sleep restriction results in a substantial change of SP in the S × R model, and this avoids the necessity to assume a “masking” of the circadian component.

Studies such as that of Paech et al. allow separation and quantification of the contribution to SP of (a) the different sleep components, (b) the circadian time, and (c) sleep pressure, systematically varied by increasing amounts of sleep restriction. Models like the one proposed by us, can make quantifiable predictions about the dose-dependent increase of SP with sleep restriction and the variation of SP along the scale of circadian time.

CITATION

Bes F; Jobert M; Schulz H. Modeling sleep propensity when sleep is severely restricted. SLEEP 2013;36(4):609-611.

DISCLOSURE STATEMENT

This was not an industry supported study. The authors have indicated no financial conflicts of interest.