Abstract
Tissue level characteristics of bone can be measured by nanoindentation and microspectroscopy, but are challenging to translate to whole bone mechanical behavior in this hierarchically structured material. The current study calculated weighted section modului from microCT attenuation values based on tissue level relationships (Zlin,a and Zlin,b) between mineralization and material properties to predict whole bone mechanical behavior. Zlin,a was determined using the equation of the best fit linear regression between nanoindentation indentation modulus and mineral:matrix ratio from Raman spectroscopy. To better represent the modulus of unmineralized tissue, a second linear regression with the intercept fixed at 0 was used to calculate Zlin,b. The predictive capability of the weighted section moduli calculated using a tissue level relationship were compared with average tissue level properties and weighted section moduli calculated using an apparent level relationship (Zexp) between Young’s Modulus and mineralization. A range of bone mineralization was created using vitamin D deficiency in growing rats. After 10 weeks, left femurs were scanned using microCT and tested to failure in 3 point bending. Contralateral limbs were used for co-localized tissue level mechanical properties by nanoindentation and compositional measurements by Raman microspectroscopy. Vitamin D deficiency reduced whole bone stiffness and strength by ~35% and ~30%, respectively, but only reduced tissue mineral density by ~10% compared with Controls. Average tissue level properties did not correlate with whole bone mechanical behavior while Zlin,a, Zlin,b, and Zexp predicted 54%, 66%, and 80% of the failure moment respectively. This study demonstrated that in a model for varying mineralization, the composite beam model in this paper is an improved method to extrapolate tissue level data to macro-scale mechanical behavior.
Keywords: Nanoindentation, composite beam theory, rat cortical bone, Raman spectroscopy, vitamin D
Introduction
Whole bone mineralization and quantity predict whole bone mechanical behavior for healthy bone (Currey, 1969, 1984, 1988); however, skeletal pathologies such as osteoporosis alter those relationships. Dual energy x-ray absorptiometry (DXA) is currently the clinical standard for assessing osteoporotic fracture risk but is not a perfect predictor of fracture (Aspray et al., 2009). Fracture risk evaluation can be improved by considering age and previous fracture status as evidenced by FRAX (Kanis, 2002; Kanis et al., 2005; Kanis et al., 2008; Watts and Diab, 2011). Areal bone mineral density (aBMD) assessed by DXA reflects both bone volume and density. Osteoporosis therapies disproportionately alter aBMD and fracture risk. Fluoride treatments were ineffective at reducing fracture risk despite 8–16% increases in aBMD (Haguenauer et al., 2000; Meunier et al., 1998), whereas antiresorptive treatments reduced fracture risk by 30–50% despite only increasing aBMD by 8–10% (Cummings et al., 2002; Ettinger et al., 1999).
The disconnect between BMD and whole bone mechanical performance in diseased bone has prompted research aimed at revealing the role of tissue level composition. Like other load bearing structures, whole bone mechanical behavior depends on geometry, volume, and tissue level properties. The application of nanoindentation and vibrational spectroscopy techniques such as Raman and Fourier transform infra-red spectroscopy to bone allow the investigation of mechanical properties and composition of individual microstructural features while avoiding pores and cellular lacunae visible on the surface. Concurrent investigations of tissue material properties from nanoindentation and tissue level composition with whole bone mechanical behavior revealed inconsistent relationships between micro- and macroscale properties (Donnelly et al., 2010; Rho et al., 2002; Silva et al., 2004; Sun et al., 2009). Both the presence and absence of correlations have been reported between whole bone and tissue level mechanical properties, indicating that the extrapolation of tissue level properties to whole bone mechanical behavior is not straightforward. The aforementioned studies averaged tissue level data points into a single value to represent the material properties of the entire bone to correlate with whole bone mechanical behavior. Averaging highly resolved tissue level properties simplifies bone into a homogeneous material and diminishes the advantage of the local tissue level measurements provided by nanoindentation and vibrational microspectroscopy. To take into account mineralization heterogeneity, studies have used composite beam theory to generate density-weighted moments of inertia or bending stiffnesses that take spatial variations in mineralization into account (Bhatavadekar et al., 2006; Corcoran et al., 1994; Hong et al., 2004). These models used apparent level relationships between Young’s modulus and mineralization, and the use of tissue level relationships may improve the predictive capability of these models.
The current study used tissue level relationships between mineralization and material properties to calculate density-weighted section moduli to predict whole bone mechanical behavior. This method preserves the spatial distribution and heterogeneity of tissue properties while using intrinsic tissue level relationships instead of apparent level relationships to calculate density-weighted section moduli. Relationships between mineralization and mechanical properties at the whole bone and tissue level length scales were characterized in rats with impaired mineralization and reduced whole bone mechanical behavior through vitamin D deficiency. Whole bone composition and geometry were quantified using micro-computed tomography (microCT) prior to whole bone mechanical testing in three point bending. Contralateral limbs were used for tissue level analyses. Tissue level mechanical properties were measured using nanoindentation and tissue composition was measured using Raman microspectroscopy. Density-weighted section moduli calculated from tissue level measurements were compared with section moduli calculated using one previously reported apparent level relationship, averaged tissue level properties, and whole bone measures of composition and geometry on their ability to predict whole bone mechanical properties.
Methods
Bone mineralization was reduced using a previously established vitamin D deficiency treatment in growing rats (Sonnenberg et al., 1984). Three week old male Sprague-Dawley rats (Charles River, Wilmington, MA) were divided into three groups: Control, and two reduced mineralization groups, NC1 and NC3 (n = 20/group) and given their respective diets and water ad libitum for the 10 wk experimental duration. Intraperitoneal injections of tetracycline and demeclocycline were administered 28 d and 14 d before euthanasia. These fluorochrome labels demarcated 3 tissue age zones, 0–14 d, 15–28 d, and 29 d+. After 10 wk, animals were euthanized by CO2 asphyxiation. Vitamin D deficiency was confirmed by an enzyme-linked immunoassay for 1,25-OH D (Immunodiagnostic Systems Inc, Scottsdale, AZ) (Control n = 12, NC1 n = 11, NC3 n = 16). All procedures were approved by Cornell University’s Institutional Animal Care and Use Committee (IACUC). See supplementary text for details.
Whole Bone Testing
Left femurs (n = 20/group) were collected for whole bone compositional and geometric measures and mechanical testing. Femurs were scanned in saline using microCT with 25 μm isotropic voxel size (eXplore CT 120, GE Healthcare, Waukesha, WI). For scan specifications see supplementary text. A global threshold equivalent to 43 mgHA/cc was used (Fritton et al., 2005). Tissue mineral density (TMD) and content (TMC) were calculated for a 3 mm thick volume of interest (VOI) from the midshaft of the femurs (MicroView 2.2, GE Healthcare, Waukesha, WI). The VOI consisted of 120 slices. The cortical cross-sectional areas (AC) was calculated for each slice then averaged, resulting in a single value for each sample (in-house MATLAB® code, The Mathworks Inc, Natick, NA).
After scanning, femurs were failed in three point bending in the anterior-posterior direction (858 Mini Bionix, MTS, Eden Prairie, MN). Outcomes from the load-displacement data included the failure moment (MF), bending stiffness (EI), effective modulus (EI/Iun), and post-yield displacement (Dpy). See supplementary text for details.
Tissue Level Measurements
A subset of the right femurs was processed for tissue level analyses (n = 4–5/group, 14 total). Femurs were dehydrated in ethanol and embedded in polymethymethacrylate. A 3 mm thick transverse section of cortical bone from the midshaft of each sample was fixed to an atomic force microscope stub and polished anhydrously (Donnelly et al., 2006a). For each sample, 5 indentations spaced at least 7 μm apart were made in the middle of the zones parallel to the labels and at the periosteal edge (Triboindentor, Hysitron, Minneapolis, MN). Four different tissue age zones were tested: periosteal zone, 0–14 d, 15–28 d, and 29 d+. Indents were created using a 500 μN trapezoidal load function. The indentation modulus (Ei) and hardness (H) were calculated from the unloading portion of the 500 μN load-displacement curve (Oliver and Pharr, 1992). See supplementary text for details.
Residual indents were indentified using the white light optical microscope attached to the Raman microscope. The laser spot (~2 μm diameter) was centered over each residual indent and corresponding Raman spectra between 800 and 1800 cm−1 were collected (inVia, Renishaw, Gloucestershire, UK). Tissue mineralization (mineral:matrix) and B-type carbonate substitution (carbonate:phosphate) were calculated (Draper et al., 2005; Timlin et al., 2000). See supplementary text for details.
Composite Beam Model
To predict whole bone mechanical behavior, composite beam theory was used to calculate density-weighted moments of inertia in addition to the commonly used geometric (unweighted) moment of inertia (Bartel et al., 2006). Similar to the cortical area measurements, the moment of inertia was calculated for each slice then averaged, resulting in a single value for each sample. An unweighted moment of inertia about the medial-lateral axis (IML) with respect to the centroid (X) was calculated (in-house MATLAB® code) assuming a homogeneous bone tissue:
| (1) |
| (2) |
where the summation is over the total pixel count (n). For each pixel containing bone, xj is the distance from the center of the j-th pixel to the y-axis and Aj is the area of the j-th pixel. Three density-weighted moments (Ilin,a, Ilin,b, Iexp) of inertia were calculated (in-house MATLAB® code) with respect to the mass-weighted centroid (Xw):
| (3) |
| (4) |
where v was the attenuation weighted value calculated for each pixel assuming the modulus was proportional to the attenuation value, either linearly according to our tissue level data from the anterior-medial quadrant (Equation 5) or exponentially according to an apparent level relationship (Equation 6).
| (5) |
| (6) |
HUj is the x-ray attenuation of the j-th pixel and TH is the global threshold value both in Hounsfield units, m is the slope, b is the intercept, and a is the exponential coefficient.
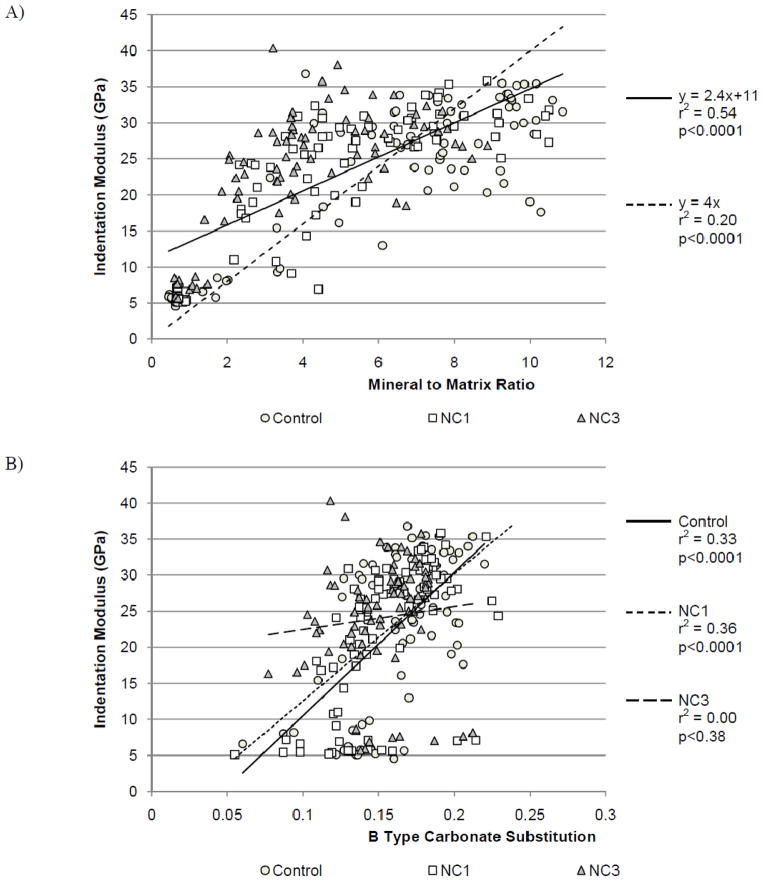
Two linear equations based on the tissue level data from this study were used to calculate density-weighted moments of inertia. The equation of the best fit linear regression between indentation modulus and mineral:matrix ratio was y = 2.4x + 11 (Figure 3a) consequently m = 2.4 and b =11 in Equation (5). Substituting Equation (5) into Equations (3) and (4) resulted in a linearly weighted centroid and moment of inertia (Ilin,a). The best fit linear regression overestimated the modulus of mineral:matrix ratios below 2. The intercept of the regression line represents the indentation modulus of tissue containing no mineral. Demineralized collagen fibrils have been shown to have a Young’s modulus of 20MPa, which is less than 1% of the best fit intercept, 11GPa (Balooch et al., 2008). To better represent the modulus of unmineralized tissue, a second linear regression with the intercept fixed at 0 was used to calculate another density-weighted moment of inertia. The equation of this line was y = 4x, with m = 4 and b= 0. Substituting Equation (5) into Equations (3) and (4) resulted in a second linearly weighted centroid and moment of inertia (Ilin,b). Respective section moduli (Zlin,a, Zlin,b) using the moments of inertia were calculated by dividing the respective moments of inertia by the maximum anterior-posterior distances from the density-weighted centroids.
Figure 3.
A) Linear regressions for mineral:matrix versus indentation modulus, solid line for y=2.4x+11 and a dashed line for y=4x. B) Analysis of covariance with B-type carbonate substitution as the covariate and diet group as the factor.
The exponential relationship we used was based a previously established relationship between ash fraction and Young’s modulus from bovine cortical bone beams where a = 3.91 in Equation (6) (Schaffler and Burr, 1988). Substitution of Equation (6) into Equations (3) and (4) resulted in an exponentially-weighted centroid and moment of inertia (Iexp). The section modulus (Zexp) was calculated by dividing the moment of inertia (Iexp) by the maximum anterior-posterior distance from the density-weighted centroid. The sensitivity of our results to the exponential coefficient chosen was investigated by looking at a range of exponential coefficients.
Statistical Analyses
For all statistical tests, p-values less than 0.05 were considered significant. Results presented are significant unless stated otherwise. See supplementary text for details.
Results
Whole Bone Properties
Serum levels of 1,25-OH D were reduced in both vitamin D deficient groups compared with Controls (36.9 ± 2.17 nmol/L), 60% and 64%, respectively. Serum levels of 1,25-OH D in the NC1 and NC3 groups were not different from each other. Final body masses were reduced by 18% and 19% compared with Controls in the NC1 and NC3 groups, respectively.
From the whole bone analyses, vitamin D deficiency reduced whole bone mechanical performance, and mineralization and geometric parameters as measured by microCT compared with Controls (Table 1, Figure 1). TMC was reduced by 20% and 27% in NC1 and NC3 compared with Controls, respectively. TMD was reduced by 8% and 12% in NC1 and NC3 compared with Controls. TMC was 8.6% lower and TMD was 4.2% lower in the NC3 group compared with NC1. Cortical area was reduced by 13% and 17% in NC1 and NC3 compared with Controls. Failure moment was reduced by 26% and 33% in NC1 and NC3 compared with Controls. EI was reduced by 32% and 38% in NC1 and NC3 compared with Controls. The effective modulus was 20% lower in the NC3 group compared with Controls. The post-yield displacement was not different with vitamin D deficiency. No differences were observed between NC1 and NC3 treatments in geometric measures or whole bone mechanical behavior.
Table 1.
Mean measures of whole bone composition, geometry and mechanical behavior. Values shown as mean (standard deviation).
| Control | NC1 | NC3 | |||
|---|---|---|---|---|---|
| Difference vs. Control (%) | Difference vs. Control (%) | ||||
| Final Body Mass (g) | 506 (39) | 416 (39) | −18* | 408 (39) | −19* |
| Tissue Mineral Content (mg) | 23.2 (1.6) | 18.6 (2.2)* | −20* | 17.0 (1.5)+ | −27*+ |
| Tissue Mineral Density (mg/cc) | 937 (23) | 864 (37)* | −8* | 825 (41)+ | −12*+ |
| Cortical Area (mm2) | 8.4 (0.5) | 7.3 (0.7)* | −13* | 7.0 (0.6)* | −17* |
| Moment of Inertia (mm4) | 17.5 (2.7) | 14.3 (2.6)* | −18* | 13.6 (2.8)* | −22* |
| Moment of Inertia Lin. A (mm4) | 165 (33) | 127 (29)* | −23* | 120 (26)* | −27* |
| Moment of Inertia Lin. B (mm4) | 90.1 (13.8) | 68.0 (13.0)* | −25* | 61.7 (12.0)* | −32* |
| Moment of Inertia Exp. (mm4) | 449 (78) | 273 (68)* | −39* | 218 (49)*+ | −52*+ |
| Section Modulus (mm3) | 5.3 (0.8) | 4.4 (0.7)* | −17* | 4.2 (0.7)* | −20* |
| Section Modulus Lin. A (mm3) | 85.4 (12) | 69.6 (11)* | −19* | 66.0 (10)* | −23* |
| Section Modulus Lin. B (mm3) | 26.9 (3.9) | 20.9 (3.7)* | −22* | 19.3 (3.0)* | −28* |
| Section Modulus Exp. (mm3) | 131 (23) | 81.5 (21)* | −38* | 68.5 (14)*+ | −48*+ |
| Failure Moment (Nmm) | 695 (94) | 517 (72)* | −26* | 469 (73)* | −33* |
| Bending Stiffness (Nmm2) | 18100 (3600) | 12400 (2800)* | −32* | 11200 (2400)* | −38* |
| Post Yield Displacement (mm) | 0.12 (0.15) | 0.13 (0.14) | +8 | 0.14 (0.16) | +17 |
| Effective Modulus (N/mm2) | 1870 (570) | 1560 (360) | −17 | 1500 (430) | −20* |
Significantly different from Control;
significantly different from NC1 treatment group.
Figure 1.
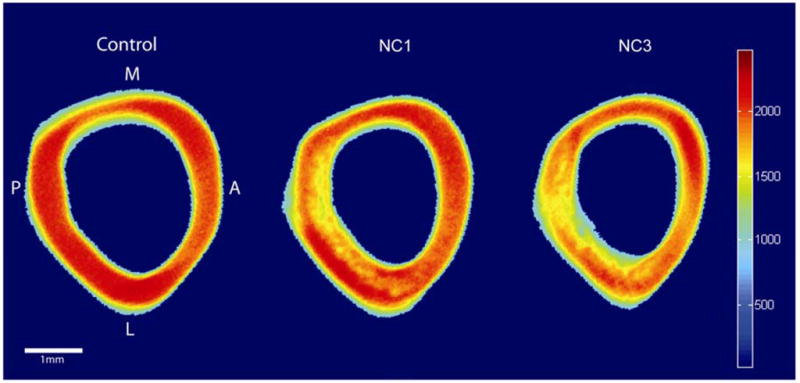
Representative microCT images of Control, NC1, and NC3 right femur cross sections. Colors represent differences in attenuation (Houndsfield Units). Vitamin D deficiency reduced mineralization of the cortical bone particularly in the posterior half of the femurs.
Tissue Level Properties
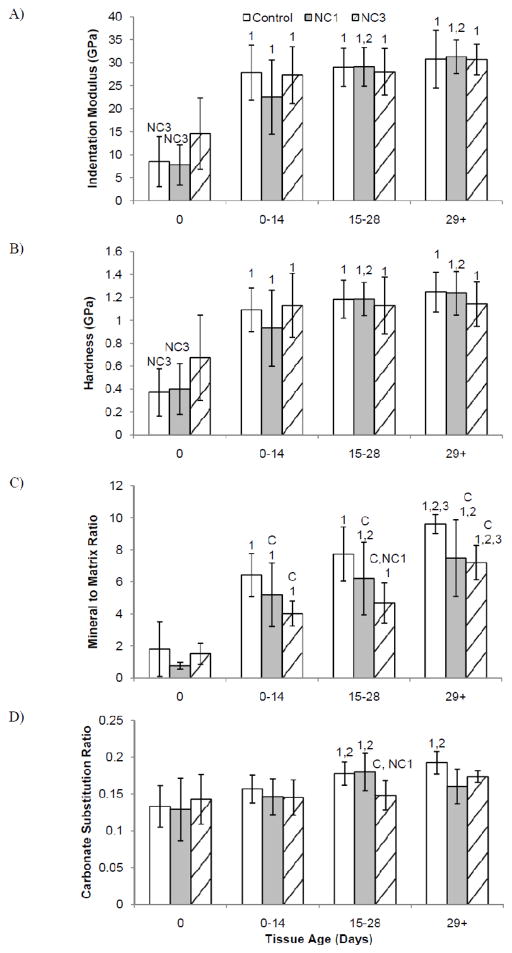
From the two-way ANOVA with diet group and tissue age zone, the indentation modulus in all groups was lower at the periosteal surface compared to the 0–29 d+ tissue zones. Additionally, in the NC1 group, the indentation modulus of 0–14 d tissue was 49% lower than the 14–29 d+ tissue (Figure 2a). Hardness results followed similar trends to the indentation modulus (Figure 2b). For all groups, the hardness was lower at the periosteal surface compared to the 0–29 d+ tissue zones. The NC1 group had a 45% lower hardness in the 0–14 d tissue than 14–29 d+ tissue.
Figure 2.
Mean A) indentation modulus, B) hardness, C) mineral:matrix ratio and D) carbonate substitution by diet group versus tissue age zone. Significantly different from Control (C), NC1 (NC1), NC3 (NC3) within a single tissue age zone. Significantly different from 0 day old tissue (1), 0–14 day old tissue (2), and 15–28 day old tissue (3) within the same group. Error bars indicate standard deviation.
The mineral:matrix ratio increased with increasing tissue age for all diet groups (Figure 2c). Vitamin D deficiency decreased the mineral:matrix ratio compared to Control animals in the intracortical tissue (0–14, 15–28 and 29 d+), but not at the periosteal edge. In the 0–14 d tissue the Control mineral:matrix ratio was higher than NC1 and NC3. In 15–28 d tissue the Control and NC1 mineral:matrix ratios were higher than NC3. In the 29 d+ tissue the Control mineral:matrix ratio was higher than both NC1 and NC3. Vitamin D deficiency delayed the increase in B-type carbonate substitution across the cortex (Figure 2d). Control animals had a significantly higher carbonate:phosphate ratio in the three older tissue age zones than at the periosteum. For NC1, the carbonate:phosphate ratio significantly increased after 15 d. The carbonate:phosphate ratio did not increase with tissue age for the NC3 group; intracortical tissue maintained similar levels to the youngest tissue.
From the analysis of covariance, diet group did not affect the relationship between mineral:matrix ratio and indentation modulus, thus indentation modulus and mineral:matrix ratio data from all groups were fit using a single linear model (r2 = 0.54, p < 0.001) (Figure 3a). The relationship between the indentation modulus and carbonate substitution varied by diet group. Although tissue level mechanical properties and the carbonate:phosphate ratio correlated in the Control and NC1 groups, no correlation existed in the NC3 group (Figure 3b).
Relating Tissue Level and Whole Bone Properties
For the samples used for tissue level analyses (n=14), linear regressions between whole bone mechanical behavior of the contralateral limbs and average intracortical tissue level properties were examined (average of the oldest 3 tissue age zones). None of the averaged tissue level properties were significant predictors for the effective modulus, bending stiffness, or failure moment.
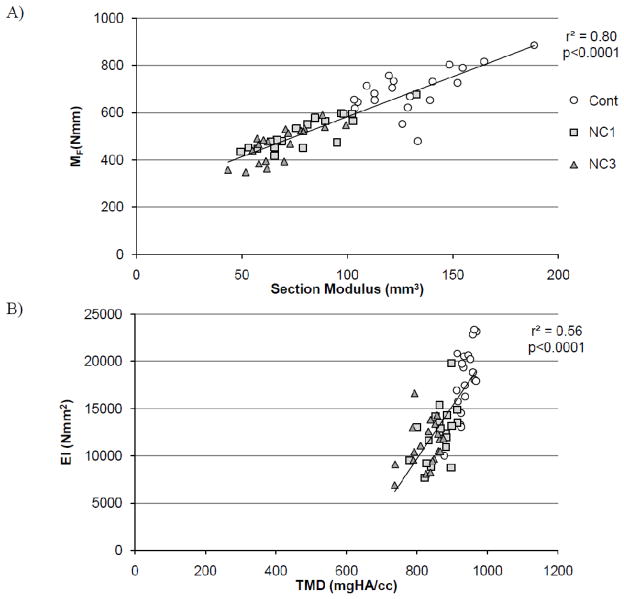
Whole bone geometric and compositional measures from microCT were used to predict EI and MF (Table 2). From the geometric and compositional data from microCT, the best predictor for EI was TMD (r2 =0.56) and for MF was TMC (r2=0.78). MF was better predicted than EI by every predictor. The linearly weighted moment of inertia (Ilin,a) increased the coefficient of determination for failure moment to r2 = 0.57 compared with the geometric moment of inertia (r2 = 0.36). Ilin,b and Zlin,b increased coefficients of determination for whole bone mechanical behavior compared to the respective values calculated using the linear equation with the non zero intercept (Ilin,a, Zlin,a). The exponentially weighted moment of inertia (Iexp) predicted 75% of the variability of the failure moment. The exponentially weighted section modulus (Zexp) predicted 80% of the variability of the failure moment (Figure 4b). The exponentially weighted section modulus had significantly greater explanatory power for the failure moment than all variables except TMC, exponentially weighted moment of inertia, and the linearly weighted section modulus with 0 intercept. For bending stiffness, the exponentially weighted section modulus had significantly greater explanatory power than all variables except TMC, TMD, and the exponentially weighted moment of inertia (Table 2).
Table 2.
Coefficients of determination (r2) for whole bone mechanical behavior, failure moment (MF) and bending stiffness (EI).
| MF | EI | ||
|---|---|---|---|
| Average material properties | Tissue mineral content | 0.78 | 0.50 |
| Tissue mineral density | 0.65* | 0.56 | |
| Geometric properties | Cortical area | 0.63* | 0.32# |
| Moment of inertia | 0.36* | 0.09# | |
| Section Modulus | 0.47* | 0.16# | |
|
| |||
| Spatially varying material properties | Moment of inertia (linearly weighted, Ilin,a) | 0.49* | 0.15# |
| Section modulus (linearly weighted, Zlin,a) | 0.54* | 0.21# | |
| Moment of inertia (linearly weighted, Ilin,b) | 0.57* | 0.23# | |
| Section modulus (linearly weighted, Zlin,b) | 0.66 | 0.29# | |
| Moment of inertia (exponentially weighted, Iexp) | 0.75 | 0.43 | |
| Section modulus (exponentially weighted, Zexp) | 0.80 | 0.49 | |
Significantly different r2 from the exponentially weighted section modulus for the failure moment.
Significantly different r2 from the exponentially weighted section modulus for the bending stiffness.
Figure 4.
A) The best predictor for failure moment (MF) was the exponentially weighted section modulus. B) The best predictor for bending stiffness (EI) was tissue mineral density (TMD).
Discussion
Vitamin D deficiency in growing rats reduced measures of whole bone mechanical behavior, mineralization, and geometry similar to previous studies (Baylink et al., 1970a; Donnelly et al., 2010; Einhorn et al., 1986). Reductions in whole bone mineralization, as indicated by reduced TMD, were paralleled by reductions in tissue level mineral:matrix ratios with vitamin D deficiency. The spatial distribution and heterogeneity of tissue properties were preserved by using intrinsic tissue level relationships instead of apparent level relationships to calculate density-weighted section moduli. Density-weighted section moduli calculated from tissue level data better predicted variability in whole bone mechanical behavior than averaged tissue level properties and unweighted measures of whole bone geometry; however, the density-weighted section moduli from apparent level data further improved the predictions.
To investigate the sensitivity of the results to the specific coefficients used in Equations (5) and (6), different intercepts and exponential coefficients were examined. For the linear equation, the predictive capability of the weighted section modulus was affected by the intercept, but not the slope. The intercept of the regression line represents the indentation modulus of tissue with no mineral, which should be much lower than bone. Hence the increased explanatory power using the equation with a 0 intercept was not surprising. In fact the relationship between mineral:matrix ratio and indentation modulus appears bimodal with a larger slope between mineral:matrix ratio of 0–4, then a smaller slope beyond a mineral:matrix ratio of 4 (Figure 3a). The bimodal response would be vital during rapid growth as the prompt establishment of mechanical competence would be necessary for the bone to withstand everyday loads during primary mineralization (Busa et al., 2005; Wergedal and Baylink, 1974). Secondary mineralization would then follow with a slow but steady accrual of mineralization and increased mechanical properties.
To examine the effect of the exponential coefficient on the prediction of whole bone mechanical behavior, weighted section moduli were calculated using a range of exponential coefficients. Between exponential coefficient values of 3 and 9, the coefficient of determination of the exponentially weighted section modulus changed less than 1%. The initial value of 3.91 selected for this experiment was within 1% of the best coefficient of determination for this data set.
An underlying assumption of our approach was that the relationship between Raman mineral content and indentation modulus was proportional to apparent density and Young’s modulus. Both TMD and mineral:matrix ratio from Raman spectroscopy are measures of mineralization, not true gravimetric densities. Vitamin D deficiency primarily affects mineralization leaving the matrix intact (Baylink et al., 1970b; Donnelly et al., 2010; Einhorn et al., 1986). If the amount of collagen and non-collagenous proteins is similar between groups, the mineral:matrix ratio should indicate relative increases in mineral in a given volume of tissue. Additionally a correlation between Raman mineral:matrix and TMD has been confirmed in growing rabbits, and a similar relationship would expected in rats (Turunen et al., 2011). Assuming a constant Poisson’s ratio (ν) across all samples, Young’s modulus is proportional to the indentation modulus scaled by (1 − ν2). Thus the proportionality of the indentation modulus and the mineral:matrix ratio to TMD and Young’s modulus is plausible.
A limitation of the study is that tissue level measurements were taken in a single quadrant of the cortex, thus a single regression equation for the mineral:matrix ratio and indentation modulus was used throughout the cortex. Quadrant-specific differences in tissue properties naturally occur in the cortex and could have obscured diet-induced changes in the indentation modulus (Akkus et al., 2004). Additional tissue level data from other quadrants of the femur could validate the use of a single expression or provide location specific tissue property relationships to improve the predictive capability of density-weighted section moduli.
Two different experimental groups were included to create a range of both bone mineralization and mechanical properties. However, whole bone mechanical behavior of the NC1 and NC3 groups was similar despite differences in mineralization density. Although MF and EI were not different between NC1 and NC3, the values were spread across a range ensuring the regressions were not influenced by highly leveraged data. Similarly at the tissue length scale, tissue level mechanical properties were unchanged despite differences in local tissue mineralization. The lack of differences in indentation modulus with dietary intervention could indicate that large changes in mineralization are needed to affect indentation modulus and is in accord with a previous study that affected mineralization in rats with a more severe diet (Donnelly et al., 2010).
Our approach to predicting mechanical behavior could be further improved by using higher resolution microCT scans. The current study used scans with 25μm voxel size that cannot resolve cellular lacunae, small pores and blood vessels. A higher resolution scan that resolves these architectural features could improve the accuracy of the model and prediction of whole bone mechanical behavior. Additionally the coefficient of determination of 0.54 between indentation modulus and mineral:matrix ratio indicates additional determinants of the indentation modulus remain. Previous studies have shown that the indentation modulus correlates with other compositional measures such as collagen alignment and carbonate substitution (Busa et al., 2005; Donnelly et al., 2006b). In the future, including compositional parameters in addition to mineralization could provide a more robust and accurate model to predict whole bone mechanical behavior.
Density-weighted section moduli are not as complex as microCT-based finite element models (FEA), but could provide a faster and more economic evaluation of whole bone mechanical behavior. MicroCT-based finite element models can predict 70–98% of the variability in the failure load based on apparent properties, but require the use of super computers or hours of computational time (Imai et al., 2008; Pistoia et al., 2002). The density-weighted section moduli calculated using composite beam theory predicted 80% of the variability in failure moment and are less computationally intensive. Improvements in the methodology used to calculate density-weighted section moduli could make this approach equivalent to microCT-based FEA models in terms of predictive capability but more time and cost efficient.
The hierarchical organization of the skeleton produces an amazingly efficient load bearing structure while simultaneously making analysis and modeling challenging. Previously, microCT images in conjunction with composite beam theory and apparent level relationships between elastic modulus and mineralization improved predictions of whole bone mechanical behavior (Bhatavadekar et al., 2006; Corcoran et al., 1994; Cory et al., 2010; Hong et al., 2004). This study is the first to use nanoindentation derived material properties from contralateral limbs of the same animal with composite beam theory to minimize assumptions about tissue heterogeneity and microarchitecture when predicting whole bone mechanical behavior. Although the apparent level derived relationships had more predictive power than the tissue level data derived linear relationships, the composite beam model in this paper is an improved method to extrapolate tissue level data to macro-scale mechanical behavior in a mineralization defect model.
Supplementary Material
Acknowledgments
This study was supported by NIH/NAIMS grant R01-AR053571 and AR046121. This work made use of the Cornell Center for Materials Research Facilities supported by the National Science Foundation under Award Number DMR-0520404. The authors would like to thank Hystitron Inc., Cornell CARE staff, Mark Riccio, Jayme Burket, Daniel Gu, and Dr. Steven Doty.
Footnotes
Conflicts of Interest
Authors have no conflicts of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Grace Kim, Email: gk242@cornell.edu.
Adele L. Boskey, Email: boskeya@hss.edu.
Shefford P. Baker, Email: shefford.baker@cornell.edu.
References
- Akkus O, Adar F, Schaffler MB. Age-related changes in physicochemical properties of mineral crystals are related to impaired mechanical function of cortical bone. Bone. 2004;34:443–453. doi: 10.1016/j.bone.2003.11.003. [DOI] [PubMed] [Google Scholar]
- Aspray TJ, Prentice A, Cole TJ, Sawo Y, Reeve J, Francis RM. Low bone mineral content is common but osteoporotic fractures are rare in elderly rural Gambian women. J Bone Miner Res. 2009;11:1019–1025. doi: 10.1002/jbmr.5650110720. [DOI] [PubMed] [Google Scholar]
- Balooch M, Habelitz S, Kinney JH, Marshall SJ, Marshall GW. Mechanical properties of mineralized collagen fibrils as influenced by demineralization. J Struct Biol. 2008;162:404–410. doi: 10.1016/j.jsb.2008.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartel DL, Davy DT, Keaveny TM. Orthopaedic biomechanics: mechanics and design in musculoskeletal systems. Prentice Hall; 2006. [Google Scholar]
- Baylink D, Stauffer M, Wergedal J, Rich C. Formation, mineralization, and resorption of bone in vitamin D-deficient rats. J Clin Invest. 1970a;49:1122–1134. doi: 10.1172/JCI106328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baylink D, Wergedal J, Stauffer M, Rich C. Year Effects of fluoride on bone formation, mineralization, and resorption in the rat. [Google Scholar]
- Bhatavadekar NB, Daegling DJ, Rapoff AJ. Application of an image-based weighted measure of skeletal bending stiffness to great ape mandibles. Am J Phys Anthropol. 2006;131:243–251. doi: 10.1002/ajpa.20397. [DOI] [PubMed] [Google Scholar]
- Busa B, Miller LM, Rubin CT, Qin YX, Judex S. Rapid establishment of chemical and mechanical properties during lamellar bone formation. Calcif Tissue Int. 2005;77:386–394. doi: 10.1007/s00223-005-0148-y. [DOI] [PubMed] [Google Scholar]
- Corcoran TA, Sandler RB, Myers ER, Lebowitz HH, Hayes WC. Calculation of cross-sectional geometry of bone from CT images with application in postmenopausal women. J Comput Assist Tomogr. 1994;18:626–633. doi: 10.1097/00004728-199407000-00021. [DOI] [PubMed] [Google Scholar]
- Cory E, Nazarian A, Entezari V, Vartanians V, Müller R, Snyder BD. Compressive axial mechanical properties of rat bone as functions of bone volume fraction, apparent density and micro-ct based mineral density. J Biomech. 2010;43:953–960. doi: 10.1016/j.jbiomech.2009.10.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cummings SR, Karpf DB, Harris F, Genant HK, Ensrud K, LaCroix AZ, Black DM. Improvement in spine bone density and reduction in risk of vertebral fractures during treatment with antiresorptive drugs. The American journal of medicine. 2002;112:281–289. doi: 10.1016/s0002-9343(01)01124-x. [DOI] [PubMed] [Google Scholar]
- Currey JD. The mechanical consequences of variation in the mineral content of bone. J Biomech. 1969;2:1–11. doi: 10.1016/0021-9290(69)90036-0. [DOI] [PubMed] [Google Scholar]
- Currey JD. Effects of differences in mineralization on the mechanical properties of bone. Philos Trans R Soc Lond B Biol Sci. 1984;304:509–518. doi: 10.1098/rstb.1984.0042. [DOI] [PubMed] [Google Scholar]
- Currey JD. The effect of porosity and mineral content on the Young’s modulus of elasticity of compact bone. J Biomech. 1988;21:131–139. doi: 10.1016/0021-9290(88)90006-1. [DOI] [PubMed] [Google Scholar]
- Donnelly E, Baker SP, Boskey AL, van der Meulen MCH. Effects of surface roughness and maximum load on the mechanical properties of cancellous bone measured by nanoindentation. Journal of Biomedical Materials Research Part A. 2006a;77:426–435. doi: 10.1002/jbm.a.30633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donnelly E, Chen D, Boskey AL, Baker SP, van der Meulen MCH. Contribution of Mineral to Bone Structural Behavior and Tissue Mechanical Properties. Calcif Tissue Int. 2010;87:450–460. doi: 10.1007/s00223-010-9404-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donnelly E, Williams RM, Downs SA, Dickinson ME, Baker SP, van der Meulen MCH. Quasistatic and dynamic nanomechanical properties of cancellous bone tissue relate to collagen content and organization. Journal of materials research. 2006b;21:2106–2117. [Google Scholar]
- Draper ERC, Morris MD, Camacho NP, Matousek P, Towrie M, Parker AW, Goodship AE. Novel Assessment of Bone Using Time-Resolved Transcutaneous Raman Spectroscopy. J Bone Miner Res. 2005;20:1968–1972. doi: 10.1359/JBMR.050710. [DOI] [PubMed] [Google Scholar]
- Einhorn TA, Bonnarens F, Burstein AH. The contributions of dietary protein and mineral to the healing of experimental fractures. A biomechanical study. The Journal of Bone and Joint Surgery. 1986;68:1389. [PubMed] [Google Scholar]
- Ettinger B, Black DM, Mitlak BH, Knickerbocker RK, Nickelsen T, Genant HK, Christiansen C, Delmas PD, Zanchetta JR, Stakkestad J, Gluer CC, Krueger K, Cohen FJ, Eckert S, Ensrud KE, Avioli LV, Lips P, Cummings SR. Reduction of vertebral fracture risk in postmenopausal women with osteoporosis treated with raloxifene: results from a 3-year randomized clinical trial. Multiple Outcomes of Raloxifene Evaluation (MORE) Investigators. Journal of the American Medical Association. 1999;282:637–645. doi: 10.1001/jama.282.7.637. [DOI] [PubMed] [Google Scholar]
- Fritton JC, Myers ER, Wright TM, van der Meulen MCH. Loading induces site-specific increases in mineral content assessed by microcomputed tomography of the mouse tibia. Bone. 2005;36:1030–1038. doi: 10.1016/j.bone.2005.02.013. [DOI] [PubMed] [Google Scholar]
- Haguenauer D, Welch V, Shea B, Tugwell P, Adachi JD, Wells G. Fluoride for the treatment of postmenopausal osteoporotic fractures: a meta-analysis. Osteoporos Int. 2000;11:727–738. doi: 10.1007/s001980070051. [DOI] [PubMed] [Google Scholar]
- Hong J, Cabe GD, Tedrow JR, Hipp JA, Snyder BD. Failure of trabecular bone with simulated lytic defects can be predicted non-invasively by structural analysis. J Orthop Res. 2004;22:479–486. doi: 10.1016/j.orthres.2003.09.006. [DOI] [PubMed] [Google Scholar]
- Imai K, Ohnishi I, Yamamoto S, Nakamura K. In Vivo Assessment of Lumbar Vertebral Strength in Elderly Women Using Computed Tomography-Based Nonlinear Finite Element Model. Spine. 2008;33:27–32. doi: 10.1097/BRS.1090b1013e31815e33993. [DOI] [PubMed] [Google Scholar]
- Kanis JA. Diagnosis of osteoporosis and assessment of fracture risk. Lancet. 2002;359:1929–1936. doi: 10.1016/S0140-6736(02)08761-5. [DOI] [PubMed] [Google Scholar]
- Kanis JA, Borgstrom F, De Laet C, Johansson H, Johnell O, Jonsson B, Oden A, Zethraeus N, Pfleger B, Khaltaev N. Assessment of fracture risk. Osteoporos Int. 2005;16:581–589. doi: 10.1007/s00198-004-1780-5. [DOI] [PubMed] [Google Scholar]
- Kanis JA, Johnell O, Oden A, Johansson H, McCloskey E. FRAX and the assessment of fracture probability in men and women from the UK. Osteoporos Int. 2008;19:385–397. doi: 10.1007/s00198-007-0543-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meunier PJ, Sebert JL, Reginster JY, Briancon D, Appelboom T, Netter P, Loeb G, Rouillon A, Barry S, Evreux JC. Fluoride salts are no better at preventing new vertebral fractures than calcium-vitamin D in postmenopausal osteoporosis: the FAVOStudy. Osteoporos Int. 1998;8:4–12. doi: 10.1007/s001980050041. [DOI] [PubMed] [Google Scholar]
- Oliver WC, Pharr GM. Improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. Journal of Materials Research. 1992;7:1564–1583. [Google Scholar]
- Pistoia W, van Rietbergen B, Lochmüller EM, Lill CA, Eckstein F, Rüegsegger P. Estimation of distal radius failure load with micro-finite element analysis models based on three-dimensional peripheral quantitative computed tomography images. Bone. 2002;30:842–848. doi: 10.1016/s8756-3282(02)00736-6. [DOI] [PubMed] [Google Scholar]
- Rho JY, Zioupos P, Currey JD, Pharr GM. Microstructural elasticity and regional heterogeneity in human femoral bone of various ages examined by nano-indentation. J Biomech. 2002;35:189–198. doi: 10.1016/s0021-9290(01)00199-3. [DOI] [PubMed] [Google Scholar]
- Schaffler MB, Burr DB. Stiffness of compact bone: effects of porosity and density. J Biomech. 1988;21:13–16. doi: 10.1016/0021-9290(88)90186-8. [DOI] [PubMed] [Google Scholar]
- Silva MJ, Brodt MD, Fan Z, Rho JY. Nanoindentation and whole-bone bending estimates of material properties in bones from the senescence accelerated mouse SAMP6. J Biomech. 2004;37:1639–1646. doi: 10.1016/j.jbiomech.2004.02.018. [DOI] [PubMed] [Google Scholar]
- Sonnenberg J, Pansini AR, Christakos S. Vitamin D-dependent rat renal calcium-binding protein: development of a radioimmunoassay, tissue distribution, and immunologic identification. Endocrinology. 1984;115:640–648. doi: 10.1210/endo-115-2-640. [DOI] [PubMed] [Google Scholar]
- Sun LW, Fan YB, Li DY, Zhao F, Xie T, Yang X, Gu ZT. Evaluation of the mechanical properties of rat bone under simulated microgravity using nanoindentation. Acta Biomater. 2009;5:3506. doi: 10.1016/j.actbio.2009.04.042. [DOI] [PubMed] [Google Scholar]
- Timlin JA, Carden A, Morris MD, Rajachar RM, Kohn DH. Raman Spectroscopic Imaging Markers for Fatigue-Related Microdamage in Bovine Bone. Anal Chem. 2000;72:2229–2236. doi: 10.1021/ac9913560. [DOI] [PubMed] [Google Scholar]
- Turunen MJ, Saarakkala S, Rieppo L, Helminen HJ, Jurvelin JS, Isaksson H. Comparison between infrared and Raman spectroscopic analysis of maturing rabbit cortical bone. Applied Spectroscopy. 2011;65:595–603. doi: 10.1366/10-06193. [DOI] [PubMed] [Google Scholar]
- Watts NB, Diab DL. A backbone for FRAX? J Bone Miner Res. 2011;26:458–459. doi: 10.1002/jbmr.351. [DOI] [PubMed] [Google Scholar]
- Wergedal JE, Baylink DJ. Electron microprobe measurements of bone mineralization rate in vivo. American Journal of Physiology--Legacy Content. 1974;226:345–352. doi: 10.1152/ajplegacy.1974.226.2.345. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.