Abstract
Leukocyte trafficking in the microvasculature during inflammatory response is known to involve multiple adhesion molecules and is referred to as the leukocyte adhesion cascade (LAC). Surface-bound selectins and their respective ligands are primarily responsible for tethering and rolling of leukocytes over inflamed endothelium. Numerical modeling of this response is challenging due to the nature of cell-cell interactions in Stokes flow (i.e., large domain of influence for each cell over its neighbors). Here, we discuss a novel simulation capable of modeling several steps of the LAC. The new model includes relevant contact and lubrication forces and extends a physics-based model for single particle rolling interactions developed by Hammer and Apte (1992), for multiparticle interactions by King and Hammer (2001a), and for deformable particles by Gee and King (2006). We initially demonstrate the model for cell-cell collisions occurring near a planar substrate, and for cell-substrate adhesive interactions. The adhesion studies provide a new perspective of the contribution of Hertzian contact mechanics towards variations in contact area at the cell-substrate interface. The results confirm that interfacial contact area will increase as a result of the contact formulation and that this mechanism may enhance cell rolling interactions for cells driven towards endothelium by cell-cell collisions. As a result of cell compliance, rolling velocity may decrease significantly, compared to noncompliant cells.
Keywords: inflammation, cell deformation, boundary element method, Poiseuille lubrication, Hertzian contact
I. INTRODUCTION
The innate immune response involves the recruitment of leukocytes that migrate to the site of injury. This response includes rolling-adhesion, firm-adhesion, chemotaxis, and transmigration. Previously, it was demonstrated that a firmly adherent rigid cell could recruit circulating cells via “hydrodynamic recruitment” (King and Hammer, 2001a, b). This has been shown experimentally in cell-free assays (King et al., 2001) and is supported by measurements of leukocyte capture in vivo using hamster cheek pouch (Lee and King, 2006). Here, we present a novel simulation and numerically investigate cell-substrate and near-wall cell-cell collisions between deformable particles. Cell deformation is widely considered to play an important biological role in inflammation by modulating rolling velocity. The resulting deformation and subsequent increase in area at the cell-substrate interface is hypothesized to enhance secondary recruitment. This mechanical factor will be evaluated numerically in a future study. Blood is a non-Newtonian fluid with erythrocytes, leukocytes, and thrombocytes suspended in viscous plasma. Following the pioneering work of Fröhlich and Sack (1946), a variety of computational techniques have been developed to solve problems involving immersed objects. Methods including volume of fluid and immersed boundary method have been used to simulate blood flow. However, such domain-based methods are computationally expensive since they necessitate a complete discretization of the fluid domain. Our strategy is based on boundary element techniques (BEM) that are well suited to deal with particle suspensions. The reduction of problem dimensionality by one enables a 3D problem to be solved by surface discretization. The method, involving a range completion of the double layer, is known as the Completed Double Layer Boundary Integral Equation Method (CDL-BIEM) (Phan-Thien and Fan, 1996; Phan-Thien et al., 1992).
Mathematical modeling of biological cells is an active area of research. Its origins can be traced to the fundamental fluid dynamics problem of the deformation and dislodging of liquid droplets. Numerical studies have generated considerable debate regarding the proper cell constitutive model. Lim et al. (2006) summarize several constitutive theories and outline the benefits and shortcomings of each model. While Dong et al. (1999) modeled the cell as a Hookean ring enclosing an incompressible fluid, N’Dri et al. (2003) proposed that the cell could be modeled as a two-dimensional compound liquid drop. These ideas have been extended to 3D by Jadhav et al. (2005) and Pappu and Bagchi (2008), by approximating the outer membrane as a non-linear hyperelastic material. The ability of leukocytes to undergo large deformations has also been modeled using compound viscoelastic drop models proposed by Khismatullin and Truskey (2005, 2012). Our approach models the leukocyte as a Hookean solid with material parameters η, νp. A linear elastic model was previously adopted by Wankhede et al. (2006) and is appropriate for representing the small deformations associated with selectin-mediated rolling (Evans et al. 2005). Clearly, a different constitutive model would be required to describe the entire range of deformation experienced by a leukocyte as it becomes progressively activated over the adhesion cascade. To our knowledge, the influence of contact and lubrication forces on the deformation of biological cells is not well documented. We revisit the theory of contact mechanics and will briefly discuss the theoretical model and overall computational technique.
II. PROBLEM FORMULATION
Dilute suspensions of blood cells are often approximated as a Newtonian fluid and mathematically described with the Navier-Stokes equations. For low Reynolds number microcirculatory flow, these PDE’s simplify to a linear set known as the Stokes equations,
| (1) |
where ν, p are velocity and pressure, respectively. Immersed cells are subject to stresses as a result of fluid shear forces, cell-cell collisions, and adhesive interactions. The resulting deformation may be computed once the surface traction distribution is known. For as an isotropic homogenous elastic solid, small displacements are governed by Navier’s equation,
| (2) |
where u, νp are displacement and Poisson’s ratio, respectively. Hence, there are three problems of interest: mobility (translational and rotational motions), exterior (surface traction), and interior (deformation).
III. BOUNDARY ELEMENT TECHNIQUE
A. Mobility Problem
The starting point is the integral representation of Stokes equation in a semi-infinite domain
| (3) |
where Gij is the i-component of velocity due to a point force acting at X in the j-direction, Σijk is the associated stress, and S = ◡Sp, where p = 1,2,…,M , and M is the number of particles. The planar assumption is used both for simplicity and due to the fact that the characteristic length scales involved (diameter of blood vessel for microvasculature varies from 10–300 µm while leukocyte diameter is approximately 10 µm) can vary by more than an order of magnitude. Here, n represents the outward normal and σ is the stress tensor,
| (4) |
The integrals on the right and left hand side of Eq. (3) are known as the single- and double-layer potentials, respectively, in analogy with potential theory. Decoupling the three problems permits the mobility step to proceed as a rigid body calculation (Phan-Thien and Fan, 1996). However, this direct formulation results in a Fredholm integral equation of the first kind and is ill-conditioned. This problem may be circumvented by dropping the single-layer and expressing the double-layer potential in terms of an unknown surface density φ,
| (5) |
where
Power and Miranda (1987) recognized the inability of the double-layer to impart forces or torques on the particle and sought to complete its range by associating the forces and torques with the six degrees of freedom of the particle. The final expression is given by
| (6) |
with
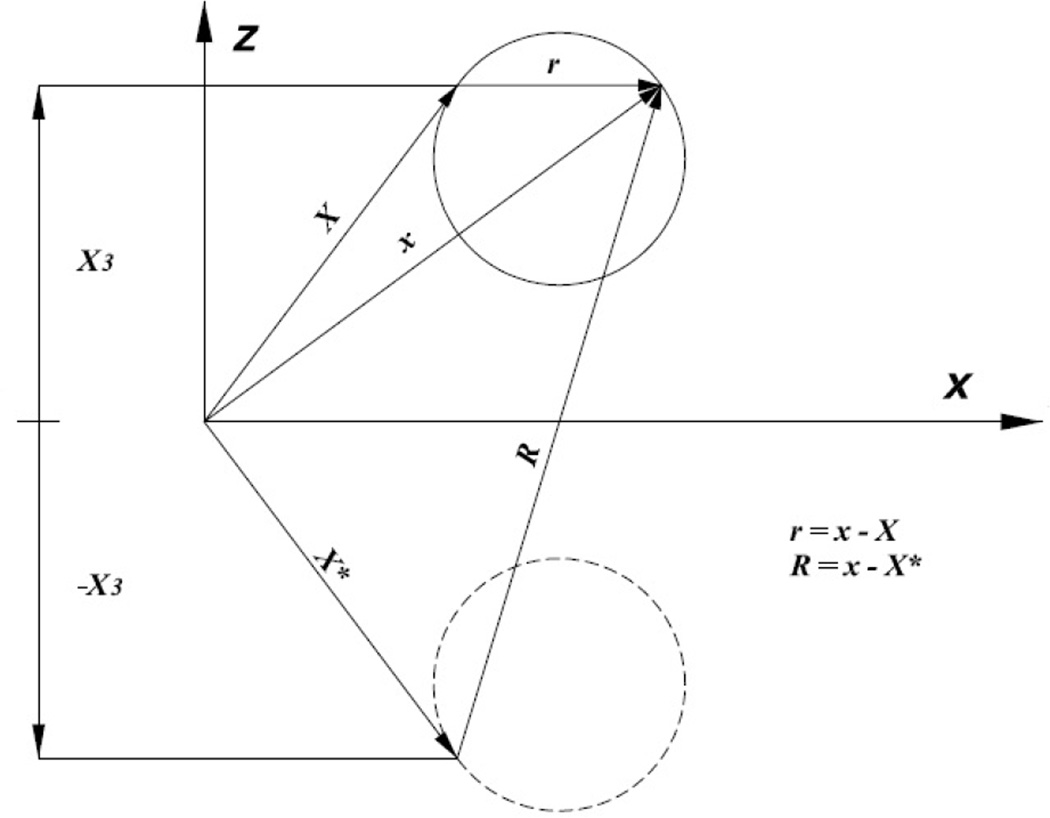
where , T(p) are the external force and torque, respectively, acting on particle p and is the farfield velocity. Here, φ(p,l) represents the translational motion (l=1,2,3) and rotational motion (l=4,5,6) of the particle, ψ(p) the eigenvector of the adjoint operator K*, and 〈·,·〉 denotes the inner product 〈a·b〉 = ∫a(x) · b(x)dS. The rigid body motions are computed once φ is determined. In the present study, no-slip velocity and zero displacement boundary conditions are enforced at all times. Significantly, the singularity solution is supplemented with an image Stokeslet (Fig. 1) and additional terms such that the no-slip condition is automatically satisfied. This implies that the planar surface need not be discretized.
Figure 1.
Source point (i.e., Stokeslet or Kelvinlet) and image source point. No-slip velocity and no-displacement boundary conditions are automatically satisfied at X3=0.
B. Exterior Problem
The starting point for the exterior problem is the single-layer representation of the velocity field,
| (7) |
The traction at point X, with unit normal nk (X), is given by
| (8) |
where is the traction due to and is the associated traction of Gij,
A detailed description of the spectral properties of the double layer and its adjoint is provided by Phan-Thien and Kim (1994) and Phan-Thien and Tullock (1993). In the limit where X approaches the particle surface, the adjoint double-layer suffers a jump discontinuity equal to −tj. Hence
| (9) |
Range completion of the adjoint double-layer is sought by imposing constraints in the form of external forces and torques on the particle. The final expression is given by
| (10) |
with
Here φ(p,l) represents the eigenfunction corresponding to the eigenvalue −1. As reported by Phan-Thien and Fan (1996), the deflation of the eigenvalue +1 is not necessary.
C. Interior Problem
We consider a linear elastic constitutive model since rolling deformations at low to intermediate shear stresses (≤ 5 dyn/cm2) are relatively small. Evans et al. (2005) demonstrated that for compressive deformations on the order of hundreds of nanometers, neutrophil response is well approximated as a linear elastic solid. Using Betti’s reciprocal theorem, Eq. (2) is recast as an integral equation for u
| (11) |
where each particle is assumed Lyapunov smooth (i.e., having continuous normal everywhere). Gij(x,ξ) represents the i-component of displacement due to a point force acting at ξ in the j-direction. For zero displacement boundary condition on the planar substrate, the singularity solution is supplemented with image and extra terms (Fig. 1). The corresponding kernel functions are given by Tran-Cong and Phan-Thien (1986) and the final expression for u is given by
| (12) |
IV. COLLOIDAL FORCES
King and Hammer (2001a) proposed that electrostatic interactions generate a repulsion force Frep between cells and the planar substrate of the type,
| (13) |
where 1/τ is a length scale and ε denotes the surface-to-surface separation distance. Here, τ = 2000 µm−1 and Fo = 1015–1018 fN and the force is directed either along the line connecting cell centers, or normal to the plane. The objective behind such short range forces is to prevent cell-cell or cell-substrate overlap. Here, colloidal forces are treated as body forces that only affect mobility.
V. AREA MODULATION OF CONTACT INTERFACE
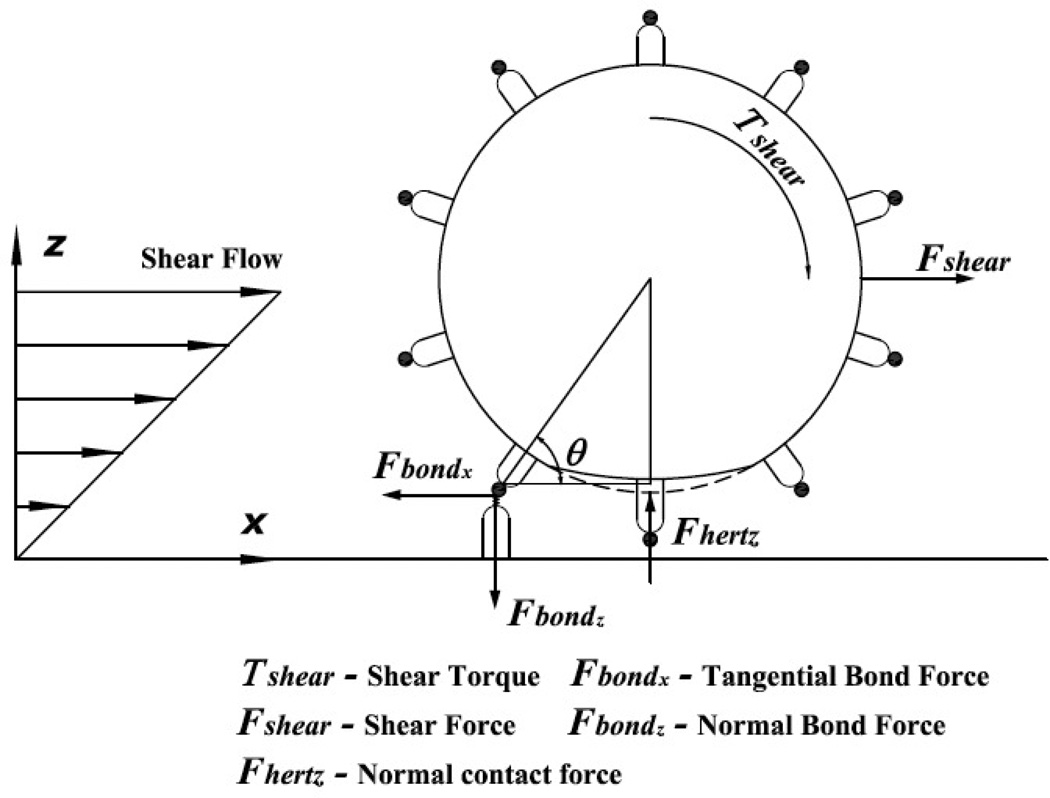
In the present study, we have used a Hertzian contact formulation to calculate an estimate of the evolving interfacial contact area which results from the formation of adhesive bonds between the two interacting surfaces. This is consistent with our approximation of the leukocyte as a linear elastic spherical solid, and we note that the contact formulation has been applied previously to leukocytes (Rosenbluth et al., 2006). For this type of contact, separating distances are of the order of 100 nm, thereby permitting a dry contact formulation (Villaggio (1996); Rognon and Gay (2008)). The forces and torques acting on a tethered cell (Alon et al., 1995) are indicated in Fig. 2, and for static equilibrium ΣFx = ΣFz = 0, ΣT = 0. Hence,
| (14) |
| (15) |
| (16) |
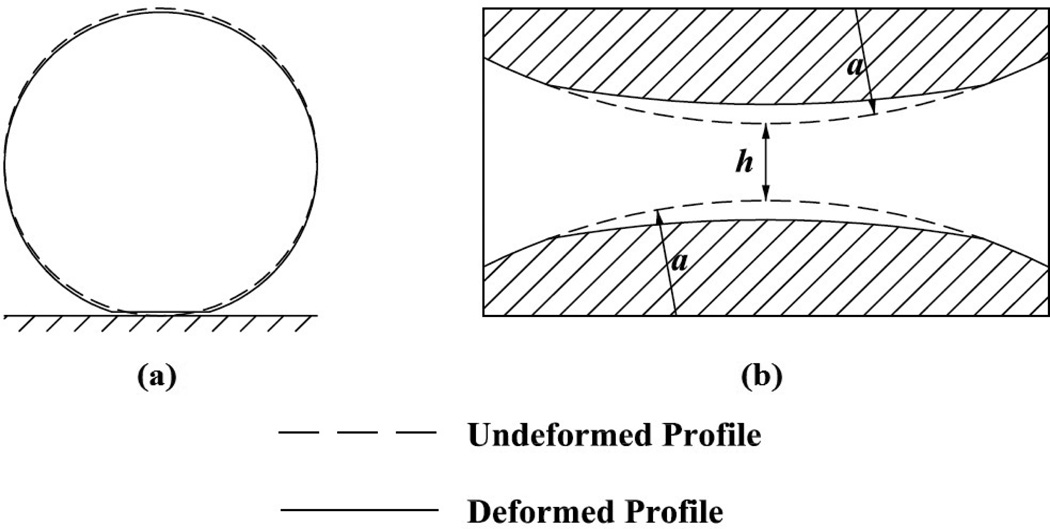
The normal component of the bond force tends to restrain the cell against the endothelium. The resulting reaction force, Eq. (16), induces cell compression (Fig. 3a) which, in turn, modulates interfacial contact area thereby modulating the number of receptors available for subsequent bond formation. The spherical contact radius as is expressed in terms of cell radius, corrected Young’s modulus, and contact force Fhertz (Chang and Wang, 1998),
| (17) |
where
| (18) |
Next, for colliding cells it is assumed that the interacting cells are in the limit of near-touching and are separated by a thin film of plasma (Goddard, 1977). The lubrication of compliant particles is governed by the theory of elastohydrodynamic lubrication, Fig. 3b. The forces arising out of the relative motion between two cells has been computed using the strategy adopted by Nasseri et al. (2000) and Rognon and Gay (2009). The force (inducing deformation), Felas, is given by the sum of the fluid shear and lubrication forces,
| (19) |
The problem formulation is based on the premise that for cell-cell interactions, Flubr is the vector addition of squeezing and shearing components arising from relative motion between cells. A minimum film thickness is adopted and it is assumed that the film does not rupture. Additionally, we assume that the variation in film thickness with deflection is infinitesimal. bj (X) in Eq. (10) has been augmented to account for contact and/or lubrication forces, as indicated in Eqs. (16) and (19).
Figure 2.
Schematic diagram indicating hydrodynamic, adhesive, and contact forces and torques acting on rolling cell.
Figure 3.
Deformation of elastic sphere: (a) interaction with planar substrate, (b) cell-cell collision. In former case, a dry contact formulation is implemented, while the latter case is due to lubricated contact.
VI. ADHESIVE INTERACTIONS
The model for adhesive interactions was developed by Bell (1978). The neutrophil was modeled as a rigid sphere with random surface distribution of adhesion molecules, while the substrate contained a random distribution of ligand. For cells in near-wall region, receptor-ligand pairs were tested for bond formation using a Monte-Carlo technique and, if formed, bonds were modeled as Hookean springs. The rate of bond dissociation, kr, depends on the magnitude of the bond force, F, as follows,
| (20) |
where , ro, have been experimentally determined. The rate of bond formation follows directly from the Boltzmann distribution for affinity,
| (21) |
where σ is the spring constant and |xb − λ| is the deviation bond length. Note, only selectin-mediated cell-substrate adhesive interactions are considered here. Leukocyte-leukocyte adhesive interactions are governed by different adhesion molecule pairs.
VII. NUMERICAL IMPLEMENTATION
Cell surfaces have been discretized using QUAD9 Lagrangian elements. The unknown variable is assumed piecewise constant and is solved for iteratively using up to 3×3 Gaussian quadrature. For the singular element, integration of the double-layer and adjoint double-layer follow the singularity subtraction technique (Phan-Thien and Fan, 1996). For cell collisions, an adaptive time-stepping algorithm has been used with steps varying between 10−4 –10−5, based on proximity of the surfaces. Substantially smaller time steps have been adopted for adhesive calculations. All material points are advected using an explicit time integration rule based on Euler’s method. Simulations have been performed on Sun X4600M2 servers with 2.3Ghz AMD Quad Core processors and on a Macintosh Pro workstation with a 2.8 Ghz Intel Xeon Quad Core processor. Additional parameters are given below:
| PARAMETER | DEFINITION | VALUE |
|---|---|---|
| a | cell radius | 5 µm |
| γ̇ | shear rate | 100 s−1 |
| μ | viscosity | 1 cP |
| ρ | fluid density | 1 gm/cc |
| ρg | cell density | 1.05 gm/cc |
| es | cell roughness | 175 nm |
| ew | substrate roughness | 50 nm |
| σ | spring constant | 100 dyn/cm |
| λ | equilibrium bond length | 30 nm |
| unstressed off-rate | 2.4 s−1 | |
| ro | reactive compliance | 0.39 A° |
| intrinsic on-rate | 365 s−1 | |
| nr | receptor density | 20 molec/µm2 |
| η | shear modulus* | 0.5–104 Pa |
| ν | Poisson’s ratio | 0.33 |
Note, some values of shear moduli have been determined using atomic force microscopy for nonadherent HL-60s, neutrophils, and Jurkat cells with ν = 0.5 (Rosenbluth et al., 2006).
VIII. RESULTS AND DISCUSSION
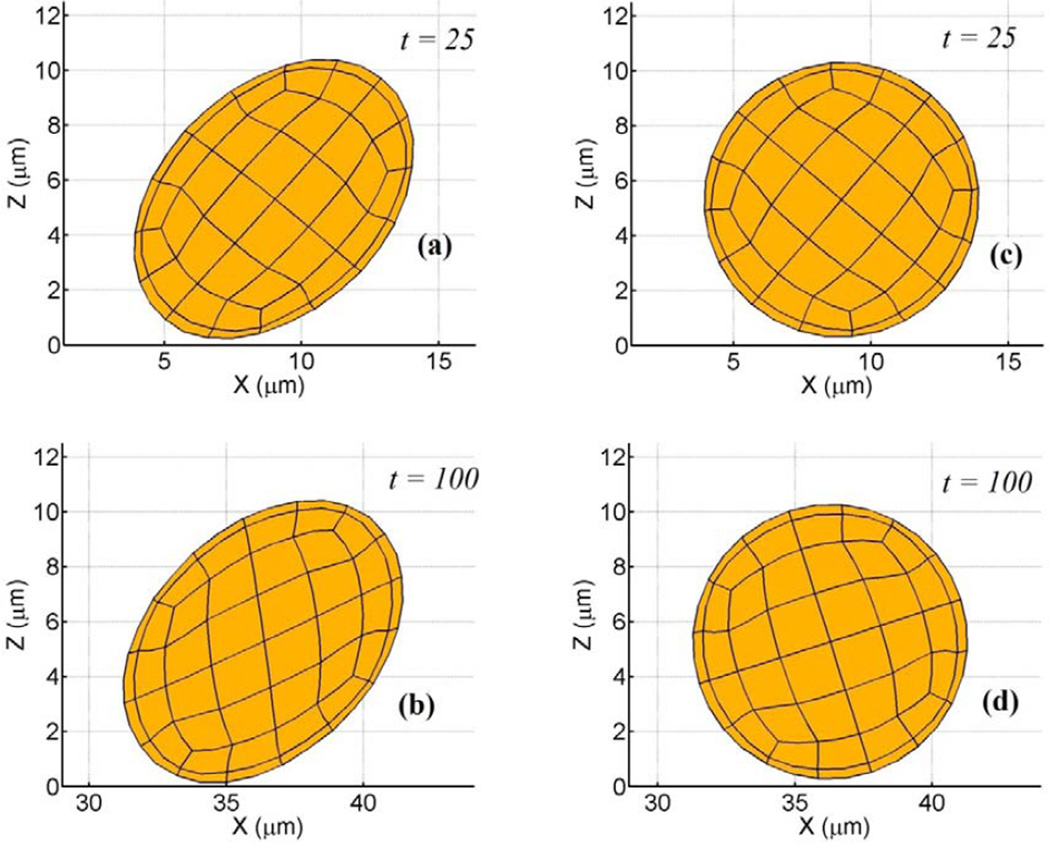
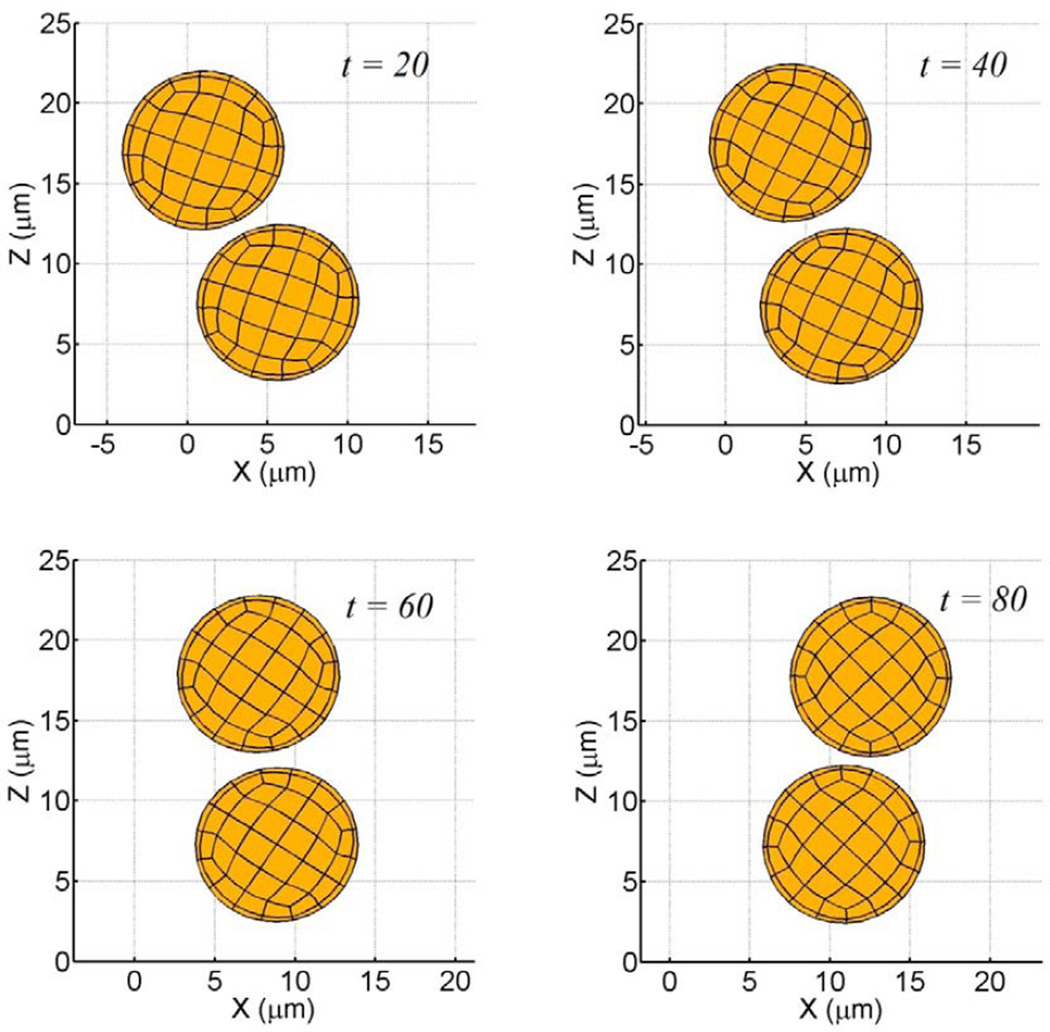
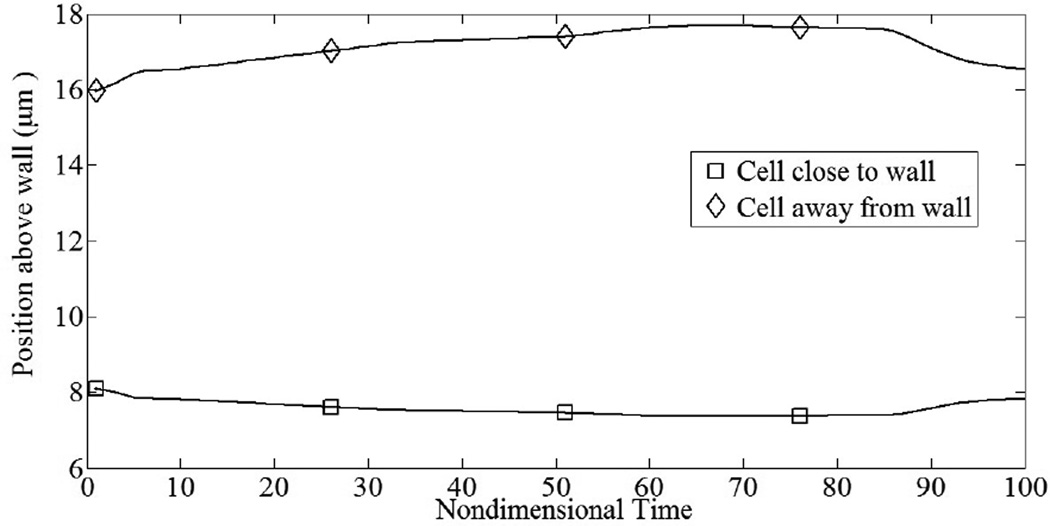
First, we simulate the tumbling motion of an elastic sphere in proximity to a planar substrate. Steady state profiles for a cell in linear shear flow are given in Fig. 4. In Fig. 4a–b, fluid shear stresses are relatively large compared to the shear modulus and the cell deforms into an ellipsoidal shape while tumbling in place (tank-treading motion). The aspect ratio of the deformed profile was observed to be ~0.69. In Fig. 4c–d, fluid shear stresses are relatively weak and the cell retains its spherical shape. Since the aspect ratio of the deformed cell depends on the viscous number (ratio of shearing force to elastic restoring force) of the membrane, leukocytes with realistic shear moduli would only deform into ellipsoids at high shear rates. The deformed profiles are in good agreement with similar studies for neo-Hookean solids (Gao and Hu, 2009) and elastic capsules (Pozrikidis, 1995). In the latter study for an equivalent viscous number of 0.02, the aspect ratio was observed to be ~0.64, indicating reasonable accuracy with our model result. A cell-cell interaction in linear shear flow is illustrated in Fig. 5. By virtue of its initial position, the upper cell catches up to and then passes the lower cell. One feature of this collision is that as the upper cell rides over the lower cell, the lower cell is nudged towards the surface, closer to the region where adhesive interactions are possible. By plotting the cell’s distance above the plane both during and after the collision, we may quantify this interaction, Fig. 6. As seen, the normal displacements are not symmetric and reflect the presence of the container wall. This idea of collisions driving cells towards the wall has been shown previously (Melder et al., 1995; Melder et al., 2000).
Figure 4.
Tumbling motion near planar substrate for elastically deformable particle (ν = 0.33, γ̇ = 100 s−1). Non-dimensional time indicated in panel. (a–b) η = 0.5 Pa, (c–d) η = 23 Pa. For the smaller shear modulus, cell deforms into ellipsoidal shape, while for the larger value the cell retains its spherical shape.
Figure 5.
Short range cell-cell interactions between particles are governed by colloidal and lubrication forces (η = 8 kPa, ν = 0.33, γ̇ = 100 s−1 ). These terms prevent cell overlap. In the model, colloidal forces are assumed to only impact particle mobility.
Figure 6.
Collision of freestream particles induces trajectory deflection during interaction. Upper particle was originally at (x,z) = (−9.0,15.6 µm), while lower particle was at (0.0,8.15 µm). Due to cell-cell collision, lower particle is driven towards the substrate.
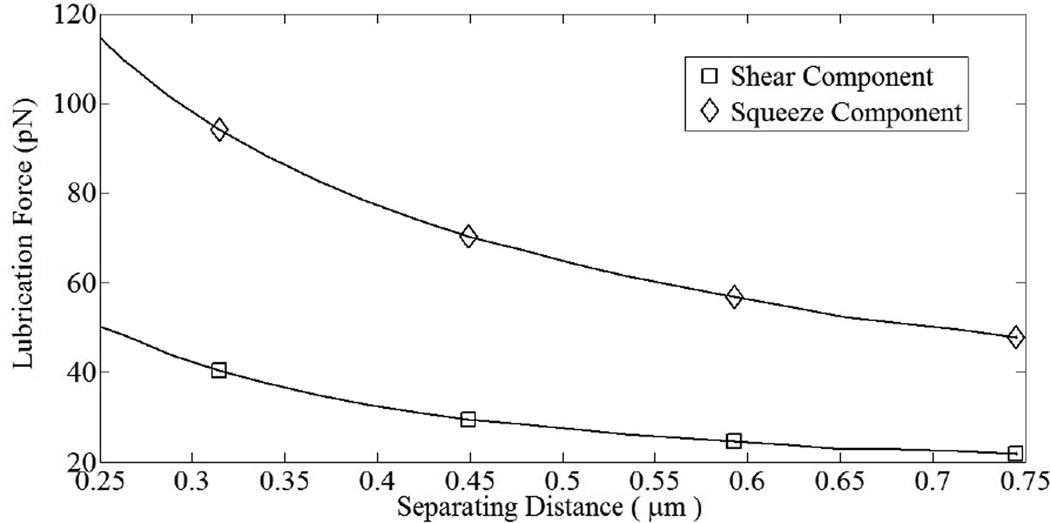
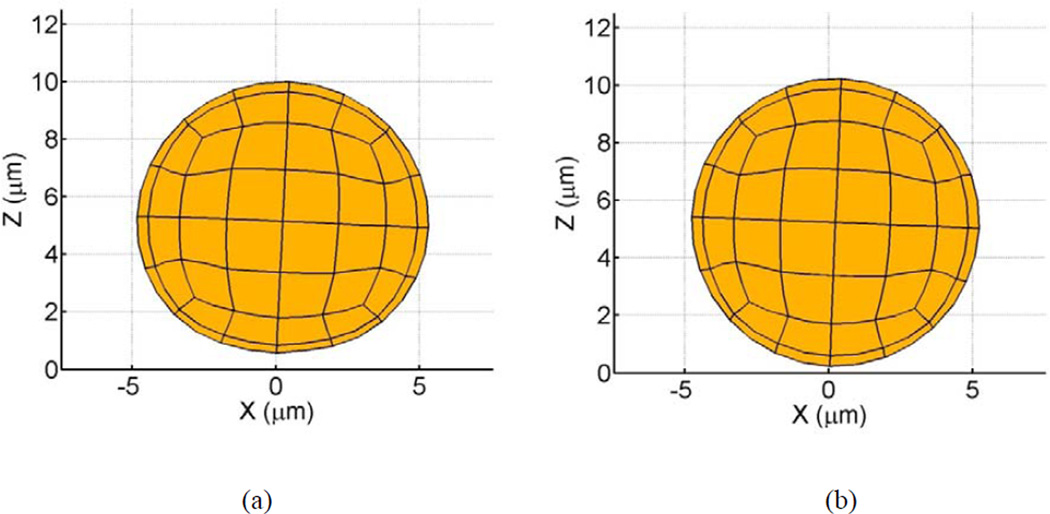
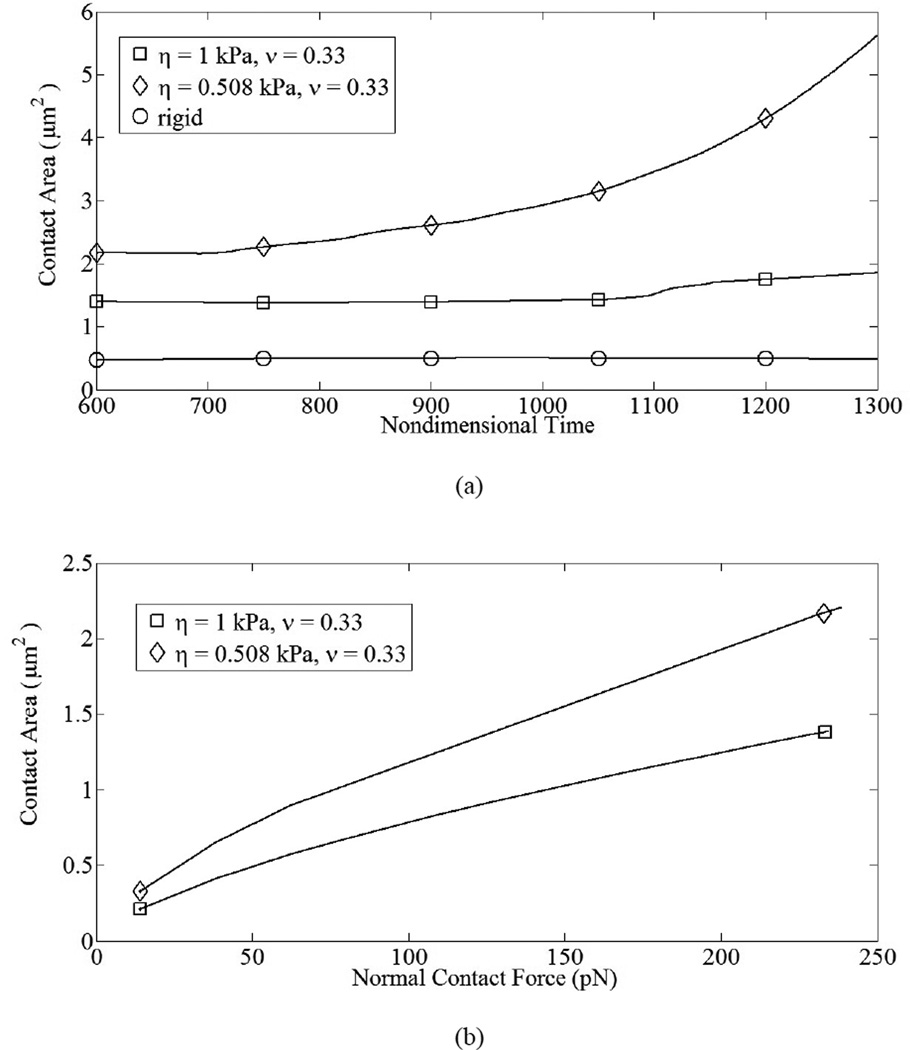
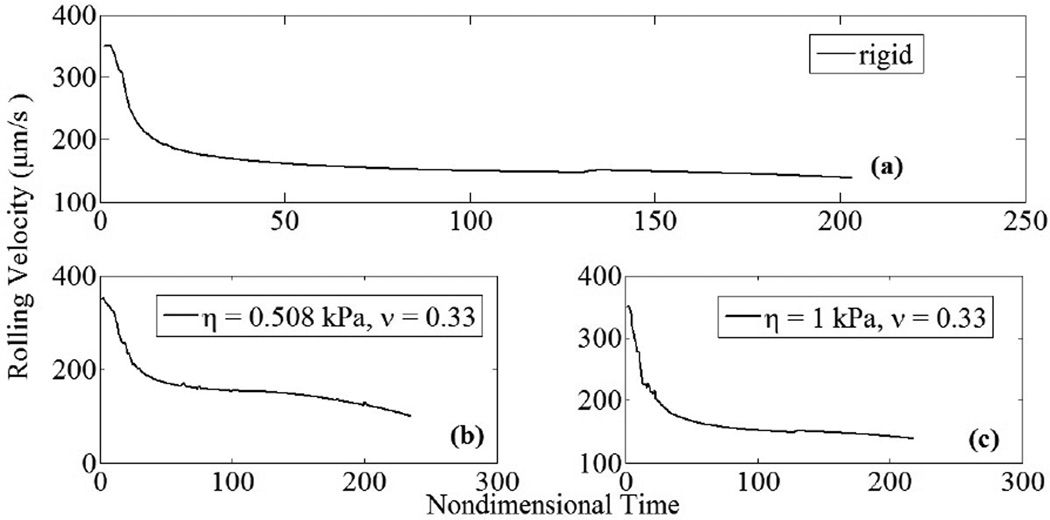
Deformable cell-cell collisions produce a pronounced increase in the contact area between the interacting cells due to elastohydrodynamic lubrication. Studies involving elastic capsules (Jadhav et al., 2007) and droplets (Loewenberg and Hinch, 1997) have been performed previously. Although the Poiseuille theory of lubrication is strictly applicable to infinitesimal deformations, a test case involving small but finite deformations has been presented to illustrate the model. The deformed cells exhibit a distinct parabolic profile which is characteristic of elastic spheres under lubricated contact. These deformations, arising from a collision between a freestream and adherent cell, have been observed in vitro in order to understand the influence of inter-cellular contact area on shear thresholding of leukocytes (Kadash et al., 2004). The asymptotic variation in the shearing and squeezing force components with gap distance is given in Fig. 7. Figure 8 indicates the effect of contact forces on cells. At the time shown, the compliant cell, Fig. 8a, is deformed and generates a flatter contact, as compared to its rigid counterpart, Fig. 8b. Moreover, contact area increases gradually with respect to time for stiff cells, and sharply for compliant cells; Fig. 9a. The variation in circular contact area with normal reaction suggests a direct proportionality between the two variables, Fig. 9b. While the average contact area for the compliant cell under the chosen conditions was calculated as 6.2 µm2, for the stiffer cell it was 1.9 µm2. A likely consequence is an increased number of bonds and subsequent slower rolling velocity, as compared to a rigid cell; Fig. 10. We estimate a drop in rolling velocity to 99 and 138 µm/s for compliant and rigid cells, respectively, as compared to an equivalent non-interacting cell. These results imply that compliant cells could roll considerably slower than their stiffer counterparts, as hypothesized by Jadhav et al. (2005).
Figure 7.
Squeeze and shear components of lubrication force vary with surface separation distance. As gap increases, both components approach zero asymptotically, in agreement with theory.
Figure 8.
Adhesive tractions induce cell rolling motion along planar substrate. (a) Compliant cell deforms as a result of adhesive and contact forces (η = 0.508 kPa, ν = 0.33, γ̇ = 100 s−1 ). Deformation depends on the number of adhesive bonds. Here, approximately 30–40 tensile and compressive bonds have formed; (b) rigid cell does not experience deformation.
Figure 9.
Adhesion and contact forces vary with time and induce variation in interfacial contact area; γ̇ = 100 s−1. (a) Variation in contact area vs. non-dimensional time. For the more compliant cell (η = 0.508 kPa), average contact area was 6.1 µm2, while for the stiffer cell the average contact area was 1.9 µm2; (b) variation in contact area vs. contact force.
Figure 10.
Cell rolling velocity decreases as adhesive tractions increase; γ̇ = 100 s−1 . (a) Rolling velocity for rigid cell decreases with respect to time due to increasing adhesive interactions; (b) for compliant cell (ν = 0.33), rolling velocity decreased by approximately 28% compared to rigid cell as a result of increased contact area, leading to increased adhesive interactions (η = 0.508 kPa); (c) rolling velocity for stiffer cell was similar to that found for rigid case (η = 1 kPa).
Acknowledgement
This research was supported in part by Grant #15651 (D.J.G.) from the Office of the Vice President for Research (RIT) and by Grant HL018208 from the National Institutes of Health (M.R.K.). We would like to acknowledge Dr. Sangtae Kim for several useful discussions.
Glossary
Nomenclature
- x, X, X*
integration variable, source point, image point
- Gij (x, X)
Stokeslet or Kelvinlet
- Σijk (x, X)
associated stress tensor
- Kij,
double-layer, adjoint double-layer
- h
cell-cell separation distance
- F,Fo
force vector, parameter in repulsive force model
- T
torque, temperature
- kb
Boltzmann’s constant
unstressed off-rate, on-rate
- ro
reactive compliance
Greek Symbols
- σ
stress tensor
- μ
viscosity
- ν
Poisson’s ratio
- η
shear modulus
- τ
parameter in repulsive force model
- λ
equilibrium bond length
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest statement
No author has any conflict of interest to declare.
REFERENCES
- Alon R, Hammer DA, Springer TA. Lifetime of the P-selectin– carbohydrate bond and its response to tensile force in hydrodynamic flow. Nature (Lond) 1995;374:539–542. doi: 10.1038/374539a0. [DOI] [PubMed] [Google Scholar]
- Bell GI. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- Chang Y-I, Wang Y-F. A preliminary study on the initial elastic adhesion behavior of leucocytes. Coll. Surf. A: Physicochem. Eng. Aspects. 1998;140:395–401. [Google Scholar]
- Dong C, Cao J, Struble EJ, Lipowsky HH. Mechanics of leukocyte deformation and adhesion to endothelium in shear flow. Annals of biomedical engineering. 1999;27:298–312. doi: 10.1114/1.143. [DOI] [PubMed] [Google Scholar]
- Evans E, Heinrich V, Leung A, Kinoshita K. Nano- to microscale dynamics of P-selectin detachment from leukocyte interfaces. I. Membrane separation from the cytoskeleton. Biophys. J. 2005;88:2288–2298. doi: 10.1529/biophysj.104.051698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fröhlich H, Sack R. Theory of the rheological properties of dispersions. Proc. Roy. Soc. Lond. A. Math. Phys. Sci. 1946;185:415–430. doi: 10.1098/rspa.1946.0028. [DOI] [PubMed] [Google Scholar]
- Gao T, Hu HH. Deformation of elastic particles in viscous shear flow. J. Comp. Phys. 2009;228:2132–2151. [Google Scholar]
- Gee DJ, King MR. Year Multiparticle adhesion of deformable cells. 15th U.S. National Congress on Theoretical and Applied Mechanics; Boulder, CO. [Google Scholar]
- Goddard JD. An elastohydrodynamic theory for the rheology of concentrated suspensions of deformable particles. J. Non-Newtonian Fluid Mech. 1977;2:169–189. [Google Scholar]
- Hammer DA, Apte SM. Simulation of cell rolling and adhesion on surfaces in shear flow: general results and analysis of selectin-mediated neutrophil adhesion. Biophys. J. 1992;62:35–57. doi: 10.1016/S0006-3495(92)81577-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jadhav S, Chan KY, Konstantopoulos K, Eggleton CD. Shear modulation of intercellular contact area between two deformable cells colliding under flow. J. Biomech. 2007;40:2891–2897. doi: 10.1016/j.jbiomech.2007.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jadhav S, Eggleton CD, Konstantopoulos K. A 3-D computational model predicts that cell deformation affects selectin-mediated leukocyte rolling. Biophys. J. 2005;88:96–104. doi: 10.1529/biophysj.104.051029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadash KE, Lawrence MB, Diamond SL. Neutrophil string formation: Hydrodynamic thresholding and cellular deformation during cell collisions. Biophys. J. 2004;86:4030–4039. doi: 10.1529/biophysj.103.035782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khismatullin DB, Truskey GA. Three-dimensional numerical simulation of receptor mediated leukocyte adhesion to surfaces: Effects of cell deformability and viscoelasticity. Phys. Fluids. 2005;17:031505. [Google Scholar]
- Khismatullin DB, Truskey GA. Leukocyte Rolling on P-Selectin: A Three-Dimensional Numerical Study of the Effect of Cytoplasmic Viscosity. Biophys. J. 2012;102:1757–1766. doi: 10.1016/j.bpj.2012.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King MR, Hammer DA. Multiparticle adhesive dynamics. Interactions between stably rolling cells. Biophys. J. 2001a;81:799–813. doi: 10.1016/S0006-3495(01)75742-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King MR, Hammer DA. Multiparticle adhesive dynamics: hydrodynamic recruitment of rolling leukocytes. Proc. Natl. Acad. Sci. USA. 2001b;98:14919–14924. doi: 10.1073/pnas.261272498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King MR, Rodgers SD, Hammer DA. Hydrodynamic collisions suppress fluctuations in the rolling velocity of adhesive blood cells. Langmuir. 2001;17:4139–4143. [Google Scholar]
- Lee D, King MR. Hydrodynamic interactions between cells on reactive surfaces. In: King MR, editor. Principles of Cellular Engineering. Burlington: Academic Press; 2006. pp. 255–266. [Google Scholar]
- Lim CT, Zhou EH, Quek ST. Mechanical models for living cells-a review. J. Biomech. 2006;39:195–216. doi: 10.1016/j.jbiomech.2004.12.008. [DOI] [PubMed] [Google Scholar]
- Loewenberg M, Hinch EJ. Collision of two deformable drops in shear flow. J. Fluid Mech. 1997;338:299–315. [Google Scholar]
- Melder RJ, Munn LL, Yamada S, Ohkubo C, Jain RK. Selectin- and integrin-mediated T-lymphocyte rolling and arrest on TNF-alpha-activated endothelium: augmentation by erythrocytes. Biophys. J. 1995;69:2131–2138. doi: 10.1016/S0006-3495(95)80087-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melder RJ, Yuan J, Munn LL, Jain RK. Erythrocytes enhance lymphocyte rolling and arrest in vivo. Microvasc. Res. 2000;59:316–322. doi: 10.1006/mvre.1999.2223. [DOI] [PubMed] [Google Scholar]
- N’Dri NA, Shyy W, Tran-Son-Tay R. Computational modeling of cell adhesion and movement using a continuum-kinetics approach. Biophys. J. 2003;85:2273–2286. doi: 10.1016/s0006-3495(03)74652-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nasseri S, Phan-Thien N, Fan XJ. Lubrication approximation in completed double layer boundary element method. Comp. Mech. 2000;26:388–397. [Google Scholar]
- Pappu V, Bagchi P. 3D computational modeling and simulation of leukocyte rolling adhesion and deformation. Comp. Biol. Med. 2008;38:738–753. doi: 10.1016/j.compbiomed.2008.04.002. [DOI] [PubMed] [Google Scholar]
- Phan-Thien N, Fan XJ. A boundary integral formulation for elastically deformable particles in a viscous fluid. Z. Angew. Math. Phys. 1996;47:672–694. [Google Scholar]
- Phan-Thien N, Kim S. On the elastic double layer: Some exact solutions and the spectrum on the sphere. J. Mech. Phys. Solids. 1994;42:1177–1197. [Google Scholar]
- Phan-Thien N, Tullock D. Completed double layer boundary element method in elasticity. J. Mech. Phys. Solids. 1993;41:1067–1086. [Google Scholar]
- Phan-Thien N, Tullock D, Kim S. Completed double layer in half-space: a boundary element method. Comp. Mech. 1992;9:121–135. [Google Scholar]
- Power H, Miranda G. Second kind integral equation formulation of Stokes' flows past a particle of arbitrary shape. SIAM J. Appl. Math. 1987;47:689–698. [Google Scholar]
- Pozrikidis C. Finite deformation of liquid capsules enclosed by elastic membranes in simple shear flow. J. Fluid Mech. 1995;297:123–152. [Google Scholar]
- Rognon P, Gay C. Soft dynamics simulation. 1. Normal approach of two deformable particles in a viscous fluid and optimal-approach strategy. Eur. Phys. J. E: Soft Matter Biol. Phys. 2008;27:253–260. doi: 10.1140/epje/i2008-10378-3. [DOI] [PubMed] [Google Scholar]
- Rognon P, Gay C. Soft dynamics simulation. 2. Elastic spheres undergoing a T1 process in a viscous fluid. Eur. Phys. J. E: Soft Matter Biol. Phys. 2009;30:291–301. doi: 10.1140/epje/i2009-10528-1. [DOI] [PubMed] [Google Scholar]
- Rosenbluth MJ, Lam WA, Fletcher DA. Force microscopy of nonadherent cells: A comparison of leukemia cell deformability. Biophys. J. 2006;90:2994–3003. doi: 10.1529/biophysj.105.067496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tran-Cong T, Phan-Thien N. Boundary element solution for half-space elasticity or Stokes problem with a no-slip boundary. Comp. Mech. 1986;1:259–268. [Google Scholar]
- Villaggio P. The rebound of an elastic sphere against a rigid wall. J. Appl. Mech. 1996;63:259–263. [Google Scholar]
- Wankhede SP, Du Z, Berg JM, Vaughn MW, Dallas T, Cheng KH, Gollahon L. Cell detachment model for an antibody-based microfluidic cancer screening system. Biotechnol. Prog. 2006;22:1426–1433. doi: 10.1021/bp060127d. [DOI] [PubMed] [Google Scholar]