Water oxidation surface mechanisms replicated by a totally inorganic tetraruthenium–oxo molecular complex

Abstract

Solar-to-fuel energy conversion relies on the invention of efficient catalysts enabling water oxidation through low-energy pathways. Our aerobic life is based on this strategy, mastered by the natural Photosystem II enzyme, using a tetranuclear Mn–oxo complex as oxygen evolving center. Within artificial devices, water can be oxidized efficiently on tailored metal-oxide surfaces such as RuO₂. The quest for catalyst optimization in vitro is plagued by the elusive description of the active sites on bulk oxides. Although molecular mimics of the natural catalyst have been proposed, they generally suffer from oxidative degradation under multiturnover regime. Here we investigate a nano-sized Ru₄–polyoxometalate standing as an efficient artificial catalyst featuring a totally inorganic molecular structure with enhanced stability. Experimental and computational evidence reported herein indicates that this is a unique molecular species mimicking oxygenic RuO₂ surfaces. Ru₄–polyoxometalate bridges the gap between homogeneous and heterogeneous water oxidation catalysis, leading to a breakthrough system. Density functional theory calculations show that the catalytic efficiency stems from the optimal distribution of the free energy cost to form reaction intermediates, in analogy with metal-oxide catalysts, thus providing a unifying picture for the two realms of water oxidation catalysis. These correlations among the mechanism of reaction, thermodynamic efficiency, and local structure of the active sites provide the key guidelines for the rational design of superior molecular catalysts and composite materials designed with a bottom–up approach and atomic control.

Photocatalytic water splitting offers a bioinspired strategy for replacing fossil fuels with clean energy vectors (1–3). The overall reaction entails a sequence of light-promoted electron and proton transfers coupled with cleavage and formation of molecular bonds, ultimately splitting H₂O molecules into O₂ and H₂. The application of such technology for a viable solar-fuel economy is at the forefront of a very intense research effort. The main issue is the design and optimization of innovative catalysts enabling the half reaction of water oxidation (2H₂O → O₂ + 4H⁺ + 4e⁻) (1) at low overpotential, high turnover frequencies, and long-term operation stability. Considering its high thermodynamic cost [E⁰ = −1.23 V at pH = 0 vs. normal hydrogen electrode (NHE)] and mechanistic complexity, water oxidation catalysis (WOC) poses severe challenges for artificial photosynthesis applications.

In plants, water oxidation is catalyzed by the Mn₄CaO₄ oxygen evolving complex of Photosystem II (PSII) enzymes. The natural catalyst exhibits a functional asset of four redox active metal centers with adjacent μ–oxo bridges to enable water oxidation with a maximal turnover frequency of 400 s⁻¹ per O₂ molecule (4). The drawback lies in the intrinsic weakness of the biological components, requiring multiple repair strategies of both the inorganic core and the enzyme proteins. Similar stability issues due to oxidative damage during water oxidation affect most of the synthetic homogeneous molecular catalysts (5, 6).

In the artificial transposition of the natural process, the attention is actually focused on metal-oxide heterogeneous catalysts, which conjugate robustness and efficiency, with the most prominent examples being RuO₂, IrO₂, or cobalt phosphate (7, 8). In particular, RuO₂-based materials for electrocatalytic water oxidation have been the subject of intense investigation, including single- or polycrystalline systems (4, 9, 10), compact RuO₂ films, and composite oxides (4, 11, 12). The structure and composition of the active sites in these materials are strongly dependent on surface morphology, preparation, and doping conditions, which hinder the precise mapping of surface-absorbed species and/or detection of short-lived high-valent intermediates. As a result, the mechanism for water oxidation promoted by metal-oxide heterogeneous catalysts such as RuO₂ remains controversial. This translates into severe hurdles to fundamental studies of elementary steps and to their optimization in terms of rates and efficiency ultimately hampering the rational design of the light-absorption/conversion interface.

In this paper we identify a well-defined molecular analog to guide our understanding of the fundamental principles governing WOC at metal-oxide materials, while offering an unprecedented bridge between homogeneous and heterogeneous catalysis. Our perspective is based on the highly promising class of polyoxometalate (POM) catalysts, which comprise multinuclear metal–oxo cores embedded in totally inorganic molecular scaffolds. One of the most efficient and robust catalytic cores reported so far is a tetraruthenate oxo fragment [Ru₄O₄(OH)₂(H₂O)₄]⁶⁺ sandwiched between two inert polyoxotungstate ligands [Ru₄–POM; Fig. 1A], displaying a discrete and nano-sized structure.

Fig. 1.

(A) Structure of the Ru₄–POM in the resting state S₀. (B–F) Octahedral environment around one Ru center of Ru₄–POM, ligands involved in water oxidation and schemes of the corresponding electronic structure of the highest occupied molecular orbitals for the Ru–ligand moyeties.

Ru₄–POM has been shown to oxidize water in the homogeneous phase with small overpotential (0.35 eV), high turnover frequency (>450 h⁻¹), and no degradation (13, 14). By virtue of the molecular nature, when coupled to photogenerated oxidants, it displays photo-induced electron transfer rates in the nano/microsecond time domain (15), thus approaching the natural paradigm, while preserving its activity also when it is interfaced with functionalized carbon nanotubes (16).

Our combined computational and spectroscopic study traces a parallel scenario of water oxidation at molecular Ru₄–POM and crystalline RuO₂ surfaces. We identify the thermodynamic origins and kinetic pathways governing the high efficiency of the molecular Ru₄–POM and demonstrate that its elementary tetraruthenate–oxo fragment complies with the same optimal thermodynamic requirement for water oxidation displayed by crystalline RuO₂ surfaces. Disclosing the atomistic origins of the high catalytic efficiency and stability of the molecular analog opens the way for a predictive catalyst upgrade and its integration in innovative photosynthetic materials.

Results and Discussion

Ru K-Edge X-Ray Absorption Spectroscopy Analysis.

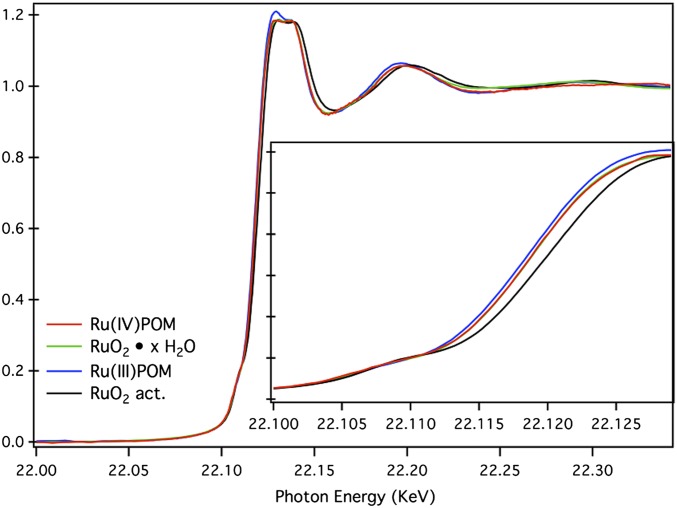
We begin by demonstrating that the local atomistic and electronic structures of the metal centers in molecular Ru₄–POM and crystalline RuO₂ surfaces are equivalent. X-ray absorption near edge spectroscopy (XANES) has been performed at Ru K-edge on Ru₄–POM as isolated crystals of the cesium salt, exhibiting all Ru(IV) centers [Ru(IV)POM in Fig. 2], on a related Ru(III) complex [Ru(H₂O)SiW₁₁O₃₉]⁵⁻, and on hydrous ruthenium oxide as prepared (RuO₂⋅xH₂O) and after thermal activation (RuO₂ act.) at 150 °C for 5 h. The latter is a key treatment for enhancing the catalytic properties of RuO₂ crystals.

Fig. 2.

XANES spectra at the Ru K edge for different Ru₄–POM [Ru(IV)POM (red) and Ru(III)POM (blue)], RuO₂ hydrous (green), and thermally activated (black). The inset shows the pre-edge and edge region of the spectra.

The XANES spectra (Fig. 2) have been recorded, for solid samples, on the XAFS beamline at the Elettra synchrotron source. The Ru(IV)POM and hydrous RuO₂ display identical XANES edge and line shape. The edge position is known to depend on the ruthenium oxidation state, shifting to higher photon energy as the valence state increases (17, 18). It can be concluded that the Ru ions in the two materials have the same Ru(IV) oxidation state. These data compare well with those reported for related Ru(IV) systems (18). Instead, the main absorption edge of Ru(III)POM is shifted to lower photon energies (by 2 eV), which is consistent with a lower oxidation state of Ru. It is worth noting that the pre-edge feature is practically the same for all of the samples. Moreover, the absence of adventitious Ru(III) species and or mixed valence states is evident from the position of the first absorption edge and from the line shape of the first absorption peak [note that in Ru(III)POM, the first structure is higher than the second one]. This is consistent with a silent EPR behavior of the freshly isolated crystals (19).

In addition, X-ray diffraction spectra shows that the Ru(IV) ions in both the Ru₄–POM and RuO₂⋅xH₂O materials have the same RuO₆ octahedral local environment with the same average Ru–O bond length, 1.98 Å (SI Text and Table S1). To complete the analogy, note that every Ru center of the Ru₄–POM core coordinates a water ligand and can be viewed as a minimal, highly hydrated, RuO₂ nanocrystal. Interestingly, thermally activated RuO₂ shows a shift of the peaks in the main absorption edge to higher photon energy, suggesting the evolution to less hydrated or anhydrous materials, with changed structure, in agreement with literature observation (20).

Reaction Intermediates and Thermodynamics.

The equivalence in the short-range atomistic and electronic structures of the molecular and bulk ruthenium–oxide catalysts is validated by our density functional theory (DFT) calculations. These predict a distorted octahedral geometry around the Ru metal centers in the Ru₄–POM active core (21) in excellent agreement with experimental data (SI Text and Table S1) and similar to the one of RuO₂ crystalline surfaces. In the absence of an applied potential or without oxidants in solution, the calculations show that every Ru atom of the Ru₄–POM is in oxidation state IV and coordinates a water ligand, thus resulting in four Ru(IV)–H₂O groups (Fig. 1A) (13, 14, 21). In this configuration, the d⁴ electrons formally residing on the metal ion in the Ru(IV)–H₂O moiety occupy the t_2g-like orbitals with two unpaired spins (Fig. 1B). This reference structure is denoted as S₀.

From this resting state, we perform a thermochemical analysis of water oxidation adopting the computational method proposed by Norskov and coworkers (22, 23). We aim at identifying the four Ru₄–POM intermediates (S_i, Fig. 3) that, through a cycle of four stepwise proton-coupled electron-transfer oxidations (PCET), make the formation of the O–O bond and the release of O₂ thermodynamically favorable.

Fig. 3.

(Upper) Calculated free energy of the four catalytic cycles for water oxidation at increasing oxidation state of Ru₄–POM. Black dots represent the available experimental values (19). Only C and D satisfy the thermodynamic requirements for water oxidation (dashed horizontal line). (Lower) Scheme of the tetraruthenium–oxo core in S₀ and description of reaction intermediates S_i.

The first cycle we consider begins from S₀ and involves all of the four Ru sites of the Ru₄–POM core: S₀ → S₄ + 4H⁺ + 4e⁻ (see cycle A in Fig. 3). The first oxidation of S₀ leads to the formation of one Ru(V)–OH moiety (Fig. 1C) according to Ru(IV)–H₂O → Ru(V)–OH + H⁺ + e⁻. We denote this state as S₁. The oxidized Ru(V) d³ ion has three unpaired electrons in the t_2g-like orbitals. The successive three oxidations via PCET steps transform the other Ru(IV)–H₂O groups of S₁ into the Ru(V)–OH ones of S₂, S₃, and S₄ states (cycle A in Fig. 3).

The energetics of these four initial oxidation steps is shown in Fig. 3 (cycle A, S₀ − S₄). The calculated values of the free energy differences (ΔG) are in very good agreement with the available experimental data (black circles) (Note that only the S₀−S₃ portion of the cycle is accessible experimentally) (19). This validates the high accuracy of the present computational approach [Becke 3 Lee Yang Parr (B3LYP) functional] for predicting the reaction thermodynamics. It turns out that the calculated ΔG for the S₀/S₄ couple is 3.38 eV (green line in Fig. 3), which is 1.18 eV below the thermodynamic limit for water oxidation (dashed line in Fig. 3) (While the experimental value the free energy change at standard conditions associated to the reaction 2H₂O→O₂+2H₂ is 4.92 eV, the B3LYP value, including zero point energy corrections and entropic contributions is 4.56 eV. Consistently, we will compare our B3LYP results for the energetics of the intermediates with this value rather than the experimental one. ). This indicates that promoting water oxidation requires catalyst oxidation states higher than S₄. It therefore rules out cycle A, which involves the simultaneous participation of the four Ru centers of the Ru₄–POM core.

Further oxidation of S₄ to S₅ leads to the formation of one formal Ru(VI)–oxo moiety (Fig. 1D) via the reaction Ru(V)–OH → Ru(VI)–O + H⁺ + e⁻. S₅ is the highest valent intermediate in the the S₁/S₅ catalytic cycle B (Fig. 3), which entails only three Ru centers. This PCET step changes the spin density localized at the Ru atom, from 1.9 (in Ru–OH) to 1.0 (in Ru–O), and a net spin polarization appears on the oxo ligand. Note that on the basis of the charge and spin analysis, it is not possible to unambiguously associate the Ru–O moiety to a Ru(VI)–oxo or to a Ru(V)–oxyl radical (Table S2). The oxyl radical, however, has been proposed to be a key intermediate in catalytic water splitting by ruthenium complexes as in the “blue dimer” (24, 25) and also for the oxygen evolving complex of PSII (26). Similarly to cycle A, also the calculated free energy of cycle B (4.21 eV) is well below the thermodynamic limit for splitting water (Fig. 3).

The calculated thermodynamics predict that water oxidation can only be promoted by the higher valent Ru₄–POM intermediates emerging in catalytic cycles C or D (Fig. 3). These cycles require the active participation of two and one Ru centers, respectively. The computed free energy difference for both the S₂/S₆ and S₃/S₇ couples is 4.82 eV. In both these cycles, the most demanding oxidation is the formation of the first oxo moiety (S₄ → S₅, ΔG = 1.53 eV), while a lower energy cost is required to form the second Ru–oxo group (S₅ → S₆, ΔG = 1.31 eV).

In the Nørskov approach, kinetic barriers separating the intermediate states are neglected, and the overpotential is approximated by the free energy cost of the most demanding oxidation step along the cycle. In this framework, the reaction overpotential of both cycles C and D is determined by the formation of the first Ru–oxo moiety, and can be computed as η = ΔG(S₄ → S₅) – ΔG(H₂O)/4= 0.39 eV, and is in excellent agreement with the experimental value of 0.35 eV (16). Here ΔG(H₂O) is the free energy change for the reaction 2H₂O → O₂ + 2H₂ at pH = 0 and room temperature.

Reaction Mechanisms for Water Splitting and O₂ Evolution.

Once the catalyst has reached the activated intermediate capable of oxidizing water (S₆), the reaction can then proceed with the key O–O bond formation step (Fig. 4). There are several possible mechanisms for this step, either intramolecular (e.g., involving an oxo ligand and an O atom of the metal-oxide core) or intermolecular (e.g., a nucleophilic attack on the Ru–oxo moiety by a solvent water molecule). The direct formation of the O–O bond from two oxo ligands in the same or in neighboring Ru₄–POM molecules can be excluded on the basis of the very large distance between the two oxo atoms in the core (> 5.26 Å) and of the reaction kinetics, respectively (13).

Fig. 4.

Free energy diagram for cycles C and D with a schematic representation of the reaction intermediates. ΔG(H₂O) is the free energy change in the reaction 2H₂O → O₂ + 2H₂ at pH = 0 and room temperature.

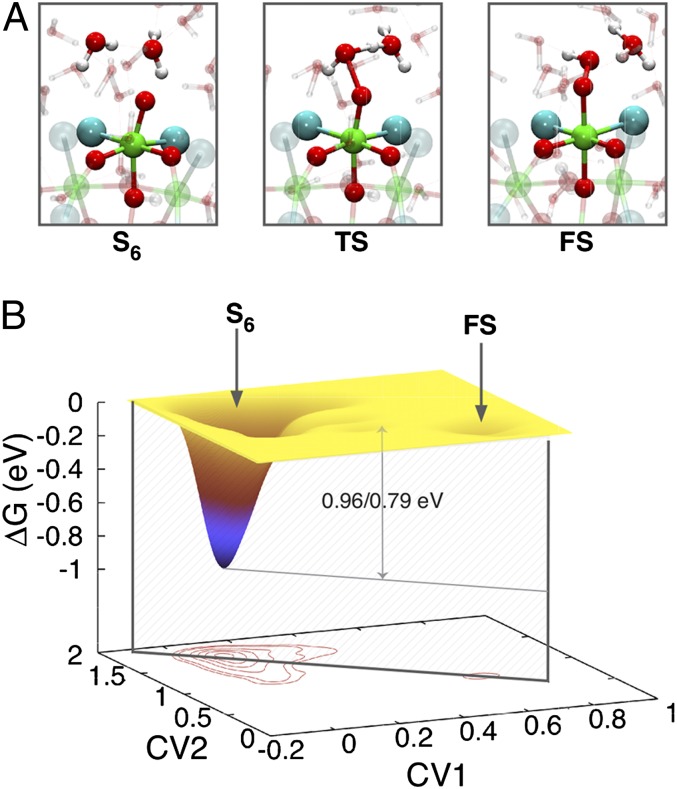
The lowest energy path for the O–O bond formation at one of the two Ru–oxo moieties of S₆ was determined by metadynamics calculations (27) using as collective variable (CV) the coordination number of the oxo ligand with any other O in the system, either from the solvent or from the catalyst (Figs. S1 and S2 and other details in SI Text). This CV allows us to capture both the intra- and intermolecular mechanisms introduced above. This metadynamics simulation predicts that the O–O bond is preferentially formed via an intermolecular mechanism (Fig. 5A). It consists in the nucleophilic attack on the Ru–oxo moiety by a solvent water molecule, which evolves to a hydroperoxo ligand and liberates a proton in solution. This path is energetically more favorable than any intramolecular reaction mechanism (SI Text). Indeed the electronic structure of the catalyst shows the presence of low-energy empty states localized around the Ru–oxo moiety, suitable for a nucleophilic attack by water (Fig. S3).

Fig. 5.

Reaction mechanisms for water splitting and O–O bond formation. (A) Nucleophilic attack: Initial (S₆), transition (TS), and final states (FS). (B) Free energy surface of the reaction as a function of the two CVs reconstructed from the metadynamics simulation. The two activation energies refer to the PBE/B3LYP functionals, respectively.

To estimate the reaction barrier more precisely, the metadynamics simulation described above was refined by a second calculation. This time two CVs were biased: (i) the coordination number of one of the oxo ligands with the oxygen atom of the water molecule involved in the nucleophilic attack (CV1) and (ii) the coordination number of the oxygen atom of this water molecule with its two hydrogens (CV2). The free energy landscape as a function of these CVs is displayed in Fig. 5B. It shows that the nucleophilic attack proceeds via a concerted mechanism, in which the formation of the O–O bond and the deprotonation of the solvent water molecule happen concurrently (Fig. S2), in analogy with what has been proposed for single-center Ru complexes (28).

Of the two Ru–oxo groups initially present in the activated S₆ state, one converts to Ru–OOH via nucleophilic attack (as shown in our metadynamics), the other to Ru–OH by a proton transfer. In the resulting 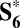intermediate (Fig. 4), all of the Ru atoms are in oxidation state V (spin density analysis in Table S2).

These simulations predict an activation energy of 0.96 eV [Perdew–Burke–Ernzerhof (PBE) functional]. Single point B3LYP calculations of two configurations representing the initial and transition states allow us to refine the free-energy barrier to 0.79 eV. By inserting this value in an Arrhenius-type equation, assuming a prefactor of 10¹³ s⁻¹ and room temperature, we estimate a turnover frequency of 0.4 s⁻¹, which is in good agreement with the experimental rate, 0.12 s⁻¹ at pH = 0 (13). On RuO₂, for the same non-Faradaic step leading to the formation of the OOH ligand, Fang et al. estimated the activation barrier to decrease linearly with the applied bias (29), with a slope consistent with the experimental Tafel slope. Extrapolating their results to zero bias one obtains a barrier of 0.74 eV, in the same range as our activation energy, suggesting similar kinetic requirements for the formation of the O–O bond in both systems.

By analyzing the final state predicted by these metadynamics simulations (Fig. 5A), we conclude that the relevant precursor of O₂ evolution is the hydroperoxo ligand of 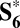(Fig. 1E). Its formation is slightly endothermic, ΔG = 0.16 eV, as shown by the calculated thermodynamics for the 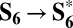step (Fig. 4). Once the hydroperoxo has been formed, the reaction cycle is downhill in energy and does not involve any net transfer of electrons or protons to the electrode or solution (dashed blue line in Fig. 4). Therefore, an external potential is not required to close cycle C.

Oxygen evolution from the hydroperoxo intermediate entails two further steps. First, one of the Ru(V)–OH is converted back to a Ru(IV)–H₂O through the migration of a proton and an electron from the hydroperoxo ligand. This leads to a 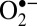superoxo bound to the Ru(V) center (S₈ in Figs. 4 and 1F). Then, an electron transfers from the superoxo to the neighboring Ru ion, and the resulting O₂ ligand is exchanged with a solvent water molecule. This leads to O₂ evolution and to the S₂ intermediate, thus closing the catalytic cycle. Overall, the proton exchange and O₂ evolution steps are exothermic by –0.05 and –0.20 eV, respectively.

Atomistic and Thermodynamic Origins of Catalytic Efficiency: Unifying Concepts in WOC.

The formation of the key hydroperoxo intermediate through the 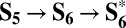sequence could also be envisioned as a single PCET step coupled to the nucleophilic attack (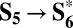, ΔG = 1.47 eV; Fig. 4). This is the same mechanism of water oxidation proposed for ideal metal and metal-oxide surfaces (30–32).

The similarity between the homogeneous and heterogeneous reaction mechanisms becomes even more evident by considering the 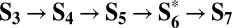path (cycle D in Fig. 3), which is energetically equivalent to the 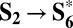one (cycle C) described above. Cycle D involves the same four PCET steps proposed for metal-oxide surfaces (32):

and

In both the crystalline RuO₂ and molecular Ru₄–POM cases (cycle D), the oxygen evolution cycle takes place at a single ruthenium site. It involves the hydroxo (OH*), oxo (O*), and hydroperoxo (OOH*) intermediates, which are formed electrocatalytically, and the formation of the O–O bond proceeds through the nucleophilic attack of a water molecule. This analogy sheds light on the origins of the efficiency of the Ru₄–POM complex and provides a unifying scenario governing water oxidation at molecular and crystalline metal-oxide catalysts.

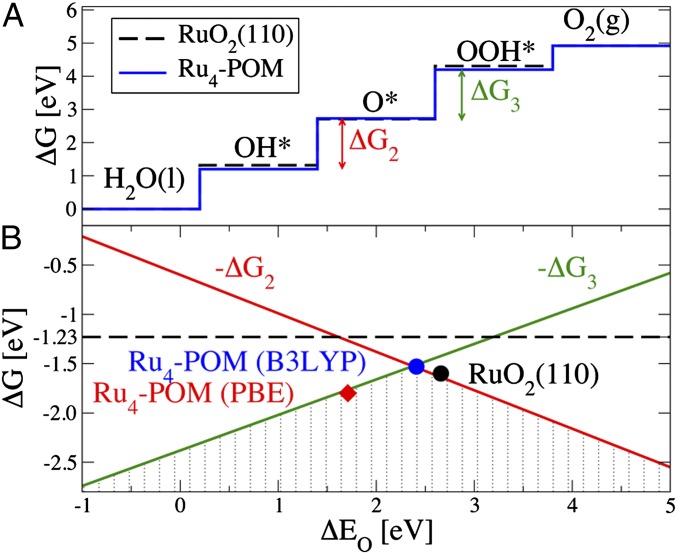
In the theory of surface catalysts, maximum thermodynamic efficiency is achieved by thermodynamic stairways of metal-based intermediates that equally distribute the free energy of water oxidation (4.92 eV at pH = 0) among the four elementary steps of Eqs. 1–4. In this way the same minimal potential (1.23 V at pH = 0, NHE) can drive all of the PCET steps, avoiding thermodynamic barriers due to uneven stability of some intermediates. For a wide class of crystalline metal and metal-oxide surfaces, the binding energies of metal-aquo/hydroxo and oxo species are shown to depend linearly one to another (32, 33). As a result, the free energy of each oxidation (ΔG_i in Eqs. 1–4) can be expressed as linear functions of the oxygen binding energy (ΔE_O), which is taken as the reaction descriptor (32). [This linear dependence has also be shown to lead to ΔG₂ + ΔG₃ = 3.2 ± 0.2 eV (33). Multi-site mechanisms, favored for proximal metal-group interactions and leading to intramolecular O–O coupling, would not obey the linear relationships described above and could thus brake the predicted 3.2 eV constraint.]

Fig. 6 reports the free energies for the two most demanding oxidations steps—the formation of the oxo (ΔG₂) and of the hydroperoxo (ΔG₃) intermediates—as a function of ΔE_O. The resulting volcano plot (shaded area) determines the thermodynamic overpotential (i.e., the largest ΔG_i) for a given value of the descriptor ΔE_O. The thermodynamic requirements at the top of the volcano plot (ΔE_O such that ΔG₂ = ΔG₃) set the optimal catalyst with the smallest overpotential (32). Extended screening of metal-oxide crystalline surfaces show that RuO₂(110) surfaces satisfy well these optimal thermodynamic requirements [black dot in Fig. 6; data from ref. 33 obtained using the restricted PBE (RPBE) functional for an O-covered surface]. [The black dot in Fig. 6 corresponds to the RuO₂–3O structure in (32), where O ligands are present at three out of four Ru surface sites. The oxygen adsorption energy is strongly influenced by the surface coverage: as the coverage is reduced, oxygen is more strongly bound and the corresponding point on the volcano moves to left (32).] This rationalizes why this material is among the ones displaying the smallest, albeit finite, overpotential (33).

Fig. 6.

(A) Free energies of the four PCET steps (reactions 1–4) for water oxidation on the crystalline RuO₂ surface (black line) and Ru₄–POM (blue). (B) Negative of free energy cost of the most demanding oxidation steps (ΔG₂ and ΔG₃) as a function of the oxygen binding energy (ΔE_O). The shaded area (volcano plot) sets the overpotential for a given value of ΔE_O.

Our calculations show that Ru₄–POM perfectly complies with the set of linear relationships established for metal oxide surfaces and is almost on top of the volcano, in close proximity with RuO₂(110) surfaces (Fig. 6). This is a clear indication that the tetraruthenate–oxo core of this molecular catalyst can be viewed as an elementary RuO₂ unit, promoting the same reaction mechanism as the parent oxide, with very similar overpotential as shown both experimentally and theoretically. In Fig. 6 we report for Ru₄–POM both data obtained with the B3LYP and PBE functionals. While for this system the use of different functionals results in significant differences in the energetics (with only hybrid functionals being able to accurately reproduce the experimental overpotential and the free energy change of the S₀ → S₃ transformation) (21), both data points lie on the volcano plot. This suggests that the linear relationships established using one particular functional (RPBE) (32) might be of general application.

Single- vs. Multisite Mechanisms by Molecular Cores.

The thermodynamic equivalence of the two reaction pathways shown in Fig. 4 suggests that the efficiency of multicenter metal–oxo cores is not necessarily determined by multisite mechanisms involving oxidation of several metal centers of the core. Instead, the minimum overpotentials can be achieved also by reaction pathways in which a single metal site within the tetraruthenium core promotes a multielectron process, like cycle D for the Ru₄–POM. In this cycle, the nonparticipating sites remain in the Ru(V)–OH state. While metal oxidation states on the bulk material have hardly been discussed, this observation traces a parallel between cycle D and water oxidation on fully hydroxylated RuO₂ surfaces, which are predicted to be stabilized under applied bias (29, 32).

Indeed a single-site Ru–POM molecule was recently shown to catalyze the oxidation of water in the homogeneous phase (34), suggesting that cycle D could be a common mechanism at play on both single- and multicenter catalysts. Although the thermodynamic efficiency of the Ru₄–POM can be controlled by only one or two sites, the presence of multiple metal centers clearly plays an important function, as shown by the significantly superior performance of Ru₄–POM (13, 14) compared with the single center catalysts (34). The difference in their efficiency is likely to arise from the local environment around the active sites, shaped and reinforced by the metal–oxo connectivity among them. This, together with the thermodynamic analogy between the homogeneous Ru₄–POM and the heterogeneous metal–oxo surfaces presented above, suggests that the Ru–O connectivity in the tetraruthenium–oxo core could be enough to mimic, at the active site, the structural and electronic effects of an extended RuO₂ surface.

In conclusion, we show that the efficiency of the Ru₄–POM complex, a unique tetranuclear water-oxidation catalyst, stems from thermodynamic and kinetic origins that are common to extended metal–oxide surfaces. The stepwise oxidation of the tetraruthenate core is instrumental to activate a single Ru–oxo moiety, triggering the water nucleophilic attack and O₂ release. The overpotential is minimized because the ruthenium centers can catalyze the formation of the oxo and hydroperoxo key intermediates with an almost identical cost, within the molecular tetrarutenium–oxo cores and on extended RuO₂ surfaces.

We identify a parallel scenario of water oxidation between two efficient classes of homogeneous and heterogeneous inorganic catalysts. The core of Ru₄–POM can be viewed as an optimal RuO₂ cluster in which every metal center is exposed to the solvent, thus exhibiting the highest surface area for catalysis. Although not directly involved in the chemical reaction, the metal spectators play a crucial role, providing the electronic stabilization for the building-up of a high-valent ruthenium–oxo site, capable of water oxidation. In the same environment, the hydroperoxo intermediate is also produced at low thermodynamic and kinetic cost for the overall cycle. Understanding the guidelines to enhance such interplay between the performance of the catalyst and local atomic environment around the active site will be crucial for the design of the next generation catalysts: molecules working as activated surfaces.

Materials and Methods

Simulations were based on DFT, using CP2K code (35). Our previous benchmarks (21) show that unrestricted B3LYP/aug–triple zeta valence double polarized (TZV2P) provides an accurate description of the energetics of the reactions, with errors of the order of 0.1 eV per PCET step. The thermodynamics of the catalytic cycle was studied with the Norskov protocol (22), which has already been applied to study water oxidation (30–32) and oxygen reduction (22) on metal and metal–oxide surfaces. Details on the application of this methodology to Ru₄–POM can be found in ref. 21. To reduce the computational cost of hybrid functional calculations, the energy differences among the various intermediates are evaluated on the simplified Ru₄–Cl model first (where POM ligands are substituted with Cl⁻ ions; ref. 21; SI Text and Fig. S4). The small contribution to the energy differences introduced by the presence of the POM ligands is evaluated at the PBE level (21). All calculations for the thermodynamics of the catalytic cycle are performed in vacuum, since solvent effects on the energetics of PCET reactions for this system have been shown to be negligibly small (21).