Phase geometries of two-dimensional excitable waves govern self-organized morphodynamics of amoeboid cells

Abstract

In both randomly moving Dictyostelium and mammalian cells, phosphatidylinositol (3,4,5)-trisphosphate and F-actin are known to propagate as waves at the membrane and act to push out the protruding edge. To date, however, the relationship between the wave geometry and the patterns of amoeboid shape change remains elusive. Here, by using phase map analysis, we show that morphology dynamics of randomly moving Dictyostelium discoideum cells can be characterized by the number, topology, and position of spatial phase singularities, i.e., points that represent organizing centers of rotating waves. A single isolated singularity near the cellular edge induced a rotational protrusion, whereas a pair of singularities supported a symmetric extension. These singularities appeared by strong phase resetting due to de novo nucleation at the back of preexisting waves. Analysis of a theoretical model indicated excitability of the system that is governed by positive feedback from phosphatidylinositol (3,4,5)-trisphosphate to PI3-kinase activation, and we showed experimentally that this requires F-actin. Furthermore, by incorporating membrane deformation into the model, we demonstrated that geometries of competing waves explain most of the observed semiperiodic changes in amoeboid morphology.

Many moving cells are amoeboid—i.e., their shape is roundish, irregular, and constantly changing to facilitate cell migration and phagocytosis (1–3). During directional cell movement, cells become polarized by forming the leading edge enriched in F-actin/phosphatidylinositol (3,4,5)-trisphosphate (PIP3)/PI3-kinase at the front and by forming the retracting trailing edge at the rear enriched in myosin II/phosphatidylinositol (4,5)-bisphosphate (PIP2)/phosphatase and tensin homolog (PTEN) (4). The patterning of signaling activities is initiated by chemoattractant-mediated activation of small GTPases and PIP3 synthesis. Such asymmetric localizations of PIP3 and F-actin, however, are also known to occur spontaneously even in the absence of chemoattractant gradient (5). It has been proposed that there are feedback loops from F-actin to PI3-kinase and from PIP2 to PTEN that amplify small differences to break the symmetry (5–7). These spontaneous dynamics potentially underlie the random motility and searching behaviors of freely moving amoeboid cells, and they could also bias directional sensing and chemotaxis.

In neutrophils, macrophages, and amoebae such as Dictyostelium, the shape of an entire cell sometimes exhibits cycles of change that are spatially and temporally ordered yet complex (8–11). Although many of the molecular mechanisms underlying actin assembly are known, how they give rise to these patterns is not well understood. In both randomly moving Dictyostelium (12–15) and mammalian cells (7), transient local syntheses of PIP3 and F-actin propagate as waves at the substrate-attached cytosolic side of the membrane. Because the phosphatidylinositol wave induces a large-scale protrusion when reaching the cell edge, it dictates timing and direction of large-scale membrane deformation (16). The localized patterns of signaling molecules and cytoskeleton that form the propagating waves resemble the phagocytic cup structure (17), and it has been proposed that the cells are scanning the glass surface for particle intake (18). Theoretical analysis has also shown that direction sensing could be biased by this spatiotemporal patterning (6, 19). Thus, the dynamics of PIP3/F-actin waves serve as a model to analyze the mechanisms and function of spontaneous large-scale cytoskeletal organization and membrane deformation (20).

The PIP3/F-actin waves in Dictyostelium are a transient de novo formation of dendritic F-actin networks that is relayed from one location to its neighbor at the cytoplasmic face of the substrate-attached cell membrane (20) (Fig. 1A, Figs. S1A and S2A, and Movie S1A). The wavefront composed of F-actin and other components associated with the leading edge of chemotactic cells such as the Arp2/3 complex (13) and PIP3 (14) propagates through the “default” basal state enriched in molecules characteristic of the side and the rear of polarized cells such cortexillin I (16), ElmoA (21), and PTEN (22). The wavefront is also accompanied by localization of PI3-kinase (Fig. S1B) and reduction in the level of PIP2 and its binding partner PTEN (22) (Fig. S1 A and B), indicating that initiation and propagation of PIP3 waves accompany consumption of its substrate PIP2. It has been described that there are distinct wave patterns and that the cells spontaneously make a transition from one form to another (22). Exactly what characterizes these forms, how their transitions are determined, and how they are related to the ordered patterns of cell deformation (11) remain unclear. To understand the geometry of the waves and their transition rules, here we use a phase-map analysis and demonstrate that interaction between waves follows the characteristic phase response property of excitatory waves. We show that spontaneous nucleations of waves compete with one another and give rise to spatial phase singularity that supports spiral waves, which in turn provides rotational membrane extension. Furthermore, by studying a simplified kinetic model coupled to membrane deformation, we see that the complex transitions between different modes of morphology dynamics can be understood under a unified framework.

Fig. 1.

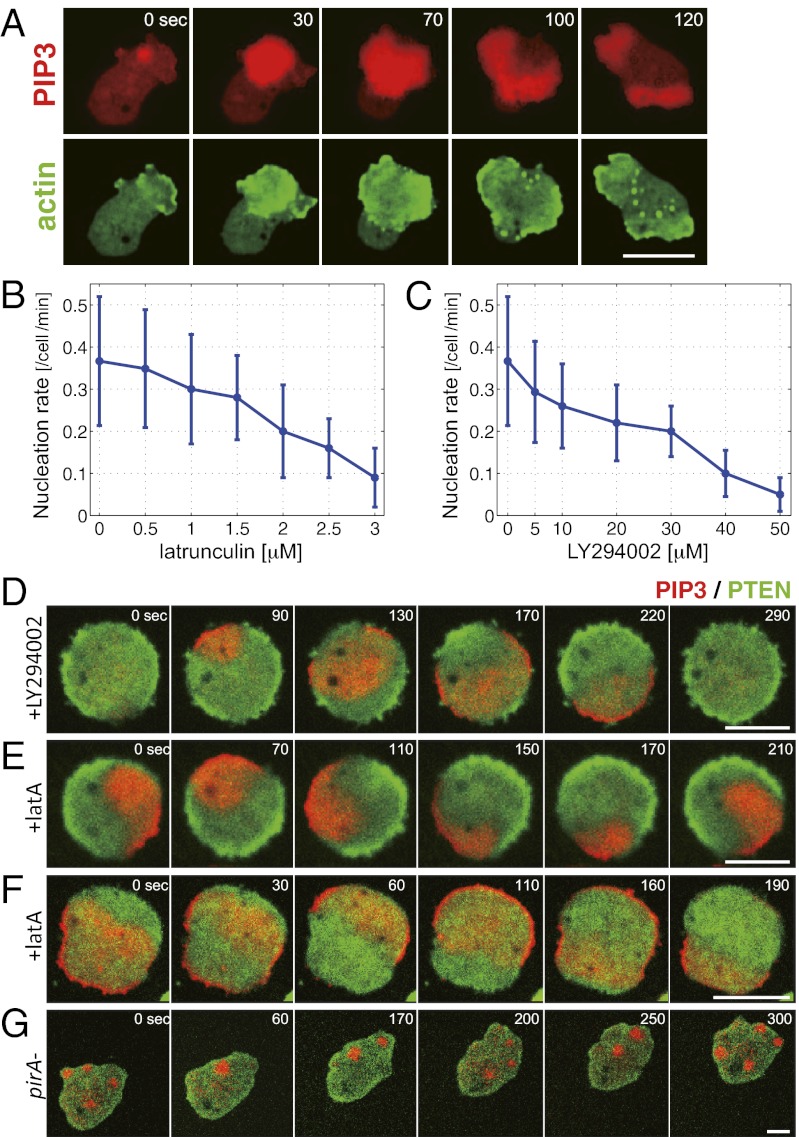
Inhibition of actin polymerization or PI3Kinase activity reduces the rate of wave nucleation and simplifies the wave patterns. (A) PIP3 (PHcrac-RFP) and F-actin (LimEΔCoil-GFP) waves at the basal membrane. (B and C) Wave nucleation rate depended on F-actin and PI3Kinase. Wave nucleation was suppressed in cells treated with latrunculin A (B) and PI3Kinase inhibitor LY294002 (C) in a dose-dependent manner. (D–G) Wave patterns in pharmacologically treated cells and a pirA⁻ cell. (D) Transient waves were observed in cells treated with 60 μM LY294002. Rotational (E) and reflecting (F) waves were observed in cells treated with 5 μM latrunculin. (G) Sporadic localized accumulation of PIP3 in a pirA⁻ cell. Red and green colors indicate fluorescence intensity of PH-cracRFP and PTEN-GFP, respectively. (Scale bars: 5 μm.)

Results and Discussion

Inhibition of F-Actin and PI3-Kinase Simplifies the Complex Wave Geometry by Reducing the Rate of Wave Nucleation.

Fig. 1A shows representative waves of PIP3 and F-actin that propagated together at the cytosolic side of the substrate-attached membrane in Dictyostelium cells (Movie S1A, SI Materials and Methods, and SI Text). Although earlier studies have studied these waves in cells recovering from inhibition of actin polymerization (23), we were able to observe these waves also in nontreated cells plated from suspension culture during growth and the early starvation stage before they become highly polarized (12, 14). Waves were restricted at the basal cell membrane (Fig. S2A) and appeared every 3–5 min (Fig. S2 B and C and Movie S1B). When these waves reach the border it promotes membrane extensions (16) (Fig. S1 C and D). One of the key determinants of the geometry of membrane extension is thus when and where the waves are initiated and what determines their frequency. Local accumulations of PIP3 at random locations were observed together with reduction in PTEN (Fig. S2D). A recent study (24) suggested PTEN depletion proceeds a few seconds ahead of PIP3 accumulation. These events appear almost simultaneously in the time resolution (10-s interval) of the present analysis. A marked F-actin accumulation was observed only when the localized enrichment of PIP3 grew in size for an extended period (Fig. S3 A and B) and gave rise to a propagating wave (Fig. S3C), an event hereafter referred to as wave nucleation. When cells were mildly treated with latrunculin A, an inhibitor of actin polymerization, PIP3 waves continued to propagate in the absence of F-actin waves (Fig. S3D). Under such conditions, occurrence of new waves was reduced by about 50% (Fig. 1B). These results suggest that F-actin facilitates PIP3 wave nucleation in keeping with earlier observations that actin waves follow local PIP3 accumulation (17). A similar decrease in the nucleation rate was observed for cells treated mildly with PI3-kinase inhibitor LY294002 (Fig. 1C). F-actin and PIP3 waves were suppressed altogether in cells treated with increased dosage of latrunculin/LY294002 or in cells lacking PI3K1/2 (Fig. S3E). Combined with our observation that transient localization of PI3-kinase to the membrane always traveled together with the PIP3 waves (Fig. S1B and Movie S1D), the results indicate that spatially and temporally regulated metabolism of PIP3 is the primary driving force for the self-organizing waves.

To deconstruct the complex wave patterns in randomly moving cells, we took advantage of the fact that in cells mildly treated with latrunculin and LY294002, nucleation of PIP3 waves was suppressed. Under these conditions, a wavefront traveled for an extended period before being disrupted by a newly formed wave (Fig. 1 D–F). In LY294002-treated cells, waves appeared periodically as planar waves that propagated from one end to the other (Fig. 1D). On the other hand, waves in latrunculin-treated cells were self-sustaining waves of two distinct forms. One was a rotational wave that propagated in either a clockwise or an anticlockwise direction at a period of about 3.5 min (Fig. 1E and Movie S2A). These waves switched direction of their rotation occasionally. The other wave geometry was of a reflection type that appeared as a translational wave propagating toward the cell border in alternating directions of 180° angle (Fig. 1F).

Phase-Map Analysis Reveals Birth and Death of Spatial Phase Singularities.

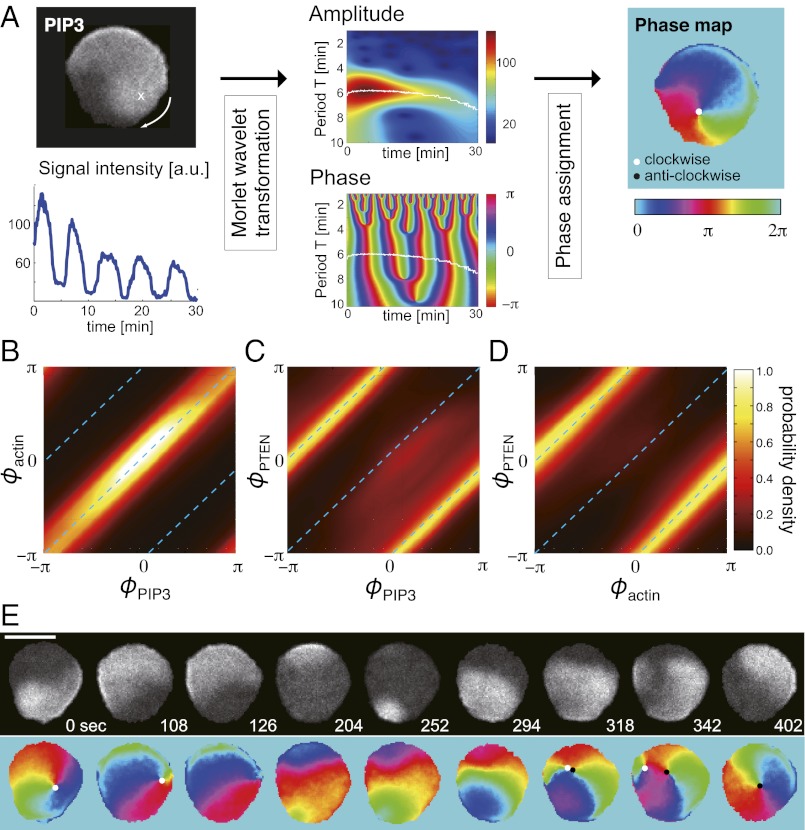
To examine 2D dynamics of the wave geometry in detail, we analyzed phase of PIP3 oscillations. To this end, we used a ridge extraction method with Morlet wavelet transformation, which effectively eliminates photobleaching and short-time noise effects (25) (Fig. 2A and SI Materials and Methods). By mapping PIP3 wave amplitude to phase, one can easily distinguish the front and the back of the wave as depicted in Fig. 2A. Phases of PIP3 and F-actin waves coincide at most spatial-time points as expected (Fig. 2B). Similar analysis for PIP3 and PTEN shows a clear antiphase relation (Fig. 2C). Consistently, the phases of F-actin and PTEN are also in antiphase relation (Fig. 2D). At the center of a rotational wave, we identified a spatial phase singularity (26–28) that represents the core of a self-sustaining spiral wave (Fig. 2A, Right). Detailed analyses of spatial phase singularities revealed that their birth and death are the key underlying process behind transitions between the wave patterns. Fig. 2E shows a representative example of the switch in the direction of spiral wave propagation observed in cells treated with latrunculin. For the sake of analysis, we computed the topological charge of a phase singularity to define the direction of the wave rotation: +1 is clockwise and −1 is anticlockwise (SI Materials and Methods). Phase singularities exhibited considerable meandering and disappeared when reaching the edge (Fig. 2E, 126 s). After the phase singularity disappeared, nucleation of a new wave occurred followed by birth of a pair of phase singularities of opposite topological charges (Fig. 2E, 204–318 s). These singularities competed for dominance until one reached the cell border and disappeared (Fig. 2E, 342–402 s). If the new singularity that survived by chance had an opposite charge as shown in this case, the resulting new wave propagated in the opposite direction.

Fig. 2.

Phase map analyses of PIP3 waves in latrunculin-treated cells. (A) Phase mapping of a single rotating wave. Phase of oscillating PIP3 at every spatial point was extracted from a grayscale image of fluorescence intensity (Upper Left) by Morlet wavelet transformation (25). (Lower Left) A representative time series from a fixed position. (Center) Amplitude (Upper) and phase (Lower) of the wavelet transform. The frequency component having the maximum magnitude at each time point was obtained by ridge extraction (white line), and the phase was calculated accordingly. (Right) White solid circle depicts a phase singularity with +1 charge that corresponds to clockwise rotation. (Scale bar, 10 μm.) (B–D) Codistribution of phases of PIP3, F-actin, and PTEN waves: ϕ_PIP3, ϕ_actin, and ϕ_PTEN, respectively. Data in B–D were obtained from Movie S1 A, C, and D respectively. (E) Time series of phase maps during spiral reversal in a cell treated with 3 μM latrunculin. A core of a clockwise rotating spiral wave disappeared at t = 126 s. A new wave that appeared at t = 252 s created a pair of phase singularities (t = 318 s). One of the singularities reached the border and disappeared, resulting in a dominance of a left-handed spiral. (Scale bar, 10 μm.)

In nontreated cells, there were on average two to three fronts of propagating PIP3 waves, and their geometries appeared more complex. Nonetheless, we found that the spiral and translational waves are the basic components of the wave geometry and that competition and switch between these waves underlie the complex membrane deformation. To illustrate the dynamics of the wave patterns in a freely moving amoeba, a representative time series is shown as snapshots in Fig. 3A. When a wavefront supported by a pair of phase singularities reached the cell edge, it gave rise to symmetric extension of the cell membrane (Fig. 3A, 54–84 s and 348–396 s, arrows). In contrast, when the wave was supported by a solitary singularity, the resulting single-arm spiral caused the membrane to extend while rotating in the same direction as the wavefront (Fig. 3A, 180–222 s, arrow). In such cases, cores of the spiral waves acted as pivots for rotational extensions. Thus, the number, the charge, and the position of spatial phase singularities are the major determinants of the observed large-scale deformation.

Fig. 3.

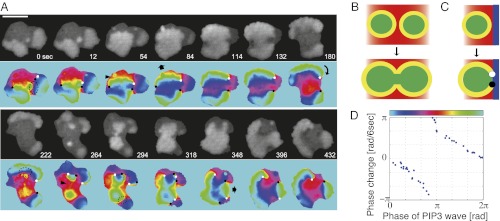
Phase map analyses of PIP3 waves in nontreated cells. (A) Phase analysis of PIP3 wave in a freely moving cell. Symmetric expansion of a circular wavefront was supported by phase singularities of +1 and −1 charge located at both ends (t = 54–84 and 348–396 s). Rotational PIP3 waves were maintained by an isolated phase singularity (t = 180–222 s). The arrowheads indicate a front–front interaction that resulted in wave merger and extinction (t = 54 and 264 s). The dotted regions indicate front–back interactions of the wave, which create a pair of phase singularities (t = 0, 222, and 294 s). (B) Front–front interaction: Wavefronts (yellow) simply merged and annihilated each other after the collision. (C) Front–back interaction: Waves did not merge but instead created a pair of phase singularities. This occurred for nucleation at the back of a wave or when a wavefront (yellow) caught up with a waveback (blue). (D) Phase change upon birth of singularities was discontinuous, indicating a strong phase resetting of type 0.

The dynamics of phase singularities can be summarized as follows. When a new wave nucleated at a random location spread and collided with the front side of another wave, they simply merged and annihilated each other (Fig. 3B, yellow–yellow collision; see also Fig. 3A, 264–294 s). However, when nucleation happened at the back of a wave or when a newly formed wave spread and caught up with the back of a preexisting wave (i.e., a region in the refractory phase), further propagation of the new wave was prohibited, and a pair of spatial phase singularities was created (Fig. 3C; see also Fig. 3A, dotted region). Experimentally observed phase shifts by front–back interactions are presented in Fig. 3D. When the interaction occurred at a particular phase that corresponds to the back of a preexisting wave (Fig. 3D, π radian, red), there was a discontinuous transition, indicating a strong phase resetting of type 0 (26, 29). Such interactions between the new and preexisting waves gave rise to phase singularities (29), and they were always born as a pair of opposite charges. On the other hand, disappearance of phase singularity mainly followed when it reached the edge after meandering (Fig. 3A, 84–114 s). In some cases, singularities disappeared by collision of those with opposite charge (Fig. 3A, 318–348 s). Frequency of such events was rare—about 1/10th of total extinction events.

Analysis of an Excitable System with 2D Morphodynamics.

To address how the observed wave patterns arise from regulation of PIP3, we studied a simplified mathematical model that describes the essence of the phosphorylation/dephosphorylation reaction of the phosphoinositides and their diffusion at the basal membrane (15, 30) (Fig. S4A; see SI Text for details). PI3-kinase that catalyzes conversion of PIP2 to PIP3 is activated upon localization to the plasma membrane and this is known to occur spontaneously in the absence of receptor-mediated chemoattractant signaling (5). In the model, we assumed that localized production of PIP3 promotes PI3-kinase activation by a positive feedback loop (5). Another positive feedback loop is the phosphatase PTEN that binds to PIP2 (31) and catalyzes desphosphorylation of PIP3 to PIP2. We found that the combined reaction exhibits excitability of PIP3 production above a certain threshold activity of PI3-kinase (SI Text). Due to the positive feedback, a small increase in PI3-kinase activity amplifies PIP3 production and further enhances its own activity and gives rise to local accumulation of PIP3. PIP3 diffuses in the membrane and further promotes PI3-kinase activity in the surrounding area. When PIP3 concentration increases, PIP2 becomes locally depleted; hence the PIP3 level is allowed to come down again. Hence this relatively simple regulation of PI3-kinase and PTEN is sufficient to explain excitability of the system. According to our analysis, the excitation threshold becomes high when either PI3-kinase activity is low or the strength of the positive feedback from PIP3 to PI3-kinase is weak (Eqs. S12 and S14). A higher excitation threshold suppresses wave nucleation; thus taken together with our experimental observations (Fig. 1 B and C), the model supports the idea that F-actin mediates the feedback from PIP3 to PI3-kinase (5).

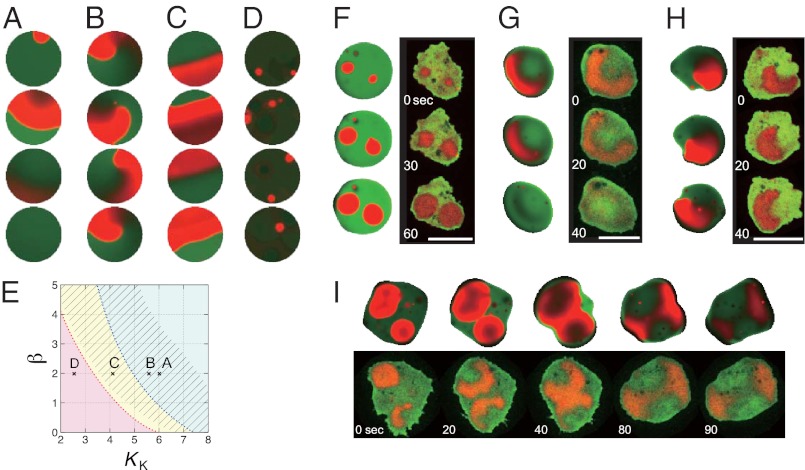
To study the effect of this feedback on the wave patterns in detail, we first performed numerical simulations with a fixed circular domain. For weak feedback strength, model simulations predicted transient planar waves that propagate from one end to the other (Fig. 4A), similar to those observed in LY294002-treated cells (Fig. 1D). As feedback was increased, we began to observe rotating (Fig. 4B) and reflecting (Fig. 4C) waves as observed in latrunculin-treated cells. In simulations too, wave nucleation occasionally induced spiral reversal as shown in Fig. S4B. These behaviors agree well with experimental observations (Figs. 1 D–F and 2E). The model predicted, on the other hand, that a further increase in the feedback strength should generate a new stable steady state. Hence excitability was lost and no waves could propagate (Fig. 4D and Fig. S4 E and H). Because there are presently no convenient means to test this prediction pharmacologically, we studied a null mutant of PIR121, a component of the SCAR/WAVE complex, that is known to exhibit an excessive amount of polymerized actin (32). We found that occurrence of PIP3 nucleation was markedly enhanced in the mutant as expected (Fig. S5 A and B); however, these areas of rich PIP3 accumulation failed to grow in size and did not give rise to propagating waves (Fig. 1G and Movie S2B). The effect was not due to direct involvement of PIR121 in wave propagation per se, because the rates of nucleation and wave propagation were restored when the mutant cells were treated with latrunculin (Fig. S5 C–E). These observations support our model prediction that PIP3 wave propagation requires the strength of the positive feedback to be at an intermediate range (Fig. 4E and SI Text).

Fig. 4.

Numerical simulations of phosphoinositide waves and membrane deformation. Concentrations of PIP3 and PIP2 in the simulations (white background panels) are colored in red and green, respectively. Experimental data (black background) shown for comparison are fluorescence intensity of PHcracRFP (red) and PTEN-GFP (green). (A–D) Simulations in a fixed circular domain. (A) For weak feedback strength, waves were extinguished at the boundary so that they propagated only transiently as observed in LY294002-treated cells (Fig. 1D). For moderate strength of feedback, the system showed either spiral (B) or reflecting (C) waves, similar to those observed in cells treated with latrunculin (Fig. 1 E and F). For exceedingly large feedback strength, the system exhibited no excitability and only small patches of transient PIP3 enrichment similar to those in the pirA⁻ mutant (Fig. 1G) were observed (D). The strength of the feedback is increased by lowering the value of K_K (SI Text). K_K = 6.0 (A), 5.7 (B), 4.2 (C), and 2.5 (D). (E) Phase diagram of the cell behavior. Parameter β indicates the strength of the PTEN-mediated dephosphorylation reaction. Red represents no excitability; yellow, reflection at the edge; and blue, extinction at the edge. Spirals are observed in the shaded region. Symbols represent parameters in A–D. (F–I) Simulation results with a deforming boundary. Concentric (F), translational (G), and rotational (H) wave propagation induced deformation of distinct forms at the cell edge. Head-to-head collision of waves induced a lateral membrane extension. (Scale bars: 10 μm.) Detailed descriptions of the model and parameters are provided in SI Text and Table S1.

To capture how the waves determine the shape of membrane deformation and vice versa, we next studied the effect of a moving boundary by describing extension of an elastic border (33) at the site of PIP3 accumulation (SI Text). Results of the simulations are compared with experimental observations (Fig. 4 F–I). Typically observed dynamics were synchronous wave nucleation (Fig. 4F), a short-lived transient wave extinguished at the boundary (Fig. 4G), and self-sustaining rotational waves (Fig. 4H). New sites of nucleation tended to be located close to the sites that previously initiated waves simply because they recovered from the refractory period earlier than other areas. Thus, pattern selection depended not only on the parameters that control excitability of the system but also on the initial condition. Consistent with the experiments described above, front–back wave interactions gave rise to phase singularities that supported rotating waves. As a result, waves propagated along the cell border and caused rotational deformation (Fig. 4H). On the other hand, a front–front collision and subsequent annihilation resulted in transient wavefronts that propagated outward toward the cell border in lateral directions (Fig. 4I, 40–80 s). This in turn switched the direction of cell elongation by 90°. The same type of collision with a short time lag between nucleations of two consecutive waves resulted in more anisotropic deformation (Fig. S1A). The wave geometry therefore provides the basis for the previously documented spatiotemporal patterns of morphology dynamics (9, 11).

In addition to the occurrence of phase singularity, persistence of waves depends much on whether they are extinguished or reflected at the cell border. Experimentally, both in latrunculin-treated (Fig. 1F) and in nontreated cells (Movie S1B, 2–5 min) waves often bounced back from the cell border. Transient waves observed in LY294002-treated cells (Fig. 1D), in principle, can turn into waves traveling back and forth as in latrunculin-treated cells (Fig. 1F) if the wave is reflected at the border. Numerical analysis of the model in one dimension indicated that reflection cannot take place at low excitability (Fig. S6A, high K_K), consistent with the transient waves observed in LY294002-treated cells (Fig. 1D). In comparison, latrunculin treatment appears to have a milder effect in terms of lowering excitability, because reflection was observed (Fig. 1F) and because birth of spiral waves (Fig. 1E) required interactions between wave nucleations. Numerical analysis also indicated that deformability of the boundary (Fig. S6A, parameter a) must be either low or high to support reflection (Fig. S6B). Thus, the difference between LY294002 and latrunculin could also be due to the latter possibly lowering both excitability and the boundary stiffness at the same time. In summary, geometries and the relative phase of colliding waves are responsible for the complex pattern transitions in cell shape (Movie S3). Waves are created and annihilated following excitable dynamics coupled to boundary deformation and take either spiral- or planar-form geometries. Because the wavelength is close to the size of a cell and because there is continuous competition between new and old waves, the resulting patterns are complex and not immediately apparent. The interdependence between the wave dynamics and boundary deformation suggests that cells could be using such a property to further modulate complexity of the wave dynamics by mechano-chemical interactions.

Concluding Remarks.

Unlike the shape and motion of keratocytes that are simple and relatively well understood (34, 35), the dynamics of amoeboid cells possess a certain mix of randomness and regularity (9, 11), making them more difficult to analyze. Our study demonstrated that the semicyclic morphologies in randomly moving Dictyostelium are determined by the phase information of the underlying excitability. It is dictated by actin-dependent nucleation of PIP3 waves that compete for dominance and propagate either as transient planar waves or self-sustaining spiral waves. Although nucleating events that trigger the waves are stochastic, dynamics that follow are deterministic—they are constrained by the topological rules of phase singularities. It should be emphasized that 2D geometry is essential for understanding dynamics of the observed pattern and their transitions. In earlier models based on one-dimensional geometry (6, 15, 30, 36), a switch of patterns such as reversion of wave propagation along the cell periphery occurs merely by stochastic noise (6). The current study suggests that such a view of pattern transition in many cases could be an oversimplification, because topological charge of the spiral core is robust and cannot simply be flipped by random noise. Rather, pattern transitions occur following a sequence of generation and disappearance of phase singularities, and these are determined by the position and timing of wave nucleation relative to the preexisting waves as well as the overall cell shape.

The current modeling framework provides a rare opportunity to integrate the interplay between the excitable molecular signaling and the cell morphodynamics and to further provide insights that are experimentally testable. Because the observed wave geometries are generic (26), earlier models of PIP3/F-actin waves in Dictyostelium, whether they are abstract (19) or detailed (6, 15), may also be able to capture some of the essential dynamics uncovered in this study. Future studies that include mutant analysis should allow comparison of details that delineate the existing models. Also of theoretical interest is to relate similar waves of PIP3 and/or F-actin observed in animal cells (7, 36–38) and other amoeba species (28). Although other feedback mechanisms in addition to the PIP3/F-actin reactions (7) appear to be in operation in animal cells—such as those that involve Hem-1—many are likely to share general characters of excitable dynamics (37). Thus, the relationship between complex morphology and geometry of excitability may be of relevance to a wide variety of cell types. Similarities between the PIP3/F-actin waves and the phagocytic cup structure have been noted previously (17). By making use of a mixture of randomness and order, cells may be effectively scanning the surrounding environment as they move and forage in the changing terrain. We note that in addition to the membrane extension, net cell translocation requires coordination between membrane tension and attachment/detachment that provides further layers of cell polarity. How the F-actin/PIP3 waves and these mechanical principles work together (39, 40) and how they are guided by extracellular cues for directional movement (19, 41) are an avenue of future work. The present study adds a revealing example to a repertoire of self-organizing spatiotemporal dynamics (42) underlying critical biological functions such as bacterial cell division (43), cell aggregation (27), and somitogenesis (44). Excitable dynamics are well studied in the Belouzov–Zhabotinsky reaction; however, how patterns are influenced by a finite boundary and its movement is largely unexplored (45, 46). Our results hint at future approaches of synthesizing complex cellular movement on a pure chemical and material basis.

Materials and Methods

Dictyostelium discoideum cells expressing a combination of PHcracRFP, PI3K-RFP, or LimEΔcoil-RFP with PTEN-GFP were constructed and cultured according to standard procedures. Live cell imaging was performed using an inverted microscope (IX81; Olympus) equipped with a multipoint laser confocal scanning unit (CSU-X1; Yokogawa). Detailed descriptions of materials and methods are provided in SI Materials and Methods.