Possible relation of water structural relaxation to water anomalies

Abstract

The anomalous behavior of thermodynamic response functions is an unsolved problem in the physics of water. The mechanism that gives rise to the dramatic indefinite increase at low temperature in the heat capacity, the compressibility, and the coefficient of thermal expansion, is unknown. We explore this problem by analyzing both new and existing experimental data on the power spectrum S(Q, ω) of bulk and confined water at ambient pressure. When decreasing the temperature, we find that the liquid undergoes a structural transformation coinciding with the onset of an extended hydrogen bond network. This network onset seems to give rise to the marked viscoelastic behavior, consistent with the interesting possibility that the sound velocity and response functions of water depend upon both the frequency and wave vector.

Although water is one of the simplest molecules, it is in reality a very complex liquid displaying more than 64 counterintuitive anomalies, most of which have not been adequately explained (1, 2). The best known of these is its density behavior: unlike most liquids, water displays a maximum at 4 °C, and becomes less dense rather than more dense when it freezes. Other unexplained anomalies occur for response functions such as the isothermal compressibility K_T, the isobaric heat capacity C_P, and the thermal expansion coefficient α_P. Moreover, if one extrapolates these functions into the metastable supercooled phase of water below the melting temperature (T_M = 273 K at atmospheric pressure), and above the homogeneous nucleation temperature (T_H ∼ 231 K), they behave as if they might diverge at a singular temperature T_S ∼ 228 K (1). Water is a glassy liquid below the glass transition temperature T_g ∼ 130 K (2). Immediately above T_g it transforms into a highly viscous fluid and ultimately crystallizes at T_X ∼ 150 K. The region between T_X and T_H is a “no-man’s land” within which bulk liquid water cannot be studied (1). For these and other reasons, liquid water is one of the most exciting research topics, and an enormous number of studies have sought to elucidate the physical reasons for water’s unusual properties.

There are four current hypotheses (1), two of which have gained considerable attention: the singularity-free hypothesis (3, 4) and the liquid–liquid critical point (LLCP) hypothesis (5). The LLCP hypothesis is based on two assumptions: (i) that water displays the phenomenon of “liquid polymorphism” (6) and (ii) as T decreases, the hydrogen bonds (HBs) begin to form an open tetrahedrally coordinated HB network. If we begin with the stable liquid phase and decrease T, the HB lifetime and the cluster stability increase, and this altered local structure continues through the no-man’s land down to the amorphous phase region. Amorphous solid water is widely believed to display polymorphism: below T_g, low-density amorphous (LDA) and high-density amorphous (HDA) structures (7) can be transformed from one to the other by tuning the pressure. Hence liquid water may have local structural features of two liquids, low-density liquid (LDL) and high-density liquid (HDL), with an altered local structure that is a continuation of the LDA and HDA phases (5). In HDL, which predominates at higher pressure and temperature, the local tetrahedrally coordinated HB structure is not fully developed, but in LDL a more open HB network begins to appear. Thus, water anomalies reflect the “competition” between these differing local forms of the two local liquid structures. The LLCP scenario also predicts a locus, the Widom line, in the T–P phase diagram along which water’s thermodynamic response functions attain their maximum values (8). The Widom line reflects water’s response functions because they are related to the correlation length. This line and the hypothesized associated polymorphic transition is difficult to study as it lies inside the no-man’s land, but the crystallization inside this region can be retarded by confining water within nanoporous structures so narrow that the liquid cannot freeze (9), or within its own ice phase (10), or by using electrolytic solutions (11, 12).

Many experiments have been carried out on water confined in nanopores (9, 13, 14). These studies show that when T is decreased to a certain point the water HB lifetime increases by approximately six orders of magnitude, indicating the location of the Widom line (9), and signs of LDL and HDL inside the supercooled region are observed (14). At ambient pressure the Widom line is crossed at T_W(P) ∼ 225 K where a fragile-to-strong dynamic crossover occurs (8, 9), the Stokes–Einstein relation is violated (13, 15), and LDL local structure predominates over HDL (14). These findings on confined water are subject to the concern that water behavior may be affected by the silica pore surfaces or the confinement constraints may affect its dynamic behavior, resulting in a physical situation very different from that of bulk water. The results on nanopore-confined water, however, have been confirmed by a number of different techniques (10, 12, 16) that also show the crossover at ∼225 K and thus are consistent with the possibility that the tetrahedral HB structure recovers at temperatures pertinent to studies of the hypothesized liquid–liquid transition (17).

To test the connection between water anomalies and water’s HB network, we consider thermodynamic results on confined water and bulk water sound propagation data. In specific, we consider the velocity dispersion (18–20) asking to what extent is sound velocity in water v a function of the probe wave vector 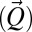and the frequency (ω). Water structure has a viscoelastic behavior that is reflected in the scattered spectra and that persists under ambient conditions. We study the two compressibilities (isothermal χ_T and adiabatic χ_S), the coefficient of thermal expansion (α_P), and the specific heat (C_p), each of which reflect a correlation with some thermodynamic fluctuation: χ_T reflects the volume 〈δV²〉, χ_S = [ρv²]⁻¹ the pressure 〈δP²〉, C_P the entropy fluctuations 〈δS²〉, and α_P the entropy and volume cross-correlations 〈δSδV〉.

In most liquids, volume and entropy fluctuations decrease as T decreases, but in water they increase. In most liquids, δS and δV are positively correlated, but in water δS and δV are anticorrelated when T < 277 K. The local ordering around each water molecule may be related to the microscopic cause of these anticorrelations and the reason that α_p can be negative at a certain temperature (1).

The relationships among the sound-propagation velocity, the isothermal and the adiabatic compressibility, the specific heat, and the coefficient of thermal expansion are

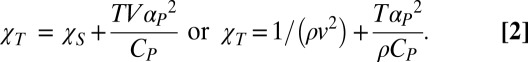Thus, studying sound velocity can help better understand water behavior.

Scattering experiments on bulk water, from the stable to the supercooled phase (14, 18, 21–24), indicate a strong dispersion, v = v(Q, ω), that on the basis of the previous equations is linked to the compressibilities.

Because of water’s viscoelastic properties, when sound propagates in bulk water it disperses. We thus observe both an “ordinary” sound velocity and a relaxed high-frequency mode, which is present when Q > 1 nm⁻¹ and propagates with a velocity close to that in amorphous ice (∼3,200 m/s) (18). This sound dispersion—observed using light scattering in the supercooled phase and inelastic X-ray scattering (IXS) in the high-frequency regime [ω/2π ∼ 10¹³ Hz (19)] inside the stable phase (260 < T < 370 K)—is due to structural relaxation, as proposed by a molecular dynamics (MD) simulation study (20). Here we show that this sound behavior is reflected in the isothermal compressibility as χ_T = χ_T(Q, ω), and hence may be a relevant factor in understanding the thermodynamic anomalies in water. Using sound-propagation experiments we can trace the effects of the structural relaxation on χ_T. As in critical phenomena, sound dispersion and attenuation in water can be attributed to the relaxation of the density fluctuations that determine the behavior not only of the isothermal compressibility K_T, but also of C_P and α_P.

The idea that HB networks characterize supercooled water has been supported by experiments on the power spectrum S(Q, ω), defined as the Fourier transform (over r and t) of the generalized pair correlation function G(r, t) (1). In this conceptual framework, many studies have produced evidence for the existence of relaxing structures in the liquid, whose size increases as T decreases (14, 18, 21–24), and for their effects on the transport, configurational, and vibrational properties of the system. In the time domain, as T decreases the HB average relaxation time (〈τ〉) strongly increases (up to many orders of magnitude), and the parallel frequency domain is characterized by viscoelasticity and strong dispersions in sound propagation (9, 18, 19).

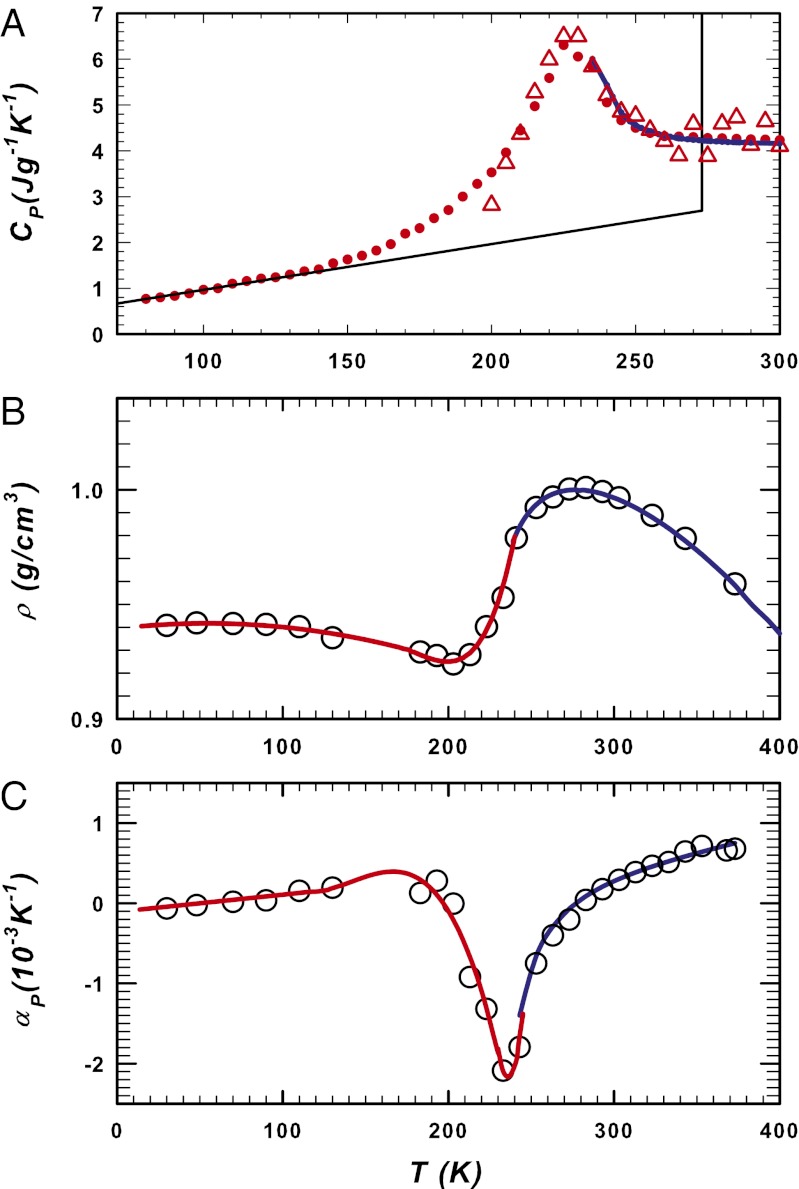
These data on three response functions of bulk water as a function of T up to ∼ 240 K indicate diverging characteristics (Methods and refs. 23–27). In confined water in which C_P(T), ρ(T), and α_P(T) have been measurable inside the no-man’s land (T ≥ 180 K), there is evidence of very different behavior. Fig. 1 shows these quantities in both the bulk and the confined phases (17, 28–31).

Fig. 1.

Experimental data for (A) C_P(T), (B) ρ(T), and (C) α_P(T) in its bulk (blue line) and confined (red line) phases. These lines connecting the experimental data points are essentially guides for the eye. The blue ones, corresponding to bulk water, are the same used to fit literature data (25, 26). Confined water data also include the C_P values measured using normal calorimetry (red dots) (28) and NMR (red triangles) (29), and the density and α_P(T) measured using FTIR spectroscopy (17, 30) (the density and thermal expansion coefficient data for T < 140 K are for amorphous water). Inside the no-man’s land, confined water exhibits a density minimum at ∼200 K (experimentally observed in confined water, ref. 30, and suggested in bulk by MD simulations, ref. 31), a C_P(T) maximum at ∼230 K, and a α_P(T) minimum, also at ∼230 K.

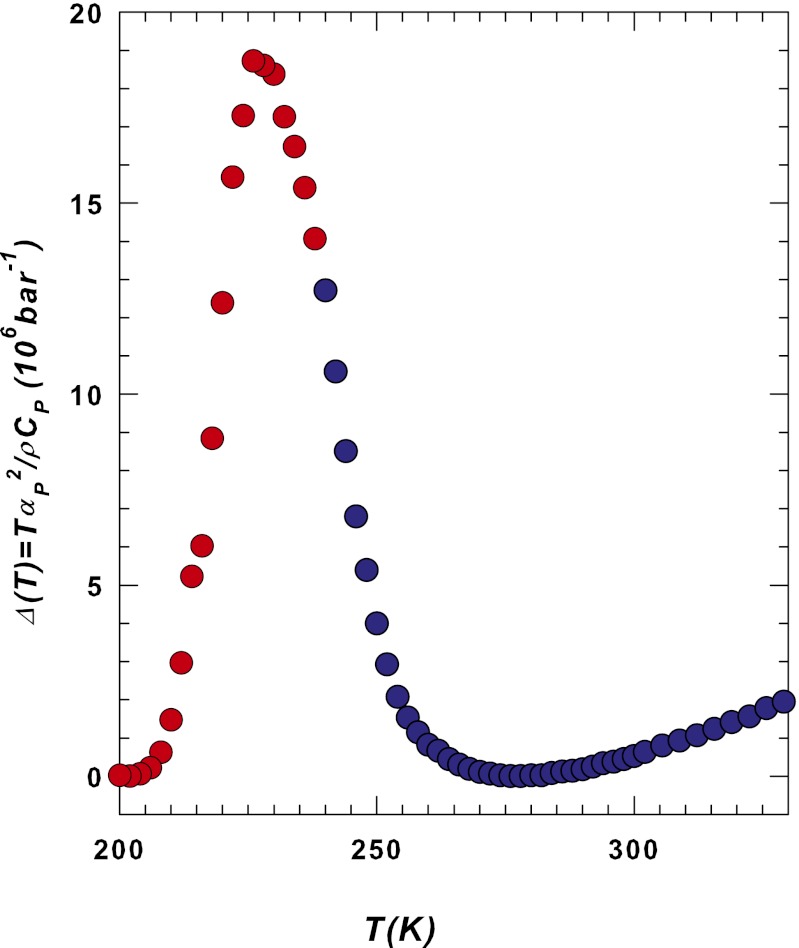
Measurements of χ_T and χ_S in confined water have not yet appeared in the literature, but the difference between the two, Δ(T) = Tα_P²/ρC_P (Eq. 2), can be obtained from the corresponding response functions (Fig. 1). Fig. 2 shows Δ(T) for 200 < T < 330 K. Because Δ = 〈δSδV²〉/〈(δS)²〉k_BTV is related to the entropy and volume cross-correlations, its maximum indicates their increase in the interval 200 < T < 270 K reflecting the HB networking (1).

Fig. 2.

The Δ(T) = Tα_P²/ρC_P obtained from the corresponding response function data measured in bulk (blue data) and confined (red data) water. Note that as T decreases the Δ values slowly decrease from the high temperature region down to approximately the density maximum temperature and then begin to rapidly increase, reaching a maximum at ∼227 K. The low values found in the high T region are recovered at ∼200 K. The temperature at which this maximum is located is approximately the same as that of the dynamical crossover and that at which the violation of the Stokes–Einstein relation in the transport functions occurs (13). In addition to the maximum obtained inside the T region for confined water, a careful observation of the Δ(T) data also reveals a flex point at ∼240 K in the T interval for bulk water.

The behavior of sound velocity dispersion is reflected in the response functions of bulk water, as is clear when one uses scattering techniques to measure S(Q, ω). Experiments covering a wide energy range (Methods and refs. 18, 19, 32–37) reveal the existence in pure bulk water of a sound velocity dispersion as the effect of a relaxing HB structure, a phenomenon that can be related to the hypothesized water polymorphism. The HB structure relaxes and exhibits both hydrodynamic “normal-liquid” and “solidlike” regimes. This latter regime is characterized by finite clusters of HB water molecules, the density fluctuations correspond to a more stable local HB structure, and the sound velocity increases rapidly (20). Note that the measured sound velocity over a wide ω range of 10⁴ < ω < 10¹³ Hz is characterized by a positive dispersion showing a minimum (v_min) at a certain temperature. For further details, see Methods.

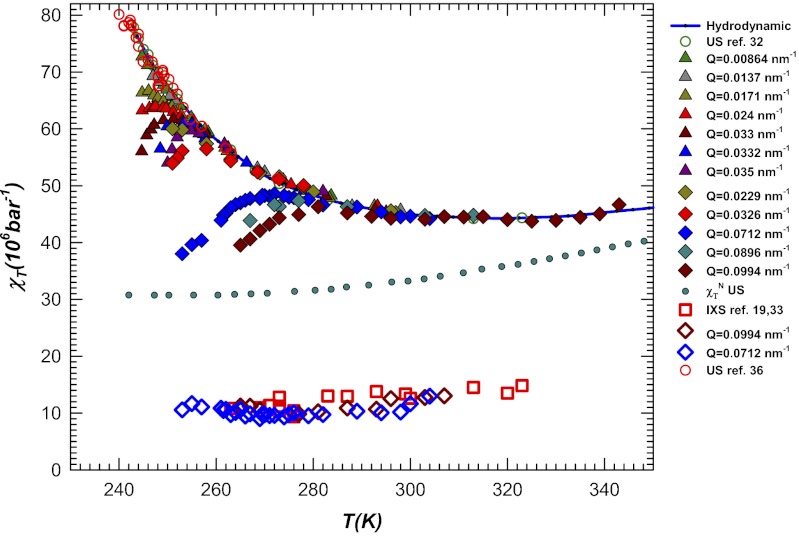
Fig. 3 shows χ_T calculated from sound propagation data using Eq. 2. Using the literature data for Δ(T) (the blue data of Fig. 2), we see that the experimentally measured isothermal compressibility of bulk water depends on the frequency and the wave vector, and thus χ_T = χ_T(Q, ω). This response function has a clear maximum that is more pronounced in the supercooled phase, especially when Q attains its largest values (the hypersound data) and when the T behavior of the “normal” sound data measured in intermediate frequency regime experiments by Brillouin scattering (BS) and inelastic UV scattering (IUVS) differs greatly from that of low-frequency ultrasound data. Hence the structural relaxations cause a maximum in χ_T 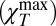 that is strongly affected by the transferred scattered momentum and the temperature. For the highest Q values (Q = 0.0994 nm⁻¹) this maximum is seen inside the stable liquid phase (T ∼ 285 K) and, if we decrease Q, it continuously evolves to the lowest T values (e.g., for Q = 0.0171 nm⁻¹ the maximum is seen deep inside the supercooled regime at T ∼ 245 K).

Fig. 3.

The bulk water isothermal compressibility χ_T = χ_T(Q, ω) evaluated according to Eq. 2 from the relaxing sound velocities. Shown are the compressibility values corresponding to the “fast” sound v_hf measured in the Brillouin, IXS, and INS (open squares) scattering techniques together with those corresponding to the US and acoustical levitation (AL) data (open circles), and the hydrodynamic values gathered from thermodynamic measurements (solid line) (25). Note that for the temperatures studied these low-frequency data coincide within experimental error, although a small rounding off in the AL data are seen at the lowest temperatures (T < 245 K). The T behavior of “normal” sound data measured in inelastic scattering experiments at the intermediate frequency regime (BS and IUVS), are reported as triangles (the BS data) and diamonds (the IUVS data).

Fig. 3 shows that the χ_T maximum 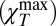is T and Q dependent. Its value increases when the temperature [like the corresponding hydrodynamic χ_T = χ_T(Q → 0) value] and the exchanged wave vector Q are decreased. In bulk water this behavior—a relaxed sound velocity v_hf and a high-frequency compressibility value 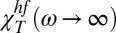—is caused by the HB network structure. This means that a dynamically correlated structure (i.e., a cluster that has a characteristic length ξ) can relax, a process that is strongly dependent on T, Q, and ω. The anomalous T dependence, unlike that in normal liquids (Methods), is a consequence of the HB lifetime. As T decreases, the HB lifetime increases rapidly, exhibiting super-Arrhenius behavior (approximately one order of magnitude in the range 293 > T > 243 K, i.e., from < 1 ps to about 10 ps). As T decreases, ξ increases and the largest cluster becomes more stable in time. This explains why, at the largest values of Q, scattering experiments in the THz regime in the stable liquid phase can detect the HB-relaxing cluster.

At a certain Q value, χ_T increases with decreasing T up to a maximum value imposed by the corresponding volume fluctuations δV. Note that the decrease in χ_T after this maximum is caused by the relaxation of its high-frequency solidlike values, as shown in Fig. 3, which appear to be temperature-independent 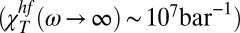. The increase in inside the metastable supercooled phase again reflects the growth of ξ (or δV) as T decreases.

Although the hydrodynamically measured χ_T appears to diverge, the presence of a structural relaxation and all of the trends observed in the χ_T = χ_T(Q, ω) suggest that the behavior of χ_T is analogous to that of Δ(T) (Fig. 2). Thus, if χ_T(Q → 0) is measured for T < 243 K (the lowest T value available, ref. 25) there will be a maximum at a certain temperature. This observation is supported by the fact that we cannot expect an indefinite decrease in the bulk water density by decreasing the temperature. Although a density minimum has been observed in confined water, the measured value (ρ = 0.94 g/cm³) in the LDA phase at 120 K (38) may be the limit for bulk water.

Figs. 2 and 3 show data associated with system fluctuations (Fig. 2 for both the bulk and the confined phases). They indicate that in bulk water, unlike in normal fluids, density fluctuations become increasingly pronounced as T decreases. Fig. 3 shows, in addition, a relaxation process revealing also that the volume fluctuations (χ_T = 〈δV²〉_P,T/k_BTV), depending on the probe wave vector Q, cannot grow indefinitely. Also the initial growth in Δ = 〈δSδV〉²/k_BTV〈δS²〉, for T < 273 K, which is related to a volume-entropy cross-correlation (and to an anticorrelation: V increases as S decreases), cannot evolve indefinitely, so the behavior of the confined water (Fig. 2), with a maximum in Δ at ∼225 ± 5 K, must be the same as for bulk water if it can be supercooled to that temperature range. The maximum in these anticorrelations must correspond to an inversion in the system fluctuations caused by a decrease in the density fluctuations as seen in confined water. The maximum in Δ(T) has the same value as the maximum in C_P(T), and the minimum in α_P(T) occurs at the crossover temperature at which the structure changes from an HDL region to an LDL region, as proposed by the hypothesized water polymorphism.

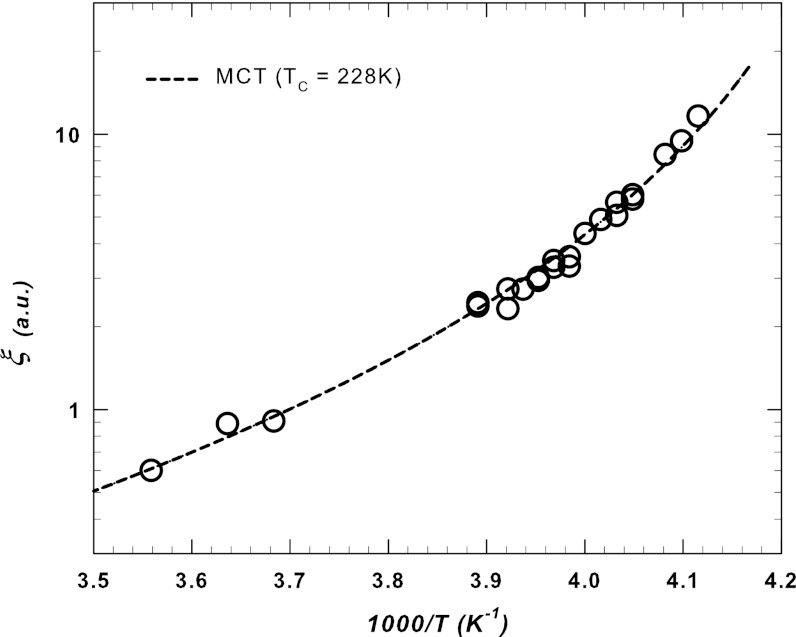
Finally, we estimate the temperature at which bulk water reaches a maximum in χ_T by considering the temperature (T^max) of the observed 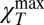, which corresponds to the experimental Q values, i.e., we evaluate the T^max value in the hydrodynamic limit (Q → 0). For the scattering models ξ ∼ 1/Q we plot ξ vs. 1/T^max (Fig. 4) and observe the same power-law fit as that derived when the mode coupling theory (MCT) approach is used to predict the temperature of the dynamic crossover, i.e., T_× = 228 ± 5 K, in terms of the transport parameters (39). This is approximately the same temperature of the Δ(T) and C_P(T) maxima and the α_P(T) minimum (Figs. 1 and 2) measured in confined water. An identical scaling result has been obtained for the corresponding structural relaxation times measured using a different spectroscopic technique, the time-resolved optical Kerr effect (40).

Fig. 4.

The water network correlation length corresponding to the temperature of χ_T(Q) maxima as a function of 1/T. Dotted line represents the ideal MCT power-law fitting curve with T_× = 228 ± 5 K, whereas the exponent is θ ∼ 2. Note that this result is approximately the same as that previously obtained by fitting the anomalous contribution 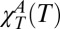(23, 24) and the specific heat C_P(T) (26) in pure bulk water. Within the framework of extended MCT such a temperature represents the crossover to a water dynamics driven by hopping processes among clusters with a characteristic length proportional to ξ.

The consistent appearance of this crossover temperature in the thermal response functions in bulk and confined water and also in their transport parameters (9, 13, 41) is surprising. We hypothesize the cause is the HB network structure of water and its relaxation, and that this relaxation strongly affects the physical properties of both bulk and confined water.

The existence of an LLCP is not the only hypothesis that attempts to explain supercooled water’s anomalous thermodynamic properties. Other scenarios range from the idea that the anomalous thermodynamic properties do not diverge at a single critical temperature but at a range of pressure-dependent temperatures to the idea that there is a multiplicity of critical points in the supercooled water phase (see, e.g., ref. 42). Simulation studies have recently proposed two interesting possibilities regarding the existence of two different phases in supercooled water. In one MD simulation the existence of a liquid–liquid critical point for the ST2 water model together with the two distinct liquid states is supported (43). In the other, a link between water anomalies and the crystallization rate of ice is demonstrated (44). This latter coarse-grained simulation suggests that the crystallization rate of water reaches a maximum around 225 K, below which ice nuclei form faster than the LDL water phase can equilibrate; i.e., spontaneous crystallization occurs before liquid–liquid separation can equilibrate. This approach is based on the assumption that the sharp increase in the fraction of four-coordinated molecules in supercooled liquid water explains its anomalous thermodynamic behavior and controls the rate and the mechanisms of ice formation. In principle, the maxima observed here in χ_T at different wave vectors and temperatures can be related to water crystallizing into ice, but for Q > 0.07 nm⁻¹ the corresponding χ_T maxima are located inside water’s stable liquid phase, i.e., T > T_M. In addition, because the relaxed high-frequency sound velocity v_hf of the HB structure has been experimentally demonstrated to be accessible within the temperature range ∼ 250–320 K, it cannot be explained by the presence of any form of ice.

A recent thermodynamic model for supercooled water, based on a scaling field approach with an appropriate parametric equation of state (42), describes all available experimental thermodynamic data for both bulk and confined water. The shape of the response functions, specifically the minimum in α_P and the maximum in C_P, are predicted for the bulk phase at approximately the same temperature as that observed in the confined state T_× = 228 ± 5 K. Hence finite-size effects may account for some of the differences between confined and bulk results, so a maximum in Δ(T) = Tα_P²/ρC_P similar to that proposed in Fig. 2 can also be the case for bulk water. Finally, the Anisimov model indicates that χ_T for bulk water has a maximum at ambient conditions located at approximately T_×. Because this χ_T maximum is pressure dependent, it is associated with the two coexisting liquid phases and relates to the LLCP hypothesis. The same arguments also hold on the basis of the water structural relaxation observed using sound relaxation. Note that further improving this approach to describing liquid–liquid criticality has demonstrated an explicit crossover equation of state that explains the liquid–liquid phase transition in metastable water through the entropy-driven nonideality of two states associated with two different HB network structures (45). Because it is renormalized by order-parameter fluctuations, the equation of state reproduces the asymptotic critical anomalies (as introduced through the original scaling theory; ref. 42) and reduced to the regular mean-field behavior away from the critical point.

We next compare the viscoelastic relaxation in supercooled liquid water with the relaxation of critical density fluctuations near the vapor–liquid critical point, where the observed sound dispersion is caused by critical density fluctuations, the isobaric heat capacity C_P anomaly cancels the χ_T anomaly, and the dispersion of the χ_S anomaly is described by the frequency-dependent fluctuation-induced anomaly in the isochoric heat capacity C_V.

This is why the hypersonic sound speed near the vapor–liquid critical point does not show a T-dependent anomaly. Hence the sound dispersion and attenuation are attributed to the relaxation of the critical fluctuations only. In other words, in the mean field approximation there is no dispersion of sound velocity near the vapor–liquid critical point because there is no C_V anomaly.

On the other hand, in supercooled water the relaxation is caused by the relaxing structure and the density fluctuations follow the structural fluctuations. Thus, it is possible that the pronounced effects of structural relaxation are associated with viscoelasticity, even in the main field approximation.

In conclusion, only by treating water as a viscoelastic system (i.e., a system governed by an underlying extended structure) is it possible to understand the microscopic origin of water anomalies. The proposed scenario here has been developed using a dynamic approach; i.e., all of the studied quantities reflected by the measured power spectrum, S(Q, ω), are explored in the wave vector and frequency phase diagram (or length and time), and thus they allow a data completion not possible in simulation studies.

Methods

Scattering experiments measure thermodynamic response functions by measuring the correlations in their fluctuations. The power spectrum S(Q, ω) is the Fourier transform with respect to both r and t of the generalized pair correlation function G(r, t). Both the adiabatic and the isothermal compressibilities of a liquid can be obtained from the S(Q, ω).

The structure factor S(Q) in the hydrodynamic limit is S(0) = k_BTρ_Nχ_T. Assuming that water exhibits “critical” behavior, it was proposed that 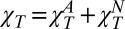(23, 24); i.e., a “normal” compressibility, 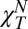, displaying the thermal behavior of a typical fluid and a “singular” compressibility, 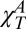, displaying critical behavior. The same approach was proposed for C_P(T) (26) and α_P(T) (25). Calorimetry, ultrasound (US) propagation, and hypersound Brillouin scattering (BS) experiments (24) were used to isolate the anomalous component in the bulk water response functions by measuring each ideal normal contribution separately. All of the apparently diverging functions fit a power-law form (the solid red line) analogous to that of ideal mode coupling theory 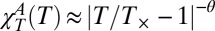and predict T_× ∼ 225 ± 2 K, a value identical to that found in the confined water transport parameters that support the existence of a dynamic crossover (9, 13).

In the case of structural relaxation, v = v(Q, T) can be evaluated as v(Q, T) = Γ(Q, T)/Q, where Γ is the maximum of the current I = ω²S(Q, ω), and the measured structure factor S(Q) gives the isothermal compressibility χ_T as S(0) = k_BTρ_Nχ_T in the hydrodynamic limit (Q → 0).

The studied response functions are: the compressibilities (isothermal and adiabatic) χ_T = (∂ ln ρ/∂ ln P)_T = −V⁻¹(∂V/∂P)_T, χ_S = (∂ ln ρ/∂ ln P)_S = −V⁻¹(∂V/∂P)_S; the coefficient of thermal expansion α_P = −(∂ ln ρ/∂T)_P = −V⁻¹(∂S/∂P)_T; and the specific heat C_p = T(∂S/∂T)_P. In terms of their corresponding thermodynamic fluctuations (δV, δP,δS), they are: χ_T = 〈δV²〉_P,T/k_BTV, χ_S = k_BT/V〈δP²〉_V,S, C_P = 〈δS²〉/k_B, and α_P = 〈δSδV〉/k_BTV.

The behavior of the response functions in bulk water can be characterized by the sound velocity dispersion, i.e., v = v(ω, Q), as evidenced by scattering, e.g., visible light Brillouin (BS) (18, 32) in the supercooled liquid region, and in the stable liquid phase [IXS (19), neutron (INS), and IUVS (33)]. These techniques have made possible the study of sound propagation from the moderately low (BS) and high (IXS and INS) ω regimes of S(Q, ω) (1–10 GHz using BS; 0.2–100 GHz using IUVS, and up to the THz range using IXS) (18, 19). The IXS scattered intensities I(E, Q) measured at different Q as a function of the energy E(meV) in the range 270 < T < 370 K, have proposed—in the plane E–Q (0 ÷ 30 meV and 1 ÷ 15 nm⁻¹)—the existence of pure liquid water with two dispersing branches of collective modes, both ω dependent. One of the branches has a sound velocity v_hf of ∼3,200 m/s, and the other a more normal v_us of ∼1,500 m/s. This sound velocity dispersion has been confirmed by using the BS, IUVS, and IXS experiments performed in supercooled bulk water in which Q is changed. This has been done in the visible light range (8 × 10⁻³ < Q < 3 × 10⁻² nm⁻¹) (18, 32), and in the IUVS range (3 × 10⁻² < Q < 0.1 nm⁻¹) (33) and, after examining the T behavior of the elastic modulus M(ω), a relaxed high-frequency sound velocity v_hf ∼ 3,000 m/s is obtained. In this latter case the process has been more correctly interpreted by assuming that water is a viscoelastic system and thus has a relaxing dynamic structure. More precisely, this dispersion is caused by relaxation processes in the local water structure originating in the HBs, exhibiting both a hydrodynamic normal liquid regime and a high-frequency solidlike regime. Because this latter regime is characterized by finite HB clusters of water molecules, the density fluctuations respond to the more stable (frozen) liquid and the sound velocity increases rapidly (20), a phenomenon that can be related to the hypothesized water polymorphism.

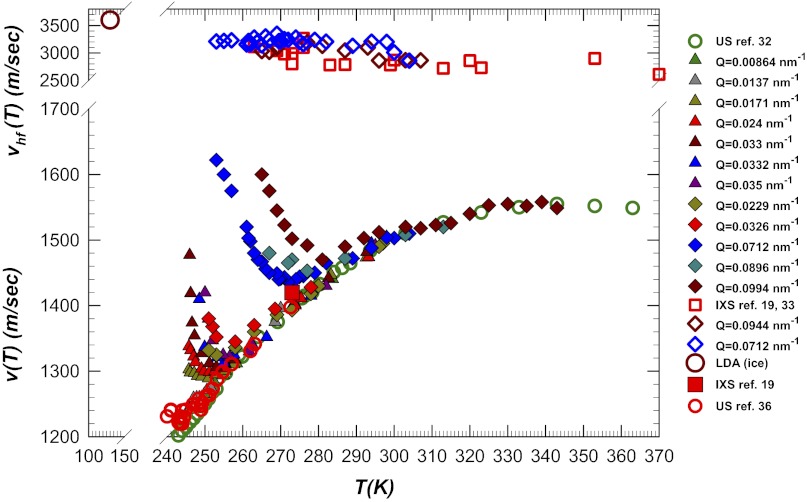
Fig. 5 shows the bulk water viscoelasticity indicated by the sound propagation results. In the BS (18, 32) and IUVS data (33) we see that the measured sound velocity v = v(Q) over a large temperature range 240 < T < 340 K (the stable liquid phase) is strongly dependent on the momentum transferred wave vector Q. Shown are data measured in three frequency regimes (over a wide ω range of 10⁴ < ω < 10¹³ Hz).

Fig. 5.

The measured viscoelastic behavior of bulk water (sound velocity data). (Bottom) The v(T) data measured using the BS (18, 32) and IUVS (full symbols) (33) techniques at different wave vectors (Q). At the top are the v_hf(T) data obtained using IXS (19, 34) and IUVS. The LDA data (large open dark red circles) (37) are also shown for comparison. The US data v_us are measured by using the AL technique at 54 kHz (35), the SS technique at 100 MHz (36), and the IXS technique in the THz regime (19, 34). The intermediate ω ranges are measured using BS (1–10 GHz) (18, 32) and IUVS (0.2–100 GHz) (33). For the sake of comparison the value of the longitudinal sound velocity measured in the LDA phase by means of the ultrasound at 5MHz (37) and the values of v_us and v_hf measured at 273 K using the IXS technique are also shown. Note that the AL data differ slightly from the US data and are, within experimental error, nearly constant when T < 245 K.

In characterizing sound velocity in bulk water we find that

• i) values of v_hf, measured at ω > 10⁹ Hz, slowly increase (within an experimental error) as T decreases;

• ii) the US–stimulated scattering (SS) velocity data, v_us(T), measured at 10⁸ Hz, nearly coincide with the corresponding data measured using the pulsed echo technique at 10⁷ Hz (23, 24), and they continue to decrease as T decreases; and

• iii) unlike the US data, the BS and the IUVS data show a strong wave-vector dependence accompanied by a positive dispersion with a minimum (v_min) at a certain temperature.

Hence the minimum velocity temperature is strongly dependent on the probe wave vector Q_exp, and for each Q_exp the speed of sound v(Q, T) evolves from the US value toward v_hf as a function of decreasing temperature. In all of the experiments producing this v(Q, T) behavior (18, 32, 33), the inelastic contributions to the S(Q, ω) are characterized by a marked broadening as T decreases. For the viscoelastic models this behavior is the result of a typical relaxation process evolving on a time scale that matches the reciprocal frequencies (time and length scales) of the longitudinal modes. Thus, when we decrease T and increase Q the structural relaxation drives the transition (Fig. 3) of the longitudinal mode v(Q, T) from the adiabatic limit v_us to the high-frequency limit v_hf. This behavior is seen in the physical properties of all glass-forming systems (and supercooled liquids)—structural relaxation allows a transition from the viscous to the elastic regime. It was recently shown that structural relaxation causes the transport properties of all supercooled liquids to be characterized by a dynamic crossover from super-Arrhenius to Arrhenius behavior (41). Using mode coupling to examine the hopping processes among these relaxing structures (39) we find the crossover temperature of the transition from liquidlike to solidlike behavior toward dynamic arrest (or glass transition). This crossover temperature can be verified using the power law form proposed by the ideal MCT.

Note Added in Proof.

After this work was submitted, we learned of some very interesting results (46) that offer theoretical arguments supporting the proposal of Kumar and Stanley (47), based on computer simulations, of a minimum of thermal conductivity, associated with the maximum of compressibility near the Widom line.