Choice-related activity and correlated noise in subcortical vestibular neurons

Abstract

Functional links between neuronal activity and perception are studied by examining trial-by-trial correlations (choice probabilities) between neural responses and perceptual decisions. We addressed fundamental issues regarding the nature and origin of choice probabilities by recording from subcortical (brainstem and cerebellar) neurons in rhesus monkeys during a vestibular heading discrimination task. Subcortical neurons showed robust choice probabilities that exceeded those seen in cortex (area MSTd) under identical conditions. The greater choice probabilities of subcortical neurons could be predicted by a stronger dependence of correlated noise on tuning similarity, as revealed by population decoding. Significant choice probabilities were observed almost exclusively for neurons that responded selectively to translation, whereas neurons that represent net gravito-inertial acceleration did not show choice probabilities. These findings suggest that the emergence of choice probabilities in the vestibular system depends on a critical signal transformation that occurs in subcortical pathways to distinguish translation from orientation relative to gravity.

Introduction

How response variability in sensory neurons is related to trial-by-trial variability in perceptual decisions is a fundamental question in systems neuroscience. To assess functional links between single neurons and perceptual decisions, neurophysiologists have measured trial-by-trial correlations between neuronal activity and perceptual reports for weak or ambiguous stimuli. By computing choice probabilities, these studies quantify the ability of an ideal observer to predict choices from neural responses¹. Choice probabilities have been measured in multiple cortical areas, including visual motion processing areas MT^1–6 and MSTd^7–9, other areas of visual cortex^10–13, and somatosensory cortex^{14, 15}.

Despite numerous studies, fundamental issues regarding the nature and origin of choice probabilities remain unresolved¹⁶. First, to our knowledge, all reports of significant choice probabilities have come from studies of cortical neurons. Thus, it is unclear whether subcortical neurons, closer to the sensory periphery, may exhibit choice probabilities. In some sensory systems, this question cannot be addressed because subcortical neurons do not exhibit the same forms of stimulus selectivity seen in cortex (e.g., binocular disparity selectivity in visual neurons). The vestibular system provides an excellent model to probe the origins of choice probability because the same basic forms of directional selectivity are seen from otolith afferents to cortical neurons¹⁷.

Second, the factors that drive the expression of choice probability in some neurons, but not others, remain unclear. For example, neurons in secondary visual cortex show significant choice probabilities during disparity discrimination whereas neurons in primary visual cortex do not¹⁰. One hypothesis is that choice probabilities appear when sensory signals are represented in an appropriate format for mediating the trained behavior, but evidence for this idea is lacking¹⁸. We examine whether choice probabilities correlate with the degree to which vestibular neurons represent translation without being confounded by orientation relative to gravity, a fundamental transformation that occurs in the vestibular brainstem and cerebellar nuclei^{19, 20}.

Third, the empirical relationship between choice probability and correlated noise among neurons remains unclear. Noise correlation provides a measure of shared input to neurons²¹, and computational studies reveal that choice probabilities depend strongly on the structure of correlated noise in neural populations^{16, 22, 23}. Without correlated noise, sizeable choice probabilities are observable only with implausibly small neuronal pool sizes. We examine whether differences in choice probabilities between subcortical and cortical neurons can be accounted for by differences in correlation structure across areas.

We address these issues by studying the vestibular nuclei (VTN) and cerebellar nuclei (CBN) during a vestibular heading discrimination task. VTN and CBN represent two important early stages of vestibular processing in the central nervous system¹⁷. Both areas, which have strong reciprocal connections²⁴, project to the thalamocortical system²⁵ and also receive projections from the vestibular cerebellum²⁶ and vestibular afferents²⁷. It is presently unknown whether VTN/CBN are polysynaptically connected with area MSTd²⁸, which was studied previously during vestibular heading discrimination⁹.

We compare data from VTN and CBN to those from area MSTd, measured under identical conditions. Our findings reveal robust choice probabilities in subcortical neurons and suggest that the emergence of choice probabilities is coupled with the ability of vestibular neurons to represent translation without being confounded by orientation relative to gravity. Our findings have important implications for understanding how response variability of sensory neurons relates to perceptual decisions.

Results

Neuronal discrimination thresholds

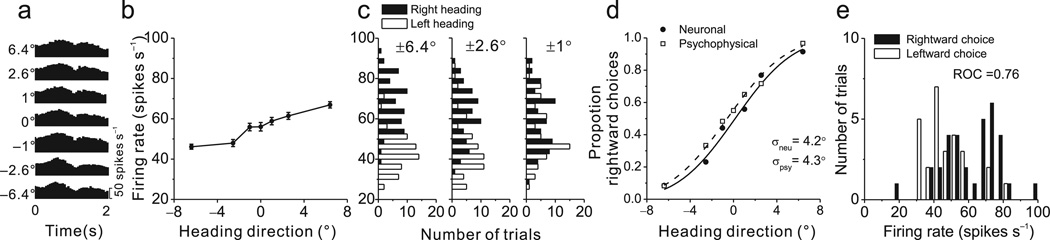
We recorded from neurons in the VTN and CBN, the latter coming mainly from the rostral fastigial nucleus and perhaps portions of the anterior interposed nuclei²⁹. Neurons with significant vestibular heading tuning in the horizontal plane (p<0.05, one-way ANOVA) were tested in a fine heading discrimination task, in which animals made saccades to indicate whether their perceived direction of translation was leftward or rightward relative to straight ahead⁹. Response histograms from an exemplar neuron reveal phasic responses to the dynamic stimulus (Fig. 1a). Over the narrow range of headings tested in the discrimination task (±6.4°), responses were monotonically tuned, with a preference for rightward motion (Fig. 1b).

Figure 1.

Quantification of neuronal sensitivity for an exemplar CBN neuron recorded during the heading discrimination task. (a) Response PSTHs for the 7 distinct heading directions. (b) Tuning curve, plotting firing rate (mean±s.e.m.) as a function of heading direction over a narrow range around straight-forward. Positive and negative headings indicate rightward and leftward directions, respectively. (c) Firing rate distributions for pairs of comparison headings, ± 6.4°, ±2.6° and ±1°. (d) Example neurometric function (filled symbols) showing proportion of ‘rightward’ decisions of an ideal observer as a function of heading direction. Each data point represents an ROC value computed from distributions like those shown in (c). The corresponding psychometric function is superimposed (open symbols). Solid and dashed lines show cumulative Gaussian fits. (e) Distribution of firing rates of the same neuron in response to an ambiguous 0° (straight forward) heading stimulus, grouped according to whether the monkey reported 'leftward' or 'rightward' motion. These distributions yielded a highly significant choice probability of 0.76 (p<<0.001).

To quantify neural sensitivity for discriminating heading, we used signal detection theory to transform firing rates into performance of an ideal observer^{9, 30}. When the difference between two headings is substantial (±6.4°), response distributions for leftward and rightward headings have little overlap (Fig. 1c), and the ideal observer makes few errors. In contrast, for a small difference in heading (±1°), response distributions overlap extensively and the ideal observer’s performance is close to chance.

This intuition is captured by using receiver-operating-characteristic (ROC) analysis⁹ to construct neurometric curves that are fit with cumulative Gaussian functions (Fig. 1d, filled symbols). The standard deviation of the Gaussian is taken as the neuronal threshold, which quantifies the precision with which an ideal observer can discriminate heading based on the neuron’s responses. The example neuron was nearly as sensitive as the animal (Fig. 1d, neuronal threshold: 4.2°, psychophysical threshold: 4.3°).

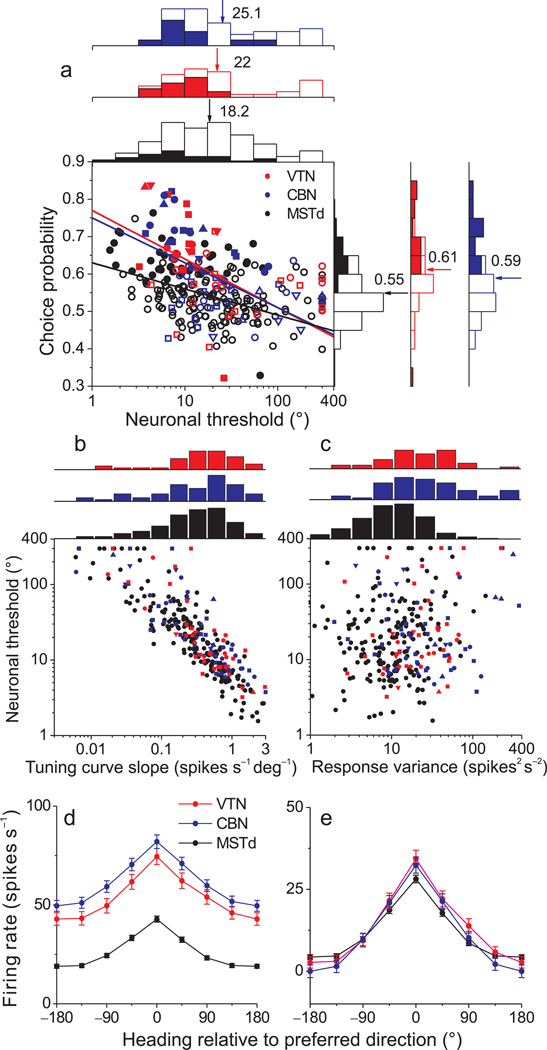
We recorded from 257 neurons (see Suppl. Fig. 1 for reconstruction of recording sites). Among these, 56 VTN and 91 CBN neurons had significant vestibular heading tuning, and 97 cells were tested with enough stimulus repetitions to be included in this analysis. Across the population, neuronal thresholds averaged 22 °±3.7 ° for VTN (geometric mean ± s.d., n=41) and 25.1°±3.4° for CBN (n=56). These values are slightly, but not significantly (p=0.4, Kruskal-Wallis test), greater than the mean neuronal threshold for area MSTd⁹ (18.2°±3.2°, n=183; Fig. 2a). When considering the 10% of neurons with the lowest thresholds, the mean neuronal threshold was significantly lower for MSTd than for the subcortical areas (MSTd: 3.0±0.24; CBN: 5.5±0.5; VTN: 4.4±0.5; Wilcoxon rank sum tests, p<0.05).

Figure 2.

Summary of neural sensitivity, choice probability, and tuning curves. (a) Scatter plot of choice probabilities against neuronal thresholds. Data are shown separately for VTN (red), CBN (blue), and MSTd (black). Solid lines indicate linear fits (type II regression, fit to threshold values ≤200). Filled symbols represent choice probability values that are significantly different from 0.5 (p < 0.05, permutation test). Symbol shapes denote data from different animals: upward triangles: monkey M (n=7); circles: monkey W (n=31); squares: monkey Y (n=49); downward triangles: monkey O (n=10). Also shown are marginal distributions of neuronal thresholds and choice probabilities. Filled and open bars indicate neurons with significant and non-significant choice probabilities, respectively. Arrows indicate the mean values. (b), (c) Relationship between neuronal threshold and local tuning curve slope (b) or response variance (c). Tuning curve slope was calculated by linear regression, over the narrow range of headings tested in the discrimination task. Response variance was computed only from the 0° heading data. (d), (e) Population heading tuning curves from CBN (blue, n=107), VTN (red, n=70) and MSTd (black, n=342) neurons before (d) and after (e) subtraction of spontaneous activity. Responses from each neuron were shifted along the horizontal axis to align the peaks of all tuning curves (at 0°) before averaging. Error bars denote s.e.m.

Only the most sensitive VTN/CBN neurons had thresholds that rivaled psychophysical performance (Suppl. Fig. 2a). Thus, the average neuronal to psychophysical (N/P) threshold ratios were >>1 (Suppl. Fig. 2a). These large N/P ratios are at least partially attributable to the fact that heading stimuli were not tailored to the tuning curves of individual neurons⁹.

Neural heading discrimination thresholds depend critically on two factors⁹: the slope of the cell’s tuning curve around straight-ahead and firing rate variability. Neuronal thresholds were strongly correlated with tuning curve slope (Fig. 2b, ANCOVA, p<0.001), and this dependence was similar across areas (interaction, p=0.08). There were no significant differences in tuning slope between VTN, CBN, and MSTd (Wilcoxon rank sum tests, p >0.13). Neuronal thresholds did not correlate significantly with response variance (Fig. 2c, ANCOVA, p=0.1), but variance was greater for both VTN and CBN neurons as compared to MSTd (Wilcoxon rank sum tests, p < 0.001), with no significant difference between VTN and CBN (p = 0.3).

We explored these issues further by fitting wrapped Gaussian functions³¹ to population heading tuning curves. Average tuning curves were similar between areas (Fig. 2d), especially when spontaneous activity was subtracted (Fig. 2e). Tuning curve amplitudes for VTN (mean 26 spikes/s) and CBN (25.1 spikes/s) were modestly but significantly greater than the amplitude for MSTd (21.1 spikes/s, p<0.05, bootstrap), with no significant difference between VTN and CBN (p>0.05). Tuning bandwidths for VTN (68.8 deg) and CBN (68.1 deg) were significantly greater than the bandwidth (59.9 deg) for MSTd (p<0.05). Note that the modestly greater tuning amplitudes in VTN/CBN vs. MSTd are somewhat counteracted by the broader bandwidths in VTN/CBN such that tuning curve slopes are similar across areas (Fig. 2b).

In contrast to these subtle differences in tuning curves, spontaneous activity was much greater in both VTN and CBN than in MSTd (Wilcoxon rank sum tests, p < 0.001; Fig. 2d), with no significant difference in mean Fano factor between areas (MSTd: 1.38; CBN 1.43; VTN 1.34; Kruskal-Wallis test: p = 0.12). Thus, differences in neural sensitivity between areas are mainly driven by differences in spontaneous activity, which translate directly into differences in response variance (Fig. 2c) by virtue of the similar Fano factors.

Relationship between neural activity and choices

For headings close to straight-ahead, monkeys make both ‘leftward’ and ‘rightward’ judgments in response to an identical sensory stimulus, and neural responses vary considerably from trial to trial. If neural activity in VTN/CBN is functionally linked to perceptual decisions, then trial-to-trial fluctuations in behavioral reports and neuronal responses should be correlated¹, as observed previously in area MSTd⁹. To quantify the relationship between neuronal activity and choice, responses were grouped according to the animal’s decision ('leftward' or 'rightward'). This is perhaps best illustrated for the ambiguous straight-forward stimulus (0° heading), which yields chance performance (50% correct). Although the sensory stimulus was identical for each trial, the neuron generally fired more strongly when the monkey made rightward decisions, in favor of the neuron’s preferred heading (Fig. 1e). This choice-related difference in activity was quantified by ROC analysis to compute choice probability, which measures how well an ideal observer can predict the monkey’s choice from the firing rate of the neuron. For this example neuron, the choice probability is 0.76, which is significantly greater than chance (permutation test, P < 0.001). Values of choice probability >0.5 indicate greater neural activity when the monkey chooses the neuron's preferred heading. In contrast, choice probability values <0.5 denotes the counterintuitive situation in which greater activity accompanies choices toward the neuron’s non-preferred heading.

At the population level, choice probabilities averaged 0.61±0.02 s.e.m. for VTN and 0.59±0.01 for CBN neurons. Both values were significantly greater than chance (P<0.001) and also significantly greater than the mean value for area MSTd (0.55±0.01) (p<0.001, Wilcoxon rank sum tests, Fig. 2a). Previous work has shown that choice probabilities are inversely correlated with neuronal thresholds^{1, 8, 9}, such that more sensitive neurons tend to show greater choice probabilities. VTN and CBN neurons both exhibited this relationship (Fig. 2a, VTN: R= −0.41, p=0.008; CBN: R= −0.48, p=<0.001; type II regression). Notably, the slope of the relationship between choice probability and neuronal threshold was steeper for VTN and CBN than for MSTd (p=0.03, interaction effect, ANCOVA), whereas the slopes were not significantly different between VTN and CBN (p = 0.8). Indeed, regression slopes for subcortical neurons were roughly double that for MSTd neurons (VTN: slope = −0.13; 95% confidence interval= [−0.25, −0.06]; CBN: −0.12, [−0.18, −0.06]; MSTd: −0.07, [−0.09, −0.04]). Thus, VTN/CBN neurons tend to have greater choice probabilities than MSTd neurons of comparable sensitivity.

Time course of neural thresholds and choice probabilities

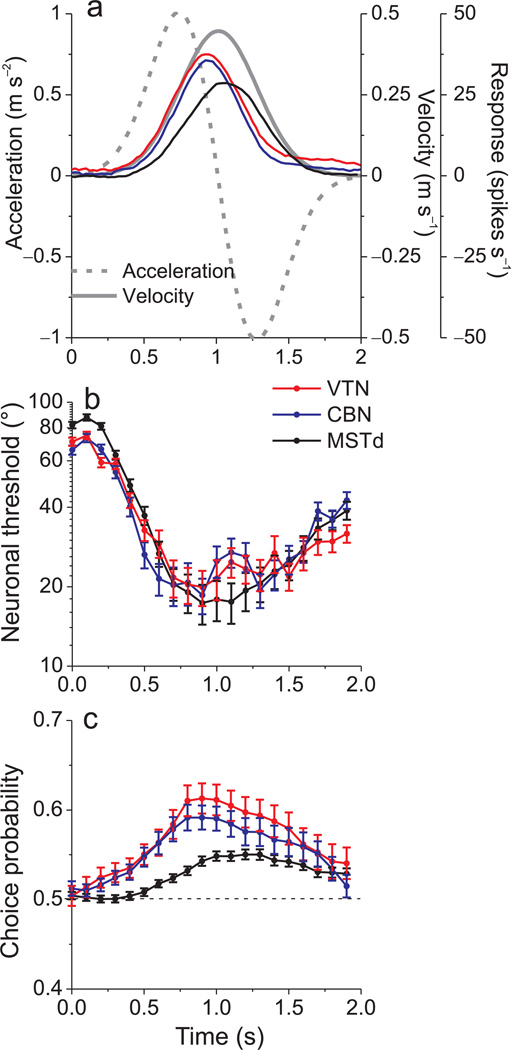
The analyses summarized above were based on firing rates computed from the middle 400ms of the 2s stimulus period (around peak stimulus velocity). However, the motion stimulus has a Gaussian velocity profile, and population responses in all 3 areas roughly follow this profile (Fig. 3a, MSTd data re-plotted from Refs^{8, 9}). By repeating our analyses for numerous 400ms time windows spaced 100 ms apart, we computed the time course of neuronal threshold and choice probability. For all three areas, thresholds were smallest around the time of peak responses and were greatest during early and late time windows, when firing rates were low (Fig. 3b). Minimum thresholds were reached slightly earlier in VTN and CBN than in MSTd (Fig. 3b), likely reflecting the fact that population responses peak somewhat earlier in VTN/CBN (Fig. 3a; see also Suppl. Fig. 3).

Figure 3.

Time courses of response amplitude, neuronal thresholds, and choice probabilities. (a) Average evoked responses at the preferred heading (with spontaneous activity subtracted) for 56 CBN neurons (blue), 41 VTN neurons (red) and 183 MSTd neurons (black). The stimulus motion profile is also shown (solid gray curve: velocity; dashed gray curve: acceleration). (b), (c) Average neuronal threshold and choice probability as a function of time. Each point represents data computed in a 400ms analysis window that is shifted by a multiple of 100ms. Error bars denote s.e.m.

Whereas neuronal thresholds were very similar across areas, the time course of choice probability reveals that VTN/CBN cells exhibited larger choice probabilities than MSTd neurons throughout the stimulus period (Fig. 3c). Choice probabilities in VTN/CBN rise significantly above chance earlier during the response, and reach substantially larger magnitudes than choice probabilities in MSTd (p< 0.001, Wilcoxon rank sum tests). Toward the end of the stimulus epoch, when mean responses decline, VTN/CBN choice probabilities decrease and become similar to those in MSTd (p=0.9, Wilcoxon rank sum tests). Because the relative values of choice probability and neuronal threshold across areas are fairly consistent over time, the following analyses focus on a 400 ms time window centered on peak stimulus velocity.

Choice probabilities correlate with translation coding

A critical question is whether choice probabilities are related to the nature of the information that is coded by sensory neurons. We examined whether choice probabilities are correlated with an important functional property of vestibular neurons—their ability to resolve the gravito-inertial acceleration ambiguity. All linear accelerometers, including the otolith organs in the inner ear, are unable to distinguish orientation relative to gravity from inertial accelerations; rather, they signal the net gravito-inertial acceleration.

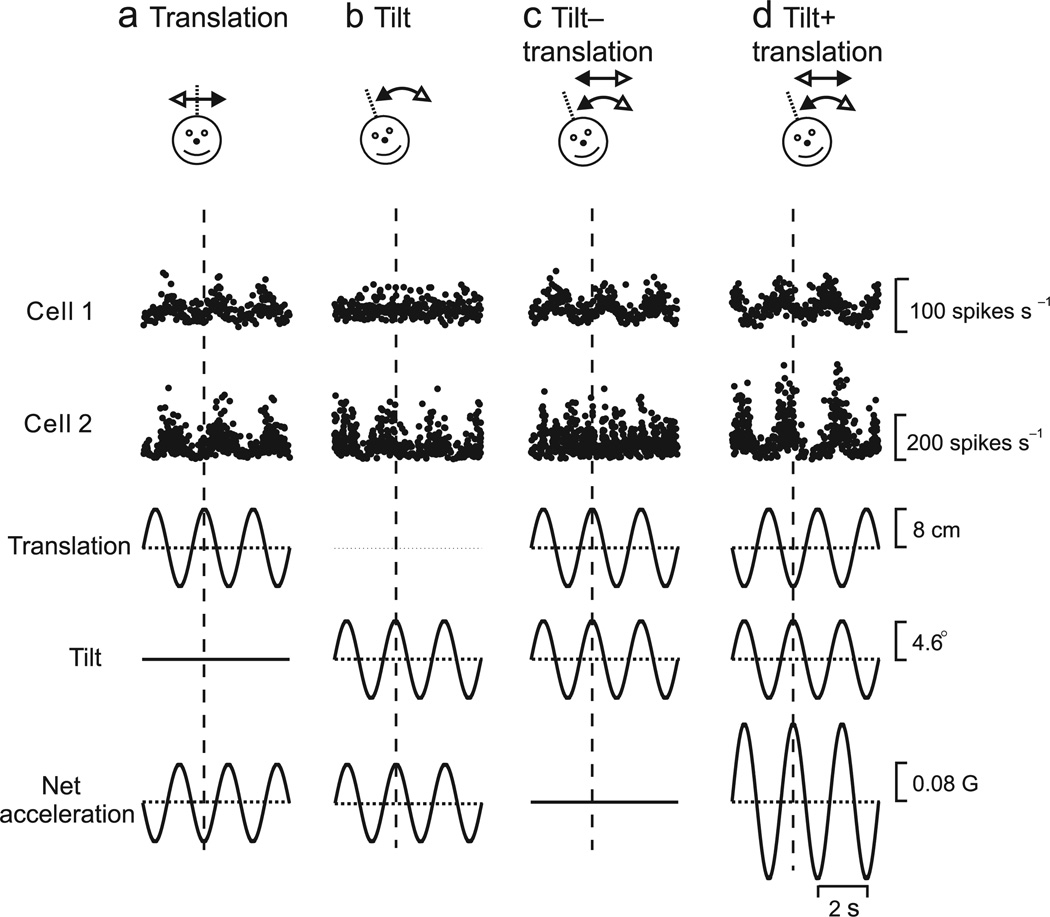
This sensory ambiguity is partly resolved at the level of VTN/CBN neurons, some of which selectively respond to translation and ignore changes in head orientation relative to gravity¹⁹. If choice probabilities reflect a functional linkage of vestibular neurons to heading perception, then we hypothesize a correlation between choice probability and the selectivity of VTN/CBN neurons for translation. To test this hypothesis, 17 VTN and 23 CBN neurons were further characterized using sinusoidal (0.5 Hz) translation, sinusoidal tilt relative to gravity, and combinations of the two stimuli¹⁹ (Fig. 4, top). Tilt amplitude was chosen such that the horizontal component of linear acceleration due to gravity equals that produced by translation (see Methods). Hence, neurons that respond like otolith afferents should respond similarly during translation and tilt (Fig. 4a,b), confounding the two variables. In contrast, neurons that respond selectively to translation but not tilt should be ideal for mediating heading perception.

Figure 4.

Examples of CBN (cell 1) and VTN (cell 2) responses during sinusoidal stimulation protocols involving (a) translation only, (b) tilt only, and (c), (d) combined translation and tilt. For ‘tilt−translation’ (c), translational and gravitational accelerations cancel each other; for ‘tilt+translation’ (d), the translational and gravitational accelerations add together. Translation and tilt waveforms (bottom traces) were tailored in both amplitude and direction to elicit identical net accelerations in the horizontal plane^{19, 20}. Vertical dotted lines mark stimulus peak.

Although net acceleration was the same during translation and tilt, translation-coding VTN/CBN neurons, such as cell 1 (Fig. 4a,b), responded robustly during translation but not during tilt. When translation and tilt combined such that the horizontal component of net linear acceleration is either nulled (tilt − translation, Fig. 4c) or doubled (tilt+translation, Fig. 4d), translation-coding neurons such as cell 1 respond as though stimulated by translation alone. Such cells can reliably represent heading without being biased by spatial orientation relative to gravity. In contrast, neurons like cell 2 respond similarly during tilt and translation (Fig. 4a,b). When tilt and translation are combined, responses of such cells follow the net gravito-inertial acceleration (Fig. 4c,d), similar to primary otolith afferents¹⁹.

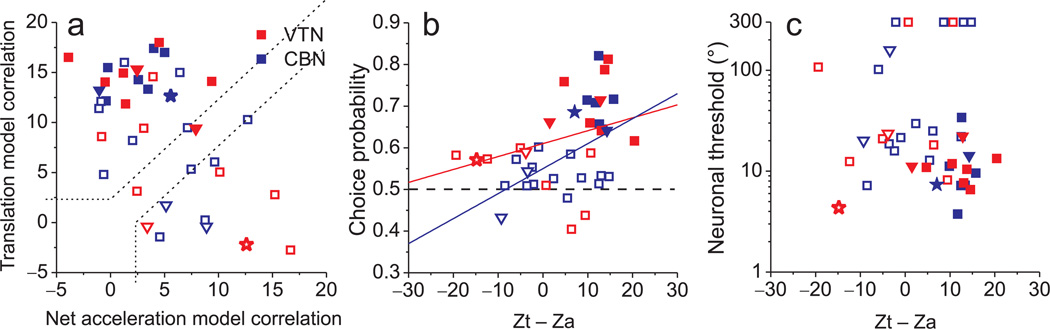
A regression analysis was used to compute partial correlation coefficients that describe how well each neuron’s responses could be predicted by net acceleration or translation. Fisher’s r-to-z transform was used to normalize the partial correlation coefficients¹⁹, which were then plotted against each other (Fig. 5a, dotted lines mark boundaries at p=0.01 significance). Almost all VTN and CBN cells with significant choice probabilities fall in the upper-left region (Fig 5a, filled symbols), indicating that their responses are significantly better correlated with translation. In contrast, most neurons with insignificant choice probabilities fall in the lower-right region, indicating a better correlation with net acceleration.

Figure 5.

Choice probabilities depend on the translation/net acceleration coding property of VTN/CBN cells. (a) Scatter plot of z-transformed partial correlation coefficients derived from fits of each cell’s responses with a translation-coding model and net-acceleration-coding model. Dashed lines divide the plots into three regions: an upper/left area corresponding to responses that are significantly better fit by the translation-coding model, a lower/right area that includes neurons that are significantly better fit by the net acceleration-coding model, and an intermediate zone in which neither model is significantly better than the other. Star-shaped symbols mark the 2 cells from Fig. 4. (b) Scatter plot of choice probability vs. the difference in z-scores between the translation and net-acceleration models (Zt – Za). Red and blue lines represent type II linear regression fits for VTN and CBN, respectively. (c) Scatter plot of neuronal threshold vs. the difference in z-score between translation and net acceleration models. In all panels, filled symbols denote cells with significant choice probabilities, whereas open symbols denote non-significant choice probabilities (CBN: blue; VTN: red; MSTd: black). Downward pointing triangles and squares indicate data from monkeys O (n=6) and Y (n=34), respectively.

This observation is clarified by plotting choice probability as a function of the difference in z-score between the translation and net acceleration models (Fig. 5b). Pooling data from VTN and CBN together, there is a highly significant correlation between choice probability and translation coding (R = 0.47, p < 0.001, Spearman correlation), which also reaches significance for each subcortical area separately (VTN: R = 0.54, p = 0.03; CBN: R = 0.55, p = 0.01). In contrast, there is no significant correlation between neuronal thresholds and the z-score difference between models (Spearman correlation, VTN: R = −0.26, p = 0.31; CBN: R = −0.08, p = 0.7; pooled: R = −0.17, p = 0.3, Fig. 5c). Thus, the larger choice probabilities of translation-coding neurons cannot be simply explained by differences in neuronal sensitivity.

Noise correlations are greater in subcortical neurons

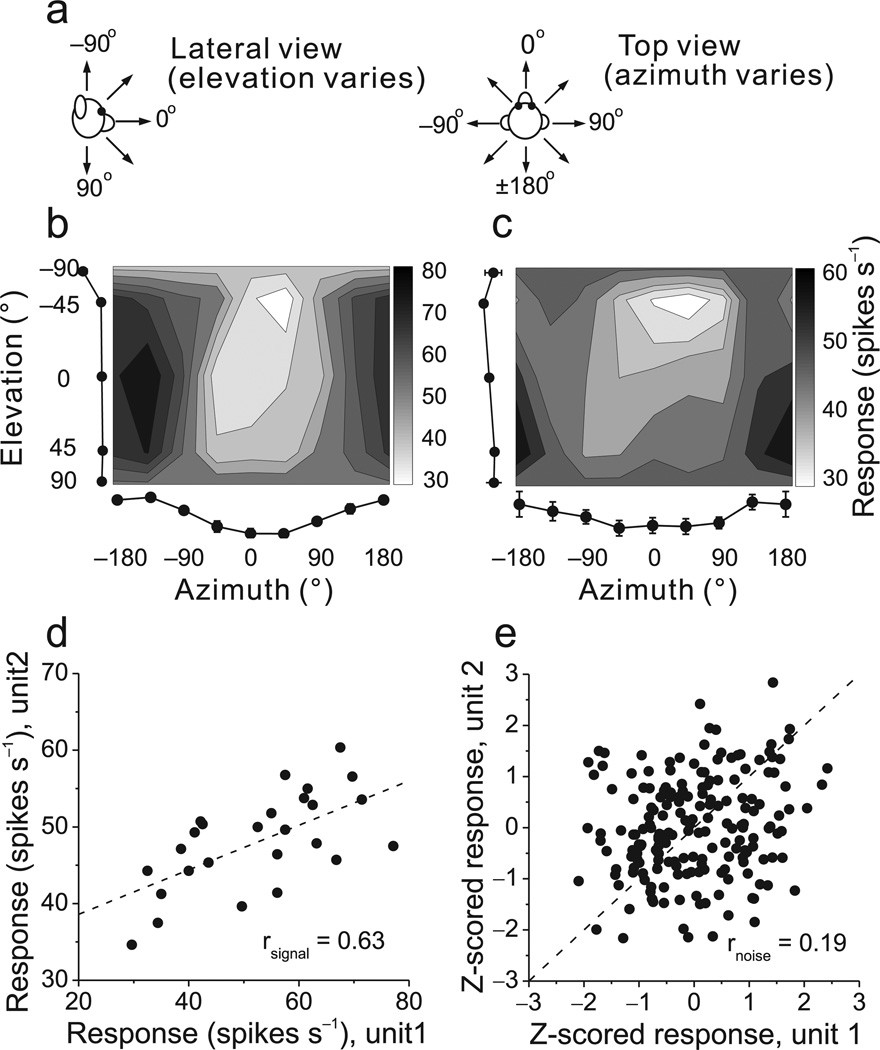
Previous work has suggested that the magnitude of choice probabilities is determined largely by the strength of correlated noise among neurons^{13, 16, 23}. To test whether the large choice probabilities found in subcortical neurons can be attributed to noise correlations, we recorded simultaneously from pairs of VTN/CBN neurons while fixating monkeys were translated along 26 directions spaced evenly in 3D (Fig. 6a)^32–35. The heading tuning profiles of an example pair of CBN cells (Fig. 6b, c) reveal that both neurons were significantly tuned (ANOVA, p<0.001 and p=0.006, respectively), with similar heading preferences given by [azimuth, elevation] = [−161°,7°] and [−183°, 32°], respectively. The similarity of tuning for such a pair of neurons, known as signal correlation (r_signal), was quantified as the Pearson correlation coefficient of mean responses from the 3D heading tuning profiles (Fig. 6d).

Figure 6.

Measuring noise correlation (r_noise) and signal correlation (r_signal) between pairs of single neurons. (a) Schematic illustration of the azimuth and elevation variables in the heading tuning protocol. (b), (c) Example heading tuning profiles for a pair of simultaneously recorded CBN neurons. Grayscale maps (Lambert cylindrical equal-area projections) show mean firing rate as a function of azimuth and elevation angles. The tuning curves along the margins of each grayscale map illustrate mean ±SEM firing rates plotted as a function of either elevation or azimuth (averaged across azimuth or elevation, respectively). (d) Comparison of the mean responses of the two neurons across all heading directions. The Pearson correlation coefficient of the mean responses quantifies ‘signal correlation’, r_signal =0.63. (e) Normalized responses from the same two neurons were weakly correlated across trials. Each datum represents z-scored responses from one trial. The Pearson correlation coefficient of the data quantifies ‘noise correlation’, r_noise =0.19. Dashed lines: unity-slope diagonals.

As in cortical areas, the spike counts of subcortical neurons in response to an identical stimulus vary from trial to trial, as illustrated for the example pair of neurons (Fig. 6e, see also Suppl. Fig. 4). Each data point in this plot represents a normalized spike count from each neuron for a single trial. Spike counts for each heading were z-scored to remove the effect of stimulus variations, thus allowing us to pool data across headings to gain statistical power (see Methods). Noise correlation (r_noise), which quantifies correlated neuronal variability across trials, was then computed as the Pearson correlation coefficient of the z-scored spike counts. For the example pair or neurons (Fig. 6d,e), r_signal = 0.63 (p<0.001) and r_noise=0.19 (p=0.008). The significant positive noise correlation indicates that, when one neuron fired more spikes than average, the other neuron tended to fire above average as well. Across the population, noise correlations averaged 0.004±0.02 s.e.m. for VTN (n=47) and 0.03±0.03 for CBN (n=63), and these values were not significantly different from zero (p = 0.17, p = 0.91, t-test).

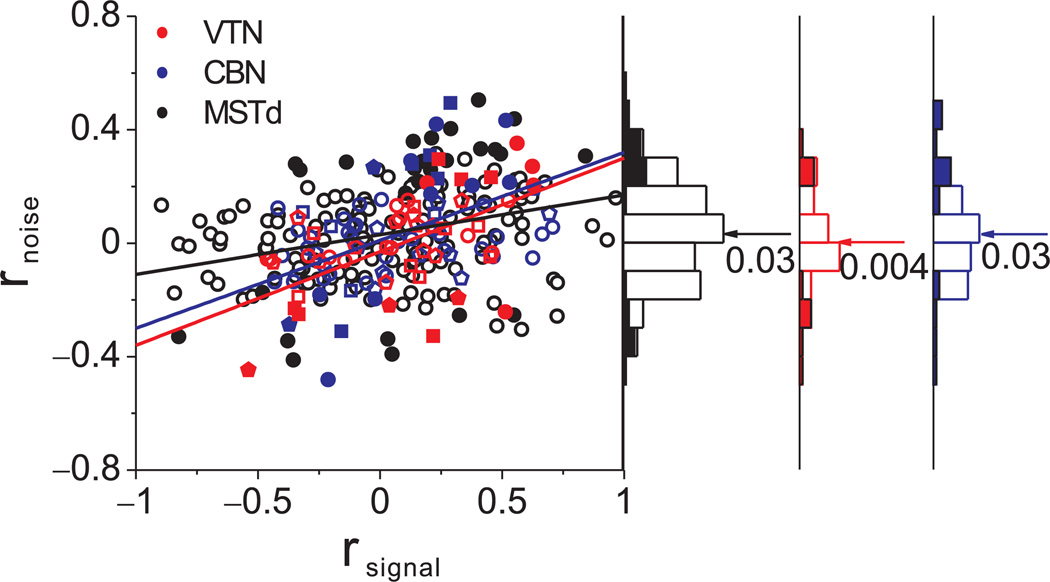
In cortical areas studied previously, including MSTd, r_noise generally shows a strong dependence on tuning similarity (r_signal)^{34, 36–40}. Similarly, there was a strong and significant correlation between r_noise and r_signal in VTN and CBN (p < 0.001, ANCOVA, Fig. 7). Notably, a substantial number of VTN/CBN pairs had large noise correlations (|r_noise|>0.4), but the population mean was not significantly different from zero because r_noise was equally likely to be positive or negative (see also Ref⁴¹). Moreover, the linear relationship between r_noise and r_signal was steeper for VTN/CBN than for MSTd (ANCOVA, p=0.03, interaction effect), even though the mean noise correlation was not significantly different among areas (Fig. 7, Wilcoxon rank sum tests, p>0.32). Hence, the difference in average choice probability between VTN/CBN and MSTd cannot simply be due to differences in average noise correlations, but may instead be due to differences in the slope of the relationship between r_noise and r_signal, as discussed below.

Figure 7.

Relationship between noise correlation (r_noise) and signal correlation (r_signal). Scatter plot of r_noise versus r_signal for pairs of neurons from VTN (red), CBN (blue) and MSTd (black). Marginal distributions of r_noise are also shown (right panels). Arrows and numbers mark the mean values of r_noise for each area. Symbol shape denotes different animals (circles: monkey W, n=59; squares: monkey Y, n=23; pentagon: monkey V, n=28), and lines represent type II linear regression fits.

A few additional differences between properties of r_noise in VTN/CBN vs. cortex should be noted. First, we found no significant dependence of r_noise on the distance between neurons in a pair for VTN and CBN (Suppl. Fig. 5a). This is different from what we observed in MSTd³⁴, and from observations in other cortical areas^{39, 42}. Second, unlike in MSTd where the mean r_noise was lower in trained than untrained animals³⁴, no significant effect of training was seen in VTN/CBN (Suppl. Fig. 5b).

Population decoding predicts choice probabilities

We now consider the possibility that the greater choice probabilities observed for subcortical neurons, relative to MSTd, can be attributed to differences in the structure of interneuronal correlations between areas (slope of r_noise vs. r_signal). To test this hypothesis quantitatively, we simulated population responses based on measured response statistics from our sample of neurons (see Methods). Correlated noise was introduced into simulated population responses by constructing a covariance matrix based on the observed relationships between r_noise and r_signal.

We decoded the simulated population responses using an empirical linear decoder based on the Support Vector Machine (SVM)⁴³. This decoder was chosen because it does not make particular assumptions about the statistics of neural activity or correlated noise. Instead, it learns the structure of spike count statistics in the training data and acquires the optimal parameters to classify whether population responses were elicited by a leftward or rightward heading. We trained the linear classifier to discriminate heading based on two sets of training data: responses pooled across all leftward headings and responses pooled across all rightward headings (see Methods). The trained decoder was then applied to a set of test trials in which the ambiguous straight-forward heading was presented, and classifier output was taken as the decision regarding perceived heading. Thus, classifier output was used to compute a predicted choice probability for each simulated neuron. In addition, neuronal thresholds were computed by applying ROC analysis to the responses of each simulated neuron. This allowed us to predict the relationship between choice probability and neuronal threshold for VTN, CBN, and MSTd, based on our measurements of tuning curves and correlation structure.

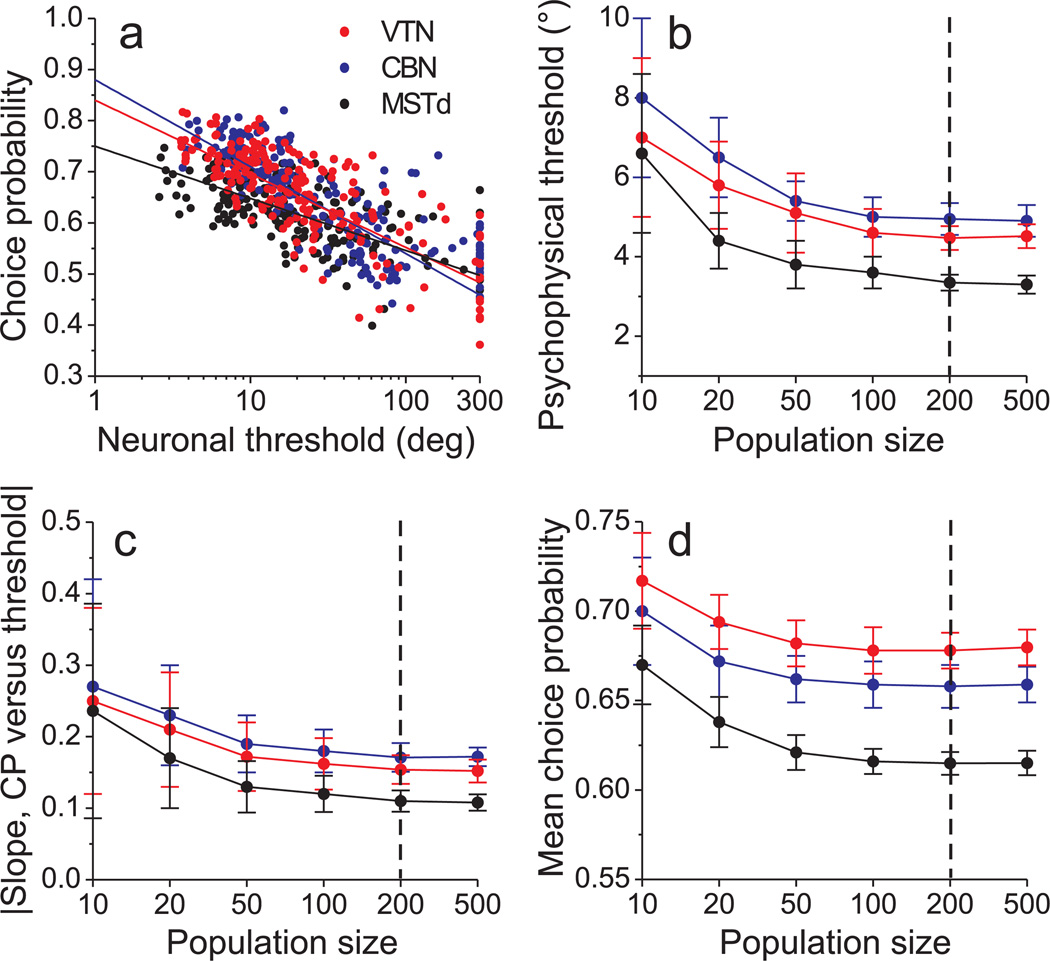
The relationship between predicted choice probabilities and neuronal thresholds is shown in Fig. 8a for one iteration of the simulation for each brain area (200 simulated neurons per area). The classifier achieved performance levels of 76% correct for VTN, 73% for CBN, and 79% for MSTd (10-fold cross-validation, pooled across all non-zero headings). Results of this simulation (Fig. 8a) capture the key features seen in the real data (Fig. 2a): higher choice probabilities for VTN/CBN, as compared to MSTd, and a steeper slope of the relationship between neuronal threshold and choice probability.

Figure 8.

Predicted relationship between choice probabilities and neuronal thresholds, derived from decoding simulated population responses. (a) Predicted choice probabilities against neuronal thresholds for a simulated population of 200 neurons from each area. Data are shown for one instantiation of the simulation. Solid lines indicate linear fits (type II regression, fit to threshold data ≤200). (b) The predicted psychophysical threshold (from decoding) is plotted as a function of the number of neurons in the simulated neural populations. Data points represent averages across 30 iterations of the simulation, with each iteration based on a different re-sampling (with replacement) of neurons from the original data sets. Error bars denote s.d. Data are shown for CBN (blue), VTN (red) and MSTd (black). (c) Average slope of the type II linear regression fit to the choice probability vs. neuronal threshold relationship as a function of population size. Each data point represents mean (±95% confidence interval) values obtained from 30 iterations of the simulation. (d) Average choice probability (±s.d.) as a function of population size for each area.

As expected^{22, 23}, decoder performance depends quantitatively on the size of simulated neural populations. The predicted psychophysical threshold of the decoder (Fig. 8b) declines with the number of neurons in the simulation, and decoder performance becomes comparable to that of most animals (Suppl. Fig. 2c) for populations larger than ~100 neurons. The slope of the relationship between neuronal threshold and choice probability also decreases with population size (Fig. 8c), reaching a plateau for populations larger than ~200 cells (see also Suppl. Fig. 6). As a result, the mean predicted choice probability for each area also declines with population size (Fig. 8d). This is expected because the contribution of each neuron becomes smaller as more cells are included in the population^{22, 23}. Critically, for all population sizes examined, the simulation predicts a steeper choice probability-threshold relationship for VTN/CBN than MSTd and the difference is significant for population sizes greater than ~50 neurons (Fig. 8c). Thus, the qualitative match between model predictions and real data (Fig. 2a) is fairly robust to population size.

These results (Fig. 8) were derived from a decoder that was not privy to the structure of interneuronal correlations among the simulated neurons. Results from a variant of the SVM decoder that knew the correlation structure (Suppl. Fig. 7) were qualitatively similar, except that predicted psychophysical thresholds continued to decline with population size (Suppl. Fig. 7b). Qualitatively similar results were also obtained when using a standard maximum likelihood decoder^{44, 45} that assumes independent Poisson statistics (Suppl. Fig. 8). Thus, our main simulation results (Fig. 8a) appear to be fairly robust to assumptions regarding interneuronal correlations and whether they are known to the decoder. However, considerable further research is needed to understand how different types of correlation structures, as well as different possible types of suboptimality in decoding, may affect the choice probabilities that are expected.

We did not attempt to fit the simulation results of Fig. 8 to empirical data. The parameters of the simulation were determined from the tuning properties and spiking statistics of recorded neurons, and the weights in the decoder were optimized only to maximize heading discrimination performance. Overall, these results suggest that the stronger choice probabilities observed in VTN and CBN, relative to MSTd, can be accounted for by the stronger dependence of r_noise on r_signal in these subcortical areas.

Discussion

We explored the relationships between neuronal sensitivity, choice probabilities, and correlated noise to better understand how sensory signals are processed to generate perceptual decisions. Our findings can be summarized as three main points: (1) Subcortical neurons exhibit robust correlations with perceptual decisions, thus establishing that choice probabilities are not only the province of cerebral cortex. Indeed, choice probabilities were found to be larger for brainstem/cerebellar neurons than for cells in area MSTd having comparable sensitivity. (2) Strong choice probabilities were observed for VTN/CBN cells that selectively encode self-translation, but not for neurons that signal net gravito-interial acceleration, which is presumably less useful for heading perception. This suggests that functional coupling between vestibular neurons and perception emerges from a critical signal transformation that converts signals into a format more appropriate to drive heading perception. (3) The dependence of noise correlation on signal correlation was substantially steeper for VTN and CBN neurons than MSTd cells. Simulations based on the measured tuning properties and correlation structure of each area were able to replicate the pattern of choice probabilities and neuronal thresholds across areas. This finding implies that differences in the strength of choice-related modulations across brain areas are attributable, at least in part, to differences in the structure of interneuronal noise correlations. These findings have important general implications for understanding how sensory neural responses are coupled to perceptual decisions.

Neuronal sensitivity

Like cortical neurons during fine discrimination tasks^{4, 8, 9, 46, 47}, the average VTN/CBN neuron in our sample was much (~6-fold) less sensitive than the animal. Neuronal thresholds were slightly greater in VTN/CBN than in MSTd, due to greater response variability that arises from higher spontaneous activity in subcortical neurons. The lowest thresholds were observed for neurons with preferred directions roughly orthogonal to straight-ahead, as expected because these neurons operate around the steep portion of their tuning curves^{4, 8, 9, 48}.

To our knowledge, only one study has previously characterized direction discrimination thresholds in the vestibular brainstem/cerebellum⁴⁹, and that study reported substantially greater neuronal thresholds relative to the present study (VTN: 72.3° vs. 22°; CBN: 58.8° vs. 25.1°). Several differences between the two studies likely account for this discrepancy: (1) Here, we used transient stimuli with a dominant frequency of 0.5 Hz, whereas Liu et al.⁴⁹ used 2 Hz sinusoidal stimuli. (2) The two studies used different motion platforms, which likely have different vibration characteristics. (3) Parameters of the ROC analysis were different. Here, we considered only a narrow range of headings (±6°), whereas Liu et al.⁴⁹ used a broader range (±20°). Here, we capped neuronal thresholds at 300°, but this was not done by Liu et al.⁴⁹. To compare more directly, we re-analyzed the data of Liu et al.⁴⁹ using parameters comparable to the present study. This yielded thresholds of 38°±3.1° for VTN and 32.8°±3.1° for CBN, which are much closer to the values obtained in the present study.

The present results are directly comparable to neuronal thresholds from area MSTd⁹, because identical stimuli and analyses were used. In both studies, stimuli were not tailored to the tuning preferences of each neuron, as done in previous studies of visual cortex³⁰. Because we recorded from every neuron that was sensitive to translation in the horizontal plane, our data represent a largely unbiased sampling of the vestibular-only cell population in VTN/CBN. It will be of great interest to characterize direction discrimination thresholds of otolith afferents and compare these to our data from VTN/CBN.

Choice probabilities

We found robust trial-by-trial correlations between responses of VTN/CBN neurons and monkeys’ perceptual decisions about heading. To our knowledge, significant choice probabilities have not been reported for neurons outside of cerebral cortex. Perhaps surprisingly, average choice probabilities in VTN/CBN were larger than average choice probabilities reported for most cortical areas, with mean choice probability values of 0.61±0.02 for VTN and 0.59±0.01 for CBN. Moreover, the most sensitive VTN/CBN neurons showed choice probabilities as large as 0.8–0.85. By comparison, the original study of choice probabilities in visual area MT found a mean value of 0.56 for coarse visual direction discrimination¹, and other MT studies reported mean choice probabilities of 0.55 for fine direction discrimination⁴, 0.52 for speed discrimination³, and 0.59 for disparity discrimination⁵. Previous studies of area MSTd have found mean choice probabilities of 0.55 for fine vestibular heading discrimination^{8, 9}. To our knowledge, only the study of Dodd et al.², involving perception of bistable structure-from-motion displays, found an average choice probability (0.67) larger than what we have observed in VTN/CBN.

A fundamental question involves the factors that determine the magnitude of choice probability effects across different brain areas. There is some evidence that choice probabilities increase from peripheral to more central stages of sensory processing. For example, binocular disparity-selective neurons in secondary visual cortex show significant choice probabilities, whereas equally sensitive neurons in primary visual cortex do not¹⁰. Similarly, choice-related effects in the somatosensory system appear to increase from primary somatosensory cortex to higher levels of processing¹⁵. One possibility is that choice probabilities emerge when sensory signals are represented in a format that is useful for the task at hand. In this respect, the vestibular system provides a unique opportunity to study the origins of choice probability because vestibular neurons have similar spatio-temporal properties all the way from vestibular afferents to the cortex. In contrast, neural correlates of heading or depth perception cannot be studied in the visual periphery of primates because neurons in the retina or thalamus do not exhibit tuning for optic flow or binocular disparity.

We found that VTN/CBN neurons which encode translation show significant choice probabilities, whereas neurons that represent net gravito-inertial acceleration do not. This finding suggests that a critical signal transformation in sensory pathways can lead to the emergence of choice probabilities. Specifically, we suggest that the transformation of vestibular signals, from representing net gravito-inertial acceleration to representing translation^{19, 20}, is the critical step that places these signals in a format that is useful for heading perception. All primary otolith afferents suffer from the linear acceleration ambiguity problem¹⁹, thus their responses would be inappropriate for driving heading perception. We predict, therefore, that otolith afferents would not exhibit significant choice probabilities in our task, and this is a current topic of investigation in the laboratory.

Our results also have relevance to the important issue of whether choice probabilities arise through a “bottom-up” or “top-down” mechanism^{13, 16}. In a bottom-up scheme, trial-to-trial variability in a population of neurons drives fluctuations in perceptual decisions. In a top-down scheme, feedback from decision-making centers (or a featural attention signal) modulates the responses of sensory neurons¹³. Our finding that only translation-coding neurons show choice probabilities (Fig. 5) is consistent with a bottom-up mechanism. The logic is that, once the signals carried by VTN/CBN neurons are transformed to represent translation, fluctuations in neural activity become linked to fluctuations in perceptual reports.

Alternatively, the result of Fig. 5 could be consistent with a top-down scheme provided that decision-related signals or featural attention signals selectively target translation-coding neurons in VTN/CBN. Although plausible, this possibility appears less likely given that there is only weak clustering of heading tuning in VTN/CBN (Suppl. Fig. 9). Without robust clustering, it may be difficult to target top-down signals to the appropriate neurons. If choice probabilities are generated by top-down feature-based attention signals, why should such attention signals propagate as far back as the brainstem? Such an interpretation would imply that subcortical areas participate in a network loop that implements decision making by altering the sensory information that reaches ‘decision-making’ areas.

Impact of noise correlations on choice probabilities

Correlated noise among neurons plays important roles in determining the information capacity of a population code⁵⁰. In general, correlated noise could either decrease or increase the amount of information represented by a population of neurons, depending on how correlated noise is structured relative to signal correlations^{23, 39, 40, 50}. Weak but significant noise correlations have been measured in a number of cortical areas^{21, 22, 40}, and the structure of noise correlations can be modified by task demands³⁷, attention³⁶, and learning³⁴.

Correlated noise should have a profound impact on choice probabilities, particularly for large neuronal populations¹⁶. Without correlated noise, sizeable choice probabilities are possible only when decisions are based on implausibly small pools of neurons²³. In contrast, when neurons share correlated noise, they may exhibit significant choice probabilities even when they do not contribute at all to decisions²². Hence, we hypothesize that differences in choice probability across brain areas are mainly driven by differences in the structure of correlated noise, but this hypothesis had not been tested previously.

In this study, we found a robust correlation structure in VTN and CBN. Critically, our simulations demonstrate that it is not the average noise correlation value that determines choice probabilities, as mean noise correlations were not significantly different from zero in VTN, CBN or MSTd. Rather, the key factor appears to be the relationship between r_noise and r_signal (Fig. 7). For a given pool size, a steeper relationship between r_noise and r_signal leads to a greater average choice probability and a steeper relationship between choice probability and neuronal threshold (Fig. 8, Suppl. Fig. 6). Indeed, our simulations, which were constrained by measured data, demonstrate that differences in choice probabilities across areas can be largely accounted for by variations in correlation structure.

In closing, our findings demonstrate that subcortical neurons exhibit robust correlations with perceptual decisions, and suggest that choice probabilities emerge when sensory signals are represented in a format that is useful for driving behavior. Moreover, the vestibular system is ideally suited to further exploration of the relationships between sensory neural activity and perceptual decisions.

Methods

Subjects and apparatus

Five rhesus monkeys (Macaca mulatta, 4–6 kg) were chronically implanted with an eye coil, head-restraint ring, and a plastic recording grid^{35, 51}. All procedures were approved by the Institutional Animal Care and Use Committee at Washington University and were performed in accordance with institutional and NIH guidelines. Motion stimuli were delivered using a six-degree-of-freedom motion platform (Moog 6DOF2000E), as described previously³⁵.

Electrophysiological recordings

We recorded extracellular activity of single neurons in VTN and CBN using tungsten microelectrodes (FHC, 5–7 MΩ impedance). We used the location of the abducens nuclei (mapped in preliminary experiments) to guide electrode penetrations into the CBN and VTN^{29, 49, 51} (Suppl. Fig. 1). We mainly targeted neurons in the medial vestibular nuclei and neurons in the rostral fastigial nucleus of the cerebellum, although some penetrations may have extended into the anterior interposed nuclei. For most recording sessions (110/215), two microelectrodes were placed inside a single guide tube (41 cell pairs) or placed in two different guide tubes (69 cell pairs) separated by 0.8 – 2.8mm. The distance between simultaneously recorded neurons was estimated from the horizontal distance between guide tubes and from recording depths.

Experimental protocols

Each cell was tested for eye movement-related responses while animals pursued a target that moved in one of the four cardinal directions: left, right, up, or down (Gaussian velocity profile, 9° amplitude, 2s duration, 5 repetitions). Firing rates during pursuit were used to determine if the neuron was tuned for direction of smooth pursuit (P < 0.05, one-way ANOVA). Only neurons without eye movement tuning, known as “vestibular-only” (VO) cells, were tested further with a 3D heading tuning protocol, in which translational motion stimuli were presented along 26 directions sampled evenly around a sphere³⁵. Animals were simply required to maintain visual fixation on a head-fixed target during this protocol. The duration of the heading stimulus was 2 s, the displacement was 13 cm, and the velocity profile was Gaussian with a peak velocity of ~30 cm/s, corresponding to a biphasic acceleration profile with peak acceleration of ~0.1 G = 0.98 m/s². Responses were computed as mean firing rates over the middle 1s period of the stimulus³⁵, or within at least five consecutive 400 ms bins, 25 ms apart. Only neurons with significant heading tuning in the horizontal plane (P < 0.05, one-way ANOVA; n=147/257) were further tested using the heading discrimination task.

Discrimination task

Four animals were trained to perform a fine heading discrimination task around psychophysical threshold⁹. During neural recordings in the discrimination task, 7 logarithmically spaced headings (±6.4°, ±2.6°, ±1°, 0° relative to straight ahead) were presented in a block of randomly-interleaved trials, while animals maintained fixation on a head-fixed target (2×2° fixation window). The range and spacing of headings were chosen to obtain near-maximal psychophysical sensitivity while allowing neural sensitivity to be reliably estimated for most neurons. The motion trajectory (30 cm displacement) was 2 s in duration and followed a Gaussian velocity profile (peak velocity: 45 cm/s), with a corresponding biphasic linear acceleration profile (±0.1G = ±0.98ms⁻²). The Gaussian velocity profile was 50% broader in the discrimination task than in the fixation task described above, such that the peak accelerations were comparable while the discrimination task had a greater peak velocity and displacement.

At the end of each discrimination trial, the fixation point disappeared, two choice targets appeared, and the monkey made a saccade to the left or right target to report his perceived heading (leftward or rightward relative to an internal standard of straight ahead). Correct choices were rewarded with a drop of liquid. For the ambiguous straight-forward heading direction (0°), rewards were delivered randomly on half of the trials. If fixation was broken at any time during the 2s motion stimulus, the trial was aborted and data were discarded. If neural isolation was lost before completion of at least 10 repetitions, that neuron was excluded from quantitative analysis. In our sample, 66% (n=97/147) of the cells were held long enough to be tested with at least 10 repetitions of each distinct stimulus.

Measuring selectivity for translation vs. net gravito-inertial acceleration

We tested whether VTN/CBN neurons signal translation of the head or whether they simply respond to net linear acceleration, such as that produced when the head is tilted relative to gravity. To distinguish these possibilities^{19, 20, 25}, four stimulus conditions were randomly interleaved: translation only, tilt only, and two combinations of translation and tilt (‘tilt−translation’ and ‘tilt+translation’). The tilt stimulus consisted of a 0.5 Hz sinusoidal rotation from an upright position with a peak amplitude of ±4.6° (peak velocity of ±14.4°/s). This stimulus reorients the head relative to gravity, such that otolith afferents are stimulated by a ±0.08 G linear acceleration component in the stereotaxic head-horizontal plane. The amplitude of translation was adjusted to match the interaural component of acceleration induced by the head tilt (±0.08 G, requiring a translational displacement of ±8 cm). During combined tilt/translation stimuli, translational and gravitational accelerations are combined in either an additive or subtractive manner, depending on the relative phases of the two stimuli. As a result, the net gravitoinertial acceleration in the horizontal plane was either doubled (tilt+translation) or nulled (tilt−translation), even though the actual translation of the head remained the same. Each cell was tested with this tilt/translation protocol along either the interaural/roll axis or the naso-occiptal/fore-aft axis, whichever produced a larger response modulation during translation.

Data Analysis: Tilt/translation discrimination

Responses to sinusoidal stimuli were quantified using instantaneous firing rate, computed as the inverse of the interspike interval¹⁹. Instantaneous firing rates were overlaid from multiple stimulus cycles, and response amplitude and phase were determined by fitting a sinusoid (clipped off at zero response) to both response and stimulus profiles. Response amplitude refers to one-half of the peak-to-trough modulation. Phase was expressed as the difference between peak response and peak stimulus velocity (rotation and tilt) or acceleration (translation). To determine whether neural responses correlated best with translation or net acceleration, linear regression analysis was used to simultaneously fit responses to all of the tilt/translation conditions with either a “net acceleration” model or a “translation-coding” model^{19, 52}. To determine how well each of the two models fit the data, we computed partial correlation coefficients that were normalized using Fisher’s r-to-z transform^{19, 20, 53}.

Behavior and single neuron responses

Behavioral performance was quantified by plotting the proportion of 'rightward' choices as a function of heading direction and fiting the data with a cumulative Gaussian function⁹:

$$P(r)=\frac{1}{\sigma \sqrt{2\pi }}{\displaystyle \underset{-\mathrm{\infty }}{\overset{h}{\int }}}{e}^{\frac{-{(x-\mu )}^2}{2{\sigma }^2}}\mathit{\text{dx}}$$ (1)

P(r) denotes the proportion of rightward choices, h is the heading direction, μ is the mean of the Gaussian (corresponding to the point of subjective equality) and σ is the standard deviation. Psychophysical threshold was defined as the standard deviation of the Gaussian fit, σ, which corresponds to 84% correct (assuming no bias).

For the analysis of neural responses, we used mean firing rates calculated during the middle 400ms interval of each stimulus presentation (in Fig. 3, the center location of this window was varied). To characterize neuronal sensitivity, we used ROC analysis to compute the ability of an ideal observer to discriminate between two oppositely-directed headings (e.g., −6.4° vs. +6.4°, see Fig. 1c) based solely on the firing rate of the recorded neuron and a presumed 'anti-neuron' with opposite tuning³⁰. ROC values were plotted as a function of heading, resulting in a neurometric function that was also fit with a cumulative Gaussian function (Fig. 1d). Neuronal threshold was defined as the standard deviation of the fitted Gaussian. For a handful of insensitive neurons, threshold values were capped at an upper limit of 300°.

To quantify the relationship between neural responses and perceptual decisions, we computed “choice probabilities” using ROC analysis¹. For each heading, neuronal responses were sorted into two groups based on the choice that the animal made at the end of each trial: ‘preferred’ choices refer to decisions that favor the preferred heading of the recorded neuron, whereas ‘null’ choices refer to decisions in the opposite direction. ROC values were calculated from these response distributions, yielding a choice probability for each heading, as long as the monkey made at least 3 choices in favor of each direction. In addition, we also computed a single “grand” choice probability for each neuron by combining responses across all heading directions that met this criterion. Grand choice probability was computed by z-scoring the data for each heading and then combining them into a single pair of distributions for preferred and null choices. ROC analysis on this pair of distributions yielded the grand choice probability. The statistical significance of choice probabilities (relative to the chance level of 0.5) was determined by permutation test (1000 permutations).

Noise and signal correlations

Noise correlation (r_noise) was computed as the Pearson correlation coefficient (ranging from −1 to 1) of the trial-by-trial responses of two simultaneously recorded neurons⁴⁰ during the 3D heading tuning protocol (passive fixation). The response in each trial was taken as the number of spikes during the middle 400ms of the stimulus duration. For each heading, responses were z-scored by subtracting the mean response and dividing by the standard deviation across stimulus repetitions. This operation removed the effect of heading on the mean response, such that noise correlation measures only correlated trial-to-trial fluctuations around the mean response. To avoid artificial correlations caused by outliers, we removed data points with z-values more than 3 standard deviations from the mean response⁴⁰. We then pooled data across different heading directions to compute r_noise. To remove slow fluctuations in response that could arise from changes in cognitive or physiological state (e.g., fluctuations of arousal), we re-normalized the z-scored responses in blocks of 20 trials^{34, 40}.

Signal correlation (r_signal) was computed as the Pearson correlation coefficient (ranging from −1 to 1) between tuning curves for two simultaneously recorded neurons. Tuning curves were constructed by plotting mean firing rates as a function of heading.

Population decoding and simulations

To simulate population responses and apply decoding techniques to predict choice probabilities, we generated simulated population responses based on the measured spiking statistics of recorded neurons. The tuning curve, F(θ), for each simulated neuron was obtained from the measured mean responses of a real neuron during the discrimination task. For each heading and simulated trial, a response of the i^th neuron was generated by randomly drawing a value from a Gaussian distribution having the same mean and variance, V_i(θ), as the measured data:

$$R_i(\theta )=F_i(\theta )+x_i\sqrt{V_i(\theta )},$$ [2]

where x is a vector of independent random deviates (one per neuron) with zero mean and unit variance. This produces simulated population responses in which each neuron’s noise is independent. To generate correlated noise among neurons, we multiplied the vector of independent deviates, x, by the square root of the covariance matrix^{22, 23}. In the covariance matrix, the correlation coefficient between neurons i and j was assigned according to:

$$r_{\mathit{\text{noise}}(i,j)}=k·r_{\mathit{\text{signal}}(i,j)}+\alpha ,$$ [3]

where r_signal represents the signal correlation between heading tuning curves for a pair of neurons. The slope k and offset α were acquired from a type II linear regression fit to the measured relationship between r_noise and r_signal in each brain area. Equation [2] then becomes:

$$R_i(\theta )=F_i(\theta )+y\sqrt{V_i(\theta )},$$ [4]

where y represents the product of the square root of the covariance matrix with the independent vector of random deviates, x. For each simulation, we generated 200 trials of responses for each neuron and each heading.

Support vector machine (SVM) decoder

To decode heading from a population of neurons, we implemented a linear decoding method⁴³ that uses a support vector machine (SVM) to determine the optimal weighting of each neuron’s response. This approach does not make specific assumptions regarding the spiking statistics of neurons (e.g., Poisson) or about the pattern of noise correlations^{43, 54, 55}. Given a sample of population activity for the j^th trial, R_j, the SVM assigns a category label C_j ∈ [−1, +1] to the population response, where +1 corresponds to a rightward choice and −1 corresponds to a leftward choice. The category label is computed as

$$C_j=\text{sgn}({\mathit{\text{wR}}}_j+b)$$ [5]

where sgn() is the signum function, w is a vector of decoding weights for each neuron, and b is a vector of bias terms. These parameters define a hyperplane that separates the population response into two classes corresponding to rightward and leftward perceived headings. To train the SVM, we pooled data from all leftward headings into one class and from all rightward headings into another class. Results were similar when only data from the largest headings (±6.4°) were used to train the classifier. Using10-fold cross-validation⁵⁶, there were 200×90%×3×2=1080 training trials for each simulation.

Once we acquired the weight vector, w, and the bias vector, b, from the training data set, we applied the decoder to the subset of trials corresponding to the ambiguous straight-forward heading. We decoded responses to 20 simulated trials for each training set, and we used 10-fold cross-validation such that 200 total trials were decoded. The ‘choice’ of the decoder on each simulated trial was used to compute choice probabilities for each simulated neuron. This allowed us to make quantitative predictions of choice probabilities for neural populations of different sizes.