Kinetics and Mechanisms of Thiol–Disulfide Exchange Covering Direct Substitution and Thiol Oxidation-Mediated Pathways

Abstract

Significance: Disulfides are important building blocks in the secondary and tertiary structures of proteins, serving as inter- and intra-subunit cross links. Disulfides are also the major products of thiol oxidation, a process that has primary roles in defense mechanisms against oxidative stress and in redox regulation of cell signaling. Although disulfides are relatively stable, their reduction, isomerisation, and interconversion as well as their production reactions are catalyzed by delicate enzyme machineries, providing a dynamic system in biology. Redox homeostasis, a thermodynamic parameter that determines which reactions can occur in cellular compartments, is also balanced by the thiol–disulfide pool. However, it is the kinetic properties of the reactions that best represent cell dynamics, because the partitioning of the possible reactions depends on kinetic parameters. Critical Issues: This review is focused on the kinetics and mechanisms of thiol–disulfide substitution and redox reactions. It summarizes the challenges and advances that are associated with kinetic investigations in small molecular and enzymatic systems from a rigorous chemical perspective using biological examples. The most important parameters that influence reaction rates are discussed in detail. Recent Advances and Future Directions: Kinetic studies of proteins are more challenging than small molecules, and quite often investigators are forced to sacrifice the rigor of the experimental approach to obtain the important kinetic and mechanistic information. However, recent technological advances allow a more comprehensive analysis of enzymatic systems via using the systematic kinetics apparatus that was developed for small molecule reactions, which is expected to provide further insight into the cell's machinery. Antioxid. Redox Signal. 18, 1623–1641.

Introduction

Reactions that result in thiol–disulfide exchange have pivotal roles in biology. For a long time these reactions were thought to only have a protein stabilizing structural purpose, but it is now evident that they are also responsible for diverse dynamic functional properties of many enzymes. The conversion of thiols into disulfides can occur via direct substitution or a series of redox reactions.

Direct thiol–disulfide interchange is the rate determining step in the folding process of proteins that have to form structural disulfide bonds. Although spontaneous thiol–disulfide interchange is slow (kinetically not competent on the folding timescale), enzyme catalysis accelerate the reactions in vivo. Chemically, similar mechanisms operate in the endoplasmic reticulum (ER; Fig. 1) (15) and mitochondrial inter membrane space (IMS; Fig. 2) (45) of eukaryotes and in the periplasm of prokaryotes (Fig. 3) (26, 68), although via different enzyme pathways. In all three cellular compartments, the new disulfide bond in the folding polypeptide is introduced by a series of inter- and intramolecular thiol–disulfide interchange reactions via oxidoreductases, and the oxidizing equivalents are supplied by molecular oxygen.

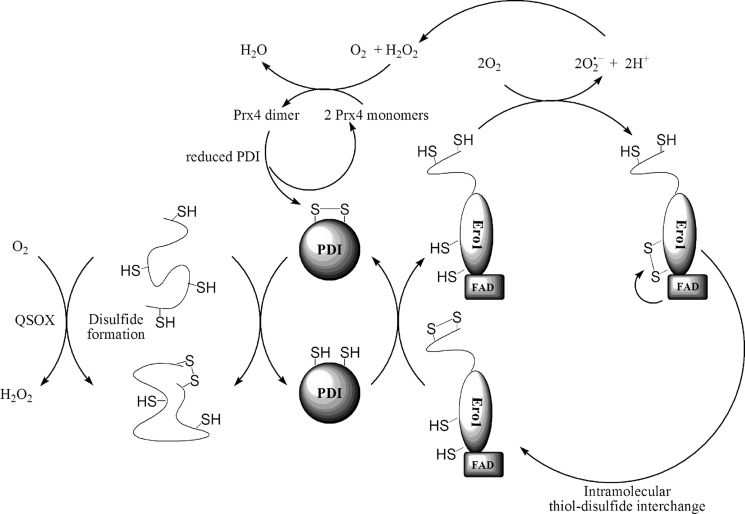
FIG. 1.

Mechanism for the folding process of polypeptides in the endoplasmic reticulum (ER) of eukaryotes. In eukaryotes folding of nonfunctional polypeptides in the ER is governed via disulfide bond formation by protein disulfide isomerase (PDI). The new protein–disulfide bond is introduced via thiol–disulfide exchange reactions between the oxidized PDI and the substrate protein thiols. In the first step, PDI forms a mixed disulfide intermediate species (not shown), which is reduced by another thiol on the substrate to give reduced PDI and the new protein-disulfide moiety. PDI is recycled via thiol–disulfide exchange reactions with the membrane-bound flavoprotein ER oxidoreductin (Ero1). Direct oxidation of PDI occurs by a disulfide that is present on a flexible loop of Ero1. Ero1 is reoxidized by oxygen reduction through its flavin adenine dinucleotide (FAD) domain, which subsequently oxidizes the so-called shuttle CXXC motif in its close proximity. The active disulfide on the loop forms via intramolecular thiol–disulfide exchange with the oxidized shuttle CXXC motif. Superoxide that forms during oxygen reduction dismutates to give H₂O₂ and O₂. H₂O₂ was recently proposed to preferentially oxidize peroxiredoxin 4 (Prx)4 to its dimeric form, which can subsequently reoxidize PDI via thiol–disulfide exchange, providing a feedback model for more efficient utilization of the oxidizing equivalents to create new disulfides. An alternative way to introduce disulfide moieties into unfolded proteins is via the quiescin-sulfhydryl oxidase (QSOX) family of enzymes. These proteins are proposed to function with a similar mechanism as Ero1 reoxidizes PDI, but they directly oxidize the unfolded proteins (60). Interestingly, beside their promiscuous substrate specificity they only poorly oxidize PDI. In addition, while the reduced form of PDI was shown to be involved in the reduction and isomerization of misfolded protein disulfides (not shown), QSOX does not catalyze these processes and in the absence of PDI, incorrectly paired disulfide bonds (generated by QSOX) accumulate (60).

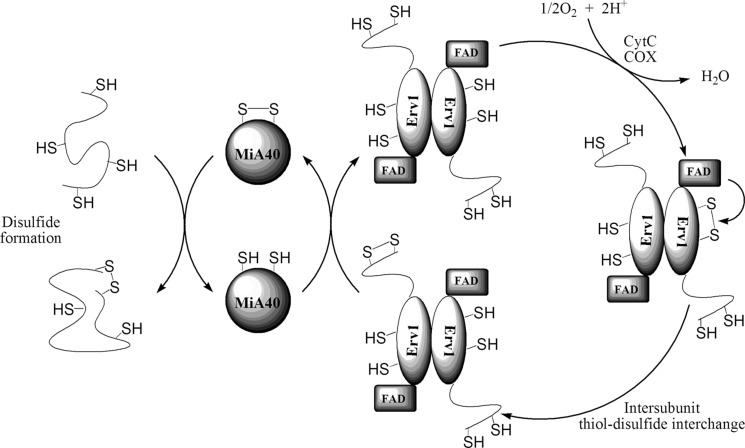
FIG. 2.

Mechanism for polypeptide folding in the mitochondrial inter-membrane space (IMS) of eukaryotes. Freshly synthesized polypeptides translocate from the cytosol to the IMS, where folding is facilitated by Mia40, via donating the disulfide bond of its CPC domain through a mixed disulfide intermediate species (45). Mia40 is subsequently reoxidized to its active form by the disulfide on the N-terminal shuttle domain of the flavoprotein essential for respiration and vegetative growth sulfhydryl oxidase (Erv1). In the homodimeric Erv1 protein, the active shuttle domain disulfide is reformed via intersubunit thiol–disulfide exchange with the CXXC motif of the other Erv1 in the homodimer. The CXXC is reoxidized via consecutive one-electron oxidation through the FAD domain of the same subunit. From the FAD, the electrons flow via the respiratory chain cytochrome C (Cyt C) and cytochrome C oxidase (COX) back to the stroma in the mitochondria to give H₂O and avoid H₂O₂ production.

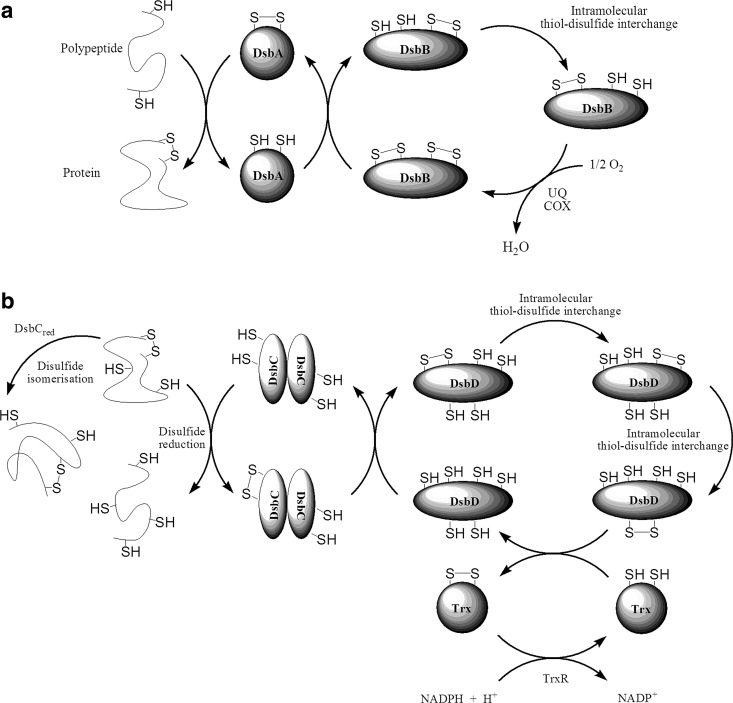
FIG. 3.

Protein folding in the periplasmic space of prokaryotes. (a) Unfolded polypeptides enter the periplasm, where the soluble disulfide bond protein family A (DsbA) protein catalyzes the folding process via introducing new disulfide bonds in thiol–disulfide exchange reactions through mixed disulfide intermediates. DsbA is reoxidized by DsbB. During the recycling of DsbB after an intramolecular thiol–disulfide interchange between two DsbB Cys pairs, the electrons flow (under aerobic conditions) via ubiquinone (UQ) and cytochrome oxidase (COX) of the electron transport chain to eventually reduce oxygen to H₂O in the cytoplasm. (b) Reduction or isomerisation of misfolded proteins occur by the homodimeric DsbC coupled to DsbD via the flow of electrons to the opposite direction. DsbC needs to be in the reduced state, which is maintained by the membrane-bound DsbD to which the reducing equivalents are supplied by cytoplasmic NADPH via thioredoxin (Trx). The oxidizing equivalents travel from the periplasm to the cytoplasm via a cascade of intramolecular thiol–disulfide interchange reactions through the transmembrane domain of DsbD on to Trx. A major difference in the protein-folding mechanism in prokaryotes versus eukaryotes is that while a separate reduction/isomerization machinery exists in prokaryotes (DsbC-DsbD), this process is catalyzed by the PDI and Mia40 disulfide relay systems in eukaryotes. Also, despite the functional similarities of Ero1 and DsbB, they lack sequence homology. The only similarity is the Cys pairs.

Protein thiols are also major targets of reactive oxygen species in vivo and oxidative conversion of thiols into disulfides and their subsequent reduction (e.g., see Figs. 4 and 5, respectively), is an alternative mechanism for thiol–disulfide exchange. In fact, the thiol–disulfide pool is thought to be primarily responsible for intracellular redox homeostasis and these reactions are important both for antioxidant defense and redox regulation of cell signaling (108). Therefore, delicate enzymatic pathways exist to control the direction of the electron-flow via cascades of one- and two-electron redox reactions (79).

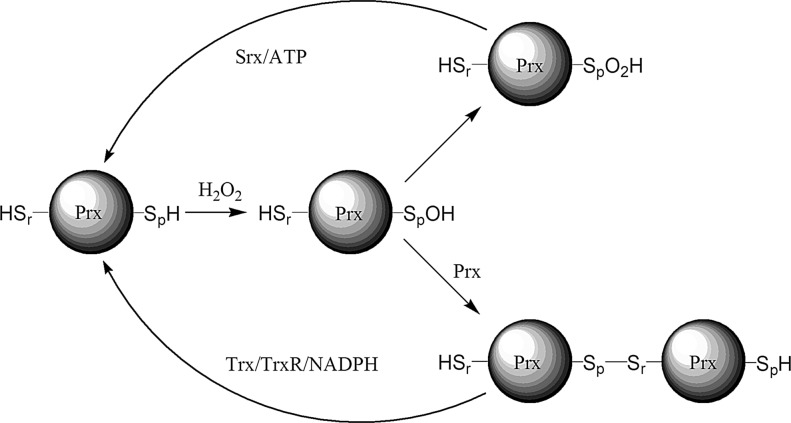
FIG. 4.

General mechanism for the peroxidase function of Prx. The peroxidative Cys (C_p) reacts with the peroxide oxidant to give a CyS_pOH derivative. Prx-CyS_pOH is reduced by a reducing Cys_r of another Prx to give the disulfide. Alternatively, CyS_pOH can be further oxidized to the corresponding CyS_pO₂H derivative by a second equivalent of peroxide. Reduction of the disulfide occurs by Trx (using NADPH) and the CyS_pO₂H derivative is slowly recycled by sulfiredoxins (using ATP).

FIG. 5.

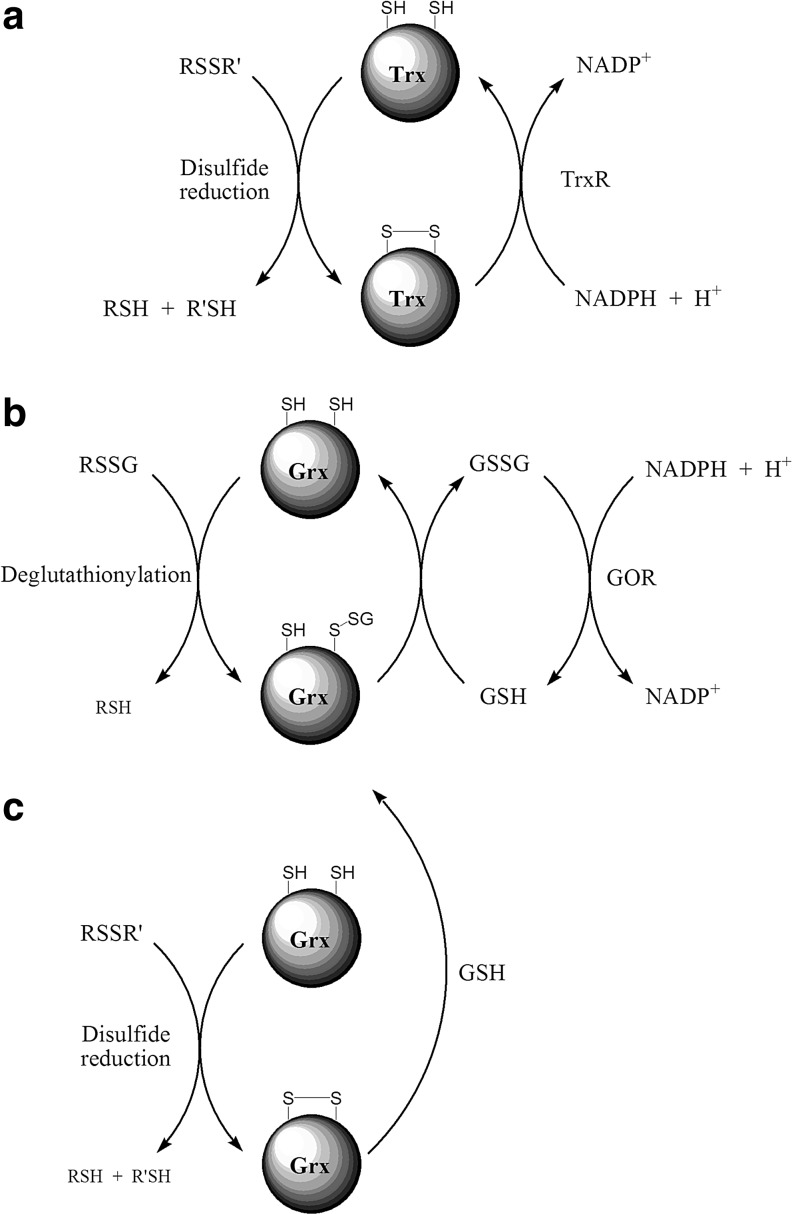
General mechanisms for disulfide reduction. (a) Trx are responsible for the reduction of a wide variety of protein disulfide bonds. Reduction occurs via formation of intermediate mixed disulfides. The reduced substrate is then released via an intramolecular nucleophilic attack of the resolving Trx thiolate on the sulfur of the N-terminal Trx Cys that is engaged in the mixed disulfide bond. Trx is recycled via thioredoxin reductase (TrxR) and the reducing equivalents are supplied by NADPH. (b) Glutathionylated protein thiols are catalytically reduced by glutaredoxin (Grx). The protein-bound glutathione is transferred to Grx through a nucleophilic attack of the Grx N-terminal Cys on the GS-sulfur. An important difference in the catalytic mechanism of Grx compared to Trx is that the glutathionylated Grx is reduced in an intermolecular reaction with another reduced glutathione (GSH) as opposed to intramolecular Trx disulfide formation. Oxidized glutathione (GSSG) is recycled via Glutathione oxido-reductase (GOR) catalyzed reduction by NADPH. (c) Grx can also reduce protein disulfides by the dithiol mechanism, which includes a nucleophilic attack of the N-terminal Cys of Grx on the disulfide moiety to give a mixed disulfide. This mixed disulfide is subsequently reduced by the C-terminal Grx Cys in a similar intramolecular fashion as for Trx (see Fig. 5a). The Grx disulfide moiety is reduced by GSH, where the intermediate glutathionylated N-terminal Cys reacts preferentially with another GSH over the C-terminal Grx Cys, just like during the reduction of glutathionylated proteins.

It is now generally accepted that in cellular systems, both thiol–disulfide interchange and thiol-oxidation/reduction reactions are nonequilibrium dynamic processes, which are kinetically, not thermodynamically controlled (51, 53, 57). In other words, redox potentials and equilibrium constants only highlight whether a reaction is favorable, but partitioning of particular pathways depend on relative rates. Enzymes play essential roles in these processes via fine tuning reaction activation energies, which determine the final outcome of the oxidative stimuli or the position of structural disulfides in native proteins. This review is focused on the kinetics and mechanisms of direct substitution (the classical thiol–disulfide interchange) and redox reactions that result in thiol–disulfide exchange. Basic kinetic and mechanistic principles as well as parameters that influence reaction rates are discussed from a chemical perspective with relevant biological examples.

The Classical Thiol–Disulfide Interchange Reaction

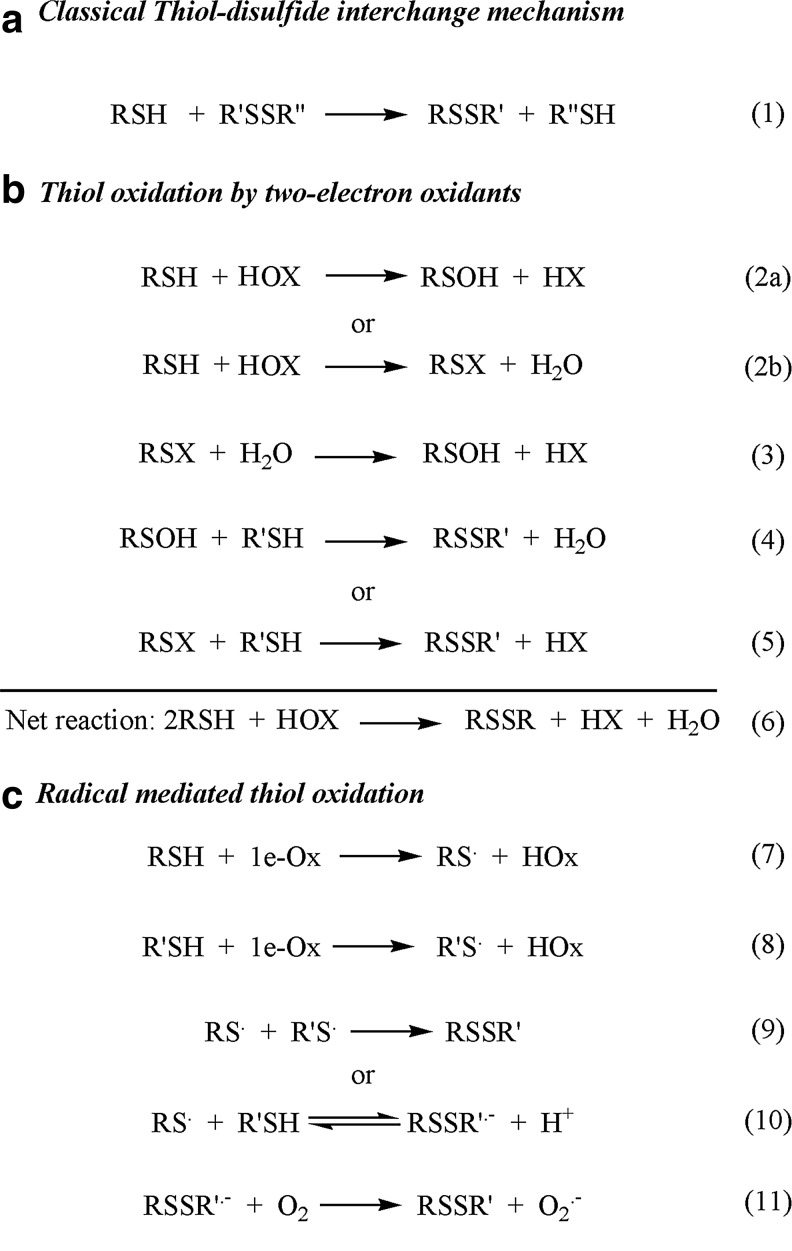
From the chemical point of view, the reaction is a nucleophilic substitution of a thiol in disulfides with another thiol (Scheme 1, Reaction 1).

Scheme 1.

General mechanisms for thiol–disulfide exchange via direct substitution (a) or (b-c) thiol oxidation. For the sake of simplicity, the depicted models do not take into account the different protonation states of the reactants and products. (a) The classical thiol–disulfide interchange mechanism is consistent with an S_N2 type model, where in a single reaction step (1) the attacking sulfur (RS-), the nucleophile, binds to the central sulfur of the disulfide (R′S-) and the leaving thiol (R′′SH) is released via a trisulfide-like transition state structure. (b) Two-electron thiol oxidation to disulfide can occur via multiple mechanisms. The most common pathways are via a sulfenic acid (RSOH; 2a) or an alternative sulfenyl (RSX, e.g., sulfenyl-halides when X=Cl, Br, or I; 2b) intermediate. RSOH reacts rapidly with thiols to give the corresponding disulfide species (4). RSX can hydrolyze to sulfenic acid (3) or it could react directly with another thiol to give the disulfide (5). (c) One-electron oxidation of Cys generates thiyl radicals (7 and 8). Recombination of two thiyl radicals results in disulfide formation (9). However, under physiological conditions, thiyl radicals are more likely to react with thiols to give the disulfide radical anion (10), which captures oxygen in a diffusion-controlled reaction to give the closed shell disulfide and superoxide (11).

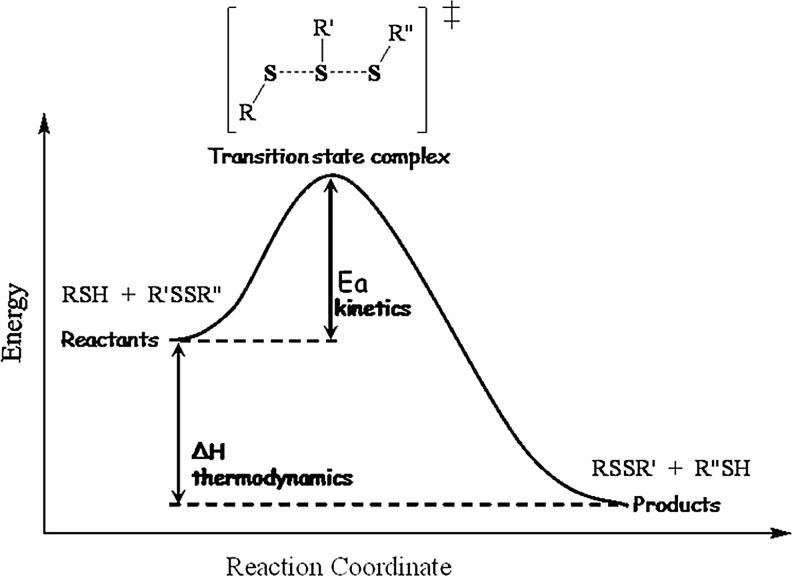
A number of studies have shown that the reaction proceeds with a simple S_N2 type nucleophilic substitution mechanism. The S_N2 mechanism is consistent with a one-step reaction via a single transition state complex with no intermediate formation (Fig. 6). The nucleophile is the deprotonated thiolate anion, which attacks the reacting sulfur of the disulfide moiety. Several pieces of theoretical and experimental evidence suggest a linear trisulfide-like transition state, with the negative charge being delocalized, but most abundant on the attacking and leaving sulfurs (10, 30, 32, 63).

FIG. 6.

Schematic energy profile of Reaction 1 as a function of the reaction coordinate. The reaction mechanism is consistent with an S_N2-type nucleophilic substitution via a linear -S-S-S- like transition state. E_a represents the activation energy (the parameter that determines the rate of the reaction) and ΔH measures the free enthalpy change during the reaction (corresponding to the thermodynamic feasibility of the reaction).

In their seminal work, Fava et al. have reported that the rate equation for Reaction 1 exhibits first order dependency on both the thiol and disulfide concentrations (30), which is indicative of a bimolecular reaction. The observed base catalysis was consistent with the deprotonated thiolate being a better nucleophile compared to the thiol. In addition, their data allowed the exclusion of an alternative mechanism, where base hydrolysis of the disulfide would result in a sulfenic acid derivative, followed by condensation with the attacking thiol to give the product disulfide.

The noncatalyzed reaction is slow (in the order of k=0.1−10 M⁻¹s⁻¹ at pH 7, see Table 1) (30, 56, 93, 100), but oxidoreductase enzymes [such as thioredoxin (Trx), glutaredoxin (Grx), the bacterial disulfide bond protein family A-D (DsbA-D), protein disulfide isomerase (PDI), Mia40, ER oxidoreductin (Ero1), essential for respiration and vegetative growth sulfhydryl oxidase, Erv1, see Figs. 1–3 and 5] are designed to accelerate the process up to k=10⁴–10⁶ M⁻¹s⁻¹ (for an abbreviated list of rate constants, see Table 1). A general feature of these enzymes is that they contain a Trx fold domain with a redox active CXXC motif at the active site, where in the reduced forms, the N-terminal Cys serves as the nucleophile. Therefore, the first bimolecular thiol–disulfide exchange reaction of a reduced oxidoreductase enzyme with its substrate results in an intermediate mixed disulfide species between the central disulfide sulfur of the substrate and the N-terminal Cys of the oxidoreductase. This is followed by an intramolecular nucleophilic attack of the C-terminal Cys on the N-terminal Cys of the oxidoreductase to give the oxidized CXXC motif and release the reduced substrate thiol. An exception is Mia40 (responsible for disulfide bond formation in the IMS see Fig. 2), which is not a member of the Trx family and has a redox active N-terminal CPC and two structural CX₉C motifs. Another distinctive feature of Mia40 is that it forms the intermediate mixed disulfides via the C-terminal Cys of its CPC (12).

Table 1.

List of Selected Second Order Rate Constants for Thiol–Disulfide Interchange Reactions in Small Molecules As Well As Proteins

Reaction partners
Thiol	Disulfide	Product disulfide	kapp(M−1s−1)	Temp (oC)	pH	Concentration conditions	Data fitting	Method	References
DTT	GSSG	ox DTT	0.235	30	7	Pseudo-first order with DTT in excess. 0.066 M iP, under Ar	Initial rate method	Enzymatic conversion of GSH into S-lactoyl glutathione (λ=240 nm)	(100)
CyS	GSSG	CySSG	0.8	25	7.5	Second order conditions, 0.15 mM NaCl no buffer	Initial rate method	1H NMR spectroscopy	(56)
CoA	GSSG	CoAS-SG	0.077	25	7.14	Second order conditions (0.15 mM NaCl no buffer)	Initial rate method	Acid quench-1H NMR spectroscopy	(56)
CoA	CoAS-SG	CoAS-SCoA	0.013	25	7.28	Second order conditions, 0.15 M NaCl no buffer	Initial rate method	Acid quench-1H NMR spectroscopy	(56)
GSH	papainS-SCH3	GSSCH3	47	30	7	Pseudo-first order with GSH in excess, 0.1 M iP, 0.1 M KCl, 5 mM EDTA, under Ar	Initial rate method	Dilution quench-enzyme activity measurement	(93)
nDsbDred	DsbCox	nDsbDox	3.9×106	25	7	Second order, 0.1 M iP, 0.1 mM EDTA	Second order fit	HPLC	(92)
DsbCred	nDsbDox	DsbCox	3.0×103	25	7	Calculated from the above forward reaction and the equilibrium constant			(92)
cDsbDred	nDsbDox	cDsbDox	1.1×105	25	7	Second order, 0.1 M iP, 0.1 mM EDTA	Second order fit	HPLC	(92)
DsbAred	DsbBox	DsbAox	2.7×105	25	7	Second order, 0.1 M iP, 0.1 mM EDTA	Second order fit	Change in Trp fluorescence (λex=280 nm, λem=330 nm)	(42)
Grx	GSSG	GrxS-SG	7.1×105	37	7.6	Pseudo first order with GSH in excess, iP=0.1 M	Pseudo first order rate constants were extrapolated from lifetime measurements	1H NMR spectroscopy, inversion-magnetization transfer	(89)
GSH	GrxS-SG	GSSG	4×104	30	9.5	Pseudo first order with GSH in excess, AMPSO=0.1 M I=0.3 M	Initial rate method	Release of radiolabelled GSH in a coupled assay with GOR	(98)
Trx	Insulin	Trxox	1×105	23	7	Pseudo first as well as second order, 0.1 M iP, 2 mM EDTA	Estimated based on turnover and change in Trp fluorescence	Coupled assay and Trp fluorescence	(47)
Trx	I27 domain of human cardiac titin	Trxox	2.2×105	25	7.2	Pseudo-first order at Trx in excess, 10 mM HEPES, 1 mM EDTA, 150 mM NaCl	Exponential fit and extrapolation to force=0	Single-molecule force-clamp spectroscopy	(105)
I27S32H	I27S24-S55	I27S24-S32	0.065 s−1	25	7.2	Intramolecular disulfide rearrangement,10 mM HEPES, 1 mM EDTA, 150 mM NaCl	Simulated based on solving the appropriate differential equation and optimized with the Downhill Simplex Method	Single-molecule force-clamp spectroscopy	(3)
I27S32H	I27S24-S55	I27S32-S55	0.25 s−1

DTT, dithiothreitol; GSSG, oxidized glutathione; iP, phosphate buffer; GSH, reduced glutathione; nDsbD, N-terminal domain of DsbD; Grx, glutaredoxin; Trx, thioredoxin; I27S²⁴-S⁵⁵, I27 domain of human cardiac titin; HPLC, high-performance liquid chromatography, GOR, glutathione oxidoreductase; CoA, coenzyme A; CoAS-SG, glutathionylated CoA; GrxS-SG, gultathionylated GrX.

Factors That Influence the Rates of Thiol–Disulfide Interchange Reactions

In this section, a number of factors will be discussed, which were proposed to have rate enhancing or inhibitory effects on thiol–disulfide interchange reactions. Most reports consider the factors (i.e., the pK_a and the nucleophilicity) that influence the reactivity of the attacking thiol. However, it is important to emphasize that from the kinetic point of view, factors that affect the stability of the leaving group or the electrophilicity of the central disulfide sulfur, will have just as important roles in decreasing the activation barrier.

Box 1: A Few General Kinetic Considerations for Studying Thiol–Disulfide Interchange Reactions.

The rate equation and rate determining concentrations

For a true bimolecular thiol–disulfide interchange reaction (Scheme 1, Reaction 1), the following rate equation applies:

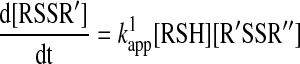(12)

As shown by Equation 12, the rate law of a bimolecular thiol–disulfide interchange reaction exhibits first order dependency on both reactant concentrations. Under pseudo-first order conditions (one of the reactants is in >10-fold excess over the other), the observed kinetic traces will fit to an exponential equation. However, if the concentrations of the two reactants are comparable (which is often the case under biological conditions), then the data has to be treated with a more complicated second order equation.

Another important implication of this phenomenon is that under pseudo-first order conditions, the half life of the reaction will only be dependent on the concentration of the reactant in excess. In contrast, under second order conditions, the half life will depend on both reactant concentrations.

Reversible reactions

The above considerations apply when the reaction essentially proceeds to completion, and hence, is practically irreversible. However, thiol–disulfide exchange reactions in many cases approach equilibrium with substantial amounts of reactants remaining (such as in the case of the oxidation of DsbA or DsbC with DsbB or DsbD, respectively).

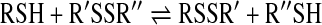(13)

In this case, the rate law will have the following form:

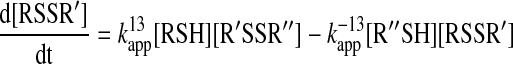(14)

and therefore, fitting the data with a single exponential (when, for example, one of the reactants is in excess over the other) does not result 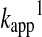. Relaxation kinetics approaches, or also called concentration jump methods, were developed to study reactions that approach equilibrium. This involves a sudden change of a parameter (concentration of a reactant, dilution, or temperature) that perturbs the already attained equilibrium, and subsequent following of the establishment of the new equilibrium. An elegant method described by King allows relatively simple interpretation of the data when small enough changes are applied (58). In such a situation, it was shown that the re-equilibration of Reaction 13 is a first order process. For more details on the kinetic analysis of reactions that approach equilibrium see Ref. (28).

The effect of pH

The kinetics of thiol–disulfide interchange reactions are pH dependent, because of the much stronger nucleophilicity of the thiolate compared to the thiol. The difference in the nucleophilicities is so dramatic that in many cases the reaction proceeds via the thiolate even when it is a minor species (i.e., at pH values far below the thiol pK_a). A model that takes into account the different protonated forms of the attacking thiol is shown below:

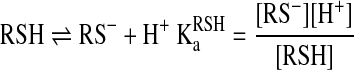(15)

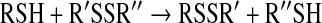(16)

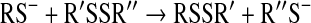(17)

From this model, the following rate equation can be derived:

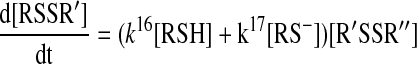(18)

Protonation–deprotonation reactions are usually fast in aqueous media, and hence, it is generally accepted that Reaction 15 can be treated using the pre-equilibrium assumption. In addition, if we assume that the reaction only proceeds via Reaction 17 under the applied experimental conditions and take into account that [RSH]_tot=[RSH] + [RS^-], then the rate equation will be:

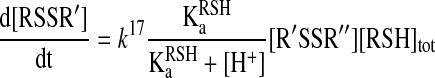(19)

Hence, the reactant concentration-independent apparent rate constant (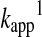 in Equation 12) will be a composite pH-dependent value with the following form:

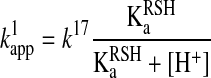(20)

where k¹⁷ is independent of pH. Practically this means that the rate of the reaction will increase with the pH up to the point where most of the attacking thiol will be deprotonated. Note that in polyprotic molecules, such as GSH, the deprotonated form of the sulfur center will be determined by microscopic acid dissociation constants (see Acid dissociation constants of reacting functional groups section), which further complicates the kinetic analyses (74, 78, 79).

Acid dissociation constants of reacting functional groups

Equation 20 in Box1 implies that at physiological pH, the rate of thiol–disulfide interchange reactions will be inversely dependent on the attacking thiol's pK_a, because the deprotonated thiolate form is a better nucleophile than the thiol. However, due to the linear-free energy relationship, the nucleophilicity of the thiolate will increase with its pK_a, which translates in an increase in k¹⁷, representing an opposite effect on the overall reaction rate (93, 100, 107). The relationship between k¹⁷ and the pK_a of the reacting thiol is described by a Brønsted equation:

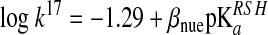(21)

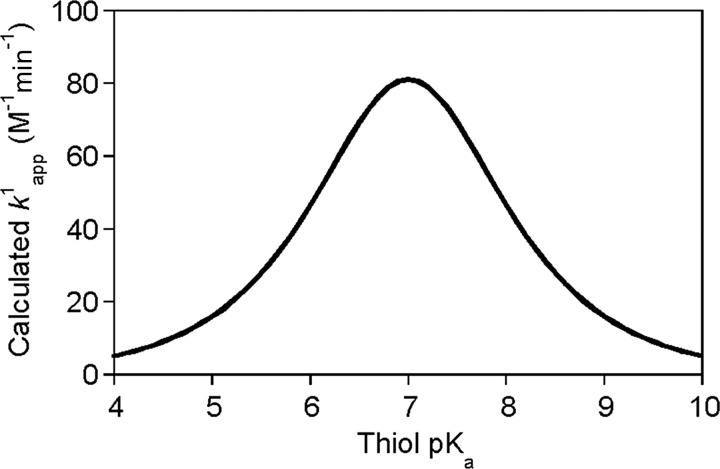
where β_nuc is the Brønsted coefficient that was established to be ∼0.5 for the reaction of various different thiols with oxidized glutathione (GSSG) (100). Based on this Brønsted relationship, Figure 7 shows the predicted 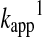rate constants (see equation 12 in Box 1) for thiol–disulfide exchange reactions of GSSG as a function of the attacking thiols' pK_a at pH=7. Based on the position of the maximum (at ∼ pK_a=7), the N-terminal Cys pK_a values of Trx (55) (∼6–7) are ideal with regard to nucleophilic power (see Fig. 7). On the other hand, the very low pK_a values of the nucleophilic Cys in reduced DsbA [pK_a=3.5(82)], DsbC [pK_a=4.1(99)], or Grx1 [pK_a=3.5 (38, 69)] do not correspond to proportionally high nucleophilicity and are likely to have additional kinetic (e.g., the effect of the leaving group pK_a, see below) or thermodynamic (i.e., an effect on the position of the corresponding thiol–disulfide equilibrium) purpose in the overall multistep thiol–disulfide exchange processes (i.e., reduction of: DsbA by DsbB, protein disulfides by DsbC, and glutathionylated proteins by Grx1, respectively).

FIG. 7.

Calculated 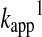for thiol-GSSG interchange reactions as a function of thiol pK_a at pH 7 based on the Brønsted relationship that was established by Whitesides. Using 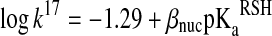(equation 21), the pH independent rate constant (k¹⁷) was calculated at different thiol pK_a values. Substituting these rate constants into eq 20 (Box 1), the obtained 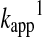at a given pH for Reaction 1 were plotted as a function of thiol pK_a (in the range of pK_a=4–10) at pH 7. The figure clearly demonstrates that decreasing the attacking thiol's pK_a will only result in an overall rate enhancement until the thiolate becomes the dominant species (i.e., until the thiol pK_a approaches the applied pH). Beyond this, the drop in the nucleophilicity of the sulfur center with the pK_a will determine the rate and result in slower kinetics.

The rate of Reaction 17 is also influenced by the pK_a values of the central and leaving groups, which is described by a more comprehensive Brønsted equation:

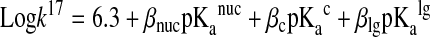(22)

where β_nuc, β_c, and β_lg are Brønsted coefficients and pK_a^nuc, pK_a^c, and pK_a^lg are acid dissociation constants for the attacking, central and leaving groups (pK_a^RSH, pK_a^R′SH, and pK_a^R′′SH for Reaction 17), respectively.

The measured Brønsted coefficients (β_nuc=0.59, β_c=−0.40, and β_lg=−0.59) indicate that the pK_a values of the attacking and leaving thiols will have a larger influence compared to the central thiol. The negative β_lg corroborates Wilson and coworkers' observation (107) that the rate decreases with the increase in the leaving thiol pK_a, representing an opposite effect compared to that of the attacking thiol's pK_a. This is explained by the increase in the stability of the leaving thiolate with the decrease of pK_a^lg, which results in a drop of the transition state energy. Therefore, the aforementioned extremely low pK_a values of DsbA, DsbC, or Grx1 Cys residues will have an accelerating effect on the reduction of the mixed disulfide bonds (which form as intermediates during the reduction of: DsbA by DsbB, protein disulfides by DsbC, or glutathionylated proteins by Grx1) via leaving group stabilization in the transition state structure (see Fig. 6).

Microscopic versus macroscopic acid dissociation constants

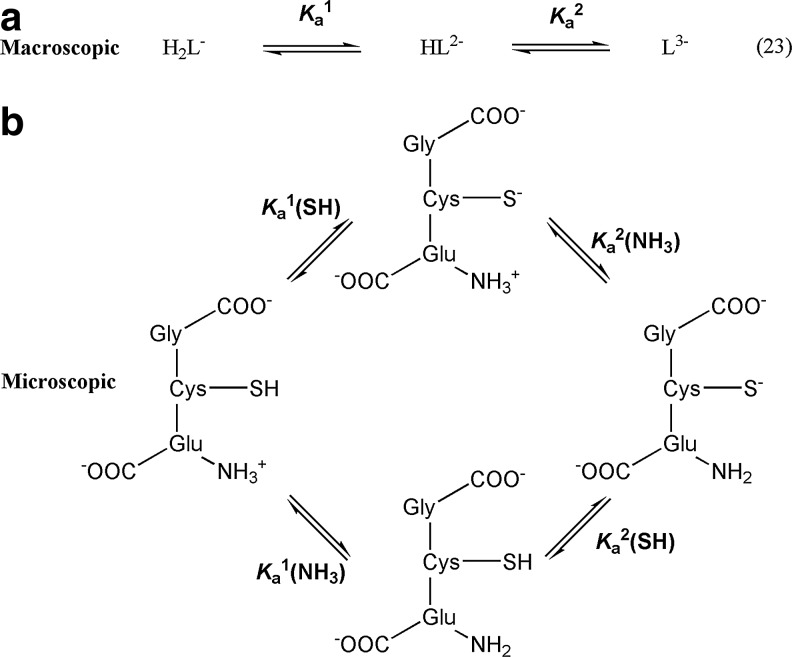
The protonation state of a functional group in a polyprotic acid is characterized by microscopic acid dissociation constants, a phenomenon that is often overlooked in kinetic studies.

For glutathione, the two carboxylic groups are both deprotonated under physiological conditions, and therefore we can assume that their pK_a values do not influence the kinetics of its thiol–disulfide exchange reactions. However, the terminal amino and sulfhydryl groups are mostly in their protonated forms at pH 7 resulting in two labile protons for reduced glutathione (GSH), see Equation 23 on Scheme 2a.

Scheme 2.

Macroscopic (a) and microscopic (b) speciation of reduced glutathione at pH>5 with the corresponding macroscopic and microscopic equilibrium constants.

K_a¹ and K_a² (in Scheme 2a) are macroscopic acid dissociation constants that determine the overall protonation state of GSH. However, these equilibrium constants cannot be assigned to individual functional groups, because HL²⁻ (Scheme 2a) represents a mixture of two protonation isomers [for a recent review of microscopic pK_a's of Cys and GSH see (79)], where the proton is either attached to the thiol or the amino group of GSH (see Scheme 2b). Therefore, microscopic acid dissociation constants are required to calculate the concentration of thiolate functional groups. It is particularly important in kinetic studies because the rate of Reaction 1 will be more influenced by the protonation state of the thiol group than by the overall protonation state of GSH. However, protonation at a different site could not only influence thiol pK_a values, but additional charge effects could also contribute to the overall reactivity of the molecule (79).

The ionizability of protein thiols is even more challenging to measure. These are influenced by many factors, including charged states, orientations, inductive effects of neighboring functional groups, and solvent accessibility (90). In addition, proteins are dynamic entities and changing the pH often results in small, but sometimes substantial conformational changes. Therefore, in a protein titration data set (which is in most cases the method of measuring the pK_a), all of the above-mentioned variables make it hard to evaluate the sole contribution of the deprotonation of a particular functional group. This gives a different chemical meaning for protein pK_a values compared to those of small molecules. On the other hand, it is important to understand how changes in pH affect the reactivities of protein thiols. Therefore, this parameter is best studied by measuring the pH profile of the kinetics of the reaction with its biologically relevant reaction partner [for more details see Ref. (79)]. For example, the pK_a value of the C-terminal Cys in Trx is likely to be different when the enzyme is in its reduced state compared to when it is engaged in a mixed disulfide intermediate (between the N-terminal Trx Cys and the substrate) (19). Indeed, it has been proposed that due to a conformational change in the Trx–arsenate reductase mixed disulfide complex, new H-bonding interactions result in a transient drop in the pK_a of the C-terminal Trx Cys, activating it for a nucleophilic attack on the N-terminal Cys to release the substrate (22, 91).

Steric factors

Steric factors play particularly important roles in the kinetics of reactions that proceed via an associative S_N2 type mechanism, because of a crowded transition state structure. A linear conformation was suggested for the attacking, central, and leaving groups for the best orientation of their molecular orbitals see, for example, (10, 30, 33). Bulky functional groups can hinder the access of the attacking thiol and increase the activation energy. On the other hand, steric interactions can also stabilize the binding of particular substrates, which is an important factor in substrate specificity of many enzymes. A nice example for a steric hindrance-mediated kinetic insulation is the periplasmic disulfide shuttle system (Fig. 3). Although the pK_a values of reduced DsbA and DsbC are very similar [pK_a=3.5(82) and 4.1(99), respectively], in the periplasm, DsbA is predominantly oxidized, while DsbC is reduced. These functional redox statuses of DsbA and DsbC are maintained by DsbB and DsbD, respectively (see Fig. 3). Since all of these proteins are in the same cellular compartment and thermodynamically, the nonfunctional reduction of DsbA by DsbD or oxidation of DsbB by DsbC would be favorable, they are under strict kinetic control: DsbD reduces DsbC (k=4×10⁶ M⁻¹s⁻¹)>3 orders of magnitude faster than DsbA (k=9×10² M⁻¹s⁻¹) and similarly DsbB oxidizes DsbA (k=3×10⁶ M⁻¹s⁻¹)>3 orders of magnitude faster than DsbC (k=2×10³ M⁻¹s⁻¹) (92), which were proposed to be due to steric factor-mediated substrate specificity (26, 49).

In addition, steric factors can introduce strain on a disulfide bond, and accelerate its interchange reactions by making it more labile. In DsbA, for example, the tense conformation of the oxidized form contributes to its oxidizing properties (112). It is also an important driving force of the folding process, where stabilization of the structured intermediate disulfide moieties are key in the overall kinetics and metastable disulfides are preferentially reshuffled (81).

An additional factor in thiol–disulfide exchange reactions is the formation of energetically favorable cyclic disulfides. This, together with the fact that cyclic disulfide formation is (i) entropy reduction facilitated and (ii) occurs at a larger effective thiol concentration compared to intermolecular reactions (due to the close proximity of the other thiol group), is the reason why dithiothreitol (DTT) is preferred over mercaptoethanol to reduce protein disulfides. In more detail, during the reduction of protein disulfides, the facilitated ring closure step results in a shift in the equilibrium toward the formation of oxidized DTT (a cyclic disulfide) and reduced protein thiols, while in the case of mercaptoethanol (even at large concentrations of the reducing agent), substantial amounts of mixed disulfide species can form. It is noteworthy that a ring opening reaction (the back reaction of the reduction of proteins with dithiols) would be faster for a more strained cyclic disulfide (as mentioned above for DsbA). However, investigating the kinetics of the reactions of many different dithiols with DTNB, Whitesides et al. reported a faster intramolecular interchange reaction (i.e., ring closure) step compared to the initial attack of the dithiol on the disulfide (in all studied cases even at very low reactant concentrations) (104). This would suggest that, even in cases when more strained intramolecular disulfides are generated, the equilibrium is shifted toward the formation of the cyclic disulfide species (when the dithiol is used in excess).

Similar principles would apply for the dithiol oxidoreductases, which also contributes to the thermodynamics and kinetics of their thiol–disulfide interchange reactions. In general, the rate of reactions of dithiols with disulfides and the reducing potentials of dithiols depend on: (i) the strain in the resulting cyclic disulfide, (ii) the conformational freedom of the dithiol, (iii) the entropy factor (which suggests a more unfavorable reaction for the formation of larger loops), and (iv) the steric proximity of the two thiol functional groups (particularly in proteins). These factors all contribute to the large differences that were observed in the equilibrium and rate constants for the reduction of disulfides by dithiols (e.g., orders of magnitude larger equilibrium constants were observed for the reactions of Trx compared to DsbA) (48, 115).

Charges, coulombic and H-bonding interactions with neighboring functional groups

In general, neighboring functional groups that stabilize the charge distribution of the transition state accelerate, and interactions that lower the energetics of the reactant complexes inhibit Reaction 1.

The aminoacid sequence of peptides was shown to have a profound effect on the rate of thiol–disulfide exchange reactions with particular influence of ionic aminoacids in close proximity to the thiolate (111). In proteins, due to their tertiary and quaternary structures, charged aminoacids that are sequentially well separated can also come close to the reaction center and affect reactivity. Positive or partial positive charges (electron withdrawing functional groups) stabilize the thiolate or the leaving group and, hence, catalyze the reactions, while negative charges have opposite effects.

Ion pairing, dipole or H-bonding interactions can also contribute to the nucleophilicity of the reacting thiolate. Electron-donating functional groups will increase its nucleophilicity, but H-bond donation will have an opposite effect (18, 33). For example, a recent report suggested an accelerating effect for the reaction of peroxiredoxins (Prx) with peroxides via a shift of H-bonds from the thiolate to the substrate to increase the nucleophilicity of the thiolate (33). Note that this latter reaction is an oxidation reaction, but the nucleophilicity of the thiolate in redox reactions is similarly an important rate-enhancing factor (see the Factors that influence the rate of thiol oxidation section).

For a direct thiol–disulfide interchange reaction, a hydrophobic environment is catalytic (32, 95). In Mia40, for example, two CX₉C connected helices create a hydrophobic pocket, which serves as a substrate-binding groove (94). Similarly, a large hydrophobic region behind the active site of PDI was demonstrated to have an important role in its activity. In addition to preferential binding of unfolded substrates and assisting conformational changes, the hydrophobic environment was shown to lower the activation energy of the thiol–disulfide interchange reaction (32, 59). Furthermore, S_N2 reactions in general favor an aprotic environment, partly because polar protic solvents tend to have a larger stabilizing effect on the reactants than on the transition state complex, which increases the activation energy. Thiol–disulfide interchange reactions indeed were found to be ∼3 orders of magnitude faster in aprotic solvents than in water (95), which is consistent with a more delocalized negative charge in the transition state, providing experimental credence for the theoretical calculations.

Inter- versus intramolecular reactions

The thiol–disulfide interchange can occur between two different reactants or in an intramolecular fashion. Intramolecular reactions can gain considerable rate enhancement compared to intermolecular reactions due to several different reasons (14, 64): (i) In an intermolecular reaction, a wide distribution of rotamers exist and statistical factors (as well as concentration) determine the probability of the conformation that undergoes reaction. On the other hand, in intramolecular reactions, the orientation of the reacting functional groups could be in the most favorable position for the molecular orbitals to overlap. (ii) In intramolecular reactions, interactions with neighboring residues could lock the reacting functional groups in a conformation that closely resembles the transition state and, thereby, considerably lower the activation energy. (iii) Intramolecular reactions are entropy reduction-facilitated via the loss of the translational entropy, which accompanies the bringing together of the reactants. For example, a highly favorable thiol–disulfide exchange between the C- and N-terminal sites of DsbD was proposed (k=1×10⁵ M⁻¹s⁻¹), although the kinetics were investigated in an intermolecular fashion via the purified C-terminal (cDsbD) and N-terminal domains of DsbD (nDsbD; see Table 1). Therefore, the true intramolecular disulfide relay in DsbD is likely to be much faster due to the above-mentioned factors and unlikely to be rate limiting in the overall reduction of DsbC (although the direct reduction of DsbC by the nDsbD is fast k=3.9×10⁶ M⁻¹s⁻¹) (92).

In addition, in intramolecular enzymatic reactions, the pK_a-s of the reacting and leaving thiol groups could be optimized for the thiol–disulfide exchange via conformational changes as proposed for Trx [see the effect of pK_a section and (19, 91)].

Grx represents a unique exception in the Trx-fold family of proteins, because the intramolecular disulfide formation between the two Cys in their CXXC motif is not favorable during the reduction of glutathionylated proteins (Fig. 5b). Grx recycle glutathionylated protein thiols (37, 50, 89, 114) via a Grx-GSH intermediate (see Fig. 5), which is subsequently reduced in an intermolecular reaction with another GSH to give GSSG and reduced Grx (31). Hence, the intramolecular Grx disulfide formation (which occurs occasionally as a side reaction) is outcompeted by the intermolecular reaction with GSH. Therefore, this is a nice example how preferential binding of a substrate (via steric, coulombic, H-bonding, etc. interactions) not only results in specificity, but has catalytic effect on the reaction (in this case, up to the extent to outcompete an entropy reduction facilitated intramolecular reaction) (50). Another factor that may contribute to the favorable intermolecular reduction of Grx-GSH is the stabilization of the bound GSH moiety (114) to inhibit the attack of the C-terminal Grx Cys via steric isolation. On the other hand, it is important to note that Grx also reduce protein disulfides (Fig. 5c). These reactions were proposed to occur via the so-called dithiol mechanism, which is different from the reduction of glutathionylated proteins. In the first step, a mixed disulfide forms as a result of a nucleophilic attack of the N-terminal Grx Cys on the protein disulfide moiety. This mixed disulfide is reduced in a Trx-like mechanism, that is, by the C-terminal Cys of the Grx CXXC motif. The Grx disulfide is recycled by GSH, where glutathionylation of the N-terminal Cys is followed by an intermolecular thiol–disulfide exchange with another GSH to give GSSG (just like in the case of the reduction of glutathionylated proteins) (65).

Mechanical force

Mechanical force can also trigger the thiol–disulfide exchange by activating the disulfide bond. For example, it was shown that in the adhesion ligand von Willebrand factor physiologically relevant fluid shear stresses promoted the thiol–disulfide exchange, which increased platelet binding (20).

Using force clamp spectroscopy, a series of publications from the Fernandez group allowed deeper insight into the molecular bases of thiol–disulfide exchange reactions (3, 63, 105). They have shown that the rate of Reaction 1 is exponentially dependent on the applied force when pulling the disulfide moiety apart. The rate is appropriately described by an Arrhenius equation (29):

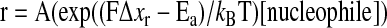(24)

where A is the pre-exponential factor, E_a is the activation energy of the reaction, k_B is the Boltzmann constant, T is the temperature, and Δx_r is the distance to the transition state along the reaction coordinate. The fitted value of Δx_r holds information on the disulfide bond elongation although theoretical calculations suggest that this parameter should be handled with care (62). Nevertheless, the fact that the reduction of a disulfide by different thiol nucleophiles resulted in very similar Δx_r values suggests that these reactions exhibit similar energetic and structural properties (2).

The kinetics and mechanisms of disulfide reduction by Trx was also investigated with this technique. The method shed light on the catalytic mechanism and suggested a force-dependent reorientation of the substrate at the active site to achieve a previously proposed linear -S-S-S- like transition state structure (105).

More recently, these investigators also managed to measure the rates of intramolecular thiol–disulfide exchange reactions (3). In the presence of two available thiol groups within the same protein, they could investigate their reactivities separately with the disulfide moiety. The obtained four-fold difference in the reactivities of the two thiol groups could be well explained by the previously discussed leaving group pK_a effects. Importantly, this investigation for the first time allowed insight into the kinetics of thiol–disulfide isomerization reactions.

Prevention of nonfavorable side reactions

In complex biological systems, unwanted side reactions could inhibit the enzymatic catalysis. A good example is the IMS disulfide relay system, which is inhibited in the absence of GSH or the Zn²⁺ binding protein (Hot13), although via different mechanisms. Accumulation of intermediate mixed disulfides between Mia40 and its substrate slows the process down significantly. The counterproductive catalytic role of GSH (a reducing agent catalyzing an oxidation process) was explained by reduction of this mixed disulfide intermediate to recycle Mia40 in its reactive form (13). On the other hand, Zn²⁺ was shown to inhibit Mia40 reduction by Erv1 (67) and the Cys-rich Hot13 protein was proposed to catalyze the overall protein-folding process in the IMS via binding Zn²⁺ (70), and thereby accelerating Erv1-mediated Mia40 reduction (see Fig. 2).

Oxidation of Thiols

In many respects, thiol oxidation is similar to the thiol–disulfide interchange and by a variety of secondary reactions, oxidation of one thiol can lead to disulfide formation on another. Thiol oxidation to disulfide is at least a two-step process involving intermediate species. Oxidation can occur via one- and two-electron redox pathways depending on the nature of the oxidant.

The thiol-mediated redox state of the cell is predominantly controlled by the Trx and glutathione systems. Both these systems use NADPH as a fuel of their reducing capacity, although via different mechanisms. Trx are kept reduced by thioredoxin reductase (TrxR), which transfers the electrons from NADPH, while GSH is kept reduced by the glutathione oxidoreductase/NADPH couple. GSH and Trx can transfer their reducing equivalents to many different enzymes, including Prx, methionine sulfoxide reductase and ribonucleotide reductase for Trx; or glutathione peroxidase (Gpx or Orp1), glutathione S-transferase (GST), and Grx for GSH. Hence, they are involved in a variety of cellular events.

Two-electron oxidation pathways

Oxidation of Cys by two-electron oxidants, in most cases, occurs via formation of a Cys sulfenic acid (RSOH) derivative (Reactions 2–6 on Scheme 1). RSOH often forms directly in a bimolecular reaction with the oxidant (e.g., with peroxides; Reaction 2a). Alternatively, it can be a secondary hydrolytic intermediate in the oxidation of thiols with, for example, hypohalous acids (HOX, X=Cl, Br or I) or hypothiocyanite (OSCN⁻) (74, 76, 96) that predominantly react via X⁺, not OH⁺, transfer (34, 74, 101) (Reactions 2b–3). Sulfenic acids are generally reactive; they are rapidly reduced by thiols to form the corresponding disulfide species (Reaction 4).

Peroxides react relatively slowly with most Cys residues with second order rate constants ranging from k=1 to a few hundred M⁻¹s⁻¹ (108) (e.g., see Table 2). However, thiol peroxidases contain Cys residues (Cys_p; called the peroxidative Cys) that exhibit exceptional reactivity with peroxides having several orders of magnitude larger second order rate constants k=10⁶–10⁸ M⁻¹s⁻¹ [such as Prx; the Escherichia coli transcription factor (OxyR); or Gpx; see Table 2] (8, 23, 36, 61, 87). Based on a crude modeling exercise on the kinetics of cellular thiol oxidation by H₂O₂ in a cytosol-like environment, we recently put forward some concepts in relation to peroxide-mediated redox signaling (79, 108): (i) Prx1 and 2 and Gpx1 are the most favored targets of H₂O₂ and if they are effectively recycled they should consume the majority of the cytosolic peroxide. Due to the high reactivity of Prx and Gpx (and abundance in the case of Prx), direct oxidation of GSH and other important redox-regulated proteins (like GAPDH or protein tyrosine phosphatase) are prevented up till the concentration of H₂O₂ reaches tens of μM-s, and hence, the redox signal that involves H₂O₂ is most likely transmitted via Prx and/or Gpx.

Table 2.

List of Selected Second Order Rate Constants for Oxidation Reactions of Small Molecule and Protein Thiols with H₂O₂

Thiol	kapp(M−1s−1)	Temp (oC)	pH	Concentration conditions	Data fitting	Method	References
Cysteine	2.9	37	7.4	Pseudo first order with thiol in excess, 50 mM iP, 10 μM DTPA	Exponential fit	H2O2 loss was monitored with a peroxide electrode or the FOX method	(109)
N-acetyl cysteine	0.16
GSH	0.89
PTP 1B	9.1	25	7	Pseudo first order with H2O2 in excess, 0.1 M acetate, 0.05 M Bis-Tris, and 0.05 M Tris	Exponential fit	Decay of enzyme activity	(25)
Cdc25B	164	20	7	Pseudo first order with H2O2 in excess, 3-C buffer	Exponential fit	Enzyme inactivation was measured with the quench method	(97)
CdC25C	120
Trx	1.05	25	7.4	second order conditions in iP	Initial rate method	Following the loss of thiol concentration	(41)
OxyR	1.1×105	25	7.4	pseudo first order with H2O2 in excess, PBS, 1 mM EDTA	Exponential fit	Change in Trp fluorescence (λex=280 nm, λem>330 nm)	(61)
Tsa1	2.2×107	25	7.4	0.1 M iP, 0.1 mM DTPA	Relative to HRP inhibition at different ratios	Competition kinetics with HRP	(83)
Tsa2	1.3×107
Prx2	2.2×107	25	7.4	0.1 M iP	Relative to HRP inhibition at different ratios	Competition kinetics with HRP	(87)
Prx3	2×107	25	7.4	0.01 M iP	Relative to HRP inhibition at different ratios	Competition kinetics with HRP	(23)

OxyR, the Escherichia coli transcription factor; Prx, peroxiredoxins; PBS, phosphate-buffered saline; DTPA, diethylene triamine penta acetic acid; HRP, horseradish peroxidase.

The second part of the aforementioned simplest oxidation-mediated thiol–disulfide conversion mechanism is an electrophilic–nucleophilic condensation reaction between RSOH and another thiol to give the disulfide (Reaction 4, where RSOH is the electrophile and RSH is the nucleophile). It is significantly more challenging to investigate the kinetics of this reaction because RSOH derivatives are in most cases very reactive and do not exhibit characteristic spectral features (36, 74, 78). Often the production of a RSOH is rate limiting and much slower than its condensation with another thiol (66). In these reactions, the steady-state approximation applies to RSOH concentrations, which makes it difficult to acquire kinetic information for Reactions 4 (or 5) in small molecules (6, 7). However, in reactions of RSH with more reactive oxidants, such as the HOX [at pH=7 k_HOCl=∼10⁷, k_HOBr=∼10⁷ (4, 74, 84, 85)], Reaction 4 becomes rate determining and could be followed by stopped-flow spectroscopy at high pH (which is necessary to slow down the reaction to the stopped-flow timescale, see Box 2 The effect of pH section) (74). Extrapolation of the data to pH 7 gave an estimate of 10⁵ M⁻¹s⁻¹ for the lower limit of the second order rate constant for the reaction of the parent CySOH with Cys under physiological conditions. (74). In contrast, in some proteins, steric hindrance restricts formation of a protein–protein disulfide and stabilizes the RSOH derivative. Notwithstanding, the RSOH derivative of human serum albumin exhibits surprisingly low reactivities even with small molecular weight thiols, having second order rate constants in the range of 2–100 M⁻¹s⁻¹ (102). In these cases, steric hindrance should be less prevalent and the proposed explanation is that the reacting Cys (CyS³⁴) is sitting in a hydrophobic pocket and not readily accessible for the solvent and the reactants. (27).

Box 2: A Few General Kinetic Considerations for Studying Thiol Oxidation Reactions.

The rate equation and rate determining concentrations

Two-electron thiol oxidation to disulfide [Scheme 1 model (b)] is a multistep process. In kinetic studies of multistep reactions, it is important to establish the rate determining step. For the simplest oxidative thiol–disulfide conversion mechanism (i.e., via a single RSOH intermediate species; Reactions 2a and 4), a similar rate equation will apply as for the interchange model if the rate determining step is the bimolecular reaction between the oxidant and the thiol:

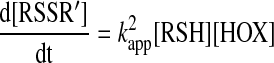(25)

This implies that all subsequent reaction steps are fast and the steady-state approximation applies for the change in the concentration of the intermediates over time. Even in this case, the relationship between the observed rate constant and the true rate constant of the initial bimolecular reaction will depend on the observable (i.e., whether we follow the decay of the thiol or the formation of the disulfide). If we follow the decay of the thiol, then the observed rate constant needs to be corrected with a proportionality constant to account for the fast loss of a second thiol in Reaction 4, and hence, the rate law will have the following form:

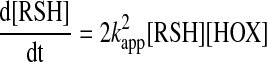(26)

In some cases, the situation can be more complicated and depending on the mechanism and conditions, the proportionality constant can be even larger (73). In these cases, a more comprehensive kinetic analysis is required to establish the concentration dependencies of the rate equation. Another important point is that if we follow the formation of the disulfide, we need to make sure that the rate determining step under the applied conditions does not change.

The effect of pH

The pH dependency of thiol oxidation reactions are generally more complicated compared to thiol–disulfide exchange reactions. For example, the pH profile of the rate law for Reaction 2 will not only depend on the protonation status of the thiol, but that of the oxidant's as well. Protonation of the oxidant accelerates the reaction because the protonated form is a better electrophile, which is an opposite effect to the aforementioned favorable deprotonation of the thiol. Therefore, the plot of k_obs as a function of pH will have a bell-shaped profile, where the pH at the maximum will correspond to the average of the pK_a values of the reactants [e.g., (78)]. Sometimes, alternative pathways via the less reactive species (e.g., the deprotonated form of the oxidant at higher pH) also exhibit competitive rates and, therefore, need to be taken into account (74, 78). Similarly to the kinetics of thiol–disulfide interchange reactions, microscopic acid dissociation constants (see Acid dissociation constants of reacting functional groups section) are required to describe speciation of thiolate derivatives of polyprotic molecules (such as Cys or GSH) (74, 78, 79). Furthermore, the rate of Reaction 4 is also pH dependent. As for the initial oxidation step (i.e., Reaction 2), the favored species are the thiolate (nucleophile) and the protonated RSOH (electrophile), and hence, a bell-shaped pH dependency is expected for this reaction too. In addition, the two consecutive reactions could exhibit pH dependencies to a different extent, which may result in a change in the rate determining step with the pH (74).

Studying fast reactions by competition kinetics

Under physiological conditions, some reactions are so fast that they cannot be followed directly. For a non-enzymatic reaction, the rate can be slowed down by a dramatic move away from pH 7 (either toward acidic or basic conditions), because of the above-mentioned reasons. However, most proteins are only stable at around pH 7, and pH-induced conformational transitions can result in changes in the mechanism. Therefore, to obtain kinetic information on fast protein oxidation reactions, the competition kinetics approach is often used [see e.g., (23, 77, 83, 87)]. This is based on the introduction into the reaction mixture of another reactant that competes for the oxidant. By changing the relative concentrations of the protein and the new reactant and taking into account the second order rate constant for the oxidation of the new reactant, the rate constant of interest (i.e., for the oxidation of the protein) can be calculated from product distribution. This approach is widely accepted, but there are potential pitfalls that are needed to be taken into account during the analysis: (i) Cross reactions of intermediates and products can change product distribution and confine the kinetic analysis. (ii) Not efficient mixing (i.e., slower mixing compared to reaction rates) can cause locally large concentrations of reactants due to inhomogenity, which could also change product ratios. (iii) For such competition kinetics measurements, the proportionality constant cannot be determined due to the lack of information on secondary reactions.

RSOH can also act as a nucleophile, for example, in its self-condensation or disproportionation reactions to give thiosulfinate ester (RS-S(=O)R′) or sulfinic acid (RSO₂H) derivatives, respectively. Both reactions were observed during the oxidation of free Cys with hypohalites even at >10-fold excess of thiol over the oxidant (74, 78). (RS-S(=O)R′) react with thiols to give a disulfide and RSOH (which is then converted to disulfide by another thiol) (39, 40, 73, 78). Therefore, these reactions can be considered as intermediate steps during thiol–disulfide conversion. However, it is important to note that in the presence of more than one type of thiol, intermediate formation of RS-S(=O)R′ can result in different product distribution, that is, different ratios of the mixed disulfides could form via the different pathways. On the other hand, RSO₂H does not react with thiols in aqueous solutions and, therefore, diverts the reactions from the disulfide formation path. Notwithstanding, reduction of RSO₂H derivatives of Prx back to the corresponding thiols by sulfiredoxin (Srx) occurs by a mechanism that involves the formation of a mixed (RS-S(=O)R′) intermediate (17, 54).

Thiol–disulfide conversion via radical-mediated oxidation pathways

One-electron oxidation of Cys thiols give thiyl radicals (Reactions 7 and 8) (103). The reaction proceeds via hydrogen abstraction from the thiol group or electron transfer through the thiolate species (9). The biologically important second order rate constants of these reactions range from 10–1000 M⁻¹s⁻¹ for superoxide [still debated due to the initiation of a chain reaction, see Refs. (52, 109, 117)] through 10⁸ M⁻¹s⁻¹ (1) for carbon centered radicals up to the diffusion-controlled limit as with the hydroxyl radical. Rapid recombination of two thiyl radicals can give a closed shell disulfide species, which would complete the thiol–disulfide conversion (Reaction 9). However, although the reaction is fast [2k=1.5×10⁹ M⁻¹s⁻¹ for GSH (46)], it is less likely to occur under physiological conditions because thiyl radicals exhibit high reactivities with other more abundant molecules. In biological systems, the most favorable is probably its reaction with thiolates (k>10⁹ M⁻¹s⁻¹) (5) to give the disulfide anion radical (RSSR′^•−; Reaction 10). RSSR′^•− are powerful reducing radicals and react favorably with oxygen (which was predicted to be their predominant reaction under physiological conditions) to give superoxide and the corresponding disulfide (Reaction 11). Alternatively, RS^. can react with oxygen (k ∼ 10⁸–10⁹ M⁻¹s⁻¹) in a reversible reaction to give a thiyl peroxyl radical RSOO^•), although this reaction is predicted to be less prevalent in biological systems. The fate of RSOO^• depends on the conditions, but many reaction pathways result in Cys derivatives with higher oxidation states (79).

In biological systems, one- and two-electron redox reactions often accompany each other. For example, in the disulfide relay systems, the oxidizing or reducing equivalents for oxidoreductases are supplied by molecular oxygen and NADPH, respectively, via one-electron redox reactions (see Figs. 1–3 and 5). The switch between the one- and two-electron transport pathways is mediated via intramolecular flavin adenine dinucleotide–disulfide interactions in flavin containing oxidoreductases, such as Erv1, Ero1, Grx, or TrxR (11, 43, 106, 118).

Although one-electron-mediated pathways are prevalent in biological systems, discussion of factors that influence their kinetics is outside the scope of this review.

Factors That Influence the Rates of Thiol Oxidation

Many of the previously mentioned determinants of the rate of thiol–disulfide interchange, including the pK_a and the nucleophilicity of the thiol (33), have similar influence on the kinetics of thiol oxidation reactions. In addition, the pK_a of the oxidant in reactions 2 and 4 will also affect its electrophilicity (see Box 2) and, thus, have a marked effect on the kinetics [see e.g., (71, 72, 75, 76)].

As with the thiol–disulfide interchange, factors that enhance the stability of the leaving group will also accelerate oxidation reactions. For example, during the reduction of different peroxide species by thiols, the effect of the reacting and leaving group pK_a values on the kinetics can also be described by Brønsted equations (33).

Reaction 2 was also suggested to proceed via an S_N2-type mechanism with a linear conformation of the thiol sulfur and the oxidant's attacking and leaving groups (33). [Although a recent insightful computational study challenges this proposal (116)]. Therefore, similarly to the thiol–disulfide exchange, larger oxidants could react slower with protein thiols due to steric hindrance. This effect might be responsible for the observed drop of the reactivities of Prx 2 and 3 with the size of the peroxide oxidant (86).

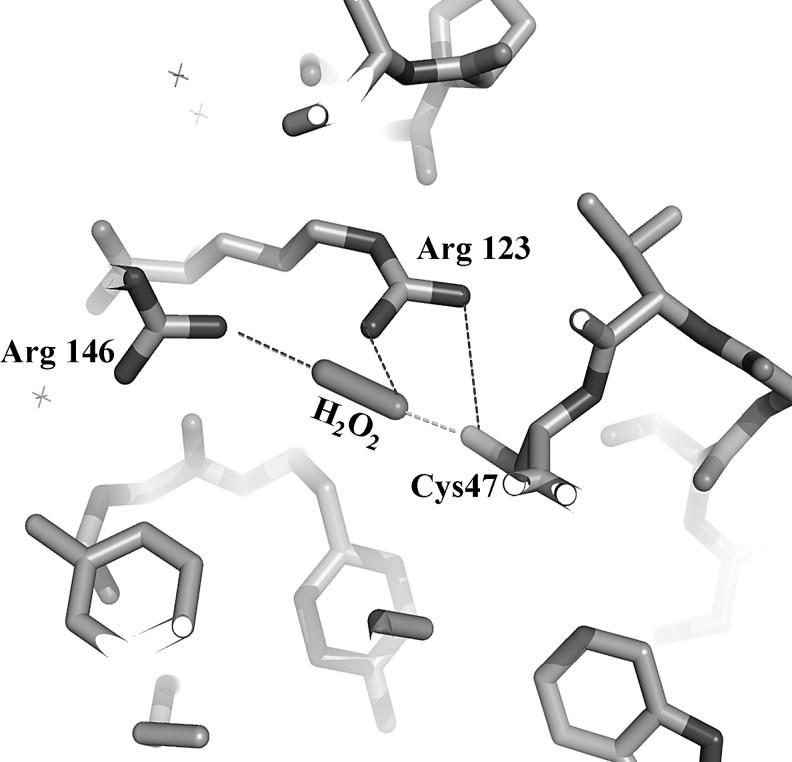
H-bond donating functional groups have profound effects on thiol oxidation reactions from many perspectives. For example, in a recent study, high-level theoretical calculations (at the G4 level) showed that the rate of the reaction of a thiol with a peroxide species is markedly accelerated via H-bond donating interactions at the sulfur as well as both oxygen centers in a cooperative manner (77). H-bond donation to the reacting oxygen has an accelerating effect via increasing its electrophilicity, and H-bond donation to the leaving oxygen stabilizes the transition state (as well as the leaving group) and decreases the activation energy. However, it is a bit less intuitive to envisage how H-bond donation to the sulfur center accelerates the reaction, because in general, H-bonding interactions to a nucleophile decrease its nucleophilic character (18). The effect was best explained by a more pronounced stabilization of the transition state structure compared to the reactant complexes, which further lowers the activation barrier of the reaction (77). On the protein level, these H-bonding effects are demonstrated by the example of the peroxidase activity of Prx, where two highly conserved Arg residues (∼3.5 and 6.5 Å away from the reacting sulfur) were proposed to serve as H-bond donors to the sulfur center as well as the two peroxide oxygens (see Fig. 8). Comprehensive kinetic analysis with a series of mutant enzymes revealed the importance of these two Arg residues in the peroxidase activities of Prx2 and Prx3. Point mutation of either of the Arg residues resulted in five orders of magnitude drop in the second order rate constants of the reactions of both isoforms with H₂O₂. When both Arg residues were mutated (in Prx2 as well as Prx3), the reactivities decreased further by two orders of magnitude resulting in similar reactivities of the double mutants as free Cys. Note that similar rate-enhancing properties of neighboring functional groups via H-bonding interactions were proposed for Prx (although via different mechanisms) in two different studies based on structural considerations of the active sites (44, 80). Structural studies also suggest that the Arg that is in the close proximity of the C_p (Arg 123 for Prx 3, see Fig. 8) plays an important role in activating the reacting peroxide oxygen, but a different orientation of the peroxide was proposed (44). Hence, further kinetic and structural analysis is required to establish which functional groups are involved in H-bond donation to the leaving oxygen in the different Prx isoforms.

FIG. 8.

Model for the activation of H₂O₂ at the active site of Prx via H-bonding interactions with two highly conserved Arg residues. The figure shows the proposed orientation of H₂O₂ at the active site of bovine Prx3 (Protein Data Bank code 1ZYE) (16). The distances of the Arg nitrogens from the peroxidative Cys47 sulfur are ideal to engage in H-bonding interactions with the sulfur center and the reacting and leaving oxygens of the peroxide. We proposed that Arg 123 anchors the reacting oxygen to the thiolate sulfur and Arg 146 stabilizes the leaving group (77). In addition, we suggested that the two Arg residues pull the oxygens apart, which activate the peroxide for the OH⁺ transfer to the thiolate.

In OxyR, an Arg residue (Arg 266) in the close proximity of the reacting thiolate serves a similar role (21). For both Prx and OxyR, disulfide formation is accompanied by a conformational change, which takes the Cys residues away from the corresponding Arg to stabilize the disulfide moiety (i.e., the close proximity of Arg would lower the pK_a and make the disulfide-bound Cys_p, a better leaving group).

Side reactions can also inhibit oxidation-mediated thiol–disulfide exchange processes. For example, during catalytic reduction of peroxides by the Prx/Trx/TrxR/NADPH system, at high peroxide concentrations, RSO₂H can form, which takes the protein out of the catalytic cycle (110, 113) (see Fig. 4). Although RSO₂H are eventually recycled by Srx, this process is significantly slower and, hence, inhibitory to the overall reduction process of oxidized Prx.

Interconversion of Substitution and Redox-Mediated Thiol–Disulfide Exchange Pathways

A beautiful example for the interconversion of oxidative and substitution-mediated thiol–disulfide exchange is the regulation of hydroperoxide homeostasis in S. cerevisiae. The peroxidase Orp1 reduces the peroxide to give an Orp1-SOH derivative, which reacts with the Yes-associated protein 1 (Yap1) to give a mixed disulfide intermediate. The mixed disulfide is subsequently reduced in an intramolecular thiol–disulfide interchange reaction to release Orp1 and give the oxidized Yap1 (a monomer with an intramolecular disulfide), which is its activated form. The signal regulatory role of Trx in this process also occurs via thiol–disulfide interchange reactions with the intramolecular Orp1 or Yap1 disulfide to recycle them in their active forms (24).

Recent kinetic considerations suggested that Prx will also serve as cellular peroxide sentinels (79, 108) and might transmit the redox signal by initiation of a cascade of subsequent reactions potentially via similar thiol–disulfide-mediated mechanisms (35, 79, 88, 108): Prx senses the signal (H₂O₂) in a rapid bimolecular reaction to give Prx-SOH. Prx-SOH then could react with another protein thiol to form a mixed disulfide, which could further engage in inter- and intramolecular thiol–disulfide exchange reactions and transmit the signal. Alternatively, the oxidized Prx dimer (as in Fig. 4) can transmit the oxidizing equivalents to other proteins via thiol–disulfide interchange. An example for this latter mechanism is Trx oxidation by the Prx dimer (as in Fig. 5a), which potentially contributes to redox regulation of cell signaling, because Trx is involved as a thiol reducing agent in many signaling pathways.

Another example for the overlap of the oxidative and redox-mediated thiol–disulfide conversion is the capture of the H₂O₂ by Prx4 that is produced by Ero1 in the ER. Oxidized Prx4 can subsequently oxidize PDI (to give its active form) via thiol–disulfide interchange, which provides a more efficient utilization of oxidizing equivalents in the protein-folding process (see Fig. 1) (119).

Conclusions and Future Directions

Thiol–disulfide interchange and thiol oxidation reactions are constantly occurring in cellular systems. It is now widely appreciated that the dynamics of these reactions are governed via kinetic rather than thermodynamic forces. Due to the promiscuous chemical properties of sulfur, the reactions can proceed via diverse pathways and give a plethora of different products and intermediate species. The lack of distinct spectroscopic signatures of the various thiol derivatives, as well as the large scale of chemical factors that influence the reaction rates poses challenges for kinetic investigations. The situation is further complicated by the fact that in cellular systems, some of the reaction cascades travel through different cellular compartments (see e.g., Figs. 1–3). Therefore, electron shuttling or diffusion/transport of reactants across membranes can become rate determining for the overall process. The above factors represent serious challenges and limitations to kinetic investigations that are aimed to better understand biological events. However, recent technological advances in kinetic, product identification/quantification, imaging, and other biochemical methodologies provide additional tools to carry out more comprehensive mechanistic studies. Therefore, a systematic rigorous chemical kinetics approach, which is routinely used in investigations of small molecule reactions, is becoming available to study more complicated enzymatic systems, which is expected to allow a deeper insight into cellular functions.

Abbreviations Used

AMPSO

3-[(1,1-dimethyl-2-hydroxyethyl)amino]-2-hydroxypropanesulfonic acid

Cdc

M-phase inducer phosphatase 2

cDsbD

C-terminal domain of DsbD

CoA

coenzyme A

CoAS-SCoA

coenzyme A dimer

CoAS-SG

gultathionylated CoA

COX

Cytochrome oxidase

CySH

Cys thiol

CySSG

Cys-GSH mixed disulfide

CySOH

Cys sulfenic acid

CySO₂H

sulfinic acid

Cys_p

peroxidative Cys of peroxiredoxins

CyS-S(=O)Cy

thiosulfinate ester

DsbA-D

the disulfide bond protein family A-D

DTPA

diethylenetriamine pentaacetic acid

DTT

dithiothreitol

ER

endoplasmic reticulum

Ero1

ER oxidoreductin

Erv1

essential for respiration and vegetative growth sulfhydryl oxidase

FAD

flavin adenine dinucleotide

FOX

Fe²⁺/xylenol orange assay

GAPDH

glyceraldehyde 3-phosphate dehydrogenase

GOR

glutathione oxido-reductase

Gpx or Orp1

glutathione peroxidases

Grx

glutaredoxin

GrxS-SG

glutathionylated Grx

GSH

reduced glutathione

GSSG

oxidized glutathione

HRP

horseradish peroxidase

Hot13

Zn binding protein

HOX

hypohalous acids

HSA

human serum albumin

I27S²⁴-S⁵⁵

I27 domain of human cardiac titin

IMS

mitochondrial inter membrane space

iP

phosphate buffer

nDsbD

N-terminal domain of DsbD

OxyR

the Escherichia coli transcription factor

PDI

protein disulfide isomerase

Prx

peroxiredoxins

PTP

protein tyrosine phosphatase

QSOX

quiescin-sulfhydryl oxidase

RSOO^•

thiyl peroxyl radical

Srx

sulfiredoxin

Trx

thioredoxin

Tsa

yeast peroxiredoxin

TrxR

thioredoxin reductase

Yap1

Yes-associated protein 1

Acknowledgments

The financial support of FP7-PEOPLE-2010-RG (Marie Curie International Reintegration Grant; grant No.: PIRG08-GA-2010-277006) is greatly acknowledged. I am grateful to Prof. Christine Winterbourn for critical reading and for my colleagues for proofreading the manuscript.