AVM Compartments: Do they modulate trasnidal pressures? An electrical network analysis

Abstract

Background:

Arteriovenous malformation (AVM) compartments are thought as independently fed, hemodynamically independent components of the AVM nidus. Its possible role in modulating transnidal pressures have not been investigated to our knowledge.

Objective:

To investigate if AVM compartments play a role in modulating transnidal pressures by using electrical models as a method of investigation.

Materials and Methods:

Monocompartmental and multicompartmental AVM models were constructed using electrical circuits- building on Dr. Guglielmi's previous work. Each compartment was fed by two feeding arteries (resistors) and had a shared draining vein with other compartments in the AVM nidus. Each compartment is composed of a series of resistors which represents the pressure gradient along the AVM (arterial, arteriolar, venular, and venous). Pressure (voltage) readings were obtained within these nidal points.

Results:

The pressure gradient (venous-arterial) is more as there are less AVM compartments in the nidus model. The monocomparmental model had a pressure gradient of 66mmHg (V); while it was 64, 61, and 59 for the 2-, 3-, and 4-compartment models, respectively. In addition, the more the number of compartments, the greater the flow (mA) is in the whole AVM nidus, 33 ml/min for the monocompartmental AVM and 121ml/min for the 4-compartment AVM; though there was greater flow per compartment as there were less compartments, 33ml/min per compartment for the monocompartmental model versus 29ml/min for the 4-compartment model.

Conclusion:

Transnidal pressure gradients may be less the more compartments an AVM has. This electrical model represents an approach that can be used in investigating the hemodynamic contributions of AVM compartments.

Introduction

A number of studies have investigated Arteriovenous malformation (AVM) hemodynamics in relation to its possible contribution to AVM rupture and consequent hemorrhage.[1–5] Hemodynamic factors that have been studied include feeding artery and draining vein pressures.

Henkes et al. found a lower difference between the Mean Arterial Pressure (MAP) and Feeding Artery Pressure (FAP) in hemorrhagic, small, and single draining AVMs.[1] These findings corroborate Spetzler's study that small AVMs had higher feeding artery pressures and larger hemorrhage volumes than larger AVMs.[2] In addition, Henkes et al. also noted an increase in feeding artery pressures upon occlusion of an AVM, more so with complete occlusion than minor occlusion, signifying that occluding an AVM may cause more flow obstruction leading to higher feeding pressures.[1] Kader et al. meanwhile hypothesize that feeding artery pressures constitute by itself a risk for spontaneous AVM hemorrhage and is not merely a consequence of AVM size.[5]

The role of venous pressures in AVM hemodynamics is of considerable significance. In principle, an AVM bleed is a venous bleed since it results from increased venous pressure transmitted through the shunt.[6] Evidence of this transnidal transmission of pressure is given by Young et al.'s finding that draining vein pressure (DVP) correlates with feeding artery pressure.[7] In addition, the drop in pressure from the feeders to the drainers (FAP-DVP) was found to be inversely correlated with AVM size – the smaller the AVM, the greater the drop in pressure from the feeding arteries to the draining veins.[7] DVP, along with FAP, was also found to be elevated in hemorrhagic AVMs than in non-hemorrhagic ones, the pressure drop, however, (FAP-DVP) was not found to be different between the two groups.[8]

AVM anatomy is essentially composed of one or more feeding arteries, a nidus, and one or more draining veins. The nidus composes the bulk of the AVM and is a cluster of venous loops that are entangled. It is connected to numerous vascular channels and is a high-flow system where arterial blood shunting occurs.[9–11] It has also been observed that the AVM nidus is composed of hemodynamically independent compartments.[9,10,12] Yamada describes AVM compartments as having separate feeding arteries and one or more draining veins; he additionally described that multiple compartments can share the same venous outflow tract.[9] Gryzska and Fiehler added that compartments are in hemodynamic balance as there was no transfer of contrast material observed from one compartment to another in digital subtraction angiography.[11] This latter finding supports Kakizawa et al.'s finding on 3D rotational angiography that nidal compartments are independently fed and do not overlap.[12] They further described that the outflow tract of the separate compartments ran mostly through a common draining vessel.

Discussed earlier are feeding artery and draining vein pressures in relation to AVM hemorrhage and angioarchitecture. Also discussed is AVM anatomy with special attention to the presence of independently fed, hemodynamically independent, nidal compartments. It is known that pressure is transmitted from the feeding arteries to the draining veins via the nidus, as blood flows from the feeding arteries to the nidus which is subsequently drained by one or more draining veins.[9,10,13] The question then is, do nidal compartments play a role in modulating pressure from the feeding arteries to the draining veins? It is hypothesized that AVM compartments may play a role in modulating the drop in pressure from the feeding arteries to the draining veins (transnidal pressure drop).

Given this problem, a study on the role of the nidal core in AVM hemodynamics would be beneficial. It, however, poses great technical challenges to measure pressures directly from the nidus.[13] It is thus proposed that a biomathemical model, based on electrical network analysis, be used as a possible approach to address the question at hand.

Materials and Methods

A compartmental brain AVM model was constructed using electrical models by using the software NI Multisim from National Instruments (www.ni.com/multisim). The model is based on Dr. Guglielmi's work which he used to measure baseline hemodynamics in the different parts of the AVM nidus as well as hemodynamic alterations as a consequence of surgery and endovascular embolization.[13]

To construct the model, he used data on pressure measurements from previous empirical studies and the value of blood flow through the brain hemisphere as well as through the AVM complex. The AVM system was simulated by a chain of resistors in series and in parallel. The flow of blood is likened to the flow of electrons and was designated as current- milliamperes (mA). The pressure drop across vascular segments- across the AVM nidus for example, was likened to the voltage drop as current flows across a resistor, the value of which was calculated using Ohm's law.[13] It was decided that we would adopt Dr. Guglielmi's low-flow model rather than the high-flow model as the former provides homogeneity among the compartments as opposed to the latter- which contains plexiform and fistulous components.[13]

Monocompartment model

The following components of the monocompartmental model/circuit is the voltage source which acts as the heart (100V or 100 mmHg), the cerebral vasculature represented by the resistor “Brain” and the AVM complex itself. The AVM complex is composed of two feeding arteries (each with 1150 ohms resistance), supplying one compartment. This is based on Yamada et al's anatomic study on brain AVMs.[10,11] Each compartment is composed of a series of resistors to represent the pressure gradient along the AVM from the arterial (N1), arteriolar (N2), venular (N3), and venous (N4) ends of the AVMs, akin to the “channels” in Dr. Guglielmi's work.[13] The compartment drains to a common draining vein with a 95 ohm resistance which eventually drains to the Transverse Sinus- Jugular vein output, set at 18 ohms. It is at this point where the AVM drainage and cerebral vasculature drainage meet [Figure 1].

Figure 1.

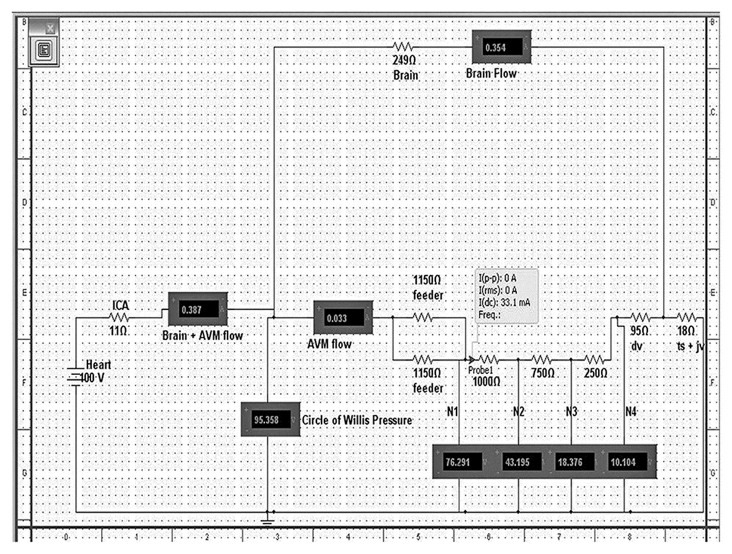
This is an electrical model of a monocompartmental AVM. The resistors simulate the vessels and they are expressed in ohms. The “Heart” is the voltage source and it simulates the human heart. “ICA” -internal carotid artery; “Brain + AVM flow” - flow (in mA) through the brain and AVM complex; “; “Brain flow”- flow through the brain alone; “feeder”- arterial feeder to the nidal compartment;” dv”-draining vein;” ts+jv”-transverse sinus + jugular vein complex; “N1”-pressure at arterial part of the nidus, “N2”- pressure at the arteriolar part of the nidus, ”N3”-pressure at venular part of the nidus, “N4”-pressure at venous part of the nidus. The probe indicates the flow per compartment: “I(dc)”

Multicompartmental models

The following models are 2-compartment, 3-compartment, and 4-compartment models, respectively [Figures 2–4]. It is generally similar to the monocompartmental AVM model described above. Each compartment is supplied by two feeding arteries, and it was decided that all compartments will have a common draining vein. This is to better demonstrate the possible role that compartments may have in modulating transnidal pressures.

Figure 2.

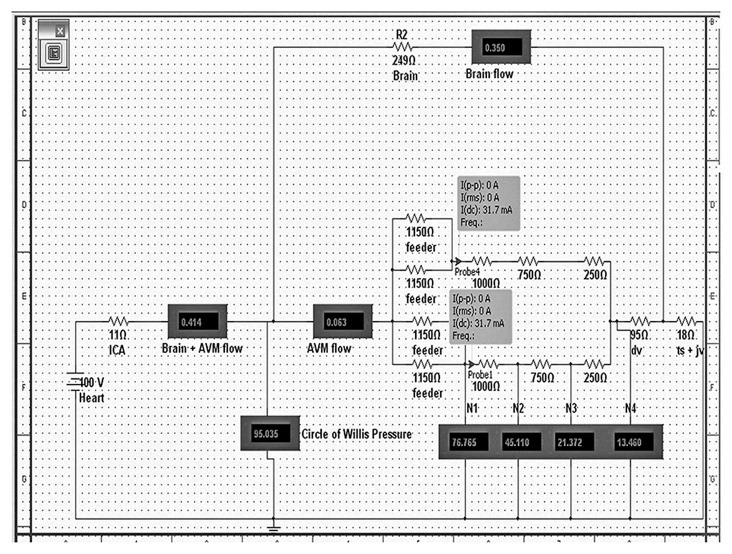
This is an electrical model of a 2-compartment AVM. The resistors simulate the vessels and they are expressed in ohms. The “Heart” is the voltage source and it simulates the human heart. “ICA” -internal carotid artery; “Brain + AVM flow” - flow (in mA) through the brain and AVM complex; “; “Brain flow”- flow through the brain alone; 2 arteries labeled as “feeder” supply each of the two nidal compartments;“ dv”-draining vein;” ts+jv”- transverse sinus + jugular vein complex; “N1”-pressure at arterial part of the nidus, “N2”- pressure at the arteriolar part of the nidus, “N3”-pressure at venular part of the nidus, “N4”-pressure at venous part of the nidus. The probes indicate the flow per compartment: “I(dc)”

Figure 4.

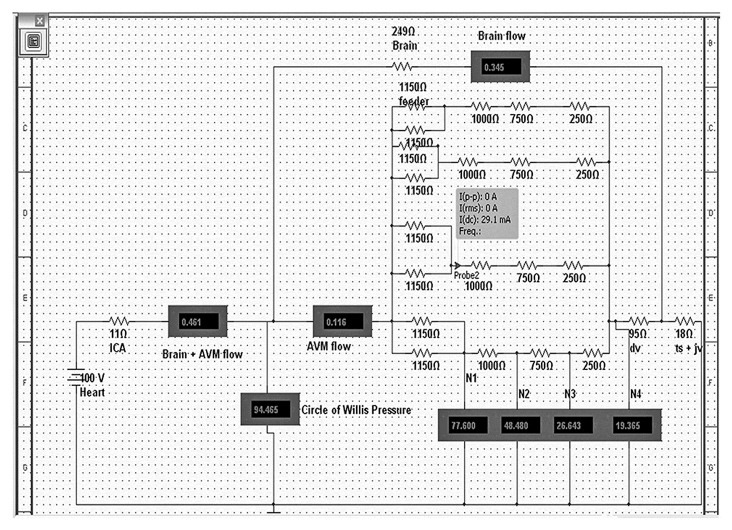
This is an electrical model of a 4-compartment AVM. The resistors simulate the vessels and they are expressed in ohms. The “Heart” is the voltage source and it simulates the human heart. “ICA” -internal carotid artery; “Brain + AVM flow” - flow (in mA) through the brain and AVM complex; “; “Brain flow”- flow through the brain alone; 2 arteries labeled as “feeder” supply each of the 4 nidal compartments; “ dv”-draining vein;” ts+jv”- transverse sinus + jugular vein complex; “N1”-pressure at arterial part of the nidus, “N2”-pressure at the arteriolar part of the nidus, “N3”-pressure at venular part of the nidus, “N4”-pressure at venous part of the nidus. The probe indicates the flow per compartment: “I(dc)”

Figure 3.

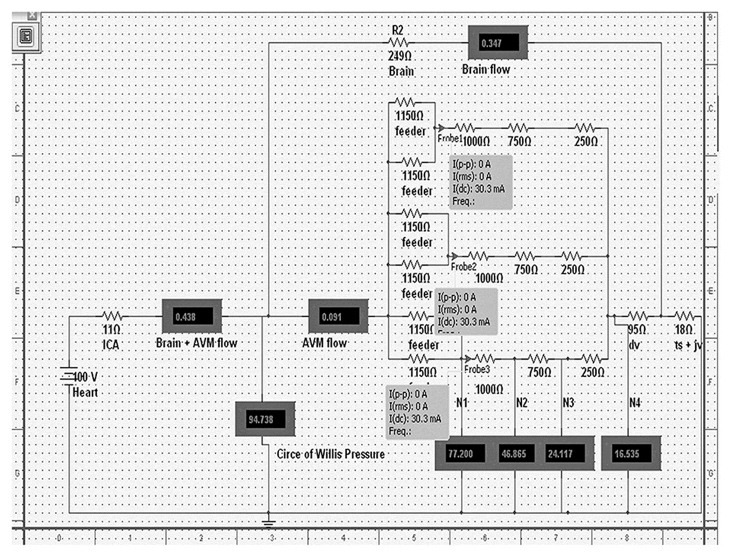
This is an electrical model of a 3-compartment AVM. The resistors simulate the vessels and they are expressed in ohms. The “Heart” is the voltage source and it simulates the human heart. “ICA” -internal carotid artery; “Brain + AVM flow” - flow (in mA) through the brain and AVM complex; “; “Brain flow”- flow through the brain alone; 2 arteries labeled as “feeder” supply each of the 3 nidal compartments; “ dv“-draining vein;” ts+jv”- transverse sinus + jugular vein complex; “N1”-pressure at arterial part of the nidus, “N2”- pressure at the arteriolar part of the nidus, “N3”- pressure at venular part of the nidus, “N4”-pressure at venous part of the nidus. The probes indicate the flow per compartment: “I(dc)”

Results

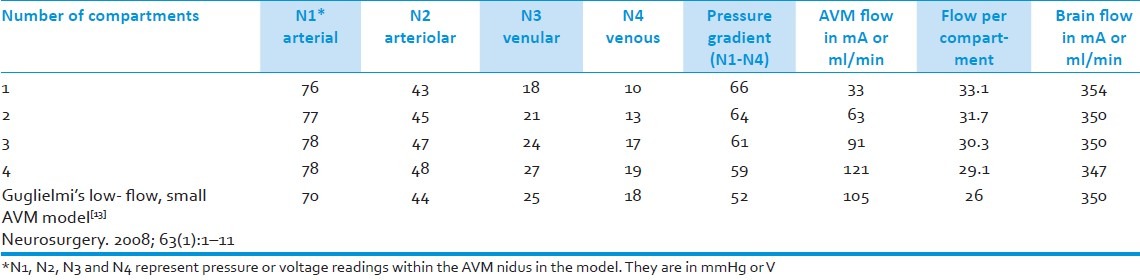
AVM flow is directly proportional to the number of compartments in the AVM model- the greater the number of compartments, the greater the flow in the AVM. However, the more the number of compartments in the model, the less the flow per compartment is. In our model, the 4-compartment AVM has an AVM flow of 121ml/min (mA) and 29.1ml/min flowing in each of its compartments; while the monocompartmental model only has 33.1ml/min flowing through it but has all of that flowing in one compartment. Also, the less blood/current flows into the AVM, the more blood/current flows into the brain. As there are more compartments in the model, the less blood flows into the brain, possibly demonstrating in these models the “steal” phenomenon that has been described in angiographic studies.[6,11]

Pressure at the arterial part of the nidus, which is empirically construed as the feeding artery pressure, is observed to be fairly constant at the arterial part of the nidus model regardless of number of compartments. A decrease in pressure is observed as the current/blood flows from the arterial to the venous point of the nidus. The drop in pressure, however, from the arterial to the venous portion of the nidus, the pressure gradient (N1-N4), differs among the AVM models. The arterial-venous gradient in the model of the AVM nidus is observed to be inversely proportional to compartment number. That is, the less the number of compartments, the more the pressure could be dissipated across the nidus and the more compartments there are, the less the pressure could be dissipated [Table 1].

Table 1.

Summary table of AVM flow, flow per AVM compartment, brain flow, pressures, and pressure gradient in relation to compartment number in the electrical AVM model

Discussion

It was described in the preceding section that the monocompartmental AVM model had the highest pressure gradient among the AVM models- with pressure gradient decreasing the more compartments there are. It was also described that the AVM models with less compartments have more flow per compartment, even though the whole AVM complex itself has less flowing into it.

AVM hemodynamics has been demonstrated to be sufficiently approximated by Poiseuille's formula. The following equations deriving from it were outlined by Hademenos et al. and these are:[14]

1. Q = [DELTA]P/R_V

Where Q is flow rate, [DELTA]P is the pressure gradient, and R_v is the vascular resistance of the vascular bed

2. V_avg = [DELTA]P(R[2]/8L[eta]).

Where V_avg = average blood flow velocity, R= inner radius of the vessel, L is the length of the vessel, and eta is blood viscosity

3. [tau] = –[([DELTA]P)R/2 L]

Where [tau] is wall shear stress, R is inner radius of vessel wall, L is length of vessel

The negative sign represents force acting in a direction opposing flow.

Given these equations, it can be conceptually observed that the greater the pressure gradient there is, the greater the flow rate, flow velocity, and wall shear stress are, assuming that the other variables are held constant. It can also be observed that the greater the flow rate is, the greater the wall shear stress is as expressed in the following equation:

[tau] = [4[eta] Q/[pi]R[3].

Where [tau] is wall shear stress, [eta] is blood viscosity, Q is flow rate, and R the inner radius of the vessel wall.

The compartmental AVM model that we constructed may provide information on pressure gradient as well as flow rate per compartment which may be tied up with the equations given above to possibly give a conceptual picture of how compartments are involved in AVM hemodynamics. Monocompartmental AVMs may possibly have greater flow rates, average blood flow velocities, and wall shear stress, given that it may have higher pressure gradients than multicompartmental AVMs. The former may also have higher wall shear stresses given that it may have higher flow rates per compartment as is observed in the model.

The findings of this study are fairly consistent with studies which have done direct measurements of feeding artery and draining vein pressures.[6,7] We did a correlation between AVM flow (to the whole AVM nidus and not on a per compartment basis) and pressure gradient based on Nornes and Grip's data set consisting of 9 AVMs.[6] This showed a negative correlation between flow and pressure gradient, r=−0.704 P=0.051, indicating that the lower the flow an AVM has, the higher the pressure gradient it may have. This is consistent with the findings of our compartmental AVM electrical model- wherein the 4-compartment AVM which has a flow rate of 121 ml/min, has a pressure gradient of 59 mmHg (V), while the monocompartmental model has a flow rate of 33 ml/min and a pressure gradient of 66 mmHg(V).

Young et al. demonstrated an inverse relationship between AVM size and trasnidal pressure drops;[7] smaller AVMs had greater drops in pressure across the nidus than larger AVMs. This could be interpreted as consistent with our findings in light of Yamada et al.'s anatomic findings that larger AVMs had more compartments than smaller AVMs.[10] In our model, the monocompartmental AVM may be construed as a small AVM while the multicompartmental AVMs are that of a larger size. Our model shows that the transnidal pressure drop is greater the less compartments there are- with the monocompartmental model having a 66 mmHg drop and the 2-, 3-, and 4- compartmental models having pressure drops of 64, 61, and 59 mmHg, respectively.

The limits of this electrical model are similar to that outlined by Guglielmi in his previous work. It does not take into account factors such as blood viscosity, nidal shear stress, pulsatile blood flow, and the distensibility of AVM vessels.[13] In addition, our model assumes that all compartments are homogenous, and run in parallel to each other- as demonstrated by them being arranged as parallel circuits. This does not account for vessel tortuosity within the nidus. Our multicompartmental models also show the compartments sharing common drainage, while Yamada et al. showed anatomically that each compartment has its own drainage.[10] Though what are mentioned above are obvious limitations, we would like to stress that simplicity in the model is what we desire as we try to establish a starting point in the study of hemodynamics vis-à-vis AVM compartments- something which we believe to have achieved.

Conclusion

We have attempted in this electrical model to demonstrate the possible role of AVM compartments in modulating transnidal pressures. It was demonstrated that the pressure gradient from the arterial to the venous portion of the nidus is greater as there are less compartments in the AVM. Differential wall shear stresses meanwhile can be deduced from differential pressure gradients- the greater the pressure gradient, the greater the wall shear stress. Mocompartmental AVMs then, may have greater wall shear stresses compared to multicompartmental AVMs. We believe that this model is helpful in studying AVM compartments in relation to AVM hemodynamics, something which at present is extremely difficult to study in-vivo. A model that would incorporate more the inherent anatomic and hemodynamic complexity of an AVM is desired in the future.