Semiparametric Regression Pursuit

Abstract

The semiparametric partially linear model allows flexible modeling of covariate effects on the response variable in regression. It combines the flexibility of nonparametric regression and parsimony of linear regression. The most important assumption in the existing methods for the estimation in this model is to assume a priori that it is known which covariates have a linear effect and which do not. However, in applied work, this is rarely known in advance. We consider the problem of estimation in the partially linear models without assuming a priori which covariates have linear effects. We propose a semiparametric regression pursuit method for identifying the covariates with a linear effect. Our proposed method is a penalized regression approach using a group minimax concave penalty. Under suitable conditions we show that the proposed approach is model-pursuit consistent, meaning that it can correctly determine which covariates have a linear effect and which do not with high probability. The performance of the proposed method is evaluated using simulation studies, which support our theoretical results. A real data example is used to illustrated the application of the proposed method.

1. Introduction

Suppose we have a random sample (y_i, x_i1, …, x_ip), 1 ≤ i ≤ n, where y_i is the response variable and (x_i1, …, x_ip) is a p-dimensional covariate vector. Consider the semiparametric partially linear model

$$y_i=\mu +\sum _{j\in S_1}{\beta }_j{x}_{ij}+\sum _{j\in S_2}{f}_j(x_{ij})+{\epsilon }_i,1\le i\le n,$$ (1)

where S₁ and S₂ are mutually exclusive and complementary subsets of {1, …, p}, {β_j: j ∈ S₁} are regression coefficients of the covariates with indices in S₁, and (f_j: j ∈ S₂) are unknown functions. In this model, the mean response is linearly related to the covariates in S₁, while its relation with the remaining covariates is not specified up to any finite number of parameters. This model combines the flexibility of nonparametric regression and parsimony of linear regression. When the relation between y_i and {x_ij: j ∈ S₁} is of main interest and can be approximated by a linear function, it offers more interpretability than a purely nonparametric additive model.

There is a large literature on the estimation in partially linear models. Examples include the partial spline estimator (Wahba 1984; Engle, Granger, Rice and Weiss 1986 and Heckman 1986) and the partial residual estimator (Robinson 1988, Speckman 1988) and polynomial spline estimator (Chen 1988). An excellent discussion of partially linear models can be found in the book by Härdle, Liang and Gao (2000), which also contains an extensive list of references on this model. A comprehensive treatment of general semiparametric theory and many related models can be found in Bickle, Klaassen, Ritov and Wellner (1993).

The most important assumption in the existing methods for the estimation in partially linear models is to assume that it is known a priori which covariates have a linear form and which do not in the model. This assumption underlies the construction of the estimators and investigation of their theoretical properties in the existing methods. However, in applied work, it is rarely known in advance which covariates have linear effects and which have nonlinear effects.

Recently, Zhang, Cheng and Liu (2010) proposed a novel method for determining the zero, linear and nonlinear components in partially linear models. Their method is a two-step regularization method in the smoothing spline ANOVA framework. In the first step, they obtain an initial consistent estimator for the components in a nonparametric additive model, and then use the initial estimator as the weights in their proposed regularized smoothing spline method in a way similar to the adaptive Lasso (Zou 2006). They obtained the rate of convergence of their proposed estimator. They also showed that their method is selection consistent in the special case of tensor product design. However, they did not prove any selection consistency results for general partially linear models. Also, in their two-step approach, a total of four penalty parameters need to be selected, which may be difficult to implement in practice.

We consider the problem of estimation in partially linear models without assuming a priori which covariates have a linear effect and which have nonlinear effects. We propose a semiparametric regression pursuit method for identifying the covariates with linear effects and those with nonlinear effects. We embed partially linear models into a nonparametric additive model. By approximating the nonparametric components using spline series expansions, we transform the problem of model specification into a group variable selection problem. We then determine the linear and nonlinear components with a penalized approach, using the minimax concave penalty (MCP, Zhang 2010) imposed on the norm of the coefficients in the spline expansion. We refer to this penalized approach as the group MCP method. We show that, under suitable conditions, the proposed approach is model pursuit consistent, meaning that it can correctly determine which covariates have a linear effect and which do not with high probability. We allow the possibility that the underlying true model is not partially linear. Then the proposed approach has the same asymptotic property as the nonparametric estimator in the nonparametric additive model. We also show that the estimated coefficients of linear effects are asymptotically normal, with the same distribution as the estimator assuming the true model were known in advance.

Some of the techniques used in this paper are similar to those in Huang, Horowitz and Wei (2010), in which the problem of variable selection in nonparametric additive models is considered. In particular, after transforming the present problem of model pursuit into a group selection problem based on spline approximation, some of the techniques in obtaining rate of convergence for the group Lasso estimator in the context of nonparametric additive models in Huang et al. (2010) can be applied here with some modiffcations, see the proof of Theorem 2 in the Appendix. However, the problem of model pursuit considered in this paper is very different from that in Huang et al. (2010). Also, here we use the group MCP rather than the group Lasso, which requires different treatment at the technical level as well.

This article is organized as follows. In Section 2 we describe our proposed semi-parametric regression pursuit (SRP) method. We transform the problem of identifying linear and nonlinear components into an group selection problem using the group MCP. In Section 3 we derived a group coordinate descent algorithm to implement the proposed method. In Section 4 we state the theoretical results concerning the selection and estimation properties of the proposed method. Section 5 includes simulation studies and an illustration of the proposed method on a data example. Proofs of the results stated in Section 3 are given in the Appendix.

2. Semiparametric regression pursuit via group minimax concave penalization

2.1. Method

The semiparametric partially linear model (1) can be embedded into the nonparametric additive model (Hastie and Tibshirani 1990),

$$y_i=\mu +f_1(x_{i1})+\cdots +f_p(x_{ip})+{\epsilon }_i.$$ (2)

Suppose that x_ij takes values in [a, b] where a < b are finite constants. To ensure unique identification of the f_j’s, we assume that Ef_j(x_ij) = 0, 1 ≤ j ≤ p. If some of the f_j’s are linear, then (2) becomes the partially linear additive model (1). The problem becomes that of determineing which f_j’s have a linear form and which do not. For this purpose, we decompose f_j into a linear part and a nonparametric part

$$f_j(x)={\beta }_{0j}+{\beta }_{j}x+g_j(x).$$

Consider a truncated series expansion for approximating g_j,

$$g_{nj}(x)=\sum _{k=1}^{m_n}{\theta }_{jk}{\phi }_k(x),$$ (3)

where φ₁, …, φ_mn are basis functions and m_n → ∞ at certain rate as n → ∞. If θ_jk = 0, 1 ≤ k ≤ m_n, then f_j has the linear form. Therefore, with this formulation, the problem now is to determine which groups of {θ_jk, 1 ≤ k ≤ m_n} are zero.

Let β = (β₁, …, β_p)′ and ${\theta }_n={({\theta }_{1n}^{\prime },\dots ,{\theta }_{pn}^{\prime })}^{\prime }$, where θ_jn = (θ_j1, …, θ_jmn)′. Define the penalized least squares criterion

$$L(\mu ,\beta ,{\theta }_n;\lambda ,\gamma )=\frac{1}{2n}\sum _{i=1}^n{\left(y_i-\mu -\sum _{j=1}^p{x}_{ij}{\beta }_j-\sum _{j=1}^p\sum _{k=1}^{m_n}{\theta }_{jk}{\phi }_k(x_{ij})\right)}^2+\sum _{j=1}^p{\rho }_{\gamma }(|\left|{\theta }_{jn}\right||A_j;\sqrt{m_n}\lambda ),$$ (4)

where ρ is a penalty function depending on the penalty parameter λ ≥ 0 and a regularization parameter γ. Here without causing confusing, we still use μ to denote the intercept. The norm $\left|\right|{\theta }_{jn}\left|\right|A_j={({\theta }_{nj}^{\prime }{A}_j{\theta }_{nj})}^{1/2}$ for a given positive definite matrix A_j. In theory, any positive definite matrix can be used as A_j, since ||θ_jn||Aj = 0 if and only if θ_jn = 0 as long as A_j is positive definite. However, it is important to choose a suitable choice of A_j to make the amount of penalization comparable across the groups and to facilitate the computation. We will specify A_j in (9) below.

We use the minimax concave penalty, or MCP introduced by Zhang (2010). This penalty function is defined by

$${\rho }_{\gamma }(t;\lambda )=\lambda {\int }_0^t{(1-x/(\gamma \lambda ))}_{+}dx,t\ge 0,$$ (5)

where γ is a parameter that controls the concavity of ρ and λ is the penalty parameter. Here x₊ denotes the nonnegative part of x, that is, x₊ = x1_{x≥0}. We require λ ≥ 0 and γ > 1. The term MCP comes from the fact that it minimizes the maximum concavity measure defined in (2.2) of Zhang (2010) subject to conditions on unbiasedness and selection features. The MCP can be easily understood by considering its derivative

$${\stackrel{.}{\rho }}_{\gamma }(t;\lambda )=\lambda {(1-t/(\gamma \lambda ))}_{+},t\ge 0.$$ (6)

It begins by applying the same rate of penalization as the lasso, but continuously relaxes that penalization until, when t > γλ, the rate of penalization drops to 0. It provides a continuum of penalties with the ℓ₁ penalty at γ = ∞ and the hard-thresholding penalty as γ → 1+. In particular, it includes the Lasso penalty as a special case at γ = ∞. Detailed discussions on the MCP can be found in Zhang (2010).

The penalty in (4) is a composite of the penalty function ρ_γ (·; λ) and a weighted ℓ₂-norm of θ_j. The ρ_γ (·; λ) is a penalty for individual variable selection. When it is applied to a norm of θ_j, it selects the coefficients in θ_j as a group. This is desirable, since the nonlinear components are represented by the coefficients in the θ_j’s as groups. Based on the definition of the penalty function in (4), it is natural to call it the group minimax concave penalty, or group MCP.

For a given (λ, γ), the penalized least squares solution is defined by

$$({\widehat{\mu }}_n,{\widehat{\beta }}_n,{\widehat{\theta }}_n)=\underset{\mu ,\beta ,{\theta }_n}{argmin}L(\mu ,\beta ,{\theta }_n;\lambda ,\gamma ),$$

subject to the constraints

$$\sum _{i=1}^n\sum _{k=1}^{m_n}{\theta }_{jk}{\phi }_k(x_{ij})=0,1\le j\le p.$$ (7)

These centering constraints are sample analogs of the identifying restriction Ef_j(x_ij) = 0, 1 ≤ i ≤ n, 1 ≤ j ≤ p.

We convert (7) to an unconstrained optimization problem by centering the response and the covariate functions. Specifically, we center the responses and covariates and standardize the covariates by imposing

$$\sum _{i=1}^n{y}_i=0,\sum _{i=1}^n{x}_{ij}=0\text{and}\sum _{i=1}^n{x}_{ij}^2=n.$$

We also center the basis functions. Let

$${\overline{\phi }}_{jk}=\frac{1}{n}\sum _{i=1}^n{\phi }_k(x_{ij}),{\psi }_{jk}(x)={\phi }_k(x)-{\overline{\phi }}_{jk}.$$ (8)

Define

$$Z_{ij}={\left({\psi }_{j1}(x_{ij}),\dots ,{\psi }_{{jm}_n}(x_{ij})\right)}^{\prime }.$$

So the z_ij consists of the centered basis functions at the ith observation of the jth covariate. Let Z = (Z₁, …, Z_p), where Z_j = (z_1j, …, z_nj)′ is the n × m_n ‘design’ matrix corresponding to the jth expansion. Let y = (y₁, …, y_n)′, x_j = (x_1j, …, x_nj)′ and X = (x₁, …, x_p). We can write

$$({\widehat{\beta }}_n,{\widehat{\theta }}_n)=\underset{\beta ,{\theta }_n}{argmin}\{L(\beta ,{\theta }_n;\lambda ,\gamma )=\frac{1}{2n}{\left|\right|y-X\beta -Z{\theta }_n\left|\right|}^2+\sum _{j=1}^p{\rho }_{\gamma }({\left|\right|{\theta }_{nj}\left|\right|}_{A_j};\sqrt{m_n}\lambda )\}.$$

Here we dropped μ from the arguments of L, since the intercept is zero due to centering. With the centering, the constrained optimization problem becomes an unconstrained one.

2.2 Penalized profile least squares

To compute (β̂_n, θ̂_n), we can use a penalized profile least squares approach. For any given θ_n, the β̂ that minimizes L necessarily satisfies

$$X^{\prime }(y-X\beta -Z{\theta }_n)=0.$$

Thus β = (X′X)⁻¹X′(y − Zθ_n). Let Q = I − P_X, where P_X = X(X′X)⁻¹X′ is the projection matrix onto the column space of X. The profile objective function of θ_n is

$$L({\theta }_n;\lambda ,\gamma )=\frac{1}{2n}{\left|\right|Q(y-Z{\theta }_n)\left|\right|}^2+\sum _{j=1}^p{\rho }_{\gamma }({\left|\right|{\theta }_{nj}\left|\right|}_{A_i};\sqrt{m_n}\lambda ).$$ (9)

As noted above, any positive definite matrix can be used for A_j. Here we use $A_j=Z_j^{\prime }{QZ}_j/n$. The rationale for this choice is based on the following considerations. First, in the profile objective function (9), the covariate matrix for group j is QZ_j. The Gram matrix associated with it is $Z_j^{\prime }{Q}^{\prime }{QZ}_j/n=A_j$, since Q is an orthonormal matrix. Although the original covariates x_ij’s are standardized, the covariate matrices for the groups are not necessarily so. Therefore, this choice of A_j standardizes the covariate matrices associated with θ_nj’s and makes the amount of penalization comparable across the groups comparable. Second, this leads to an explicit expression in the update steps in the group coordinate algorithm described below. This facilitates the implementation of the algorithm, since computation in each update step can be carried out using explicit expressions. For any given (λ, γ), the penalized profile least squares solution is defined by θ̂_n = arg min_θn L(θ_n; λ, γ). We compute θ̂_n using a group coordinate descent algorithm described in Section 3.

The set of indices of the covariates that are estimated to have the linear form in the regression model (1) is Ŝ₁ ≡ {j: ||θ̂_nj|| = 0}. Thus,

$${\widehat{g}}_{nj}(x)=0,j\in {\widehat{S}}_1\text{and}{\widehat{g}}_{nj}(x)=\sum _{k=1}^{m_n}{\widehat{\theta }}_{jk}{\psi }_{jk}(x),j\notin {\widehat{S}}_1.$$

Denote X̂₍₁₎ = (x_j, j ∈ Ŝ₁), Ẑ₍₂₎= (Z_j: j ∉ Ŝ₁) and ${\widehat{\theta }}_{n(2)}={({\widehat{\theta }}_{nj}^{\prime },j\notin {\widehat{S}}_1)}^{\prime }$. We have β̂_n = (X′X)⁻¹X′(y − Ẑ₍₂₎θ̂_n(2)). The estimator of the coefficients of the linear components is β̂_n1 = (β̂_j: j ∈ Ŝ₁)′. Let

$${\widehat{f}}_{nj}(x)={\widehat{\beta }}_{j}x+{\widehat{g}}_{nj}(x),j\notin {\widehat{S}}_1.$$

Denote f̂_nj(x_j) = (f̂_nj(x_1j), …, f̂_nj(x_nj))′. Then the estimator of the coefficient vector of the linear components can also be written as

$${\widehat{\beta }}_{n1}={({\widehat{X}}_{(1)}^{\prime }{\widehat{X}}_{(1)})}^{-1}{\widehat{X}}_{(1)}^{\prime }(y-\sum _{j\notin {\widehat{S}}_1}{\widehat{f}}_{nj}(x_j)).$$

2.3 Spline approximation

We use polynomial splines to approximate the non-parametric components g_j, 1 ≤ j ≤ p. Let a = t₀ < t₁ < ··· < t_K < t_K+1 = b be a partition of [a, b] into K subintervals I_Kk = [t_k, t_k+1), k = 0, …, K − 1 and I_KK = [t_K, t_K+1], where K ≡ K_n = O(n^v) with 0 < v < 0.5 is a positive integer such that max_1≤k≤K+1 |t_k − t_k−1| = O(n^−v). Let S_n be the space of polynomial splines of degree l ≥ 1 consisting of functions s satisfying: (i) the restriction of s to I_Kk is a polynomial of degree l for 1 ≤ k ≤ K; (ii) for l ≥ 2 and 0 ≤ l′ ≤ l − 2, s is l′ times continuously differentiable on [a, b] (Schumaker 1981). There exists normalized B-spline basis functions {φ_k, 1 ≤ k ≤ m_n} for S_n, where m_n ≡ K_n + l (Schumaker 1981). We can use these basis functions in the approximation (3).

3. Computation

We derive a group coordinate descent algorithm for computing θ̂ _n. This algorithm is a natural extension of the standard coordinate descent algorithm (Fu 1998; Friedman et al. 2007; Wu and Lange 2007) used in optimization problems with convex penalties such as the Lasso. It has also been used in calculating the penalized estimates based on concave penalty functions (Breheny and Huang 2010).

The group coordinate descent algorithm optimizes a target function with respect to a single group at a time, iteratively cycling through all groups until convergence is reached. This algorithm is particularly suitable for computing θ̂_n, since it has a simple closed form expression for a single-group model as given in (10) below.

We write $A_j=R_j^{\prime }{R}_j$ for an m_n × m_n upper triangular matrix R_j via the Cholesky decomposition. Let b_j = R_jθ_j, ỹ = Qy and ${\stackrel{\sim }{Z}}_j={QZ}_j{R}_j^{-1}$. Simple algebra shows that

$$L(b;\lambda ,\gamma )=\frac{1}{2n}{\left|\right|\stackrel{\sim }{y}-\sum _{j=1}^p{\stackrel{\sim }{Z}}_j{b}_j\left|\right|}^2+\sum _{j=1}^p{\rho }_{\gamma }(|\left|b_j\right||;\sqrt{m_n}\lambda )$$

Note that $n^{-1}{\stackrel{\sim }{Z}}_j^{\prime }{\stackrel{\sim }{Z}}_j={R_j^{-1}}^{\prime }(n^{-1}{Z}_j^{\prime }{QZ}_j)R_j^{-1}=I_{m_n}$. Let ${\stackrel{\sim }{y}}_j=\stackrel{\sim }{y}-{\sum }_{k\ne j}^p{\stackrel{\sim }{Z}}_k{b}_k$. Denote

$$L_j(b_j;\lambda ,\gamma )=\frac{1}{2n}{\left|\right|{\stackrel{\sim }{y}}_j-{\stackrel{\sim }{Z}}_j{b}_j\left|\right|}^2+{\rho }_{\gamma }(|\left|b_j\right||;\sqrt{m_n}\lambda ).$$

Let ${\eta }_j={\stackrel{\sim }{Z}}_j{({\stackrel{\sim }{Z}}_j^{\prime }{\stackrel{\sim }{Z}}_j)}^{-1}{\stackrel{\sim }{y}}_j=n^{-1}{\stackrel{\sim }{Z}}_j^{\prime }\stackrel{\sim }{y}$. For γ > 1, it can be verified that the value that minimizes L_j with respect to b_j is

$${\stackrel{\sim }{b}}_{j,GM}(\lambda ,\gamma )=M({\eta }_j;\lambda ,\gamma )\equiv \{\begin{array}{ll}0,\hfill & \text{if}\left|\right|{\eta }_j\left|\right|\le \sqrt{m_n}\lambda ,\hfill \\ \frac{\gamma }{\gamma -1}(1-\frac{\sqrt{m_n}\lambda }{\left|\right|{\eta }_j\left|\right|}){\eta }_j,\hfill & \text{if}\sqrt{m_n}\lambda <\left|\right|{\eta }_j\left|\right|\le \gamma \sqrt{m_n}\lambda ,\hfill \\ {\eta }_j,\hfill & \text{if}\left|\right|{\eta }_j\left|\right|>\gamma \sqrt{m_n}\lambda .\hfill \end{array}$$ (10)

In particular, when γ = ∞, we have

$${\stackrel{\sim }{b}}_{j,GL}={\left(1-\frac{\sqrt{m_n}\lambda }{\left|\right|{\eta }_j\left|\right|}\right)}_{+}{\eta }_j,$$

which is the group Lasso estimate for a single-group model (Yuan and Lin 2006).

With the above expressions, the group coordinate descent algorithm can be implemented as follows. Suppose the current values for the group coefficients ${\stackrel{\sim }{b}}_k^{(s)}$, k ≠ j are given. We want to minimize L with respect to b_j. Define

$$L_j(b_j;\lambda ,\gamma )=\frac{1}{2n}{\left|\right|\stackrel{\sim }{y}-\sum _{k\ne j}{\stackrel{\sim }{Z}}_k{\stackrel{\sim }{b}}_k^{(s)}-{\stackrel{\sim }{Z}}_j{b}_j\left|\right|}^2+{\rho }_{\gamma }(|\left|b_j\right||;\sqrt{m_n}\lambda ).$$

Denote ${\stackrel{\sim }{y}}_j={\sum }_{k\ne j}{\stackrel{\sim }{Z}}_k{\stackrel{\sim }{b}}_k^{(s)}$ and ${\stackrel{\sim }{\eta }}_j=n^{-1}{\stackrel{\sim }{Z}}_j^{\prime }(\stackrel{\sim }{y}-{\stackrel{\sim }{y}}_j)$. Let b̃_j denote the minimizer of $L_j(b_j;\sqrt{m_n}\lambda ,\gamma )$. When γ > 1, we have ${\stackrel{\sim }{b}}_j=M({\stackrel{\sim }{\eta }}_j;\sqrt{m_n}\lambda ,\gamma )$, where M is defined in (10).

For any given (λ, γ), we use (10) to cycle through one component at a time. Let ${\stackrel{\sim }{\beta }}^{(0)}={({{\stackrel{\sim }{\beta }}_1^{(0)}}^{\prime },\mathrm{...},{{\stackrel{\sim }{\beta }}_p^{(0)}}^{\prime })}^{\prime }$ be the initial value. The proposed coordinate descent algorithm is as follows.

Initialize vector of residuals r = y − ỹ, where $\stackrel{\sim }{y}={\sum }_{j=1}^p{\stackrel{\sim }{Z}}_j{b}_j^{(0)}$. For s = 0, 1, …, carry out the following calculation until convergence. For j = 1, …, p, repeat the following steps:

1. Calculate ${\stackrel{\sim }{\eta }}_j=n^{-1}{\stackrel{\sim }{Z}}_j^{\prime }r+{\stackrel{\sim }{b}}_j^{(s)}$.

2. Update ${\stackrel{\sim }{b}}_j^{(s+1)}=M({\stackrel{\sim }{\eta }}_j;\lambda ,\gamma )$.

3. Update $r\leftarrow r-{\stackrel{\sim }{Z}}_j({\stackrel{\sim }{b}}_j^{(s+1)}-{\stackrel{\sim }{b}}_j^{(s)})$ and j ← j + 1.

The last step ensures that r always holds the current values of the residuals. Although the objective function is not necessarily convex, it is convex with respect to a single group when the coefficients of all the other groups are fixed. Thus, Theorem 5.1 of Tseng (2001) implies that the group coordinate descent algorithm described above always converges.

4. Theoretical properties

We present the results on the model-pursuit consistency, rate of convergence and asymptotic normality of the proposed SRP estimator. In particular, our model-pursuit consistency result shows that the proposed method can correctly determine the linear and nonlinear components in the partially linear model with high probability.

Denote the underlying regression components by f_0j and write

$$f_{0j}(x)={\beta }_{0j}x+g_{0j}(x).$$

Suppose the series expansion for approximating g_0j is

$$g_{0j}(x)=\sum _{j=1}^{m_n}{\theta }_{0jk}{\phi }_k(x).$$

Let θ_0jn = (θ_0j1, …, θ_0jmn)′. Denote ${\left|\right|g\left|\right|}_2={({\int }_a^b{g}^2(x)dx)}^{1/2}$ for any square integrable function g on [a, b]. We have S₁ = {j: ||g_0j||₂ = 0} and ||θ_0nj|| = 0 for j ∈ S₁. Let ${\theta }_{0n}={({\theta }_{0n1}^{\prime },\mathrm{...},{\theta }_{0np}^{\prime })}^{\prime }$.

Let q = |S₁| be the cardinality of S₁, which is the number of linear components in the regression model. Define

$${\stackrel{\sim }{\theta }}_n=\underset{{\theta }_n}{argmin}\{\frac{1}{2n}{\left|\right|Q(y-Z{\theta }_n)\left|\right|}^2:{\theta }_{nj}=0,j\in S_1\}.$$ (11)

This is the oracle estimator of θ_0n assuming the identity of the linear components were known. We note that the oracle estimator is not computable since S₁ is unknown. We use it as the benchmark for our proposed estimator.

Analogous to the actual estimates defined at the end of Section 2.2, define the oracle estimators

$${\stackrel{\sim }{g}}_{nj}(x)=0,j\in S_1\text{and}{\stackrel{\sim }{g}}_{nj}(x)=\sum _{k=1}^{m_n}{\stackrel{\sim }{\theta }}_{jk}{\psi }_{jk}(x),j\notin S_1.$$

Denote X₍₁₎ = (x_j, j ∈ S₁), X₍₂₎ = (x_j: j ∈ S₂) and ${\stackrel{\sim }{\theta }}_{n(2)}={({\stackrel{\sim }{\theta }}_{nj}^{\prime },j\in S_2)}^{\prime }$. Let

$${\stackrel{\sim }{f}}_{nj}(x)={\stackrel{\sim }{\beta }}_{j}x+{\stackrel{\sim }{g}}_{nj}(x),j\in S_2.$$

Denote f̃_nj(x_j) = (f̃_nj(x_1j), …, f̃_nj(x_nj))′. The oracle estimator of the coefficients of the linear components is

$${\stackrel{\sim }{\beta }}_{n1}={(X_{(1)}^{\prime }{X}_{(1)})}^{-1}{X}_{(1)}^{\prime }(y-\sum _{j\in S_2}{\stackrel{\sim }{f}}_{nj}(x_j)).$$

Without loss of generality, suppose that S₁ = {1, …, q}. Write ${\stackrel{\sim }{\theta }}_n={({\mathbf{0}}_{{qm}_n}^{\prime },{\stackrel{\sim }{\theta }}_{n(2)}^{\prime })}^{\prime }$, where 0_qmn is a (qm_n)-dimensional vector of zeros and

$${\stackrel{\sim }{\theta }}_{n(2)}={(Z_{(2)}^{\prime }{QZ}_{(2)})}^{-1}{Z}_{(2)}^{\prime }Qy.$$ (12)

Define θ_*= min_j∈S1 ||θ_0nj||, which is the smallest norm of the coefficients in the spline expansions of the nonlinear components.

Let k be a non-negative integer, and let α ∈ (0, 1] be such that d = k + α > 0.5. Let 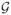be the class of functions g on [0, 1] whose kth derivative g^(k) exists and satisfies a Lipschitz condition of order α:

$$\mid g^{(k)}(s)-g^{(k)}(t)\mid \le C{\mid s-t\mid }^{\alpha }\text{for}s,t\in [a,b].$$

Define ${\left|\right|g\left|\right|}_2={[{\int }_a^b{g}^2(x)dx]}^{1/2}$ for any function g, whenever the integral exists.

We make the following assumptions.

(A1) The p and q are fixed and ε₁, …, ε_n are independent and identically distributed with Eε_i = 0 and Var(ε_i) = σ². Furthermore, P(|ε_i| > x) ≤ K exp(−Cx²), i = 1, …, n, for all x ≥ 0 for some constants C and K.

(A2) Eg_j(x_j) = 0 and g_j ∈ , j = q + 1, …, p.

(A3) The covariate vector X has a continuous density and there exist constants C₁ and C₂ such that the density function η_j of x_j satisfies 0 < C₁ ≤ η_j(x) ≤ C₂ < ∞ on [a, b] for every 1 ≤ j ≤ p.

Theorem 1

Suppose that m_n = O(n^1/(2d+1)), $1/\sqrt{m_n}\gamma$ is less than the smallest eigen-value of Z′QZ/n, and

$$\frac{1}{m_n^{(2d-1)/2}({\theta }_{\ast }-\gamma \lambda )}+\frac{1}{\lambda \sqrt{n}}\to 0.$$ (13)

Then under (A1)–(A3),

$$\text{P}({\widehat{\theta }}_n\ne {\stackrel{\sim }{\theta }}_n)\to 0.$$

Consequently,

$$\begin{array}{c}\text{P}({\widehat{S}}_1=S_1)\to 1,\\ \text{P}({\widehat{\beta }}_{n1}={\stackrel{\sim }{\beta }}_{n1})\to 1,\mathit{and}\text{P}({\left|\right|{\widehat{f}}_{nj}-{\stackrel{\sim }{f}}_{nj}\left|\right|}_2=0,j\in S_2)\to 1.\end{array}$$

Therefore, under the conditions of Theorem 1, the proposed estimator can correctly distinguish linear and nonlinear components with high probability. Furthermore, the proposed estimator has the oracle property in the sense that it is the same as the oracle estimator assuming the identity of the linear and nonlinear components were known, except on an event with probability tending to zero.

We note that, except the assumption on the tail probabilities in (A1), (A1)–(A3) are standard conditions for nonparametric additive models. They would be needed to estimate the additive components at the optimal ℓ₂ rate of convergence in standard nonparametric additive model setting. The main extra condition needed here is (13), which requires λ = o(n^−1/2) and ${\theta }_{\ast }>\gamma \lambda +a_n{m}_n^{-(2d-1)/2}$ for some a_n → ∞ simultaneously. The first part of this requirement ensures that the bias resulting from the penalty is small so that it does not interfere with selection, and the second part requires that the smallest norm θ_* of the coefficients in the spline expansions of the (nonzero) nonlinear components should be larger than the penalty level plus a term due to the spline approximation error.

Theorem 2

Suppose (A1)–(A3) hold. Under model (2), we have

$$\sum _{j=1}^p{\left|\right|{\widehat{f}}_{nj}-f_{0j}\left|\right|}_2^2\le O_p\left(\frac{m_n}{n}\right)+O\left(\frac{1}{m_n^{2d}}\right)+O(m_n{\lambda }^2).$$

This theorem gives rate of convergence of the proposed estimator under the non-parametric additive model (2), which contains the partially linear models as special cases. In particular, if we assume that each component in (2) is second order differentiable (d = 2) and take m_n = O(n^1/5) and λ = n^−1/2+δ for a small δ > 0, then ${\sum }_{j=1}^p{\left|\right|{\widehat{f}}_{nj}-f_{0j}\left|\right|}_2^2=O_p(n^{-4/5})$, which is the optimal rate of convergence in nonparametric regression.

We now consider the asymptotic distribution of β̂_n1. Denote

$$H_j=\{h_j={(h_{jk}:k\in S_1)}^{\prime }:{\text{E}h}_{jk}^2(x_j)<\infty ,{Eh}_{jk}(x_j)=0\},j\in S_2.$$

Each element of H_j is a |S₁|-vector of square integrable functions with mean zero. Denote the sumspace

$$H=\{h=\sum _{j\in S_2}{h}_j:h_j\in H_j\}.$$

The projection of the centered covariate vector x₍₁₎ − E(x₍₁₎) ∈ R^q onto the sumspace H is defined to be the ${(h_1^{\ast },\dots ,h_r^{\ast })}^{\prime }$ with ${\text{E}h}_j^{\ast }(x_j)=0$, j ≤ Ŝ₂ that minimizes

$$W(h)\equiv \text{E}{\left|\right|x_{(1)}-\text{E}(x_{(1)})-\sum _{j\in S_2}{h}_j(x_j)\left|\right|}^2.$$ (14)

For x₍₂₎ = (x_j: j ∈ S₂), denote

$$h^{\ast }(x_{(2)})=\sum _{j\in S_2}{h}_j^{\ast }(x_j).$$ (15)

Under condition (A3), by Lemma 1 of Stone (1985) and Proposition 2 in Appendix 4 of Bickel, Ritov, Klaassen and Wellner (1993), the sumspace H is closed. Thus the orthogonal projection h^* onto H is well defined and unique. Furthermore, each individual component $h_j^{\ast }$ is also well defined and unique. In addition to (A1)–(A3), we also need the following condition for asymptotic normality of the linear component estimator.

(A4) Let w ≥ 1 be a positive integer. The wth partial derivatives of the joint density of x₍₂₎ = (x_j, j ∈ S₂) are bounded by a constant and the qth derivative of each component of &xi;(v) = E(x₍₁₎|x_j = v), j ∈ S₂ is bounded by a constant.

Let A = E[x₍₁₎ − E(x₍₁₎ − h* (x₍₂₎)]^⊗2, where h* is defined in (15). Here x^⊗2 = xx′ for any column vector x ∈ R^d.

Theorem 3

Suppose that the conditions in Theorem 1 and (A4) are satisfied and that A is nonsingular. Then,

$$n^{1/2}({\widehat{\beta }}_{n1}-{\beta }_{(1)}){\to }_{d}N(0,\mathrm{\sum }),$$

where β₍₁₎ = (β_j: j ∈ S₁)′ and Σ = σ²A⁻¹.

Theorem 3 provides sufficient conditions under which the proposed estimator β̂_n1 of the linear components in the model is asymptotically normal with same the limit normal distribution as the oracle estimator β̃_n1.

5. Numerical studies

5.1 Simulation studies

We use simulation to evaluate the finite sample performance of the proposed method. Two examples are considered in the simulation. In each of the simulated models, two sample sizes (n=100, 200) are considered and a total of 100 replications are conducted. Consider the following six functions defined on [0, 1]:

$$\begin{array}{l}{f}_1(x)=x,f_2(x)=sin(2\pi x)/(2-sin(2\pi x)),\\ f_3(x)=0.1sin(2\pi x)+0.2cos(2\pi x)+0.3{sin}^2(2\pi x)+0.4{cos}^3(2\pi x)+0.5{sin}^3(2\pi x),\\ f_4(x)={(3x-1)}^2,f_5(x)=cos(2\pi x)/(2-cos(2\pi x)),\\ f_6(x)=0.1cos(2\pi x)+0.2sin(2\pi x)+0.3{cos}^2(2\pi x)+0.4{sin}^3(2\pi x)+0.5{cos}^3(2\pi x).\end{array}$$

In the implementation, we use cubic B-spline with seven basis functions to approximate each function.

Example 1

Let p = 6. Consider the model

$$y=3f_1(x_1)+4f_1(x_2)-2f_1(x_3)+8f_2(x_4)+6f_3(x_5)+5f_4(x_6)+\epsilon .$$

In this model, the first three variables have linear effect and the last three variables have nonlinear effect. The p covariates are simulated in the following way. First we simulate w₁, ···, w_p and u independently from U [0, 1]. Then x_ik = (w_k + u)/2 for k = 1, ···, p. The correlation among predictors is Corr(x_ij, x_ik) = 0.5. The error term ε is chosen from N(0, 1.57²) to give a signal to noise ratio 3.

Example 2

Let p = 10. Consider the model

$$y=3f_1(x_1)+4f_1(x_2)-f_1(x_3)-f_1(x_4)+2f_1(x_5)+5f_2(x_6)+4f_3(x_7)+5f_4(x_8)+5f_5(x_9)+4f_6(x_{10})+\epsilon .$$

In this model, the first 5 components are linear and the remaining 5 are nonlinear. The covariates are simulated in the same way as in Example 1. The error term ε ~ N(0, 1.80²), which gives a signal to noise ratio 3.

The group coordinate descent algorithm described in Section 3 is used repeatedly to compute θ̂_n over a grid of (λ, γ) values in a rectangle [λ_max, λ_min] × [γ_max, γ_min]. Here ${\lambda }_{max}={max}_{1\le j\le p}\left|\right|n^{-1}{\stackrel{\sim }{Z}}_j^{\prime }\stackrel{\sim }{y}\left|\right|$, which is the smallest value of λ that forces all the solutions to be zero, and we take λ_min = 0.0001λ_max. We use a set of 100 equally spaced grid points on the logarithmic scale in [λ_max, λ_min]. For the γ parameter in the group MCP, we consider a grid of equally spaced points in the interval [γ_max, γ_min] = [8.0, 1.1] with grid size 0.1. We note that Zhang (2010) suggested using γ = 2.7 for standardized covariates in linear regression. In our simulation studies, we found that the value of γ also has considerable impact on the results. Thus instead of using a fixed γ value, we consider a range of γ values.

For the group Lasso, which can be considered a special case of the group MCP with γ= ∞, the algorithm starts at λ_max where θ̂_n equals 0 and proceeds along the grid values of λ, using the previous solution as the initial value at each grid point. For the group MCP, for each value of λ in the λ-grid and the corresponding initial value from the group Lasso, the algorithm proceeds along the grids of γ in [8.0, 1.1], that is, for each λ grid value, we start the algorithm at γ = 8 using the group Lasso solution as the initial value. This approach follows that of Mazumder, Friedman and Hastie (2009). We then apply the BIC (Schwarz 1978) to select (λ, γ). Here the BIC is defined as

$$\mathit{BIC}(\lambda ,\gamma )=log({\mathit{RSS}}_{\lambda ,\gamma })+logn\cdot \frac{m_n{df}_{\lambda ,\gamma }}{n},$$

where RSS_{λ; γ} is the residual sum of squares and df_{λ; γ} is the number of the nonzero selected groups for a given (λ, γ). Recall m_n is the number of spline basis functions given in (3). The optimal value of (λ, γ) is chosen to be the one that minimizes the BIC.

The simulation results based on 100 replications are presented in Tables 1–3. The columns in Table 1 are: the average number of nonlinear components being selected (NL), the average model error (ER), the percentage of occasions on which the correct nonlinear components are included in the selected model (IN%) and the percentage of occasions on which the exactly nonlinear components are selected (CS%) in the final model. Enclosed in parentheses are the corresponding standard errors. Table 2 includes the number of times each component being estimated as nonlinear function. Table 3 shows the average mean square error for each function. Enclosed in parentheses are the corresponding standard errors.

Table 1.

Simulation results for Examples 1–2. NL, the average number of the nonlinear components being selected; ER, the average model error; IN%, the percentage of occasions on which the correct nonlinear components are included in the selected model; CS%, the percentage of occasions on which exactly correct nonlinear components are selected, averaged over 100 replications. Enclosed in parentheses are the corresponding standard errors.

	n = 100				n = 200
	NL	ER	IN%	CS%	NL	ER	IN%	CS%
Example 1, Group Lasso	3.46 (0.76)	2.66 (0.66)	100 (0.00)	67 (0.47)	3.10 (0.39)	2.71 (0.39)	100 (0.00)	92 (0.27)
Group MCP	3.18 (0.39)	2.28 (0.47)	100 (0.00)	82 (0.39)	3.01 (0.10)	2.43 (0.30)	100 (0.00)	99 (0.10)
Example 2, Group Lasso	4.37 (2.90)	6.26 (4.84)	51 (0.50)	17 (0.38)	5.41 (0.71)	3.55 (0.59)	98 (0.14)	62 (0.49)
Group MCP	5.25 (1.37)	2.98 (1.22)	76 (0.43)	43 (0.50)	5.22 (0.54)	3.09 (0.38)	98 (0.14)	78 (0.42)

Table 3.

The average mean square error for each component based on 100 replications by the group Lasso and group MCP methods in Examples 1–2.

	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10
	n = 100
Example 1, Group Lasso	0.64 (0.93)	0.66 (0.79)	0.67 (1.05)	7.52 (1.48)	12.23 (6.68)	25.50 (10.02)
Group MCP	0.54 (0.83)	0.55 (0.70)	0.49 (0.65)	7.51 (1.45)	11.39 (6.72)	25.34 (9.77)
Oracle	0.11 (0.25)	0.11 (0.17)	0.12 (0.23)	2.22 (1.07)	0.76 (0.46)	10.05 (2.39)
	n = 200
Group Lasso	0.21 (0.28)	0.19 (0.27)	0.20 (0.26)	7.29 (1.05)	12.08 (4.47)	27.24 (7.04)
Group MCP	0.20 (0.28)	0.16 (0.21)	0.19 (0.26)	7.25 (1.03)	11.35 (4.77)	27.08 (7.12)
Oracle	0.09 (0.07)	0.08 (0.06)	0.09 (0.07)	1.88 (0.65)	0.50 (0.18)	9.93 (1.72)
Example 2, Group Lasso	1.22 (1.45)	1.55 (2.63)	1.58 (2.08)	1.40 (2.06)	1.87 (2.95)	3.66 (1.43)	10.24 (7.17)	23.80 (12.7)	3.03 (2.76)	10.09 (5.80)
Group MCP	0.87 (1.02)	1.05 (1.91)	0.90 (1.16)	0.89 (1.51)	1.03 (1.33)	3.55 (1.24)	9.27 (6.88)	22.30 (10.6)	1.96 (1.98)	9.85 (5.08)
Oracle	0.52 (1.00)	0.17 (0.60)	0.27 (0.36)	0.31 (0.63)	0.44 (0.79)	2.57 (0.90)	1.09 (1.54)	13.31 (13.9)	1.28 (1.80)	1.85 (10.45)
	n = 200
Group Lasso	0.34 (0.45)	0.36 (0.40)	0.30 (0.41)	0.38 (0.61)	0.39 (0.56)	3.34 (0.71)	8.55 (3.19)	20.09 (6.61)	0.95 (0.81)	9.26 (3.86)
Group MCP	0.30 (0.40)	0.32 (0.39)	0.28 (0.39)	0.31 (0.55)	0.34 (0.52)	3.32 (0.70)	8.52 (3.24)	19.91 (6.50)	0.87 (0.81)	9.19 (3.66)
Oracle	0.23 (0.20)	0.16 (0.23)	0.05 (0.02)	0.16 (0.33)	0.16 (0.41)	0.88 (0.30)	0.36 (0.14)	9.83 (1.68)	0.50 (0.17)	0.33 (0.14)

Table 2.

Number of times each component being selected as nonlinear component in the 100 replications by the group Lasso and group MCP methods in Examples 1–2.

	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10
	n = 100
Example 1, Group Lasso	21	13	12	100	100	100
Group MCP	9	4	5	100	100	100
	n = 200
Group Lasso	3	4	3	100	100	100
Group MCP	1	0	0	100	100	100
	n = 100
Example 2, Group Lasso	19	21	14	17	18	54	73	95	69	57
Group MCP	16	13	9	9	11	89	99	100	97	82
	n = 200
Group Lasso	9	8	7	9	11	99	100	100	100	98
Group MCP	5	6	6	5	2	99	100	100	100	99

Several observations can be made from Tables 1 and 2. Table 1 shows that the proposed method with the group MCP performs better than the proposed method with the group Lasso in terms of the percentage of occasions on which the correct nonlinear components are included in the selected model (IN%) and the percentage of occasions on which the exactly nonlinear components are selected (CS%) in the final model. For instance, in Example 1, when n = 100, the percentage of correct selection (CS%) is 82% with the group MCP and is 67% with the group Lasso. Also, when the sample size increases from 100 to 200, the percentage of including all the nonlinear components (IN%) and selecting the exactly correct model (CS%) by both methods are increased. This is not surprising since data with a larger sample size contain more information about the underlying model. Table 2 shows that the group MCP is more accurate in distinguishing the linear functions from the nonlinear functions than the group Lasso. When n = 200, the group MCP can correctly distinguish the linear from nonlinear components 99% of the times in Example 1 and 78% of the times in Example 2. In Table 3, we examine the performance of the proposed method for estimating the linear and nonlinear components in the simulated models. In general, the proposed method with the group MCP have smaller mean square errors. Overall, the proposed method with the group MCP is effective in distinguishing the linear components from the nonlinear ones in the simulation models.

5.2 Diabetes data example

This data set is from a study reported in Willems et al. (1997). The data consist of 19 variables on 403 subjects from 1046 African Americans who were interviewed in a study to understand the prevalence of obesity, diabetes, and other cardiovascular risk factors in central Virginia. Diabetes Mellitus Type II (adult onset diabetes) is associated with obesity. The 403 subjects were the ones who were screened for diabetes. Glycosolated hemoglobin > 7.0 is usually taken as a positive diagnosis of this disease.

We consider Glycosolated hemoglobin as the response variable and the other 15 variables as the covariates excluding. These 15 variables are: cholesterol (chol), stabilized glucose (stab.glu), high density lipoprotein (hdl), cholesterol/hdl ratio (ratio), location, age, gender, height, height, weight, frame, first systolic blood pressure (bp.1s), first diastolic blood pressure (bp.1d), waist, hip, postprandial time when labs were drawn (time.ppn). Among these 15 variables, 3 are categorial variables (location, gender, frame), 12 are continuous variables. We are interested in finding which continuous covariates have nonlinear effects on the response variable. In our study, we only consider the subjects which have all the information, without missing values. Thus the number of subjects are n = 366, p = 15.

The results are summarized in Tables 4 and 5. The top panel of Table 4 lists the 12 continuous variables being selected by the group MCP and the group Lasso as linear or nonlinear variables, indicated by 0/1 (1, nonlinear; 0, linear). The top panel of Table 5 shows the number of variables being selected as nonlinear variables and the residual sum of squares by both the group MCP and the group Lasso methods.

Table 4.

Diabetes data: Number of each component being selected by the group Lasso and group MCP methods as nonlinear components. The top panel of Table lists the 12 continuous variables being selected by the group MCP and the group Lasso as linear or nonlinear variables, indicated by 0 or 1 (0, linear; 1, nonlinear). The bottom panel shows the number of times a variable has a nonlinear effect in the 100 partitions.

	chol	stab.glu	hdl	ratio	age	height	weight	bp.1s	bp.1d	waist	hip	time.ppn
	whole data set
group Lasso	0	1	0	0	0	1	0	0	0	0	0	0
group MCP	1	1	0	1	1	1	0	0	0	0	0	1
	training and testing sets
group Lasso	29	66	7	1	0	72	0	0	0	0	0	0
group MCP	89	100	30	99	65	100	9	2	0	0	4	89

Table 5.

Diabetes data: The top panel shows that the number of selected nonlinear components (NL) and the residual sum of squares (RSS) based on the whole data. The bottom panel shows the NL, the RSS and the prediction error (PE), averaged over 100 replications. Enclosed in parentheses are the corresponding standard errors.

	NL	RSS	PE
	whole data
group Lasso	2.00	3.06
group MCP	6.00	2.53
	training and testing sets
group Lasso	1.75 (0.76)	3.01 (0.19)	3.44 (1.02)
group MCP	5.87 (0.87)	2.53 (0.16)	3.27 (0.89)

To evaluate the prediction performance of the methods, we randomly select a training set with 300 subjects from the data to do the estimation and selection and use the remaining 66 subjects at the test set for prediction. We repeat this process 100 times and the results are summarized in the bottom panel of Tables 4 and 5. The bottom panel of Table 4 shows the number of times a variable has a nonlinear effect. The bottom panel of Table 5 shows the number of variables being selected (NL) as nonlinear components, the residual sum of squares (RSS) and the prediction error (PE), averaged over 100 replications with standard error in the parentheses. Table 5 shows that the proposed method with the group MCP performs better than with the group Lasso in terms of the residual sum of squares and the prediction error.

6. Concluding remarks

In this paper, we proposed a semiparametric regression pursuit method for distinguishing linear from nonlinear components in semi-parametric partially linear models. This approach determines the parametric and non-parametric components in a semiparametric model adaptively based on the data. Our proposed method is fundamentally different from the standard semiparametric inference approach where the parametric and nonparametric components in a model are pre-specified. We showed that our method has the asymptotic oracle properties, meaning that it is the same as the standard semiparametric estimator assuming the model structure were known with high probability. The asymptotic rates of the penalty parameters required for our theoretical results are derived. However, as in many recent studies, it is not clear whether the penalty parameters selected using the BIC or other procedures can match the asymptotic rates. This is an important and challenging problem that requires further investigation, but is beyond the scope of the current paper. Our simulation study indicates that the proposed method works well in finite sample situations.

We have only considered the proposed semiparametric regression pursuit method in the partially linear model with fixed p. In many applications such as genomic data analysis, it is possible to have data with p > n. In this case, our proposed method is not directly applicable. In the p > n case, assuming the model is sparse in the sense the number of important covariates is much smaller than n, we can first reduce the model dimension and then apply the proposed method. For example, we can first use the adaptive group Lasso method to select the important variables in the nonparametric additive model (Huang, Horowitz and Wei 2010). We then use the proposed method in this paper to determine linear and nonlinear components in the model. Under the conditions given in Huang et al. (2010) and those given in this paper, this two-step approach has the asymptotic oracle property even in p > n settings. Further work is needed to evaluate the finite sample performance and spelled out the technical details of this two-step approach in p > n settings.

The proposed semiparametric regression pursuit method extends the scope of the application of penalized methods from variable selection to model specification. We have focused on the proposed method in the context of semiparametric partially linear models. This method can be extended to other models, such as the generalized partially linear and partially linear proportional hazards models (Huang 1999). It would be interesting to generalized the results of this paper to these more complicated models.

Appendix

Proof of Theorem 1

Since $1/\sqrt{m_n}\gamma$ is less than the smallest eigenvalue of Z′QZ/n, L(·; λ, γ) in (9) is a convex function. By the Karush-Kuhn-Tucker conditions, a necessary and sufficient condition for θ̂_n is

$$\{\begin{array}{ll}{Z}_j^{\prime }Q(y-Z{\widehat{\theta }}_n)=n\stackrel{.}{\rho }(|\left|{\widehat{\theta }}_n\right||;\lambda ),\hfill & {\left|\right|{\widehat{\theta }}_j\left|\right|}_2\ne 0,\hfill \\ {\left|\right|Z_k^{\prime }Q(y-Z{\widehat{\theta }}_n)\left|\right|}_2\le n\lambda ,\hfill & \left|\right|{\widehat{\theta }}_{nj}\left|\right|=0.\hfill \end{array}$$ (16)

For j ∉ S₁, if ||θ̃_nj|| ≥ γλ then ρ̇(||θ̃_nj||; λ) = 0. Thus θ̃_n satisfies (16) if also ${\left|\right|Z_j^{\prime }Q(y-Z{\stackrel{\sim }{\theta }}_n)\left|\right|}_2\le n\lambda$ for j ∈ S₁. Therefore, θ̂_n = θ̃_n in the intersection of the events

$${\mathrm{\Omega }}_1(\lambda )=\left\{\underset{j\notin S_1}{min}\left|\right|{\stackrel{\sim }{\theta }}_{nj}\left|\right|\ge \gamma \lambda \right\}\text{and}{\mathrm{\Omega }}_2(\lambda )=\left\{\underset{j\in S_1}{max}\left|\right|Z_j^{\prime }Q(y-Z{\stackrel{\sim }{\theta }}_n)\left|\right|\le n\lambda \right\}.$$ (17)

Let g_0j(x_j) = (g_0j(x_1j), …, g_0j(x_nj))′ and δ_n = Σ_j∉S1g_0j(x_j) − Z₍₂₎θ_n(2). By the approximation properties of splines to a smooth function, we have

$$n^{-1}{\left|\right|{\delta }_n\left|\right|}^2=O_p((p-q)m_n^{-2d}).$$ (18)

Let $C_{(2)}=Z_{(2)}^{\prime }{QZ}_{(2)}$ and $H=Q-{QZ}_{(2)}{(Z_{(2)}^{\prime }{QZ}_{(2)})}^{-1}{Z}_{(2)}^{\prime }Q$. By (12),

$${\stackrel{\sim }{\theta }}_{n(2)}-{\theta }_{n(2)}=C_{(2)}^{-1}{Z}_{(2)}^{\prime }Q({\mathit{\epsilon }}_n+{\delta }_n),$$ (19)

and

$$Z_j^{\prime }Q(y-Z_{(2)}{\stackrel{\sim }{\theta }}_{n(2)})=Z_j^{\prime }H({\mathit{\epsilon }}_n+{\delta }_n).$$ (20)

Recall θ_* = min_j∈S1 ||θ_nj||. If ||θ_nj − θ_nj|| ≤ θ_* − γλ, then min_j∉S1||θ̃_nj|| ≥ γλ. Therefore,

$$1-\text{P}({\mathrm{\Omega }}_1(\lambda ))\le \text{P}(\underset{j\notin S_1}{max}||{\stackrel{\sim }{\theta }}_{nj}-{\theta }_{nj}||>{\theta }_{\ast }-\gamma \lambda ).$$

We also have

$$1-\text{P}({\mathrm{\Omega }}_2(\lambda ))\le \text{P}(n^{-1}\underset{j\in S_1}{max}||(Z_j^{\prime }H({\mathit{\epsilon }}_n+{\delta }_n)\left|\right|>\lambda ).$$

Lemma 1 below shows that, when

$$\begin{array}{c}\frac{{(p-q)}^{1/2}{m}_n^{-(2d-1)/2}}{{\theta }_{\ast }-\gamma \lambda }\to 0,\\ \text{P}(\underset{j\notin S_1}{max}||{\stackrel{\sim }{\theta }}_{nj}-{\theta }_{nj}||>{\theta }_{\ast }-\gamma \lambda )\le \frac{(p-q)m_n}{\sqrt{n}({\theta }_{\ast }-\gamma \lambda )}.\end{array}$$

and Lemma 2 below shows that, when

$$\begin{array}{c}\frac{1}{\lambda m_n^{(2d+1)/2}}\to 0,\\ \text{P}(n^{-1}\underset{j\in S_1}{max}||+Z_j^{\prime }H({\mathit{\epsilon }}_n+{\delta }_n)||>\lambda )\le \frac{{\{log({qm}_n)\}}^{1/2}}{\lambda \sqrt{n})}.\end{array}$$

Note that when m_n = n^1/(2d+1), we have $m_n{n}^{-1/2}=m_n^{-(2d-1)/2}$. Therefore, under the conditions of Theorem 1, we have P(θ̂_n ≠ θ̃_n) → 0. This completes the proof.

Lemma 1

Suppose that

$$\begin{array}{c}\frac{{(p-q)}^{1/2}}{m_n^{(2d-1)/2}({\theta }_{\ast }-\gamma \lambda )}\to 0,\\ \text{P}(\underset{j\notin S_1}{max}||{\stackrel{\sim }{\theta }}_{nj}-{\theta }_{nj}||>{\theta }_{\ast }-\gamma \lambda )\le O(1)\frac{(p-q)m_n}{\sqrt{n}({\theta }_{\ast }-\gamma \lambda )}\end{array}$$ (21)

Proof of Lemma 1

Let T_nj be an m_n × (p − q)m_n matrix with the form

$$T_{nj}=(0_{m_n},\dots ,0_{m_n},I_{m_n},0_{m_n},\dots ,0_{m_n}),$$

where 0_mn is an m_n × m_n matrix of zeros and I_mn is an m_n × m_n identity matrix in the jth block. By the triangle inequality,

$${\left|\right|{\stackrel{\sim }{\theta }}_{nj}-{\theta }_{nj}\left|\right|}_2\le {\left|\right|T_{nj}{C}_{(2)}^{-1}{Z}_{(2)}^{\prime }Q{\mathit{\epsilon }}_n\left|\right|}_2+{\left|\right|T_{nj}{C}_{(2)}^{-1}{Z}_{(2)}^{\prime }Q{\delta }_n\left|\right|}_2.$$ (22)

Let C be a generic constant independent of n. For the first term on the right-hand side, we have

$$\begin{array}{l}\text{E}\underset{j\notin S_1}{max}{\left|\right|T_{nj}{C}_{(2)}^{-1}{Z}_{(2)}^{\prime }Q{\mathit{\epsilon }}_n\left|\right|}_2\le n^{-1}{\rho }_{n1}^{-1}\text{E}{\left|\right|Z_{(2)}^{\prime }Q{\mathit{\epsilon }}_n\left|\right|}_2\\ =n^{-1/2}{\rho }_{n1}^{-1}\text{E}{\left|\right|n^{-1/2}{Z}_{(2)}^{\prime }Q{\mathit{\epsilon }}_n\left|\right|}_2\\ =n^{-1/2}{\rho }_{n1}^{-1}{m}_n^{-1/2}{((p-q)m_n)}^{1/2}\end{array}$$ (23)

$$=O(1)(p-q)n^{-1/2}{m}_n.$$ (24)

Thus

$$\text{P}(\underset{j\notin S_1}{max}|\left|T_{nj}{C}_{(2)}^{-1}{Z}_{(2)}^{\prime }Q{\mathit{\epsilon }}_n\right||\ge ({\theta }_{\ast }-\gamma )/2)\le \frac{O(1)(p-q)m_n}{\sqrt{n}({\theta }_{\ast }-\gamma \lambda )}.$$

By (18), the second term

$$\begin{array}{l}\underset{j\notin S_1}{max}{\left|\right|T_{nj}{C}_{(2)}^{-1}{Z}_{(2)}^{\prime }Q{\delta }_n\left|\right|}_2\le {\left|\right|{nC}_{(2)}^{-1}\left|\right|}_2\cdot {\left|\right|n^{-1}{Z}_{(2)}^{\prime }{Z}_{(2)}\left|\right|}_2^{1/2}\cdot {\left|\right|n^{-1/2}{\delta }_n\left|\right|}_2\\ =O_p(1){\rho }_{n1}^{-1}{\rho }_{n2}^{-1/2}{(p-q)}^{1/2}{m}_n^{-d}\\ =O_p(1){(p-q)}^{1/2}{m}_n^{-(2d-1)/2}.\end{array}$$ (25)

Therefore, when

$$\frac{(p-q)m_n}{\sqrt{n}({\theta }_{\ast }-\gamma \lambda )}\to 0,$$

(21) holds. This proves the lemma.

Lemma 2

Suppose that

$$\frac{1}{\lambda m_n^{(2d+1)/2}}\to 0,$$

we have

$$\text{P}(n^{-1}\underset{j\in S_1}{max}||Z_j^{\prime }H({\mathit{\epsilon }}_n+{\delta }_n)||>\lambda )\le O(1)\frac{{\{log\{(q\vee 1)m_n\}\}}^{1/2}}{\lambda \sqrt{n}}$$ (26)

Proof of Lemma 2

Write

$$n^{-1}{Z}_j^{\prime }H({\mathit{\epsilon }}_n+{\delta }_n)=n^{-1}{Z}_j^{\prime }{H}_n{\mathit{\epsilon }}_n+n^{-1}{Z}_j^{\prime }{H}_n{\delta }_n.$$ (27)

By Lemma 2 of Huang et al. (2010),

$$\text{E}\left(\underset{j\in S_1}{max}{\left|\right|n^{-1/2}{Z}_j^{\prime }{H}_n{\mathit{\epsilon }}_n\left|\right|}_2\right)\le O(1){\{log((p-\mid S_1\mid )m_n)\}}^{1/2}.$$ (28)

Therefore,

$$\text{P}(n^{-1}\underset{j\in S_1}{max}{\left|\right|Z_j^{\prime }{H}_n{\mathit{\epsilon }}_n\left|\right|}_2>\lambda /2)\le O(1)\frac{{\{log({qm}_n)\}}^{1/2}}{\lambda \sqrt{n}}.$$ (29)

By (18), the second term on the right hand side of (27)

$$\begin{array}{l}{n}^{-1}\underset{j\in S_1}{max}{\left|\right|Z_j^{\prime }{\mathrm{{\rm H}}}_{\nu }{\delta }_n\left|\right|}_2\le n^{-1/2}\underset{j\in S_1}{max}{\left|\right|n^{-1}{Z}_j^{\prime }{Z}_j\left|\right|}_2^{1/2}·{\left|\right|H_n\left|\right|}_2·{\left|\right|{\delta }_n\left|\right|}_2\\ =O(1){\rho }_{n2}^{1/2}{(p-q)}^{1/2}{m}_n^{-d}\\ =O(1){(p-q)}^{1/2}{m}_n^{-(2d+1)/2}.\end{array}$$ (30)

Therefore, when

$$\frac{1}{\lambda m_n^{(2d+1)/2}}\to 0,$$

(26) follows from (29) and (30).

Proof of Theorem 2

By the definition of ${\widehat{\theta }}_n\equiv {({\widehat{\theta }}_{n1}^{\prime },\dots ,{\widehat{\theta }}_{np}^{\prime })}^{\prime }$,

$$\frac{1}{2n}{\left|\right|Q(y-Z{\widehat{\theta }}_n)\left|\right|}_2^2+\sum _{j=1}^p{\rho }_{\gamma }\left|\right|{\widehat{\theta }}_{nj}\left|\right|;\lambda )\le \frac{1}{2n}{\left|\right|Q(y-Z{\theta }_n)\left|\right|}_2^2+\sum _{j=1}^p{\rho }_{\gamma }\left|\right|{\theta }_{nj}\left|\right|;\lambda ).$$ (31)

Let η_n = Q(y − Zθ_n) and ν_n = QZ(θ̂_n − θ_n). Write

$$Q(y-Z{\widehat{\theta }}_n)=Q(y-Z{\theta }_n)-QZ({\widehat{\theta }}_n-{\theta }_n)={\eta }_n-{\nu }_n.$$

We have ${\left|\right|Q(y-Z{\widehat{\theta }}_m)\left|\right|}_2^2={\left|\right|{\nu }_n\left|\right|}_2^2-2{\eta }_n^{\prime }{\nu }_n+{\left|\right|{\eta }_n\left|\right|}^2$. We can rewrite (31) as

$${\left|\right|{\nu }_n\left|\right|}_2^2-2{\eta }_n^{\prime }{\nu }_n\le 2n\sum _{j=1}^p({\rho }_{\gamma }|\left|{\theta }_{nj}\right||;\lambda )-{\rho }_{\gamma }(|\left|{\widehat{\theta }}_{nj}\right||;\lambda ).$$ (32)

Since

$$\mid {\rho }_{\gamma }(|\left|{\theta }_{nj}\right||;\lambda )-{\rho }_{\gamma }(|\left|{\widehat{\theta }}_{nj}\right||;\lambda )\mid \le \lambda \left|\right|{\theta }_{nj}-{\widehat{\theta }}_{nj}\left|\right|,$$ (33)

combining (32) and (33), we get

$${\left|\right|{\nu }_n\left|\right|}_2^2-2{\eta }_n^{\prime }{\nu }_n\le 2n\lambda \sqrt{p}\left|\right|{\widehat{\theta }}_n-{\theta }_n\left|\right|.$$ (34)

Let ${\eta }_n^{\ast }=QZ{(Z^{\prime }QZ)}^{-1}{Z}^{\prime }Q{\eta }_n$. By the Cauchy-Schwartz inequality,

$$2\mid {\eta }_n^{\prime }{\nu }_n\mid \le 2{\left|\right|{\eta }_n^{\ast }\left|\right|}_2·{\left|\right|{\nu }_n\left|\right|}_2\le 2{\left|\right|{\eta }_n^{\ast }\left|\right|}_2^2+\frac{1}{2}{\left|\right|{\nu }_n\left|\right|}_2^2.$$ (35)

From (34) and (35), we have

$${\left|\right|{\nu }_n\left|\right|}_2^2\le 4{\left|\right|{\eta }_n^{\ast }\left|\right|}_2^2+4n\lambda \sqrt{p}·{\left|\right|{\widehat{\theta }}_n-{\theta }_n\left|\right|}_2.$$

Let c_n* be the smallest eigenvalue of Z′QZ/n. By Lemma 1 of Huang, Horowitz and Wei (2010), $c_{n\ast }{\asymp }_p{m}_n^{-1}$. Since ${\left|\right|{\nu }_n\left|\right|}_2^2\ge {nc}_{n\ast }{\left|\right|{\widehat{\theta }}_n-{\theta }_n\left|\right|}_2^2$ and 2ab ≤ a² + b²,

$${nc}_{n\ast }{\left|\right|{\widehat{\theta }}_n-{\theta }_n\left|\right|}_2^2\le 4{\left|\right|{\eta }_n^{\ast }\left|\right|}_2^2+\frac{{(2n\lambda \sqrt{p})}^2}{2{nc}_{n\ast }}+\frac{1}{2}{nc}_{n\ast }{\left|\right|{\widehat{\theta }}_n-{\theta }_n\left|\right|}_2^2.$$

It follows that

$${\left|\right|{\widehat{\theta }}_n-{\theta }_n\left|\right|}_2^2\le \frac{8{\left|\right|{\eta }_n^{\ast }\left|\right|}_2^2}{{nc}_{n\ast }}+\frac{4{\lambda }^{2}p}{C_{n\ast }^2}.$$ (36)

Let $f_0(x_i)={\sum }_{j=1}^p{f}_{0j}(x_{ij})$. Write

$${\eta }_n=Q({\epsilon }_i+(\mu -\overline{y})\mathbf{1}+f(x_i)-Z{\theta }_n).$$

Since | μ − ȳ|² = O_p(n⁻¹) and ${\left|\right|f_{0j}-f_{nj}\left|\right|}_{\infty }=O(m_n^{-d})$, we have

$${\left|\right|{\eta }_n^{\ast }\left|\right|}_2^2\le 2{\left|\right|{\mathit{\epsilon }}_n^{\ast }\left|\right|}_2^2+O_p(1)+O({\mathit{npm}}_n^{-2d}),$$ (37)

where ${\mathit{\epsilon }}_n^{\ast }$ is the projection of ε_n = (ε₁, …, ε_n)′ to the span of QZ. We have

$${\left|\right|{\mathit{\epsilon }}_n^{\ast }{\left|\right|}_2^2={(Z^{\prime }QZ)}^{-1/2}{Z}^{\prime }Q{\mathit{\epsilon }}_n\left|\right|}_2^2\le O_p({pm}_n)$$ (38)

Combining (36), (37), and (38), we get

$${\left|\right|{\widehat{\theta }}_n-{\theta }_n\left|\right|}_2^2\le O_p\left(\frac{{pm}_n}{{nc}_{n\ast }}\right)+O_p\left(\frac{1}{{nc}_{n\ast }}\right)+O\left(\frac{d_{n2}{m}_n^{-2d}}{c_{n\ast }}\right)+\frac{4p{\lambda }^2}{c_{n\ast }^2}.$$

Since $c_{n\ast }{\asymp }_p{m}_n^{-1}$ and $c_n^{\ast }{\asymp }_p{m}_n^{-1}$, we have

$${\left|\right|{\widehat{\theta }}_n-{\theta }_n\left|\right|}_2^2\le O_p\left(\frac{{pm}_n^2}{n}\right)+O_p\left(\frac{m_n}{n}\right)+O\left(\frac{1}{m_n^{2d-1}}\right)+O(m_n^2{\lambda }^2).$$

Now the result follows from the properties of polynomial splines (Schumaker 2001). This completes the proof of the theorem.

Proof of Theorem 3

Let θ̃_n be the oracle estimator defined in (11). Define

$${\stackrel{\sim }{g}}_{nj}(x)=0,j\in S_1\text{and}{\stackrel{\sim }{g}}_{nj}(x)=\sum _{k=1}^{m_n}{\stackrel{\sim }{\theta }}_{jk}{\psi }_{jk}(x),j\in S_2.$$

Let

$${\stackrel{\sim }{f}}_{nj}(x)={\stackrel{\sim }{\beta }}_{j}x+{\stackrel{\sim }{g}}_{nj}(x),j\in {\widehat{S}}_2.$$

Denote f̃_nj(x_j) = (f̃_nj(x_1j), …, f̃_nj(x_nj))′. The estimator of the coefficients of the linear components is

$${\stackrel{\sim }{\beta }}_{n1}={(X_{(1)}^{\prime }{X}_{(1)})}^{-1}{X}_{(1)}^{\prime }(y-\sum _{j\in S_2}{\stackrel{\sim }{f}}_{nj}(x_j)).$$

Using the standard techniques in semiparametric models such as those described in Huang (1996), we can show that

$$\sqrt{n}({\stackrel{\sim }{\beta }}_{n1}-{\beta }_{01}){\to }_{D}N(0,\mathrm{\sum }).$$

By Theorem 1, P(β̂_n1 = β̃_n1) → 1, which implies $\sqrt{n}({\widehat{\beta }}_{n1}-{\stackrel{\sim }{\beta }}_{n1}){\to }_{P}0$. Therefore, by Slutsky’s lemma, we also have

$$\sqrt{n}({\widehat{\beta }}_{n1}-{\beta }_{01})=\sqrt{n}({\stackrel{\sim }{\beta }}_{n1}-{\beta }_{01})+\sqrt{n}({\widehat{\beta }}_{n1}-{\stackrel{\sim }{\beta }}_{n1}){\to }_{D}N(0,\mathrm{\sum }).$$

This completes the proof of Theorem 3.