Abstract
Quantum Key Distribution is carving its place among the tools used to secure communications. While a difficult technology, it enjoys benefits that set it apart from the rest, the most prominent is its provable security based on the laws of physics. QKD requires not only the mastering of signals at the quantum level, but also a classical processing to extract a secret-key from them. This postprocessing has been customarily studied in terms of the efficiency, a figure of merit that offers a biased view of the performance of real devices. Here we argue that it is the throughput the significant magnitude in practical QKD, specially in the case of high speed devices, where the differences are more marked, and give some examples contrasting the usual postprocessing schemes with new ones from modern coding theory. A good understanding of its implications is very important for the design of modern QKD devices.
Quantum key distribution (QKD) allows for the unlimited growth of a secret key guaranteed to be known only to the two legitimate parties connected by a quantum channel1. The technique solves, with information theoretical security, the long-standing problem of secret key distribution. Technologically, QKD has been coming of age quite rapidly: from the first experimental demonstration of the original Bennett-Brassard 1984 (BB84) protocol2 in 19893, where the quantum channel was a few centimeters long and worked at ≈ 1 KHz, to the first systems commercially available as early as 2003, reaching more than 50 km and with a single photon source working at a few MHz. Nowadays, QKD devices with speeds in excess of one GHz4,5,6,7,8 are customarily developed in laboratory, a prelude to their commercial production9.
A QKD link obviously requires the existence of a quantum channel, used to transmit the prepared qubits, but also needs a classical authenticated channel to extract a secret key from a set of raw detections. For high speed QKD, this postprocessing step — a key distillation process including key reconciliation and privacy amplification — is the part that takes more time, becoming a bottleneck for the secret key generation process.
The body of work about key reconciliation has been growing steadily during the last years. From the initial Cascade10 — an interactive syndrome exchange and binary search over blocks of raw data— to modern information theory applied to error reconciliation11. Usually, the main claims of these algorithms are based on the efficiency: the quotient of the information published in the authenticated channel over the Shannon conditional entropy of the correlated strings belonging to the emitter and receiver at the ends of the quantum channel. Most key distillation studies up to now use efficiency as the key figure to quote10,11,12,13,14.
While it is clear that a higher efficiency reduces the number of bits lost in the reconciliation process, improving the secret key rate, this tells us nothing about its real world throughput. The faster the QKD device, the more significant is the gap between both magnitudes. A highly efficient but slow protocol, whether because of the need of communications or heavy processing, would be eventually forced to discard bits if it cannot keep pace with the speed at which raw key is generated. This is a long standing issue in the QKD community7,15. Because of the increase in speed of recent devices, it is also receiving more attention from many research groups9,16. However, no previous works focus on the compromise between reconciliation efficiency and performance, and the impact of both parameters in the secret key throughput.
This work presents a study of real throughput measures of modern postprocessing protocols, contrasting the differences with the usual efficiency-oriented studies, in an attempt to clarify the questions that arise in the design of a high speed QKD device. In order to highlight the differences between the existing theoretical studies and its practical application plication optimized for different settings, a range of high performance, short block length, low-density parity-check (LDPC) codes are used for the key reconciliation process. This family of codes is commonly employed in wireless networks due to its performance and low resources requirements, which make them well suited for HW implementation. Its application to QKD illustrate quite well which are the tradeoffs and parameters that have to be taken into account in the design of the classical postprocessing part of a high performance QKD systems. During the study, the well-known Cascade protocol is used for comparison purposes as representative of the traditional reconciliation methods.
Results
Simulation results were computed to analyze the secret key rate and throughput in QKD using low-density parity-check (LDPC) codes for reconciling errors. Several techniques to improve their reconciliation efficiency13,14 are compared. In all the cases, a perfect reconciliation efficiency is also considered together with the performance of Cascade10. Simulations were performed using short-length LDPC codes and a few number of decoding iterations to additionally improve the overall throughput. In particular, quasi-cyclic LDPC codes were used, since they are of interest for hardware implementations (a layered decoding scheme over a partial-parallel architecture can be implemented for these matrices17). They are also part of a number of new communications standards, such as IEEE 802.11n (Wi-Fi), 802.16e (WiMAX) and ETSI DVB-S218,19,20, where a optimal set of codes is standardized. A GPU-based implementation of the sum-product algorithm for decoding LDPC codes (over a NVIDIA GeForce GTX 670 card) was used. The interest of using specialized HW to speed up the calculations is double. On one hand, because the simulations are extremely time consuming, to insure that we have good statistics in a reasonably short computing time and, on the other, to have a reconciled key throughput that comfortably exceeds the secret key throughput, hence exposing deficiencies in the reconciliation algorithms rather than in the inability of the implementation to keep up.
Secret key rate for the BB84 protocol is calculated as a function of the distance using the Gottesman et al. formula21,22 for a lossless QKD system (i.e. a system without transmission losses within the devices) exchanging weak coherent (attenuated) pulses. Calculations were then performed by considering α = 0.2 dB/km losses in the communication channel (typical for optical fiber and a 1550 nm wavelength) and a single photon detection efficiency of η = 10% with dark count probability of pd = 10−5. The protocol efficiency was considered to be q = 1/2. Raw key and secret key throughputs were calculated assuming a gigahertz clocked QKD system, i.e. assuming a source emitting single photon pulses at clock rates of 1 GHz.
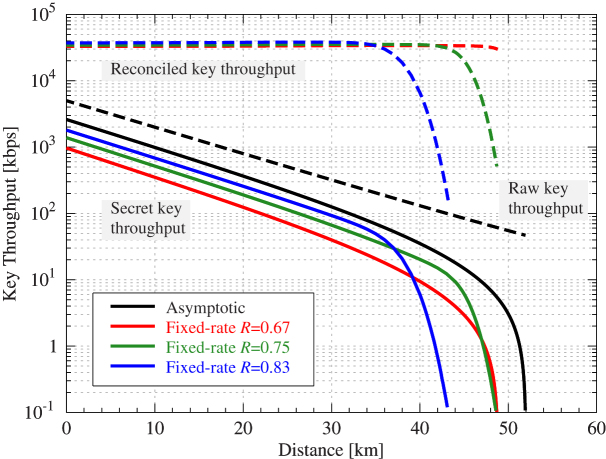
Fig. 1 shows secret key and reconciled key throughput using only one LDPC code for reconciling errors throughout the entire range of achievable distances. This first approach is computed using the correcting code without rate modulation, i.e. with a fixed information rate. As reference codes to illustrate our findings, those in the Wi-Fi standard mentioned above are used. Their length and rates are 1944 and R = 0.67, R = 0.75 and R = 0.83, respectively. As shown in the figure, the reconciled key throughputs (colour dashed lines) are considerably higher than the raw key throughput (black dashed line) and, therefore, information reconciliation with the simulated protocol is not a bottleneck in the key postprocessing. The secret key is, however, severely affected by the high amount of information disclosed for reconciliation. In the figure it can also be seen how the secret key throughput using correcting codes with low coding rate is always worse for short distances, and it only improves the secret key throughput of codes with higher coding rate when the latter are not able to distill keys (i.e. when the error is so high that no secret key can be distilled during the privacy amplification phase, or when the frame error rate in the reconciliation procedure becomes close to 1).
Figure 1. Secret key and reconciled key throughput for fixed-rate reconciliation with three LDPC codes of rates R = 0.67, R = 0.75, and R = 0.83.
Raw key throughput is for the BB84 protocol. Asymptotic secret key throughput is calculated assuming perfect reconciliation. Reconciled key throughput is constant while the code is correcting properly, since a constant number of decoding iterations are used without syndrome validation, and it starts to decrease as soon as the FER approaches 1 (i.e. errors grow beyond the capability of the code to correct them). This happens first for higher rate codes. The distance limit for the secret key throughput is higher for low rate codes since they have more redundancy. For the same reason throughput at lower distances is also smaller for low rate codes. Secret key throughput with low and high rate codes cross when the degradation due to increased FER in the higher rate code equals the information leakage in the lower rate curve.
The frame error rate (FER) is a parameter commonly used in communication theory that represents the ratio of transmitted words that cannot be corrected. In this context it represents the ratio of keys that cannot be reconciled, and therefore it is a factor that directly acts on the secret key rate. Its effect can be easily seen in Fig. 1 where only fixed rate codes are used for reconciling errors. For instance, using a short length correcting code of rate R = 0.81, FER is above 80% with a 2% of errors in the communication channel, which occurs in the simulated scenario at a distance of 40 km. At this point the secret key rate drops. A similar behavior occurs when reconciling with a code of rate R = 0.75 at a distance of approx. 46 km. However, as the figure shows, lower coding rates (e.g. R = 0.67) cannot be used to reach longer distances. This is because, for a given channel, there is a certain coding rate under which the FER is no longer the limiting factor: the secret key rate is now limited by the error rate in the channel.
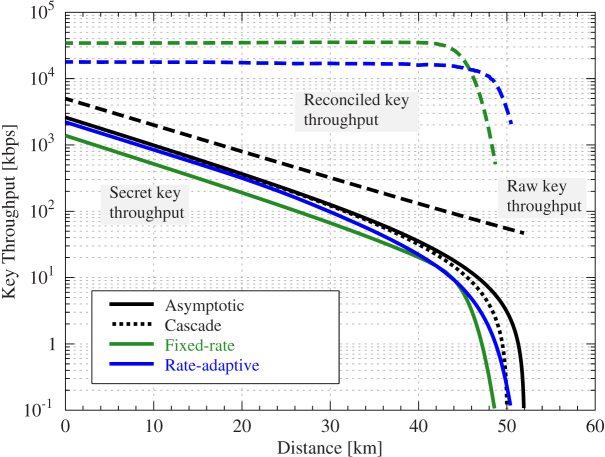
We next consider the possibility of modulating the coding rate of an LDPC code in order to reduce the excess of information disclosed, thus improving the reconciliation efficiency. A rate-adaptive technique as proposed in13 for short-length quasi cyclic LDPC codes is analyzed in Fig. 2. As shown in the figure, the secret key improves over the full range of distances, while the reconciled key throughput is not severely affected (it remains well above the throughput of raw key).
Figure 2. Secret key and reconciled key throughput for fixed-rate and rate-adaptive reconciliation with an LDPC code of rate R0 = 0.75.
Raw key and asymptotic secret key throughput are as in Fig. 1. Secret key throughput using the reconciliation efficiency of Cascade without taking into account the penalty introduced by the extra communications required by this protocol. The rate adaptive protocol reduces the reconciled key throughput due to its complexity compared to the fixed rate protocol. However, because of its higher efficiency the secret key throughput improves over the whole range of distances, reaching slightly farther than Cascade.
For this second reconciliation approach we use the optimal proportion of punctured and shortened symbols that maximizes the secret key rate. This proportion is obtained from simulations for a particular correcting code and different error rate values with the number of modulated symbols fixed to 350, the maximum allowed using he intentional puncturing algorithm described in23. Note that, for short length codes, punctured symbols should be chosen according to an intentional puncturing algorithm, such as the one cited above, to improve the overall performance. On the other hand, shortened symbols can be chosen randomly without compromising the performance, and thus the proportion of modulated symbols when puncturing and shortening simultaneously is only limited by the maximum number of symbols that can be punctured.
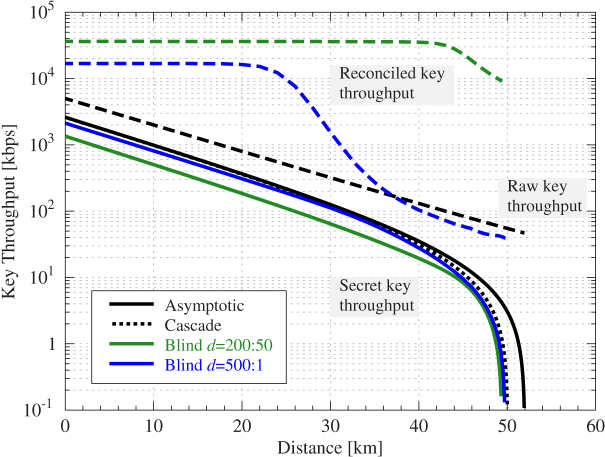
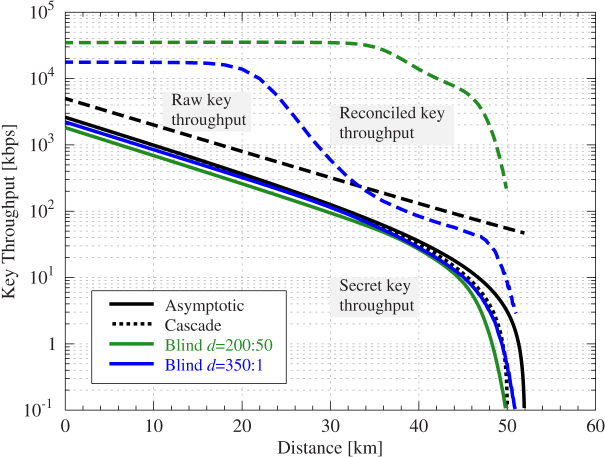
Finally, an interactive LDPC-based reconciliation is analyzed. The rate-adaptive version discussed above is extended with the use of feedback information as proposed in14, named blind reconciliation. This new technique, commonly known as incremental redundancy hybrid automatic repeat request (IR-HARQ) in the information and communication theory literature, allows to improve the average efficiency and key throughput as shown in Fig. 3 and Fig. 4. In the rate-adaptive approach simulated in Fig. 2, reconciliation is done with just one decoding procedure using the stochastically averaged optimal proportion of punctured and shortened symbols. Therefore, only one message with the syndrome and information of shortened bits has to be exchanged. However, an slightly interactive version of this protocol, such as the one proposed in14, improves the average efficiency by repeating the decoding procedure with different proportions of punctured and shortened symbols.
Figure 3. Secret key and reconciled key throughput for blind reconciliation with an LDPC code of rate R0 = 0.67.
Two different sets of parameters controlling the number of steps in the blind reconciliation are chosen: one for almost ideal behavior regardless of the performance (blue line), and other for a good balance between both (green). It can be seen how the secret key throughput of the former follows closely the throughput of the idealized — without communications — Cascade over the whole distance range, improving the rate-adaptive case of Fig. 2. Raw key, asymptotic secret key, and Cascade throughput are as in Fig. 2.
Figure 4. Secret key and reconciled key throughput for blind reconciliation with an LDPC code of rate R0 = 0.75.
As in Fig. 3 two different sets of parameters are chosen. The higher rate of the code increases the secret key throughput, improving on Cascade at the longest distances. This is because the rate fits appropriately the error range to be corrected. It can be seen that in the best point almost no secret key is lost with respect to the asymptotic case.
Although such schemes require the exchange of multiple network messages, the average throughput was calculated without taking into account this latency given that the HW used to implement the reconciliation protocol essentially operates as a pipeline (in a GPU multiple blocks can be processed in parallel): communication latency is thus hidden and paid only once at the start of the whole process.
Furthermore, note that the proportion of modulated symbols differs in both figures since the maximum number of punctured symbols depends on the coding rate. Accordingly, the number of modulated symbols may be higher for correcting codes with higher coding rates.
Discussion
The classical leakage of information during the key post-processing in QKD is dominated by the amount of information disclosed for reconciling discrepancies in an exchanged key. This leakage is lower bounded by the Shannon limit, and is usually parameterized by the reconciliation efficiency, i.e. the ratio of information disclosed for reconciliation with respect to the minimum leakage. Most techniques for reconciling errors in QKD try to optimize this parameter, such as the well-known Cascade10, the most widely used procedure for reconciling errors in QKD. However, while an efficient reconciliation improves the secret key rate, the performance of real devices must be measured in terms of secret key length per second and take into account the bandwidth of every step involved in a QKD protocol, i.e. raw key exchange, information reconciliation and privacy amplification. In this regard, reconciled key throughput is here compared to the raw key bandwidth in order to identify any setting where reconciliation is a bottleneck during postprocessing. Secret key throughput is then optimized looking for a trade-off between the customarily cited reconciliation efficiency versus the more practically significant throughput.
Fig. 1 shows reconciled and secret key throughput for a set of three different LDPC codes as a function of the distance (absorptions). These codes are used for reconciliation purposes without modulating the coding rate. The asymptotic key throughput for a perfect code is shown for comparison purposes. The reconciled key throughput is similar for all three rates up to a certain distance. After this distance (36 km for the LDPC code with coding rate R = 0.83, 44 km for R = 0.75, and 50 km for R = 0.67) the error correction method starts to fail and the correspondingly high frame error rate (FER, see the Methods section) imposes a heavy penalty on the secret key. Secret key throughput for the different rates start within a factor of two among them and decrease in a similar way with distance due to the extra information leaked. Once the point at which the code loses efficiency, i.e. when the FER grows, it becomes the main source of error, heavily penalizing the secret key. The curves for different rates cross at the point where the degradation due to increased FER in the higher rate code equals the information leakage in the lower rate curve, since the FER effects appear later because of the higher redundancy of a lower rate code.
Fig. 2 compares a fixed rate code (with coding rate R = 0.75) to a rate adaptive one (with mother code of rate R0 = 0.75). The reconciled key throughput of the rate adaptive code is slightly lower than the fixed rate due to the higher complexity of the algorithm. However, its adaptivity means that the amount of information published during reconciliation is smaller, hence its secret key throughput is always higher and remarkably closer to the asymptotic case, beating Cascade at the longest distances. Rate adaptive and fixed rate curves coincide at the point where the modulated rate equals the fixed or mother rate.
From the simulations, an interesting effect was also seen here: when the FER is depicted as a function of the distance (QBER), a region of very low FER is obtained for short distances (<20 km), as expected for a region with low errors and in which almost any code is going to work very well. In the same way, at very long distances, the amount of errors is so big that not even the code with the lowest rate would be able to correct them, thus failing very often and producing a very high FER. The somewhat unexpected result is in between both regions, where the simulations show that most of the time the code is correcting with a comparatively high FER of the order of 10−2 ~ 10−1. In communications it is usual to target a FER well below 10−3, whereas from the simulations it is clear how important is to extend the use of the code to regions of higher FER, which allows to distill key without discarding information, thus achieving a high key throughput.
Figs. 3 and 4 compare Cascade with the blind algorithm, an interactive version of the rate-adaptive reconciliation (multiple messages are exchanged between the parties) that adds feedback information to increase its performance. In this case, the average information revealed is reduced, at the expense of the reconciliation throughput due to the interactivity of the algorithm. Fig. 3 shows the results when using a mother code of rate R0 = 0.67 and Fig. 4 for R0 = 0.75. In both figures, two different sets of parameters to regulate the blind algorithm are used. One is chosen in order to obtain the maximum number of secret key bits regardless of its throughput and the other represents a balance among both. In the case of rate 0.67 this implies to start the algorithm with a number, d, of punctured symbols equal to 500 (the maximum according to23), and reveal information one bit at a time for the maximizing case; and d = 200 and reveal 50 at a time for the balanced one. For rate 0.75, the maximum number of punctured symbols is 350. In both cases it is seen that the secret key throughput is even closer to the asymptotic limit, closely matching Cascade, improving its throughput at the highest distances and extending its reach in the case of rate 0.75.
A technical note is in order regarding reconciled key throughput: as long as it is high enough to sustain the asymptotic case, its variations will not affect the secret key throughput. Apart from the reconciliation algorithm complexity, this is mostly a matter of implementation or of the HW used. This is a point that can be improved just by changing to a faster HW or optimizing the code, hence, in the points in Figs. 3 and 4 in which the achieved reconciled key throughput went below the asymptotic case, it was artificially raised above it, assuming that a better HW would solve the issue without changing the conclusions.
Methods
Secret key rate
The general expression for the secret key fraction with one-way postprocessing is given by22:
where IE is the fraction of information about the raw key that is known to the eavesdropper, Eve, and leakEC the fraction of information disclosed during the reconciliation phase.
We consider the QKD protocol BB84 and a realistic scenario: the emitting device is an attenuated laser (emitting weak coherent pulses), an optical fiber is used as communications channel and at the receiving end, the incoming signals are detected with an avalanche photodiode.
In the source, pulses with two or more photons are emitted with non zero probability and Eve can collect all the information from these pulses without being detected. In consequence, the secret key fraction is calculated using only single photon pulses and assuming that Eve can gain information at the expense of introducing errors in the communication:
Y1 is the fraction of single photon pulses detected, 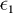 is the quantum bit error rate (QBER) corresponding to the pulses with only one photon, and h(x) the binary Shannon entropy.
is the quantum bit error rate (QBER) corresponding to the pulses with only one photon, and h(x) the binary Shannon entropy.
A lower bound for the secret key rate can be calculated by upper bounding Y1 and 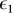 . For the fraction of 1-photon pulses detected an upper bound is given by:
. For the fraction of 1-photon pulses detected an upper bound is given by:
where μ is the average number of emitted photons per pulse, such that pmulti(μ) = 1 − (1 + μ)e−μ is the probability of emitting two or more photons, and pexp is the total detection rate. The error rate of single photon pulses is upper-bounded by 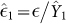 .
.
For simulation purposes, an analytical estimation of the detected pulses can be done considering the transmitivity in the fiber, t = 10−αL/10 where α is the attenuation constant and L is the distance in km, and the quantum efficiency η in the detectors. The signal detection rate is approximated by psignal ≈ μtη (where a typical choice is to set μ equal to the total transmitivity μ = tη22). And the total detection rate can be estimated considering the dark count rate pd too:
The error rate is estimated considering only dark counts.
Information reconciliation
The amount of information disclosed to reconcile errors in QKD, leakEC( ), can be lower bounded using the Slepian-Wolf limit24. When a binary symmetric channel with parameter
), can be lower bounded using the Slepian-Wolf limit24. When a binary symmetric channel with parameter  (QBER in the QKD case) is used as a model for the side-information, the minimal encoding rate is given by the binary entropy,
(QBER in the QKD case) is used as a model for the side-information, the minimal encoding rate is given by the binary entropy, 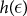 . Since any realistic reconciliation procedure would disclose more information, an efficiency factor
. Since any realistic reconciliation procedure would disclose more information, an efficiency factor 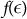 has to be included. The leakage is then expressed as:
has to be included. The leakage is then expressed as:
We restrict our attention to binary correcting codes since they are sufficient to approach the Slepian-Wolf limit. These codes transform words of k bits of information into codewords of length n. The extra n − k bits add redundancy such that, even if the codeword suffers from errors after being transmitted through a communication channel, the decoder would recover the original codeword. The leakage due to a reconciliation procedure based on an error correcting code using syndrome coding25 is given by the relation between the length of the added redundancy and the length of the codeword, (n − k)/n.
The information rate, and in consequence the leakage of information during the error reconciliation, can be modulated. Two common techniques are puncturing and shortening26. The leakage caused by a binary correcting code with p punctured bits and s shortened bits is given by the following relation:
Secret key throughput
The discussion above holds whenever the reconciliation procedure succeeds. Real reconciliation methods on noisy strings have always a non zero probability of failure. The figure of merit associated with the failure probability is the frame error rate (FER). It is defined as the mean of the random variable that outputs 0 when the reconciliation protocol is successful and 1 whenever it fails. Non reconciled words can be discarded from the process or publicly disclosed for a more refined estimation of the QBER. This gives the following final form for the secret key rate taking into account realistic reconciliation methods:
where q is the protocol efficiency.
The final key throughput of the system is found by multiplying the secret key rate by the frequency of the source.
Author Contributions
J.M. and V.M. designed the study. J.M. carried out the simulations. D.E., J.M. and V.M. discussed the results, wrote and reviewed the manuscript.
Acknowledgments
This work has been partially supported by the projects Quantum Information Technologies in Madrid (QUITEMAD), Project P2009/ESP-1594, Comunidad Autónoma de Madrid, and Hybrid Quantum Networks (HyQuNet), TEC2012-35673, Ministerio de Economía y Competitividad, Spain. The authors acknowledge the resources and assistance provided by the Centro de Supercomputación y Visualización de Madrid.
References
- Gisin N., Ribordy G., Tittel W. & Zbinden H. Quantum Cryptography. Rev. Mod. Phys. 74, 145–195 (2002). [Google Scholar]
- Bennett C. H. & Brassard G. Quantum Cryptography: Public Key Distribution and Coin Tossing. IEEE International Conference on Computers, Systems, and Signal Processing 175–179 (1984). [Google Scholar]
- Bennett C. H., Bessette F., Brassard G., Salvail L. & Smolin J. Experimental Quantum Cryptography. J. Cryptology 5, 3–28 (1992). [Google Scholar]
- Stucki D. et al. High rate, long-distance quantum key distribution over 250 km of ultra low loss fibres. New J. Phys. 11, 075003 (2009). [Google Scholar]
- Yuan Z. L., Dixon A. R., Dynes J. F., Sharpe A. W. & Shields A. J. Practical gigahertz quantum key distribution based on avalanche photodiodes. New J. Phys. 11, 045019 (2009). [Google Scholar]
- Eraerds P., Walenta N., Legre M., Gisin N. & Zbinden H. Quantum key distribution and 1 Gbps data encryption over a single fibre. New J. Phys. 12, 063027 (2010). [Google Scholar]
- Jouguet P. et al. Field test of classical symmetric encryption with continuous variables quantum key distribution. Opt. Express 20, 14030–14041 (2012). [DOI] [PubMed] [Google Scholar]
- Patel K. A. et al. Coexistence of high-bit-rate quantum key distribution and data on optical fiber. Phys. Rev. X 2, 041010 (2012). [Google Scholar]
- NanoTera Project. QCrypt: Secure High-Speed Communication based on Quantum Key Distribution. http://www.nano-tera.ch (Accessed on March 6, 2013).
- Brassard G. & Salvail L. Secret-Key Reconciliation by Public Discussion. Eurocrypt'93, Workshop on the theory and application of cryptographic techniques on Advances in cryptology. 765, 410–423 (1994). [Google Scholar]
- Van Assche G. Quantum Cryptography and Secret-Key Distillation. Cambridge University Press, (2006).
- Kasai K., Matsumoto R. & Sakaniwa K. Information reconciliation for QKD with rate-compatible non-binary LDPC codes. International Symposium onInformation Theory and its Applications 922–927 (2010). [Google Scholar]
- Elkouss D., Martinez-Mateo J. & Martin V. Information Reconciliation for Quantum Key Distribution. Quantum Inform. Comput. 11, 226–238 (2011). [Google Scholar]
- Martinez-Mateo J., Elkouss D. & Martin V. Blind Reconciliation. Quantum Inform. Comput. 12, 791–812 (2012). [Google Scholar]
- Fossier S. et al. Field test of a continuous-variable quantum key distribution prototype. New J. Phys. 11, 045023 (2009). [Google Scholar]
- HiPANQ Project. High Performance Algorithms for Next Generation Quantum Key Distribution. http://sqt.ait.ac.at/software/projects/hipanq/ (Accessed on March 6, 2013).
- Studer C., Preyss N., Roth C. & Burg A. Configurable high-throughput decoder architecture for quasi-cyclic LDPC codes. 42nd Asilomar Conference on Signals, Systems and Computers, 1137–1142 (2008).
- IEEE P802.11n. IEEE Standard for Information Technology–Telecommunications and information exchange between systems–Local and metropolitan area networks–Specific requirements, Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) specifications.
- IEEE P802.16e. IEEE Standard for Local and Metropolitan Area Networks, Part 16: Air Interface for Broadband Wireless Access Systems.
- ETSI EN 302 307. Digital Video Broadcasting (DVB), Second generation framing structure, channel coding and modulation systems for Broadcasting, Interactive Services, News Gathering and other broadband satellite applications (DVB-S2). European Standard (Telecommunications series). [Google Scholar]
- Gottesman D., Lo H.-K., Lutkenhaus N. & Preskill J. Security of quantum key distribution with imperfect devices. Quantum Inform. Comput. 4, 325–360 (2004). [Google Scholar]
- Scarani V. et al. The security of practical quantum key distribution. Rev. Mod. Phys. 81, 1301–1350 (2009). [Google Scholar]
- Elkouss D., Martinez-Mateo J. & Martin V. Untainted Puncturing for Irregular Low-Density Parity-Check Codes. IEEE Wireless Communications Letters 1, 585–588 (2012). [Google Scholar]
- Slepian D. & Wolf J. Noiseless coding of correlated information sources. IEEE Trans. Inf. Theory 19, 471–480 (1973). [Google Scholar]
- Wyner A. Recent results in the shannon theory. IEEE Trans. Inf. Theory 20, 2–10 (1974). [Google Scholar]
- Huffman W. & Pless V. Fundamentals of Error-Correcting Codes. Cambridge University Press, (2003).