NeuroGPS: automated localization of neurons for brain circuits using L1 minimization model

Abstract

Drawing the map of neuronal circuits at microscopic resolution is important to explain how brain works. Recent progresses in fluorescence labeling and imaging techniques have enabled measuring the whole brain of a rodent like a mouse at submicron-resolution. Considering the huge volume of such datasets, automatic tracing and reconstruct the neuronal connections from the image stacks is essential to form the large scale circuits. However, the first step among which, automated location the soma across different brain areas remains a challenge. Here, we addressed this problem by introducing L1 minimization model. We developed a fully automated system, NeuronGlobalPositionSystem (NeuroGPS) that is robust to the broad diversity of shape, size and density of the neurons in a mouse brain. This method allows locating the neurons across different brain areas without human intervention. We believe this method would facilitate the analysis of the neuronal circuits for brain function and disease studies.

Neural circuit is the physical basis of the brain function. Drawing the map of neuronal circuits at microscopic resolution is important to explain how the brain works, which requires tracing the neurons from its branches to the cell body (soma)¹,²,³,⁴,⁵,⁶. Therefore locating the soma of the neuron is a first step for boosting tracing accuracy and further quantifying the neuronal circuits⁷,⁸,⁹. Meanwhile, localization of neurons has also been widely used to discover the scientific fact in other researches. For example, it has been applied in computing the positions of the neural stem-cell in the adult sub ventricular zone to analyze niche cell-cell interactions¹⁰, in discovering whether the cancer stem cell are independent on the neural microenvironments or not¹¹, and in quantifying the relation between the distribution of neurons and blood vessel¹². Recent progresses in fluorescence labeling and imaging techniques, that have enabled measuring the whole brain connections of a rodent like a mouse at submicron-resolution¹³,¹⁴,¹⁵ or micron-resolution¹⁶, have piled up very huge volume of data, which made manual location the neurons painful for large scale analysis such as the mouse brain.

Substantial progresses have been made in automatically locating and segmenting cells from the image stacks. Typical methods¹⁷,¹⁸,¹⁹,²⁰,²¹,²²,²³,²⁴,²⁵,²⁶,²⁷,²⁸,²⁹ including watershed algorithm¹⁷,¹⁸,¹⁹,²⁰,²¹, tracking the gradient flows²²,²³, multi-scale filters²⁴,²⁵, and minimum-model²⁹ etc., mainly focus on locating and segmenting cells with simple rather than complicated morphology. Recently proposed FARSIGHT software²⁵ can address the neurons with specific complicated morphology³⁰. Automatic segmentation tool like V3D⁶ is widely used to track complicated neuronal fibers. However localization the neuron is typically done manually due to the broad diversity of shape and size of neurons, especially the thick dendritic truck is still challenging.

Here, to overcome the above challenges, a novel method, called as Neuronal Global Position System (NeuroGPS), was developed. Based on a new biophysical model, it applies optimization method to locate neuron by introducing L1 minimization³¹ (L1-M) with a guiding hypothesis that each neuron has only one soma, which is not densely overlapped with its neighbors. NeuroGPS locates the cell body by computing the radius of each soma, and finding the most preferred radius and its corresponding coordinates. This method efficiently eliminates the interference from the complicated neurites, especially the thick dendritic truck, on localization, and is robust to the diverse shape, size, and density of neurons. With NeuroGPS, we demonstrate automatic localization of neurons across different regions in the mouse brain without human intervention.

Results

The L1 minimization model of neurons localization

Using binarization and erosion operation (See Methods), a binarized signal B_L (the foreground and background values were set to value one and zero respectively) can be extracted from the initial image stacks. Usually, B_L contains the images of neurons with soma and thick dendritic trucks. The neuronal soma could be roughly described as a sphere, while thick dendritic truck cannot be easily described by a given template for its complicated and highly diversed pattern. So, we make a new model to describe the neuronal image. Assumed that B_Lcan be modeled as the summarization of a series of spheres and a residual part, i. e.,

where f (o, o_i, r_i) is the i th sphere function given as

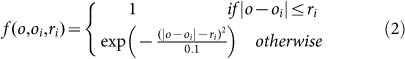res (o) is residual signal, o is the coordinates of volume pixels in B_L, k is the number of spheres, o_i and r_i are the initial position and radius of the sphere function, respectively.

The fact that B_L contains thick dendritic trucks results in some false positive positions in these k initial positions (o₁,o₂,…,o_k). So, the task of localization of neurons is thus transferred to identifying real positions from the positions (o₁,o₂,…,o_k). In Eq. (1), the unknown parameters, i.e., the radiuses and positions of sphere function, need to be estimated. The classic way to estimate the parameters is using nonlinear least squares fitting³², namely, finding the optimal parameters for Eq. (1) with a minimum residual function. Accordingly, the optimal problem can be written as

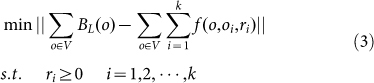where || || represents 2- norm squared and V is the coordinate sets of volume pixels in B_L.

This model (optimization problem (3)) was further characterized or modified by including the prior property of the neuronal dataset, i.e. the spatial distribution of the neuron is sparse. This is explained in details as follows. The territory of one neuron often significantly overlaps with that of another neuron with the extending neurites, however, the soma of one neuron naturally never overlaps with that of another neuron. This means the neuron is sparse when considering its position in the three dimensional space. If we set many potential soma positions for a certain dataset, most of these positions should be false, and the correlated radius should be zero. Therefore, the radius of the sphere functions has the property of sparsity. Considering this sparsity, inspired by compressive sensing³³, we use a signal processing technique called L1 minimization technique, which works on a similar principle for sparse signal reconstruction, to recover the non-zero radiuses of sphere functions, and thus modify the optimization problem (3) as

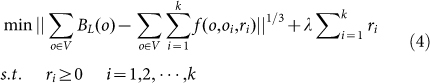where λ is the tradeoff between the error in fitting parameters of sphere function to B_L and the sparseness of the radius of the sphere functions. Here, optimization problem (4) (O.P. (4)) can be regarded as L1 minimization model (L1-M) that is used to locate neurons. λ is set to be 0.025 for the datasets analysis. Note that in optimization problem (4), to keep the same physical dimension, the first term of the objective function was modified to the 1/3 power of 2-norm squared of the error.

Solving the L1 minimization model

O.P. (4) can be solved using the method proposed by Candes³⁴. However, considering B_L is image stacks with large volume, we applied modification to the frame work of Candes³⁴, to improve the computational efficiency. Rather than updating all the parameters using gradient projection³⁵ in the iteration optimization process, we divided the parameters in O.P. (4) into two groups: radius and position of sphere functions, and updated the radius and position using gradient projection and averaging method, respectively. This operation can significantly decrease the computational time (10 × faster, data not shown). The algorithm for O.P. (4) was described in Methods-The algorithm. For all optimal radiuses, if r_i is bigger than a given threshold (see Methods-Parameters set), the corresponding position o_i is regarded as a valid position.

The feature of L1 minimization model

In L1-M model (O.P. (4)), besides it requires the simulated image reach a minimum error over the measured image, in the meantime, it requires the summarization of the radius of the many soma candidates also reach a minimum value. This additional constrain lead to shrinkage in these radiuses correlated to the neurites including thick trucks. To prove this, we examined the efficacy of introducing L1 minimization model to locate neurons. As shown in Fig. 1a, the signal labeled in light blue corresponds to the foreground of B_L, and the red spots are the initial candidate positions (or seeds) which lie in the soma and thick truck. Without L1-M, i.e., λ = 0 in O.P. (4), the radiuses corresponding to positions in thick truck were calculated to be about 4.0 μm, which are almost equal to the value of radius of some small neuronal somas. While using L1-M, except the radius of soma, the values of other radiuses were close to zero (Fig. 1b). These results clearly demonstrated that L1-M model can eliminate the interference of thick trucks when locating neurons.

Figure 1. L1 minimization suppresses the tough constrain posed by thick trucks of the pyramidal cells.

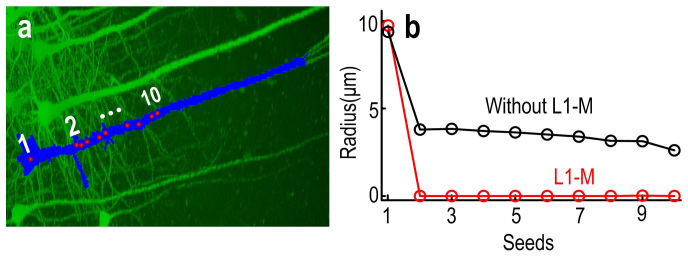
(a) The extracted signals (blue) and the initial positions of sphere functions (red dots). Analyzed using model with and without L1-M, the radiuses corresponding to each positions of sphere functions were shown in (b).

Localization neurons with broad diversity in shape and size

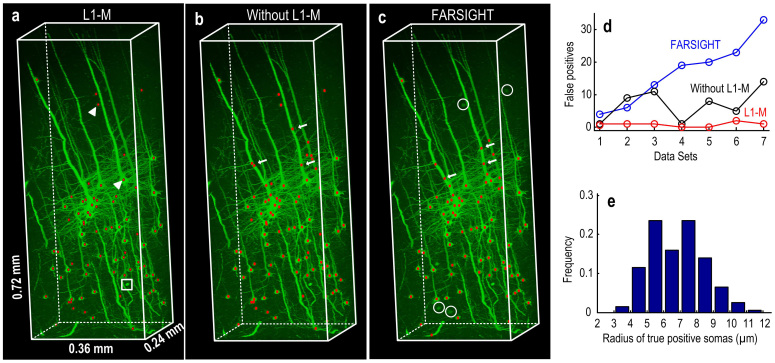
To evaluate NeuroGPS, we applied it to seven typical image stacks from different cortical regions. Each contains 300 × 200 × 600 volume pixels. Fig. 2a shows typical results, and Fig. 2d,e shows the statistics of the seven data sets. In Fig. 2a, as white triangle labeled, the shape of cells has a variety of patterns. Some pyramidal neurons show long and thick trucks, resulting in difficulties to describe their morphology, while some others cells show simple shape, can easily be modeled with a sphere function. In the meantime, the size of the soma also varies largely. In Fig. 2e, we calculated the radiuses of the true positive neurons of all the seven datasets and noted their values widely range from about 4.0 μm to 11.0 μm. For comparison, these datasets were substituted to the same optimization processing system but without L1-M (Fig. 2b), and to the popular neuron tracing software like FARSIGHT²⁵ (Fig. 2c). Thick trucks are sometimes recognized as somas (arrows in Fig. 2b,c). This will increase the overall false positive numbers in locating neurons (Fig. 2d). Some neurons cannot be detected (circles in Fig. 2c)) by FARSIGHT for low signal intensity. Consider all the neurons in the several dataset, the overall false positive rate and true positive rate are 4% and 100% for NeuroGPS, 25% and 100% for NeuroGPS without L1-M, and 61% and 88% for FARSIGHT. According to the general way of image processing, image content around the boundary of images stacks are directly ignored, that's why some bright spots are not identified as somas (the square in Fig. 2a). These spots are not included in the ground truth, and not affect the positive rate. From the above results, we can conclude that NeuroGPS is powerful to locate neurons with broad diversity of shape and size.

Figure 2. The capability of NeuroGPS for locating neurons with complicated morphology and different size.

The comparison of locating neurons from the image stacks (data set #3 in (d))) with L1 minimization (NeuroGPS) (a), without L1 minimization (b), and with FARSIGHT method(c). Some examples of the cell patterns (triangles), false-positive positions (arrows) and undetected positions (circles) were given in (a), (b) and (c). (d) The number of false positive positions for the three localization method. (e) Distribution of the radiuses of true positive neuronal somas.

Localization high-density neurons

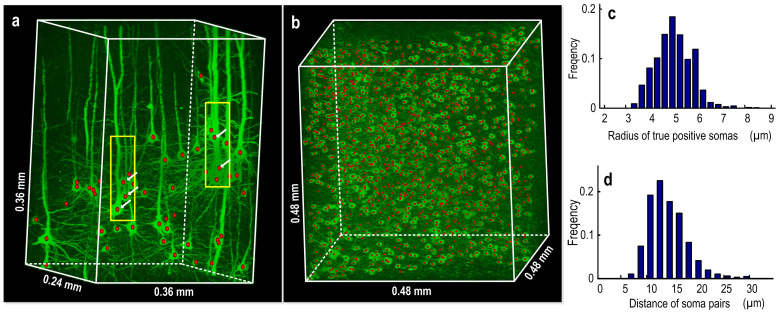
We used the experimental data sets to illustrate NeuroGPS can locate neurons with highly dense spatial distribution. Typical region such as cortical (Fig. 3a) and hippocampus (Fig. 3b) regions were given as examples of two types of high-density. The clustered neurons with complicated neuritis, labeled by arrows in Fig. 3a, were successfully located using NeuroGPS. For the image stacks in Fig. 3b, the false positive rate and true positive rate are 6% and 86%. We also quantitatively estimate the spatial density of the neurons in Fig. 3b. More than 95% radius of the neuronal soma ranges from 3.0 μm to 8.0 μm (Fig. 3c), and the distance between pairs of cells, defined as the distance from the manually-determined position of one neuron to the nearest position of the other neuron, is 13.6 ± 3.8 μm (Fig. 3d). If measured the density of the true positive somas by the pair distance smaller than 1×, or 1.2× of the sum of the radiuses, respectively, about 14% or 35% of the cells touched each other. This value indicates that a part of cells experienced dense distribution.

Figure 3.

NeuroGPS locates high-density neurons with typical regions such as cortical (a) and hippocampus (b) area. Neurons with (a) and without complicated neurites (b) were shown. The red dots represent the recognized positions. Arrows in the rectangle (a) are show cases neurons overlapped but the soma not overlapped. From the image stacks of (b), there gives the distribution of the magnitude of radiuses of real positive neurons (c), and the distance of neuron pairs (d).

Automated localization of neurons across different brain areas

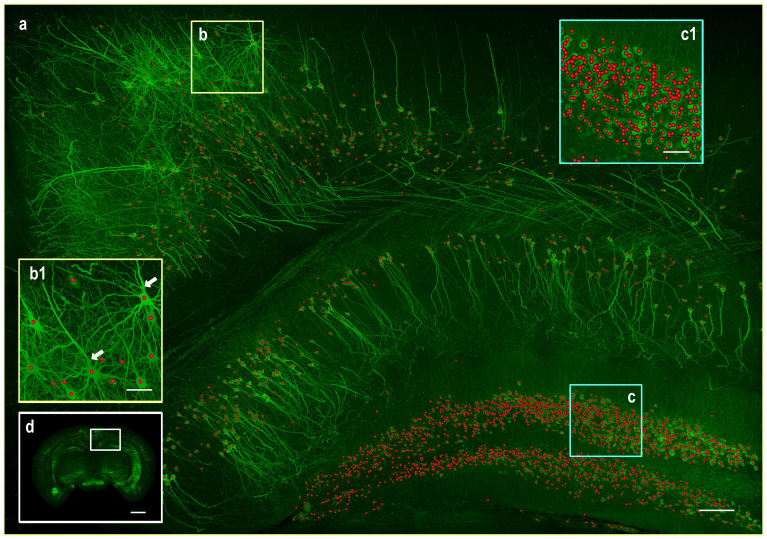
With the above two features, NeuroGPS is able to locate neuron automatically across different brain area without any manual mediation. This point is illustrated with a large scale fluorescence images dataset which includes part of the cortical and the hippocampal area, and whose max-intensity projection is shown in Fig. 4a. The images dataset is the part of the whole coronal profile (labeled by white rectangle in Fig. 4d), and its size is 1300 × 1850 × 150 volume pixels. In spite of a variety of cell shapes, sizes and densities, including very thick and complicated dendrites, (typically shown in Fig. 4b,c or b1,c1), we located about 2500 neurons using NeuroGPS, and get an overall true positive rate of 88%, and a false positive rate of 8% compared with manual detected positions as the ground truth. It is noted in this demonstration that the radiuses of some thick trucks are almost 4.0 μm, equal to or bigger than the size of small neurons, as the radius of true positive neuronal somas ranges from about 3.5 μm to 10.0 μm. Without L1-M, the positions in thick trucks were easily recognized the position of neurons (arrows Fig. 4b1). This result indicates that NeuroGPS can be applied in handling large scale data sets, which is surely beneficial for further reconstructing neuronal morphology or quantifying large neuronal circuits.

Figure 4. Automated localization of neurons across different mouse brain areas by using NeuroGPS.

(a) The max-intensity projection of image stacks and the recognized positions of neurons (red dots). The regions (b) and (c) were typical examples showing the complexity of the signals, and were enlarged to (b1) and (c1) respectively. The insect (d) shows the whole coronal profile. Arrows show thick trucks easily recognized as soma when not using the L1-M model. Scale bar, 100 μm for (a), 20 μm for (b1) and (c1), and 1000 μm for (d).

Discussion

Localization of neurons has the promise boosting neuronal trace and quantifying the large scale neuronal circuits. In this paper, we have proposed NeuroGPS method to locate neurons across different brain areas and have demonstrated its high robustness to the shape, size and spatial distribution of neurons. Specifically, this method eliminated the negative influence of the complicated neurites, especially from the thick dendritic truck, on localization.

Essentially, we made a new biophysical model to locate the neuron which only concerns the morphology of the neuronal soma, rather than the entire neuron. In the biophysical model, we introduced L1 minimization to maximize image sparsity, and identify the false positive positions in thick dendritic truck which is based on the biophysical/neurobiological assumption that each neuron has only one soma that does not overlap with its neighbors. This biophysical model and its successful solution play a key role in successfully locating neurons with complicated morphology.

Due to the complexity and diversity of neuronal structure in mammals like mouse, neurons across different brain have a wide variation of shape, size and spatial distribution. Therefore localization of these neurons without human interference is a challenging work. Typically, when we analyzed our data sets, the radiuses of some thick trucks are close to 4.0 μm (Fig. 1b), which are almost equals to or even bigger than the radius of some neuronal somas (Fig. 2e & Fig. 3c). Previous works¹⁷,¹⁸,¹⁹,²⁰,²¹,²²,²³,²⁴,²⁵,²⁶,²⁷,²⁸,²⁹ have not involved this problem, and thus experience difficulties in resolving it. For example, though the classical method like FARSIGHT can overcome the challenges in locating neurons with variation of size and spatial distribution²⁵, it cannot distinguish thick trucks and some small neurons (Fig. 2d). NeuroGPS, as described earlier, can induce shrinkage in the radiuses of thick trucks by introducing L1-M and effectively identify the false positions of thick trucks (Fig. 1a, b & Fig. 2a, b). In addition, NeuroGPS possesses high robustness to the size and spatial distribution of neurons (Fig. 2e & Fig. 3a, c). These advantages of NeuroGPS make it possible to locate neurons across different brain areas.

In optimization problem (4), the parameter λ is used to control the tradeoff between the fitting error and the sparsity of radiuses of sphere function. When we choose a big value of λ to enforce this sparsity, the fitting error will increase. Conversely, the small fitting error is built on the sacrifice of the sparsity. So finding the appropriate tradeoff may be important for the localization performance. Fortunately, the algorithm of reweighted L1 minimization³⁴ can automatically modify the strength of the sparsity in solving optimization problem (4) and provide strong sparsity even when a small value of λ is set, e.g. strong sparsity can be gained with a wide λ value range. This feature enables that the localization performance is robust to the tradeoff λ. In experiment, specific λ value was roughly estimated by analyzing a few images. If the localization result is right, the corresponding λ is set, and then extend to the rest volume datasets. If the result is not right, tune λ again to get better performances. In our experience, λ remains unchanged for any image stacks provided that the size of volume pixels and the radius of the soma are within a certain range.

In our experimental data sets analysis, a small amount of positions of neurons has not been detected as expected. There are some reasons for this phenomenon. Firstly, in the process of sample preparing or imaging, the shape of some neuronal soma may be seriously distorted and deviated far from its normal morphology. Secondly, information loss from neuronal somas in the binarization and erosion operation has a negative influence on seeds selection and sphere functions fitting. Depending on the feature of neuronal morphology, using the improved binarization and erosion method may improve the localization performance.

The computation time of NeuroGPS depends on the number, morphology and spatial distribution of neurons. As described earlier, we used the averaging method combined with gradient projection to speed the iteration optimization process and increase the computation efficiency of NeuroGPS. This operation is effective based on the fact the shape of neuronal soma basically meets spherical symmetry. As verified by Berglund³⁶, an object can be located by averaging method provided that its shape meets the spherical symmetry. Typically, analyzing an 600 × 200 × 75 volume pixels image stacks takes about 30 seconds in an Inter(R)Xeon(R)CPU 3.46 GHz computing platform. On the other hand, NeuroGPS performs independent optimizations on different extracted regions, so it can be easily implemented on massive parallel computing for more enhanced speed.

Although we built this NeuroGPS using fluorescent brain image stacks, it can also be applicable to other kinds of images, for example, Nissl staining neuronal images (576 × 1623 × 20 volume pixels). NeuroGPS well located these neurons with the false positive rate of 6% and true positive rate of 93% compared with manual detected positions. Interestingly, the signal intensity of neuronal soma in this example is not uniform. In this case, NeuroGPS is still effective. These results may indicate that NeuroGPS can be applied in a variety of data sets.

It should be noted that our NeuroGPS only focus on the localization of neurons, and cannot be implemented on segmentation of neurons at present. The main reason is that the complicated morphology and the dense distribution of neurons make high-accuracy segmentation of neurons become an acknowledged difficulty⁴,³⁷,³⁸, beyond our current concerns. Nevertheless, NeuroGPS provide a tool to automatically and accurately locate neurons, which is helpful for neuronal dendritic tracing. Some newly developed neuron tracing methods⁷,⁸,⁹ experience difficulties in rejecting the neuronal soma interference. Future work is expected to combine NeuroGPS with automatic segmentation method and facilitating automatic neuronal circuits tracing.

Methods

The algorithm

The algorithm for the optimization problem (4) is described as follows:

Step 1. Set initial weights: w_i = 1, i = 1, 2, … ,k

Step 2. Solving the optimization problem

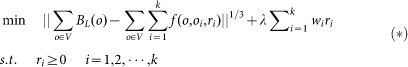2a. Set the initial value (o₁^t, r₁^t), (o₂^t, r₂^t), … , (o_k^t, r_k^t), t = 0

2b. Use the gradient projection algorithm³⁵ to obtain (r₁^{t + 1}, r₂^{t + 1}, … , r_k^{t + 1} )

2c. Use the averaging method to obtain (o₁^{t + 1}, o₂^{t + 1}, … , o_k^{t + 1} )

For each pair of parameter (o_i^t, r_i^{t + 1}), compute o_i^{t + 1}

Where I_i(o^φ) (φ = 1,2,…,m_i) is the original signal from the inner region of a ball with center position o_i^t and radius r_i^{t + 1}.

o_i^{t + 1}→o_i^t, and the computing of o_i^t is carried out again.

2d. Terminate on convergence and go to step 3, otherwise, t + 1→t, and repeat Step 2b–2c.

Step 3. Update weights:

Step 4. Repeat Step 2–3 until all parameters converge.

Brain tissue preparation

All experiments were performed in accordance with the guidelines of the Experimental Animal Ethics Committee at Huazhong University of Science and Technology. A total of 10 Thy-1-eGFP-H or Thy1-YFP-M Transgenic fluorescence mice (2–10 weeks old) were anaesthetized, and intracardially perfused. The whole brain was brought out, fixed and embedded in GMA media, by following a similar protocol used in Li et al.¹³ and Gong et al.¹⁵. A detailed description can be found there.

Imaging system

The whole brain was sliced and imaged using a fluorescence micro-optical sectioning tomography system. The image reconstruction used the frame work presented in Li et al.¹³ and Gong et al.¹⁵. Basically, image tiles are mosaicked together to form a whole section, and in each section, image pre- processing procedures were applied to remove the inhomogeneous illumination pattern, and redundant portions.

The entire image processing of NeuroGPS

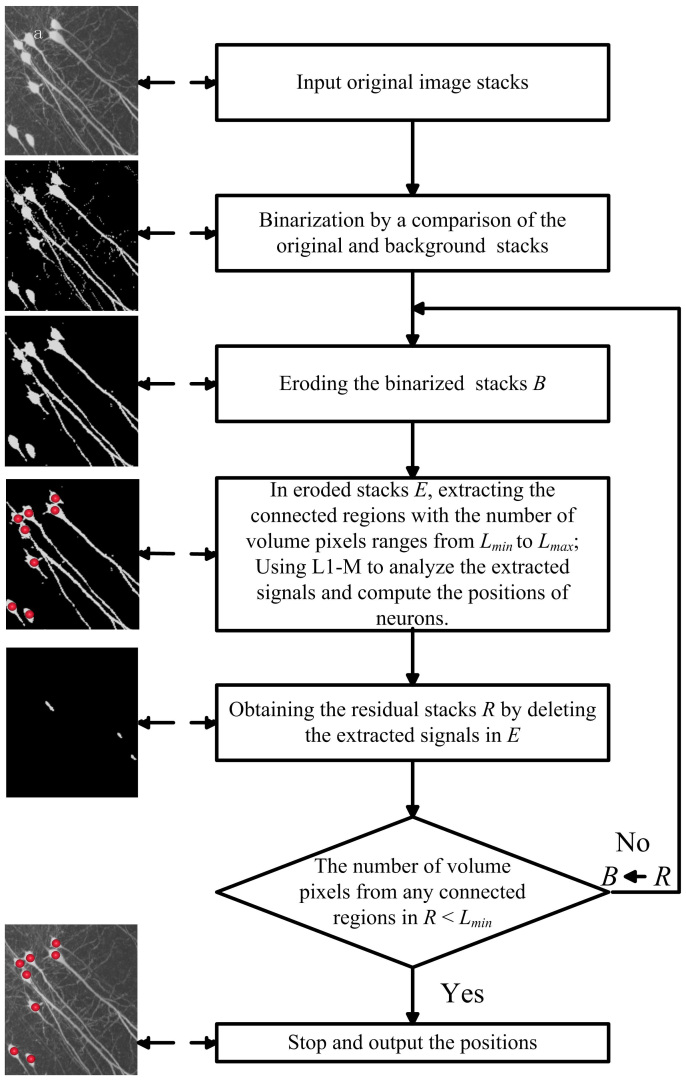
The entire image analysis procedures of NeuroGPS includes sub-region extraction, seeds selection, localization of neurons using L1 minimization and detected positions merging, which were illustrated in the flowchart of Fig. 5. Its detailed description is as follows.

Figure 5. Scheme for the image stacks analysis routine of NeuroGPS.

Sub-region extraction

Due to a sparse distribution of neurons in the image stacks, extracting sub-regions and analyzing the extracted signals can significantly increase the computational efficiency, compared with analyzing the entire image stacks. Before sub-regions extraction, the original image stacks needed to be binarized. The binarized image stacks B are calculated by

Here I(o) and C(o) represent the gray-level value of volume pixel coordinate o in the original images and background images respectively. The image stacks I*, calculated as I*(o) = min(I(o), thre), is convoluted 20 times with the averaging template (9 × 9 × 1 pixels³) and we can get the background images. Here thre is a roughly estimated value used to distinguish foreground from background.

Dense distribution and complicated morphology of neurons usually lead to the large connected regions in the binarized image stacks, which requires huge amount of computation resources to analyze these regions. To reduce the computational time, the large connected region was divided into several parts using the erosion operation.

Step1. Eroding the binarized image stacks B. If the sum of the value of the volume pixel and its 26-connected volume pixel is less than the erosion threshold T, then the value of this volume pixel is set to be 0, otherwise, it remains unchanged.

Step2. In eroded B, the connected region with volume pixels ranged in number from 100 to 20000 extracted and analyzed in the latter subsections. Then, the value of volume pixels in the extracted region is set to be 0.

Step3. Update B from Step 1 & 2, and repeat Step 1 & 2 until the number of volume pixels of any connected region in B is less than 100.

Note that, the erosion threshold T is set to be 9 in the first erosion operation and continuously increase with a step of 0.027 for subsequent erosions; the parameter, i.e. the valid number of volume pixels in the extracted region, can be determined by the smallest size of the neuron, the size of volume pixels and the largest pre-defined number of neurons in the extracted region, and automatically estimated by NeuroGPS.

Seeds selection

For simplification during subsequent processing, the binarized and original signals with respect to the extracted sub-region were completely embedded into a cuboid region, as remarked by B_L and I_L respectively. B_L and I_L are convoluted with a template (7 × 7 × 5 pixels³) in which the value of volume pixel is set to be 1, and the corresponding filtered signal B⁺ and I⁺ are generated. We regarded the position o satisfying that B⁺(o) is beyond 70 and I⁺(o) is local peak value as a candidate seed. The uniform spatial distribution and the moderate number of the candidate seeds may be of benefit to computational efficiency. Therefore, we deleted some redundant seeds using the following procedure. Selecting the seed o₁ with the highest value of I⁺ (o) from the candidate seeds and deleting the candidate seed o satisfying the condition that the Euclidean distance between position o and position o₁ is less than 4.8 μm. Repeating this procedure until the candidate seeds set is null or the number of the extracted seeds is more than 10.

Localization of neurons using L1 minimization

For the given binarized signal B_Land the extracted seeds, by introducing L1 minimization, we design the optimization problem (4). Its optimal solutions can be obtained by using the algorithm described in Methods. According to the optimal solutions, the valid positions were identified.

The valid position merging

In reality, it is unavoidable that using two sphere functions to approach some special neuronal somas is superior to using one sphere function. Based on this consideration, we take the valid position merging as a part of our method. If the distance between two valid positions is less than 70% of the sum of radius of these two positions, we merge these two positions to one position, otherwise, keep it unchanged. At last, the merging or unmerging positions are regarded as the recognized neuronal positions.

Parameters set

Here, we must point out that all the parameters involved in entire image analysis are only determined by two predefined parameters, the size of volume pixels, and the minimum radius of neuronal soma. With these two parameters, the soma locations can be automatically estimated by our NeuroGPS. In our experimental data sets, without specification, the size of volume pixels is 1.2 × 1.2 × 2.4 μm³ and an estimated value of the minimum radius is 3 μm for neurons without complex morphology and 3.6 μm for those with complex morphology.

The indicators for evaluation of the localization algorithm

The localization performance was measured using the false-positive rate, the true positive rate and the localization precision. The false-positive rate is defined as the ratio of false-positive positions to recognized positions found by the algorithm. The true positive rate is defined as the ratio of real positive positions from recognized positions to manual positions (true positions). A recognized position is defined as a true positive position providing that the distance between the recognized and true positions is less than 4.8 μm, and false-positive position otherwise.

Author Contributions

S.Z. and H.G. conceived the project. S.Z. and T.Q. design the model, and wrote the manuscript. T.Z., S.Z. and Q.L. design the imaging system, H.G., Z.Y. and T.Z. performed sample preparation, data acquisition and image experiments, T.Q. and H.Z. developed the algorithm and software, S.L., J.L., W.D. and H.G. performed the image analysis and processing.