Variability in bimanual wheelchair propulsion: consistency of two instrumented wheels during handrim wheelchair propulsion on a motor driven treadmill

Abstract

Background

Handrim wheelchair propulsion is a complex bimanual motor task. The bimanually applied forces on the rims determine the speed and direction of locomotion. Measurements of forces and torques on the handrim are important to study status and change of propulsion technique (and consequently mechanical strain) due to processes of learning, training or the wheelchair configuration. The purpose of this study was to compare the simultaneous outcomes of two different measurement-wheels attached to the different sides of the wheelchair, to determine measurement consistency within and between these wheels given the expected inter- and intra-limb variability as a consequence of motor control.

Methods

Nine able-bodied subjects received a three-week low-intensity handrim wheelchair practice intervention. They then performed three four-minute trials of wheelchair propulsion in an instrumented hand rim wheelchair on a motor-driven treadmill at a fixed belt speed. The two measurement-wheels on each side of the wheelchair measured forces and torques of one of the two upper limbs, which simultaneously perform the push action over time. The resulting data were compared as direct output using cross-correlation on the torque around the wheel-axle. Calculated push characteristics such as power production and speed were compared using an intra-class correlation.

Results

Measured torque around the wheel axle of the two measurement-wheels had a high average cross-correlation of 0.98 (std=0.01). Unilateral mean power output over a minute was found to have an intra-class correlation of 0.89 between the wheels. Although the difference over the pushes between left and right power output had a high variability, the mean difference between the measurement-wheels was low at 0.03 W (std=1.60). Other push characteristics showed even higher ICC’s (>0.9).

Conclusions

A good agreement between both measurement-wheels was found at the level of the power output. This indicates a high comparability of the measurement-wheels for the different propulsion parameters. Data from both wheels seem suitable to be used together or interchangeably in experiments on motor control and wheelchair propulsion performance. A high variability in forces and timing between the left and right side were found during the execution of this bimanual task, reflecting the human motor control process.

Background

Handrim wheelchair propulsion is the means of ambulation for a large group of people with a disability. However, handrim wheelchair propulsion is straining and (overuse) injuries to the upper extremities, e.g. shoulder pain or carpal tunnel syndrome, among wheelchair-dependent persons are common [1-3]. Therefore, a better understanding of wheelchair skill, physical capacity and the impact of wheelchair mechanics and fitting on performance are important [4-6]. Research over the past 30 years has led to a number of studies on the physiology and biomechanics of wheeled mobility [7,8]. Due to the complexity of instrumentation this research was primarily lab-based. Only more recently ambulant instrumentation for both physiological and biomechanical outcomes became available, which today even evolved into commercially available clinical tools [9,10].

Measurements of forces and torques on the handrim of a wheelchair are important to study change of propulsion technique due to learning, training or the effect of changes to the wheelchair. From a scientific point of view this provides a deeper understanding of the universal principles regarding the motor control of wheelchair propulsion, while from a clinical perspective it can help to better tailor the properties of a wheelchair to a patients needs’ and develop intervention protocols with respect to propulsion technique and strategy [11]. Over time, different studies have used different ways to instrument the wheels to gain insight in the forces and timing involved in wheelchair propulsion, varying from instrumented ergometers to specialized wheels [9,10,12-16]. These measurement systems have been used to describe unilaterally the cyclic nature of handrim propulsion analogous to gait analysis. For example, frequency of pushes, peak forces and torques and the wheel angle covered within a push have been used to describe the motor learning process of novel wheelchair users [17]. Besides propulsion technique these wheels are able to measure the power output of the wheelchair-user combination, making it possible to calculate mechanical efficiency when combined with cardio-respiratory measurements and energy calculations [18].

Most studies on propulsion technique measured this essentially bimanual propulsion task unilaterally and focused on the description of propulsion characteristics in dependence of a variety of different interventions. Yet, due to both internal control processes and external perturbations interlimb variation is expected [19]. Studying unilateral wheelchair propulsive mechanics provide biomechanical information about propulsion technique measures like peak forces and push time. However, wheelchair propulsion is a bimanual task, and studies in the area of bimanual motor control have shown that the limbs are not controlled independently, but are coupled to each other. This implies that principles of interlimb coordination cannot be derived from the study of single-limb movements [20].

Only few studies addressed bimanual upper limb consistency or the variability for that matter of motor performance in this task by using two instrumented wheels simultaneously [16,21,22]. Moreover, the provided data on reliability or validity of these measurement-wheels or related ergometer technology in literature are very scarce [10,23-25], let alone the comparability of different measurement-wheels.

In order to evaluate the consistency of such measurement systems during steady-state wheelchair propulsion on a motor driven treadmill, the current study simultaneously assesses two commercially available instrumented wheelchair wheels: the Smartwheel^a and the Optipush^b (Figure 1). The Smartwheel uses instrumented beams to measure torques and forces, whereas the Optipush uses a commercial force-torque sensor at the center, which attaches to the rim through rigid beams. Both come with a clinical software package that can be used for guidance and evaluation of wheelchair adaptations and training programs in clinical or adapted sports practice. An important question is how these measurement-wheels compare to each other, and whether they consistently measure similar technique phenomena since they are based on different measurement approaches, yet are suggested to measure the same variables in the same range of accuracy. Thus from a clinical as well as a scientific perspective, it is important to know whether these wheels are interchangeable and whether we can compare the studies using these different wheels.

Figure 1.

Smartwheel^a (left) and Optipush^b (right). Both wheels measure three-dimensional forces and torques on the handrim, combined with the angle under which the wheel is rotated. The local coordinate systems are defined as: x- and y-axis, orthogonal to each other in the plane of the handrim, z axis orthogonal to the plane of the handrim and pertruding from the wheel axle. The direction of positive torque is mirrored for the wheels so that they measure positive torque when pushing forward.

One way to compare the measurement-wheels is to fit them to both sides of the same wheelchair, during a steady-state propulsion task on a treadmill. Although both wheels examine the same performance of wheelchair propulsion, the motor control process involves a combined movement of the two upper limbs, which determines speed and direction. When comparing the pushes on both wheels, one faces the problem that human movement is intrinsically variable, both within and between individuals [26]. At present, there is a growing recognition that this variability (e.g. intra- and interlimb variability) is not simply the reflection of noise, but contains features that provide insight about normal learning and pathological processes [27-29]. Consequently for comparison of the wheels it is necessary to isolate the consistency of measurement from the variability inherent to the motor control process. Therefore a time dependent one-on-one comparison between pushes of the left and right arm are not expected to provide a suitable outcome measure for comparing the measurement-wheels against each other. Namely at this relatively small time-scale variability due to motor control and task variability, despite propelling at a constant speed on a motor driven treadmill, is to be expected. Indeed, one study using two Smartwheels specifically looked at the asymmetry of wheelchair propulsion and showed side-to-side differences when matching three pushes left and right [21].

Yet, the set task of straightforward steady-state propulsion on a level treadmill should be intrinsically stable over a larger time-scale and should lead to comparable mean outcome values for the left and right side, resulting in a constant mean power output (product of torque and angular velocity) over time. In the current study it is therefore assumed that systematic differences in unilateral mean power output between both wheels, when propelling at constant speed on a motor driven treadmill, should indicate differences in measurement systems rather then motor variability. For instance van der Woude et al. showed a high correlation (r=0.97) of left- and right-hand sprint power averaged over 30 seconds for 67 wheelchair athletes on a computer controlled wheelchair simulator [30]. Although steering on this ergometer is not critical like on a motor driven treadmill, this high interlimb consistency in power production still exists.

Traditionally power output on a motor-driven treadmill is determined through a separate drag test [31]. In the current study, the drag test, combined with the use of a pulley system is used to impose an additional drag force of known magnitude to the wheelchair-user combination on the treadmill [32]. The outcomes of the measurement wheels are compared with this other form of measuring power output.

Specifically we studied 1) if the two measurement-wheels (Optipush^b, Smartwheel^a) provided comparable time-averaged data for the left and right hand side during steady-state wheelchair propulsion on a motor-driven treadmill in a group of trained able-bodied subjects and 2) if the power output values for the measurement-wheels were comparable to the power output based on a separate drag test.

Answering these questions will enable researchers and practitioners to better interpret results from both measurement-wheels published in previous studies, and use both wheels in the same evaluation setup in the future. Furthermore it gives information on how earlier estimations of power output, using a drag test and a pulley system, compare to the outcomes of the measurement-wheels. Finally this study will help to further our understanding of details of bimanual variability in propulsion technique during steady-state handrim wheelchair propulsion.

Methods

Subjects

After having given written informed consent, 9 able-bodied subjects participated in the study. Criteria for inclusion were male, between 18–65 years, no prior experience in wheelchair propulsion, and absence of any medical contra-indications. To compare with earlier research in our laboratory only male subjects were selected. The study was performed according to the guidelines of the Ethics Committee of the Faculty of Human Movement Sciences, VU University Amsterdam (ECB 2011–46).

Protocol

Prior to our study, subjects practiced wheelchair propulsion in 9 practice trials over 3-weeks. Every trial comprised two 4-min exercise blocks at variable low-intensity levels of external power output. The first and the last trial were used as a pre- and post-test and were both extended with one 4-min exercise block. 2-Min rest was given between any two adjacent exercise blocks. Subjects received no specific instructions other than to stay on the treadmill using the handrims. The data for the current study were taken from the post-test that thus consisted of three four-minute blocks (T1, T2, T3) at 1.11 m/s and 0.18 W/kg. Figure 2 shows how the power was imposed by adding mass to a pulley system after having performed an individual drag test [31,32]. Experiments and practice sessions were all conducted on a level treadmill of 2.4 m length by 1.2 m width (Forcelink^c) in the same experimental wheelchair (Double Performance^d) with 24-inch measurement-wheels.

Figure 2.

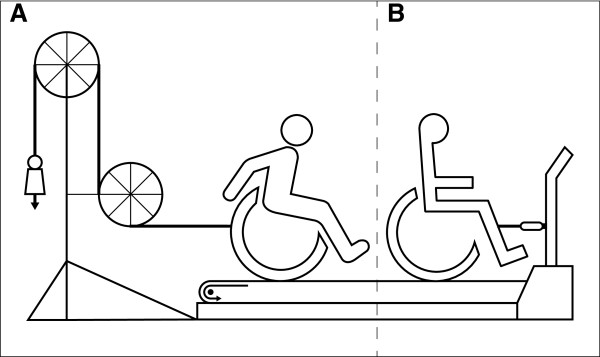
Experimental setup. A) To impose the desired power output a pulley-system attaches to the instrumented wheelchair on the treadmill. B) A dragtest is performed beforehand, to determine power output of the user-wheelchair combination.

Measurement-wheels

The regular rear 24 inch wheels of the standardized wheelchair were replaced with two instrumented wheels; on the left the OptiPush^b (6.0 kg, Max Mobility) and on the right the Smartwheel^a (4.9 kg, 3-Rivers). Both wheels measure 3-dimensional forces and torques applied to the handrim, combined with the angle under which the wheel is rotated. These variables were the only ones used in this experiment for data processing; further data processing and interpretation as done by the respective software packages was not included in the current study. Data were wirelessly transferred to a laptop at 200 Hz (Optipush) and 240 Hz (Smartwheel). Both wheels were synchronised by an electronic pulse at the start of each measurement.

Data analysis

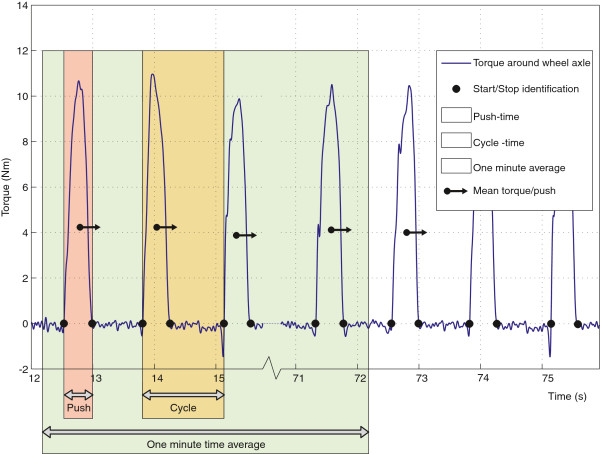
The rawest data from the instrumented wheels available to the researchers were further analysed using custom-written Matlab routines. Data of all three practice blocks including the rests in between were collected in one continuous measurement. To be sure of stable, steady-state propulsion, each last minute from the three 4-min exercise blocks (T1-T3) was used for the analysis. After data collection the Smartwheel output (240 hz) was downsampled to the frequency of the Optipush (200 hz) using a cubic spline. Per subject and exercise block, nine columns of data output were further used in the comparison between the measurement-wheels. These were the x, y and z components of force (N) and torque (Nm) as expressed by the wheels in their local coordinate systems (Figure 1), angle (rad), time (s) and sample number. First, individual pushes were defined as each period of continuous positive torque with a minimum of at least 1 Nm. Over the identified pushes biomechanical characteristics were calculated and later averaged over all pushes within the fourth minute of each practice block per subject. Calculated characteristics are defined in Table 1 and Figure 3.

Table 1.

Propulsion variables

Variable:	Description:	Equation:
Push time (s)	Time from the start of positive torque to the stop of positive torque for an individual push.	tend(i) - tstart(i)
Cycle time (s)	Time from the start of positive torque to the next start of positive torque.	tend(i) − tend(i − 1)
Contact angle (rad)	Angle at the end of a push minus the angle at the start.	Øend(i) − Østart(i)
Fpeak (N)	3d peak force during the push phase	Maxstart : end(Fx2 + Fy2 + Fz2)0.5
Mean Power/push (W)	The mean power during the push phase.	Meanstart : end(Tz • ΔØ)
Work/push (J)	The power integrated over the duration of the push.	∑start : end(Tz • ΔØ)
Frequency (push/min)	Pushes per minute.	Npushes/Δt
Mean power/minute (W)	The mean total (unilateral) power (Tz*Angular velocity) during a complete series of cycles in a minute multiplied by 2.	2 • (∑start(i) : start(n)(Tz • ΔØ))

Abbrevations: t, time(s); _start(i), start of the current push (sample); _end(i), end of the current push (sample); Ø, angle (rad); Fx, Fy and Fz, force components (N); Tz, torque around wheel axle (Nm).

Figure 3.

Definitions of push variables. Push identification, push-time, cycle-time, work per push, and mean torque. Variables were calculated per puss or over all full push cycles within one minute.

Statistics

First, a cross-correlation was performed between the torque signals around the axle of each of the wheels for each subject, over the whole last minute of each practice block. We were specifically interested in correlation and the time lag between the two measurement-wheels. Possible differences in correlation and time lag were evaluated with repeated-measures Anova.

Secondly, the different biomechanical variables averaged over a minute were compared between the measurement-wheels with an intra-class correlation (ICC) over the different trials. A case 3 ICC was used to compare the degree of absolute agreement of the measurements that are the averages of the three independent 4-minute blocks with the two measurement-wheels as fixed judges [33]. A case 1 ICC was also performed over the three 4-minute blocks within each wheel to relate these within wheel outcomes to the between wheel outcomes. ICC values higher than 0.85 are considered good and measures below 0.7 as poor [34]. To further inspect the differences in power output Bland-Altman plots and limits of agreement were used [35].

Finally the total mean power output measured from the wheels was compared to that estimated by the drag test - pulley combination using an Anova for the different mean power outputs of the different measurement systems. Overall statistical significance was set at p<0.05.

Results

The nine male subjects had a mean age of 25.9 years (std = 9.6), a mean body mass of 90.3 kg (std = 12.5) and a mean height of 1.90 m (std = 0.04). All subjects enrolled in the study after 8 sessions (1 first session of 12min and 7sessions of 8min) of low-intensity steady-state wheelchair exercise on the motor driven treadmill.

Cross-correlation

Table 2 shows the cross-correlation between the torque signals around the wheel-axle (Figure 3) of both measurement-wheels for the three different practice blocks for each subject separately as well as the mean over n=9 subjects. For all three blocks we found a high cross correlation (respective means: 0.97, 0.97, 0.98) that did not change significantly (p=0.46). However, the lag between the two signals (see Table 2) for the three blocks did change significantly from a mean of 7.2 samples on T1 to 19.3 on T2 and 31.7 on T3 (p<0.001), indicating a shift in time of 0.06 ms between the signals obtained by both wheels between each practice trial.

Table 2.

Cross correlation and the corresponding phase lag between the two torque signals around the wheel axis, for the different trials

	T1		T2		T3
Subjects	Cross correlation	lag	Cross correlation	lag	Cross correlation	lag
1	0.97	8	0.98	21	0.97	33
2	0.98	4	0.97	17	0.98	31
3	0.98	7	0.98	17	0.98	28
4	0.96	7	0.97	20	0.98	33
5	0.96	11	0.97	23	0.97	32
6	0.98	8	0.97	17	0.98	32
7	0.98	4	0.98	17	0.98	29
8	0.97	8	0.97	20	0.97	32
9	0.96	8	0.96	22	0.97	35
Mean:	0.97	7.2	0.97	19.3	0.98	31.7
Std:	0.01	2.2	0.01	2.4	0.01	2.2

Intra-class correlation

Mean power output between both wheels had a good intra-class correlation of 0.89 (Table 3). Within the different wheels the ICC for mean power output over the three 4-minute blocks was considerably higher, 0.97 and 0.98 for the Optipush and Smartwheel respectively. For the other biomechanical variables ICC’s between the wheels are high (>0.9), indicating good agreement between both wheels. The variables that took more calculation steps (Work/push, mean power output two-sided and speed) had lower ICC’s (Table 3).

Table 3.

Means and standard deviation (between brackets) of propulsion characteristics for the different measurement-wheels (Optipush (Op) en Smartwheel (Sw)) over the three 4-minute blocks (n=9 AB subjects)

Variable:	T1 Op	T1 Sw	T2 Op	T2 Sw	T3 Op	T3 Sw	ICC Betw.	ICC Op Within	ICC Sw Within
Push time (s)	0.37 (0.05)	0.38 (0.05)	0.38 (0.06)	0.37 (0.06)	0.37 (0.06)	0.38 (0.07)	0.97	0.96	0.95
Cycle time (s)	1.24 (0.24)	1.29 (0.27)	1.29 (0.31)	1.24 (0.25)	1.27 (0.27)	1.28 (0.31)	1	0.94	0.95
Contact angle (rad)	1.36 (0.16)	1.37 (0.19)	1.38 (0.2)	1.33 (0.2)	1.34 (0.21)	1.37 (0.24)	0.97	0.96	0.95
Fpeak (N)	66.87 (14.75)	68.92 (16.72)	67.47 (16.34)	63.47 (16.25)	65.25 (19.72)	62.79 (17.3)	0.94	0.92	0.94
Work/push (J)	10.47 (1.76)	10.66 (2.15)	10.72 (2.34)	10.21 (1.88)	10.38 (2.78)	10.57 (2.59)	0.89	0.91	0.94
Mean Power/push (W)	27.73 (5.21)	27.8 (5.35)	27.67 (5.34)	27.82 (5.82)	27.79 (7.01)	27.84 (6.25)	0.9	0.93	0.96
Frequency (push/min)	50.69 (8.87)	49 (9.5)	49.55 (10.16)	50.33 (8.92)	49.27 (9.2)	49.47 (10.18)	1	0.94	0.95
Mean power/ minute (W)	16.4 (2.48)	16.05 (2.63)	16.11 (2.48)	16.28 (2.39)	16.08 (2.61)	16.31 (2.47)	0.89	0.97	0.98

The first ICC is between the wheels. Reported ICC’s in the last 2 columns are calculated between the mean per subject of the three blocks for each of the wheels.

Bland altman plots

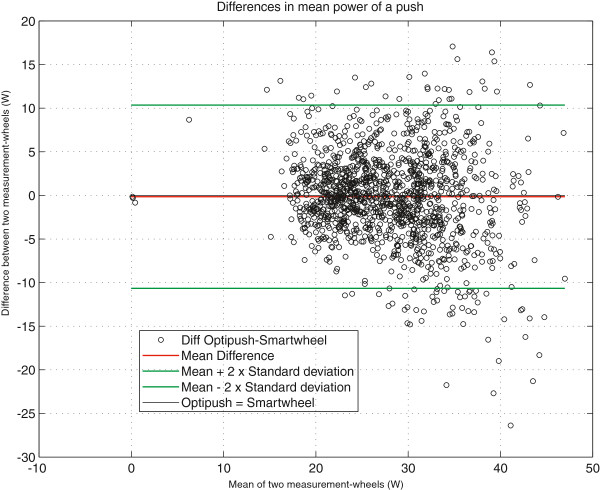
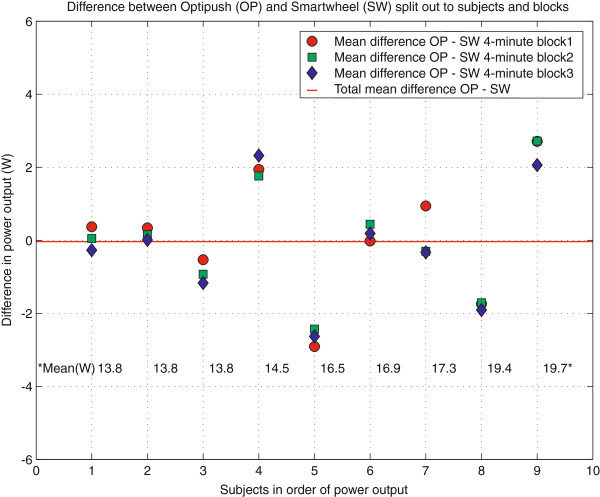
The results on mean power output per push are shown in the Bland Altman plot in Figure 4. In this plot over n=9 subjects, each individual push of the Optipush has been matched to a time-synchronized push of the Smartwheel and the difference of these pushes is plotted against the mean of those two pushes. As expected, differences between left and right occurred, but the mean difference over the group and measurement period was very close to zero (−0.03 W). This low mean difference over the group and time, exemplifies that mean power left and right did not differ significantly. Further, Figure 5 shows the average power output over one minute for each subject (displayed on the x-axis) for each 4-minute block (displayed as different markers). The figure shows that for the individual subjects’ differences in power did occur as a consequence of the human motor control process and assumed detailed elements of task variation. Yet on group level (average difference over the group) no systematic differences were found (Mean difference −0.03 W).

Figure 4.

Bland-Altman plot of all pushes, for all practice blocks of all subjects. Each push of the Optipush^b is matched to the simultaneous one of the Smartwheel^a. For each push the difference of the two is plotted against the mean of the two (black circles). It is clearly seen that they differ a lot on individual pushes, but on average (red line) there is no clear systematic difference between the wheels.

Figure 5.

Adjusted Bland Altman plot. The differences between Optipush^b and Smartwheel^a are split out for each subject (x-axis) for each 4-minute block (symbols). Subjects are ranked according to their mean power output level.

Measurement-wheels and drag test

Mean total power output was compared for both wheels and with an external criterion; the calculations of a drag test in combination with a pulley system shown in Table 4, column 3. The measurement-wheels did not significantly differ from each other (means 16.2 and 16.2 W, p=0.73), but measured a significantly higher power output than estimated from the drag test – pulley combination (mean 14.0 W, p<0.00).

Table 4.

Power output (Pout) as determined by three different methods. There is a significant difference between the measurement-wheels and the drag test

Subject	Handedness	Mean Pout x2 Op(Watt)	Mean Pout x2 Sw(Watt)	Pout dragtest (Watt)
1	Right	18.5	20.3	15.8
2	Left	17.0	16.8	13.2
3	Right	13.9	13.7	13.7
4	Left	15.5	13.5	11.1
5	Right	13.4	14.3	11.6
6	Right	15.2	17.9	16.0
7	Right	17.4	17.3	15.9
8	Right	13.8	13.8	11.9
9	Right	21.0	18.5	16.5
Mean:		16.2	16.2	14.0

Discussion

The aim of the present study was to compare two different measurement-wheels with supposedly the same data output under a real life dynamic, yet standardized submaximal wheeling condition. The results will help interpretation in future research regarding wheelchair propulsion with the use of these wheels, and will help to further investigate the intricate interlimb coupling during this bimanual task. The results showed good agreement between both wheels during steady-state propulsion on a treadmill. Both in time (cross-correlation) and in amplitude (intra-class correlation) a high correlation between the wheels was found (Tables 2 and 3). With regard to the power output both wheels showed comparable and consistent results.

Cross correlation

The directly measured torque signals had a high cross-correlation, but over the different 4-minute blocks the time lag between the two signals became larger, from 0.04 s after 4 minutes to 0.16 s after 12 minutes. While the wheels were synchronized at the start a synchronous stop was not possible for the Optipush. The two internal clocks of both devices probably differed, yet in the current setup it was not possible to say in which way since a third source of known reliability was not available. Had a synchronous stop been possible we could have corrected for this phenomenon. Despite the small magnitude such options would be greatly appreciated in the future, especially if these measures are to be combined with other measurement systems like EMG or position registration.

Intra-class correlation

Most push characteristics had an ICC higher than 0.9. The timing parameters push time, cycle time and frequency approach an ICC of 1.00 and so did the contact angle. These results all added to the conclusion that the provided signals by both wheels were highly comparable in the time and space profiles. The force-related parameters peak force, work per push and power had slightly lower ICC’s, but were still sufficiently high given that they measured different limb actions, which force profiles had to be produced individually and might also depend on hand dominance [36,37]. Since the data were collected within a larger framework of experiments it was decided not to change the sides of the different measurement-wheels, which could have shown differences due to hand dominance. Yet the studies that did look into the interlimb coupling and relationship between dominant and non-dominant hand in wheelchair propulsion did not yet show a clear effect of handedness [16,21]. Future experiments using both wheels could further investigate this possible confounder of the results.

Bland altmann plots

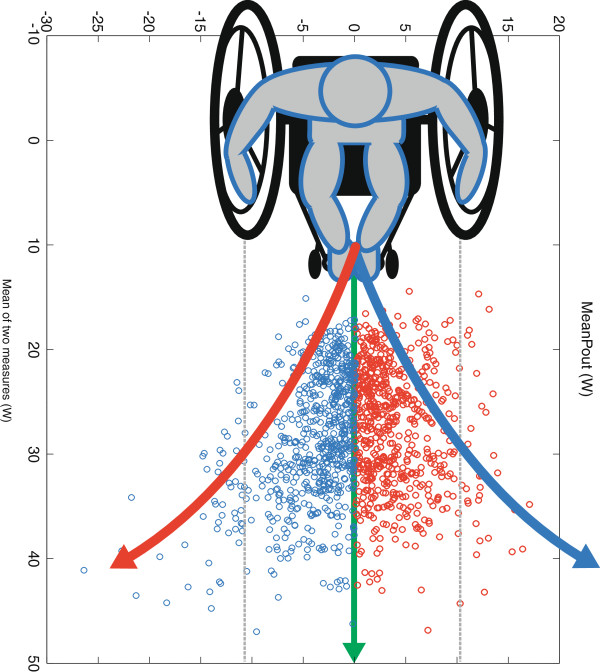
The coupling of propulsion to steering in real life and on the motor driven treadmill seems to make wheelchair propulsion an intrinsic variable task requiring continuous coordination by the human motor system. Considerable left-right differences were found when comparing single pushes, showing variation in power output between the different sides, as was expected from a motor control perspective [19] The Bland Altman plot in Figure 4 is alternatively visualized in Figure 6. This figure illustrates how left-right differences influence direction and how eventually subjects manage to stay on the treadmill. Whether wheelchair propulsion is considered an asymmetrical act depends on the research interest. Clearly pushes left and right are not exactly the same and even differ considerably from time to time. As such, research fields like motor learning would greatly benefit from the use of two wheels to see how this variability changes because of a practice or feedback intervention. On the other hand over a larger time scale in a straightforward steady state submaximal propulsion task both limbs show very comparable propulsion performance allowing for generalization of findings from one side to the other. For instance seat height changes might be studied with just one measurement-wheel [38].

Figure 6.

Top view visualization of steering and propulsion. This adapted version of Figure 4 shows the effect of the differences in mean power output of individual pushes with regard to steering. Blue circles are pushes where the Smartwheel measured more power leading to a change in the direction of the blue arrow. Vice versa for the Optipush the red circles lead to a change in the direction of the red arrow. Result is the green arrow, which was the overall outcome (staying on the treadmill).

Left-right power output

Power output is a complex output measure, using different components of a measurement-wheel, in this case torque multiplied by angular velocity averaged over time. Assuming a balanced, well-maintained and good quality wheelchair system on a stable and level treadmill, average power output at the left and right side should be identical over time during steady-state wheelchair propulsion on a motor driven treadmill. Although on group level the average difference in power output indeed was almost zero, individual subjects clearly showed differences between the mean power output left and right (Figure 5). Accordingly the ICC for mean power output was lower than for some of the other propulsion characteristics and remarkably lower than the ICC within the measurement-wheels for the three different trials. This means that as expected mean power output of the three different trials was more consistent within the wheels than between wheels.

The individual differences in power output left and right might have different causes. First, dependent on the weight distribution of the subject in the chair and the position fluctuations of the subject-wheelchair combination on the treadmill belt, rolling friction in both the rear wheels and the front castor wheels might be different left and right. More weight on the left or right front castor wheel will increase friction on that side, leading to a higher necessary power output on that side. Second, the weight distribution by the subject between both wheels also proportionally influences the power output; leaning over to one side makes the power output on that side necessarily larger. Third, the pulley system was positioned in line with the center of the treadmill, however subjects propel an approximately 0.75 m wide wheelchair on a 1.20 m wide treadmill, which allowed for movement toward either side of the treadmill. Propelling the chair more to the side will give a force component from the pulley system orthogonal to the wheels resulting in more power output on the outer side with respect to the pulley system. Also, the belt tension of the treadmill is somewhat different at the sides versus the center of the belt, which may also lead to slightly higher levels of rolling resistance when coasting left or right on the treadmill instead of in the middle.

Finally, the wheels under study might be of influence on the measured power output. The differences in mass and inertia of both wheels could potentially have influenced left-right power output. The suppliers did unfortunately not make inertial properties available, which would be greatly appreciated in the future development. Secondly the two wheels could measure torque and angle differently resulting in different power output. While the first three arguments are assumed to be distributed equally over all subjects, the argument of the measurement-wheels is a systematic difference. Although the other reasons might have masked a difference due to the measurement-wheels, the absence of a systematic difference in power output or any of the other outcomes in our view supports the conclusion that differences between subjects seem to be caused rather by their own propulsion behavior and geometrical characteristics than by the measurement systems used.

The agreement in power output as found in the present study is in line with earlier studies [30,39]. In different experimental setups these studies also found good agreement on power output for both sides. Important in this respect is also the operationalization of the term power output. As mentioned in the introduction Hurd et al. [21] averaged the power over only three push cycles while the other studies averaged power over more cycles. Therefore their finding of asymmetry in power output, averaged over just three consecutive pushes, seems to be in line with our finding of high variability in the left-right difference in power output (Figure 4).

Measurement-wheels and dragtest

The wheels measured more power than estimated from the dragtest-pulley combination. In addition to the aforementioned consequence of task variation on power output other factors might have contributed to this difference. First the drag test was performed without speed changes, but at a constant speed. Secondly, additional losses when going to the front and back of the treadmill or left-right are not measured by the drag test, but are measured by the wheels. Thirdly, the friction on the front wheels is also dependent on weight distribution. During the drag test subjects were seated in a uniform position (sitting upright with the trunk; hands on the lap), while during propulsion they were free to move in their wheelchair (e.g. with trunk flexion/extension) possibly leading to more rolling friction and thus a higher power. The measurement-wheels seem to measure power in a more accurate way, because they are sensitive to change of torque and angular velocity, still the drag test is the only external comparison currently possible and is relatively cost effective and easy to use

Conclusion

A good agreement between both measurement-wheels was found in this study. Data from both wheels seem consistent and suitable to be used together in experiments on wheelchair propulsion. Both wheels measure a higher mean total power output compared to the estimation of power output using a drag test. If a standardization of an experiment is done using a drag test this should be taken into account. Variability in the execution of wheelchair propulsion seems an essential part in the motor control of this bimanual task. Further research into the interlimb coupling during this bimanual task might use bilateral measurement-wheels to explain and understand the variability between and within the push cycles of both wheels.

Endnotes

^a Three Rivers Holdings, Mesa, AZ, USA.

^b MAX Mobility, LLC, Antioch, TN, USA.

^c Forcelink b.v, Culemborg The Netherlands.

^d Double Performance BV, Gouda, The Netherlands.

Abbreviations

Op: Optipush ^b; Sw: Smartwheel ^a; Pout: Power output; ICC: Intraclass Correlation; Anova: Analysis of Variance

Competing interests

The authors declare that they have no competing interests.

Authors’ contributions

RJKV was involved in the conception of the research project, the design, the execution, the analysis and the interpretation thereof and the writing of the manuscript. CJL and SG were involved in the design, analysis and interpretation of the data analysis and writing of the manuscript. HEJV contributed to the conception of the study, interpretation of the data analysis and revising the manuscript. LHVW participated in the conception and organization of the study, interpretation of the data analysis and revising of the manuscript. All authors read and approved the manuscript.

Acknowledgements

The Open Access publication of this paper was funded by the Netherlands Organization for Scientific Research (NWO).