Modeling the Calcium Sequestration System in Isolated Guinea Pig Cardiac Mitochondria*

Abstract

Under high Ca²⁺ load conditions, Ca²⁺ concentrations in the extra-mitochondrial and mitochondrial compartments do not display reciprocal dynamics. This is due to a paradoxical increase in the mitochondrial Ca²⁺ buffering power as the Ca²⁺ load increases. Here we develop and characterize a mechanism of the mitochondrial Ca²⁺ sequestration system using an experimental data set from isolated guinea pig cardiac mitochondria. The proposed mechanism elucidates this phenomenon and others in a mathematical framework and is integrated into a previously corroborated model of oxidative phosphorylation including the Na⁺/Ca²⁺ cycle. The integrated model reproduces the Ca²⁺ dynamics observed in both compartments of the isolated mitochondria respiring on pyruvate after a bolus of CaCl₂ followed by ruthenium red and a bolus of NaCl. The model reveals why changes in mitochondrial Ca²⁺ concentration of Ca²⁺ loaded mitochondria appear significantly mitigated relative to the corresponding extra-mitochondrial Ca²⁺ concentration changes after Ca²⁺ efflux is initiated. The integrated model was corroborated by simulating the set-point phenomenon. The computational results support the conclusion that the Ca²⁺ sequestration system is composed of at least two classes of Ca²⁺ buffers. The first class represents prototypical Ca²⁺ buffering, and the second class encompasses the complex binding events associated with the formation of amorphous calcium phosphate. With the Ca²⁺ sequestration system in mitochondria more precisely defined, computer simulations can aid in the development of innovative therapeutics aimed at addressing the myriad of complications that arise due to mitochondrial Ca²⁺ overload.

Introduction

Under certain conditions, isolated mitochondria can accumulate up to 3000 nmol Ca²⁺ per mg of mitochondrial protein [1–4]. Such extreme mitochondrial Ca²⁺ loads result in loss of respiratory control and irreversible damage to the mitochondria. At lower, yet very high loads (100’s of nmol/mg), the mitochondria maintain their ability to phosphorylate ADP [5, 6]. Assuming that the matrix water volume of isolated mitochondria is on the order of 1 μl/mg, this amount would exceed 100 mM if all of the Ca²⁺ was free. Clearly, the vast majority of Ca²⁺ taken up by mitochondria must be sequestered in a relatively non-reactive, osmotically inactive state; otherwise, the mitochondria would be unable to remain functional. To this day, the precise mechanism that enables this massive Ca²⁺ uptake and sequestration remains enigmatic. In our companion paper [7], we introduce experimental data that sheds light on this elusive phenomenon.

Mitochondrial Ca²⁺ is buffered by a complex set of binding events and reactions involving protein buffers and amorphous calcium phosphate (ACP) formation [8–12]. Unfortunately, the modeling community has not addressed this manner of Ca²⁺ buffering and has relied on simple Ca²⁺ buffering models that do not account for mitochondrial Ca²⁺ sequestration. This is in part due to the limited available data and uncertainty in the measurement of mitochondrial Ca²⁺ concentration ([Ca²⁺]_m) [13]. As such, most mathematical models that included mitochondrial Ca²⁺ dynamics have relied on a constant Ca²⁺ buffering coefficient [14–16] with the exception of Bazil et al. [17, 18] and Warashina [19]. In Bazil el al., a simple Ca²⁺ buffering system was employed based on the available data from rat heart mitochondria [10, 11]. Warashina developed a similar Ca²⁺ buffering system and included a phenomenological model of calcium phosphate precipitation; however, the mechanism relied on a calcium phosphate solubility constant outside the in vitro measured range. None of the above models possess sufficient mitochondrial Ca²⁺ buffering mechanisms capable of simulating the experimental data presented in the companion paper [7]. Thus, a new model of mitochondrial Ca²⁺ dynamics including Ca²⁺ sequestration is necessary to satisfactorily explain the data.

Herein, we present a mathematical model of mitochondrial Ca²⁺ dynamics that is capable of reproducing the observed ability of isolated cardiac mitochondria from guinea pig to take up, sequester and release Ca²⁺. It is based on an existing model of mitochondrial Ca²⁺ dynamics and includes updated models of the Na⁺/Ca²⁺ cycle transporters and a novel model of the Ca²⁺ sequestration system. The Ca²⁺ sequestration system relies on at least two classes of Ca²⁺ buffers and implicitly includes the formation of ACP. Both the uptake and efflux dynamics of Ca²⁺ are quantitatively captured by the model. The Ca²⁺ sequestration system helps elucidate the mechanism by which isolated mitochondria from guinea pig heart maintain their Ca²⁺ concentration in the low μM levels (1–5 μM) despite the presence of total amounts of Ca²⁺ on the order of 10’s of mM.

Methods

Description of the Experimental Data

The Ca²⁺ uptake, sequestration and release data from the companion paper [7] are used to develop a mathematical model of the guinea pig cardiac mitochondrial Ca²⁺ sequestration system. In this study, isolated mitochondria from guinea pig heart were challenged with a wide range of CaCl₂ boluses followed by ruthenium red and a wide range of NaCl boluses. In brief, the extra-mitochondrial Ca²⁺ concentration ([Ca²⁺]_e) and [Ca²⁺]_m dynamics were monitored in parallel using the fluorescent Ca²⁺-sensitive dye, indo-1, in a suspension of isolated mitochondria (0.5 mg/ml) with the following protocol: First, 0.5 mM pyruvic acid was added to the suspension at 0 s to energize the mitochondria. Second, various amounts of CaCl₂ were added at 120 s to initiate Ca²⁺ uptake. Third, ruthenium red was added at 300 s to stop Ca²⁺ uptake via the Ca²⁺ uniporter (CU). Finally, various amounts of NaCl were added at 360 s to initiate Ca²⁺ efflux via the Na⁺/Ca²⁺ exchanger (NCE). The dynamics were monitored until 840 s. The data used to estimate the model parameters were slightly modified as follows: First, five seconds were added to the time series when a reagent was added to the suspension to account for the delay caused by stopping the measurements, opening the spectrophotometer, adding the reagent, closing the spectrophotometer and resuming the measurements. Second, for some data, the measurement error was less than 10% due to scaling; thus, a minimum error of 10% was used to better reflect the true measurement uncertainty. Finally, the standard deviation is shown instead of the standard error of the mean.

Derivation of the Mitochondrial Calcium Buffering Power

The mitochondrial Ca²⁺ buffering power is a manifestation of the mitochondrial Ca²⁺ sequestration system. Knowledge of how the buffering power changes with the [Ca²⁺]_m facilitates the development of a mathematical model capable of characterizing this system. To derive the mitochondrial Ca²⁺ buffering power, the principle of mass conservation is used. Thus, the total Ca²⁺ in the mitochondria is the sum of the free Ca²⁺ and bound Ca²⁺:

$${[\mathit{TCa}]}_m={[{Ca}^{2+}]}_m+{[\mathit{BCa}]}_m.$$ (1)

Differentiating Eq. 1 with respect to time,

$$\frac{d{[\mathit{TCa}]}_m}{dt}=\left(1+\frac{\partial {[\mathit{BCa}]}_m}{\partial {[{Ca}^{2+}]}_m}\right)\frac{d{[{Ca}^{2+}]}_m}{dt}.$$ (2)

Rearranging Eq. 2,

$$\frac{d{[{Ca}^{2+}]}_m}{dt}=\frac{1}{{\beta }_{Ca,m}}\frac{d{[\mathit{TCa}]}_m}{dt}$$ (3)

with

$${\beta }_{Ca,m}=1+\frac{\partial {[\mathit{BCa}]}_m}{\partial {[{Ca}^{2+}]}_m}.$$ (4)

We define β_Ca,m as the mitochondrial Ca²⁺ buffering power. For highly buffered conditions, β_Ca,m is ≫ 1; therefore, large changes in total mitochondrial Ca²⁺ concentration ([TCa]_m) only lead to small changes in [Ca²⁺]_m. Although the functional relationship between bound mitochondrial Ca²⁺ concentration ([BCa]_m) and [Ca²⁺]_m is unknown, solving Eq. 3 for β_Ca,m reveals how the mitochondrial Ca²⁺ buffering power is related to the ratio of the rate of change of [TCa]_m and [Ca²⁺]_m,

$${\beta }_{Ca,m}=\frac{d{[\mathit{TCa}]}_m}{dt}/\frac{d{[{Ca}^{2+}]}_m}{dt}.$$ (5)

We can approximate the rate of change of [Ca²⁺]_m directly from the dynamical data. But to estimate β_Ca,m, we need an additional method to compute the rate of change of the total Ca²⁺ transport into/out of the mitochondria.

Derivation of the Total Calcium Transport Into/Out of the Mitochondria

The total Ca²⁺ transport into/out of the mitochondria is obtained from the [Ca²⁺]_e time courses. In the experiments of the companion paper [7], the extra-mitochondrial Ca²⁺ is buffered with 40 μM EGTA. Unlike the mitochondrial Ca²⁺ buffering, the Ca²⁺ buffering in the extra-mitochondrial space can be accurately approximated using known mechanisms. Assuming that all other Ca²⁺ chelators that are present in the isolated mitochondrial suspension are outcompeted by EGTA, the extra-mitochondrial Ca²⁺ buffering power is computed as:

$${\beta }_{Ca,e}=1+\frac{\partial {[\mathit{CaEGTA}]}_e}{\partial {[{Ca}^{2+}]}_e}=1+\frac{{[\mathit{EGTA}]}_e\left(1+\frac{{[H^{+}]}_e}{K_{H1}}+\frac{{[H^{+}]}_e^2}{K_{H1}{K}_{H2}}\right)}{K_{Ca}{\left(1+\frac{{[H^{+}]}_e}{K_{H1}}+\frac{{[H^{+}]}_e^2}{K_{H1}{K}_{H2}}+\frac{{[{Ca}^{2+}]}_e}{K_{Ca}}\right)}^2},$$ (6)

where K_Ca is the CaEGTA dissociation constant, K_H1 is the HEGTA dissociation constant and K_H2 is the H₂EGTA dissociation constant. Equation 6 assumes that H⁺ and Ca²⁺ bind to EGTA much more significantly than other ions such as Na⁺, K⁺ or Mg²⁺. Table S2.1.2 in Supplement 2 contains the dissociation constants used to estimate the extra-mitochondrial Ca²⁺ buffering power. As in the case of mitochondrial Ca²⁺, the rate of change of total Ca²⁺ in the extra-mitochondrial compartment is related to the rate of change of free Ca²⁺ by:

$$\frac{d{[\mathit{TCa}]}_e}{dt}={\beta }_{Ca,e}\frac{d{[{Ca}^{2+}]}_e}{dt},$$ (7)

where β_Ca,e is given by Eq. 6.

According to mass conservation, the rate of change of [TCa]_m is related to the total extra-mitochondrial Ca²⁺ concentration ([TCa]_e) by

$$\frac{d{[\mathit{TCa}]}_m}{dt}=-V_r\frac{d{[\mathit{TCa}]}_e}{dt},$$ (8)

where V_r is the volume ratio of the extra-mitochondrial space and mitochondrial matrix. Given an average matrix water volume of 1 μl/mg, a mitochondrial load of 0.5 mg/ml and a suspension volume of 1 ml, the volume ratio is equal to 2000.

Computing the Mitochondrial Calcium Buffering Power

Combining Eqs. 5–8, the mitochondrial Ca²⁺ buffering power is related to the rate of change of [Ca²⁺]_e and [Ca²⁺]_m by

$${\beta }_{Ca,m}=-{\beta }_{Ca,e}{V}_r\frac{d{[{Ca}^{2+}]}_e}{dt}/\frac{d{[{Ca}^{2+}]}_m}{dt}.$$ (9)

As with the rate of change of [Ca²⁺]_m, we can approximate the rate of change of [Ca²⁺]_e from the dynamical data. Now that we have a method to compute the mitochondrial Ca²⁺ buffering power, we need to estimate these rates from the Ca²⁺ dynamics.

Estimation of the Rate of Change of the Extra-Mitochondrial and Mitochondrial Calcium Concentrations

The rates of change of [Ca²⁺]_e and [Ca²⁺]_m are estimated using smooth trend curves. At each phase specified in Fig. S1 in Supplement 1, a multi-exponential function was fit to the data,

$$y(t)=p_1+p_2{e}^{(t-p_3)/p_4}+p_5{e}^{(t-p_6)/p_7},$$ (10)

where y(t) was either [Ca²⁺]_e or [Ca²⁺]_m evaluated at some time, t. The seven parameters are offset values, pre-exponential constants, time lags and time constants. Biologically meaningful interpretations of the parameter values were not attempted. Two exponentials are sufficient to fully capture the dynamics of [Ca²⁺]_e and [Ca²⁺]_m regardless of concavity or convexity. These rates are estimated at any given time by evaluating the analytical derivative of Eq. 10,

$$\frac{dy}{dt}(t)=\frac{p_2}{p_4}{e}^{(t-p_3)/p_4}+\frac{p_5}{p_7}{e}^{(t-p_6)/p_7}.$$ (11)

Uncertainty Propagation

The uncertainty in the estimated mitochondrial Ca²⁺ buffering power is computed using the standard engineering approach (for details, see [20]). Only the first order effects are considered, and non-identifiable parameters are removed so that the Fisher Information Matrix is invertible. In brief, for a given arbitrary function, f, that is dependent on some set of parameters, p, the uncertainty associated with the measured data is propagated into f, up to first order, using

$${\sigma }_f^2=\frac{\partial f}{\partial p}\mid \mathrm{\sum }\mid \frac{\partial f^T}{\partial p},$$ (12)

where σ_f is the propagated uncertainty at some evaluation of f, $\frac{\partial f}{\partial p}$ is the gradient of f with respect to p and Σ is the parameter covariance matrix. The covariance matrix is approximated using the Fisher Information Matrix. The uncertainty in the mitochondrial Ca²⁺ buffering power is estimated by setting f equal to Eq. 9 and solving Eq. 12.

Mathematical Model of Mitochondrial Calcium Dynamics

Our previous corroborated model of mitochondrial Ca²⁺ dynamics [15] is updated to include binding of protons (H⁺) and metal ions (Na⁺, K⁺, Mg²⁺ and Ca²⁺) to metabolites (ATP, ADP and Pi). In addition, extra-mitochondrial and mitochondrial cation buffering, including the formation of ACP, and models of the CU [21], rapid mode of Ca²⁺ uptake (RaM) [22], NCE [23] and the Ca²⁺/H⁺ exchanger (CHE) are incorporated. The CHE model is based on simple mass action kinetics and is required to simulate Na⁺-independent Ca²⁺ efflux. The pH regulatory parameter of the NCE is adjusted to better reproduce the data in Fig. 4 of Paucek and Jaburek [24] as shown in Supplement 2. Moreover, it was found that the best fits to the data presented in our companion paper [7] were obtained when this parameter was adjusted as discussed in Supplement 3. The cation ordinary differential equations (ODEs) are extended to include Na⁺ and Ca²⁺ dynamics using the method outlined in Vinnakota et al. [25]. The model details, including ODEs, rate equations and parameter values are located in the Supplemental Materials. The schematic representation of the model is depicted in Fig. 1.

Fig. 1. The schematic of the integrated mathematical model of mitochondrial Ca²⁺ dynamics.

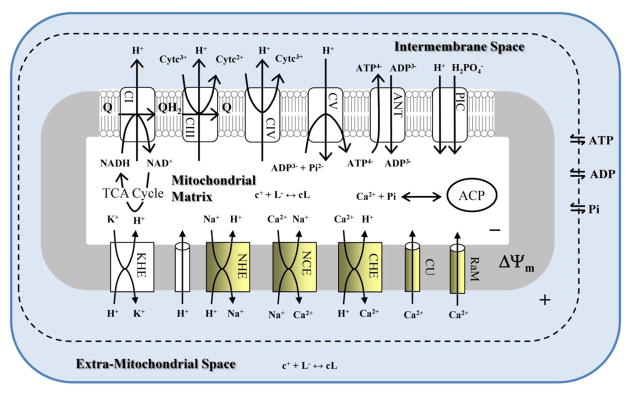
Our previously corroborated model of the mitochondrial Ca²⁺ dynamics is updated with our new transporter models for the CU, RaM, NCE, a new model of CHE and a model of the Ca²⁺ sequestration system. The model implicitly includes the binding of Ca²⁺ to mobile and immobile buffers and the formation of ACP. The expression “c⁺ + L⁻ ↔ cL” represents cation-anion complexation. In the mitochondrial matrix, the anions include ATP, ADP and Pi. In the extra-mitochondrial space, the anions are ATP, ADP, Pi and EGTA.

The model was developed, parameterized and simulated on a Dell Precision T3500 workstation with a 3.2 GHz Intel® Xeon quadcore processor and 16 GB RAM using MATLAB® version 2010b. A custom, parallelized simulated annealing algorithm was used to globally search the parameter space before identifying a local minimum with a gradient-based local optimizer.

Results and Discussion

The mitochondrial Ca²⁺ sequestration system is described in mathematical terms by the mitochondrial Ca²⁺ buffering power. A minimal model for the mitochondrial Ca²⁺ buffering power was developed before fitting the entire dynamical data set with the integrated model of mitochondrial Ca²⁺ dynamics. This approach avoids unnecessary exploration of the model structural and parameter space. Therefore, the analysis of the data set is discussed first.

Data Analysis of the Mitochondrial Calcium Sequestration System

The mitochondrial Ca²⁺ uptake, sequestration and extrusion data in [7] show several intriguing phenomena. Specifically, isolated mitochondria from guinea pig heart possess a remarkable ability to take up a large bolus of Ca²⁺ while maintaining a fixed [Ca²⁺]_m. The results demonstrate that for increasing amounts of CaCl₂ boluses added to the suspended mitochondria, [Ca²⁺]_m quickly reach a maximum concentration despite continual uptake. Moreover, after a large NaCl bolus at high mitochondrial Ca²⁺ loads, [Ca²⁺]_m is only marginally decreased despite a massive amount of Ca²⁺ removed from the mitochondria via the NCE. This introduces a paradox in which guinea pig cardiac mitochondria buffer Ca²⁺ stronger when the total Ca²⁺ load is high.

In order to estimate the mitochondrial Ca²⁺ buffering power as a function of [Ca²⁺]_m, the ratio of the rate of change of [TCa]_m and [Ca²⁺]_m is necessary. These rates were estimated from the trend curves as described in the Methods and shown in Fig. S1. The data corresponding to the Ca²⁺ efflux phase were used to estimate the mitochondrial Ca²⁺ buffering power as shown in Fig. 2a. A near identical buffering profile is obtained by repeating the analysis for the Ca²⁺ uptake phase, but the propagated uncertainties associated with the buffering function are larger due to the larger uncertainties in both the [Ca²⁺]_e and [Ca²⁺]_m measurements.

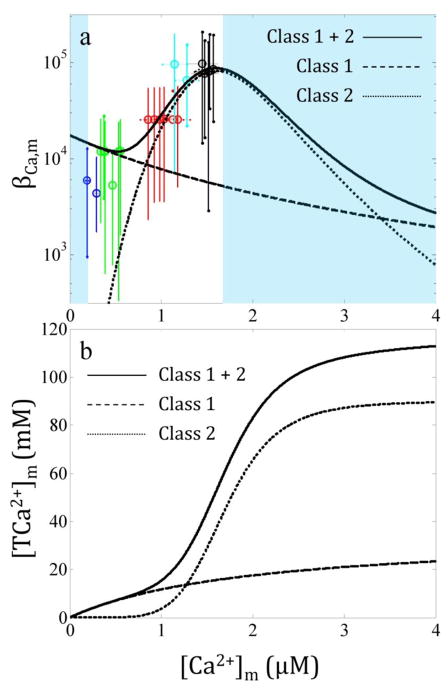
Fig. 2. The mitochondrial Ca²⁺ buffering power increases as the Ca²⁺ load increases for isolated cardiac mitochondria from guinea pig.

The data from our companion paper [7] were used to compute the Ca²⁺ buffering power as described in the Methods section (a). The colors correspond to the following CaCl₂ boluses: blue, 0 μM; green, 10 μM; red, 20 μM; cyan, 30 μM; and black 40 μM. The solid line is the minimal model defined in Eq. 13. The dashed and dotted lines correspond to the contribution of the class 1 and 2 buffers to the Ca²⁺ buffering power, respectively. The shaded regions indicate where the mitochondrial Ca²⁺ buffering power cannot be estimated from the data. The total sequestered Ca²⁺ predicted by the Ca²⁺ sequestration system demonstrates that after 120 mM total Ca²⁺, the buffering system is near maximum capacity (b). At high Ca²⁺ loads, the vast majority of Ca²⁺ buffering is from the class 2 buffers.

Modeling the Mitochondrial Calcium Sequestration System

Once the general shape of the mitochondrial Ca²⁺ buffering power is identified, a minimal model may be derived:

$${\beta }_{Ca,m}=\left(1+\sum _i\frac{n_i^2{[{Ca}^{2+}]}_m^{n_i-1}{[B_{Ca,i}]}_m}{K_{Ca,i}^{n_i}1+{[{Ca}^{2+}]}_m^{n_i}/{K_{Ca,i}^{n_i}}^2}\right),$$ (13)

where i is the index indicating individual components of the buffering model, [B_Ca,i]_m is the total concentration of buffer component i, K_Ca,i is the Ca²⁺ dissociation constant for component i and n_i is the number of binding sites per component i. For n_i > 1, it is assumed that Ca²⁺ binding to the buffering components is fully cooperative. The minimal model that best fit the data shown in Fig. 2a was one with two classes of buffers. The optimal parameter set is presented in Table 1. The class 1 buffers possess a single Ca²⁺ binding site, and the class 2 buffers contain multiple binding sites. The classes are designated in no particular order. There are at least two essential features the model must possess in order to facilitate data-consistent simulations. i) For [Ca²⁺]_m less than 1 μM, the buffering power is less than 10⁴. ii) For [Ca²⁺]_m greater than 1 μM, the buffering power must increase 10 fold and reaches 10⁵ by the time the [Ca²⁺]_m is 1.5 μM.

Table 1.

Calcium Sequestration System Model Parameters

Name	Definition	Value	Units
Class 1 buffer
[BCa,1]x	Total binding sites	35.0	mM
KCa,1	Ca2+ binding constant	2.0	μM
n1	Number of binding sites	1	-
Class 2 buffer
[BCa,2]x	Total binding sites	15.0	mM
KCa,2	Ca2+ binding constant	1.7	μM
n2	Number of binding sites	6	-

The minimal model for the mitochondrial Ca²⁺ buffering power detailed above is plotted with the data along with the contribution of the individual components identified by the dashed and dotted lines in Fig. 2a. The model describes the data very well. For cases where [Ca²⁺]_m lies below 200 nM and above 1.6 μM, the mitochondrial Ca²⁺ buffering power cannot be defined using the experimental data from our companion paper [7]. Assuming that this minimal model was sufficient to characterize the guinea pig cardiac mitochondrial Ca²⁺ sequestration system, the system will begin to fail when [Ca²⁺]_m exceeds 4 μM. This corresponds to the sequestration of approximately 120 mM of total mitochondrial Ca²⁺ (equivalent to 120 nmol/mg Ca²⁺) as shown in Fig. 2b. This lower estimate is in agreement with a previous study showing a limit near 100 mM (100 nmol/mg) in the absence of adenine nucleotides (AdNs), Mg²⁺ or cyclosporin A [26]. Under the experimental conditions modeled herein, the mitochondria sequestering Ca²⁺ would undergo non-specific permeabilization soon after the uptake of 120 mM Ca²⁺ since [Ca²⁺]_m would dramatically increase due to the decrease in the Ca²⁺ buffering power. This conceptual model is explicitly demonstrated in Fig. 8 of Chalmers and Nicholls [8] with rat brain mitochondria, but the permeabilization occurs at higher Ca²⁺ loads due to the presence of ADP in the incubation medium. The Ca²⁺ buffering capacity provides a great deal of information on the intrinsic limits of the mitochondrial Ca²⁺ sequestration system. Thus, future work is planned to identify these limits in mitochondria from guinea pig heart.

Integrated Mitochondrial Calcium Dynamics Model

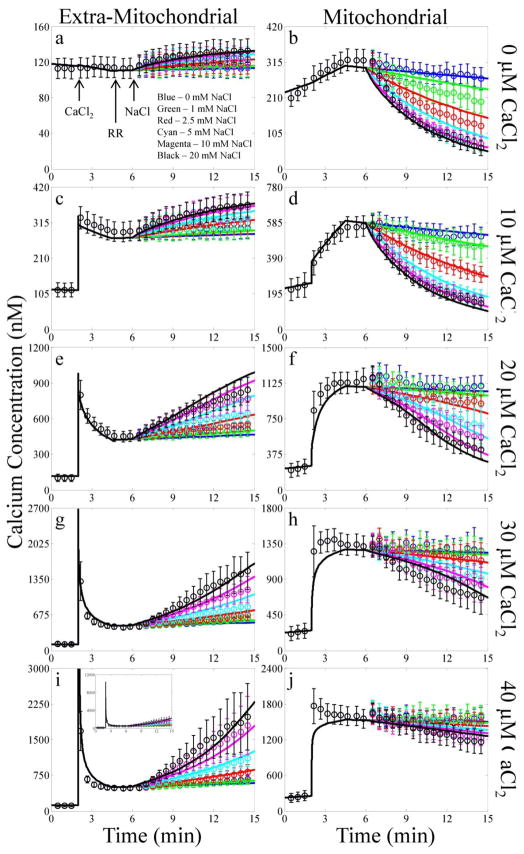
With the minimal model of the mitochondrial Ca²⁺ sequestration system identified, the [Ca²⁺]_e and [Ca²⁺]_m dynamics observed in the companion paper [7] can be simulated with an integrated model of mitochondrial Ca²⁺ dynamics. The integrated model parameter values that were updated from their published values are listed in Table 2. The integrated model equations are presented in Supplement 2. The basic simulated environment consisted of 0.5 mM pyruvate, 130 mM KCl, 5 mM K₂HPO₄, 0.1% BSA, 40 μM EGTA and 20 mM MOPS at pH 7.15 and a temperature of 25°C. The model reproduces the Ca²⁺ uptake, sequestration and release dynamics of isolated mitochondria from guinea pig heart as shown in Fig. 3. The model explains why the rise in [Ca²⁺]_m is blunted despite continual Ca²⁺ uptake. Also, when the mitochondrial Ca²⁺ load is high (30–40 μM boluses), the model shows that the observed massive Na⁺-dependent Ca²⁺ efflux does not necessarily cause an equally reciprocal change in [Ca²⁺]_m. This is because at these high Ca²⁺ loads, the [Ca²⁺]_m is strongly buffered by the class 2 buffers.

Table 2.

Updated Integrated Model Parameter Values^a

Name	Definition	Value
XCU	CU activity	1.5 nmol/min/mg
$K_{Ca}^{CU}$	Ca2+ binding constant for CU	3.69 μM
XRaM	RaM activity	0.25 nmol/min/mg
XNCE	NCE activity	0.5056 nmol/min/mg
$K_{Na}^{\mathit{NCE}}$	Na+ binding constant for NCE	2 mM
$K_{Ca}^{\mathit{NCE}}$	Ca2+ binding constant for NCE	110 nM
$n_H^{\mathit{NCE}}$	NCE H+ dependence	3
XCHE	CHE activity	4.0×1019 nmol/min/mg/M3
[BH]tot	Total mitochondrial H+ binding sites	1.8 M
$K_H^{B_H}$	H+ binding constant for the H+ binding sites	10−7.5 M

^aAll other model parameters were not changed from their original published values.

Fig. 3. Experimental data compared with model simulation results of the CaCl₂ and NaCl bolus combinations.

The simulation results of each bolus CaCl₂ addition are plotted by row with the extra-mitochondrial (left) and mitochondrial (right) Ca²⁺ concentrations plotted by column. The color of each line corresponds to the following NaCl boluses: blue, 0 mM; green 1 mM; red, 2.5 mM; cyan, 5 mM; magenta, 10 mM; and black, 20 mM. The times that reagents were added to the mitochondria are indicated by the arrows. Due to Ca²⁺ contamination present in the mitochondrial suspension, the extra-mitochondrial free Ca²⁺ concentration reaches approximately 10 μM for the 40 μM CaCl₂ bolus addition as shown by the inset in panel G. To account for experimental variability in a few cases when simulating the experiments, the mitochondrial load, EGTA concentration and/or CaCl₂ bolus concentration were allowed to vary +/−15%.

The model is qualitatively (and to some extent quantitatively) corroborated by predicting the mitochondrial redox potential (NADH), the membrane potential (ΔΨ), pH and [Na⁺]_m responses to the Ca²⁺ uptake, sequestration and release protocol as shown in Fig. 4. For clarity, the simulation results for selected CaCl₂ and NaCl bolus combinations are shown and detailed in the figure legend. The NADH and ΔΨ simulations both demonstrate a qualitative match to the data in the companion paper [7]. Immediately after the CaCl₂ bolus, both the NADH and ΔΨ transiently dip approximately 10% but recover as the Ca²⁺ is taken up and sequestered by the mitochondria. The simulated mitochondrial pH was in the range of 7.34 and also possessed similar dynamics as reported in [7]. The mitochondrial pH alkalinizes due to charge compensation from the incoming Ca²⁺ ions, but the pH in mitochondria is buffered. Therefore, it only increases approximately 0.05 pH units for a CaCl₂ bolus of 40 μM. Upon the application of the NaCl bolus, the mitochondrial pH initially alkalinizes due to reversal of the Na⁺/H⁺ exchanger (NHE); however, it quickly acidifies when NHE transitions to forward mode once sufficient Na⁺ is taken up by the mitochondria. The corresponding mitochondrial [Na⁺] demonstrates that the model simulates reasonable Na⁺ dynamics and concentrations. Specifically, the [Na⁺]_m/[Na⁺]_e is near equal to [H⁺]_m/[H⁺]_e (not shown) as expected from the high NHE activity [27].

Fig. 4. Corroboration simulation results of additional model state variables.

The simulated mitochondrial ΔΨ (a), NADH fraction (b), mitochondrial pH (c) and [Na⁺]_x (d) are plotted for each CaCl₂ and NaCl bolus combination. The color of each line corresponds to the following CaCl₂ boluses: blue, 0 μM; green 20 μM and black, 40 μM. The style of each line corresponds to the following NaCl boluses: dotted, 0 mM; dashed, 5 mM and solid, 20 mM.

The simulation of the relevant Na⁺/Ca²⁺ cycle transporter fluxes during the Ca²⁺ uptake, sequestration and release protocol are shown in Fig. 5. As with Fig. 4, selected CaCl₂ and NaCl bolus combinations are shown for clarity and detailed in the figure legend. The CU flux reaches 220 nmol/mn/mg for the largest CaCl₂ bolus, but quickly diminishes below 1 nmol/mn/mg as a result of Ca²⁺ uptake. The NCE flux peaks at 4 nmol/mn/mg; however, this is primarily due to limiting [Ca²⁺]_m. By weakening the mitochondrial Ca²⁺ buffering power and thus allowing [Ca²⁺]_m to increase, Nicholls and co-workers showed that the NCE flux could increase > 10 fold [28, 29]. The integrated model supports this conclusion (not shown). In all cases, the CHE flux never exceeds 10% of the total Ca²⁺ efflux. This is corroborated by previous experimental results that estimated the relative contribution of the Na⁺-independent pathway during Ca²⁺ efflux in excitatory tissues [30]. The simulation results for the NHE flux show an initial reversal whereby Na⁺ is imported by both the NCE and NHE due to no Na⁺ present in the mitochondria. After [Na⁺]_m is sufficiently elevated, the NHE begins to extrude Na⁺ imported by the NCE.

Fig. 5. Model predictions of the Na⁺/Ca²⁺ cycle related fluxes.

The simulated fluxes for the CU (a), NCE (b), CHE (c) and NHE (d) are plotted for selected CaCl₂ and NaCl bolus combinations. The color and style of each line correspond to the same scheme of CaCl₂ and NaCl bolus combinations given in the legend of Fig. 4.

Simulating the Set-Point Phenomenon with Isolated Mitochondria

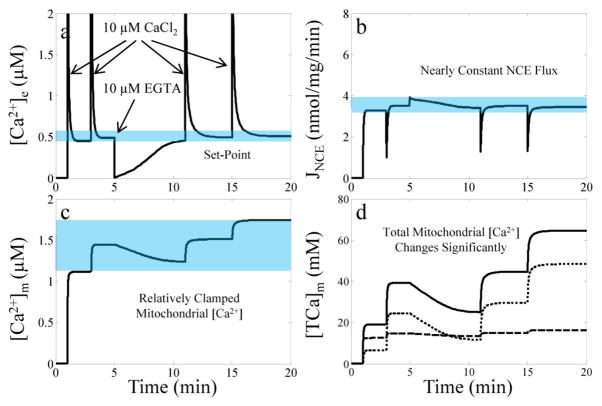
Starting from the late 70’s, Nicholls and colleagues published a series of papers that successfully demonstrated isolated mitochondria’s unique ability to regulate [Ca²⁺]_e at a fixed value [8, 29, 31, 32]. They called this fixed value the set-point and deduced that it was a result of a steady state condition whereby Ca²⁺ influx via the CU is equal to Ca²⁺ efflux via the NCE and/or the CHE. They also found that it was remarkably stable over a wide range of mitochondrial Ca²⁺ loads [8, 32] and dependent on a number of factors known to enhance the Ca²⁺ loading capacity of isolated mitochondria (for example, see [6, 26, 33]). They identified that the primary controller of the set-point was the Ca²⁺-efflux mechanism. When [Ca²⁺]_m is essentially clamped by ACP formation, a component of the Ca²⁺ sequestration system, the rate that mitochondria extrude Ca²⁺ is nearly constant. If Ca²⁺ is added or removed from the extra-mitochondrial space, [Ca²⁺]_e decreases or increases, respectively, until the set-point is reestablished.

As a further corroboration of the integrated model of mitochondrial Ca²⁺ dynamics, the model simulation of the set-point phenomenon is shown in Fig. 6. For the set-point simulations, a series of two 10 μM CaCl₂ boluses, followed by a bolus of 10 μM EGTA and then a series of two more 10 μM CaCl₂ boluses are given to respiring mitochondria. The [Na⁺]_e is set to 10 mM throughout the simulation. The time CaCl₂ or EGTA is added is indicated by the arrows in panel A. The simulation results reveal the origin of the set-point phenomenon: a nearly constant Ca²⁺ extrusion rate via the NCE due to a relatively clamped [Ca²⁺]_m regardless of [TCa²⁺]_m. This is only possible due to the presence of the class 2 buffers buffering the majority of the mitochondrial Ca²⁺ as demonstrated in panel d.

Fig. 6. Simulation results of the set-point phenomenon.

Simulated [Ca²⁺]_e (a), NCE flux (b), [Ca²⁺]_m (c) and [TCa²⁺]_x (d) dynamics are plotted for the simulation of the set-point protocol. The blue regions highlight the origin of the phenomenon – nearly constant NCE flux due to a relatively clamped [Ca²⁺]_m regardless of [TCa²⁺]_x. For the simulations, matrix pH is initialized to 7.15 by increasing the [K⁺]_x to 140 mM to facilitate Ca²⁺ extrusion by the NCE. The mitochondrial load is 0.5 mg/ml. In panel D, the dashed and dotted lines are the contribution to total Ca²⁺ of the class 1 and class 2 buffers, respectively.

The Mitochondrial Calcium Sequestration System

The class 1 buffers of the Ca²⁺ sequestration system are interpreted as being the combination of many different components with various affinities for Ca²⁺. These would include acid phospholipids in the membrane, enzymes, metabolites and other soluble proteins in mitochondria that are not already accounted for by the model. Although the model includes the formation of Ca²⁺ complexes with ATP, ADP and Pi in mitochondria, the Ca²⁺ dissociation constants range from 100 μM to 10 mM (see Table S2.1.2). Thus, they contribute very little to the Ca²⁺ buffering power when [Ca²⁺]_m is below 10 μM.

The class 1 buffers closely resemble the ones found in [10, 11] with a notable exception. The Ca²⁺ sequestration system predicts a similar “activity coefficient” (as defined in [10]) when [Ca²⁺]_m is below 1 μM, and the class 1 buffers have very similar properties to the Ca²⁺ buffering component found in Corkey et al. (see Tables IV and V in [11]). A major difference, however, is observed for [Ca²⁺]_m above 1 μM. The amount of bound Ca²⁺ is very different due to the class 2 buffers. This could be attributed to the species difference (rat versus guinea pig), measurement methodology (null point versus molecular dye) or that the class 2 buffers may be sensitive to the perturbations employed when measuring mitochondrial Ca²⁺. Regardless, this class requires a more careful interpretation.

It is not likely that there exists nearly 15 mM of soluble proteins in mitochondria that are capable of binding multiple Ca²⁺ ions (of the class 2 type found in this study). What is more likely is that the proteins responsible for this class are some sort of nucleation factors that bind to the membrane in a Ca²⁺-dependent manner. These nucleation factors would serve as a scaffold for more Ca²⁺ to bind along with some other counter-ion, putatively Pi. (Note that for the experiments examined herein, Pi was not limiting. Experiments are currently being conducted under limiting Pi conditions to identify Pi’s mechanistic role with these class 2 buffers.) Each nucleation site could then spawn many more new binding sites reducing the total concentration of necessary proteins from 15 mM to 100’s or 10’s of μM, a more reasonable value. The only known proteins to possess such properties are the ones belonging to the annexin family (for reviews, see [34–36]). Annexins are a diverse class of proteins that serve in a variety of roles that bind to acidic phospholipid membranes, particularly cardiolipin [37] and phosphotidylserine [38], in a Ca²⁺-dependent manner. It is interesting to note that their ubiquitous presence in mitochondria [39–42] is yet to be fully explained.

An alternative hypothesis is that the observed mitochondrial Ca²⁺ buffering is simply due to Ca²⁺ directly bound to the membrane. The most abundant acidic phospholipid in mitochondria that is capable of binding Ca²⁺ is cardiolipin [43, 44]. But despite its abundance, there is not enough present to support the amount of Ca²⁺ sequestration needed to explain the data [45]. Moreover, Plager and Nelsestuen showed that the amount of Ca²⁺ that is directly bound to phospholipids is low with nearly all of the Ca²⁺ associated with the annexin-phospholipid complex [46].

Annexin-Mediated ACP versus ACP Precipitation Formation

The necessary concomitant Pi uptake with Ca²⁺ during Ca²⁺ loading of isolated mammalian mitochondria has been known for several decades, but the mechanism behind this sequestration phenomenon has been obscure [4]. Nicholls and colleagues were one of the first to elucidate a feasible mechanism. This phenomenon was attributed to the formation of ACP precipitation [8, 32]. In this mechanism, ACP precipitation is limited by the concentration of the phosphate ion (PO₄³⁻), which in turn, is set by the third power of the mitochondrial pH. As such, ACP precipitation is extremely sensitive to pH and requires alkaline conditions (pH > 7.7) to effectively buffer [Ca²⁺]_m in the low μM range. If this mechanism was correct, then acidic mitochondrial pH would prevent robust Ca²⁺ uptake and sequestration. However, Chinopoulos and co-workers demonstrated the contrary [47]. Also, the mitochondrial pH reported in the companion paper was 7.4, yet the [Ca²⁺]_m was maintained below 2 μM. Moreover, the model analysis herein suggests that ACP formation is better characterized by sequestration versus precipitation. Thus, a new mechanism is required to explain this phenomenon.

Massive Ca²⁺ sequestration involves the formation of dense granules that are nearly always located at or near the cristae within the mitochondrial matrix [4]. These granules possess electron transparent cores surrounded by electron opaque shells which suggests that they consist of an organic moiety surrounded by ACP [4, 48]. Moreover, immunogold electron microscopy has detected annexins located in the mitochondrial matrix on the inner mitochondrial membrane at or near the cristae [39, 49]. Also, it has been recently demonstrated that annexins are necessary for potent ACP nucleation in vitro [50]. Therefore, we postulate that the Ca²⁺ and Pi uptake associated with Ca²⁺ loading of isolated mitochondria, is not solely associated with the formation of ACP precipitates but primarily involves the formation of readily dissociable complexes of Ca²⁺ and Pi mediated by annexins. This process is illustrated in Fig. 7. In this scenario, annexins are recruited to the inner mitochondrial membrane in a Ca²⁺-dependent manner near the cristae (location of Ca²⁺ influx). Once bound to the membrane, the annexins nucleate ACP formation until their capacity is exceeded.

Fig. 7. Cartoon of the mitochondrial Ca²⁺ sequestration system.

The Ca²⁺ sequestration system consists of at least two types of Ca²⁺ buffers. The first type, class 1, binds Ca²⁺ in a 1:1 stoichiometry. The second type, class 2, facilitates the formation of ACP via nucleation and binds Ca²⁺ with a greater stoichiometric ratio than the class 1 buffers.

Modulating the Mitochondrial Calcium Sequestration System

An important question regarding the mitochondrial Ca²⁺ sequestration system in mammals is whether or not the maximum capacity or its affinity for Ca²⁺ can be modulated. It has long been known that Mg²⁺ and AdNs have the ability to enhance the Ca²⁺ retention capacity in isolated mitochondria [4, 26, 33, 51–53]. In fact, AdNs are required to produce large electron dense granules in the mitochondrial matrix [3, 26, 48]. However, the mechanism is currently not well understood. Moreover, it is unclear whether or not this phenomenon is restricted to isolated mitochondria. Surprisingly, it is not. It has recently been demonstrated that this phenomenon also occurs in situ [54]. Despite the evidence, it cannot be conclusively determined how AdNs influence Ca²⁺ uptake. Chelation by CaATP complexation is unlikely (see above). A more plausible scenario is that AdNs increase the mitochondrial Ca²⁺ buffering power via interaction with annexins already present in the mitochondria. It has been shown that ATP increases the Ca²⁺-binding affinity of annexins in an isolated protein setup [55]. In fact, there is an entire class of annexins that shows this AdN-dependent Ca²⁺-binding (for reviews, see [56, 57]). This might explain some of our recent experimental data on the sudden rise in [Ca²⁺]_m during oxidative phosphorylation [58]; however, much more work remains to be done before any conclusion is reached. As such, the integrated model is currently being utilized to design future experiments aimed at teasing out how AdNs affect the mitochondrial Ca²⁺ sequestration system. The answer to this important question has implications reaching far beyond the nature of Ca²⁺ uptake in isolated mitochondria.

Conclusions

Here we introduce a model of the Ca²⁺ sequestration system in mitochondria that implicitly includes Ca²⁺ binding to the inner membrane, metabolites and formation of ACP. The system developed herein is able to facilitate data-consistent simulations when integrated into our model of mitochondrial Ca²⁺ dynamics. The integrated model explains how isolated guinea pig cardiac mitochondria take up, sequester and release a wide range of CaCl₂ boluses followed by ruthenium red and a wide range of NaCl boluses. Future work entails using the model to design experiments in order to dissect the model of the mitochondrial Ca²⁺ sequestration system into components that explicitly describes this system in a biophysically detailed, mechanistic manner. Extending the mitochondrial Ca²⁺ sequestration system to include the known regulatory components and predict the Ca²⁺ loading capacity before the onset of mitochondrial Ca²⁺ dysfunction would prove to be a powerful tool for the development of alternative therapies aimed at preventing this form of dysfunction.