Electric double-layer capacitance between an ionic liquid and few-layer graphene

Abstract

Ionic-liquid gates have a high carrier density due to their atomically thin electric double layer (EDL) and extremely large geometrical capacitance C_g. However, a high carrier density in graphene has not been achieved even with ionic-liquid gates because the EDL capacitance C_EDL between the ionic liquid and graphene involves the series connection of C_g and the quantum capacitance C_q, which is proportional to the density of states. We investigated the variables that determine C_EDL at the molecular level by varying the number of graphene layers n and thereby optimising C_q. The C_EDL value is governed by C_q at n < 4, and by C_g at n > 4. This transition with n indicates a composite nature for C_EDL. Our finding clarifies a universal principle that determines capacitance on a microscopic scale, and provides nanotechnological perspectives on charge accumulation and energy storage using an ultimately thin capacitor.

Single-layer graphene (SLG) has two kinds of singularities. One is a topological singularity at K points in non-doped SLG, called the Dirac point. The carrier transport at the Dirac point, with a vanishing density of states D(E), has been intensively studied¹,²,³,⁴,⁵. The other is the van Hove singularity at M points in highly doped SLG, which has recently attracted significant attention due to predictions of several novel phenomena such as superconductivity⁶,⁷, ferromagnetism⁸, and charge/spin density waves⁹,¹⁰ caused by divergent D(E) and a band structure with high symmetry. We can reach this state by doping SLG with 0.25 electrons or holes per carbon atom (~1 × 10¹⁵ /cm²). This high carrier density is expected to be attainable with an ionic-liquid gate because of its thin electronic double layer (EDL)¹¹,¹²,¹³,¹⁴, i.e. large geometrical capacitance determined by C_g = ε_ILε₀/d. Here, ε_IL, ε₀ and d are the relative permittivity of the ionic liquid, vacuum permittivity, and thickness of EDL, respectively. However, studies have demonstrated that carrier doping into SLG with ionic liquids is much lower than expected¹⁵,¹⁶. This is because the potential difference between an ionic liquid and SLG is made smaller than the applied gate voltage V_g by the shift of the Fermi energy E_F when doping SLG with an additional charge of Q. This phenomenon can be interpreted in terms of the quantum capacitance C_q, defined as C_q = eQ/E_F = e²D(E_F)¹⁵,¹⁷,¹⁸, which is connected to C_g in series. Thus, the total capacitance C_EDL between the ionic liquid and SLG is understood as follows:

The effect of C_q is prominent when C_q ≪ C_g, which is characteristic of the combination of SLG with small C_q and an ionic liquid with a large C_g. Thus, even if an ionic liquid has a large C_g, small C_q limits C_EDL to make high charge density unattainable. Here, increasing the layer number n might solve this problem, because D(E) increases with n, and accordingly C_q increases. To find an optimal n for carrier doping with an ionic liquid is thus quite important for the discovery of novel ordered states in graphene. In addition, the C_EDL will increase with n, but the specific surface area (the surface area per unit of mass) of few-layer graphene (FLG) decreases. In a practical viewpoint to realise the superior characteristics in graphene-based supercapacitor¹⁹,²⁰, therefore, it is of significance to elucidate the optimal n producing both the large C_EDL and specific surface area. In this letter, we examine the capacitance of SLG and FLG while systematically changing n.

Results

Our results are summarized in Figs. 1a and 1b. The capacitance C_EDL between the ionic liquid and FLG was measured as a function of n by two methods, a transport measurement using graphene field effect transistors (FETs) (Fig. 1a), and a capacitance measurement using AC (Fig. 1b). When the gate voltage V_g induces the charge Q(V_g), C_EDL^DC = Q/V_g and C_EDL^AC = dQ/dV_g are obtained by the transport and capacitance measurements, respectively. These two measurements are complementary to each other and are especially important in the estimation of C_EDL, which depends significantly on measurement frequency due to the slow transport of the ions in an ionic liquid. The calculated values of C_EDL are also shown in Figs. 1a and 1b, and are in good agreement with the experimental data. At n = 1, a small C_EDL is observed, as in previous studies¹⁵,¹⁶. With increasing n, C_EDL increases and saturates at n > 4. In the following, we describe the experimental and theoretical details.

Figure 1.

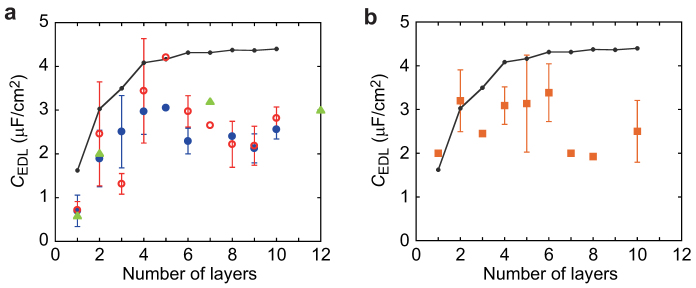
Layer-number dependence of EDL capacitance between graphene and ionic liquid (a), C_EDL evaluated from conductivity measurements (Fig. 2 and Supplementary Fig. S2 online) for SLG and FLG devices. The C_EDL values measured in hole-carrier and electron-carrier regimes using two-terminal devices are indicated by blue solid circles and red open circles, respectively. The C_EDL values evaluated from Hall coefficients are indicated by green triangles. (b), C_EDL directly measured with AC (Fig. 3). The minimum C_EDL values from V_tg = −1 to 1 V are plotted. In (a) and (b), the error bars are the standard deviation of the data measured for each n device. The black solid lines in (a) and (b) represent calculated C_EDL based on a simple theoretical model (Fig. 4). Dependencies of experimental data on n are consistent with the model.

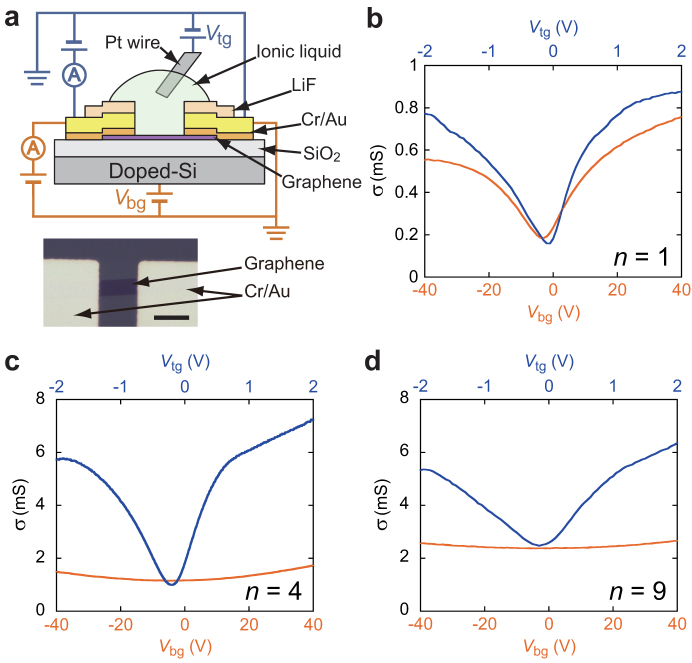
First, we evaluated C_EDL from transport measurements. Two-terminal graphene FETs were prepared on SiO₂ 300 nm/highly doped Si substrate. The structure of the device and the optical microscope image are shown in Fig. 2a. In order to obtain a reliable n dependence, we used only uniform graphene layers without any overlaps of different layers, wrinkles or folds. If the device has overlaps of different layers, the exposure of interstices between the neighbouring graphene layers to the ionic liquid might lead to inaccurate n and errors in estimation of surface area. The uniformity of graphene layer was clearly confirmed by the optical contrast of micrographs¹⁶,²¹,²²,²³,²⁴. Raman spectroscopy mapping and atomic force microscope (AFM) image also evidenced the uniformity of the graphene layer. The number of devices used in this measurement is shown in Table 1; good reproducibility was obtained. The sheet conductivity σ was measured as a function of back gate voltage V_bg applied to the Si substrate. Next, a droplet of ionic liquid was placed on the graphene surface, and σ was measured again as a function of the top gate voltage V_tg applied to the ionic liquid with a Pt wire (100 μm in diameter). In Figs. 2b–2d, σs of FLG FETs with n = 1, 4, and 9 are plotted as functions of V_bg and V_tg. Note that the horizontal scales are different for V_bg and V_tg. It was found that σ was modulated with a lower gate voltage for V_tg than V_bg. The conductivity varied with gate voltage in proportion to the capacitance as follows, 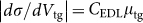or 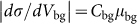, where μ is electric field mobility and the subscript tg (bg) means top (back) gate. Thus, C_EDL is given by

Here, 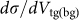is defined as the steepest slope of the experimental data around the charge neutrality point. Assuming μ_bg/μ_tg = 1 and substituting the experimental value of C_bg = 11.5 nF/cm², C_EDL is calculated for each device and plotted in Fig. 1a. A clear n dependence of C_EDL is found in Fig. 1a. C_EDL is a minimum at n = 1. With increasing n, C_EDL shows a maximum at n = 4 and decreases smoothly as n approaches 10. Maximum carrier density was estimated to be 0.003 /C atom (4.7 × 10¹³ /cm²) at n = 4 and V_tg = 2 V.

Figure 2.

C_EDL obtained by 2-terminal transport measurement (a), Schematic side view of two-terminal graphene FET and optical microscope image of a device. Scale bar is 10 μm. Materials and terminal configurations are indicated. After σ(V_bg) was measured using the circuit shown by orange lines, an ionic liquid was applied and σ(V_tg) was measured using the circuit shown by blue lines. Actual size of Pt wire (100 μm in diameter) is much larger than the channel length (10 μm), but it is depicted as a thin wire in the figure for clarity. (b), (c), (d), Comparison of σ(V_bg) (orange line) and σ(V_tg) (blue line) for SLG (b), 4-layer (c), and 9-layer graphene (d). Note that the horizontal scales are different for V_bg and V_tg. To determine C_EDL from equation (2), we estimated dσ/dV_tg(bg) as the steepest slope of the σ(V_tg(bg)) curve. The gate voltages were swept from negative to positive values.

Table 1. Number of FLG devices prepared in this study.

layer number	1	2	3	4	5	6	7	8	9	10	total
Transport measurement	4	4	4	3	1	5	1	2	3	3	30
Capacitance measurement	1	2	1	4	2	3	1	2	0	2	18

In order to prove the validity of C_EDL(n) obtained by the transport technique, we directly measured the capacitance using AC. The device structure and the optical microscope image are shown in Fig. 3a. Uniform graphene layers are carefully chosen in this measurement. The graphene layer was covered with photoresist except for a region about 15 μm square, on which a droplet of the ionic liquid was placed. AC voltage was applied across the interface between the ionic liquid and FLG, and the capacitance C_EDL was evaluated by the out-of-phase components of the detected current. C_EDL was measured with an excitation amplitude of 10 mV at a frequency of 500 Hz and with a superimposed DC bias voltage V_tg ranging from −1 to +1 V. The equivalent circuit of our system is shown in Fig. 3a¹⁶. Here, it should be noticed that the contact area between the ionic liquid and Pt electrode is much larger than the area between the ionic liquid and FLG. Hence, the impedance of C_Pt is negligible compared to that of C_EDL. This means that V_tg is effectively applied at the interface between the ionic liquid and FLG. Note that V_tg is uniform along this interface, because the impedance of C_EDL (~ 10⁸ Ω) is much larger than the resistance of FLG (10³ – 10⁴ Ω). The measured impedance is typically Z ~ 10⁶ – 10⁸ i Ω at a frequency of 500 Hz. Therefore, the capacitive component dominates the total impedance, showing that C_EDL can be directly determined by the measurement with LCR meter as described in the method section.

Figure 3.

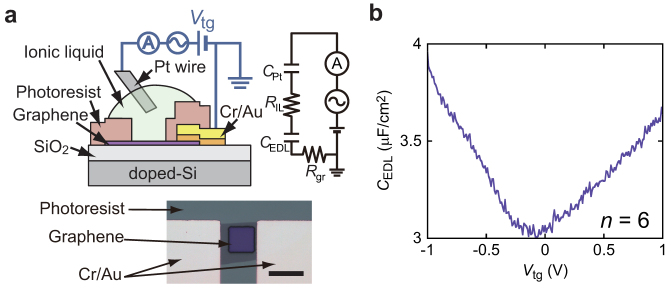
C_EDL obtained from direct AC measurement (a), Schematic side view of a device for capacitance measurement and the equivalent circuit. Materials and terminal configurations are indicated. R_IL and R_gr are the electric resistance in the ionic liquid and graphene, respectively. C_Pt is the capacitance between Pt wire and the ionic liquid. Actual size of Pt wire (100 μm in diameter) is much larger than the square window (15 μm on a side), but it is depicted as a thin wire in the figure for clarity. Optical microscope image of a sample is also indicated. Scale bar shows 20 μm. (b), V_tg dependence of C_EDL for 6-layer graphene. The gate voltage was swept from negative to positive values.

In Fig. 3b, C_EDL for n = 6 is plotted as a function of V_tg. We found that C_EDLs for all the devices significantly depended on V_tg, which corresponds to the ambipolar behaviour in D(E). Here it is important to notice that V_tg in our experiment may be different from the actual voltage applied to the FLG since the potential drop caused by the interface of the Pt wire is not considered. The accurate dc bias in the electrochemical impedance analysis may be defined as the potential difference from the reference electrode using a three-terminal setup¹⁵. However, in our devices used in this study, the potential drop at the Pt interface is expected to be so small that applied voltage from the ground is approximately equal to the actual voltage, because the Pt electrode is much wider than the channel region of FLG, as described above. To compare with the transport measurement, the C_EDL for each device, obtained at the charge neutrality point, is plotted as a function of n in Fig. 1b. Here the charge neutrality point is defined as the V_tg where C_EDL exhibited the lowest value, and is located around V_tg = 0 V as shown in Fig. 3b. Since V_tg ~ 0 V, the value of minimum capacitance is obtained without any ambiguities of the bias voltage. Consequently, the discussion on n dependence of capacitance shown in Fig. 1b is appropriate. As shown in Figs. 1a and 1b, a C_EDL - n plot is substantially consistent with that from the transport measurement, which supports the validity of our estimation of C_EDL from the transport measurement.

Discussion

Here, we discuss the validity of the C_EDL obtained by two-terminal transport measurements. The analysis using equation (2) might oversimplify the estimation of C_EDL because the contribution of μ_bg/μ_tg is bypassed. First, we consider the validity of the assumption of μ_bg/μ_tg = 1. This assumption is required because C_EDL and μ_tg cannot be determined independently without the result of Hall effect. In order to investigate the validity of this assumption, we carried out additional transport measurement using the multi-terminal Hall bar devices with n = 1, 2, 7, and 12. (see Supplementary Fig. S2 online). In this method, we can independently determine C_EDL and μ_tg without any assumption. By measuring the Hall coefficient, R_H, and σ in four-terminal geometry under the gate voltage V_g (V_bg and V_tg), we can evaluate μ (μ_bg and μ_tg) and C (C_bg and C_EDL) independently by using the following equations²⁵,²⁶.

These equations are satisfied in the doped region where only one kind of carrier presents. R_H was measured as a function of V_tg under perpendicular magnetic field of 6 kOe. The values of C_EDL were estimated from the slope of 1/R_H - V_tg curve in the range where equation (4) holds. The C_EDL - n plot is shown in Fig. S2b and C_EDLs are added in the graph in two-terminal measurement (Fig. 1a). This shows a good agreement between the C_EDL values obtained from two-terminal transport with assumption of μ_bg/μ_tg = 1 and Hall effect without any assumption. Therefore, this result proves the validity of the assumption of μ_bg/μ_tg ~ 1 in the analysis in two-terminal geometry.

Furthermore, we deduced μ_bg and μ_tg separately by substituting both R_H and σ in four-terminal geometry into equation (3), and evaluated μ_bg/μ_tg. The result is shown in Fig. S2c. The μ_bg/μ_tg scarcely depends on n and is regarded as a constant around 0.5. The difference, 1 and 0.5, in μ_bg/μ_tg between two analyses described above may be closely associated with the contact resistance. The contact resistance reduces the conductance measured in two-terminal geometry, and this effect becomes more significant in highly doped graphene. Accordingly, μ_tg in two-terminal measurement could be underestimated, because μ_tg is estimated in more carrier-accumulated region than μ_bg, while μ_tg and μ_bg evaluated from R_H and σ measured in four-terminal geometry are not affected by the contact resistance. This may be one of the reasons why the difference in μ_bg/μ_tg takes place between two analyses. It is reasonable that μ_bg/μ_tg using two-terminal mobility enhances from the value (~ 0.5) of μ_bg/μ_tg estimated from Hall bar devices (R_H and σ in four-terminal geometry). Thus, μ_bg/μ_tg in two-terminal geometry can be concluded to be close to unity as we assumed in the analysis of equation (2).

Finally, to give physical meaning to the experimental result, we calculated the charge distribution in the FLG that forms the EDL capacitor, and obtained C_EDL as a function of n. We define U_EDL ( = Q²/2C_EDL) as the total energy stored in the EDL capacitor where charges +Q and −Q are condensed in the ionic liquid and FLG boundaries, respectively. As shown in Fig. 4a, the charge −Q is distributed over the layers so as to screen penetration of the electric field into the interior. The electric field E_i between the i-th and i+1-th layer becomes smaller than E_i-1 owing to the charge −q_i lying on the i-th layer, where i = 1, ..., n is numbered from the ionic liquid side. Then, C_g is obtained by C_g = Q²/2U_g, where U_g is the static field energy due to E_i:

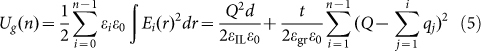where ε_gr = 5.7 is the relative permittivity of graphite²⁷ and t = 0.34 nm is the distance between graphene layers²⁸. The first term in the right-side expression shows the classical electric field energy accumulated in EDL and the second term indicates that in n-layer graphene. Note that a familiar formula 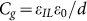is obtained for SLG owing to n = 1. On the other hand, we can relate C_q to the band filling energy U_q²⁹, C_q = Q²/2U_q. Originally C_q was introduced to explain the incomplete shielding of the electric field effect for a two-dimensional electron gas¹⁷. We extend this concept to thicker films that can completely screen the electric field by expressing U_q as a summation of the band-filling energy in each layer;

where E_Fi is the Fermi energy of the i-th layer. For simplicity, we used a constant D(E) to deduce the second equality. As mentioned before, C_q = e²D is obtained for SLG. We minimized U_EDL ( = U_g + U_q) with respect to each q_i of the variational parameters and thereby determined U_g, U_q, and U_EDL. Using these energies, capacitances were deduced. C_g, C_q, and C_EDL are plotted as a function of n in Fig. 4b. All the capacitances significantly depend on n: C_q increases and C_g decreases with n, and both capacitances saturate to constant values at n ≫ 4. This saturation behaviour corresponds to the fact that the electric field is screened by the charge distributed within 3–4 layers²⁹,³⁰ in FLG. Note that the charge distribution over 3–4 layers in FLG significantly reduces C_g because the effective EDL thickness expands from d to ~ d + αt; α is on the order of unity and determined by the effective charge distribution. Therefore, even if an ionic liquid with extremely thin d were used, C_g could not be increased due to the additional EDL thickness of αt (see Supplementary Fig. S4 online). Although layered material is considered to be the most suitable for use with an ionic liquid gate, the effect of decreasing C_g must be taken into account.

Figure 4.

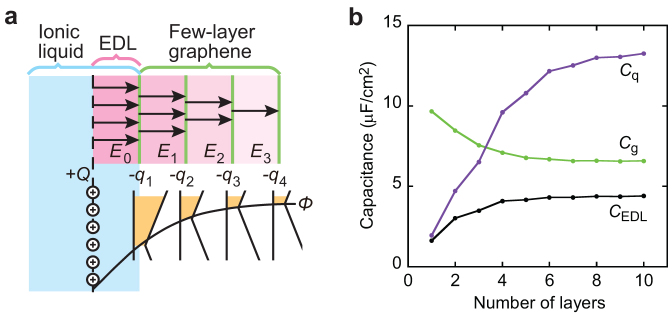
Model calculation of C_EDL (a) Schematic representation of the charge distribution -q_i in FLG, which shields the electric field. (b) Calculated capacitances as a function of n. Geometrical capacitance C_g, quantum capacitance C_q, and EDL capacitance C_EDL are indicated by green, purple, and black lines, respectively. Details of the calculation can be found in the main text and Supplementary Information. We find that the C_EDL is limited by C_q for n < 4 and by C_g for n > 4.

In conclusion, we have clarified the microscopic principles determining the capacitance of n-layer graphene by systematic study. The carrier distribution and the band structure in the electrodes of a capacitor define C_g and C_q, respectively, both of which contribute to the total capacitance. This study demonstrates that we may not in principle achieve the high-density carrier accumulation required for E_F to reach the van Hove singularity even with ionic liquid gated FLG. This result suggests that we need chemical doping⁶,³¹,³² or band control⁹ to bring the van Hove singularity close to the Fermi energy. Our finding for EDL capacitor may establish a nanotechnological guideline to improve ultrathin capacitors for charge doping, energy storage, and electric power supply.

Methods

FLGs were prepared on a SiO₂/highly doped Si substrate by the micromechanical cleavage of Kish graphite (Covalent Materials Co.). The SiO₂ was 300 nm thick and its surface was coated with a hydrophobic hexamethyldisilazane (HMDS) layer³³ to improve the FET characteristics. The number of graphene layers was distinguished by the contrast of the optical microscope image¹⁶,²¹,²²,²³,²⁴, atomic force microscopy (AFM) and Raman spectroscopy³⁴,³⁵,³⁶,³⁷ (see Supplementary Fig. S1 online). As described in the main text, we only used uniform graphene layers without any overlaps of different layers, wrinkles and folds in order to obtain a reliable n dependence. FLG devices for two-terminal transport measurement were fabricated by photolithography and the vacuum evaporation of metal (Cr 5 nm/Au 50 nm) and insulator (LiF 30 nm) to passivate the electrodes. FLG devices with a Hall bar structure were prepared using the electron beam lithography and oxygen plasma etching. FLG devices for capacitance measurement were coated with 800 nm thick photoresist (Tokyo Oka, TSMR8900) instead of LiF, followed by photolithography to open a window on the graphene layer. All the measurements were carried out in Ar at room temperature. The transport property was measured with a semiconductor device analyser (Agilent B1500A). We evaluated the conductivity from the slope of I – V curves measured at a drain voltage of ±1 mV. Except for the transport measurement using a Hall bar structure, a gel of bmim[PF₆] was used as the top gate dielectric (preparation details described elsewhere³⁸). The geometrical capacitance of this ionic liquid was estimated to be 9.7 μF/cm² by extrapolating the measured capacitance at 20 Hz – 100 kHz to 0 Hz. This value corresponds to d = 0.6 nm, assuming ε_IL = 7 ¹⁵. The capacitance measurement was carried out with a precision LCR meter (Agilent E4980A) applying an AC voltage of 10 mV at 500 Hz and superimposed DC voltage V_tg from −1 to 1 V. Only the FLG devices with a Hall bar structure were measured by applying V_tg with an electrolyte LiClO₄/PEO. The mixing molar ratio of LiClO₄/PEO is 1/20. The geometrical capacitance of this electrolyte is reported to be 15 μF/cm^{2 39}, which is of the same order as that in bmim[PF₆].

Author Contributions

H. G. and Y. K. planned the experiments. E. U. prepared graphene devices and carried out the transport and capacitance measurements. All authors analysed and discussed the experimental results.

Supplementary Material

Supplementary Information

Supplementary information