Abstract
The lack of practicable nonlinear elastic contact models frequently compels the inappropriate use of Hertzian models in analyzing indentation data and likely contributes to inconsistencies associated with the results of biological atomic force microscopy measurements. We derived and validated with the aid of the finite element method force-indentation relations based on a number of hyperelastic strain energy functions. The models were applied to existing data from indentation, using microspheres as indenters, of synthetic rubber-like gels, native mouse cartilage tissue, and engineered cartilage. For the biological tissues, the Fung and single-term Ogden models achieved the best fits of the data while all tested hyperelastic models produced good fits for the synthetic gels. The Hertz model proved to be acceptable for the synthetic gels at small deformations (strain < 0.05 for the samples tested), but not for the biological tissues. Although this finding supports the generally accepted view that many soft materials can be assumed to be linear elastic at small deformations, the nonlinear models facilitate analysis of intrinsically nonlinear tissues and large-strain indentation behavior.
Keywords: Indentation, Elasticity, Hyperelasticity, Mechanical properties
1 Introduction
In numerical simulations or uniaxial and biaxial tests, the mechanical response of polymer gels and biological tissues are often described successfully using linear elasticity theory at small strains and rubber elasticity theory at both small and large strains. For polymer gels subjected to conventional mechanical modes of loading (e.g., uniaxial and equibiaxial tests), various models have been developed and applied—see, e.g., review by Horkay and McKenna (2007). For measurement of elasticity at micron and submicron length scales, the prevalence of atomic force microscopy in materials research has established micro- and nanoindentation as two of the leading techniques. In particular, the unique capabilities of the AFM (e.g., concurrently imaging and probing samples of minute size submerged in liquid) have made it an indispensable tool in the study of biological materials. However, despite advancements in instrumentation and analysis methods, its application to soft matter is still complicated by tip-sample interactions and the lack of practical nonlinear contact mechanics models. It is common practice to rely on models based on the classical Hertz theory, with its assumptions of linear elasticity and infinitesimal strains, to analyze force curves. Consequently, errors are frequently incurred by applying these representations beyond their validity range or at the small-strain range where the indentation process is most prone to noise.
Lin et al. (2007b) had previously developed an approximate relation for the spherical indentation of rubber-like, Neo-Hookean and Mooney-Rivlin materials. Assuming that the contact radius varies in the Hertzian manner with indentation depth, a force–indentation relationship was formulated and validated for the AFM microindentation of poly(vinyl alcohol) (PVA) gels. In this work, we refine the approach and extend it to other non-Hookean constitutive laws including the two-term reduced polynomial (Mooney 1940), single-term Ogden (1972), Fung (Fung 1967; Fung et al. 1979), Gaylord and Douglas (1987, 1990), Tschoegl–Gurer (Gurer and Tschoegl 1985; Tschoegl and Gurer 1985), and van der Waals (Kilian 1985) models. We begin by introducing the various hyperelastic strain-energy potential functions and describing the theoretical framework for deriving contact mechanics equations based upon them. Next, the use of finite element analysis (FEA) to validate and further improve the closed-form force–indentation relationships is discussed. We then reanalyze literature data obtained from the large-strain AFM indentation of swollen PVA gels and cartilage samples in terms of each model. Strategies developed previously (Lin et al. 2007a) were utilized in the automated analysis and evaluation of the performance of the different theoretical approaches. The models found to be most suitable for rubber-like gels and biological extracellular matrices and cells are identified. We propose the use of these models when analyzing data from the AFM indentation of soft materials at large strains.
2 Theory
2.1 Contact mechanics
Hertz’s seminal treatise on the contact of ellipsoidal bodies remains the analytical basis for the majority of indentation experiments. In spherical indentation, the Hertzian relationship between the applied force (F) and the resulting indentation (δ) is (Johnson 1985)
| (1) |
where E and ν are Young’s modulus and Poisson’s ratio of the indented material, respectively, and R is the radius of the rigid indenter. The contact radius (a) varies with δ according to
| (2) |
Because the Hertz formalism is based on the theory of linear elasticity, it must be possible to define measures of stress and strain that satisfy a Hookean relationship. The concept of an analogy between uniaxial compression and spherical indentation was first explored by Tabor (1948, 1951) for the elastic-plastic indentation of metals and has since been extended to other classes of materials (Briscoe et al. 1998; Fischer-Cripps and Lawn 1996; Hochstetter et al. 2003; Iwashita et al. 2001; Swain and Hagan 1976). Widely accepted definitions of indentation stress (or mean pressure, σ*) and strain (ε*) are given by
| (3) |
The strain prefactor of 0.2 was empirically determined by Tabor (1951) and has since been verified by other investigators (Field and Swain 1995; Herbert et al. 2001; Taljat et al. 1998). Thus defined, indentation stress and strain are similar to their counterparts in uniaxial loading. In fact, indentation is essentially a compressive process since only the edge of the contact region experiences tension (Johnson 1985). Dividing stress by strain and substituting Eqs. (1) and (2) for Hertzian indentation, the following linear (i.e., Hookean) relationship is obtained:
| (4) |
From the parallels between indentation and uniaxial compression, it stands to reason that non-Hookean, uniaxial stress–strain relations can be extended to non-Hertzian contact. Table 1 lists the hyperelastic strain energy functions and corresponding uniaxial stress (σ)–stretch (λ) equations used in this study and described in more detail in the next section. By substituting the definitions of σ* and ε* given in Eq. (3) for stress and strain, respectively, the uniaxial relations are transformed into contact equations in terms of force and contact radius. In most instrumented indentation tests, however, the contact radius is not a measurable quantity. Instead, the variation of indentation depth with increasing magnitude of the applied force is monitored directly or indirectly; an expression such as Eq. (2) relating a and δ is therefore necessary. Assuming material incompressibility and that the contact radius varies with indentation depth according to Eq. (2), Lin et al. applied an alternative definition of strain, ε* = a/R (Briscoe et al. 1998; Hochstetter et al. 2003; Iwashita et al. 2001; Mesarovic and Fleck 1999; Swain and Hagan 1976), to the Mooney-Rivlin Lagrangian uniaxial engineering stress–stretch equation to arrive at the contact relation (Lin et al. 2007b)
| (5) |
where B1 and B2 are fitting parameters related by
| (6) |
in which E0 denotes the initial or infinitesimal Young’smodulus. Here, we apply Tabor’s definition of strain given in equations (3) and implement the following approach:
- The general form of the uniaxial stress–stretch relations shown in Table 1 can be expressed as
where the stress σ is some function f of the fitting coefficients Ci and the stretch ratio λ, which is related to uniaxial strain ε by λ = 1 + ε.(7) - It is necessary at this point to resolve differences in sign convention between the standard engineering notation employed by Eq. (7) and that commonly used in indentation. In engineering notation, stresses and strains are positive in tension and negative in compression. However, in general force-indentation equations, both force and indentation are taken to be positive. As a result, both σ* and ε* are also positive despite being essentially compressive in nature. In transforming equation (7) into a relation between σ* and ε*, we therefore redefine the stretch ratio as
and replace σ with −σ*. Equation (7) becomes(8)
where Ci has been replaced with Bi.(9) - Dividing Eq. (9) by ε*, we obtain
(10) - As its name implies, the initial or infinitesimal shear modulus G0 (equal to 1/3 of the initial Young’s modulus E0 for incompressible materials) found in Table 1 is equivalent to the modulus in the linear elastic regime (i.e., as ε → or λ → 1). Hence, if we take the limit as ε* → 0 in Eq. (10), the left-hand side is equal to the proportionality constant in Eq. (4) while the right-hand side tends toward some value Bi βi, where βi are constants:
(11) - A relationship between a and the indentation δ is necessary to complete the derivation. Equation (2) applies in the case of Hertzian contact, but it is not known whether it applies to hyperelastic contact. For the general case, we search for a function of the form
where x, y, and z are constants. As will be shown, the finite element method is a powerful tool for determining this relationship.(13)
Table 1.
Hyperelastic strain energy functions and corresponding uniaxial stress-strain equations
| Name | Strain energy potential (W) Uniaxial stress (α)—stretch (λ) equation Initial shear modulus (G0) |
|
|---|---|---|
| Mooney-Rivlin, Neo-Hookean (Mooney 1940; Treloar 1975) | W = C1 (I1 – 3) + C2 (I2 – 3); C2 = 0 for Neo-Hookean model | |
| σ = 2C1 (λ – λ−2) + 2C2 (1 – λ−3) | ||
| G0 = 2 (C1 + C2); Fitting parameters: C1, C2 | ||
| Reduced polynomial (Mooney 1940) | ||
| G0 = 2C1; Fitting parameters: Ci | ||
| Ogden (1972) | ||
| ; Fitting parameters: Ci, αi | ||
| Fung (Fung 1967; Fung et al. 1979) | ||
| σ = C (λ − λ−2) exp [b (I1 − 3)] | ||
| G0 = C; Fitting parameters: C, b | ||
| Van der Waals (Kilian) (Kilian 1985) | ||
| G0 = C; Fitting parameters: C, b | ||
| λm is the limiting tensile stretch; I1m is the corresponding first invariant | ||
| Gaylord—Douglas (1987,1990), Tschoegl—Gurer (Gurer and Tschoegl 1985; Tschoegl and Gurer 1985) | ||
| σ = C1 (λ − λ−2) + (2C2/b) [λb − λ−b/2] | ||
| G0 = C1 + C2; Fitting parameters: C, C2 | ||
| Gaylord–Douglas: b = 1 Tschoegl–Gurer: b = 0.34 |
Assuming material incompressibility, in uniaxial loading in the x-direction, I1 first strain invariant = ; I2 second invariant = , σ = λ (∂W/∂λ), λx = λ, λy = λz = λ−1/2 and strain ε = λ − 1
Using the above procedure, the resulting force-contact radius relations corresponding to the strain energy functions from Table 1 are listed in Table 2. Note the similarity between the Mooney-Rivlin equation (5) and that shown in Table 2.
Table 2.
Force-indentation relations for the hyperelastic strain energy functions
| Name | Force (F)— indentation (δ) equations | |
|---|---|---|
| Mooney-Rivlin, Neo-Hookean | ||
| ; B2 = 0 for Neo-Hookean model | ||
| 2-term reduced polynomial | ||
| Ogden | ||
| Fung | ||
| Van der Waals (Kilian) | ||
| ; εm is the limiting tensile strain | ||
| Gaylord–Douglas, Tschoegl–Gurer | ||
| Gaylord–Douglas: b = 1 Tschjoegl–Gurer: b = 0.34 |
E0 is the initial Young’s modulus and R is the radius of the indenter a is the contact radius and is a function of indentation, e.g., Eq. (2)
2.2 Hyperelastic models
Following the pioneering works of Treloar, Rivlin, and Mooney that resulted in the Neo-Hookean, Mooney-Rivlin, and polynomial mathematical descriptions of material behavior, a number of other hyperelastic models have been developed. Each is based on a strain energy density function that relates the energy stored in a material to the deformation, and can be categorized as being molecular or phenomenological in nature according to the basis for its formulation (Aklonis and MacKnight 1983; Treloar 1975). In this study, we compare a subset of models representing different approaches.
Molecular models are generally premised on the statistical thermodynamics of the underlying macromolecular structure of the network. These models consider the discrete structure of the material by focusing on a characteristic unit cell with a certain number of constituent chains. The chains are randomly oriented and connected at junction points, which in networks are the covalent cross-links between the molecules. The Neo-Hookean form is the most well known and mathematically simple of all the hyperelastic models. Treloar (1947) presented a summary of its derivation, which assumes the network to be consisted of freely jointed chains that obey Gaussian statistics. Non-Gaussian statistics were applied subsequently to account for the finite extensibility of the polymer molecules. Treloar (1975) derived the free energy of chains using Langevin statistics, which incorporates the finite extensibility effects of network deformation. A historical overview of the theoretical framework established by Flory, James, Guth, Kuhn, Mark, Treloar, Wall, and others can be found in texts that cover the subject (Aklonis and MacKnight 1983; Sperling 2001; Treloar 1975). Although the Neo-Hookean stored energy function appears to be a special case of the Mooney-Rivlin equation, the latter was derived from different principles.
Efforts to include a more rigorous molecular representation of polymer gels have yielded many functions more advanced than the Neo-Hookean form. Concepts from the field of rheology have been adopted to develop new models based on the force equilibration principle of viscoelastic deformation. Different models (tube models, constraint junction fluctuation model, slip-link model, etc.) employ different treatments of entanglement effects (Horkay and McKenna 2007). Here we consider the Gaylord–Douglas tube model (1987, 1990), which incorporates contributions to the network free energy change of deformation from the chain connectivity of the polymer segments and the restrictions on chain configurations due to entanglements. As pointed out by Gaylord and Douglas, their model is consistent with the continuum mechanics approach used in deriving the Tschoegl–Gurer equation. Other molecular formulations include the Arruda–Boyce non-Gaussian, eight-chain model (Arruda and Boyce 1993).
Deformations of soft tissues as well as synthetic polymers involve complex mechanisms that are not fully understood. On the basis of macroscopic experimental observations “phenomenological” models have been developed with the objective of describing the elastic response of the materials. These models are generally based on continuum theories. Mooney (1940) first proposed that a general strain energy function could be obtained by an infinite series expansion in terms of the first and second strain invariants. The polynomial and reduced polynomial models are therefore generalizations of a number of other functions. The Mooney-Rivlin model was introduced as one specific case of the polynomial form (Mooney 1940); it was also studied by Rivlin in a series of papers on large elastic deformations (Rivlin and Saunders 1951) and is widely used in fitting experimental data. However, an important limitation of the Mooney-Rivlin model is that it is not able to predict large strain behavior (Han et al. 1999). Moreover, the Mooney-Rivlin constants determined from one deformation type have limited value for predicting behavior in other deformation types. It should be noted that the Neo-Hookean model has similar limitations.
Although biological tissues and synthetic polymer networks exhibit several common features (in both cases the primary building blocks are long polymer chains held together by chemical or physical cross-links, van der Waals bonds, etc.), in general, biopolymers are much stiffer than synthetic polymers. One of the most successful phenomenological models that has been applied to soft tissues is that of Fung (Fung 1967; Fung et al. 1979). It describes the strain stiffening behavior as an exponential relation in terms of the first strain invariant. Another widely used constitutive model developed by Ogden (1972) also predicts large strain behavior well. The Ogden general strain energy formulation is a linear combination of an algebraic power dependence of strain invariants. Like the polynomial models, fitting of experimental data is usually performed by retaining up to several terms in the summation. The Tschoegl–Gurer model (Gurer and Tschoegl 1985; Tschoegl and Gurer 1985) combines the Neo-Hookean strain energy function with one based on algebraic power dependence similar to the single-term Ogden function (Blatz et al. 1974).
Several attempts were made to combine molecular and phenomenological approaches by developing so-called “hybrid” models. We mention the van der Waals strain energy function proposed by Kilian (1985) that accounts for finite chain extensibility and draws on the analogy between the phenomenological van der Waals equation of state for ideal gases and the equation of state of rubber elasticity. In the Gent model (1996), the strain energy density is a logarithmic function of the first strain invariant and involves two material parameters: the shear modulus and a constant defined by the limiting chain extensibility.
3 Materials and methods
3.1 Finite element modeling
The indentation was simulated as contact between a rigid sphere (R = 5 µm) and an elastic slab (1 mm diameter, 0.25 mm thick) in an axisymmetric model using a commercial FEA package (Abaqus, Dassault Systèmes). Models were executed for either 1 µm (small displacement) or 5 µm (large displacement) of indentation in 250 ms. Although no viscoelastic effects were assumed, this displacement rate was chosen to be comparable to that from the AFM experiments (see below). The mesh size was graded to be more refined in the vicinity of the sphere and coarse at the model extremes (see Fig. 1). The bottom and side of the slab were fixed in space, and both the rigid sphere and axis of symmetry for the slab were only permitted to move in the vertical direction. Contact between the sphere and slab was assumed to be frictionless. Three material models were simulated, each with an effective shear modulus of 10.2 kPa and Poisson’s ratio of 0.499: a linear elastic model (properties as above), a Mooney-Rivlin hyperelastic model (C1 = 4.702 kPa, and C2 = 0.47 kPa), and an Ogden hyperelastic model (G0 = 10.2 kPa, α = 0.81). From the simulations, the relationship between contact radius and indentation depth was extracted.
Fig. 1.
Finite element displacement magnitude map at the maximum displacement of 5 µm. The radius of the sphere is also 5 µm. The gradation of mesh size and the point at which the contact radius is measured are clearly seen
3.2 Synthetic gels
We cast PVA gel cylinders (1 cm diameter, 1 cm height) and films (>2 mm thick) for macroscopic displacement-controlled compression and AFM nanoindentation, respectively (Lin et al. 2007a). The polymer concentration was ~6% by weight. Aqueous PVA solutions (MW 70,000–100,000) were crosslinked with glutaraldehyde at pH ~1.5, with an appropriate amount of crosslinker (one unit per 100 monomer units) to ensure that all polymer chains were attached to a continuous network structure. All samples were equilibrated with water prior to testing. The Young’s modulus of these gels is approximately 20 kPa, which is within the range of many biological soft tissues.
A bench top materials testing system (Stable Micro Systems, UK) was used to perform displacement-controlled compression of the cylinders at a ramp speed of 1 mm/s. Volume change and barreling were visually monitored and found to be negligible during the test. The shear modulus was determined by fitting the engineering stress–stretch data with the uniaxial hyperelastic equations given in Table 1. Assuming material incompressibility, the infinitesimal Young’s modulus was then calculated by multiplying the shear modulus by a factor of three. Triplicate samples, each tested three times to ascertain elasticity, were used.
3.3 Mouse articular cartilage
Sixty-micrometer thick cartilage samples were transversely sectioned from the femoral heads of one-day old wild-type mice using a microtome. Samples were lightly fixed in 3% formaldehyde, rinsed thoroughly in PBS, and frozen in embedding medium prior to sectioning. Slices were immediately transferred to glass slides, where the embedding medium was allowed to dry and bond the tissue samples to the glass surface. The samples were then rinsed several times with a buffer solution (10 mM HEPES, 2 mM CaCl2, 150 mM NaCl; pH 7.5) and equilibrated to room temperature. AFM imaging and microindentation were performed with the samples submerged in the buffer.
3.4 Tissue-engineered cartilage
Preparation of the tissue-engineered constructs have been detailed elsewhere (Horkay et al. 2005). In brief, chondrocytes harvested from chick embryo sternum were statically seeded on PVA hydrogel disks and cultured under static conditions for up to five weeks. The samples used for the measurements presented here were removed from the surface of the gel scaffold after 19 days, sectioned to a thickness of approximately 1 mm, glued to a glass slide using a small amount of cyanoacrylate adhesive, rinsed and immersed in PBS, and frozen until testing.
3.5 AFM microindentation
For the synthetic gels, general-purpose silicon nitride tips with 5.5 µm glass or 9.6 µm polystyrene beads attached were used for the AFM measurements, performed using a commercial AFM (Bioscope I with Nanoscope IV controller, Veeco). Polystyrene beads of 5 and 9.6 µm were used for the native and engineered cartilage, respectively. The spring constants of the cantilevers were measured by the thermal tune method while bead diameters were measured from images acquired during the attachment process. A raster scanning approach (“force-volume”) was applied to automatically perform indentations over an area of ~20×20 µm, at a resolution of 16×16 (256 total indentations) for the PVA gels and over an area of ~30×30 µm at a resolution of 32×32 (1,024 indentations) for the native cartilage. In all measurements, a tip velocity of approximately 814 nm/s was applied. For the mouse cartilage, surface topography images were used to determine whether each measurement location corresponded to the extracellular matrix or to the cells. In the case of the engineered tissue, the dataset consisted of individual indentations acquired at random locations over the sample.
Code written in Matlab was used to automatically process each dataset and extract values of Young’s modulus using an optimization-based approach. Because the AFM is not capable of directly measuring force and indentation depth, these values must be inferred from directly measurable quantities, the cantilever spring constant kc, and knowledge of the point of contact. The directly measured values are typically the bending position of the cantilever (d) and the position of the cantilever base (z), the zero points of which are usually arbitrary. It is necessary to determine the reference values or the values at the contact point, of the deflection (d0) and position (z0). In terms of the reference values, force (F) and indentation (δ) in the absence of attractive or repulsive interactions are
| (14) |
| (15) |
Fitting the force-indentation equations in Table 2 to an AFM dataset of (z, d) pairs necessitates identifying the contact point (z0, d0) and solving the regression problem for the fitting coefficients.
4 Results
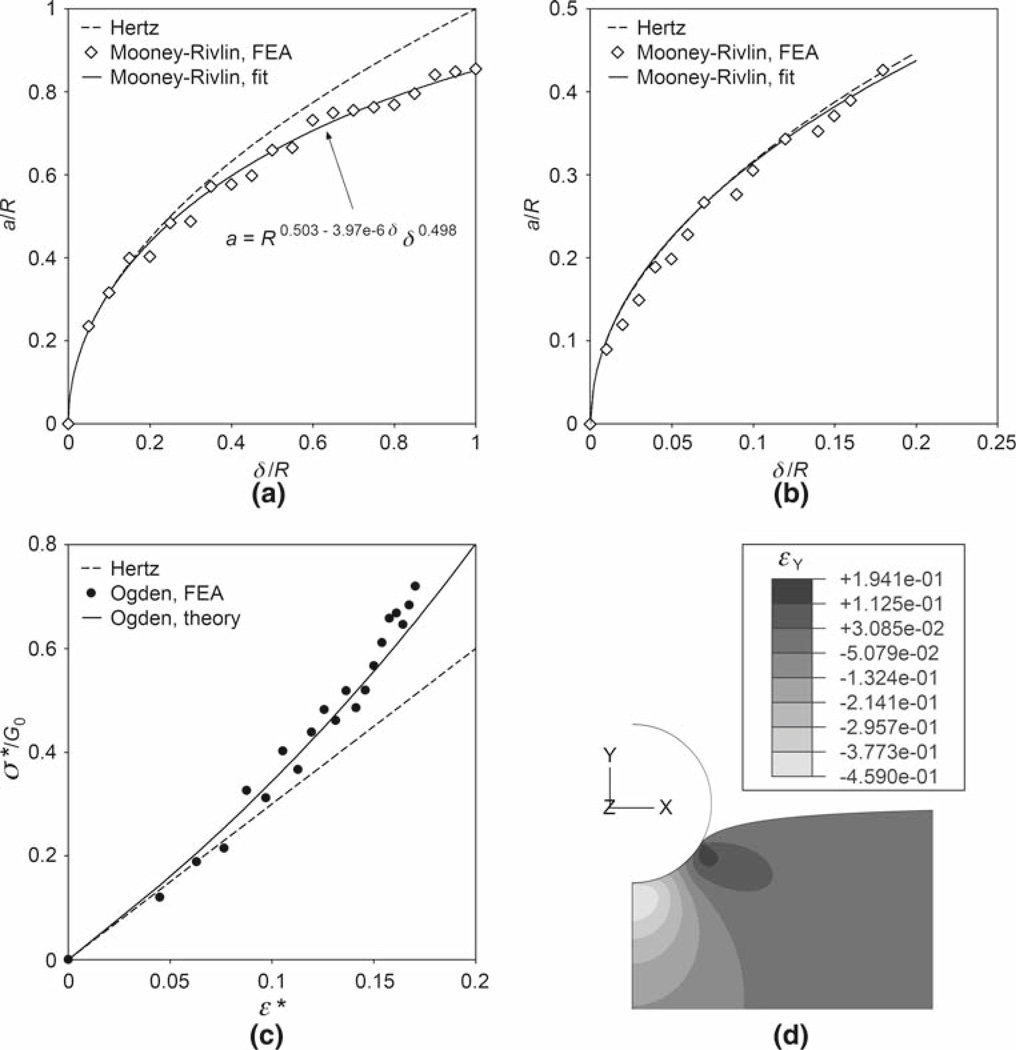
The dependence of the contact radius on the indentation as evaluated by nonlinear FEA is shown in Fig. 2a and b. A generalized relationship between a and δ in the form of Eq. (13) was used to fit the large displacement FEA data (Fig. 2a). For both the large and small displacement cases, a comparison is made between the FEA solution and Eq. (2). In Fig. 2c, the indentation stress–strain response predicted by the FEA is compared to the theoretical model from Table 2. The predicted strain field is presented in Fig. 2d.
Fig. 2.
FEA results for the Mooney-Rivlin and Ogden hyperelastic materials. a Theoretical equation (2) and FEA-derived, Mooney-Rivlin contact radii as functions of the indentation. Both contact radius and indentation are normalized by the radius of the sphere. The least squares fit of the large displacement FEA data was performed using Eq. (13); the unit of length is nm. Note that since Eq. (13) has three fitting parameters, this solution is not unique. Data for the Ogden case is virtually identical. b Comparison of Eq. (2) and FEA-derived, Mooney-Rivlin contact radii at small displacement. For this case, differences between Mooney-Rivlin, Ogden, and Hertz models were negligible. c Indentation stress–strain curves using the definitions in Eqs. (3). FEA and the theoretical Ogden model from Table 2 both indicate significant nonlinearity. d Vertical strain field in the Ogden material at maximum indentation (δ = R). The maximum compressive strain of ~46% occurs at the point of initial contact, but the average value is in line with the definition ε* = 0.2a/R
From the compression tests, the means and standard deviations of the initial Young’s modulus E0 of the PVA gel, obtained using a Hookean relationship at limited strain (0 < ε < 0.05, where compressive strains are taken to be positive) and the various hyperelastic models, are summarized in Table 3. A representative dataset fit with the Mooney-Rivlin uniaxial equation is shown in Fig. 3. Also listed in Table 3 are the corresponding values obtained from the AFM microindentation of three different samples (256 indentations per sample). The mean coefficient of determination (r2) is also listed for each model. In the case of the Mooney-Rivlin equation, previously reported results using Eq. (5) (Lin et al. 2007b) are also listed for comparison.
Table 3.
Young’s modulus (mean ± st. dev.) of PVA gels from two methods and various models
| Model | Macro. compressiona |
AFM indentationb |
||
|---|---|---|---|---|
| E0 (kPa) | Mean r2 | E0 (kPa) | Mean r2 | |
| Hookean/Hertzian/(Hz) | – | – | 24.13 ± 3.56 | 0.9926 |
| Small strain Hookean/Hertzian (sHz)c | 20.49 ± 2.67 | 0.9846 | 21.36 ± 3.61 | 0.9978 |
| Neo-Hookean (NH) | 20.74 ± 0.76 | 0.9994 | 21.92 ± 2.88 | 0.9967 |
| Moone-Rivlin (MR) | 20.26 ± 1.00 | 0.9997 | 20.96 ± 2.75 | 0.9975 |
| 18.23 ± 2.38d | – | |||
| 2-term reduced polynomial (2p) | 20.30 ± 0.90 | 0.9998 | 18.05 ± 4.84 | 0.9997 |
| Fung (Fu) | 20.31 ± 0.90 | 0.9998 | 18.63 ± 4.49 | 0.9997 |
| Ogden (Og) | 19.85 ± 1.23 | 0.9998 | 22.95 ± 4.23 | 0.9997 |
| van der Waals (vdW) e | 20.12 ± 1.12 | 0.9998 | 21.32 ± 2.85 | 0.9974 |
| Gaylord–Douglas (GD) | 19.77 ± 1.30 | 0.9998 | 21.69 ± 2.82 | 0.9969 |
| Tschoegl–Gurer (TG) | 19.86 ± 1.21 | 0.9998 | 21.54 ± 2.80 | 0.9971 |
Macroscopic compression: 3 samples, 3 loading cycles/sample
AFM indentation: 3 samples, 256 indentations/sample
Data limited to strains trains < 0.05
Values using Eq. (5), applied to two samples (Lin et al. 2007b)
Limiting tensile strain of εm = 4 was as used
Fig. 3.
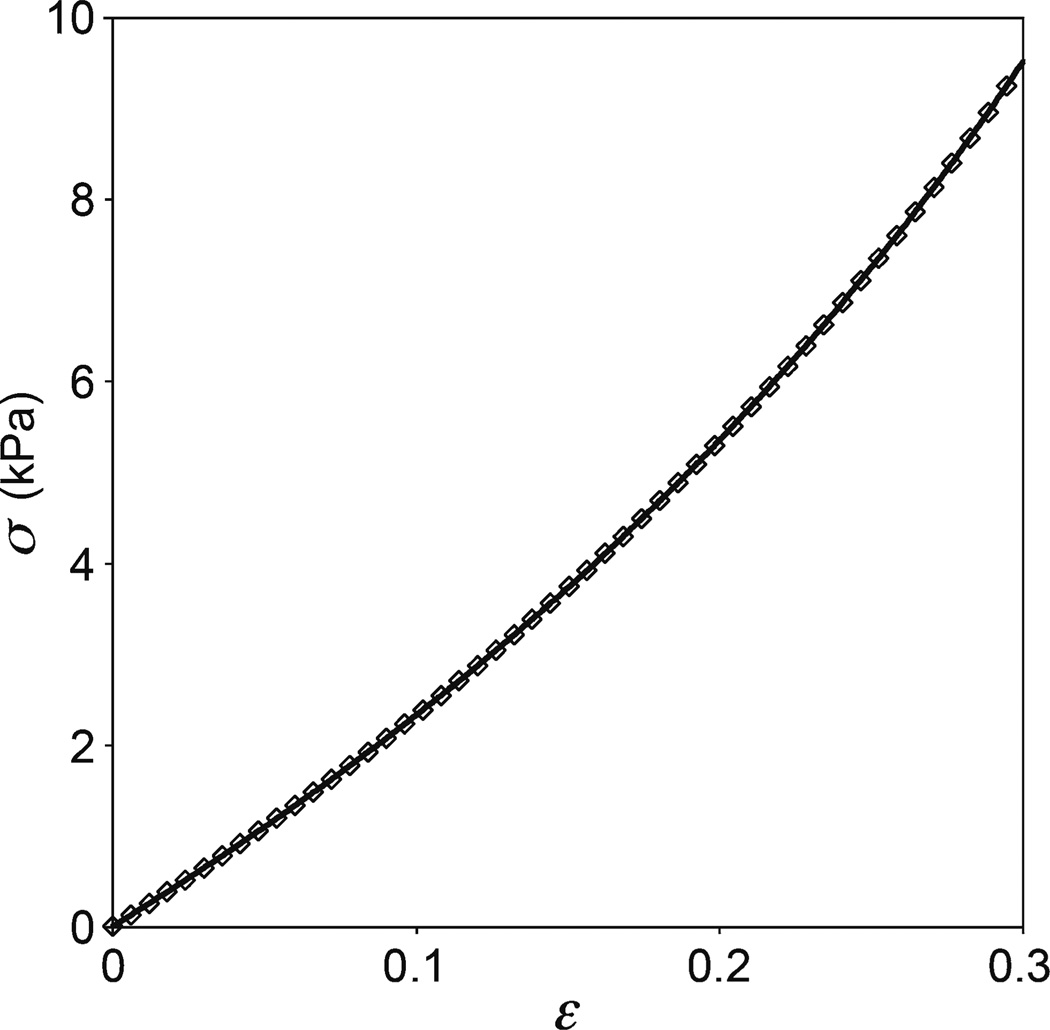
Sample compressive engineering stress–strain behavior of a PVA gel cylinder. Every tenth data point is plotted. Compressive stresses and strains are taken to be positive for consistency with the convention used in indentation. The solid curve is the best fit (r2 = 0.9999) to the data using the uniaxial Mooney-Rivlin equation (see Table 1). The analysis was limited to the deformation range 0 < ε < 0.3. For this particular case, E0 = 20.69 kPa and the fitting parameters are C1 = 3.214 kPa and C2 = 0.235 kPa. The quality of fit is virtually indistinguishable among the various hyperelastic models
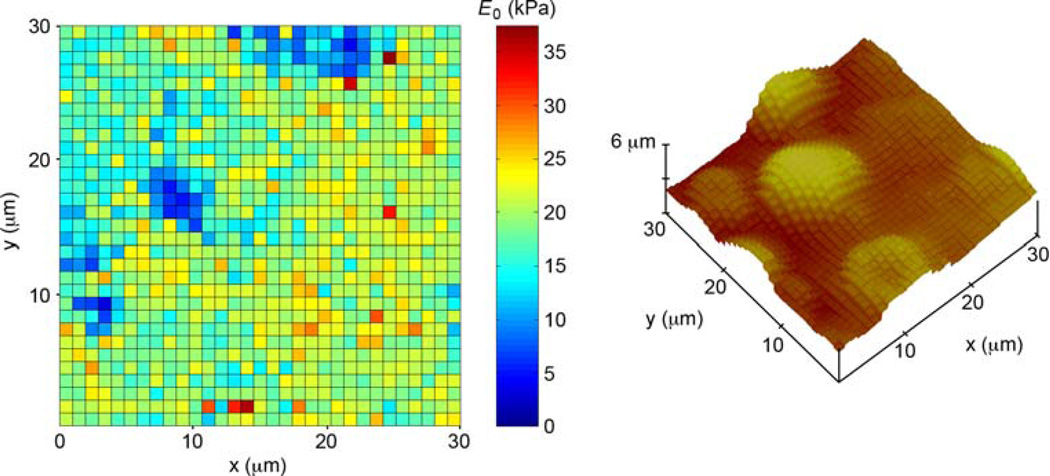
Figures 4 and 5 show datasets representative of the indentation response of mouse cartilage matrix and chondrocytes, respectively. Fits to the data using the Fung and Mooney-Rivlin models are compared in Fig. 4 while the Ogden and Tschoegl-Gurer models are compared in Fig. 5. In Fig. 6, the full results of analyzing a complete force–volume set of data (1,024 indentations) using the Fung model are presented in the form of an elastic modulus map. Ten random datasets each from the extracellular matrix and the chondrocytes, selected with the aid of five AFM topography images such as shown in Fig. 6, were also analyzed using each model. We chose points near the centers of cells and near the middle of the intercellular spaces. The results are tabulated in Table 4 along with those from the indentation of the engineered cartilage.
Fig. 4.
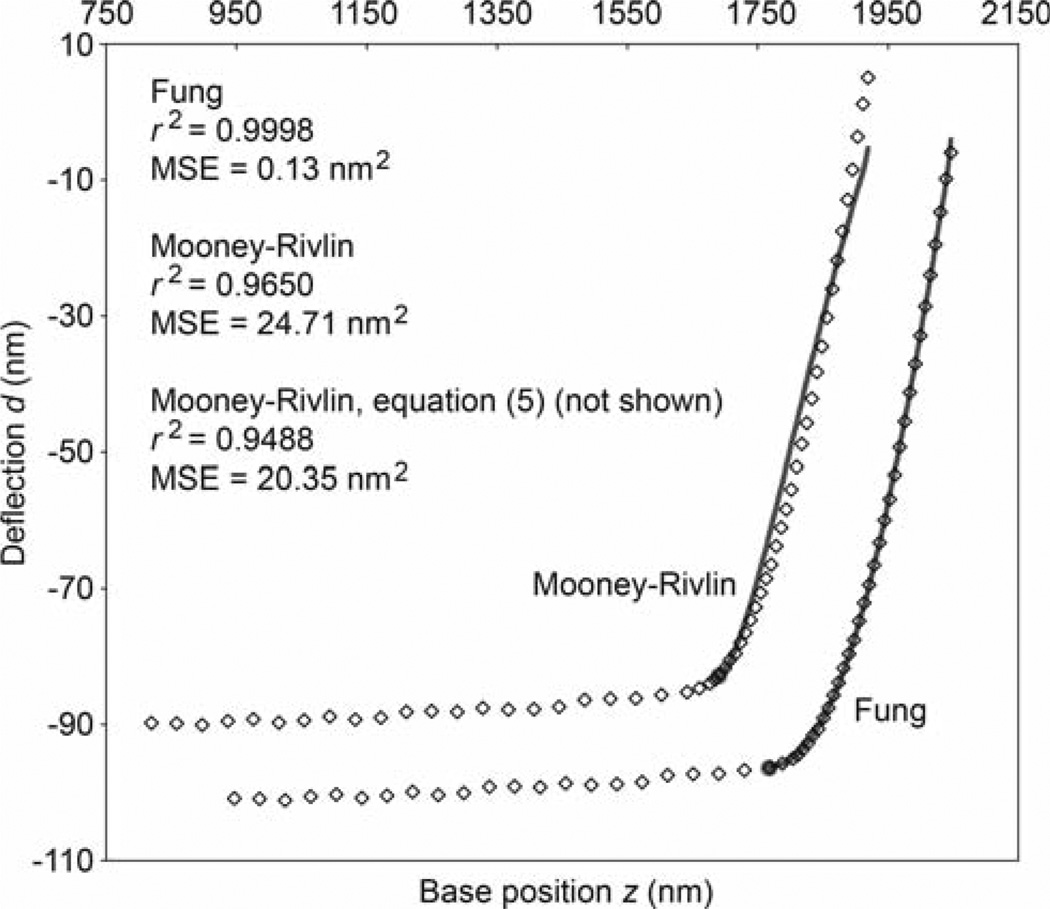
Sample deflection-position data showing every tenth data point from the AFM indentation of the extracellular matrix of mouse cartilage. The data is plotted twice, with the two sets shifted apart for clarity. The solid curves are the best fits using the Fung (fitting parameters B = 19.59 kPa and b = 196.5, E0 = 20.78 kPa) and Mooney-Rivlin (fitting parameters B1 = 2.289 × 10−5 kPa and B2 = 149.35 kPa, E0 = 158.36 kPa) force-indentation equations (see Table 2). The points of contact are indicated by the filled circles. Also shown are the coefficient of determination and mean-squared-error (MSE) for each fit. These values are also listed for the fit using the older form of the Mooney-Rivlin equation given by Eq. (5)
Fig. 5.
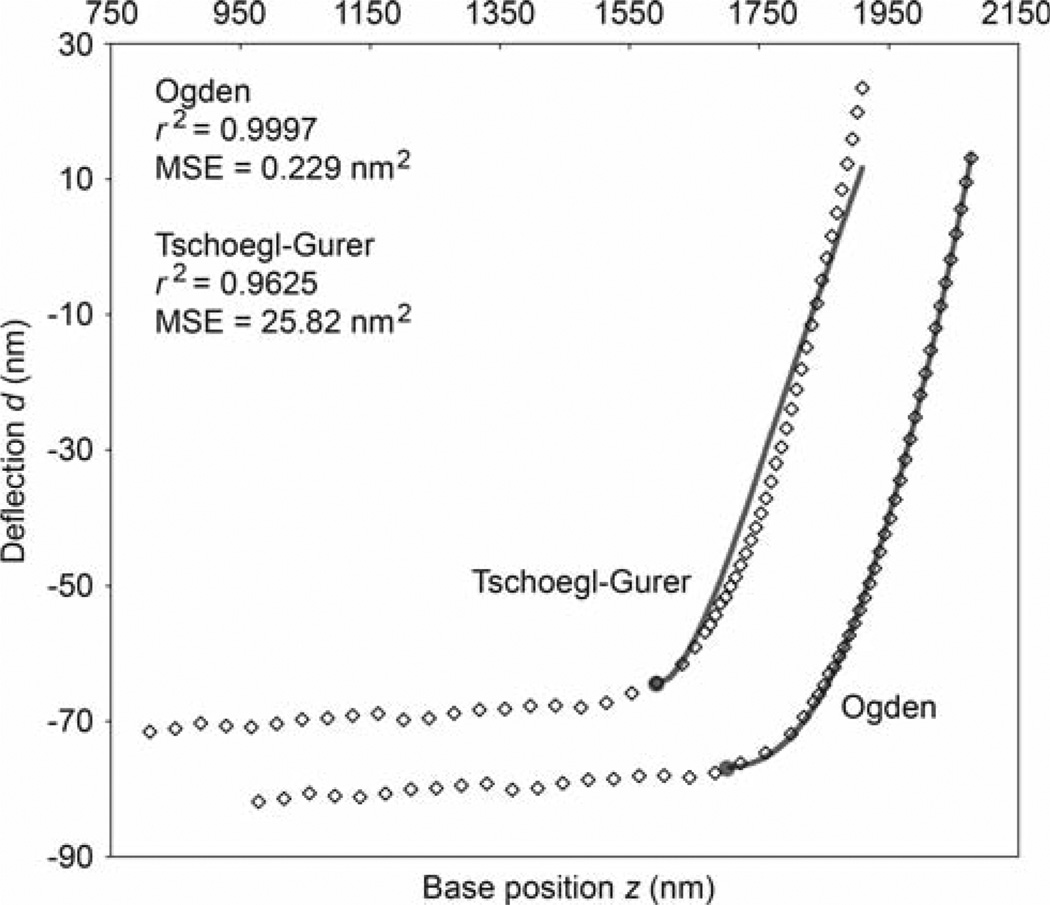
Sample deflection-position data showing every tenth data point from the AFM indentation of a mouse cartilage chondrocyte. The data is plotted twice, with the two sets shifted apart for clarity. The solid curves are the best fits using the Ogden (fitting parameters B = 25.41 kPa and α = 115.4, E0 = 13.47 kPa) and Tschoegl-Gurer (fitting parameters B1 = 6.804 × 10−6 kPa and B2 = 430.8 kPa, E0 = 77.65 kPa) force-indentation equations (see Table 2). The points of contact are indicated by the filled circles. Also shown are the coefficient of determination and mean-squared-error (MSE) for each fit
Fig. 6.
Young’s modulus map and surface plot of a 30 × 30 µm region of mouse cartilage. Moduli were computed using the Fung model. Mean coefficient of determination of the 1,024 fits: 0.999
Table 4.
Young’s modulus (mean ± st. dev.) of cartilage matrix and cells from the models
| Modela | Eng. cartilageb,c |
Mouse matrixb |
Mouse Cells b |
|||
|---|---|---|---|---|---|---|
| E0 (kPa) | Mean r2 | E0 (kPa) | Mean r2 | E0 (kPa) | Mean r2 | |
| Hz | 0.81–5.08 | 0.9359 | 97.79 ± 16.78 | 0.8755 | 45.64 ± 12.46 | 0.9025 |
| sHz | 0.45–3.59 | 0.9635 | 56.69 ± 15.54 | 0.9291 | 19.39 ± 4.74 | 0.9725 |
| NH | 0.68–4.39 | 0.9528 | 99.92 ± 19.08 | 0.8982 | 41.81 ± 12.27 | 0.9098 |
| MR | 0.60–4.04 | 0.9584 | 95.21 ± 18.50 | 0.9215 | 39.18 ± 11.76 | 0.9153 |
| 2pd | Failed | – | Failed | – | Failed | – |
| Fu | 0.46–3.03 | 0.9962 | 19.64 ± 2.30 | 0.9996 | 11.05 ± 2.01 | 0.9997 |
| Og | 0.54–3.97 | 0.9976 | 19.71 ± 3.40 | 0.9995 | 12.47 ± 2.44 | 0.9996 |
| vdW | 0.62–4.12 | 0.9573 | 96.33 ± 18.64 | 0.8871 | 39.79 ± 11.88 | 0.9141 |
| GD | 0.66–4.31 | 0.9540 | 98.79 ± 18.93 | 0.8847 | 41.18 ± 12.14 | 0.9110 |
| TG | 0.65–4.25 | 0.9548 | 98.02 ± 18.84 | 0.8854 | 40.76 ± 12.06 | 0.9118 |
Abbreviations from Table 3
Ten randomly selected samples
Range of values shown rather than mean ± standard deviation since measurements for matrix and cells could not be separated
Two-term polynomial model failed to produce viable fits in the majority of cases
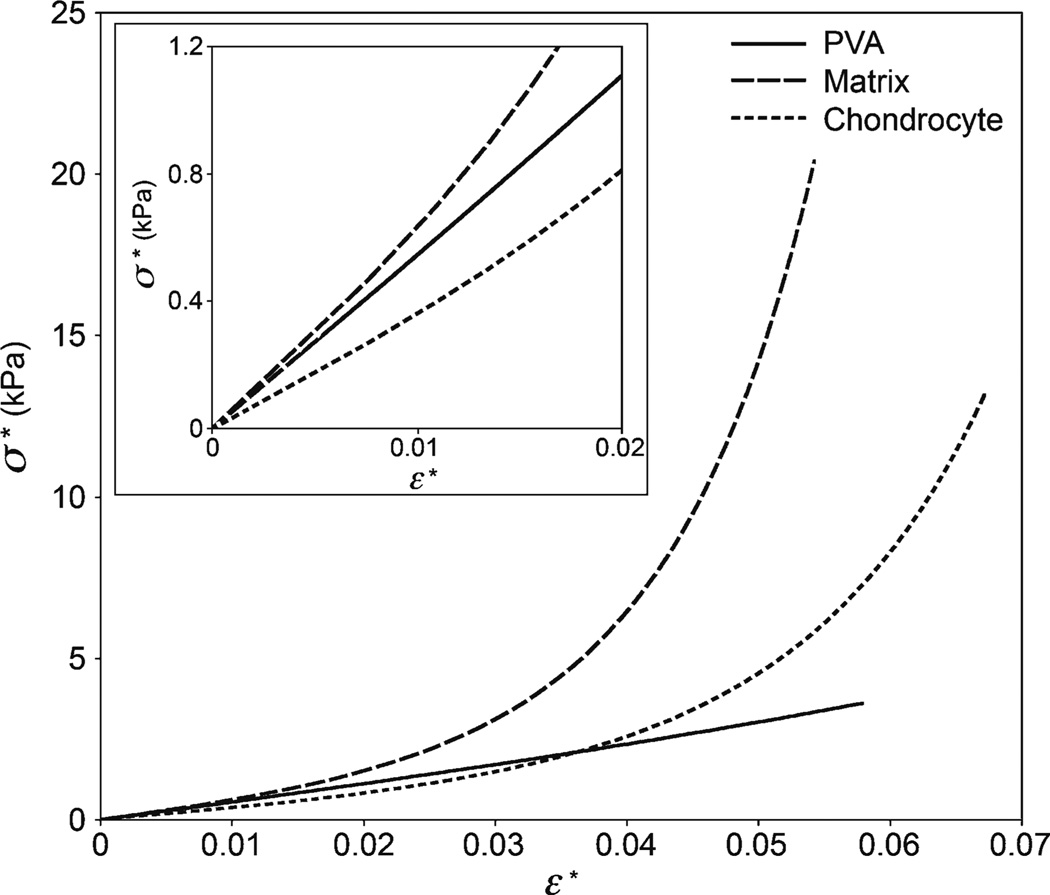
Finally, Fig. 7 shows a comparison of the extent of linearity among the mouse cartilage matrix, cells, and the PVA gel. The data are represented by their respective fits using the Fung model.
Fig. 7.
Indentation stress versus strain (0.2 a/R) for representative microindentations of the PVA gel, mouse cartilage extracellular matrix, and chondrocytes. Data are from the Fung fit of sample AFM datasets (PVA E0 = 19.1 kPa, matrix E0 = 20.7 kPa, chondrocyte E0 = 12.2 kPa). The stress–strain response of the PVA gel appears linear (due to the scaling, nonlinearity is not obvious) while the cartilage components are highly nonlinear. Inset shows the relationship up to 2% strain
5 Discussion
The finite element method proved to be a powerful tool for validating and establishing the limit of the contact radius relationship given by Eq. (2). Figure 2a and b indicate that Eq. (2) holds for a/R below ~0.4 or indentation strains of less than 8%. We expect this limit to hold for each hyperelastic model studied. Beyond a/R = 0.4, the relationship given in Fig. 2a or one that is similar can be used. Computational modeling of indentation by FEA therefore serves the additional, integral purpose of extending the applicability and accuracy of the analytical force–indentation equations beyond this limit. It should be pointed out that we did not attempt to numerically validate the a–δ relationship for each model. Since the normalized indentation δ/R never exceeded 0.2 (and hence, a/R never exceeded 0.4 according to Fig. 2b) in the indentation tests regardless of the size of the bead used, it was possible to apply Eq. (2) in conjunction with the equations in Table 2 to fit the AFM deflection-position data.
As shown by Fig. 2c and d for the representative Ogden hyperelastic material, FEA also verified Tabor’s empirical definitions of stress and strain given by Eqs. (3). The simulated stress–strain response is in reasonable agreement with the theoretical relationship found in Table 2. Moreover, the strain field supports that theoretical prediction of the existence of tensile strains solely at the edge of contact (Johnson 1985.
Chemically crosslinked PVA in swelling equilibrium with water is known to be rubber elastic and obeys the simple Neo-Hookean constitutive model under uniaxial loading (Horkay and Nagy 1980). The results shown in Fig. 3 and Table 3 indicate that each of the hyperelastic models examined in this study capably describes rubber elastic behavior (i.e., both the initial linear elastic response and the strain stiffening are accurately captured by the mathematical fits). This is not true when applied to the indentation of the cartilage samples. In fact, only the Fung and Ogden models were found to be viable for both native and engineered tissues, as seen by comparing the average coefficients of determination (r2) in Table 4 and illustrated by the representative datasets shown in Figs. 4 and 5. In analyzing the indentation of cartilage and the PVA gels, the single-term Ogden model often yielded elastic moduli that slightly exceeded those obtained from the Fung model. We surmise that this discrepancy may be related to retaining only one term in the Ogden strain energy potential.
The suitability of the Fung and Ogden hyperelastic models for the indentation of cartilage and cells is not unexpected since they have been applied successfully to a number of other soft biological tissues. Fung formulated the exponential strain energy function based on mechanical testing of mesentery and arterial tissues (Fung 1967; Fung et al. 1979); his model is widely used in describing blood vessel elasticity (Pandit et al. 2005; Schulze-Bauer et al. 2002). The single-term Ogden model has been found to be capable of accurately representing the elastic response of the vocal fold (Zhang et al. 2006), spinal cord (Bilston and Thibault 1996), brain tissue (Prange and Margulies 2002), and dura mater from the brain and spinal cord (Maikos et al. 2008). Use of these models in biological indentation should allow enhanced sensitivity in detecting spatial variations in elastic moduli and promote greater accuracy of tissue elasticity maps. Figure 6 indicates that when an appropriate fitting function is applied, even a relatively large spherical probe is capable of delineating differences in stiffness within a cell’s perimeter (i.e., the elastic modulus map reveals that the cells are softer close to their centers and stiffer near their edges). We note the possibility that some models not included in our list may perform as well as the Fung and Ogden equations. Even disregarding those that were eliminated by necessity (e.g., higher order polynomials with more than two fitting parameters), it was not our intent to conduct a comprehensive comparison of hyperelastic models. Other indentation equations can easily be derived from strain energy functions using the approach described.
In the macroscopic compression tests, limiting the strain in the Hookean analysis to 5% still ensured that an adequate number of data points remained such that the effects of random noise were essentially obviated. Because the indentation strain does not scale linearly with δ, limiting ε* to a similar range leaves a smaller portion of the data for analysis; at the 5% strain level, each truncated dataset contained approximately one tenth of the total points in the contact regime. For the soft tissue samples, onset of stress–strain nonlinearity prior to ε* = 0.05 and the presence of higher levels of noise in the vicinity of initial contact rendered the Hertzian approach nonviable. Figure 7 shows that the cartilage extracellular matrix and cells exhibited highly nonlinear elasticity when indented, with the nonlinear response of the matrix already pronounced at an indentation strain of 3%. The poor results we obtained when attempting to fit our experimental results with the Hertz equation (see Table 4) are consistent with the findings of Costa and Yin (1999), who conducted finite element studies on the indentation of materials whose behavior conformed to the Mooney-Rivlin, two-term reduced polynomial, or Fung strain energy functions. In their simulations of finite indentation with a conical tip, large errors were incurred in the estimated elastic moduli when using linear elastic models to fit the data except in the case of the Mooney-Rivlin material. Hence, it was concluded that linear elastic models are inappropriate for fitting AFM indentation data at the deformations applied in typical tests.
The pronounced nonlinearity of the cartilage and chondrocytes in comparison to the response of the PVA is likely associated with the innately more complex structure of the biological materials. Furthermore, unlike PVA, cartilage is not expected to obey rubber-like elasticity since the majority of its constituents are rigid. Although the effects of finite chain extensibility are expected to be important contributors to strain stiffening, interactions in the cartilage extracellular matrix between the collagen and glycosaminoglycan networks as well as the presence of fixed and mobile charges must also be considered. The cellular cytoskeleton and cytoplasm can be viewed as parts of an even more intricate network. It is not surprising, therefore, that none of the molecular models, which cannot possibly account for such structural features, proved capable of fitting the experimental data. For the measurement of elastic properties, phenomenological models are viable alternatives to complicated constitutive laws such as Mow’s biphasic theory of cartilage (Mow et al. 1980) and the molecular theory of semiflexible biopolymer networks proposed by Janmey and coworkers (Storm et al. 2005).
Analysis using the Fung model yields a value of approximately 20 kPa for the Young’s modulus of neonatal mouse ECM. For comparison, we also found a maximum value of 3 kPa for the engineered constructs (Table 4). A survey of the literature shows these measurements to be within the range typical of immature native and statically engineered tissue. Some relevant results are listed in Table 5. Although the stiffness of the engineered cartilage appears to be significantly less than that of the native tissue, a direct comparison between the two types of samples is not expedient due to differences in preparation. It is possible that even light fixation of the native cartilage may have a particularly marked effect on the mechanical properties of the cells, which contain various macromolecules that are susceptible to crosslinking. In fact, the average elastic modulus we measured for the mouse chondrocytes (Table 4, using the Fung and Ogden models as the basis for comparison) is relatively high compared to values reported in the literature using a number of different techniques—see, e.g., comparison by Darling et al (2006), where the instantaneous Young’s modulus ranged from 0.29 to 8 kPa, and results listed in Table 5. Despite the lack of surface plots and hence, a means of segregating indentations of chondrocytes from those performed on the matrix, our measurements on the engineered tissue indicate that the average elastic modulus of the cells is within the range of values reported by other investigators.
Table 5.
Reported values of Young’s modulus for engineered and immature native cartilage
| Reference | Source of tissue and culture conditions | Technique | E (kPa) |
|---|---|---|---|
| Ficklin et al. (2007) | Newborn bovine knee joint patellofemoral groove explants, load applied normal to articular surface | Macro compression | 22 |
| Klein et al. (2007) | Fetal and bovine knee joints, surface region | Macro compression | 28 |
| Park et al. (2004) | 4–6 month old bovine humeral heads | AFM indentation (Hertz model) | 45.8 |
| Schinagl et al. (1997) | Adult bovine knee joint patellofemoral groove, superficial layer | Micro compression | 79 |
| Darling et al. (2006) | Porcine chondrocytes | AFM indentation, micropipette aspiration | 0.6–1.2 |
| Guilak et al. (2005) | Adult canine hip joints, pericellular matrix (PCM) | Micropipette aspiration | 23–24 |
| Guilak et al. (1999) | Adult human hip joints, pericellular matrix | Micropipette aspiration | 1.54 |
| Ng et al. (2007) | Bovine chondrocytes cultured in growth factor stimulated medium | AFM indentation (Hertz model) | 0.7–1 (cells), 0.1–4.15 (PCM) |
| Huang et al. (2008) | Engineered tissue from bovine chondrocytes, static culture, no growth factors | Macro tension | ~20–107 |
| Janjanin et al. (2008) | Engineered tissue from human bone marrow derived stem cells, bioreactor culture | Macro compression | ~3–12 |
| Mauck et al. (2003) | Engineered tissue from bovine chondrocytes, static and dynamically loaded culture | Macro compression | ~20–186 |
The elastic moduli measured in this study are instantaneous values calculated using the loading data and disregarding the effects of loading rate. For the tip velocity applied in our indentation of the PVA gels and soft tissues, use of indenters of different radii resulted in strain rates (ε̇*) varying from 0.08–0.11 s−1. It is reasonable to assume that there exists a threshold of ε̇* above which viscoelastic effects can be considered insignificant (Cheng and Cheng 2005; Franke et al. 2007). At the aforementioned rates, it is likely that most of the stress–strain response is independent of fluid flow, and therefore virtually elastic. In a study using bovine articular cartilage (DiSilvestro et al. 2001), it was found that peak reaction forces were dependent on strain rate (ε̇* = 0.0001–0.01 s−1), but instantaneous Young’s modulus was unaffected. For studies of creep-compliance, mathematical methods such as utilization of the Laplace transform to map the time-dependent contact solution to a corresponding elastic solution (Lee 1955), can be extended to the elastic contact models in Table 2. This method was employed in the spherical indentation of chondrocytes (Darling et al. 2006). The hereditary integral operator approach proposed by Lee and Radok (1960), which has been applied to the indentation of polymers (Kumar and Narasimhan 2004; Lu et al. 2003; Oyen 2005; Tweedie and Van Vliet 2006) and soft tissues (Mattice et al. 2006), is generally regarded as more accurate since it pertains to time-varying boundary conditions (Lu et al. 2003).
Conclusions
We have demonstrated the validity of the hyperelastic force-indentation equations introduced herein for describing the indentation of materials that obey simple rubber elastic behavior as exemplified by the PVA gels. The equations based on the Fung and Ogden models also show promise in modeling the indentation of biological tissues beyond the Hertzian regime. The relative simplicity of these closed-form equations makes them attractive for applications in biological indentation, where the ability to detect local variations in elastic properties is of significant benefit. The combined numerical–analytical approach of deriving force-indentation equations can also be applied to other nonlinear elastic, stress–strain constitutive laws.
Acknowledgments
This work was supported by the Intramural Research Program of the NIH, NICHD. The authors are grateful to Dr. Edward Mertz of NICHD for providing the mouse cartilage samples and assisting in their preparation.
Contributor Information
David C. Lin, Section on Tissue Biophysics and Biomimetics, NICHD, National Institutes of Health, 9 Memorial Drive, Bethesda, MD 20892, USA, lindavid@mail.nih.gov
David I. Shreiber, Department of Biomedical Engineering, Rutgers, The State University of New Jersey, 599 Taylor Road, Piscataway, NJ 08854, USA
Emilios K. Dimitriadis, Laboratory of Bioengineering and Physical Science, NIBIB, National Institutes of Health, 13 South Drive, Bethesda, MD 20892, USA
Ferenc Horkay, Section on Tissue Biophysics and Biomimetics, NICHD, National Institutes of Health, 13 South Drive, Bethesda, MD 20892, USA.
References
- Aklonis JJ, MacKnight WJ. Introduction to polymer viscoelasticity. New York: Wiley; 1983. [Google Scholar]
- Arruda EM, Boyce MC. A three-dimensional constitutive model for the large deformation stretch behavior of rubber elastic materials. J Mech Phys Solids. 1993;41:389–412. [Google Scholar]
- Bilston LE, Thibault LE. Themechanical properties of the human cervical spinal cord in vitro. Ann Biomed Eng. 1996;24:67–74. doi: 10.1007/BF02770996. [DOI] [PubMed] [Google Scholar]
- Blatz PJ, Sharda SC, Tschoegl NW. Strain energy function for rubberlike materials based on a generalized measure of strain. J Rheol (NYNY) 1974;18:145–161. [Google Scholar]
- Briscoe BJ, Fiori L, Pelillo E. Nano-indentation of polymeric surfaces. J Phys D. 1998;31:2395–2405. [Google Scholar]
- Cheng Y, Cheng C. Relationships between initial unloading slope, contact depth, and mechanical properties for spherical indentation in linear viscoelastic solids. Mater Sci Eng A. 2005;409:93–99. [Google Scholar]
- Costa KD, Yin FCP. Analysis of indentation: implications for measuring mechanical properties with atomic force microscopy. J Biomech Eng. 1999;121:462–471. doi: 10.1115/1.2835074. [DOI] [PubMed] [Google Scholar]
- Darling EM, Zauscher S, Guilak G. Viscoelastic properties of zonal articular chondrocytes measured by atomic force microscopy. Osteoarthr Cartil. 2006;14:571–579. doi: 10.1016/j.joca.2005.12.003. [DOI] [PubMed] [Google Scholar]
- DiSilvestro MR, Zhu Q, Suh JK. Biphasic poroviscoelastic simulation of the unconfined compression of articular cartilage: II—Effect of variable strain rates. J Biomech Eng. 2001;123:198–200. doi: 10.1115/1.1351887. [DOI] [PubMed] [Google Scholar]
- Ficklin T, Thomas G, Barthel JC, Asanbaeva A, Thonar EJ, Masuda K, Chen AC, Sah RL, Davol A, Klisch SM. Articular cartilage mechanical and biochemical property relations before and after in vitro growth. J Biomech. 2007;40:3607–3614. doi: 10.1016/j.jbiomech.2007.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Field JS, Swain MV. Determining the mechanical properties of small volumes of material from submicrometer spherical indentations. J Mater Res. 1995;10:101–112. [Google Scholar]
- Fischer-Cripps AC, Lawn BR. Indentation stress–strain curves for"quasi-ductile” ceramics. Acta Mater. 1996;44:519–527. [Google Scholar]
- Franke O, Durst K, Maier V, Goken M, Birkholz T, Schneider H, Hennig F, Gelse K. Mechanical properties of hyaline and repair cartilage studied by nanoindentation. Acta Biomater. 2007;3:873–881. doi: 10.1016/j.actbio.2007.04.005. [DOI] [PubMed] [Google Scholar]
- Fung YC. Elasticity of soft tissues in simple elongation. Am J Physiol. 1967;213:1532–1544. doi: 10.1152/ajplegacy.1967.213.6.1532. [DOI] [PubMed] [Google Scholar]
- Fung YC, Fronek K, Patitucci P. Pseudoelasticity of arteries and the choice of its mathematical expression. Am J Physiol. 1979;237:H620–H631. doi: 10.1152/ajpheart.1979.237.5.H620. [DOI] [PubMed] [Google Scholar]
- Gaylord RJ, Douglas JF. Robber elasticity: a scaling approach. Polym Bull. 1987;18:347–354. [Google Scholar]
- Gaylord RJ, Douglas JF. The localisation model of rubber elasticity. II. Polym Bull. 1990;23:529–533. [Google Scholar]
- Gent A. A new constitutive relation for rubber. Rubber Chem Technol. 1996;69:59–61. [Google Scholar]
- Guilak F, Jones WR, Ting-Beall HP, Lee GM. The deformation behavior and mechanical properties of chondrocytes in articular cartilage. Osteoarthr Cartil. 1999;7:59–70. doi: 10.1053/joca.1998.0162. [DOI] [PubMed] [Google Scholar]
- Guilak F, Alexopoulos LG, Haider MA, Ting-Beall HP, Setton LA. Zonal uniformity in mechanical properties of the chondrocyte pericellular matrix: micropipette aspiration of canine chondrons isolated by cartilage homogenization. Ann Biomed Eng. 2005;33:1312–1318. doi: 10.1007/s10439-005-4479-7. [DOI] [PubMed] [Google Scholar]
- Gurer C, Tschoegl NW. Behavior of elastomer networks inmoderately large deformations. 2. Determination of the parameters of the elastic potential from measurements in small deformations. Macromolecules. 1985;18:687–690. [Google Scholar]
- Han WH, Horkay F, McKenna GB. Mechanical and swelling behaviors of rubber: a comparison of some molecular models with experiment. Math Mech Solids. 1999;4:139–167. [Google Scholar]
- Herbert EG, Pharr GM, Oliver WC, Lucas BN, Hay JL. On the measurement of stress–strain curves by spherical indentation. Thin Solid Films. 2001;398–399:331–335. [Google Scholar]
- Hochstetter G, Jimenez A, Cano JP, Felder E. An attempt to determine the true stress–strain curves of amorphous polymers by nanoindentation. Tribol Int. 2003;36:973–985. [Google Scholar]
- Horkay F, Nagy M. Elasticity of swollen polyvinyl alcohol and poly(vinyl acetate) networks. Polym Bull. 1980;3:457–463. [Google Scholar]
- Horkay F, McKenna GB. Polymer networks and gels. In: Mark JE, editor. Physical properties of polymers handbook. New York: Springer; 2007. [Google Scholar]
- Horkay F, Horkayne-Szakaly I, Basser PJ. Measurement of the osmotic properties of thin polymer films and biological tissue samples. Biomacromolecules. 2005;6:988–993. doi: 10.1021/bm049332c. [DOI] [PubMed] [Google Scholar]
- Huang AH, Yeger-McKeever M, Stein A, Mauck RL. Tensile properties of engineered cartilage formed from chondrocyteand MSC-laden hydrogels. Osteoarthr Cartil. 2008;16:1074–1082. doi: 10.1016/j.joca.2008.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwashita N, Swain MV, Field JS, Ohta N, Bitoh S. Elasto-plastic deformation of glass-like carbons heat-treated at different temperatures. Carbon. 2001;39:1525–1532. [Google Scholar]
- Janjanin S, Li WJ, Morgan MT, Shanti RM, Tuan RS. Moldshaped, nanofiber scaffold-based cartilage engineering using human mesenchymal stem cells and bioreactor. J Surg Res. 2008;149:47–56. doi: 10.1016/j.jss.2007.12.788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson KL. Contact mechanics. Cambridge: Cambridge University Press; 1985. [Google Scholar]
- Kilian HG. An interpretation of the strain-invariants in largely strained networks. Colloid Polym Sci. 1985;263:30–34. [Google Scholar]
- Klein TJ, Chaudhry M, Bae WC, Sah RL. Depth-dependent biomechanical and biochemical properties of fetal, newborn, and tissue-engineered articular cartilage. J Biomech. 2007;40:182–190. doi: 10.1016/j.jbiomech.2005.11.002. [DOI] [PubMed] [Google Scholar]
- Kumar MV, Narasimhan R. Analysis of spherical indentation of linear viscoelastic materials. Curr Sci. 2004;87:1088–1095. [Google Scholar]
- Lee EH. Stress analysis in visco-elastic bodies. Q Appl Math. 1955;13:183–190. [Google Scholar]
- Lee EH, Radok JRM. The contact problem for viscoelastic bodies. J Appl Mech. 1960;27:438–444. [Google Scholar]
- Lin DC, Dimitriadis EK, Horkay F. Robust strategies for automated AFM force curve analysis—I. Non-adhesive indentation of soft, inhomogeneous materials. J Biomech Eng. 2007a;129:430–440. doi: 10.1115/1.2720924. [DOI] [PubMed] [Google Scholar]
- Lin DC, Dimitriadis EK, Horkay F. Elasticity of rubber-like materialsmeasured by AFM nanoindentation. Express Polym Lett. 2007b;1:576–584. [Google Scholar]
- Lu H, Wang B, Ma J, Huang G, Viswanathan H. Measurement of creep compliance of solid polymers by nanoindentation. Mech Time-Depend Mater. 2003;7:189–207. [Google Scholar]
- Maikos JT, Elias RA, Shreiber DI. Mechanical properties of dura mater from the rat brain and spinal cord. J Neurotrauma. 2008;25:38–51. doi: 10.1089/neu.2007.0348. [DOI] [PubMed] [Google Scholar]
- Mattice JM, Lau AG, Oyen ML, Kent RW. Spherical indentation load-relaxation of soft biological tissues. J Mater Res. 2006;21:2003–2010. [Google Scholar]
- Mauck RL, Wang CC, Oswald ES, Ateshian GA, Hung CT. The role of cell seeding density and nutrient supply for articular cartilage tissue engineering with deformational loading. Osteoarthr Cartil. 2003;11:879–890. doi: 10.1016/j.joca.2003.08.006. [DOI] [PubMed] [Google Scholar]
- Mesarovic SDJ, Fleck NA. Spherical indentation of elastic– plastic solids. Proc R Soc Lond A Math Phys Eng Sci. 1999 [Google Scholar]
- Mooney M. A theory of large elastic deformation. J Appl Phys. 1940;11:582–592. [Google Scholar]
- Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression. Theory and experiments. J Biomech Eng. 1980;102:73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- Ng L, Hung HH, Sprunt A, Chubinskaya S, Ortiz C, Grodzinsky A. Nanomechanical properties of individual chondrocytes and their developing growth factor-stimulated pericellular matrix. J Biomech. 2007;40:1011–1023. doi: 10.1016/j.jbiomech.2006.04.004. [DOI] [PubMed] [Google Scholar]
- Ogden RW. Large deformation isotropic elasticity—on the correlation of theory and experiment for incompressible rubberlike solids. Proc R Soc Lond A Math Phys Sci. 1972;326:565–584. [Google Scholar]
- Oyen ML. Spherical indentation creep following ramp loading. J Mater Res. 2005;20:2094–2100. [Google Scholar]
- Pandit A, Lu X, Wang C, Kassab GS. Biaxial elastic material properties of porcine coronary media and adventitia. Am J Physiol Heart Circ Physiol. 2005;288:H2581–H2587. doi: 10.1152/ajpheart.00648.2004. [DOI] [PubMed] [Google Scholar]
- Park S, Costa KD, Ateshian GA. Microscale frictional response of bovine articular cartilage from atomic force microscopy. J Biomech. 2004;37:1679–1687. doi: 10.1016/j.jbiomech.2004.02.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prange MT, Margulies SS. Regional, directional, and agedependent properties of the brain undergoing large deformation. J Biomech Eng. 2002;124:244–252. doi: 10.1115/1.1449907. [DOI] [PubMed] [Google Scholar]
- Rivlin RS, Saunders DW. Large elastic deformations of isotropic materials. VII. Experiments on the deformation of rubber. Philos Trans R Soc A. 1951;243:251–288. [Google Scholar]
- Schinagl RM, Gurskis D, Chen AC, Sah RL. Depth-dependent confined compression modulus of full-thickness bovine articular cartilage. J Orthop Res. 1997;15:499–506. doi: 10.1002/jor.1100150404. [DOI] [PubMed] [Google Scholar]
- Schulze-Bauer CA, Regitnig P, Holzapfel GA. Mechanics of the human femoral adventitia including the high-pressure response. AmJ Physiol Heart Circ Physiol. 2002;282:H2427–H2440. doi: 10.1152/ajpheart.00397.2001. [DOI] [PubMed] [Google Scholar]
- Sperling LH. Introduction to physical polymer science. 3rd edn. Wiley; New York: 2001. [Google Scholar]
- Storm C, Pastore JJ, MacKintosh FC, Lebensky TC, Janmey PA. Nonlinear elasticity in biological gels. Nature. 2005;435:191–194. doi: 10.1038/nature03521. [DOI] [PubMed] [Google Scholar]
- Swain MV, Hagan JT. Indentation plasticity and the ensuing fracture of glass. J Phys D. 1976;9:2201–2214. [Google Scholar]
- Tabor D. A simple theory of static and dynamic hardness. Proc R Soc Lond A Math Phys Sci. 1948;192:247–274. [Google Scholar]
- Tabor D. The hardness of metals. Oxford: Oxford University Press; 1951. [Google Scholar]
- Taljat B, Zacharia T, Kosel F. New analytical procedure to determine stress–strain curve from spherical indentation data. Int J Solids Struct. 1998;35:4411–4426. [Google Scholar]
- Treloar LRG. The photo-elastic properties of rubber. Part I: Theory of the optical properties of strained rubber. Trans Faraday Soc. 1947;43:277–283. [Google Scholar]
- Treloar LRG. The physics of rubber elasticity. 3rd edn. Oxford: Oxford University Press; 1975. [Google Scholar]
- Tschoegl NW, Gurer C. Behavior of elastomer networks inmoderately large deformations. 1. Elastic equilibrium. Macromolecules. 1985;18:680–687. [Google Scholar]
- Tweedie CA, Van Vliet KJ. Contact creep compliance of viscoelastic materials via nanoindentation. J Mater Res. 2006;21:1576–1589. [Google Scholar]
- Zhang K, Siegmund T, Chan RW. A constitutive model of the human vocal fold cover for fundamental frequency regulation. J Acoust Soc Am. 2006;119:1050–1062. doi: 10.1121/1.2159433. [DOI] [PubMed] [Google Scholar]