Abstract
A system capable of tracking radiation force induced shear wave propagation in a 3D volume using ultrasound is presented. In contrast to existing systems, which use 1D array transducers, a 2D matrix array is used for tracking shear wave displacements. A separate single element transducer is used for radiation force excitation. This system allows shear wave propagation in all directions away from the push to be observed. It is shown that for a limit of 64 tracking beams, by placing the beams at the edges of the measurement region of interest (ROI) at multiple directions from the push, time-of-flight (TOF) shear wave speed (SWS) measurement uncertainty can theoretically be reduced by 40% compared to equally spacing the tracking beams within the ROI along a single plane, as is typical when using a 1D array for tracking. This was verified by simulation, and a reduction of 30% was experimentally observed on a homogeneous phantom. Analytical expressions are presented for the relationship between TOF SWS measurement uncertainty and various shear wave imaging parameters. It is shown that TOF SWS uncertainty is inversely proportional to ROI size, and inversely proportional to the square root of the number of tracking locations for a given distribution of beam locations relative to the push. TOF SWS uncertainty is shown to increase with the square of the SWS, indicating that TOF SWS measurements are intrinsically less precise for stiffer materials.
Index Terms: acoustic radiation force, shear wave imaging, elastography, ultrasound
I. Introduction
Shear wave imaging is a quantitative method of measuring tissue stiffness non-invasively and in vivo. Shear waves can be generated in tissue by muscle activity [1]–[4], external mechanical excitation [5]–[7], or using acoustic radiation force [8]–[11]. The shear wave speed (SWS) in tissue is directly related to its stiffness. By monitoring shear wave propagation using a real-time imaging modality such as magnetic resonance imaging (MRI) [5], [6], [12] or ultrasound [7]–[11], the underlying tissue stiffness can be estimated.
A commonly used technique for SWS estimation from ultrasonically tracked tissue displacement is the so-called time-of-flight (TOF) method [7], [13], [14]. The shear wave arrival time is measured at several locations within a spatial region of interest (ROI), or kernel. Under assumptions of homogeneity, negligible dispersion, and a fixed direction of propagation within the ROI, a linear model can be fit to the arrival times. The linear relationship between spatial location and arrival times can then be used to calculate the SWS.
This paper presents an ultrasonic system capable of monitoring acoustic radiation force induced shear wave displacement within a volume of tissue. In contrast to previous systems which use 1D array transducers mechanically swept to acquire volumetric data [15], a 2D matrix array transducer capable of electronic beamforming in both the lateral and elevation dimensions is used for tracking shear wave displacement. This enables shear wave arrival times to be measured in multiple directions from the radiation force excitation axis without the need for manual repositioning of the probe. The ability to monitor shear wave propagation in multiple directions has several advantages. First, it allows anisotropic mechanical properties to be characterized [16]. Second, it increases the amount of data that can be acquired and used for SWS estimation. Finally, it enables additional flexibility in the placement of tracking beam locations.
In this paper, the potential for improving SWS measurement precision in a homogeneous material by utilizing additional tracking beam locations available from a 2D matrix array is investigated. The first portion of this paper derives theoretical expressions for the uncertainty in TOF SWS estimation. It is then shown that given a fixed number of tracking locations, and ROI size, the precision of TOF SWS estimation in a homogeneous material can be improved by increasing the spread of the tracking beam locations relative to the push using a 2D array. These theoretical results are then verified by simulations and experimental data acquired on phantoms using the 2D matrix array transducer.
II. Uncertainty in TOF SWS Estimation
Measurement uncertainty can be classified into two groups: random, and systematic [17]. In TOF SWS estimation using acoustic radiation force induced shear waves, the measured SWS is dependent on factors such as the frequency content of the shear wave [10], [18], and the location of the reconstruction region relative to the excitation geometry [19]. These factors result in a systematic bias of the measured SWS. TOF SWS measurement is also subject to random errors such as jitter in ultrasonic displacement tracking [20]. These type of errors have zero mean and give rise to a range of SWS in repeat measurements. In general, systematic errors are difficult to analyze because the underlying ‘true’ value of the SWS is usually unknown. In contrast, random error can be assessed by examining the spread of repeat measurements. Although systematic bias among different SWS measurement systems pose a significant challenge to the clinical acceptance of this technology [21], [22], the analysis of sources of bias in SWS estimation is outside the scope of this study. Instead, the focus of this paper is restricted to random measurement error in TOF SWS estimation. The terms ‘uncertainty’ and ‘precision’ throughout this paper refer to the spread, or error bar size, of repeat measurements, and do not include bias. When the spread of repeat SWS measurements is low, the measurement is described as having high precision, or low uncertainty.
The uncertainty in TOF SWS measurement due to random error (unbiased with zero mean) is now derived. Consider least squares fitting of a line to a set of n shear wave arrival times t = {t1, t2, . . . , tn} measured at distances r = {r1, r2, . . . , rn} orthogonal to the push axis (the assumed direction of shear wave propagation). Note that r can represent spatial locations within the entire 2D plane orthogonal to the push axis. Multiple points within this plane can have the same value of r (the locus of these points is a circle of radius r with its center at the push). Let t̂ denote the least squares fit line, β̂1 the corresponding slope, and β̂0 the intercept, such that
| (1) |
The least squares solution is given by [23]:
| (2a) |
| (2b) |
where
| (3a) |
| (3b) |
| (3c) |
| (3d) |
The covariance Cov(r, t) is a measure of the extent to which variations in t can be predicted by a linear function in r. When the covariance is zero, the minimum mean square error linear estimator for t in terms of r is simply the mean value of t (3d). When t is perfectly correlated with r, the covariance is equal to the product of the standard deviation of the two variables, Cov(r, t) = σrσt (note that σt is calculated the same way as σr in (3b)). The least squares slope (2a) in this case becomes the ratio σt/σr (intuitively, the variance in r is rescaled to have the same variance as t).
Deviations in the arrival times about the least squares line are given by
| (4) |
It is assumed that these deviations are due to random errors in measuring the arrival time of the shear wave. Sources of measurement error include ultrasonic displacement tracking jitter due to speckle decorrelation and finite tracking kernel size [20], [24], as well as under-sampling due to the finite pulse repetition frequency (prf) used for tracking. These type of errors are normally distributed, and do not include gross outliers, which can be removed by an algorithm such as RANSAC [25]. Assuming that the variance of arrival time measurement error is σε2 such that
| (5) |
then the least squares estimated slope β̂1 will also be a normally distributed random variable [23]:
| (6) |
where β1 is the true TOF slope, and the standard deviation is given by
| (7) |
To estimate the TOF SWS (ct), one calculates the inverse slope of the above linear model relating measured arrival times and distance from the push location:
| (8) |
We are interested in the statistical distribution of ĉt, namely, the uncertainty in ĉt due to uncertainty in the estimated slope β̂1. To find this, we begin by writing the probability density function (pdf) of β̂1:
| (9) |
Making the change of variable
| (10) |
such that
| (11a) |
| (11b) |
and using the rule for transformation of random variables [26]
| (12) |
(9) can be converted into the standard normal distribution:
| (13) |
Applying the same change of variable to (8) gives
| (14) |
Equation (14) can be expanded as a binomial series as follows
| (15) |
The term (σβ̂1/β1) in (15) represents the ratio between the standard deviation of the estimated slope and its true value, and is equivalent to the inverse of the signal to noise ratio (SNR) of the arrival time data.
If we assume that β1 ≫ σβ̂1, or that we have high SNR arrival time data, (15) can be linearized by ignoring higher order terms:
| (16) |
Rearranging (16), one finds that
| (17a) |
| (17b) |
By the rule for transformation of random variables,
| (18) |
Substituting (17) into (18) yields
| (19) |
From (19), it can be seen that the estimated SWS ĉt has a normal distribution of
| (20) |
Since the inverse of the true TOF slope β1 is equivalent to the true TOF SWS ct, one finds that
| (21) |
As expected, the mean value of ĉt is the true TOF SWS ct. The standard deviation of the estimated SWS is given by
| (22) |
Substituting (7) into (22), one finds:
| (23) |
The above result indicates that the uncertainty of TOF SWS estimation is proportional to the square of the SWS. It is linearly proportional to the arrival time measurement error, and inversely proportional to the standard deviation of the radial distances sampled by the tracking beams. For a fixed distribution of radii, the SWS error is also inversely proportional to the square root of the number of tracking beams, as would be expected from averaging multiple measurements. Thus, given the same arrival time measurement error, and the same tracking locations, the uncertainty in TOF SWS measurement increases with the square of the SWS. This is a fundamental limit for the performance of the TOF SWS estimation method. Equation (23) is valid for any wave arrival time estimation technique. As an example, two common approaches include detecting the time to peak (TTP) and the time to peak slope (TTPS) of the shear wave displacement. In a dispersive medium, these two methods may result in different biases in the measured SWS (a systematic error). However, the distribution of the SWS about its mean value from repeat measurements is still given by (23). In the next section, the potential for improving the precision of TOF SWS measurements by increasing σr through the use of the 2D matrix array for tracking shear waves are explored.
III. Methods
It can be seen from (23) that by increasing σr, the standard deviation of TOF SWS measurements can be reduced. The term σr is a measure of the spread of the radial distances sampled by the tracking beams, r, about its mean value r̅. Increasing σr can be accomplished by increasing the number of tracking beams at the edges of the ROI. Zhai et al. [27] has previously shown that when only 4 tracking beams are available from a 1D array, positioning the beams at the ends of the ROI leads to the lowest SWS estimation uncertainty. As will be demonstrated in the following subsections, by taking advantage of the additional flexibility in the placement of the tracking beam locations afforded by the 2D matrix array, a large number of tracking beams can be positioned at the edges of the ROI to increase σr. The next subsection will present theoretical predictions of improvement in SWS estimation precision for various possible beam location configurations using the 2D matrix array. This is followed by descriptions of experimental and simulation studies performed to verify these results.
A. Theory
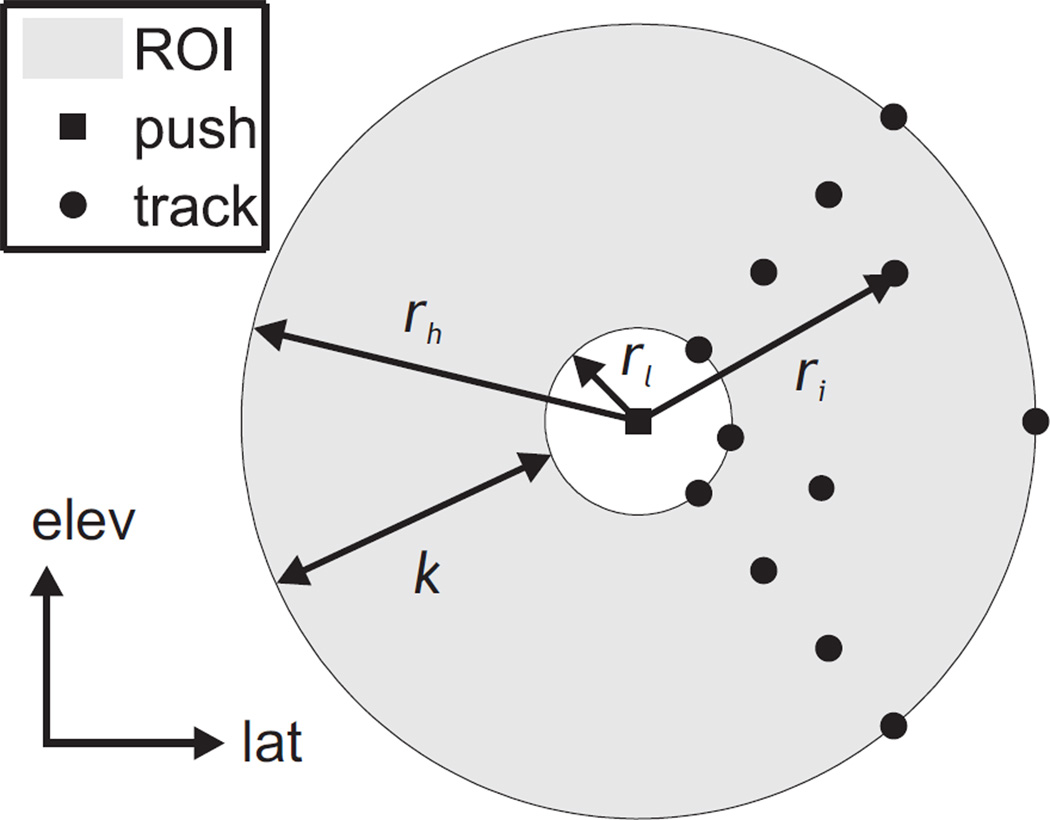
Consider a ROI with radial range between rl and rh from the axis of excitation such that rl ≤ r ≤ rh, as shown in Fig. 1. The size of the ROI, k, is given by k = rh − rl. Geometrically, this corresponds to an annulus within the plane orthogonal to the push axis centered at the push. Let the number of unique radial positions sampled by the tracking beams be nr. Note that more than one beam can have the same radial position r. Let the total number of tracking beams n be distributed such that there are an equal number of beams, nθ, at each radius. That is,
| (24) |
Fig. 1.
Geometry of the kernel over which shear wave arrival times are measured for TOF SWS estimation in the coronal (lateral-elevation) plane. The kernel (shaded gray) extends between rl and rh with a range k, and is centered on the push location (black square). The push axis is assumed to coincide with the axial dimension, which is orthogonal to the page in this view. Example tracking beam locations measuring shear wave arrival times are shown (black circles), and the radial position of one beam, ri, is marked. For this example configuration, four unique radial positions are sampled by the tracking beams (nr = 4) and there are three beams at each radius (nθ = 3).
In such a configuration, the variance in tracking beam radii, σr2, can be found using only the unique radial positions sampled (since each one is weighted equally by the same number nθ). If the radii are evenly spaced within the extent of the ROI, then the location of the ith unique radius, ri, is given by
| (25) |
Substituting (25) into (3b) and simplifying, one finds that the variance of the tracking beam radii of such a configuration is given by the function
| (26) |
Substituting (26) into (23), it can be seen that
| (27) |
and that the TOF SWS uncertainty is inversely proportional to the ROI size k.
Let us now consider a typical tracking beam configuration available from a conventional 1D array transducer for monitoring radiation force induced shear wave propagation. The SWS precision from tracking using a 2D matrix array will be compared to this reference configuration throughout this paper. Let the push be located at the center of the imaging field of view (FOV), and shear wave propagation tracked both to the left and right of the push. If half the total number of tracking beams are allocated to each side of the push (i.e., nθ = 2, nr = n/2), and they are equally spaced within the annular ROI, then
| (28) |
where the subscript 1D denotes a 1D array beam configuration.
Using a 2D matrix array capable of beamforming in both elevation and lateral dimensions, the shear wave arrival time can be monitored in an arbitrary number of directions from the push. This additional flexibility enables the number of arrival time measurements taken at each radius, nθ, to be greater than two. To keep the total number of tracking beams constant, the number of unique radii sampled can be set to nr = n/nθ. If these are again evenly spaced within the radial extent of the ROI, then
| (29) |
where the subscript 2D denotes a 2D array beam configuration.
Let R be the ratio of the TOF SWS uncertainty obtained using the beam configurations for a 2D matrix array as described above versus the reference configuration for a 1D array transducer:
| (30) |
It is clear from (23) that if the number of beams n, arrival time measurement uncertainty σε, and underlying SWS ct are equal for both the 1D and 2D array configurations, then R is given by the ratio of the spread in beam locations:
| (31a) |
| (31b) |
Finally, substituting (26) into (31) and assuming equal ROI range k, one finds
| (32) |
When nθ = 2, the beam configuration corresponding to a 1D array transducer is obtained, and R = 1. As nθ increases, R decreases, and a reduction in TOF SWS uncertainty is obtained. The maximum decrease in R occurs when (nθ, nr) = (n/2, 2), corresponding to the case when arrival times are only measured at the edges of the ROI, with half the tracking beams allocated to each edge. Intuitively, this makes sense, since the spread in the beam distances to the push is maximized in this configuration, leading to a large value of σr.
B. Experiment
1) Data Acquisition
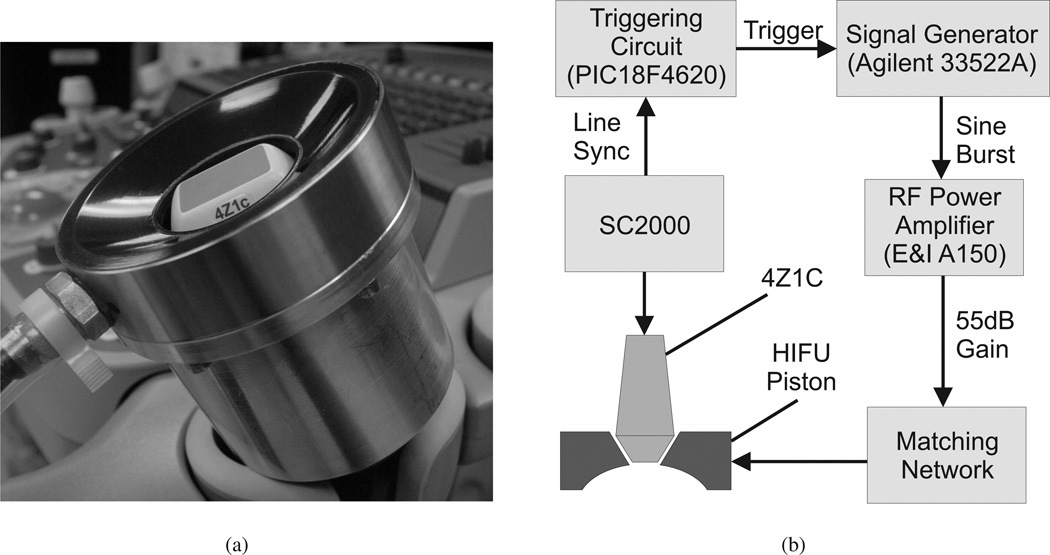
To experimentally demonstrate the reduction in TOF SWS uncertainty possible through multi-directional tracking in homogeneous materials, the Siemens 4Z1C matrix array transducer and the SC2000 scanner (Siemens Healthcare, Ultrasound Business Unit, Mountain View, CA, USA) were used to monitor acoustic radiation forced induced shear waves in phantoms. The 4Z1C array contains 48 × 36 (lateral × elevation) square elements 0.4mm in dimension. An annular focused HIFU piston transducer (H-101, Sonic Concepts, Bothell, WA) was used for acoustic radiation force impulse (ARFI) excitation (1.1 MHz, F/1, 63.2mm focal depth). The 4Z1C was inserted into the central opening of the HIFU piston and the two transducers were rigidly coupled using a specially designed holder, as shown in Fig. 2(a). The two transducers were synchronized using a custom triggering circuit, as shown in the system block diagram in Fig. 2(b).
Fig. 2.
(a) The 4Z1C imaging transducer inserted into the central opening of the HIFU piston and rigidly fixed with the holder. (b) System block diagram of the experimental setup used for tracking radiation force induced shear wave propagation in 3D. The shear wave is generated with the HIFU piston, and tracked using the 4Z1C matrix array. The two transducers are synchronized by the line sync signal from the SC2000, which provides precise timing of transmit events on the 4Z1C. When the appropriate number of transmits have occurred, the triggering circuit causes the signal generator to emit a 1.1MHz burst of selected amplitude and duration (200–400 cycles). This signal is amplified by 55 dB by an RF power amplifier (E&I A150, Electronics & Innovation, Rochester, NY), and goes through an impedance matching network, before finally driving the HIFU piston to generate the acoustic radiation force push.
Shear waves were induced in homogeneous phantoms of varying Young’s modulus between 4.8–127 kPa (CIRS, Norfolk, VA, USA). For a linear, isotropic, elastic medium, the relationship between Young’s modulus (E) and shear wave speed is
| (33) |
where ν is the Poisson’s ratio (assumed to be 0.5) and ρ the density of the material (assumed to be 1000 kg/m3). Multiple interrogations in different locations of the phantoms were performed to obtain different B-mode speckle and different realizations of arrival time measurement noise. An excitation pulse with a derated intensity of ISPPA.3 = 3175W/cm2 (in situ ISPPA.7 = 1674W/cm2) was used, and the same excitation pulse length was used for repeated interrogations in the same phantom. This pulse length was varied between 200–400 cycles for the different phantoms to ensure adequate displacement (> 1 µm) was obtained in all cases. The resulting shear waves were imaged using the 4Z1C at a center frequency of 2.8MHz.
Due to current limitations of the SC2000 beamforming hardware, arbitrary placement of beam locations was not possible. To overcome this deficiency, a finely spaced rectangular grid of 72 × 72 (lateral × elevation) beams was used for monitoring the shear wave to provide a large number of possible tracking beam locations. Desired beam configurations were then tested by using the data from a subset of the beams from this grid. At an imaging depth of 60mm, which is near the push focal depth when the two transducers are coupled, the average beam spacing is 0.54mm in both lateral and elevation dimensions, and the FOV is 38 × 38mm. The radiation force excitation was located approximately at the center of the FOV, so that the resultant shear wave propagation can be visualized in all directions. 64:1 parallel receive was used to beamform a grid of 8 × 8 beams on every transmit so that only 81 transmits were required to interrogate the entire grid of 72 × 72 beams. Shear wave displacement was monitored by repeating the push, and sequentially monitoring each of the 81 parallel receive beam groups in turn, until data from the entire FOV was acquired. The time interval between pushes was 22 sec, and was limited by the data transfer rate on the SC2000. Using this method, a high tracking prf of 7.7 kHz is obtained. Although this approach requires a relatively long acquisition time, and 81 pushes to acquire data from the entire FOV, these drawbacks are not critical issues when imaging phantoms. The benefit is that shear wave displacement data with high sampling rates both spatially and temporally is obtained.
2) Data Processing
Axial displacement along each beamline was measured using the zero-phase displacement estimation algorithm described by Pesavento et al. [28] on IQ data. Acoustic radiation force induced displacements in the lateral and elevational directions are on the order of a magnitude smaller than the axial component [29], and cannot be monitored by ultrasonic speckle tracking methods. Therefore, only 1D displacement tracking was performed. Shear wave arrival times were measured by finding the time to peak slope (TTPS) of the displacement time profile at each location. Arrival times were analyzed at a imaging depth of 60mm near the excitation focus.
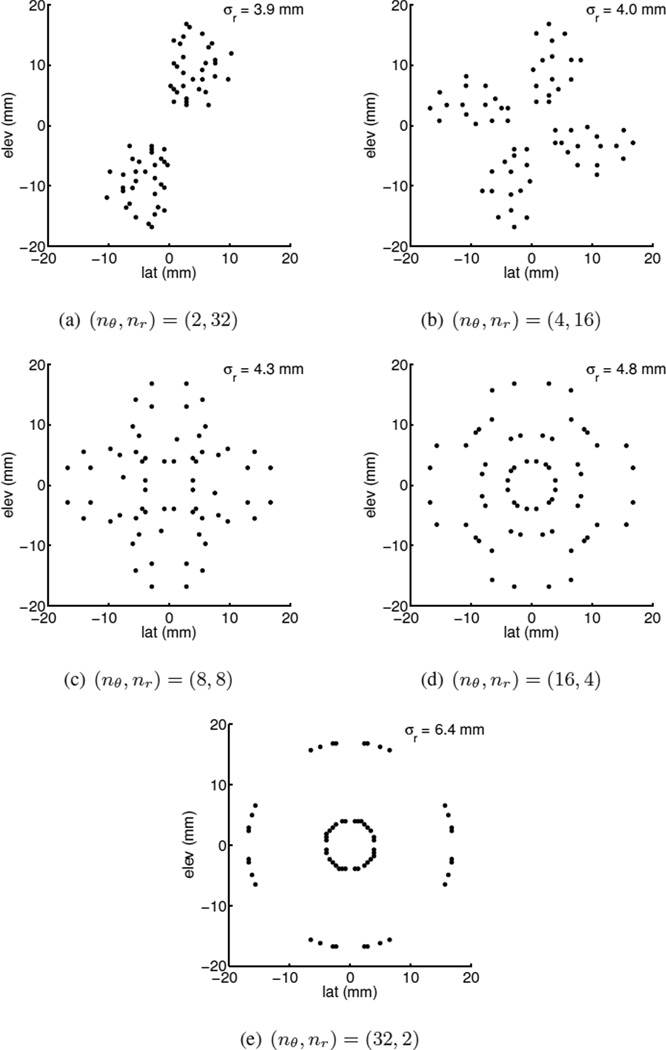
The number of tracking beams (n) used for SWS reconstruction was limited to 64. This is the number of parallel receive channels available from the SC2000, and represents the maximum number of locations the shear wave from a single ARFI excitation can be monitored with this scanner. Five different configurations for the 64 tracking beams were tested: (nθ, nr) = {(2, 32), (4, 16), (8, 8), (16, 4), (32, 2)}, with radii equally spaced between 4–17mm from the push, corresponding to a ROI size of 13mm. With a more extensively programmable system, or with a software beamforming system interfaced with the matrix probe, all the data from these beam configurations could be acquired with a single transmit and ARFI excitation. However, as previously mentioned, due to the current limitations of the SC2000, these beam configurations were implemented by choosing a subset of beams from a rectangular grid of 72 × 72 beam locations. For each configuration, beam locations from the 72×72 grid closest to the desired set of radii, assuming the push was located at the center of the FOV, were selected for SWS estimation. Data at remaining beam locations were not used. Thus, data for all five different beam configurations were synthesized from each full 72 × 72 grid data-set. The beam locations selected for all configurations are illustrated in Fig. 3. Note that in order to obtain the required set of distances between the beams and the push axis from the limited grid locations, the beam patterns are not arranged in straight lines radiating out from the center of the FOV as one would expect.
Fig. 3.
Beam locations from a 72 × 72 grid at 60mm imaging depth used for SWS estimation. The standard deviation of the beam distances from the push at the center of the FOV, σr, is shown for each configuration. Although the beams for the (nθ, nr) = (2, 32) case do not lie on a straight line, they have the same σr as a typical configuration when using a 1D array for shear wave imaging. The other cases correspond to additional configurations possible using a 2D array.
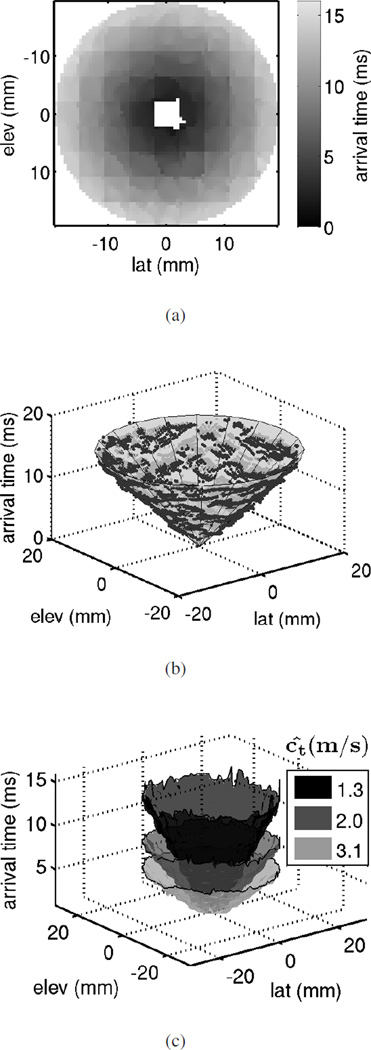
Since the location of the ARFI push from the HIFU piston relative to the 4Z1C is not known precisely, SWS estimation using experimental data was performed by least squares fitting a conical surface to the arrival times, as shown in Fig. 4(b). The axis of the cone corresponds to the axis of the ARFI excitation relative to the 4Z1C. When the HIFU piston and the 4Z1C are perfectly aligned, the cone axis coincides with the arrival time axis (the z-axis in Fig. 4(b)) and goes though the origin. The remaining two degrees of freedom, the cone opening angle, and the location of its apex along its axis, directly correspond to the slope and intercept parameters of the linear model relating arrival times to distance from the push (see equation (1)). For each data-set, the arrival times as a function of location from all the beams in the 72 × 72 grid at 60mm depth were fit to a cone to estimate the actual orientation and position of the push axis. To compensate for misalignment between the HIFU probe and the 4Z1C, cones with this same axis were fit to the arrival time data from the selected beam locations for each configuration. In other words, only the opening angle and the apex location of the cone were allowed to vary. Least squares optimization of these two parameters is equivalent to finding the slope and intercept in line-fitting. The SWS is estimated using the opening angle of the least squares cone for each configuration.
Fig. 4.
(a) Shear wave arrival times measured from the 4.8 kPa homogeneous phantom in the plane orthogonal to the push axis at an imaging depth of 60mm, which is near the excitation focal depth. The push is approximately at the center of the FOV. Arrival time measurements close to the push near the center of the FOV were not possible, as a result of reverberation echoes of the radiation force excitation. (b) Least squares cone-fit to the arrival times shown in (a). The actual push axis location and orientation, as well as the SWS can be estimated from the parameters of the cone. (c) Surface plots of arrival times at the same imaging depth (60mm) measured from three homogeneous phantoms of different stiffness. The estimated SWS from cone-fits to the data shown are displayed.
C. Simulation
Simulations were performed in MATLAB (The MathWorks, Natick, MA, USA) to verify the theoretical reduction in TOF SWS uncertainty shown in (31). Shear wave arrival times were generated for the five beam configurations experimentally tested ((nθ, nr) = {(2, 32), (4, 16), (8, 8), (16, 4), (32, 2)}) within the same radial domain (4–17mm from the push). The beam locations used were exact, and not quantized by the 72×72 grid as for the experiment. The arrival times were generated as follows. First, the ideal arrival time at each beam location was calculated using its distance from the push and a SWS of 1.26m/s, which is the same SWS as the 4.8 kPa phantom. Then, normally distributed noise with zero mean and a standard deviation of σε = 0.6 ms, similar to experimentally observed noise levels [25], was added to the ideal arrival times to simulate measurement noise. SWS estimation was performed by calculating the inverse slope of the least-squares fit line to these noisy arrival times, as previously described. This was repeated for 10000 realizations of noisy arrival time data-sets for all five beam configurations. The standard deviation (precision) of the SWS over the 10000 realizations for the five different beam configurations was finally compared.
IV. Results
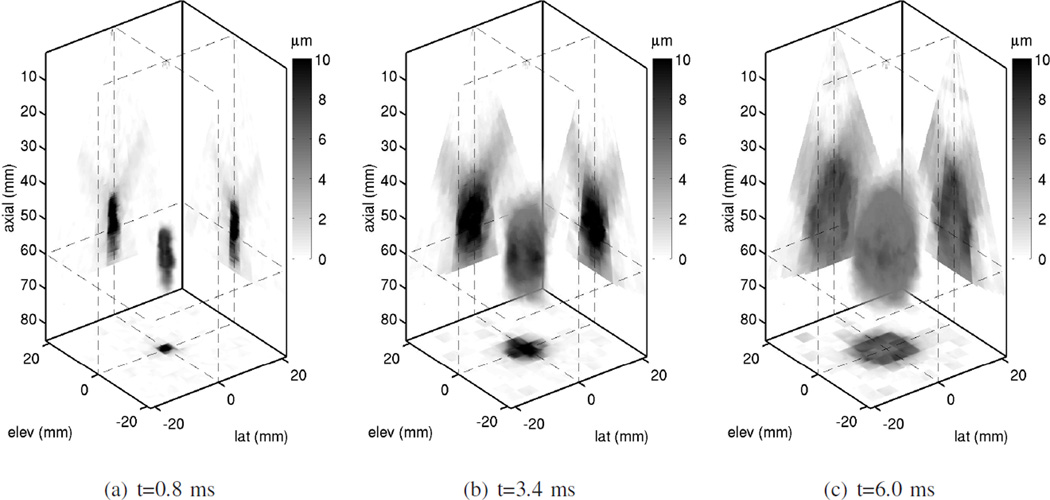
Three dimensional displacement fields measured using the 4Z1C after ARFI excitation in the 4.8 kPa phantom with the HIFU piston are shown in Fig. 5. Although a HIFU piston was used for radiation force excitation, due to the short duration of the ARFI pulse (182 − 364 µs), displacement magnitudes on the order of microns are obtained axially along the beamline direction. As previously mentioned, displacement in the lateral and elevation directions are negligible in comparison [29], and were not measured. It is evident from Fig. 5 that as time after the excitation increases, locations increasingly further away from the push are perturbed by the shear wave. Although shear wave data is analyzed in only one plane near the excitation focus in this paper, ARFI induced shear wave displacement throughout a 3D volume can be monitored using the matrix array.
Fig. 5.
3D displacement field measured by the 4Z1C after ARFI excitation using the HIFU piston in a 4.8 kPa phantom. The displacements measured along the beamline direction using 1D speckle tracking are shown as a volume rendering at three different time steps after the excitation. Darker pixels correspond to larger displacement amplitude. The push axis is parallel to the axial direction and is centered at the origin in the lateral and elevation dimensions. Orthogonal sections of the displacement field at planes indicated by the dashed lines are also projected onto the back walls of the plot. One of these planes is a coronal view (orthogonal to the push axis) at an axial depth of 60mm, which is close to the excitation focus. Throughout this paper, shear wave data from this plane is analyzed (i.e., the plane shown in Fig. 4).
The shear wave arrival times in the FOV at 60mm for one acquisition on the 4.8 kPa phantom are shown in Fig. 4(a). Due to reverberation echoes of the radiation force excitation, displacement estimates early in time after the push were not available. Therefore, arrival time measurements close to the push near the center of the FOV were not possible. As expected, the shear wave takes longer to reach locations further from the push. The arrival time appears isotropic, as would be expected for a homogeneous isotropic material. Due to the slow SWS in this phantom, the shear wave did not reach the corners of the FOV within the tracking duration. Fig. 4(b) illustrates the cone-fit to the arrival times for the example in Fig. 4(a). The SWS can be estimated from the opening angle of the cone. A faster SWS corresponds to lower arrival times, and consequently, a bigger opening angle. Fig. 4(c) shows surface plots of arrival times from acquisitions on three homogeneous phantoms of different stiffness (E = 4.8, 12, 30 kPa), and estimated SWS from each using cone-fits to the data.
The accuracy of the alignment between the HIFU probe and the 4Z1C was assessed from the axis of the cones fit to arrival times from 200 acquisitions collected on the 4.8 kPa phantom over multiple days, during which the HIFU probe was repeatedly disassembled and re-attached to the 4Z1C. The axis of the HIFU piston and the 4Z1C had an average difference of 0.5 ± 0.3° in orientation and 0.5 ± 0.2mm in position at an imaging depth of 60mm. Thus, the radii of the tracking beams in Fig. 3, which were computed assuming a perfectly aligned push axis and the 4Z1C, should not be significantly different from their intended values.
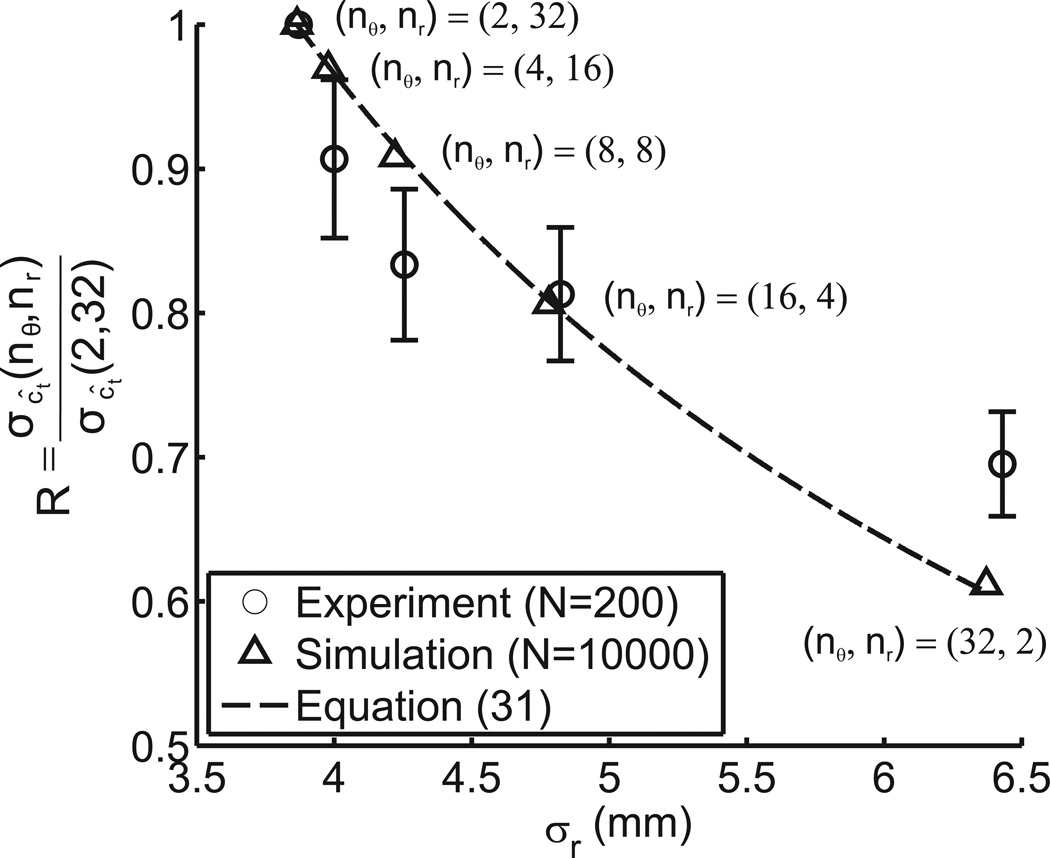
The reduction in SWS uncertainty predicted by (31) for 64 tracking beams with different σr is plotted in Fig. 6. The standard deviation of the estimated SWS from 10000 sets of simulated arrival times was calculated for the five beam configurations (nθ, nr) = {(2, 32), (4, 16), (8, 8), (16, 4), (32, 2)}. These values were normalized by the standard deviation for the reference 1D array case ((nθ, nr) = (2, 32)), and are shown on the same plot. Similarly, the SWS standard deviation from 200 acquisitions on the 4.8 kPa phantom was calculated for the five beam configurations, and the experimentally achieved reduction in SWS standard deviation is also shown on the same figure. Note that the σr values plotted in Fig. 6 for the experimentally implemented configurations are from the actual beam locations used. These differ from the σr values of the prescribed beam configurations (shown by the x-axis location of the simulated data points) due to quantization error from the limited beam locations available from the 72 × 72 grid. However, the differences in σr were small (on average 0.03 mm for the five configurations), as can be seen by comparing the x-axis locations of the experimental and simulated data points on Fig. 6. To calibrate the reader, the experimental SWS standard deviation for the baseline (nθ, nr) = (2, 32) case was 0.016m/s. Due to practical restrictions, the number of experimental data-sets used to assess TOF SWS precision was limited to 200. To illustrate the uncertainty in estimating the standard deviation from 200 samples, the SWS standard deviation from a subset of 200 samples randomly selected from the 10000 simulated data-sets for each beam configuration was compared to the standard deviation for the entire 10000 samples. This was repeated for 1000 randomly selected subsets. The mean difference in standard deviation evaluated over 200 and 10000 samples are plotted as error bars in Fig. 6.
Fig. 6.
SWS standard deviation for the five tracking beam configurations tested as a ratio of the standard deviation for the reference 1D array case ((nθ, nr) = (2, 32)). The predicted values for this ratio using the σr values of the beams and (31) are shown by the dashed curve. The reduction obtained from 10000 simulated noisy arrival time data-sets is marked by triangles, and that from 200 experimentally acquired data-sets from a homogeneous phantom is marked by circles. Note that the σr values for the experimental data are slightly different from the prescribed beam configurations due to the limited beams available from the 72 × 72 grid. The error bars on the experimental data show the expected uncertainty in estimating the standard deviation from only 200 samples. These were determined by comparing the standard deviation of 1000 sets of 200 randomly selected samples from the 10000 data-sets simulated for each configuration with the standard deviation obtained over all 10000 samples. Note that there is no error bar for the reference 1D array case ((nθ, nr) = (2, 32)), because this is used for normalization, and by definition equals to 1.
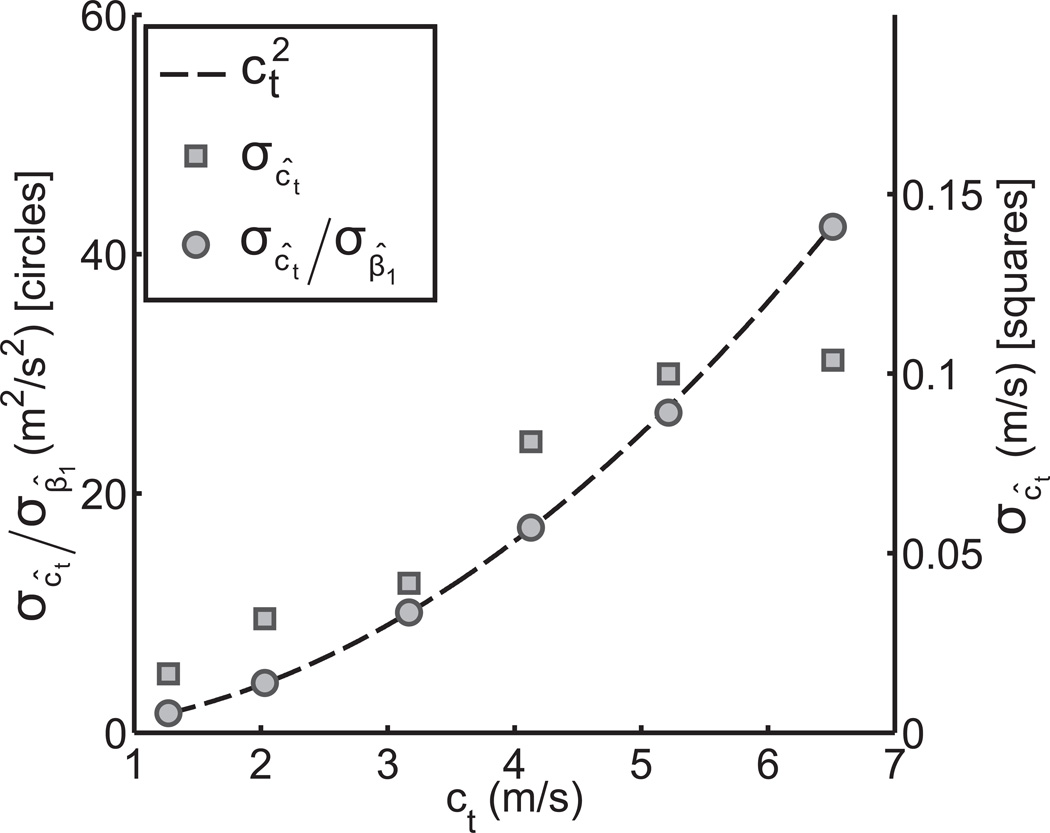
In addition to the 200 acquisitions on the 4.8 kPa phantom, an additional 20 data-sets were acquired on each of five other phantoms with varying stiffness up to 127 kPa. The SWS standard deviation was calculated for each using the (nθ, nr) = (2, 32) configuration. These were then normalized by the standard deviation of the fitted slope, σβ̂1. This effectively normalizes differences in the arrival time measurement error for the different phantoms. A plot of the normalized SWS standard deviation is shown in Fig. 7 versus the mean SWS obtained from all acquisitions on each phantom. The theoretically predicted curve for this relationship from (22) is shown on the same figure.
Fig. 7.
TOF SWS standard deviation versus the mean SWS in six homogeneous phantoms of different stiffness (squares), and after normalizing for the arrival time estimation error by dividing by the standard deviation of the fitted slope, σβ̂1 (circles). The relationship between the normalized SWS standard deviation and the SWS predicted using (22) is shown by the dashed line. The (nθ, nr) = (2, 32) beam configuration was used for SWS estimation in all cases. The sample size was 200 for the phantom with a mean SWS of 1.3m/s, and 20 for the others.
V. Discussion
As shown in Fig. 6, there is excellent agreement between the reduction in SWS uncertainty achieved on simulated data and that predicted by theory. The experimental results, however, show deviations about the expected values of R. Nevertheless, the overall trend of decreasing SWS standard deviation with increasing σr is maintained. The largest reduction occurred for the (nθ, nr) = (32, 2) beam configuration, where a 30% decrease in SWS uncertainty compared to the baseline (nθ, nr) = (2, 32) case was achieved experimentally, and a 40% decrease was predicted by theory and simulation. The disparity between the experimental results and theory may be due in part to the relatively small number of acquisitions (N=200) used to assess the SWS standard deviation compared to the simulations (N=10000). The uncertainty associated with estimating the standard deviation from 200 samples is shown by the error bars in Fig. 6. As the sample size increases, a more accurate estimate of the SWS standard deviation for the various beam configurations should be obtained.
A limitation of the theoretical derivation for the TOF SWS estimation uncertainty presented in Section II is that constant arrival time measurement noise is assumed at all beam locations. This is unlikely to be true in practice, and is another factor which could cause the discrepancy between the experimental and theoretical results in SWS uncertainty reduction observed in this study. There are two reasons why the arrival time measurement noise may be unequal at different beam locations: 1) variation in beam point spread function (PSF) due to beamforming, and 2) attenuation of the shear wave as it propagates through the medium.
The tracking beam PSF directly impacts the accuracy of ultrasonically tracked displacements. Indeed, the main source of noise in ultrasonic tracking of radiation force induced displacement is due to the distortion of the scatterer distribution within the tracking beam caused by spatial gradients in the displacement field [30], [31]. Beams with higher sidelobe levels are subject to higher levels of tracking noise due to the greater contribution of scatterer motion from the sidelobes. Thus, when the PSF of the tracking beams vary, the accuracy of the measured arrival times from those beams will also be different.
As described in Section III-B, 64:1 parallel receive beamforming was used to acquire grids of 8 × 8 beams experimentally in this study. A single transmit focused at the center of the grid was used for isonification. Data at all 64 beam locations was acquired by shifting the receive focus away from the transmit focus to every location in the grid. This has the effect of increasing the sidelobe magnitude of the track beam PSF [32]. As the receive focus is shifted further away from the transmit focus, the sidelobe level increases. Thus, the outer beams in the 8 × 8 grid has higher sidelobe levels than beams located near the center of the grid. Therefore, in the experiments performed for this study, a beam configuration in which more beams near the edges of the 8 × 8 parallel receive beam groups are selected for SWS estimation will have lower than expected SWS precision. To mitigate non-uniform tracking jitter due to parallel receive beamforming, a transmit beam with a higher F/#, or a plane wave transmit could be used.
The other factor which can cause the accuracy of arrival time estimates to vary with location is shear wave attenuation. As shear wave propagates through tissue, its amplitude can be attenuated by geometric spreading or viscosity [10], [18]. This causes the displacement amplitude at locations further from the push to be smaller, leading to larger arrival time measurement error at these locations. Since this factor was not taken into account in the derivation of (31), the experimental beam configurations in this study which utilize more beams far from the push will have lower than expected SWS precision.
Least squares fitting with unequal arrival time measurement accuracy at different locations will still give an unbiased estimate of the SWS. To extend the analysis of TOF SWS estimation uncertainty to account for unequal measurement accuracy, the following form for the standard deviation of the slope parameter β̂1 can be used [23]:
| (34) |
where is the scaling factor for the noise variance at each beam location. It can be shown that if the weights are uniformly equal to one (i.e., ), then (34) reduces to (7). Equation (22) relating the standard deviation of the SWS and the standard deviation of the estimated slope still applies in this situation. Therefore, the SWS uncertainty can still be reduced by minimizing (34). In minimizing (34), both the location (ri) and measurement noise () of the beams must be taken into account to ensure that decreases in σβ̂1 from spreading the beam locations is not offset by beams with higher measurement noise due to beamforming or shear wave attenuation. The determination of the weights is a difficult problem, because they are dependent on many factors, including the source of the shear wave, the beamforming technique used for tracking, and the viscoelastic properties of the underlying medium. One approach for determining would be to simulate both the response of the tissue to the radiation excitation force field experimentally used [33], and ultrasonic imaging of the induced displacements [30]. In practice, the exact viscoelastic properties of the medium to be imaged is unlikely to be known a priori, so a range of material properties likely to be encountered could be simulated.
As shown in Fig. 7, the experimentally measured TOF SWS uncertainty increased with mean SWS value in phantoms. Since the underlying viscoelastic properties of the phantoms were different, shear waves of varying bandwidths were induced with impulsive radiation force excitation, leading to differences in the arrival time measurement accuracy between the phantoms. After normalizing for this effect, the SWS uncertainty increased with the square of the SWS, as was predicted by (22). The fact that the uncertainty in TOF SWS measurements increases with the square of the SWS has implications for the interpretation of experimental results using TOF SWS estimation. Firstly, a greater sample size is needed for SWS measurements in stiffer materials to achieve the same power in statistical analysis as in softer materials. Secondly, in studies which involve the analysis of variability in SWS, for example, in comparing stiffness heterogeneity in the liver as a function of fibrosis stage, the inherent increase in the variance of SWS measurements in stiffer media must be taken into account.
The analytical relationships for the uncertainty in TOF SWS measurement presented in this paper are applicable to tissue as well as homogeneous phantoms. However, the tracking beam configurations presented in this paper are not intended for use in all situations. Their purpose is merely to illustrate that by increasing the spread in the beam locations, a more precise measurement of the SWS can be obtained. The specific tracking beam locations to use in any application should be chosen based on the goal of the experiment, as well as the material properties of the underlying medium. Additional considerations to be taken into account when selecting tracking beam locations for imaging tissue include shear wave attenuation due to viscosity as was previously mentioned, potential variation in stiffness with location (heterogeneity), and potential variation in stiffness with direction (anisotropy).
The main drawback of the approach used in this paper for improving SWS measurement precision is the assumption of tissue homogeneity within the ROI. It was shown in (27) that TOF SWS precision and ROI size have an inverse relationship. Therefore, there is an inherent trade-off between SWS precision and spatial resolution. In applications where the tissue stiffness is relatively homogeneous and spatial resolution is not critical, for example in assessing liver stiffness, measurement of the average SWS over a large ROI is useful. However, in applications where an image of stiffness is desired, smaller ROIs must be employed, which limits the spacing between tracking beam locations, and result in lower TOF SWS measurement precision.
The tracking beam configurations presented in this paper also assume the underlying medium to be isotropic, so that SWS does not vary with direction. Therefore, beams were placed at arbitrary angles relative to the push in the lateral-elevation plane. However, in tissues which are anisotropic, where the SWS is directionally dependent, it is not possible to measure a single SWS over the entire annular ROI. Instead, independent SWS measurements must be made in different directions from the push. This additional restriction requires beams to be placed in a sufficiently wide variety of angles to obtain the desired angular resolution in SWS. Nevertheless, the general principle of maximizing the spread in the beam locations and the expression for TOF SWS measurement uncertainty (Equation (23)) can still be applied independently for each direction.
For end users of quantitative SWS imaging systems, a useful feature would be some indication of the expected accuracy of their measurements. If there was a method to ascertain the arrival time estimation error σε, an estimate for the SWS measurement uncertainty could be calculated using (23):
| (35) |
where sĉt is the estimated SWS uncertainty, and sε is an estimate for the arrival time error. Fortunately, sε can be estimated by the deviations of the arrival times about the least squares fit line [23]:
| (36) |
where ε · ε is the sum of the square errors, and n the number of arrival times used for the fit. Equation (35) gives a direct estimate of the uncertainty, or error bar size, of the shear wave speed measurement in m/s. It is easy to show that when Cov(r, t) = σrσt (perfect correlation between arrival times and position), the uncertainty is 0m/s, and when Cov(r, t) = 0 (no correlation), the uncertainty is infinite. Thus, in addition to obtaining a SWS estimate ĉt from a single acquisition, one can also estimate the uncertainty in that estimate, sĉt, from the quality of the fit and (35).
Besides the ability to optimally position tracking beam locations to improve SWS measurement precision, another benefit of tracking shear wave propagation in 3D using a 2D matrix array is the increase in the amount of data that can potentially be acquired. If the number of tracking beams n is not held fixed, but allowed to increase by either increasing nθ or nr, then a reduction in SWS measurement standard deviation would be achieved (see equation (23)). This would be feasible using a matrix array system capable of single channel acquisition and software beamforming.
While the 3D shear wave imaging system described in this paper is a useful research tool, it has not been optimized for data acquisition in in vivo experiments. Although capable of acquiring high quality data with high sampling rates both spatially and temporally, the long acquisition time and large number of pushes required to sample the entire rectangular FOV is impractical for clinical studies. For practical purposes, both the number of tracking beams and the prf can be reduced to increase acquisition speed and decrease the number of radiation force excitations needed. If current limitations of the beamformer hardware can be overcome, then arbitrary beam locations, such as one of the configurations tested in this paper, may be realizable with a single transmit and 64 parallel receive. Alternatively, if single channel data can be acquired from the 2D array, beamforming can be performed offline in software.
Ideally, both radiation force excitation and shear wave tracking is performed with a single transducer. However, due to the high cost of the 4Z1C probe, this has not yet been attempted in our lab. Nevertheless, this is a possibility that is under investigation.
VI. Conclusion
TOF SWS measurement uncertainty is inversely proportional to ROI size, and inversely proportional to the square root of the number of tracking beam locations. TOF SWS uncertainty increases with the square of the SWS. This means that TOF SWS measurements are intrinsically less precise for stiffer materials.
For a fixed number of tracking beams and ROI size, the TOF SWS uncertainty can be reduced by increasing the spread of the tracking beam locations relative to the push within the ROI. This was experimentally demonstrated using a 2D matrix array ultrasound transducer to monitor radiation force induced shear wave propagation in a 3D volume. By taking advantage of the additional beam locations available from the 2D matrix array compared to a conventional 1D array transducer, an increase in the spread of the beam locations relative to the push was able to be achieved. Using a limit of 64 tracking beams, a reduction in TOF SWS measurement uncertainty of 40% was shown to be theoretically possible by placing the beams at the edges of the ROI at multiple directions from the push, instead of spacing the beams equally within the ROI along a single plane, as is typically done for shear wave imaging using a 1D array. This is corroborated with simulated data, and a reduction of 30% was achieved in practice using experimental data acquired with the 2D matrix array on a homogeneous phantom. Although the SWS standard deviation obtained on a phantom using the experimental setup in this study was small (< 0.016m/s), in practical imaging situations where a lower tracking prf, smaller number of tracking beams and smaller ROI size is used, and increased displacement jitter may be present due to lower B-mode SNR, the SWS uncertainty will be larger. For example, for repeated acquisitions in in vivo liver using 32 parallel beams uniformly spaced in a single plane, we observed SWS standard deviations of up to 0.2m/s [25]. The improvement in SWS precision obtained by tracking shear waves with the 2D matrix array should be most beneficial in these situations and when imaging stiff materials.
In an ideal shear wave imaging system, the SWS measurement would have both high accuracy (low bias) and high precision (low spread). This paper has proposed methods for characterizing SWS measurement precision and an approach for increasing the precision of SWS measurements by increasing the spread in tracking beam locations. However, the analysis and methods presented herein do not extend to systematic sources of errors, such as shear wave dispersion, which cause measurement bias. Depending on the application, systematic errors, which contribute to differences in the SWS measured by different systems, may pose a more significant problem than deviations in repeated measurements, which was analyzed in this paper. Investigation of potential systematic sources of SWS measurement error in shear wave imaging systems must be performed in future studies to facilitate wider clinical use of this technology.
Acknowledgment
The authors would like to thank Siemens Healthcare, Ultrasound Business Unit, Mountain View, CA, USA, for their system support.
This work was supported by NIH grant 2R01 EB-002132 and 1R01 CA142824.
References
- 1.Kanai H. Propagation of spontaneously actuated pulsive vibration in human heart wall and in vivo viscoelasticity estimation. IEEE Trans. Ultrason., Ferroelectr., Freq. Control. 2005;vol. 52(no. 11):1931–1942. doi: 10.1109/tuffc.2005.1561662. [DOI] [PubMed] [Google Scholar]
- 2.Couade M, Pernot M, Prada C, Messas E, Emmerich J, Bruneval P, Criton A, Fink M, Tanter M. Quantitative assessment of arterial wall biomechanical properties using shear wave imaging. Ultrasound in medicine & biology. 2010;vol. 36(no. 10):1662–1676. doi: 10.1016/j.ultrasmedbio.2010.07.004. [DOI] [PubMed] [Google Scholar]
- 3.Gallot T, Catheline S, Roux P, Brum J, Benech N, Negreira C. Passive elastography: shear-wave tomography from physiological-noise correlation in soft tissues. IEEE Trans. Ultrason., Ferroelectr., Freq. Control. 2011;vol. 58(no. 6):1122–1126. doi: 10.1109/TUFFC.2011.1920. [DOI] [PubMed] [Google Scholar]
- 4.Sabra K, Conti S, Roux P, Kuperman W. Passive in vivo elastography from skeletal muscle noise. Applied physics letters. 2007;vol. 90(no. 19):194 101–194 101. [Google Scholar]
- 5.Yin M, Talwalkar JA, Glaser KJ, Manduca A, Grimm RC, Rossman PJ, Fidler JL, Ehman RL. Assessment of hepatic fibrosis with magnetic resonance elastography. Clin Gastroenterol Hepatol. 2007;vol. 5(no. 10):1207–1213. doi: 10.1016/j.cgh.2007.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Huwart L, Peeters F, Sinkus R, Annet L, Salameh N, ter Beek LC, Horsmans Y, Van Beers BE. Liver fibrosis: non-invasive assessment with MR elastography. NMR Biomed. 2006;vol. 19:173–179. doi: 10.1002/nbm.1030. [DOI] [PubMed] [Google Scholar]
- 7.Sandrin L, Fourquet B, Hasquenoph J-M, Yon S, Fournier C, Mal F, Christidis C, Ziol M, Poulet B, Kazemi F, Beaugrand M, Palau R. Transient elastography: a new noninvasive method for assessment of hepatic fibrosis. Ultrasound Med Biol. 2003;vol. 29(no. 12):1705–1713. doi: 10.1016/j.ultrasmedbio.2003.07.001. [DOI] [PubMed] [Google Scholar]
- 8.Sarvazyan AP, Rudenko OV, Swanson SD, Fowlkes JB, Emelianov SY. Shear wave elasticity imaging: a new ultrasonic technology of medical diagnostics. Ultrasound Med Biol. 1998;vol. 24(no. 9):1419–1435. doi: 10.1016/s0301-5629(98)00110-0. [DOI] [PubMed] [Google Scholar]
- 9.Bercoff J, Tanter M, Fink M. Supersonic shear imaging: a new technique for soft tissue elasticity mapping. IEEE Trans. Ultrason., Ferroelectr., Freq. Control. 2004;vol. 51(no. 4):396–409. doi: 10.1109/tuffc.2004.1295425. [DOI] [PubMed] [Google Scholar]
- 10.Chen S, Fatemi M, Greenleaf JF. Quantifying elasticity and viscosity from measurement of shear wave speed dispersion. J Acoust Soc Am. 2004;vol. 115(no. 6):2781–2785. doi: 10.1121/1.1739480. [DOI] [PubMed] [Google Scholar]
- 11.Nightingale K, McAleavey S, Trahey G. Shear-wave generation using acoustic radiation force: in vivo and ex vivo results. Ultrasound Med Biol. 2003;vol. 29(no. 12):1715–1723. doi: 10.1016/j.ultrasmedbio.2003.08.008. [DOI] [PubMed] [Google Scholar]
- 12.Muthupillai R, Lomas D, Rossman P, Greenleaf J, Manduca A, Ehman R. Magnetic resonance elastography by direct visualization of propagating acoustic strain waves. Science. 1995;vol. 269(no. 5232):1854–1857. doi: 10.1126/science.7569924. [DOI] [PubMed] [Google Scholar]
- 13.Tanter M, Bercoff J, Athanasiou A, Deffieux T, Gennisson JL, Montaldo G, Muller M, Tardivon A, Fink M. Quantitative assessment of breast lesion viscoelasticity: initial clinical results using supersonic shear imaging. Ultrasound Med Biol. 2008;vol. 34(no. 9):1373–1386. doi: 10.1016/j.ultrasmedbio.2008.02.002. [DOI] [PubMed] [Google Scholar]
- 14.Palmeri ML, Wang MH, Dahl JJ, Frinkley KD, Nightingale KR. Quantifying hepatic shear modulus in vivo using acoustic radiation force. Ultrasound Med Biol. 2008;vol. 34(no. 4):546–558. doi: 10.1016/j.ultrasmedbio.2007.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bercoff J, Sinkus R, Tanter M, Fink M. Ultrasonics Symposium, 2004 IEEE. vol. 1. IEEE; 2004. 3d ultrasound-based dynamic and transient elastography: first in vitro results; pp. 28–31. [Google Scholar]
- 16.Lee W, Pernot M, Couade M, Messas E, Bruneval P, Bel A, Hagege A, Fink M, Tanter M. Mapping myocardial fiber orientation using echocardiography-based shear wave imaging. IEEE Trans. Med. Imag. 2012;vol. 31(no. 3):554–562. doi: 10.1109/TMI.2011.2172690. [DOI] [PubMed] [Google Scholar]
- 17.Taylor J. An introduction to error analysis: the study of uncertainties in physical measurements. Univ Science Books; 1997. [Google Scholar]
- 18.Deffieux T, Montaldo G, Tanter M, Fink M. Shear wave spectroscopy for in vivo quantification of human soft tissues visco-elasticity. IEEE Trans. Med. Imag. 2009;vol. 28(no. 3):313–322. doi: 10.1109/TMI.2008.925077. [DOI] [PubMed] [Google Scholar]
- 19.Zhao H, Song P, Urban M, Kinnick R, Yin M, Greenleaf J, Chen S. Bias observed in time-of-flight shear wave speed measurements using radiation force of a focused ultrasound beam. Ultrasound in Medicine & Biology. 2011 doi: 10.1016/j.ultrasmedbio.2011.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Walker WF, Trahey >GE. A fundamental limit on delay estimation using partially correlated speckle signals. IEEE Trans. Ultrason., Ferroelectr., Freq. Control. 1995;vol. 42(no. 2):301–308. [Google Scholar]
- 21.Friedrich-Rust M, Wunder K, Kriener S, Sotoudeh F, Richter S, Bojunga J, Herrmann E, Poynard T, Dietrich C, Vermehren J, et al. Liver fibrosis in viral hepatitis: Noninvasive assessment with acoustic radiation force impulse imaging versus transient elastography1. Radiology. 2009;vol. 252(no. 2):595–604. doi: 10.1148/radiol.2523081928. [DOI] [PubMed] [Google Scholar]
- 22.Colombo S, Buonocore M, Del Poggio A, Jamoletti C, Elia S, Mattiello M, Zabbialini D, Del Poggio P. Head-to-head comparison of transient elastography (te), real-time tissue elastography (rte), and acoustic radiation force impulse (arfi) imaging in the diagnosis of liver fibrosis. Journal of gastroenterology. 2012:1–9. doi: 10.1007/s00535-011-0509-4. [DOI] [PubMed] [Google Scholar]
- 23.Mendenhall W, Sincich T. Statistics for Engineering and the Sciences. 3rd ed. New York: Macmillan; 1992. [Google Scholar]
- 24.Lindop JE, Treece GM, Gee AH, Prager RW. Estimation of displacement location for enhanced strain imaging. IEEE Trans. Ultrason., Ferroelectr., Freq. Control. 2007;vol. 54(no. 9):1751–1771. doi: 10.1109/tuffc.2007.460. [DOI] [PubMed] [Google Scholar]
- 25.Wang MH, Palmeri ML, Rotemberg V, Rouze NC, Nightingale KR. Improving the robustness of time-of-flight based shear wave speed reconstruction methods using RANSAC in human liver in vivo. Ultrasound Med Biol. 2010;vol. doi: 10.1016/j.ultrasmedbio.2010.02.007. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Papoulis A. Probability, Random Variables and Stochastic Processes. 3rd ed. New York: McGraw-Hill; 1991. [Google Scholar]
- 27.Zhai L, Hsu S, Bouchard R, Nightingale K. 2008 IEEE Ultrasonics Symposium. Beijing, China: IEEE; 2008. A combined ARFI sequence for 2D displacement imaging and shear wave velocity mapping; pp. 2013–2016. [Google Scholar]
- 28.Pesavento A, Perrey C, Krueger M, Ermert H. A time-efficient and accurate strain estimation concept for ultrasonic elastography using iterative phase zero estimation. IEEE Trans. Ultrason., Ferroelectr., Freq. Control. 1999;vol. 46(no. 5):1057–1067. doi: 10.1109/58.796111. [DOI] [PubMed] [Google Scholar]
- 29.Bouchard R, Palmeri M, Pinton G, Trahey G, Streeter J, Dayton P. Optical tracking of acoustic radiation force impulse-induced dynamics in a tissue-mimicking phantom. The Journal of the Acoustical Society of America. 2009;vol. 126(no. 5):2733–2745. doi: 10.1121/1.3238235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Palmeri ML, McAleavey S, Trahey G, Nightingale K. Ultrasonic tracking of acoustic radiation force-induced displacements in homogeneous media. IEEE Trans. Ultrason., Ferroelectr., Freq. Control. 2006;vol. 53(no. 7):1300–1313. doi: 10.1109/tuffc.2006.1665078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.McAleavey S, Nightingale K, Trahey G. Estimates of echo correlation and measurement bias in acoustic radiation force impulse imaging. IEEE Trans. Ultrason., Ferroelectr., Freq. Control. 2003;vol. 50(no. 6):631–641. doi: 10.1109/tuffc.2003.1209550. [DOI] [PubMed] [Google Scholar]
- 32.Dahl JJ, Palmeri ML, Agrawal V, Nightingale KN, Trahey GE. A parallel tracking method for acoustic radiation force impulse imaging. IEEE Trans. Ultrason., Ferroelectr., Freq. Control. 2007;vol. 54(no. 2):301–312. doi: 10.1109/tuffc.2007.244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Palmeri ML, Sharma AC, Bouchard RR, Nightingale RW, Nightingale KR. A finite-element method model of soft tissue response to impulsive acoustic radiation force. IEEE Trans. Ultrason., Ferroelectr., Freq. Control. 2005;vol. 52(no. 10):1699–1712. doi: 10.1109/tuffc.2005.1561624. [DOI] [PMC free article] [PubMed] [Google Scholar]