Abstract
Drug eluting stent designs abound and yet the dependence of efficacy on drug dose and elution duration remains unclear. We examined these issues within a mathematical framework of arterial drug distribution and receptor binding following stent elution. Model predictions that tissue content linearly tracks stent elution rate were validated in porcine coronary artery sirolimus-eluting stents implants. Arterial content varied for stent types, progressively declining from its Day 1 peak and tracking with rate-limiting drug elution – near zero-order release was three-fold more efficient at depositing drug in the stented lesion than near first-order release. In vivo data were consistent with an overabundance of non-specific sirolimus-binding sites relative to the specific receptors and to the delivered dose. The implication is that the persistence time of receptor saturation and effect is more sensitive to duration of elution than to eluted amount. Consequently, the eluted amount should be sufficiently high to saturate receptors at the target lesion, but dose escalation alone is an inefficient strategy for prolonging the duration of sirolimus deposition. Moreover, receptor saturating drug doses are predicted to be most efficacious when eluted from stents in a constant zero order fashion as this maximizes the duration of elution and receptor saturation.
Keywords: Drug eluting stents, Tissue distribution, mTOR inhibitors
1. Introduction
Drug eluting stents (DES) have transformed the practice of vascular medicine with the simple idea that local delivery of potent compounds can provide high local concentrations with minimal systemic exposure. Yet the effects of drug dose and elution kinetics on tissue content and biological effects have yet to be defined [1,2]. There is as yet no rational basis for extrapolating clinical experience with existing DES to expected performance of new DES, necessitating examination of each new DES prototype in vivo, even when only drug dose or elution rate is varied. This problem is now especially acute as novel drug loading technologies that minimize polymer contact, such as polymer free and reservoir technology DES, display a wider range of potential elution kinetics than traditional DES [3,4]. The advent of these next generation devices does provide however a means of addressing some of the remaining questions – especially vis-à-vis release kinetics and dose. The recently developed NEVO™ Sirolimus eluting Coronary Stent elutes its entire drug load in a sustained fashion. By contrast, the first FDA approved DES, the CYPHER® Sirolimus eluting Coronary Stent exhibits a first order burst in addition to a sustained mode of elution, allowing the examination of the significance of the mode of sirolimus elution.
We can then compare vessel wall retention of one drug when released with two devices of similar dimensions and loads in animal models and interpret these findings with computational models. Computational modeling offers an attractive framework that complements empiric studies of the influence of dose and elution duration on local drug deposition and anticipated biological effects [1,5–8]. Numerical models that account for drug elution from stent coatings, luminal convection and arterial diffusion have shown that stent-based delivery improves deposition of weakly retained drugs but only when the rate of drug absorption by the stented artery exceeds the rate of drug elution [1,9], otherwise drug is diluted systemically prior to arterial uptake. These models provide an intuitively appealing rationale for the efficacy of sustained-elution DES, yet fail to explain clinical experience. Whereas the models predict a graded dependence of tissue content on drug dose and duration of delivery, in vivo studies suggest the existence of dose and duration thresholds that must be exceeded in order to exert biologic effect [3,10–14]. Here we analyze the dependence of tissue content and receptor-mediated drug effects on the coupled effects of drug elution kinetics, tissue transport and binding to non-specific proteins and receptors. We used a combination of in vivo experiments, computational modeling and analytical approximations to elucidate that the density of non-specific binding sites in the tissue relative to the eluted amount and the density of drug receptors determine the dependence of tissue content and receptor saturation on stent elution kinetics.
2. Materials and methods
2.1. Stents
We compared arterial drug content achieved with sirolimus eluting stents (SES) chosen to provide mono-phasic and bi-phasic elution kinetics. The CYPHER® Stent (Cordis Corporation, NJ) and a prototype of the NEVO™ Stent (Cordis Corporation, NJ) are appealing comparators as they have similar dimensions and equivalent doses per stent surface area, but distinct designs that provide different elution kinetics (Fig S1 Online supporting material). CYPHER® Stents (3.5 mm×18 mm) incorporate a nominal sirolimus dose of 175 μg that is immiscible within a multi-component carrier matrix, poly(n-butyl methacrylate) [PBMA] and poly(ethylene-co-vinyl acetate) [PEVA] that conforms to the surfaces of the stent scaffold [15]. The coating is applied on a poly(o-chloro-p-xylylene) [parylene-C] treated stainless steel stent. Prototype NEVO™ Stents (3.5 mm×17 mm) incorporate a nominal sirolimus dose of 166 μg that is formulated with poly(dl-lactic-co-glycolic acid) [PLGA] as matrix-type release systems. Hundreds of discrete holes are drilled through the metal stent scaffold and loaded with drug–polymer–solvent formulation using a high-speed, optically-guided, nanodroplet injection system [16,17]. Multiple injections of uniform droplet size deliver the polymer–drug solution to form individual matrix systems. Cycles of filling and drying are repeated until the desired drug load is attained.
2.2. Porcine coronary artery model
48 CYPHER® Stents and 45 prototype NEVO™ Stents were implanted in the coronary arteries of Yorkshire swine (1 stent/artery, n=77 pigs). All procedures and conditions of testing were performed at CBSET Inc. (Lexington, MA) adherent to the Guide for the Care and Use of Laboratory Animals [18] under an approved Institutional Animal Care and Use Committee (IACUC) protocol, in compliance with the Animal Welfare Act and the Food and Drug Administration Good Laboratory Practice (GLP) Regulations and their amendments. Stents were deployed to a target balloon-artery ratio of 1.1:1. At 1, 3, 8, 14, or 30 days post-implantation, stented arteries (n=9 per time point) were harvested and stored frozen on dry ice; subsequently, stents were removed from the stented artery segment and both samples separately prepared for quantification of sirolimus content. Sirolimus was extracted from the stents in 3 ml of HPLC grade methanol. Tissue samples were weighed, homogenized in PBS and the aqueous phase extracted into methyl-t-butyl ether/n-butyl chloride (1:1), evaporated to dryness and reconstituted in 0.5 ml HPLC grade methanol. Sirolimus extracted from the stent and arterial wall samples was quantified using a validated LC/MS/MS method. Percentage recoveries for stent and tissue extracts were 97.0–103.0% and 102.3–110%, respectively. Coefficients of variation (CV) for stent analyses were <2% across all assay days. For tissue analyses, quality controls were prepared at 3 levels (0.75, 1.5, 7.5 ng/mg tissue) and all analytical runs met the validated acceptance criteria of <20% CV. In vivo data reported are the mean±standard deviation. If data normality and variance homogeneity were observed, Student’s t-test was used to compare sirolimus stent elution, and arterial sirolimus content between SES types. If data normality and variance homogeneity were not observed, outcomes were compared using Kruskal–Wallis ANOVA on Ranks and Dunn’s test. Statistical tests were conducted using statistical functions in Sigma Plot 11.0 (Systat Software, Inc., San Jose, CA) and p<0.05 was considered significant. Average cumulative elution data for CYPHER® Stents and prototype NEVO™ Stents were fit to Eq. (1) using GraphPad Prism 3.02.
3. Mathematical modeling
3.1. Drug elution kinetics
Understanding the determinants of drug elution kinetics from stents is a topic of ongoing research and some controversy [19]. Early models of drug elution from CYPHER® Stent coatings described the tri-layer coating as a reservoir/membrane system, whereas a fast eluting two-layer prototype was described as a drug in matrix (monolith) system [2]. However, the elution kinetics of standard CYPHER® Stents significantly deviate from the expected zero-order kinetics of reservoir/membrane systems, whereas the bi-layer does display zero order elution. Subsequently, imaging studies of CYPHER® Stent coatings [20,21] and similar conformal coated DES [22–24] explained that drug distribution can deviate from the idealized layered designs due to the influence of mixing and drying that occurs during coating manufacture. Specifically, images of the coatings revealed significant concentrations of dispersed drug in the top-coat [21,24–26] that are inconsistent with the reservoir/membrane description and explain observations of early drug bursts from CYPHER® Stents and other conformal coated stents[5,24,27]. In light of these studies, we idealize CYPHER® Stent coatings as monolithic films that contain two pools of dispersed drug, one that is surface-connected and elutes through a percolating network of drug filled pores, and another that is embedded within the matrix and diffuses more slowly through the percolating polymer phase. Following Hossainy and Prabhu [5] we assumed that elution of the surface-connected pool of drug is governed by diffusion; and as its elution is fast relative to the elution of the second drug pool, we invoked the late time approximation [28] and modeled cumulative elution of surface enriched drug as a first-order process. Following Barocas et al. [27] we assumed that elution of the matrix-embedded pool of drug follows Higuchi-type diffusion-limited dissolution kinetics [29]. Thus, cumulative sirolimus elution kinetics from CYPHER® Stent coatings were parameterized as
| (1) |
where Mstent(0) denotes the initial load of drug per stent (μg), Mfo is the initial pool of first order eluting drug (μg) with rate constant Kfo (d−1), and Qsus (μg·d−1/2) is the Higuchi rate constant. As each of the holes drilled into NEVO™ Stents incorporates a matrix-type release system, Eq. (1) was also used to describe the elution kinetics of NEVO™ stents.
3.2. Tissue content and receptor binding
Sirolimus inhibition of intimal hyperplasia is attributed to its ability to inhibit mTOR signaling following its specific binding to intracellular FKBP12 [30,31]. Sirolimus bound FKBP12 binds to FRAP (FKBP-rapamycin associated protein=mTOR1), a member of the phosphatidylinositol-kinase related kinase family. FRAP kinase activity, via signaling to p70 S6 kinase and eIF4E-binding protein (4E-BP1) is essential for progression of the cell cycle from G1 to S. Blockade of FKBP12-rapamycin binding domain of FRAP arrests the cell cycle at the G1 stage. Thus, FKBP12 acts as a well defined pharmacological receptor for sirolimus, and inhibition of mTOR signaling correlates positively with the concentration of FKBP12-bound sirolimus. To concomitantly predict drug distribution and biological effects, we therefore extended previous models of drug convection and diffusion [1,6,32] to account for saturable binding to specific receptors [33] and general ECM sites [34] (Fig. 1)
| (2) |
| (3) |
| (4) |
Fig. 1.
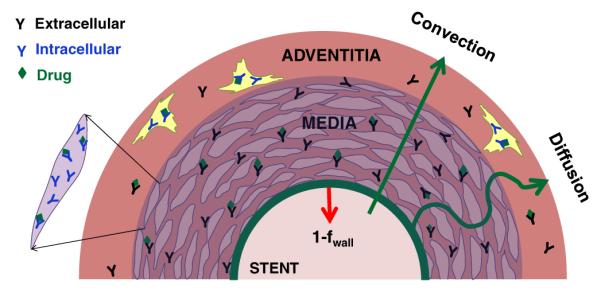
Endovascular DES are idealized as phantom interface separating arterial tissue from luminal blood, delivering a fraction fwall of their drug load to the arterial wall and the remaining fraction 1-fwall is cleared by luminal blood. Transmural distribution of absorbed sirolimus is governed by transmural convection and diffusion (Eq. (2)), binding to ECM sites (Eq. (3)), binding to pharmacological receptors (Eq. (4)), and adventitial clearance (Eq. (7)).
Here t denotes time since stent implantation, r is the distance from the intima, c is the molar concentration of free drug per unit tissue volume, bECM and bREC are the molar concentrations of ECM- and receptor-bound drug, respectively; bECM,max and bREC,max denote the local molar concentration of ECM- and receptor drug binding sites, and are the respective binding on-rate constants, and are the respective equilibrium dissociation constants, Dwall is the transmural diffusivity of the drug and Vwall is its transmural convective velocity.
As stent struts are thin relative to the arterial wall, we neglect their actual geometry and approximate the drug eluting stent using an equivalent phantom surface that elutes a defined drug load to the arterial lumen and wall (Fig. 1). Elution from the phantom surface is modeled by prescribed luminal and wall fluxes that are proportional to the in vivo net flux as inferred from residual drug content on the stent Mstent (Eq. (1)). Denoting the surface area of the blood/wall interface as Slumen, and the efficiency factor for delivery into the wall as fwall, we obtain the following intimal boundary condition
| (5) |
with
| (6) |
Here rmin is the radius of the expanded stent (1.75 mm) and Adrug is the drug’s molecular weight (914.2 g/mol). Such modeling presumes that the rate of stent elution is much slower than the rate of drug absorption by the arterial wall and can therefore be considered an independent variable [32]. This assumption is typically valid, as most stents deliver their drug load over weeks to months [35–37], whereas drugs can traverse across the arterial wall within hours of delivery [7,38,39]. The periadventitial surface is assumed to act as a perfect sink for free drug
| (7) |
where W denotes the thickness of the arterial wall. To allow a comparison to experimental results we analyzed the relationship between drug elution rate and the total drug content per tissue weight (μg drug/g tissue)
| (8) |
Here ρtissue=0.983 g/ml is the density of wet arterial tissue [40]. Similarly, we estimate the specific in vivo inhibition of the mTOR signaling pathway by sirolimus [30,31,41] through the evaluation of the average fraction of bound FKBP12 in the stented lesion
| (9) |
This formulation accounts for the essential determinants of drug content and effect in stented arterial segments. To simplify the presentation, we suppressed potential differences between drug transport and binding parameters in each of the three arterial layers [34,40,42,43]. However, we verified that accounting for such differences does not alter the qualitative results as presented in this manuscript (Section SII Online supporting material). Eqs. (5)–(7) were solved numerically using the commercial finite element package COMSOL 3.5a (numerical methods are detailed in Section SIII Online supporting material). All reported numerical simulations account for arterial curvature through the inclusion of the second term in the right hand of Eq. (2). Note, however, that the latter term is of lower order than the first diffusion term for healthy porcine coronary arteries, as these are thin relative to their radius (W/rmin=0.25). Numerical simulations illustrated that maximal tissue content was 10% lower when neglecting the curvature dependent term. Thus, in deriving analytical approximations of the model equations we neglected curvature effects to obtain an intuitive if approximate feel of the underlying dynamics.
4. Results
4.1. Drug elution kinetics
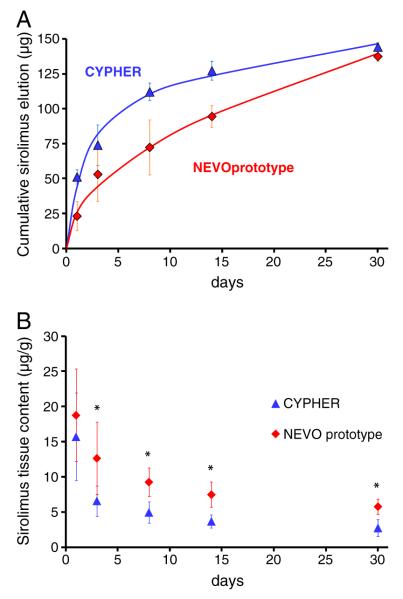
Sirolimus loads in CYPHER® Stent and prototype NEVO™ Stent lots implanted in vivo were within 10% of each other (Mstent(0), Table 1). Though CYPHER® Stents eluted significantly more sirolimus than prototype NEVO™ Stents in the first day (51.26±5.05 μg vs 23.20±10.38 μg, p<0.05), both SES eluted similar amounts by Day 30 (144.29 μg vs 137.50 μg). Elution from prototype NEVO™ Stents (Fig. 2A) was linear when plotted versus the square root of time, consistent with a single sustained diffusion-controlled mechanism (R2=0.988, Table 1). Though an unrestricted fit of NEVO™ Stent elution data to Eq. (1) also provides an excellent interpolation of the data (R2=0.993) with a reasonably tight estimate of the Higuchi rate constant (Qsus=23.19±2.67 μg d−1/2), the standard error of the estimated pool of first order eluting drug (9.1 μg) is unacceptably high (11.2 μg). Since 9.1 μg corresponds to 5.8% of the total drug load of NEVO™ Stents, we neglected this small pool of drug heretofore (Table 1 and Fig. 2). By contrast, CYPHER® Stents exhibited biphasic elution kinetics (Fig. 2A) consistent with 42.4% of the initial load eluting at a fast first order rate, the remainder eluting by diffusion-limited dissolution (R2=0.976, Table 1) at a 2-fold slower rate than that of prototype NEVO™ Stents.
Table 1.
Parameterization of in vivo sirolimus elution kinetics
Initial drug content Mstent(0) was evaluated in unimplanted balloon expanded DES from the same lots that were used in vivo. All other parameter values were estimated by fitting in vivo elution curves (Fig. 2A) to Eq. (1) using GraphPad Prism 3.02. Standard errors are reported in parenthesis.
| Stent type | Elution kinetics parameters |
|||
|---|---|---|---|---|
| Mstent(0) (μg) | Mfo (μg) | Kfo (d−1) | Qsus (μg·d−1/2) | |
| CYPHER® | 174.89 (0.98) | 74.21 (19.73) | 0.53 (0.20) | 13.22 (4.63) |
| NEVO™ prototype |
161.52 (1.04) | 0 | Not applicable | 25.48 (0.64) |
Fig. 2.
In vivo pharmacokinetics of CYPHER® Stent (blue) and prototype NEVO™ Stent (red) in the porcine coronary artery model. (A) Cumulative sirolimus elution (symbols) versus best fits (lines) of Eq. (1) (Table 1). (B) Tissue content. Asterisks denote statistically significant differences observed between SES at Days 3–30 (p<0.05).
4.2. Tissue content and receptor-mediated drug effects
Similar patterns of arterial content were observed for both SES types (Fig. 2B), with sirolimus arterial content progressively declining from its Day 1 peak. Despite the consistently higher cumulative elution by CYPHER® Stents and greater net polymer:tissue contact per stent length, prototype NEVO™ Stents provided consistently higher sirolimus tissue contents (Fig. 2B). Were tissue absorbed sirolimus perfectly retained, one would expect tissue content to scale with the cumulative amount of eluted drug. The demonstration that cumulative elution is a poor predictor of tissue content therefore suggests that tissue absorbed sirolimus molecules undergo significant clearance. Thus, one may expect the rate of sirolimus absorption to be a better predictor of tissue content. According to our model, the rate of drug elution is the driving force for absorption into the wall (Eq. (5)). However, if elution rate is predictive of tissue content, why is it that CYPHER® Stents elute sirolimus at a significantly higher rate than prototype NEVO™ Stents during the first day of stent implantation yet do not achieve higher tissue contents at Day 1?
These intriguing findings highlight the difficulty of interpreting the determinants of tissue content by intuition alone. To overcome this difficulty, we analyzed a coupled mathematical model of stent elution and sirolimus transport and binding in arterial tissue. As the equations of drug absorption and distribution (Eqs. (2)–(7)) are non-linear and depend on 11 independent parameters, it is anticipated that the model will exhibit qualitatively different dynamics for different ranges of parameter values [44]. Some of the parameters can be estimated based on stent and tissue geometry, while others were estimated based on our group’s previous benchtop experiments with excised arteries (Table 2).
Table 2.
Arterial-wall transport and equilibrium binding parameters of sirolimus.
| Parameter | Meaning | Estimate | Source |
|---|---|---|---|
| W | Arterial wall thickness | 450 μm | [45] |
| rmin | Radius of expanded stent | 1.75 mm | Stent dimensions |
| Slumen | Area of stented lumen | 1.98–2.05 cm2 | Stent dimensions |
| fwall | Drug transfer efficiency | 0.06–0.16 | This study |
| Adrug | Drug molecular weight | 914.2 g/mol | [46] |
| Vwall | Transmural velocity | 5.8×10−6 cm/s | [47,48] |
| Dwall | Transmural diffusivity | 1.5– 2.5×10−6 cm2/s |
This study |
|
bECM,max +bREC,max |
Total binding site density | 366 μM | [7] |
| b REC,max | Receptor density | 3.3±0.3 μM | This study |
| ECM dissociation constant | 2.6 μM | [7] | |
| Receptor dissociation constant |
0.2 nM | [33] | |
| ECM binding on-rate | 0.002 μM−1 s−1 | [7] | |
| Receptor binding on-rate | 0.8 μM−1 s−1 | [49] |
Parameters such as the density of drug receptors in the tissue and the efficiency factor for delivery into the wall can only be estimated through analysis of the in vivo data. Moreover, our previous studies have demonstrated discrepancies between in vivo and benchtop estimates of diffusion coefficient of sirolimus in arterial tissue [7,32,42]. To realistically simulate tissue content as a function of prescribed elution kinetics, we must therefore first estimate the remaining parameters based on a qualitative interpretation of the in vivo data, and use numerical simulations to validate these estimates. First, we note that the decline of tissue content during Days 1–30 for both SES (Fig. 2B) implies that during this entire time frame, the rate of periadventitial sirolimus clearance exceeds the rate of sirolimus absorption at the luminal interface. This in turn suggests that sirolimus traversed the full thickness of the arterial wall within 24 h of stenting with either SES, which is plausible based on previous data [7,38,39]. The implication is that transmural sirolimus absorption and clearance are rapid relative to the rate of stent elution, so that once drug has fully traversed the thickness of the wall, concentration gradients in the arterial wall quasi-statically track the declining rate of drug elution [8,50], and can be solved for by neglecting the temporal derivatives of the arterial transport equations (Eqs. (2)–(4)) to find
| (10) |
| (11) |
| (12) |
As explained in Section 3.2, Eq. (10) is an approximate form of the quasi-steady state transport equation as it neglects the curvature term that scales as W/rmin=0.25 for healthy porcine coronary arteries. Solving Eq. (10) subject to the intimal (Eq. (5)) and adventitial (Eq. (7)) boundary conditions we find that the distribution of free drug during the clearance phase
| (13) |
is proportional to the intimal influx of drug into the stented artery wall
| (14) |
Here
| (15) |
is the Peclet number, a dimensionless parameter that measures the relative importance of diffusion and convection across the wall. The magnitude of Pe will be estimated along with the diffusion coefficient. These approximations imply that once quasi-steady state is established the content of free drug in coronary tissue should proportionally track the rate of drug elution
| (16) |
The proportionality coefficient in this relationship depends on the rate constants of drug diffusion, convection, and the efficiency of drug transfer into the wall (Table S1 Online supporting material). Accounting for differential transport parameters in each of the ultrastructural layers of the arterial wall only alters the term in parenthesis which becomes a function of the intimal, medial, and adventitial Peclet numbers (Eq. SII.44 Online supporting material). In the presence of drug binding sites, Eq. (16) only accounts for the free drug content (Eq. (8)) and total tissue content depends nonlinearly on the rate of stent elution (Eq. SI.5 Online supporting material). Namely, the hyperbolic dependence of ECM-bound (Eq. (11)) and receptor-bound (Eq. (12)) drug on the local concentration of free drug renders the total content of bound drug in the tissue a function of the maximal concentration of free drug in the tissue
| (17) |
normalized to the drug binding dissociation constants of ECM proteins and pharmacological receptors. Notably, ECM dissociation constants are typically 3–4 orders of magnitude larger than the respective receptor dissociation constants (Table 2). A detailed analysis (Section SI Online supporting material) reveals that such disparity between ECM and receptor dissociation constants renders tissue content a linear function of the rate of drug elution in three distinct drug binding regimes (Fig. 3)
| (18) |
In this relationship, the intercept corresponds to the saturated binding sites in the stented tissue segment, whereas the slope constitutes a steady state rate of drug absorption (per total tissue mass) and therefore is only influenced by unsaturated drug binding sites (Table S1 Online supporting material).
Fig. 3.
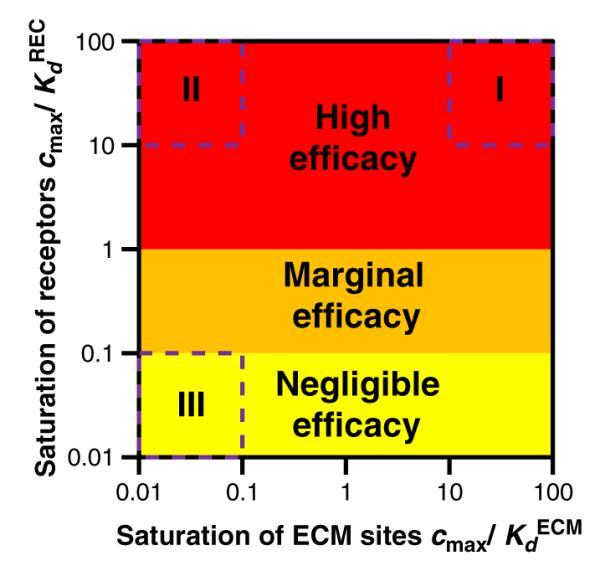
Regimes of drug binding and receptor mediated efficacy. Intimal free drug concentrations in excess of the receptor’s dissociation constant are highly efficacious (bREC/bREC, max>0.5) and encompass binding regimes I and II (Table S1 Online supporting material). Lower intimal free drug concentrations provide marginal (0.5>bREC/bREC, max>0.1) or low (bREC/bREC, max<0.1) receptor mediated effects. The favoring of specific over non-specific binding implies that regime I will evolve into regime II in an almost straight horizontal trajectory, and that regime II will evolve into regime III via a virtually vertical trajectory.
4.2.1. Regime I: saturated ECM binding, maximal efficacy
Maximal receptor-mediated drug effects require complete receptor-saturation. In one extreme (regime I, Fig. 3), drug influx is so high as to also saturate ECM binding sites
| (19) |
In this regime, the intercept of tissue content versus DES elution rate is equal to the total density of drug binding sites in the lesion, bECM,max+bREC,max, and the slope is the same as in the absence of drug binding sites (Table S1 Online supporting material). The disparity between the dissociation constants favors specific over non-specific binding and implies that as the rate of drug elution declines over time, drug first dissociates from non-specific sites. This continues even as drug-bound ECM sites decline to a small fraction of total ECM binding sites (regime II).
4.2.2. Regime II: unsaturated ECM binding, maximal efficacy
The affinity advantage of specific binding allows for drug influx to saturate receptors while only binding a negligible fraction of non-specific ECM binding sites
| (20) |
In this regime, the intercept of tissue content versus DES elution rate is equal to the density of receptors in the lesion and the slope is proportional to the non-specific binding potential of the drug in the tissue, (Table S1 Online supporting material). As the rate of drug elution declines over time, drug first dissociates from non-specific sites even though only a negligible fraction of these sites is drug-bound. Eventually receptor-bound drug begins to dissociate and regime II evolves into regime III of negligible binding and efficacy.
4.2.3. Regime III: unsaturated extracellular binding, low efficacy
At sufficiently low drug influx into the stented wall, free concentration is too low to even saturate the high affinity pharmacological receptors
| (21) |
In this regime, DES efficacy is low due to negligible receptor binding, the intercept of tissue content versus DES elution rate is vanishingly small and the slope is proportional to the total binding potential of the drug in the tissue, (Table S1 Online supporting material). For DES of proven efficacy, this regime only sets in at negligible elution rates.
4.2.4. CYPHER® Stent and prototype NEVO™ Stent saturate FKBP12 but not ECM binding sites
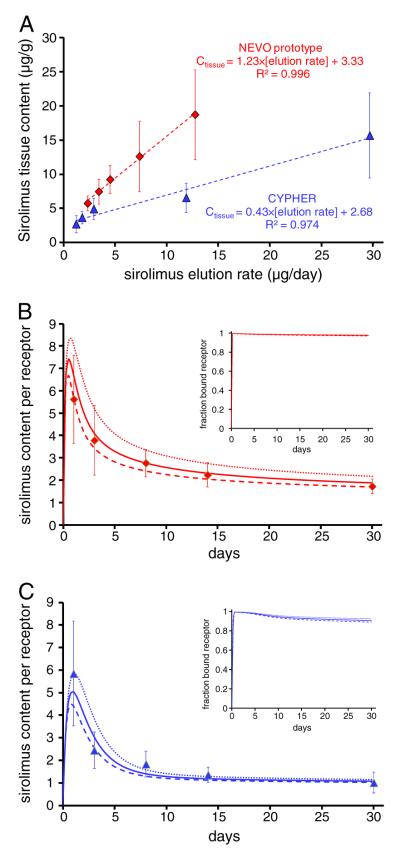
Binding regimes I–III account for all the scenarios in which tissue content linearly tracks the rate of drug elution, though not for all possible influx and binding scenarios (Fig. 3). In particular, tissue content is predicted to depend non-linearly on the rate of elution when the associated cmax is either comparable to the dissociation constants of ECM proteins or receptors . To determine the binding regimes maintained by CYPHER® Stent and prototype NEVO™ Stent we re-plotted their associated tissue contents (Fig. 2B) against their respective rates of sirolimus elution. Both plots are linear (Fig. 4A) and while the intercepts for both SES are positive and of similar magnitude (3.3 μg/g vs 2.7 μg/g), the slope for prototype NEVO™ Stents is 2.9-fold larger than that of CYPHER® Stents. Linearity validates our analysis, and since zero intercepts are only expected in the absence of drug binding sites or when only a negligible fraction of drug binding sites are occupied, positive intercepts are evidence for the significant contribution of drug binding to total tissue content. Moreover, as maximal tissue content (20 μM) achieved by both SES prototypes (Fig. 2B) is negligible relative to the estimated total density of sirolimus binding sites in the arterial wall (366 μM, Table 2), saturation of non-specific binding sites (e.g. regime I) can also be ruled out for both SES. Taken together, these results imply that sirolimus influx from both SES was too low to occupy a large fraction of ECM binding sites yet sufficiently high to saturate pharmacological receptors (regime II) throughout 30 days of implantation in porcine coronary arteries. Moreover, the intercepts in Fig. 4A estimate the density of sirolimus receptors (FKBP12) in healthy porcine arteries as bREC,max =2.9–3.6 μM, 100-fold lower than the density of ECM sirolimus-binding sites. As reference, T-cells express 6–7 μM of FKBP12 protein [51].
Fig. 4.
Model validation and calibration. (A) In vivo issue content (symbols) of arteries is rendered linear when plotted against the in vivo rate of elution. Linear fits (dashes) exhibit a 2.9-fold higher slope for prototype NEVO™ Stents (red) compared to CYPHER® Stent (blue) but similar positive intercepts that correspond to the density of sirolimus receptors. In vivo tissue content of coronary arteries stented with prototype NEVO™ Stent (B) or CYPHER® Stent (C) are normalized to receptor density and contrasted with numerical simulations of Eqs. (2)–(7) with Dwall=1.5×10−6 cm2/s (dots), Dwall=2.0×10−6 cm2/s (lines) and Dwall=2.5×10−6 cm2/s (dashes). Insets depict the predicted fraction of sirolimus-bound receptors (Eq. (8)) and illustrate that tissue contents in excess of receptor density ensure receptor saturation for both SES.
As both SES maintain the same sirolimus binding regime, the ratio of the slopes in Fig. 4A reveals that prototype NEVO™ Stents transfer a 2.9-fold larger fraction (fwall) of eluted sirolimus to the arterial wall compared to CYPHER® Stents. To directly estimate transfer efficiencies we evaluated the ratio of Day 1 sirolimus content in the stented tissue to Day 1 cumulative elution, yielding fwall=0.0601±0.0242 for CYPHER® Stents and fwall=0.1601±0.0677 for prototype NEVO™ Stents. That the ratio of these estimated transfer efficiencies only slightly under-estimates the ratio at quasi-steady state (2.7 vs 2.9) suggests steady-state is established around Day 1. Having estimated all the parameters except the in vivo diffusion coefficient of the sirolimus in arterial tissue we now estimate this remaining parameter. To focus our search we note that interpretation of the slope of tissue content versus stent elution rate (Fig. 4A) based on the approximate formula for regime II (Table S1 Online supporting material) implies that sirolimus transport is diffusion controlled, Pe⪡1. Limiting our search to diffusivity values such that Pe<0.5 (e.g. Dwall>5.2×10−7 cm2/s) we find through numerical simulation of Eqs. (2)–(8) that tissue contents of arteries that received prototype NEVO™ Stents (Fig. 4B) or CYPHER® Stents (Fig. 4C) are well fit by Dwall=(2.0±0.5)×10−6 cm2/s (0.10≤Pe≤0.17). This estimate of free sirolimus diffusivity in arterial tissue is significantly higher than our benchtop estimates [42], but is consistent with the value (Dwall =1.07×10−6) predicted by Swabb’s correlation of tissue diffusivity with molecular weight [52]. Normalization of in vivo tissue contents relative to the estimated density of sirolimus receptors illustrates that both SES saturate sirolimus receptors (FKBP12) by Day 1 and that tissue content becomes dominated by receptor-bound sirolimus at late times. Simulations of receptor binding (Fig. 4B,C insets) confirm this interpretation and directly illustrate that both SES saturate sirolimus-receptors throughout Days 1–30.
4.2.5. Elution kinetics can optimize receptor mediated effects
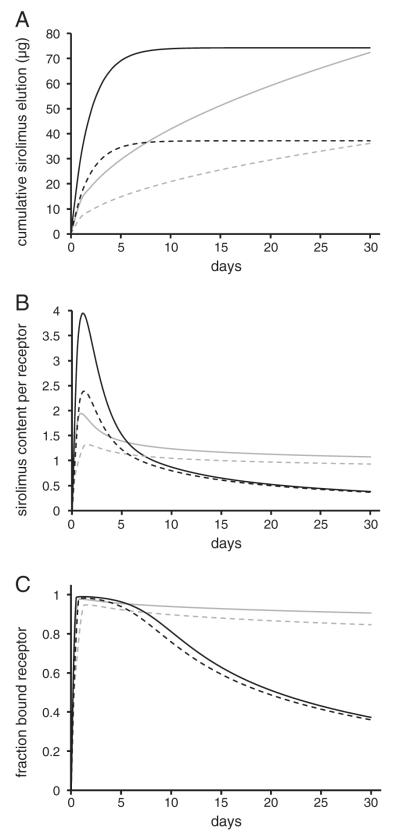
Though both SES are predicted to quickly saturate sirolimus receptors, receptor-bound sirolimus is predicted to dissociate slightly faster in CYPHER® stented arteries than NEVO™ stented arteries (Fig. 4C, inset). To examine whether this slight difference arises from the differential drug transfer efficiencies of these SES or from their differential elution kinetics, we conducted a numerical study which held the latter parameter constant and only varied the rate at which a constant dose of sirolimus (~74 μg) elutes over 30 days. Tissue content (Fig. 5B) and receptor binding (Fig. 5C) were simulated for two idealized elution kinetics, one that corresponds to the first order mode of elution from CYPHER Stents, another that corresponds to the Higuchi-mode of drug elution of CYPHER® Stents (Fig. 5A). Predicted tissue content peaked at Day 1 for the first-order mode of elution, and was equal to the density of receptors by Day 8. Tissue content displayed a lower Day 1 peak for the Higuchi mode of elution, and then slowly declined to the density of receptors by Day 30. Though both modes of elution saturated more than 98% of receptors by Day 1, by Day 30 only 36% of receptors remained bound for the first order mode of elution compared to 90% for the Higuchi mode of elution. Notably, though tissue content declined rapidly after Day 1 for the first order mode of elution, receptor saturation was virtually unchanged as long as tissue content was higher than the density of receptors (Fig. 5C) thus endowing tissue content data with new significance, at least for sirolimus and its analogs. Remarkably, halving the eluted amounts (Fig. 5A) only reduced the timing and magnitude of peak tissue content (Fig. 5B), while minimally influencing late tissue content and kinetics of receptor binding (Fig. 5C). These simulations illustrate that receptor binding is more sensitive to the kinetics of cumulative drug elution (e.g. duration) than to the eluted amount. Thus, the differential tissue content and receptor saturation prototype NEVO™ Stents (Fig. 4B) and CYPHER® Stents (Fig. 4C) seem to primarily reflect their differential cumulative elution kinetics, namely that a sizable fraction of the initial load elutes in an early burst for the latter but not the former.
Fig. 5.
Receptor binding state is more sensitive to elution kinetics than dose. Eqs. (2)–(7) were simulated for hypothetical stents that elute 74 μg (lines) or 37 μg (dashes) by pure first order (Kfo =0.53 d−1, black lines) or Higuchi (Qsus=13.22 μg·d−1/2, gray lines) kinetics (A). Tissue content (B) and receptor binding levels (C) were evaluated by integrating, respectively, the simulated distributions of total drug and receptor-bound drug across the thickness of the arterial wall. All simulations employed the same tissue transport parameter values (fwall=0.06, Dwall=2.0×10−6 cm2/s with all other values listed in Table 2).
5. Discussion
Intravascular drug delivery has revolutionized the practice of cardiovascular medicine, and yet there is still no clear understanding as to how the timing, duration and dose of delivered drug influence biological outcome. The difficulty lies in balancing the complex multi-scale processes underlying drug elution, device induced injury, drug distribution and intracellular drug effects. Moreover, the various processes and scales can feed back positively or negatively with each other. Thus for example, slow tissue absorption might limit drug elution from the local delivery device [5,9], expression of drug binding sites can modulate drug distribution [7,34,38,40,42,53] and injury can modulate the expression of drug receptors and ECM binding sites [53–56]. Such complexity eludes simple intuition and limits the value of clinical, animal and computational studies that only examine elution kinetics, tissue content or pharmacological dose response. Mathematical modeling embraces this complexity and offers a unique framework for integrating existing knowledge on the underlying processes and predicting how their interplay determines biological outcomes under realistic in vivo conditions. We used this integrative modeling paradigm to provide novel insights into the determinants of sirolimus deposition and effect in stented arteries, and a tool by which to compare different SES prototypes.
5.1. Inferring sirolimus effects from tissue content
Though tissue content of drug has been touted as essential for evaluation of DES designs no theoretical or even empirical relationships has been established between in vivo efficacy and drug content. Cell culture dose response studies do not have direct bearing on the in vivo setting where the concentration of drug varies in space and receptors have to compete with nonspecific binding sites. Mathematical modeling offers a means of accounting for spatial variations and binding interactions and deducing in vivo efficacy [8,50], but its utility depends on the availability of transport parameters and binding coefficient estimates. In lieu of estimates of binding coefficients, previous models of stent based drug delivery [1,6,9,32] used classical (linear) convection–diffusion models that are valid when tissue binding sites are far from saturation. Though such models were able to account for the influence of coating geometry, elution kinetics and thrombus on tissue content [1,32], they could not explain observations of dose and duration thresholds that must be exceeded in order to exert biologic effect [3,10–14]. Therefore, a central aim of the current work was to attain a comprehensive understanding of the coupled effects of non-specific and receptor binding on tissue content for the widest possible range of doses and delivery kinetics. This aim was achieved through scaling analysis which took advantage on the one hand of the disparity in the rates of drug elution and tissue absorption, which justified a quasi-steady state approximation, and on the other hand of the 4-log order disparity in dissociation constants (Table 2) which favors sirolimus binding to receptors over binding to non-specific tissue sites, implying that the amounts eluted from typical SES can saturate the former but not the latter. Taken together, these attributes were shown to result in a linear tracking of tissue content with elution rate. In vivo data validated this prediction (Fig. 4A) and allowed the estimation of three critical model parameters, the density of sirolimus receptors in porcine coronary tissue, transmural drug diffusivity, and the fraction of eluted sirolimus that is transferred to the artery wall.
While all three parameters were critical for validating the model against in vivo data (Fig. 4B and C), the estimate that sirolimus receptors (FKBP12) are scarce relative to general sirolimus binding sites is of particular significance as it implies that binding to the latter may mask any difference in the specific binding to the former that might be seen with formulations that elute sirolimus with different kinetics. The disparity between the dissociation constants favoring specific over non-specific binding implies that such masking is prominent at high rates of drug elution and high tissue contents. As the rate of DES elution declines over time, drug first dissociates from non-specific sites, increasing the relative contribution of receptor binding to total tissue content (Figs. 4 and 5). As long as the rate of drug elution remains sufficiently high to saturate receptors, tissue content should linearly track the rate of stent elution with a vertical intercepts that is the density of receptors (regime II). These inferences and their validation (Fig. 4A) allowed us to conclude that while NEVO™ prototype Stents achieved consistently higher tissue contents in healthy porcine coronary arteries, both SES provided receptor-saturating tissue contents during 30 day implantations (Fig. 4B and C), and likely well beyond. As inhibition of intimal hyperplasia by sirolimus is attributed to its binding to FKBP12, these data offer a mechanistic underpinning for the equivalent efficacy of CYPHER® Stents [57] and NEVO™ prototype Stents [17] in similar populations. Moreover, the greater variability in clinical response to the former might be explained by the slight difference in the predicted rates at which sirolimus dissociates from its receptor in arteries that received these stents (Fig. 4B and C).
Though our data were acquired in healthy animals, there exists supporting evidence as to their relevance to atherosclerotic arteries in animals and humans. Through histological staining of animal and human tissue samples, we [53] and others [54] have found that injury and high cholesterol diets only minimally impact the steady-state expression of sirolimus receptors (FKBP12) relative to the control state. Thus, our estimate that 1 g of arterial tissue contains approximately 3 μg of FKBP12 should remain valid in stented human arteries. Moreover, through tissue incubation studies in receptor-saturating concentrations of radiolabeled drugs we previously showed that the drug content of atherosclerotic human tissue samples scaled inversely with cholesterol content and that cholesterol poor tissue samples of human and bovine arteries displayed similar capacities for these drugs [53]. At the extreme, cholesterol rich human artery samples exhibited an almost two-fold lower non-specific capacity for sirolimus. Though this suggested that interstitial cholesterol can displace up to half of the non-specific extracellular sirolimus-binding sites, this would only have the effect of reducing the ratio of non-specific binding sites to receptors from ~100 to ~50. Thus, while sirolimus content in SES stented arteries may vary with species and or disease state, such expected differences likely mask similar concentrations of sirolimus binding to its receptor FKBP12.
5.2. Dependence of efficacy on DES dose and duration of elution
In lieu of experimental means of assessing drug-receptor binding state in real time, we used mathematical modeling to predict the fraction of sirolimus-bound FKBP12 as a metric for in vivo drug effects (Fig. 3). Scaling analysis provided a means of associating the rate of drug delivery with a proportional concentration scale (cmax, Eq. (17)) that can be contrasted with the dissociation constant of receptor binding to estimate the level of receptor saturation and drug effects (Fig. 3 and Table S1 Online supporting material). Due to the nanomolar dissociation constant of sirolimus binding to its receptors, biological effects will display apparent threshold-dependence on drug elution rate, and thereby on dose or duration of elution (Eqs. (12)–(13)). As this scaling applies after the completion of the first wave of drug absorption, it is particularly powerful when applied to stents that elute slowly relative to the rate of absorption, including CYPHER® Stent and prototype NEVO™ Stent. In contrast, though the computational model was validated and calibrated on the basis of these scaling approximations (Fig. 4), it is generally valid and can be used to predict the tissue content and receptor binding achieved by general SES. The utility of the computational model is well demonstrated by our finding of differential tissue content and receptor binding kinetics for first order and Higuchi type elution kinetics that are only weakly dependent on the dose of eluted drug (Fig. 5). Thus, the persistence time of receptor saturation and effect is more sensitive to duration of elution than to eluted amount. The implication then is that dose escalation is inefficient at compensating for sub-optimal duration of elution, so that efforts should be focused on sustaining elution rather than elevating the load. Clinical experience with sirolimus loaded polymer free stents supports these inferences [3,58].
Supplementary Material
Acknowledgments
This study was supported in part by grants from the NIH (RO1 GM-49039) and an unrestricted gift from Cordis Corporation (a Johnson and Johnson Company). The authors thank Drs. Micheline Markey and Yi-Ping Sun, and Michele Zhan and Christine Bascara of Cordis Corporation for technical support, and Drs. Cynthia Maryanoff, Karin Balss and Kumaran Kolandaivelu for their review of the manuscript and insightful comments.
Footnotes
Disclosure statement Dr. Price was an employee of Cordis a Johnson & Johnson Company when this study was conducted and holds Johnson & Johnson equity. Dr. Edelman spoke at a conference sponsored by Cordis.
Appendix A. Supplementary data Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.jconrel.2012.05.039.
References
- [1].Balakrishnan B, Dooley JF, Kopia G, Edelman ER. Intravascular drug release kinetics dictate arterial drug deposition, retention, and distribution. J. Control. Release. 2007;123:100–108. doi: 10.1016/j.jconrel.2007.06.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Venkatraman S, Boey F. Release profiles in drug-eluting stents: issues and uncertainties. J. Control. Release. 2007;120:149–160. doi: 10.1016/j.jconrel.2007.04.022. [DOI] [PubMed] [Google Scholar]
- [3].Hausleiter J, Kastrati A, Wessely R, Dibra A, Mehilli J, Schratzenstaller T, Graf I, Renke-Gluszko M, Behnisch B, Dirschinger J, Wintermantel E, Schomig A. Prevention of restenosis by a novel drug-eluting stent system with a dose-adjustable, polymer-free, on-site stent coating. Eur. Heart J. 2005;26:1475–1481. doi: 10.1093/eurheartj/ehi405. [DOI] [PubMed] [Google Scholar]
- [4].Finkelstein A, McClean D, Kar S, Takizawa K, Varghese K, Baek N, Park K, Fishbein MC, Makkar R, Litvack F, Eigler NL. Local drug delivery via a coronary stent with programmable release pharmacokinetics. Circulation. 2003;107:777–784. doi: 10.1161/01.cir.0000050367.65079.71. [DOI] [PubMed] [Google Scholar]
- [5].Hossainy S, Prabhu S. A mathematical model for predicting drug release from a biodurable drug-eluting stent coating. J. Biomed. Mater. Res. A. 2008;87:487–493. doi: 10.1002/jbm.a.31787. [DOI] [PubMed] [Google Scholar]
- [6].Hwang CW, Wu D, Edelman ER. Physiological transport forces govern drug distribution for stent-based delivery. Circulation. 2001;104:600–605. doi: 10.1161/hc3101.092214. [DOI] [PubMed] [Google Scholar]
- [7].Tzafriri AR, Levin AD, Edelman ER. Diffusion-limited binding explains binary dose response for local arterial and tumour drug delivery. Cell Prolif. 2009;42:348–363. doi: 10.1111/j.1365-2184.2009.00602.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Tzafriri AR, Lerner EI, Flashner-Barak M, Hinchcliffe M, Ratner E, Parnas H. Mathematical modeling and optimization of drug delivery from intratumorally injected microspheres. Clin. Cancer Res. 2005;11:826–834. [PubMed] [Google Scholar]
- [9].Mongrain R, Faik I, Leask RL, Rodes-Cabau J, Larose E, Bertrand OF. Effects of diffusion coefficients and struts apposition using numerical simulations for drug eluting coronary stents. J. Biomech. Eng. 2007;129:733–742. doi: 10.1115/1.2768381. [DOI] [PubMed] [Google Scholar]
- [10].Serruys PW, Sianos G, Abizaid A, Aoki J, den Heijer P, Bonnier H, Smits P, McClean D, Verheye S, Belardi J, Condado J, Pieper M, Gambone L, Bressers M, Symons J, Sousa E, Litvack F. The effect of variable dose and release kinetics on neointimal hyperplasia using a novel paclitaxel-eluting stent platform: the Paclitaxel In-Stent Controlled Elution Study (PISCES) J. Am. Coll. Cardiol. 2005;46:253–260. doi: 10.1016/j.jacc.2005.03.069. [DOI] [PubMed] [Google Scholar]
- [11].Gershlick A, De Scheerder I, Chevalier B, Stephens-Lloyd A, Camenzind E, Vrints C, Reifart N, Missault L, Goy JJ, Brinker JA, Raizner AE, Urban P, Heldman AW. Inhibition of restenosis with a paclitaxel-eluting, polymer-free coronary stent: the European evaLUation of pacliTaxel Eluting Stent (ELUTES) trial. Circulation. 2004;109:487–493. doi: 10.1161/01.CIR.0000109694.58299.A0. [DOI] [PubMed] [Google Scholar]
- [12].Teirstein PS. A chicken in every pot and a drug-eluting stent in every lesion. Circulation. 2004;109:1906–1910. doi: 10.1161/01.CIR.0000127448.25065.6E. [DOI] [PubMed] [Google Scholar]
- [13].Hausleiter J, Kastrati A, Mehilli J, Vogeser M, Zohlnhofer D, Schuhlen H, Goos C, Pache J, Dotzer F, Pogatsa-Murray G, Dirschinger J, Heemann U, Schomig A. Randomized, double-blind, placebo-controlled trial of oral sirolimus for restenosis prevention in patients with in-stent restenosis: the Oral Sirolimus to Inhibit Recurrent In-stent Stenosis (OSIRIS) trial. Circulation. 2004;110:790–795. doi: 10.1161/01.CIR.0000138935.17503.35. [DOI] [PubMed] [Google Scholar]
- [14].Rodriguez AE, Alemparte M. Rodriguez, Vigo CF, Pereira C. Fernandez, Llaurado C, Vetcher D, Pocovi A, Ambrose J. Role of oral rapamycin to prevent restenosis in patients with de novo lesions undergoing coronary stenting: results of the Argentina single centre study (ORAR trial) Heart. 2005;91:1433–1437. doi: 10.1136/hrt.2004.050617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Parker T, Dave V, Falotico R. Polymers for drug eluting stents. Curr. Pharm. Des. 2010;16:3978–3988. doi: 10.2174/138161210794454897. [DOI] [PubMed] [Google Scholar]
- [16].Falotico R, Parker T, Grishaber R, Price S, Cohen SA, Rogers C. NEVO: a new generation of sirolimus-eluting coronary stent. EuroIntervention. 2009;5(Suppl. F):F88–F93. doi: 10.4244/EIJV5IFA15. [DOI] [PubMed] [Google Scholar]
- [17].Ormiston JA, Abizaid A, Spertus J, Fajadet J, Mauri L, Schofer J, Verheye S, Dens J, Thuesen L, Dubois C, Hoffmann R, Wijns W, Fitzgerald PJ, Popma JJ, Macours N, Cebrian A, Stoll HP, Rogers C, Spaulding C. Six-month results of the NEVO Res-Elution I (NEVO RES-I) trial: a randomized, multicenter comparison of the NEVO sirolimus-eluting coronary stent with the TAXUS Liberte paclitaxel-eluting stent in de novo native coronary artery lesions. Circ. Cardiovasc. Interv. 2010;3:556–564. doi: 10.1161/CIRCINTERVENTIONS.110.946426. [DOI] [PubMed] [Google Scholar]
- [18].NRC (National Research Council) Guide for the Care and Use of Laboratory Animals. National Academy Press; Washington, DC: 1996. [Google Scholar]
- [19].Sirianni RW, Jang EH, Miller KM, Saltzman WM. Parameter estimation methodology in a model of hydrophobic drug release from a polymer coating. J. Control. Release. 2010;142:474–482. doi: 10.1016/j.jconrel.2009.11.021. [DOI] [PubMed] [Google Scholar]
- [20].Balss KM, Llanos G, Papandreou G, Maryanoff CA. Quantitative spatial distribution of sirolimus and polymers in drug-eluting stents using confocal Raman microscopy. J. Biomed. Mater. Res. A. 2008;85:258–270. doi: 10.1002/jbm.a.31535. [DOI] [PubMed] [Google Scholar]
- [21].Balss KM, Long FH, Veselov V, Orana A, Akerman-Revis E, Papandreou G, Maryanoff CA. Multivariate analysis applied to the study of spatial distributions found in drug-eluting stent coatings by confocal Raman microscopy. Anal. Chem. 2008;80:4853–4859. doi: 10.1021/ac7025767. [DOI] [PubMed] [Google Scholar]
- [22].Ranade SV, Miller KM, Richard RE, Chan AK, Allen MJ, Helmus MN. Physical characterization of controlled release of paclitaxel from the TAXUS Express2 drug-eluting stent. J. Biomed. Mater. Res. A. 2004;71:625–634. doi: 10.1002/jbm.a.30188. [DOI] [PubMed] [Google Scholar]
- [23].Verhoeven ML, Driessen AA, Paul AJ, Brown A, Canry JC, Hendriks M. DSIMS characterization of a drug-containing polymer-coated cardiovascular stent. J. Control. Release. 2004;96:113–121. doi: 10.1016/j.jconrel.2004.01.014. [DOI] [PubMed] [Google Scholar]
- [24].Belu A, Mahoney C, Wormuth K. Chemical imaging of drug eluting coatings: combining surface analysis and confocal Raman microscopy. J. Control. Release. 2008;126:111–121. doi: 10.1016/j.jconrel.2007.11.015. [DOI] [PubMed] [Google Scholar]
- [25].Acharya G, Park K. Mechanisms of controlled drug release from drug-eluting stents. Adv. Drug Deliv. Rev. 2006;58:387–401. doi: 10.1016/j.addr.2006.01.016. [DOI] [PubMed] [Google Scholar]
- [26].Wu M, Kleiner L, Tang FW, Hossainy S, Davies MC, Roberts CJ. Surface characterization of poly(lactic acid)/everolimus and poly(ethylene vinyl alcohol)/everolimus stents. Drug Deliv. 2010;17:376–384. doi: 10.3109/10717541003762847. [DOI] [PubMed] [Google Scholar]
- [27].Barocas V, Drasler W, 2nd, Girton T, Guler I, Knapp D, Moeller J, Parsonage E. A dissolution–diffusion model for the TAXUS drug-eluting stent with surface burst estimated from continuum percolation. J. Biomed. Mater. Res. B Appl. Biomater. 2009;90:267–274. doi: 10.1002/jbm.b.31282. [DOI] [PubMed] [Google Scholar]
- [28].Baker RW, Lonsdale HS. Controlled released: mechanisms and rates. In: Tanquary AC, Lacey RE, editors. Controlled Release of Biologicallyl Active Agents. Plenum Press; New York: 1974. pp. 15–71. [Google Scholar]
- [29].Higuchi T. Mechanism of sustained-action medication. Theoretical analysis of rate of release of solid drugs dispersed in solid matrices. J. Pharm. Sci. 1963;52:1145–1149. doi: 10.1002/jps.2600521210. [DOI] [PubMed] [Google Scholar]
- [30].Marx SO, Jayaraman T, Go LO, Marks AR. Rapamycin–FKBP inhibits cell cycle regulators of proliferation in vascular smooth muscle cells. Circ. Res. 1995;76:412–417. doi: 10.1161/01.res.76.3.412. [DOI] [PubMed] [Google Scholar]
- [31].Poon M, Marx SO, Gallo R, Badimon JJ, Taubman MB, Marks AR. Rapamycin inhibits vascular smooth muscle cell migration. J. Clin. Invest. 1996;98:2277–2283. doi: 10.1172/JCI119038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Balakrishnan B, Dooley J, Kopia G, Edelman ER. Thrombus causes fluctuations in arterial drug delivery from intravascular stents. J. Control. Release. 2008;131:173–180. doi: 10.1016/j.jconrel.2008.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Bierer BE, Mattila PS, Standaert RF, Herzenberg LA, Burakoff SJ, Crabtree G, Schreiber SL. Two distinct signal transmission pathways in T lymphocytes are inhibited by complexes formed between an immunophilin and either FK506 or rapamycin. Proc. Natl. Acad. Sci. U. S. A. 1990;87:9231–9235. doi: 10.1073/pnas.87.23.9231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Levin AD, Jonas M, Hwang CW, Edelman ER. Local and systemic drug competition in drug-eluting stent tissue deposition properties. J. Control. Release. 2005;109:236–243. doi: 10.1016/j.jconrel.2005.09.041. [DOI] [PubMed] [Google Scholar]
- [35].Bartorelli AL, Trabattoni D, Fabbiocchi F, Montorsi P, de Martini S, Calligaris G, Teruzzi G, Galli S, Ravagnani P. Synergy of passive coating and targeted drug delivery: the tacrolimus-eluting Janus CarboStent. J. Interv. Cardiol. 2003;16:499–505. doi: 10.1046/j.1540-8183.2003.01050.x. [DOI] [PubMed] [Google Scholar]
- [36].Perkins LE, Boeke-Purkis KH, Wang Q, Stringer SK, Coleman LA. XIENCE V™ Everolimus-eluting coronary stent system: a preclinical assessment. J. Interv. Cardiol. 2009;22:S28–S40. [Google Scholar]
- [37].Drachman DE, Edelman ER, Seifert P, Groothuis AR, Bornstein DA, Kamath KR, Palasis M, Yang D, Nott SH, Rogers C. Neointimal thickening after stent delivery of paclitaxel: change in composition and arrest of growth over six months. J. Am. Coll. Cardiol. 2000;36:2325–2332. doi: 10.1016/s0735-1097(00)01020-2. [DOI] [PubMed] [Google Scholar]
- [38].Creel CJ, Lovich MA, Edelman ER. Arterial paclitaxel distribution and deposition. Circ. Res. 2000;86:879–884. doi: 10.1161/01.res.86.8.879. [DOI] [PubMed] [Google Scholar]
- [39].Lovich MA, Creel C, Hong K, Hwang CW, Edelman ER. Carrier proteins determine local pharmacokinetics and arterial distribution of paclitaxel. J. Pharm. Sci. 2001;90:1324–1335. doi: 10.1002/jps.1085. [DOI] [PubMed] [Google Scholar]
- [40].Lovich MA, Edelman ER. Tissue average binding and equilibrium distribution: an example with heparin in arterial tissues. Biophys. J. 1996;70:1553–1559. doi: 10.1016/S0006-3495(96)79719-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Brown EJ, Albers MW, Shin TB, Ichikawa K, Keith CT, Lane WS, Schreiber SL. A mammalian protein targeted by G1-arresting rapamycin–receptor complex. Nature. 1994;369:756–758. doi: 10.1038/369756a0. [DOI] [PubMed] [Google Scholar]
- [42].Levin AD, Vukmirovic N, Hwang CW, Edelman ER. Specific binding to intracellular proteins determines arterial transport properties for rapamycin and paclitaxel. Proc. Natl. Acad. Sci. U. S. A. 2004;101:9463–9467. doi: 10.1073/pnas.0400918101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Lovich MA, Edelman ER. Mechanisms of transmural heparin transport in the rat abdominal aorta after local vascular delivery. Circ. Res. 1995;77:1143–1150. doi: 10.1161/01.res.77.6.1143. [DOI] [PubMed] [Google Scholar]
- [44].Tzafriri AR, Edelman ER. Endosomal receptor kinetics determine the stability of intracellular growth factor signalling complexes. Biochem. J. 2007;402:537–549. doi: 10.1042/BJ20060756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Lu X, Yang J, Zhao JB, Gregersen H, Kassab GS. Shear modulus of porcine coronary artery: contributions of media and adventitia. Am. J. Physiol. Heart Circ. Physiol. 2003;285:H1966–H1975. doi: 10.1152/ajpheart.00357.2003. [DOI] [PubMed] [Google Scholar]
- [46].Napoli KL, Taylor PJ. From beach to bedside: history of the development of sirolimus. Ther. Drug Monit. 2001;23:559–586. doi: 10.1097/00007691-200110000-00012. [DOI] [PubMed] [Google Scholar]
- [47].Tedgui A, Lever MJ. Filtration through damaged and undamaged rabbit thoracic aorta. Am. J. Physiol. 1984;247:H784–H791. doi: 10.1152/ajpheart.1984.247.5.H784. [DOI] [PubMed] [Google Scholar]
- [48].Huang ZJ, Tarbell JM. Numerical simulation of mass transfer in porous media of blood vessel walls. Am. J. Physiol. 1997;273:H464–H477. doi: 10.1152/ajpheart.1997.273.1.H464. [DOI] [PubMed] [Google Scholar]
- [49].Wear MA, Walkinshaw MD. Determination of the rate constants for the FK506 binding protein/rapamycin interaction using surface plasmon resonance: an alternative sensor surface for Ni2+-nitrilotriacetic acid immobilization of His-tagged proteins. Anal. Biochem. 2007;371:250–252. doi: 10.1016/j.ab.2007.06.034. [DOI] [PubMed] [Google Scholar]
- [50].Lovich MA, Edelman ER. Tissue concentration of heparin, not administered dose, correlates with the biological response of injured arteries in vivo. Proc. Natl. Acad. Sci. U. S. A. 1999;96:11111–11116. doi: 10.1073/pnas.96.20.11111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Dumont FJ, Kastner C, Iacovone F, Jr., Fischer PA. Quantitative and temporal analysis of the cellular interaction of FK-506 and rapamycin in T-lymphocytes. J. Pharmacol. Exp. Ther. 1994;268:32–41. [PubMed] [Google Scholar]
- [52].Swabb EA, Wei J, Gullino PM. Diffusion and convection in normal and neoplastic tissues. Cancer Res. 1974;34:2814–2822. [PubMed] [Google Scholar]
- [53].Tzafriri AR, Vukmirovic N, Kolachalama VB, Astafieva I, Edelman ER. Lesion complexity determines arterial drug distribution after local drug delivery. J. Control. Release. 2010;142:332–338. doi: 10.1016/j.jconrel.2009.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Bauriedel G, Jabs A, Kraemer S, Nickenig G, Skowasch D. Neointimal expression of rapamycin receptor FK506-binding protein FKBP12: postinjury animal and human in-stent restenosis tissue characteristics. J. Vasc. Res. 2007;45:173–178. doi: 10.1159/000110417. [DOI] [PubMed] [Google Scholar]
- [55].Buerke M, Guckenbiehl M, Schwertz H, Buerke U, Hilker M, Platsch H, Richert J, Bomm S, Zimmerman GA, Lindemann S, Mueller-Werdan U, Werdan K, Darius H, Weyrich AS. Intramural delivery of sirolimus prevents vascular remodeling following balloon injury. Biochim. Biophys. Acta. 2007;1774:5–15. doi: 10.1016/j.bbapap.2006.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Zohlnhofer D, Klein CA, Richter T, Brandl R, Murr A, Nuhrenberg T, Schomig A, Baeuerle PA, Neumann FJ. Gene expression profiling of human stent-induced neointima by cDNA array analysis of microscopic specimens retrieved by helix cutter atherectomy: detection of FK506-binding protein 12 upregulation. Circulation. 2001;103:1396–1402. doi: 10.1161/01.cir.103.10.1396. [DOI] [PubMed] [Google Scholar]
- [57].Moses JW, Leon MB, Popma JJ, Fitzgerald PJ, Holmes DR, O’Shaughnessy C, Caputo RP, Kereiakes DJ, Williams DO, Teirstein PS, Jaeger JL, Kuntz RE. Sirolimus-eluting stents versus standard stents in patients with stenosis in a native coronary artery. N. Engl. J. Med. 2003;349:1315–1323. doi: 10.1056/NEJMoa035071. [DOI] [PubMed] [Google Scholar]
- [58].Mehilli J, Byrne RA, Wieczorek A, Iijima R, Schulz S, Bruskina O, Pache J, Wessely R, Schomig A, Kastrati A. Randomized trial of three rapamycin-eluting stents with different coating strategies for the reduction of coronary restenosis. Eur. Heart J. 2008;29:1975–1982. doi: 10.1093/eurheartj/ehn253. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.