Abstract
In constructing predictive models, investigators frequently assess the incremental value of a predictive marker by comparing the ROC curve generated from the predictive model including the new marker with the ROC curve from the model excluding the new marker. Many commentators have noticed empirically that a test of the two ROC areas [1] often produces a non-significant result when a corresponding Wald test from the underlying regression model is significant. A recent article showed using simulations that the widely-used ROC area test produces exceptionally conservative test size and extremely low power [2]. In this article we demonstrate that both the test statistic and its estimated variance are seriously biased when predictions from nested regression models are used as data inputs for the test, and we examine in detail the reasons for these problems. While it is possible to create a test reference distribution by resampling that removes these biases, Wald or likelihood ratio tests remain the preferred approach for testing the incremental contribution of a new marker.
Keywords: receiver operating characteristic curve, biomarker, predictive model, area under the ROC curve, logistic regression, predictive accuracy, discrimination
1. Introduction
Receiver operating characteristic (ROC) curves provide a standard way of evaluating the ability of a continuous marker to predict a binary outcome. The area under the ROC curve (AUC) is a frequently used summary measure of diagnostic/predictive accuracy. Comparison of two or more ROC curves is usually based on a comparison of the area measures. The standard method comparing AUCs is a non-parametric test [1], hereafter referred to as the “AUC test,” although a method developed earlier is also used widely [3]. The AUC test uses the fact that the AUC is a U-statistic and incorporates the dependencies caused by the fact that the markers are usually generated in the same patients, and are thus “paired.”
Although the AUC test was originally developed in the context of comparing distinct diagnostic tests or markers, it has increasingly been adopted for use in evaluating the incremental effect of an additional marker in predicting a binary event via a regression model. Indeed authors of several methodological articles on predictive modeling have advocated the use of ROC curves for this purpose though these groups have generally not advocated statistical testing of the ROC curves specifically [4, 5, 6, 7, 8]. In this setting investigators typically use the fitted values from the regression model to construct an ROC curve and to compare this with the ROC curve derived similarly from the fitted values from the regression excluding the new marker. However, a recent article provided several examples of the use of this strategy in the literature, and demonstrated using simulations that the AUC test has exceptionally conservative test size in this setting, and much lower power than the Wald test of the new marker in the underlying regression model [2].
We show here that in the context of comparing AUCs from fitted values of two nested regression models the AUC test is invalid. That is the nominal reference distribution does not approximate the distribution of the test statistic under the null hypothesis of no difference between the models. Note that this is a common sense use of the term validity rather than the narrow use of this term to reflect whether or not the test size is less than (valid) or greater than (invalid) the nominal significance level. We use the Wald test as a benchmark in recognition of its wide usage and the well-known result that Wald test is asymptotically equivalent to the likelihood ratio test and the score test [9, Chapter 9].
2. AUC Test for Nested Binary Regression Models
2.1. A Review of the AUC Test
Consider first the comparison of the predictive accuracy of two independently generated predictive markers, denoted W1i and W2i for cases i = 1, …, n. We are interested in predicting a binary outcome Yi, where Yi = 1 or 0. The estimate of the AUC for marker k can be written as a U-statistic:
| (1) |
where , and I (.) is the indicator function. The AUC is equivalent to the Mann-Whitney estimate of the probability that a randomly selected marker with a positive outcome is greater than a randomly selected marker with a negative outcome.
It is important to note that (1) assumes that high marker values are more indicative of positive outcomes, Yi = 1, than low marker values. This assumption, often relegated to small print or overlooked, is highly consequential for our purposes. We will call it known directionality. Known directionality accompanies most single-marker analyses but this is not the case for markers derived as predictions from multivariable regression models.
An estimate of the difference between A2 and A1 is given by δ̂ = Â2 − Â1. DeLong et. al. [1] derived a consistent estimate for the variance V̂ = Var(δ̂) and proposed the test statistic which has an asymptotic standard normal distribution under the null hypothesis that δ = 0. We heretofore refer to this as the AUC test.
2.2. AUC test is invalid with nested binary regression models
The original derivation of the AUC test assumes that the two markers are to be compared head-to-head [1]. If the goal is to evaluate the incremental value of a marker in the presence of another marker then the AUC test cannot be used directly. Instead one needs to create a “composite” marker that captures the combined effect of the two markers, and then compare this with the first marker. This aggregation of predictive information is usually accomplished using regression. For example in the setting of logistic regression we would compare the first marker W1 = {W1i} with a composite marker derived from the risk predictors from a logistic regression of Y = {Yi} on W1 and W2 = {W2i}. Frequently there are other variables (Z) in the regression and so the comparison is between two composite predictors, derived from the following two models:
| (2) |
| (3) |
In this context we are interested in testing the null hypothesis that β2 = 0. One can then form the linear predictors using the MLEs of the parameters
| (4) |
| (5) |
Let and denote the AUCs estimated from (1) using and in place of W1 and W2. Also let and let T* denote the test statistic corresponding to δ̂* calculated in the manner outlined in Section 2.1. We heretofore refer to T* as the AUC test statistic. As reasonable and straightforward as it seems, the comparison using the AUC test in this manner is not valid for two reasons.
The first reason is that the variance estimate V̂* is based on the assumption that the observations from the patients are mutually independent, i.e. for all i ≠ j. With and defined as in (4-5) this assumption is clearly violated. In fact, typically and are strongly correlated, as we demonstrate by example later in Section 4.
The second reason concerns the construction of as defined in (1). From the perspective of predictive accuracy of an individual marker it should make a difference whether Wki is ranked from the smallest to the largest or from the largest to the smallest. We know whether a high value of a diagnostic test should be associated with increased risk of disease. That is, we know a priori how to order W with respect to Y. If we define , ∀i, and the AUC for to be then it is easily shown that . With known directionality, an AUC estimate less than 0.5 is admissible, though it would be recognized that the decrement from 0.5 is likely to be due to random variation. But in the context of a regression model it is not possible to invoke known directionality. In this context the model typically produces an ordering that leads to an increase in the area estimate. That is, for M2 for example, if W2 is observed to be positively associated with Y after adjusting for W1 and Z then the sign of β̃2 will be positive. If, on the other hand W2 is observed to be negatively associated with Y then the sign of β̃2 will be negative. Either way, the net effect will usually be to increment the AUC estimate upwards. This phenomenon is especially problematic when testing the null hypothesis that β2 = 0. The reference distribution for the AUC test is constructed under the assumption that half the time the results should lead to a decrement in AUC, but in fact this happens much less frequently. This creates a bias in T* such that it no longer has zero mean under the null hypothesis. However, as the true value of β2 departs from the null value the probability of observing a negative residual association of W2 and Y by chance becomes less likely.
2.3. Simulations
The extent and magnitude of the problem explained in the preceeding sections has been investigated by Vickers et. al. [2] who performed simulations to show that the use of the AUC test in nested regression contexts is problematic under several scenarios. In the following we have reproduced simulations constructed in the same way as in [2] and we augment these with graphs that help to explain the problems in the AUC test. Details of the data generation are provided in [2], but briefly the simulations are constructed as follows. The outcomes {Yi} are generated as Bernoulli random variables with varying probability (0.5 and 0.2 are presented). Pairs of marker values {W1i, W2i} are generated as bivariate standard normal variates with correlation ρ, conditional on {Yi}. The mean is (0, 0) when Yi = 0 and (μ1, μ2 + ρμ1) when Yi = 1. Two logistic regressions are then performed: logit(Yi) = β0 + β1W1i and logit(Yi) = β0 + β1W1i + β2W2i, and pairs of predictors generated as in Section 2.2. These are analyzed using the Wald test (for testing β2 = 0) and the AUC test based on the statistic T* [1].
Results are displayed in Table 1 for different combinations of ρ, μ1, μ2, and for two different sample sizes. Note that μ2 represents the conditional predictive strength of W2, with the null hypothesis equivalently represented by μ2 = 0 and β2 = 0. The parameter μ1 represents the underlying predictive strength of W1. The actual AUCs represented by these configurations are also displayed in the Table. These results indicate clearly that the AUC test is extremely insensitive with exceptionally conservative test size and low power. Under the null hypothesis, i.e. when μ2 = 0, the AUC test is significant typically only once in 5000 simulations (at the nominal 5% significance level) whereas the Wald test has approximately the correct size. As μ2 moves away from 0, the AUC test is substantially inferior to the Wald test in terms of power. We also see that doubling the sample size from 250 to 500 does not remedy the problem. This is because the bias involved in the estimation of the mean and the variance of the AUC test statistic does not diminish with increasing sample size. Poor performance of the AUC test is also largely unaffected by the degree of correlation between the markers (represented by ρ). Table 1 also makes clear that the performance of the AUC test under the null remains equally unacceptable when disease prevalence changes from 0.5 to 0.2.
Table 1.
Rejection probabilities of the tests.
| E(Y) | μ2 | Test | AUC1a = 0.50 | AUC1a = 0.58 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| μ1 = 0, ρ = 0 | μ1 = 0, ρ = 0.5 | μ1 = 0.3, ρ = 0 | μ1 = 0.3, ρ = 0.5 | |||||||||||
| n | n | n | n | |||||||||||
| 250 | 500 | 250 | 500 | 250 | 500 | 250 | 500 | |||||||
| AUC2b | P(Reject)c | AUC2b | P(Reject)c | AUC2b | P(Reject)c | AUC2b | P(Reject)c | |||||||
| 0.5 | 0 | Wald | 0.50 | 0.04 | 0.05 | 0.50 | 0.05 | 0.05 | 0.58 | 0.06 | 0.06 | 0.58 | 0.05 | 0.05 |
| AUC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||||||
| PPRd | 0.04 | 0.05 | 0.05 | 0.05 | 0.06 | 0.06 | 0.04 | 0.05 | ||||||
|
| ||||||||||||||
| 0.1 | Wald | 0.53 | 0.12 | 0.19 | 0.53 | 0.14 | 0.24 | 0.59 | 0.12 | 0.18 | 0.59 | 0.16 | 0.25 | |
| AUC | 0.01 | 0.02 | 0.02 | 0.04 | 0.00 | 0.01 | 0.02 | 0.01 | ||||||
| PPRd | 0.11 | 0.17 | 0.15 | 0.23 | 0.11 | 0.18 | 0.15 | 0.22 | ||||||
|
| ||||||||||||||
| 0.2 | Wald | 0.56 | 0.36 | 0.59 | 0.57 | 0.44 | 0.75 | 0.60 | 0.36 | 0.60 | 0.61 | 0.43 | 0.70 | |
| AUC | 0.08 | 0.18 | 0.11 | 0.29 | 0.04 | 0.11 | 0.06 | 0.17 | ||||||
| PPRd | 0.36 | 0.57 | 0.42 | 0.72 | 0.32 | 0.53 | 0.41 | 0.68 | ||||||
|
| ||||||||||||||
| 0.3 | Wald | 0.58 | 0.66 | 0.93 | 0.60 | 0.76 | 0.96 | 0.62 | 0.67 | 0.91 | 0.63 | 0.75 | 0.96 | |
| AUC | 0.22 | 0.56 | 0.33 | 0.73 | 0.13 | 0.39 | 0.22 | 0.54 | ||||||
| PPRd | 0.63 | 0.91 | 0.75 | 0.95 | 0.65 | 0.88 | 0.72 | 0.95 | ||||||
|
| ||||||||||||||
| 0.2 | 0 | Wald | 0.50 | 0.04 | 0.05 | 0.50 | 0.06 | 0.05 | 0.58 | 0.05 | 0.06 | 0.58 | 0.05 | 0.05 |
| AUC | 0.01 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||||||
| PPRd | 0.04 | 0.05 | 0.06 | 0.05 | 0.05 | 0.06 | 0.04 | 0.05 | ||||||
|
| ||||||||||||||
| 0.1 | Wald | 0.53 | 0.10 | 0.16 | 0.53 | 0.11 | 0.17 | 0.59 | 0.10 | 0.14 | 0.59 | 0.10 | 0.17 | |
| AUC | 0.01 | 0.03 | 0.02 | 0.03 | 0.01 | 0.01 | 0.01 | 0.01 | ||||||
| PPRd | 0.11 | 0.14 | 0.10 | 0.17 | 0.09 | 0.13 | 0.10 | 0.16 | ||||||
|
| ||||||||||||||
| 0.2 | Wald | 0.56 | 0.24 | 0.43 | 0.57 | 0.32 | 0.55 | 0.60 | 0.25 | 0.40 | 0.61 | 0.30 | 0.53 | |
| AUC | 0.05 | 0.12 | 0.07 | 0.19 | 0.03 | 0.05 | 0.04 | 0.08 | ||||||
| PPRd | 0.22 | 0.41 | 0.29 | 0.52 | 0.23 | 0.38 | 0.27 | 0.50 | ||||||
|
| ||||||||||||||
| 0.3 | Wald | 0.58 | 0.46 | 0.76 | 0.60 | 0.59 | 0.87 | 0.62 | 0.45 | 0.74 | 0.63 | 0.57 | 0.86 | |
| AUC | 0.12 | 0.34 | 0.17 | 0.46 | 0.08 | 0.20 | 0.12 | 0.35 | ||||||
| PPRd | 0.44 | 0.74 | 0.57 | 0.85 | 0.43 | 0.70 | 0.54 | 0.84 | ||||||
AUC of model M1
AUC of model M2
Probability of rejection. Equal to size for μ2 = 0 and power for μ2 > 0.
Using the projection permutation reference distribution (Section 4)
To better illustrate the biases in using the AUC test we display in Figure 1 results from a specific run of simulations (μ1 = 0.3, μ2 = 0 and ρ= 0 with n = 500). The horizontal axis is the standardized AUC test statistic T* which should have zero mean and unit variance. The solid line is the kernel density estimate of the observed test statistic over 5000 simulations; it has mean 0.353 and variance 0.232. The dotted line is a standard normal density which is the reference distribution of the AUC test statistic calculated in the conventional way [1]. Clearly, the difference between the two densities is substantial, both with respect to mean and variance. The graph shows the paradoxical effects of the two major sources of bias. The mean of the test statistic has a positive bias. However this is more than offset by the fact that the variance is greatly reduced relative to the asymptotic variance of the estimator with the result that very few realizations of this process achieve a significant test result.
Figure 1.
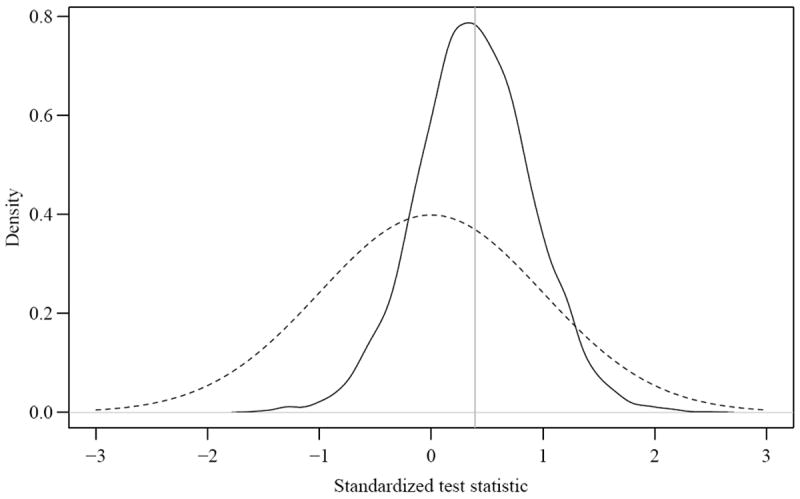
Distribution of the AUC test statistic under the null hypothesis. The solid curve depicts the density of the observed test statistic from 5000 simulations and the dashed curve is a standard normal, the presumed asymptotic distriution of the test statistic under the null hypothesis. Data are generated using μ1 = 0.3, μ2 = 0, ρ = 0 and n = 500.
The occasional negative values of the AUC test statistic in Figure 1 reveal another source of discrepancy between the AUC and Wald tests. This is due to dissonance between the maximum likelihood and AUC estimates. Parameters that maximize the likelihood do not necessarily maximize the AUC, so there will be some data sets where the residual association between and Y is positive yet the corresponding increment in AUCs is less than zero. In other words, the parameter values that maximize the likelihood result in a positive Wald test statistic but a decrement in the AUC. In our simulations under the null we observed a negative AUC test statistic approximately 20% of the time. This phenomenon becomes less common when W2 has incremental information, since the estimated coefficient is not only positive but also distant from 0 in most circumstances.
It is instructive to examine graphically the way the bias in the mean of the AUC test statistic operates. Figure 2 plots the standardized Wald test statistic against the AUC test statistic for two scenarios: no incremental information in W2 (left panel) and strong incremental information in W2 (right panel). In both cases the statistics should exhibit strong positive correlation. For the left panel, since there is no incremental information, data sets that lead to strongly negative Wald tests produce strongly positive AUC tests due to known directionality. For the right panel, as indicated in Section 2.2, these discrepancies are unlikely to occur. Hence the V-shaped pattern on the left and this V-shape is the source of the bias described in Section 2.2. The magnitude of the problem becomes smaller as the signal increases; the figure on the right exhibits the positive correlation between the two tests that we would expect. This is because it is increasingly unlikely, as β2 increases, that the residual association between W2 and Y is negative.
Figure 2.
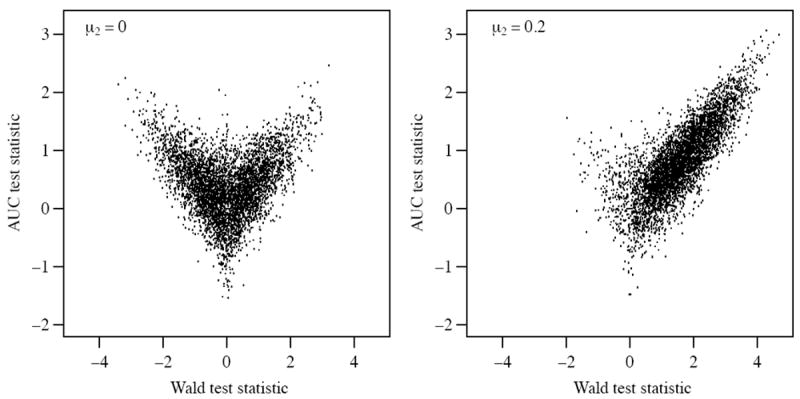
Wald statistic and the AUC test statistic under the null (left panel) and alternative (right panel) hypotheses. Both graphics are generated using 5000 draws from M2 with μ1 = 0.3 and n = 500 for both panels, μ2 = 0 for the left panel and 0:2 for the right panel (ρ = 0 for both panels).
Figure 2 explains the source of the discrepancy with respect to the location of the two densities in Figure 1. An explanation of the scale discrepancy is elusive graphically but is suggested by examining the following between subject correlations: and all of which are induced by the derived nature of W*s. The variance of the asymptotic reference distribution in Figure 1 is computed under the assumption that . Estimates of these correlations obtained from our simulations indicate that these are consistently, and frequently strongly, positive. For example for the configurations used in Figures 1 and 2 with μ1 = 0.3, μ2 = 0 and ρ = 0, we obtained and . These correlations were estimated empiricially from the predictors generated from multiple simulations.
We note that it is not self-evident that introduction of correlated data and known directionality will undermine the asymptotic properties of the U-statistics that comprise the AUC test. In fact, the AUC test statistic does not appear to converge to a limiting distribution with zero mean and unit variance. To illustrate this, using the same parametric configurations as in Figure 1, we computed the empirical mean and standard deviation of the AUC test statistic over 1000 simulated data sets for sample sizes ranging from 200 to 10000 (Figure 3). The mean of the AUC test statistic (circles) should converge to zero while the standard deviation (triangles) should converge to 1. Clearly neither convergence is apparent within reasonable sample sizes.
Figure 3.
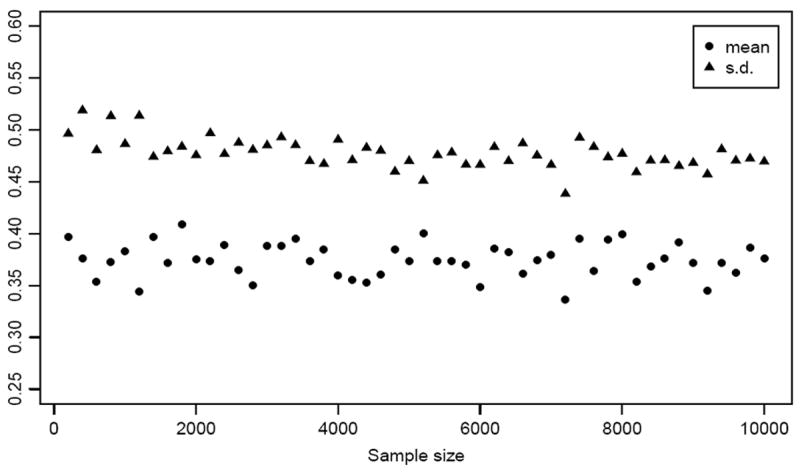
The mean (circles) and standard deviation (triangles) of the AUC test statistic from simulations at sample sizes ranging from 200 to 1000 in steps of 200. Each point is calculated from 1000 simulated data sets using the configuration μ1 = 0.3, μ2 = 0 and ρ = 0.
3. Performance of the Area Test in Non-Nested Models and Validation Samples
3.1. Non-Nested Models
Our primary objective has been to evaluate the incremental value of a new marker which inherently gives rise to the nested regression model. It is, however, logical to ask if the AUC test is valid if the comparison is between the distinct incremental contributions of two different markers. That is we wish to compare non-nested models specifically in the following way. Replace models M1 and M2 (2-3) with
and the linear predictors (4-5) now become
As before, the AUC test is used to compare and , in this case representing the hypothesis that β2 = β3.
Table 2 reports the results of simulations conducted under this scenario. Here μ2 = E(W2), μ3 = E(W3) and ρ = Cor(W2,W3). The “AUC” column in the table represents the common expected AUCs that are being compared. The table shows that the test is conservative when the common increment from the markers (μ2, μ3) is small but approaches the nominal level when this increment becomes larger. However, the negative bias in the test appears to be unrelated to the overall AUC. For example the common AUC is 0.584 when μ1 = 0, μ2 = μ3 = 0.3 but is also 0.584 when μ1 = 0.3, μ2 = μ3 = 0. The test is strongly biased in the latter case but approaches nominal test size in the former case. The empirical distributions of the AUC Test in these two scenarios are plotted in Figure 4 in red and black, respectively, versus the theoretical reference distribution (dashed line). The Figure shows that the distribution of the test statistic closely matches the reference distribution when the common signal in the two markers being compared is large (μ2 = μ3 = 0.3) but the reference distribution substantially overestimates the variance when the common signal is small or zero.
Table 2.
Size of the AUC test in non-nested models for n=250 and 500.
| μ2 = μ3 | μ1 = 0, ρ = 0 | μ1 = 0, ρ = 0.5 | μ1 = 0.3, ρ = 0 | μ1 = 0.3, ρ = 0.5 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | n | n | n | |||||||||
| 250 | 500 | 250 | 500 | 250 | 500 | 250 | 500 | |||||
| AUC | Size | AUC | Size | AUC | Size | AUC | Size | |||||
| 0 | 0.50 | 0.00 | 0.00 | 0.50 | 0.00 | 0.00 | 0.58 | 0.00 | 0.00 | 0.58 | 0.00 | 0.00 |
| 0.1 | 0.53 | 0.01 | 0.01 | 0.53 | 0.00 | 0.01 | 0.59 | 0.02 | 0.01 | 0.59 | 0.01 | 0.00 |
| 0.2 | 0.56 | 0.03 | 0.02 | 0.57 | 0.01 | 0.02 | 0.60 | 0.05 | 0.04 | 0.61 | 0.03 | 0.04 |
| 0.3 | 0.58 | 0.04 | 0.04 | 0.60 | 0.03 | 0.04 | 0.62 | 0.06 | 0.06 | 0.63 | 0.04 | 0.03 |
| 0.4 | 0.61 | 0.04 | 0.05 | 0.63 | 0.05 | 0.06 | 0.64 | 0.05 | 0.05 | 0.65 | 0.05 | 0.05 |
| 0.5 | 0.64 | 0.07 | 0.06 | 0.66 | 0.04 | 0.04 | 0.66 | 0.04 | 0.06 | 0.68 | 0.05 | 0.05 |
| 0.6 | 0.66 | 0.05 | 0.06 | 0.69 | 0.04 | 0.04 | 0.68 | 0.06 | 0.05 | 0.70 | 0.06 | 0.06 |
| 0.7 | 0.69 | 0.05 | 0.05 | 0.72 | 0.05 | 0.05 | 0.71 | 0.06 | 0.04 | 0.73 | 0.05 | 0.04 |
Figure 4.
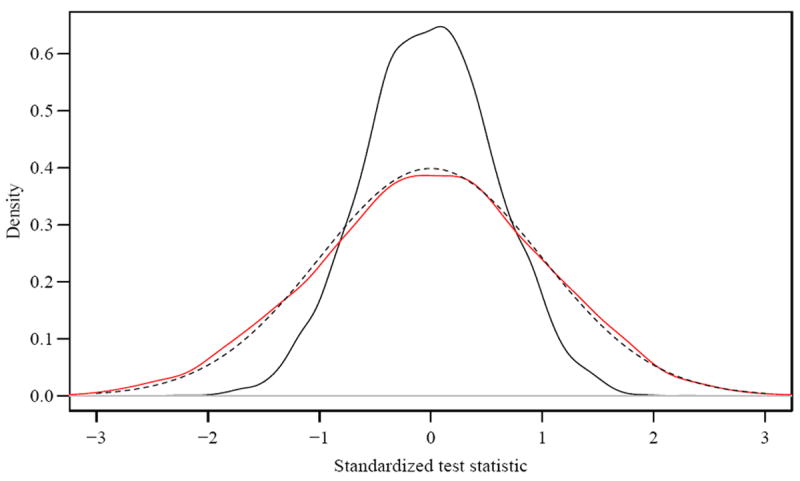
The empirical distributions of the AUC Test in two specific instances of a non-nested model: red curve for μ1 = 0, μ2 = μ3 = 0.3 and black for μ1 = 0.3, μ2 = μ3 = 0. In both cases the common AUC is 0.584 and the theoretical reference distribution is given by the dashed line.
3.2. Validation Samples
The scenarios we have considered so far have been limited to the case where estimation of regression parameters and comparison of the ROC curves were performed on the same data set. It is not uncommon for marker studies to employ validation samples where coefficients are estimated in a training set and derived predictors are constructed and compared only on a test set. Use of independent validation samples is considered to be the gold standard method for marker studies since it can eliminate optimistic bias. Is this appropriate when the data being used are calculated predictors from a nested regression model?
We conducted a set of simulations in which the data are generated in exactly the same way as in Section 2.3. Each simulated data set is then randomly split into training and test sets of equal size. Two logistic regressions are estimated using only the training set: logit(Yi) = β̂0 + β̂1W1i and logit(Yi) = β̃0 + β̃1W1i + β̃2W2i. Following this, pairs of predictors are calculated using solely the test data but with the β̂s and β̃s obtained from the training set.
In using validation data investigators are usually interested primarily in generating valid estimates of the AUCs, since these are known to be biased upwards in training data, rather than repeating tests of significance. Thus in Table 3 we present the difference in the non-parametric AUC estimates from the test data set, denoted “estimated ΔAUC”. These can be compared with the “true ΔAUC”s in the table to infer bias. We observe a modest negative bias in the estimated ΔAUC across all configurations in the table. To understand this we observe that empirical AUCs are based on ranks and and that the ranks are invariant under a location and scale shift (provided the scale factor is positive). Consequently a comparison of versus is equivalent to a comparison of versus where and . Thus we are in effect comparing a single marker {W1i} with the same marker with additional noise. The expectation of the difference in AUCs is negative unless β̃2 is exactly zero in the training set. However, this decrement is zero when μ1 = μ2 = 0 since both AUCs are 0.5 in this scenario.
Table 3.
Performance of the nested model with validation samples
| ρ | E(Y) μ2 | μ1 = 0 | μ1 = 0.3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n = 250 | n = 500 | n = 250 | n = 500 | ||||||||
| 0.2 | 0.5 | 0.2 | 0.5 | 0.2 | 0.5 | 0.2 | 0.5 | ||||
| True ΔAUC | Estimated ΔAUC | True ΔAUC | Estimated ΔAUC | ||||||||
| 0 | 0 | 0 | -0.001 | 0.000 | 0.000 | 0.000 | 0 | -0.010 | -0.008 | -0.006 | -0.004 |
| 0.1 | 0.028 | 0.009 | 0.014 | 0.014 | 0.016 | 0.005 | -0.004 | -0.003 | -0.001 | 0.001 | |
| 0.2 | 0.056 | 0.036 | 0.041 | 0.046 | 0.050 | 0.017 | 0.011 | 0.011 | 0.011 | 0.013 | |
| 0.3 | 0.084 | 0.070 | 0.075 | 0.078 | 0.080 | 0.034 | 0.027 | 0.029 | 0.030 | 0.031 | |
|
| |||||||||||
| 0.5 | 0 | 0 | -0.002 | 0.000 | 0.000 | -0.001 | 0 | -0.010 | -0.009 | -0.007 | -0.004 |
| 0.1 | 0.032 | 0.016 | 0.019 | 0.019 | 0.022 | 0.006 | -0.003 | -0.002 | 0.000 | 0.002 | |
| 0.2 | 0.065 | 0.048 | 0.053 | 0.053 | 0.059 | 0.022 | 0.016 | 0.017 | 0.018 | 0.018 | |
| 0.3 | 0.097 | 0.085 | 0.089 | 0.092 | 0.092 | 0.043 | 0.038 | 0.038 | 0.041 | 0.042 | |
4. Correcting the Reference Distribution for the AUC Test
The insensitivity of comparing AUCs in the nested setting in relation to the results of the Wald or likelihood ratio tests has been noticed by several commentators in recent years, and this has led to a perception that change in AUC is insensitive as a metric for comparison [10]. However, our results from Section 2.3 show that use of the AUC test is fundamentally biased in this context. This raises the question of whether adaptations to the reference distribution of the AUC test statistic can correct the problem. In the following we outline a modification to the derivation of the reference distribution for the AUC test to demonstrate that it is possible to construct a valid AUC test in this context. We construct an orthogonal decomposition of W2 from Section 2.2:
where P = (X′X)−1 X and X = (1 W1 Z). That is, is the projection of W2 on to the vector space spanned by (1 W1 Z) and is the orthogonal complement of . By definition is uncorrelated with and hence all the information in W2 that is incremental to (W1Z) must be contained in . Under the null hypothesis forms an exchangeable sequence. This suggests that permuting and fitting the same logistic regression models as in Section 2.2 will generate a realization of the data generating mechanism under the null hypothesis. We have examined this conjecture using a reference distribution for T* in which the test statistic is calculated after repeated permutations of .
This “Projection-Permutation” reference distribution is constructed as follows:
Compute the projection matrix P = (X′X)−1 X where X = (1 W1 Z).
Compute and
Obtain a permutation of the vector , call it
Construct
Fit models M1 and M2 replacing W2 with W2,perm from Step 4, and compute the area test statistic T*
Repeat 3-5 B times
Construct the reference distribution from the B values of the test statistic computed in step 6.
Figure 5 illustrates the validity of the Projection-Permutation reference distribution graphically for n = 250, ρ = 0.5 and μ = 0.3. The empirical density of the difference in areas (δ̂*) under the null hypothesis (i.e., when μ2 = 0) is given by the black curve and the density of the Projection-Permutation reference distribution is given by the red curve. The two are almost exactly the same, demonstrating by example that the reference distribution generated by projection-permutation closely matches the simulated distribution of the AUC test statistic. Further, the blue curve depicting the reference distribution under the alternative hypothesis, i.e. when μ2 = 0.3 is virtually identical to the black and red curves, showing that the null distribution is computed correctly when the data are generated under the alternative hypothesis. The green curve represents the distribution of δ̂* under this alternative.
Figure 5.
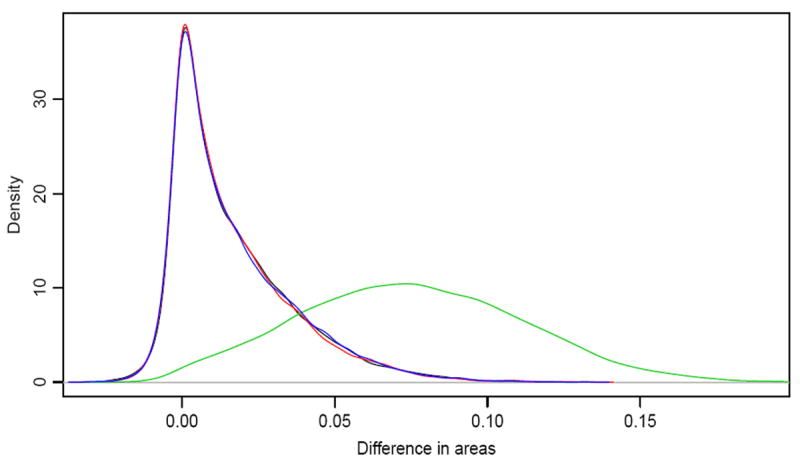
Distribution of δ̂ for ρ = 0.5. The black (μ2 = 0) and green (μ2 = 0.3) curves are estimated from the data over 10000 simulations. The red (μ2 = 0) and blue (μ2 = 0.3) curves are estimated from the reference distribution obtained by Projection-Permutation.
Construction of Figure 5 deserves some explanation. For each simulated data set δ̂* is computed and the values over 10000 simulations are used to construct the density estimates depicted by the black (null) and the green (alternative) curves. Each simulated data set is also used to construct the Projection-Permutation reference distribution. To obtain a single reference distribution from these 10000 reference distributions we randomly sampled one permutation for each data set and then used those samples to construct the reference distributions shown in the figure.
The operating characteristics of this approach have been examined in the same configurations as we used to evaluate the Wald test and the AUC test, and the results are presented in Table 1 in the rows marked “Projection-Permutation Ref.” The results demonstrate that this reference distribution leads to a test of AUCs that has the correct size and comparable, though slightly lower, power to the Wald test.
5. Discussion
In this article we have provided an explanation to the baffling observation that use of the AUC test to compare nested binary regression models is invalid [2]. We found that the validity problems of the AUC test in this context are due to two principal reasons. The first reason is that the test is based on the assumption that the data from individual subjects (W1i, W2i) and (W1j, W2j) are mutually independent. This is grossly violated when using predictors from a regression model. This leads to an incorrect variance estimate of the test statistic as described in Section 2.3 and illustrated in Figure 1. The second major problem is that in its proper construction the AUC test is fundamentally one-sided in that we know in advance the anticipated directionality of the relationship between predictor and outcome, allowing the possibility of negative effects by chance. In the regression context the methodology does not distinguish any such “known directionality” of the markers and instead constructs predictors to maximize the likelihood. In most cases this results in an optimized ROC curve. Consequently both ROC curves being compared are optimized in the same direction. Both of these phenomena lead to bias in the test statistic. The effect of these two factors is to greatly reduce the sensitivity of the AUC test. Using analogous simulations we have also established that the AUC test is also biased in some configurations when the comparison is between two predictors drawn from non-nested regression models.
Since ROC curves are widely used for assessing the discriminatory ability of predictive models, comparing the ROC curves derived from predictive models is commonplace. In the first four months of 2011 alone, we easily identified seven articles in clinical journals that used the AUC test to compare nested logistic regression models [11, 12, 13, 14, 15, 16, 17] which speaks to the prevalence of the problem in applications of biostatistics. Specific instructions on comparing AUCs from logistic regression models using STATA are already published [18]. A recent feature in PROC LOGISTIC of SAS (ROCCONTRAST statement in version 9.2) enables users to specify nested logistic regression models, estimate their ROC curves and compare them using the AUC test. Availability of this feature in some of the most commonly used statistical packages is likely to increase the use of this invalid procedure.
We have shown that it is possible to construct a valid reference distribution for the AUC test using permutation. In so doing we have shown that the problem is not due to the AUC test statistic but is instead a consequence of the fact that the standard asymptotic reference distribution is inappropriate in the context of modelled predictors. Nevertheless comparison of two nested models using the AUC test statistic and its valid reference distribution (from Section 4) is unncessary since its operating characteristics are inferior to those of the Wald test, which is widely available in standard statistical software.
In all of our simulations we generated marker values and other covariates from the multivariate normal distribution. This represents a framework in which the logistic regression model is fully valid. Given that the derived AUC test is grossly invalid in these circumstances in which the data generation is a perfect fit for the assumed model, we consider it unnecessary to investigate alternative sampling models for which observed biases may be caused either by inappropriate modeling assumptions or the phenomena we have described.
The performance of the AUC test has perplexed other investigators, including Demler et. al. [19] who assumed multivariate normality of the markers and employed linear discriminant analysis to construct the risk prediction tool. While these authors also seem to be motivated with the underperformance of the AUC test, they show that the AUCs of M1 and M2 are the same if and only if α2 = 0, where α2 is the coefficient of the second marker from a linear discriminant analysis. They show that the F-test for testing α2 = 0 has the correct size for comparing the AUCs. These authors did not use the empirical estimate of the AUC nor did they consider the AUC test of DeLong et. al. [1], the most commonly used method of comparing the AUCs. Our results specifically explain the poor performance observed in Vickers et. al. [2] by showing that the AUC test is biased and its variance is incorrect in this specific setting.
Finally, we clarify that the tests we have investigated are designed to test whether or not a new marker has any incremental value in predicting the outcome. Even if the marker is found to have significant incremental value, it is important to gauge the magnitude of the incremental information to determine if the marker has pratical clinical utility. ROC curves and the change in ROC area in particular have often been used for this purpose, although various other measures and approaches have been proposed[20, 21].
Acknowledgments
Contract/grant sponsor: National Cancer Institute Award CA 136783
References
- 1.DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988;44(3):837–845. [PubMed] [Google Scholar]
- 2.Vickers AJ, Cronin AM, Begg CB. One statistical test is sufficient for assessing new predictive markers. BMC Medical Research Methodology. 2011;11 doi: 10.1186/1471-2288-11-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hanley JA, McNeil BJ. A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology. 1983;148(3):839–843. doi: 10.1148/radiology.148.3.6878708. [DOI] [PubMed] [Google Scholar]
- 4.Harrell FE, Califf RM, Pryor DB. Evaluating the yield of medical tests. Journal of the American Medical Association. 1982;247(18):2543–2546. [PubMed] [Google Scholar]
- 5.Kattan MW. Judging new markers by their ability to improve predective accuracy. Journal of the National Cancer Institute. 2003;95(9):634–635. doi: 10.1093/jnci/95.9.634. [DOI] [PubMed] [Google Scholar]
- 6.Pepe MS, Janes H, Longton G, Leisenring W, Newcomb P. Limitations of the odds ratio in gauging the performance of a diagnostic, prognostic, or screening marker. American Journal of Epidemiology. 2004;159(9):882–890. doi: 10.1093/aje/kwh101. [DOI] [PubMed] [Google Scholar]
- 7.Cook NR. Statistical evaluation of prognostic versus diagnostic models: Beyond the roc curve. Clinical Chemistry. 2008;54(1):17–23. doi: 10.1373/clinchem.2007.096529. [DOI] [PubMed] [Google Scholar]
- 8.Hlatky MA, Greenland P, Arnett DK, Ballantyne CM, Criqui MH, Elkind MSV, Go AS, Harrell FE, Howard BV, Howard VJ, et al. Criteria for evaluation of novel markers of cardiovascular risk: A scientific statement from the american heart association. Circulation. 2009;119(17):2408–2416. doi: 10.1161/CIRCULATIONAHA.109.192278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cox DR, Hinkley DV. Theoretical Statistics. Chapman and Hall; 1974. [Google Scholar]
- 10.Ware JH, Cai T. Comments on evaluating the added predictive ability of a new marker by pencina et al. Statistics in Medicine. 2008;27:185–187. doi: 10.1002/sim.2985. [DOI] [PubMed] [Google Scholar]
- 11.Kwon S, Kim Y, Shim J, Sung J, Han M, Kang D, Kim JY, Choi B, Chang HJ. Coronary artery calcium scoring does not add prognostic value to standard 64-section ct angiography protocol in low-risk patients suspected of having coronary artery disease. Radiology. 2011;259(1):92–99. doi: 10.1148/radiol.10100886. [DOI] [PubMed] [Google Scholar]
- 12.Berg K, Stenseth R, Pleym H, Wahba A, Videm V. Mortality risk prediction in cardiac surgery: Comparing a novel model with the euroscore. Acta Anaesthesiologica Scandinavica. 2011;55(3):313–321. doi: 10.1111/j.1399-6576.2010.02393.x. [DOI] [PubMed] [Google Scholar]
- 13.Resnic F, Normand SL, Piemonte T, Shubrooks S, Zelevinsky K, Lovett A, Ho K. Improvement in mortality risk prediction after percutaneous coronary intervention through the addition of a compassionate use variable to the national cardiovascular data registry cathpci dataset: A study from the massachusetts angioplasty registry. Journal of the American College of Cardiology. 2011;57(8):904–911. doi: 10.1016/j.jacc.2010.09.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Roe C, Fagan A, Williams M, Ghoshal N, Aeschleman M, Grant E, Marcus D, Mintun M, Holtzman D, Morris J. Improving csf biomarker accuracy in predicting prevalent and incident alzheimer disease. Neurology. 2011;76(6):501–510. doi: 10.1212/WNL.0b013e31820af900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Thuret R, Sun M, Abdollah F, Budaus L, Lughezzani G, Liberman D, Morgan M, Johal R, Jeldres C, Latour M, et al. Tumor grade improves the prognostic ability of american joint committee on cancer stage in patients with penile carcinoma. Journal of Urology. 2011;185(2):501–507. doi: 10.1016/j.juro.2010.09.111. [DOI] [PubMed] [Google Scholar]
- 16.Hammill B, Curtis L, Fonarow G, Heidenreich P, Yancy C, Peterson E, Hernandez A. Incremental value of clinical data beyond claims data in predicting 30-day outcomes after heart failure hospitalization. Circulation: Cardiovascular Quality and Outcomes. 2011;4(1):60–67. doi: 10.1161/CIRCOUTCOMES.110.954693. [DOI] [PubMed] [Google Scholar]
- 17.Liang Y, Ankerst D, Ketchum N, Ercole B, Shah G, Shaughnessy J, Jr, Leach R, Thompson I. Prospective evaluation of operating characteristics of prostate cancer detection biomarkers. Journal of Urology. 2011;185(1):104–110. doi: 10.1016/j.juro.2010.08.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cleaves MA. From the help desk: Comparing areas under receiver operating characteristic curves from two or more probit or logit models. The Stata Journal. 2002;2:301–313. [Google Scholar]
- 19.Demler OV, Pencina MJ, D’Agostino RB. Equivalence of improvement in area under roc curve and linear discriminant analysis coefficient under assumption of normality. Statistics in Medicine. 2011;30:1410–1408. doi: 10.1002/sim.4196. [DOI] [PubMed] [Google Scholar]
- 20.Pencina MJ, D’Agostino RBD, V RS. Evaluating the added predictive ability of a new marker: From the area under the roc curve and beyond. Statistics in Medicine. 2008;27(2):157–172. doi: 10.1002/sim.2929. [DOI] [PubMed] [Google Scholar]
- 21.Cook NR, Ridker PM. Advances in measuring the effect of individual predictors of cardiovascular risk: the role of reclassification measures. Ann Intern Med. 2009;150(11):795–802. doi: 10.7326/0003-4819-150-11-200906020-00007. [DOI] [PMC free article] [PubMed] [Google Scholar]


