Reducing elective general surgery cancellations at a Canadian hospital

Abstract

Background

In Canadian hospitals, which are typically financed by global annual budgets, overuse of operating rooms is a financial risk that is frequently managed by cancelling elective surgical procedures. It is uncertain how different scheduling rules affect the rate of elective surgery cancellations.

Methods

We used discrete event simulation modelling to represent perioperative processes at a hospital in Toronto, Canada. We tested the effects of the following 3 scenarios on the number of surgical cancellations: scheduling surgeons’ operating days based on their patients’ average length of stay in hospital, sequencing surgical procedures by average duration and variance, and increasing the number of post-surgical ward beds.

Results

The number of elective cancellations was reduced by scheduling surgeons whose patients had shorter average lengths of stay in hospital earlier in the week, sequencing shorter surgeries and those with less variance in duration earlier in the day, and by adding up to 2 additional beds to the postsurgical ward.

Conclusion

Discrete event simulation modelling can be used to develop strategies for improving efficiency in operating rooms.

Operating rooms (ORs) are a hospital’s largest cost centre and greatest source of revenue.¹ Consequently, there is substantial incentive to recognize greater efficiencies within OR management.² Operating room efficiency may be improved by shorter surgical durations, rational scheduling of various types of surgeries and minimization of the nonoperative time by reorganizing OR activities.³ However, managing ORs is a complex task owing to conflicting priorities and preferences of its stakeholders and to scarcity of costly resources.⁴ In Canadian hospitals, which are funded by global budgets, OR inefficiency may result in elective surgery cancellations. Many factors impact OR efficiency, such as the operating surgeon, type of surgical procedure, emergency cases, delays at the start of surgery and the number of beds in postsurgical units.

The dynamics governing a hospital system demand capacity models that reflect the complexity, uncertainty, variability and limited resources.⁵ Operating room planning and scheduling may be addressed by simulation modelling. Simulation modelling is a virtual representation of a system or process that mimics, or simulates, a real system. By analyzing simulation results, opportunities for system improvement can be identified without expending substantial resources in the examination process.⁶ Simulation models conform to the direct representation of the system’s structure, logic and the available data.⁷ The main advantage of simulation over other modelling techniques is its ability to perform “what-if” scenarios by changing the model’s rules and assumptions. The model not only provides information to managers, but also engages them in the development process so as to allow them to use the model independently as a decision support tool.⁸ Computer simulation is shown to support process engineering in perioperative processes and identify potential process improvements.

The present study uses discrete event simulation (DES) to analyze planning and scheduling problems encompassing the OR. Our objective was to identify potential improvements in the flow of patients through the surgical process, to reduce the number of surgical case cancellations and to use hospital resources more efficiently. Specifically, we sought to observe the effects of applying scheduling rules on the weekly schedule of surgeons and on the surgeons’ daily cases and the effects of adding beds to postsurgical units on the number of surgical cancellations. The purpose of this research was to develop novel, generalizable knowledge regarding the impact of different elective surgical scheduling rules on elective surgery cancellation rates.

Methods

Perioperative process

The research ethics board of the University Health Network (UHN) approved our study protocol.

We used information from the Toronto General Hospital (TGH), which is part of the UHN and is a major teaching hospital in downtown Toronto. There are 19 ORs and 406 in-patient beds, of which 2–3 ORs and 30 in-patient beds are used by the general surgery department each day. The hospital handles about 9000 surgical cases per year, and the emergency department serves 30 000 patients annually.

The perioperative process for general surgery patients at TGH includes various services, including the preadmit clinic, preoperative care unit (POCU), postanesthesia care unit (PACU), medical surgical intensive care unit (MSICU), step down unit (SDU), medical day unit (MDU), ward, and alternate level of care (ALC) facilities.

Depending on the type of surgery and the level of care required, patients are taken to a combination of these units. The route taken through the perioperative process depends on the type of patient (same-day patients, elective in-patients or emergency patients). Emergency general surgery patients are categorized into 3 groups: emergency type A patients, type B patients and type C patients. Emergency type A patients require surgery within 2 hours of their arrival to the hospital, whereas emergency type B patients require surgery within 2–8 hours of their arrival to the hospital. Emergency type C patients require surgery during hospitalization.

Patient flow on surgical day

The longest surgical cases must be scheduled as the first cases of the day, according to the existing hospital scheduling rules. On the arrival of an emergency type A patient, the first available OR is assigned to that patient, and all other patients whose procedures are scheduled for that OR are held in the holding area. Emergency type B patients do not usually disrupt the daily elective schedule. These cases are held until all elective patients of an OR are finished (i.e., either undergo surgery or are cancelled) for the day. After the regular hours, ORs are kept open for certain hours for emergency type B patients. If an emergency type B patient cannot undergo surgery during these hours and waits for more than 48 hours, his or her case is given priority over daily elective patients and must be performed as the first case of the next day.

Scheduling

First, available ORs are assigned to different clinical services in a hospital. Second, the master surgical schedule (MSS) is developed. The MSS is a cyclic time table that defines the number and type of ORs available, the hours the rooms will be open and the surgical unit associated with each OR time block.⁹ Third, the OR time available in each service is distributed among its surgeons. Elective cases are scheduled in each allocated time block and the sequence of surgical cases is determined.

The general surgery service at TGH is assigned 2 or 3 ORs per day during weekdays. The regular OR hours are from 8:00 am to 3:30 pm or from 8:00 am to 5:30 pm. After regular hours, ORs are kept open until 11:00 pm for emergency type B patients. One OR is kept open for 24 hours with on-call staff to accommodate emergency type A patients.

One OR is assigned to 1 surgeon per day, and surgeons rarely switch ORs in a day. Therefore, in the model we assigned 1 surgeon to 1 OR in a day. To reasonably represent the surgeons’ daily schedules, we acquired a sampling from real schedules of particular surgeons.

Simulation model

To capture the complexity of TGH’s perioperative process and develop a flexible and reliable representation, we constructed a DES model using the Simul8 software package (Visual8 Corp.). The model used visual logic codes to create modules that mimic the real, complex tasks of the perioperative process. Various decision-making points concerning patient status were modelled, including the type of patients, their priority, expected duration of the operation, bed requirements and patients’ lengths of stay (LOS) in the MSICU, SDU and the surgical ward.

Flow of patients through the surgical process

Before the start of every day, the model created the schedule for the coming day. First, the model determined the day of the week. Second, using the MSS, it determined how many ORs ran for that day and which surgeons were assigned to the ORs. Third, for every surgeon, a random day from the hospital’s historical data was selected; these data included the surgeon’s actual caseload and showed the number, type and sequence of procedures of that day.

Using the daily schedule, the model determined the patient path. For instance, if the PACU field was zero, the patient was not intended to go to the PACU; therefore, the LOS in the PACU was also zero. The model also indicated the status of patients during the simulation time (e.g., cancelled).

Patients flowed through the surgical process according to their path. Their LOS in the PACU, MSICU, SDU and ward beds were specified from the historical data. Since no data were available with regard to the same-day patients’ LOS in the MDU, and since patients were scheduled to stay in the MDU for 1 hour, patients’ LOS in MDU beds were considered to be 1 hour in the model. The model also considered that some patients had to be discharged from the PACU when the MDU stopped accepting patients after 4:00 pm.

Once a patient was chosen, the model determined whether the OR time available was adequate to finish the surgery. If the surgery could be finished before the cut-off time plus the allowed overtime, and if postsurgical resources were available at the expected end time of the procedure, the patient could be checked into the OR. Otherwise the procedure was cancelled.

Assumptions and limitations

Owing to the lack of available data and to simplify some aspects of the model, we made the following assumptions.

• Surgeons and nurses in ORs and postsurgical units were available at all times.

• The surgeon’s weekly schedule was fixed over the period of 1 year (in reality, the schedule may change periodically).

• All inpatients were sent home from the surgical ward (in reality, some inpatients may be transferred to ALC facilities from the surgical ward, and the unavailability of resources in those institutes may cause delays in discharging patients from the ward).

• The number of PACU, MSICU and SDU beds assigned to the general surgery service was chosen based on the average number of bed occupancies by this service.

• The model only considered 1 department of 1 hospital for a period of 1 year.

• The model did not take into account transplant cases or the emergency case interruptions from services other than general surgery at TGH.

• The model did not take into account patients who died in the OR or in any of the postsurgical units.

• The model did not include emergency type C patients, who are uncommon in the general surgery service.

• When there was more than 1 emergency patient who required surgery, the model did not take into account priority owing to the severity of the case.

Model validation

Historical data for the number of surgery cancellations at TGH by month for a period of 1 year were used to validate the simulation model. The number of surgery cancellations per month was counted as the simulation progressed over a 1-year period.

Since the 95% confidence interval (CI) around the difference between the number of cancellations was −1.191 to 2.008, the difference between the actual data and simulation output was not significant, and we concluded the simulation model was valid.

“What-if” scenarios

We examined the effects of the following 3 scenarios’ on the number of surgery cancellations:

1. ranking surgeons according to the average LOS of their patients, such that surgeons whose patients had shorter lengths of stay were ranked lower and thus were scheduled earlier in the week (in order of increasing rank);

2. changing the sequence of surgical procedures based on increasing and decreasing booked surgery time (Time↑ and Time↓, respectively) and increasing and decreasing expected surgical time variation (Var↑ and Var↓, respectively); and

3. adding 2 beds to the surgical ward.

The interactions among these scenarios were also explored. Simulations were run for the base model with all possible combinations of the preferred schedules and sequences, and then the same scenarios were run in a model with 2 extra ward beds. Each scenario was compared with every other scenario to detect and quantify significant pairwise differences.

For uncorrelated data, we used a modified 2-sample (Welch) 95% CI; we constructed 95% CIs for correlated data using a paired t test approach.

Results

Two rules for the surgeons’ weekly schedule were considered according to their patients’ average LOS on the ward, calculated from historical data. The surgeons were ranked such that those whose patients had longer average LOS on the ward received a higher rank. The first rule orders surgeons from lowest rank to highest throughout the week (LOS↑), and the second rule orders surgeons in the reverse order (LOS↓).

Four rules for scheduling patients within each surgeon’s day were considered: surgery duration from short to long (Time↑); surgery duration from long to short (Time↓); surgery variance from low to high (Var↑); and surgery variance from high to low (Var↓). The surgical times and variances were calculated from historical data.

Table 1 shows the change in the number of cancellations using these scheduling rules. For example, the Time↑ surgery schedule in combination with the LOS↑ surgeon schedule resulted in a change of −19.7 cancellations (that is, a reduction of 19.7 cancellations) compared with the historical schedule (95% CI −30.9 to −8.5).

Table 1.

Cancellations using scheduling rules

Sequence of surgical operations	Surgeon schedule, mean (95% CI)
	Base	LOS↑	LOS↓
Time↑	−10.5 (−14.8 to −6.1)	−19.7 (−30.9 to −8.5)	−3.5 (−19.1 to 12.1)
Time↓	4.2 (−3.2 to 11.6)	−10.9 (−26.3 to 4.5)	18.4 (−2.7 to 39.4)
Var↑	−14.0 (−19.5 to −3.7)	−28.3 (−42.6 to −14.0)	−15.0 (−23.1 to 21.3)
Var↓	6.7 (3.4 to 9.9)	−4.3 (−16.4 to 7.9)	14.9 (−0.3 to 30.0)

CI = confidence interval; LOS = length of stay; Time = length of booked surgery time; Var = expected surgical variation.

We further considered the possibility of adding beds to the ward. Table 2 shows the change in the number of cancellations with 2 beds added to the ward with the base surgeon schedule and the LOS↑ surgeon schedule, as well as the 4 patient scheduling rules.

Table 2.

Change in the number of cancellations with 2 beds added to the ward^*

Sequence of surgical operations	Surgeon schedule, mean (95% CI)
	Base + 2 beds	LOS↑ + 2 beds
Base sequence	−27.5 (−34.3 to −21.4)	−38.1 (−49.6 to −26.6)
Time↑	−34.7 (−42.6 to −26.7)	−40.7 (−52.5 to −28.9)
Time↓	−27.9 (−33.7 to −22.2)	−35.7 (−44.5 to −26.9)
Var↑	−44.4 (−50.5 to −38.3)	−47.9 (−68.9 to −26.8)
Var↓	−19.7 (−33.9 to −5.5)	−24.8 (−36.7 to −12.9)

CI = confidence interval; LOS = length of stay.

^*We took into account the base surgeon schedule and the LOS↑ surgeon schedule, as well as the 4 patient scheduling rules.

Modifying the surgeons’ weekly schedule

The difference between the number of surgical cancellations in the base and LOS↑ schedules were compared. Against the base schedule, LOS↑ resulted in −17.6 (95% CI −29.0 to −6.1) fewer surgical cancellations. Assigning surgeons with patients who had short ward LOS and same-day discharge at the start of the week and surgeons with patients who had long ward LOS to the end of the week reduced the chance of surgery cancellations. This schedule allowed patients with long ward LOS to take advantage of ward beds during weekends. The LOS↓ schedule did not significantly affect the number of cancellations (mean 0.5, 95% CI −14.3 to 15.2).

Sequence of operations

Sequencing the surgeries in order of increasing length and variance reduced the number of surgical cancellations. Sequencing by variance had the greatest effect on the number of cancellations. The number of cancellations was further reduced by applying the sequencing rules to the LOS↑ schedule. However, when the rules were applied to the LOS↓ schedule, the observed change was not significant (Table 1).

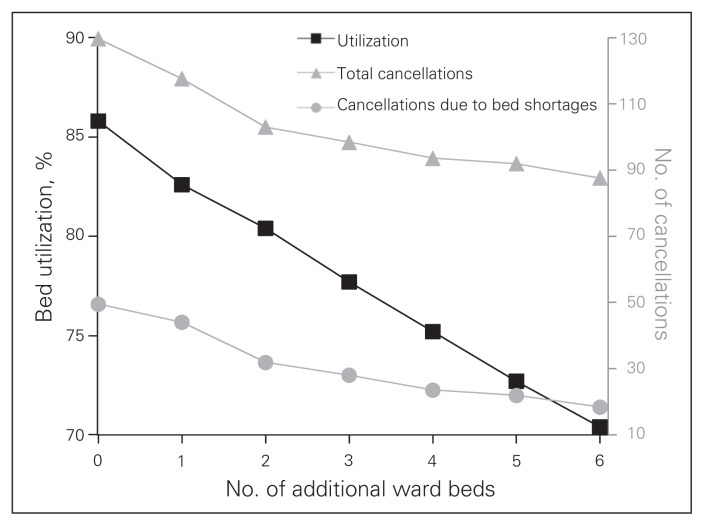
Increasing the number of ward beds

When 1–6 beds were added to the surgical ward, the number of surgical cancellations was reduced. As seen in Figure 1, adding more than 2 beds did not have a large benefit and caused the average bed utilization to fall below 80%.

Fig. 1.

Number of additional ward beds.

As seen in Table 2, adding 2 beds to the ward without even changing the schedule reduced the number of cancellations. Ordering the surgeons by increasing LOS and adding 2 beds to the ward further reduced the number of surgical cancellations, as did sequencing the surgical procedures in increasing order of length and variance. However, adding 2 beds with the LOS↓ schedule did not reduce the number of cancellations. Sequencing surgeries in order of decreasing length and variance in the base and LOS↑ schedules reduced the number of cancellations, although this reduction was caused by increasing the number of ward beds rather than the sequencing rule. Applying sequencing rules to the LOS↓ schedule did not reduce the number of cancellations.

Discussion

We used a DES to model the perioperative process in a general surgery service. The objective was to reduce the number of surgical cancellations and thereby improve the overall process. The model considered emergency case interruptions with different levels of urgency, as well as the availability of 3 types of postsurgical beds (MSICU, SDU and surgical ward) at the decision-making level.

In our DES, patients are modelled as entities with specific attributes. These entities pass through a series of queues and discrete event activities that influence their journey through the system. The activities that patients undergo provide a basis for estimating the use of resources, while the time they spend in queues provided the basis for estimating wait times.¹⁰ Computer simulation has previously been shown to support process engineering in perioperative processes and identify potential improvements. Yang and colleagues¹¹ provide several successful studies that use simulation modelling in emergency, pharmacy and out-patient departments as well as ORs and conclude that traditional approaches to scheduling, such as mathematical programming, are of limited use in medical scheduling owing to the complexity and involvement of human factors. Testi and colleagues¹² applied a simulation model to identify the best admission rule for selecting patients to be scheduled in each OR session. However, other resources involved in the process, such as recovery and ICU beds and staff, do not define bottlenecks. Dexter and colleagues¹³ used a computer simulation to model OR scheduling to maximize the OR time utilization. This study made use of waiting lists: the longer the patients waited for surgery, the greater the percentage of OR time used. Since most critical surgeries cannot be delayed, this approach is not feasible in all circumstances. There is also no clear strategy for handling emergency cases.

The present research considered the inevitability of emergency cases, which disrupt the daily OR schedule and cause surgical delays and cancellations. We did not reserve ORs exclusively for emergency cases. Whereas Lovett and Katchburian¹⁴ stressed that assigning dedicated ORs to urgent cases can decrease overtime and the number of urgent surgeries performed after working hours, Barlow and colleagues,¹⁵ Brasel and colleagues¹⁶ and Wullink and colleagues¹⁷ concluded that setting ORs aside for emergency cases is costly owing to low utilization rates of ORs. Instead, Davenport and colleagues¹⁸ Herroelen and Leus¹⁹ and Wullink and colleagues²⁰ stated that a buffer of extra time and/or resources can be used to deal with the disruptions caused by emergency cases on the daily elective schedule.

We found that sequencing shorter surgical cases with minimal variance earlier in the day reduced the number of surgical cancellations. Testi and colleagues¹² and Marcon and Dexter²¹ drew similar conclusions. Using a simulation model, they selected patients from the surgical list based on different priority rules: longest wait time, longest processing time and shortest processing time. They examined different sequencings of surgical cases to improve the OR time usage and showed that the shortest processing time is the best admission rule. Alternatively, Denton and colleagues²² applied a 2-stage stochastic programming model to determine the optimal surgery schedule. Based on numerical experiments using real-life surgery duration data, they compared optimal schedules with actual schedules and showed that the common practice of scheduling longer and more complex cases earlier in the day may have a significant negative impact on OR performance measures. We found that scheduling surgeons whose patients had shorter LOS to operate earlier in the week resulted in fewer cancellations. Presumably, this result is because patients with longer LOS use the weekend as part of their recovery time, during which there are no elective surgical admissions.

We also found that adding 2 extra beds to the surgical ward reduced the number of surgical cancellations. While adding more than 2 beds further reduced the number of cancellations, bed utilization rates decreased below 80%. After reviewing hospital bed use statistics and scheduled surgical procedures, Calichman²³ reported that the efficient OR schedule should result in a balance between the supply and demand of ward beds during the week. Van Berkel and Blake²⁴ also used a DES model for capacity planning and management of patient wait times for general surgery. They concluded that the availability of beds — not OR time — is the bottleneck of the system. However, owing to the type of surgical procedures performed in their particular system, ICU beds were excluded from their study.

Limitations

Our research provides a basis for further model development and system investigation. This model can be used to better understand the effects of new scheduling scenarios on other measures of OR efficiency and cost. Our model, though, has limitations. We only analyzed the effect of scheduling changes on surgical cancellations. In reality, other outcomes, such as cost, must be considered in addition to minimizing surgical cancellation rates. Expansion of the model can provide TGH with an integrated perioperative decision tool to reduce the number of surgical cancellations for all services. Another area for future work would be to investigate surgery durations in greater detail to identify the root causes of surgical variances. This investigation would entail gathering data on the duration of anesthesia administration, surgical duration, turnover time and unnecessary LOS in the OR.

In addition to the limitations discussed previously, it is important to remember that each hospital has its own unique patient population, case mix and other local circumstances that influence cancellation rates and scheduling rules. Our study looked at only 1 hospital; a different hospital with a different set of cancellation and emergency case management rules would look different. The purpose of this study was not to uncover a universal set of scheduling rules, but rather to demonstrate the use of simulation to guide local interventions.

Conclusion

Scheduling surgeons whose patients have shorter average LOS on the ward earlier in the week (in increasing order), sequencing surgeries in order of increasing length and variance, and adding beds to the surgical ward are expected to reduce the number of elective surgical cancellations at the hospital we studied. Depending on the hospital’s budget and managers’ preferences, this study can guide decision-makers in realizing which alternatives are preferable.