Canonical Azimuthal Rotations and Flanking Residues Constrain the Orientation of Transmembrane Helices

Abstract

In biological membranes the alignment of embedded proteins provides crucial structural information. The transmembrane (TM) parts have well-defined secondary structures, in most cases α-helices and their orientation is given by a tilt angle and an azimuthal rotation angle around the main axis. The tilt angle is readily visualized and has been found to be functionally relevant. However, there exist no general concepts on the corresponding azimuthal rotation. Here, we show that TM helices prefer discrete rotation angles. They arise from a combination of intrinsic properties of the helix geometry plus the influence of the position and type of flanking residues at both ends of the hydrophobic core. The helical geometry gives rise to canonical azimuthal angles for which the side chains of residues from the two ends of the TM helix tend to have maximum or minimum immersion within the membrane. This affects the preferential position of residues that fall near hydrophobic/polar interfaces of the membrane, depending on their hydrophobicity and capacity to form specific anchoring interactions. On this basis, we can explain the orientation and dynamics of TM helices and make accurate predictions, which correspond well to the experimental values of several model peptides (including dimers), and TM segments of polytopic membrane proteins.

Introduction

The majority of integral membrane proteins contain at least one α-helix embedded across the lipid bilayer (1). The structure and function of these proteins depend critically on the alignment of their constituent transmembrane (TM) segments with respect to the bilayer plane, which is defined by their tilt angle (τ) and their azimuthal rotation angle (ρ) (Fig. 1 a). Although both parameters are readily accessible by experiment (2–5), τ is usually the preferred subject of research due to its direct and intuitive structural meaning (6,7) and its relevance for function (8). In contrast, the azimuthal ρ angle, which governs the lateral interactions between helices (9), has not been rationalized yet. Through a number of systematic studies with symmetrical model TM helices of the WALP/WLP and KALP/KLP families (3,6,10,11) different ρ angles have been found, depending on the presence of tryptophan or lysine as flanking residues. These two residues were chosen for the design of membrane peptides because of their statistical abundance at the ends of TM helices in natural proteins (12) and because of their role in anchoring to the membrane interface through specific interactions (13–15). Recently, it was shown that tyrosine may replace tryptophan as a flanking residue with minimal changes in helix orientation (16). Although these studies provide precise measurements of the rotational orientation of TM helices in membranes, we lack a conceptual framework for the understanding and prediction of these values (17). When this important development is added to topology (18), tilt (7), and contact predictions (19–21) of TM segments, it can contribute to achieve the ambitious goal of complete membrane structure prediction from corresponding genetic sequences (22–24).

Figure 1.

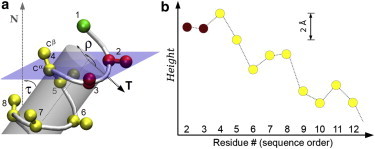
(a) A TM helix tilted by an angle τ with respect to the membrane normal N. The azimuthal rotation angle ρ, here referring to the first residue C^α (1), is defined with respect to the tilt vector T. The semitransparent plane represents the interface between the hydrophobic and polar regions in the upper monolayer leaflet of the membrane. The helix geometry leads to a characteristic immersion height for each residue (i.e., projections onto N). (b) These heights are plotted for the C^β atoms (which represent the side chains) of consecutive flanking residues (2,3) and hydrophobic core residues (shown 4 to 12). For the depicted example, arbitrary values of τ = 40° and ρ = 150° were chosen (see Methods for modeling details).

In this work, we demonstrate that the azimuthal rotation angles of tilted TM α-helices are constrained around well-defined values. These are determined by the intrinsic geometrical properties of the tilted helix, and by the preferential placement of residues that are flanking the hydrophobic core. A rationalization of these effects allows explaining the characteristic azimuthal rotations of TM helices flanked by polar versus aromatic residues. This sets the basis for accurate predictions of orientation even for cases of helix-helix dimers and segments of polytopic membrane proteins.

Methods

Model peptides

For the TM model peptides KLP23, WLP23 (11), GWALP23, WWALP23 (17), and KLAm versions (25), where no experimental structures are available, molecular models were constructed as ideal α-helices using Swiss-PdbViewer, DeepView v4.04 (http://spdbv.vital-it.ch/) (26), run under Linux with the help of WINE^HQ (http://www.winehq.org/). No attention was paid to the (unknown) conformation of the side chains, because this is not relevant here as we work with the C^β positions of the residues, which are rigidly defined by the structure of the backbone. The side chains correspond to flanking (eventually anchoring) residues and to residues at the boundaries of the hydrophobic core (see Figs. 3, 4, and 5). These are shown only for illustrative purposes and were taken in arbitrary conformations.

Figure 3.

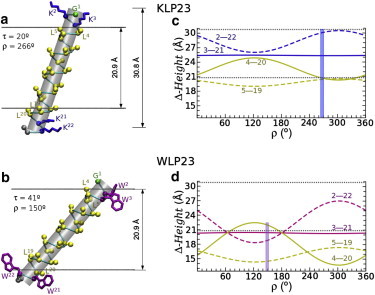
Structures of WLP23 (a) and KLP23 (b) TM helices, in DLPC bilayers at their given experimental orientations (τ and ρ stated in the figure) (6,11). The horizontal lines display the boundaries of the hydrophobic core of the bilayer. The C^α atom of G¹ (reference for ρ) and the C^α–C^β of hydrophobic-core residues (L⁴ to L²⁰) are represented with balls. For the flanking W and K residues, we represent the complete side chain in an arbitrary conformation. Panels (c and d) show the Δ-height for pairs of hydrophobic (4–20,5–19) and flanking (2–22,3–21) residues for KLP23 and WLP23, respectively, as a function of ρ and at their experimental τ. The vertical bars mark the experimentally determined ρ value for each peptide. The horizontal dotted lines correspond to the known dimensions of liquid-crystalline DLPC bilayers (28), as also illustrated in (a and b): The hydrophobic bilayer thickness is 20.9 Å, and the distance between the phosphate groups is ∼30.8 Å.

Figure 4.

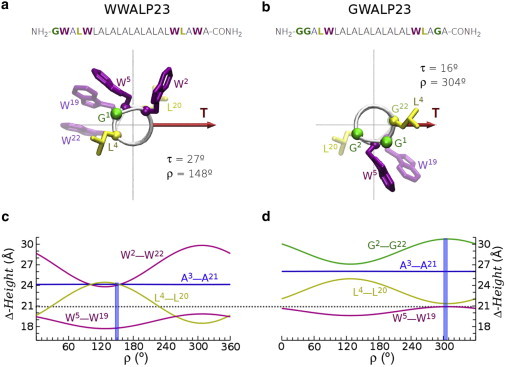
Sequences and structure models of helical peptides WWALP23 (a) and GWALP23 (b). The helices are viewed from the N-terminus along their long axis, such that the tilt vector (T) is pointing to the right and has a length proportional to the experimental τ angle (values corresponding to DLPC membranes, determined in (6) using ²H NMR splittings from (17)). The azimuthal rotation ρ, also from experiments (6,17), is defined relative to the radial position of the C^α of residue G¹. The side chains of the flanking tryptophans (W², W²², W⁵, and W¹⁹) and relevant hydrophobic residues (L⁴, L²⁰) are represented by sticks, in arbitrary conformation. Underneath are shown the hydrophobic and flanking Δ-heights for relevant residues (labeled in the graphs) of WWALP23 (c) and GWALP23 (d) as functions of ρ for their respective experimental τ. The experimental values of ρ are marked in the plots with vertical bars. The horizontal dotted line corresponds to the estimated hydrophobic thickness of liquid crystalline DLPC (20.9 Å (28)).

Figure 5.

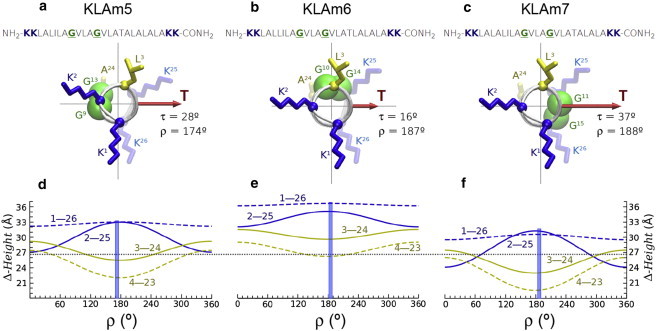
Sequences and structural models of the synthetic peptides KLAm5 (a), KLAm6 (b), and KLAm7 (c), harboring the GpA dimerization motif. The helices are viewed from the N-terminus along their long axis, such that the tilt vector (T) is pointing to the right and has a length proportional to the experimental τ (25). The azimuthal rotation ρ, also from experiments (25), is defined in this system relative to the radial position of the C^α of residue L²⁰ (equally oriented as K², shown). The two glycine residues of the GpA motif, underlined in the sequences, are represented by their C^α (balls with van der Waals radii). The side chains of the flanking lysines (K¹, K², K²⁵, K²⁶) and relevant core residues (L³, L²⁴) are represented by sticks, in arbitrary conformation. The hydrophobic and flanking Δ-heights for relevant residues (labeled in the graphs) of KLAm5 (d), KLAm6 (e), and KLAm7 (f) are shown underneath as a function of ρ, each for their respective experimental τ. The experimental values of ρ are marked in the plots with vertical bars. The horizontal dotted line corresponds to the hydrophobic estimated thickness (6,44) of liquid crystalline 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine (26.8 Å).

The structures of the peptide models, in pdb format, were loaded into VMD v1.9.1 (http://www.ks.uiuc.edu/Research/vmd/) (27) and handled using TCL scripting (http://www.tcl.tk/). For each peptide, the principal axis was aligned with the x, y, and z directions, using orient (http://www.ks.uiuc.edu/Research/vmd/script_library/scripts/orient/). In this coordinate system, the plane of the membrane is represented by the x-y plane; hence, the z axis corresponds to the membrane normal. Additionally, the center of coordinates, which is taken at the center of mass of the peptide backbone, also represents the center of a virtual bilayer. The hydrophobic slab of the membrane then occupies the region of space extending between z = +D_c and z = –D_c, where 2 D_c is the experimentally determined hydrophobic thickness (28) of the bilayer under consideration.

The peptide models were then rotated by a fixed angle around y. This corresponds to a tilt angle between the helix axis (H vector, from C- to N-terminus) and the z axis (normal N vector) and was chosen to be the mean experimental tilt angle τ of the peptide in a particular lipid system, as reported in the literature from ²H NMR data (6,11,17,25). The peptides were also rotated about their helix axis to achieve an initial azimuthal rotation ρ = 0°, i.e., making the radial vector of the C^α of a chosen reference residue (G¹ in the cases of KLP23, WLP23, GWALP23, and WWALP23; L²⁰ in the case of KLAm peptides) run parallel to the tilt vector, T = (N × H) × H. Readings of the z coordinate of the C^β atom of selected residues were then determined for rotations of the helix around its axis (ρ values from 0° to 360°) in steps of 1°, while keeping τ always fixed. These z-coordinates represent ρ-dependent heights (or depths of immersion in the membrane) of the residues on the tilted helix. Because the center of mass of the helix backbone is set at z = 0, and the N-terminus is toward +z, the heights have a positive value for residues in the N-terminal half of the peptide and a negative value for residues in the C-terminal half. The ρ-dependent height differences (Δ-height) between residues at the N-terminus and residues at the C-terminus of the helix were calculated as the sum of absolute values of their corresponding heights.

Experimental values of orientational angles, τ and ρ, are used here for comparison with our predictions. There are in some cases multiple sources for these values, due to the recently discovered influence of dynamic averaging on the NMR observables used for their determination (29,30). This affects mainly the peptide tilts, which in general are underestimated if the model used for analysis does not consider explicitly the possible fluctuations of the orientation angles (31–35). However, the azimuthal rotation angles, which are the main topic of this work, are essentially model independent (31–33). For the sake of clarity and coherency in this study all angles named as experimental for model WLP23, KLP23, GWALP23, and WWALP23 peptides are those determined using our implementation of Gaussian fluctuations and statistical analysis of fits in the dyn-GALA method (6), which we cite together with the corresponding original publications where ²H NMR splitting were reported (11,17). Because the KLAm peptides were originally analyzed using a strategy similar to ours (25), for these cases we took the values directly from the original publication.

Helix H3 from the KcsA potassium channel

The PDB coordinates (ID 3eff) of the structure of the full-length tetrameric KcsA potassium channel in its closed conformation, determined by x-ray diffraction (36), were used for representation and analysis with the help of VMD. The symmetry axis of the KcsA tetramer was aligned with the z axis of the coordinates system, which in turn was taken as the normal of an implicit membrane (centered at the origin of coordinates). Helix H3 (residues 86 to 115) from one of the four chains (K, L, M, N, equivalent by symmetry) was selected and its tilt (named the experimental tilt) was measured as the angle between the helix axis and the z axis. The experimental ρ of the helix was then measured as the angle between the tilt vector (as previously defined) and the radial vector of the C^α of G⁸⁸, taken arbitrarily as the reference for the helix azimuthal rotation. Depths of immersion of residues at the limits of the hydrophobic core and flanking residues of helix H3, as well as heights between pairs of residues from the two terminal ends of the helix, were recorded at the experimental tilt as a function of ρ, using the same strategy as for the model peptides described previously. To pinpoint the relevant pairs of residues the two outermost Trp residues were paired first, and the rest of the pairs were chosen by moving inward stepwise.

Results and Discussion

The geometry of a tilted helix conditions its orientation in membranes

The spatial position of any side chain (other than glycine) can be represented by its C^β atom (Fig. 1 a), as it depends directly on the τ/ρ orientation of the backbone. Obviously, all residues are regularly spaced along the helix axis, with a consecutive rise of ∼1.5 Å per residue. However, for a tilted helix (τ > 0), the projections of C^β onto the membrane normal N correspond to a nonuniform periodical pattern (37) (Fig. 1 b). This wave-like pattern is the key concept in rationalizing the role of ρ in TM helices, as it represents the individual height (or depth of immersion) of each residue within the membrane. The height of any selected residue varies with ρ in a cosine fashion, and it scales with r × sin(τ), where r is the radial distance from the helix axis to a point representing the residue (∼3.4 Å for C^β). Notably, this geometry has a pronounced effect on the relative heights of consecutive residues, with displacements up to a few Å (Fig. 1 b). This may even lead to a change in their order compared to the trivial expectation from the polypeptide sequence.

To understand the consequences of these structural effects, we first study the general case of an ideal α-helix with 23 residues. At either end of the helix, we consider two flanking residues (2nd, 3rd, 21st, and 22nd) around a hydrophobic core of 17 residues (4th to 20th, Fig. 2, a and b). Note that the same generalized helix is valid to analyze multiple other examples, including cases with fewer flanking residues, by simply relabeling the affected residues to their new quality (as hydrophobic of flanking). Specific cases will be discussed below. This helix is centered at the origin of the coordinate system in an implicit membrane slab, with a fixed tilt angle with respect to the z axis (see Methods for details). As the helix is rotated around its long axis, the ρ-dependent height of each residue (z-coordinate of C^β) describes a cosine wave, with a ∼100° phase shift (the α-helix pitch angle) between consecutive residues (Fig. 2, c and d). The pattern of waves for the relevant amino acids at the N-terminus (Fig. 2 c) is the same as for the C-terminus (Fig. 2 d), though with a corresponding phase shift that depends on the helix length (see other examples in Fig. S1 in the Supporting Information).

Figure 2.

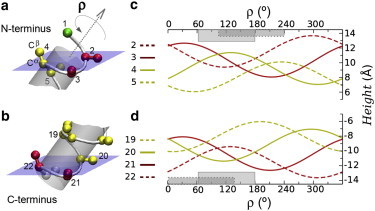
The side-chain heights of the flanking (2,3) and hydrophobic (4 to 20) residues vary as a function of ρ for a tilted ideal α-helix (τ = 40°) centered in a virtual membrane. (a) N-terminus and (b) C-terminus of the helix (23 residues long, hydrophobic core of 17 residues). The z-coordinates of the corresponding C^β atoms are plotted in (c) and (d) for the relevant residues (as numbered in a and b). The horizontal bars indicate those ρ-regions in which some flanking and core residues invert their order with regard to the peptide sequence.

For typical helix tilt angles between 10° and 40°, the ρ-waves oscillate within a range of ±0.6 Å to ±2.2 Å. These are lower limits, because the radial distance from the helix center to the side chain will extend beyond the considered C^β atom for most residues. Notably, as already mentioned (Fig. 1 b), for many ρ values the order of height positions differs from the order along the peptide sequence. This effect is most critical at the hydrophobic-hydrophilic boundary between the core residues and flanking residues. Namely, for ρ between ∼100° and ∼240° the residue 3 (which we consider flanking in this particular example) is more deeply immersed into the membrane than residue 4 (from the hydrophobic core), and for ρ between ∼65° and ∼180° even the outer flanking residue 2 comes to lie beneath residue 4 (Fig. 2 c, highlighted ρ regions). On the other hand, around ρ ≈ 300° the flanking residues (especially 2 and 22) are elevated, whereas the outermost hydrophobic core residues (4,20) are immersed, in the same order as expected from the peptide sequence (Fig. 2 c, nonhighlighted regions). Similar relationships are seen for the C-terminus (Fig. 2 d), where the corresponding ρ-regions are phase-shifted according to the helix length (Fig. S1). Most importantly, on the basis of these waves we can distinguish characteristic rotations (canonical ρ values) for which such geometrical effects, combined with the nature of the flanking residues play a decisive role on the preferred value of ρ, as we explain in detail below.

How the flanking residues optimize their position near canonical azimuthal rotations

We now consider the specific cases of a number of model TM helices. We start with the cases of KLP23 and WLP23 (6,10,11). The orientations of these and related peptides in different lipid systems are well known from experiments (3,6,10,11) and simulations (29,30,37,38). KLP23 and WLP23 have the same length and hydrophobic core (equal to the case described previously, Fig. 2), but they differ in the type of flanking residues: W²W³/W²¹W²² in WLP23, compared to K²K³/K²¹K²² in KLP23. As a result, the helices clearly prefer different rientations in membranes. Fig. 3, a and b, shows the backbone structures of the peptides, at their measured orientations, as determined by ²H-NMR in 1,2-dilauroyl-sn-glycero-3-phosphocholine (DLPC) bilayers (τ = 20 ± 4° and ρ = 266 ± 3° for KLP23, and τ = 41 ± 2° and ρ = 150 ± 3° for WLP23) (6,11). Although there are data available for the same peptides in different lipid systems, we choose the lipid with the shortest acyl chains, because this gives rise to larger tilts (6) and thus more pronounced effects of the azimuthal rotation. To analyze the ρ-dependence at the experimental τ in each case, we will now represent height differences (Δ-height) between pairs of relevant residues at either end of the helix, located symmetrically with respect to the core center. These height differences correspond to lengths between residues projected on to the membrane normal. They have an important structural meaning, as they can be compared with the thickness of the bilayer (6). The Δ-height between the inner 3–21 and between the outer 2–22 pairs of flanking residues, and the hydrophobic Δ-height for core residues, 5–19 and 4–20, are plotted in Fig. 3, c and d, as functions of ρ for KLP23 and WLP23, respectively. The amplitude of ρ-dependent oscillations now changes with the relative radial placement around the helix of the two residues of the pair. For example, residues 3 and 21 (separated by 5 complete turns) fall exactly onto the same face of the helix; thus, although their individual heights change with ρ (Fig. 2, c and d), the Δ-height of these inner flanking residues is independent of ρ (Fig. 3, c and d, straight lines). On the other hand, the Δ-height between the core residues 4–20 (or the outer flanking residues 2–22) show maximal changes with ρ, because the residues in the pair are on nearly opposite faces of the helix (separated by 200°). Furthermore, due to the sequence symmetry of the residues that define a Δ-height, the maxima and minima of different ρ-waves coincide at the same positions, with characteristic ρ values that depend only on the arbitrary definition of the azimuthal angle (for any given helix length). These extreme (canonical) values, for a case with length of 23 residues, a core centered in residue 12, and ρ defined with respect to G1, are ρ ≈ 120° and 300°. They relate to the special ρ regions identified from the analysis of individual height positions in Fig. 2 (see above). However, the Δ-height waves recapitulate the information from the two helix termini, giving rise to a much more simplified picture.

A closer look at the structures and graphs of Fig. 3, with the bilayer thickness marked at the appropriate scale, shows how well the helices have optimized their tilt angles to match the hydrophobic thickness of DLPC bilayers (20.9 Å) (12). Both, KLP23 and WLP23 have to accommodate a positive hydrophobic mismatch, as their hydrophobic length (along the helix axis) is longer than the hydrophobic thickness of DLPC (6,11). However, the optimum match for the two peptides corresponds to very different ρ values, which lay in either of the two distinct regions of the ρ waves, around the canonical ρ values (120° and 300°). Remarkably, the experimental ρ angles of KLP23 and WLP23 fall near the points of hydrophobic matching between the (projected) peptide hydrophobic core and the membrane hydrophobic thickness (Fig. 3, c and d, vertical bars).

Inspection of the patterns of hydrophobic and flanking Δ-heights helps to explain the observed azimuthal rotations and the differences between the two types of peptides. Starting with the case of KLP23, hydrophobic matching occurs at the minimum in the L⁴–L²⁰ Δ-height, in a broad region around ρ ≈ 300°. Indeed, the experimental ρ ≈ 266° (6,11) corresponds to the crossing point between the L⁴–L²⁰ and L⁵–L¹⁹ Δ-heights (Fig. 3 c). The observed ρ can thus be rationalized as favorable for positive mismatch (occurs at the minimum of the hydrophobic Δ-height). Additionally, in the same ρ region the K²–K²² Δ-height is maximum (Fig. 3 c) and matches the distance between the phosphate groups of the DLPC bilayer (∼30.8 Å) (28). Because lysine residues bind preferentially to the phosphate groups via electrostatic interactions with their side-chain N^εH₃⁺ group, the observed azimuthal rotation of KLP23 is also optimal for anchoring the outer K²–K²² pair. For the inner flanking pair K³–K²¹, the Δ-height is independent of ρ and ∼3 Å shorter than that of the outer pair. Nevertheless, K³ and K²¹ should still be able to reach their anchoring positions via snorkeling (39), as often found for lysine side chains.

In the case of WLP23, an orientation as in KLP23 would place the flanking W residues much too far away from their preferred location near the lipid carbonyl groups (15,40), i.e., at the boundary to the acyl-chain region (28). An increase in the peptide tilt angle (beyond τ = 20° of KLP23) enables the W residues to reach their preferred anchoring position. Indeed, WLP23 at its experimental τ ≈ 41° (in DLPC) (6,11) matches the W³–W²¹ Δ-height with the hydrophobic thickness of the membrane (Fig. 3 d). The ρ contribution now provides a way to bring the outer pair of tryptophan residues into optimal anchoring positions by decreasing the W²–W²² Δ-height (Fig. 3 d). These conditions explain the experimental ρ ≈ 150° for WLP23 (6,11), which falls into the region around 120°, near a crossing point of the W²–W²², W³–W²¹, and L⁴–L²⁰ Δ-heights (Fig. 3 d). Notably, this orientation allows a simultaneous anchoring of the W²/W³ and W²¹/W²² residues, as it has been suggested (6,16,41), although still keeping the L⁴/L²⁰ residues confined within the hydrophobic core of the bilayer. We should add that the good matching of Δ-heights of the peptide hydrophobic core of both KLP23 and WLP23 with the width of the hydrophobic membrane, as well as the agreement of the interanchor Δ-heights with the expected distances along the normal between their respective anchoring partners in the membrane, is a strong support for validity of the τ and ρ angular values determined from ²H NMR data (11) using our dynamic implementation of GALA (6,31,42). This is important, because it has been argued that the orientation analysis of TM helices using only ²H NMR data would be intrinsically ambiguous (32,33).

To further illustrate the usefulness of the ρ-dependent Δ-heights we consider briefly two variants related to the above model peptides, with a poly-(A-L) hydrophobic core and with the inner W-flanking pair moved to a more internal position (W⁵,W¹⁹). These are the so-called GWALP23 and WWALP23 peptides (17) (Fig. 4, a and b). The outer most flanking pair in WWALP23 (W²,W²²) is exactly as in WLP23. This seems to be important for the average azimuthal rotation, because WWALP23 and WLP23 have almost the same ρ in DLPC (148 ± 5° and 150 ± 3°, respectively (6,11,17)). Thus, as we have just seen for WLP23, the W²–W²² Δ-height at the experimental ρ of WWALP23 is near the minimum of the ρ-dependence (∼120° canonical value, Fig. 4 c), suggesting that this orientation is set to place the outermost pair of tryptophans close to anchoring positions at the hydrophobic/polar interface. However, in WWALP23 the inner flanking tryptophans are two sequence positions deeper than in WLP23, and the orientation should find a compromise for allowing also anchoring through these residues (W⁵,W¹⁹). This appears to be the reason for the smaller tilt of WWALP23, compared to WLP23 (τ = 27° vs. τ = 41°, respectively (6)). Indeed, in the former the hydrophobic width of the bilayer (dotted line in Fig. 4 a) lays almost exactly between the W²–W²² and W⁵–W¹⁹ Δ-heights. Of note, this ρ orientation also places the L⁴–L²⁰ Δ-height above the level of the hydrophobic width, which is unfavorable, thus highlighting the importance of anchoring via the outer tryptophans.

It is now interesting to look at the orientation of GWALP23, where W² and W²² are substituted by G² and G²², respectively, leaving this peptide with only one potentially anchoring tryptophan on each side (W⁵ and W¹⁹), whereas the hydrophobic residues L⁴ and L²⁰ remain outside the core limited by the flanking tryptophans. Strikingly, this change gives rise to a very different ρ (304 ± 2° (6,17), see Fig. 4 b) compared to the one of WWALP23 (Fig. 4 a). Again, we can rationalize this otherwise puzzling behavior by examining the corresponding Δ-height waves. In the absence of an outer pair of tryptophans the peptide will now rotate to reach optimal anchoring of the inner pair, approaching the W⁵–W¹⁹ Δ-height to the value of the membrane width (Fig. 4 d). For the tilt of GWALP23 in DLPC ( τ = 16 ± 1° (6)), this happens theoretically at the canonical ρ ∼300°, which overlaps nicely with the experimental ρ (Fig. 4 b). This orientation is now also favorable with respect to hydrophobic matching, because it gives a minimum for the height between the L⁴ and L²⁰, almost coincident with the more internal W⁵–W¹⁹ Δ-height. In fact, burying the external L⁴ and L²⁰ hydrophobic residues should be an important contribution to peptide anchoring. We add that these simple clues are enough to understand also the azimuthal angle orientation of other peptide variants of the same family, where the G² and G²² have been substituted by the charged residues lysine (KWALP23) or arginine (RWALP23). In both cases the experimental ρ is ∼300° (6,17), which maximizes the Δ-height of the corresponding L/R²–L/R²² pairs, thus being favorable for anchoring in a way similar to the KLP23 case.

Additionally, this analysis offers a qualitative explanation of the large whole-body orientational dynamics of WLP23 and WWALP23, versus the much smaller dynamics of GWALP23 (17). The rotational orientation of GWALP23 is optimized around the same ρ value both for anchoring the W⁵ and W¹⁹ residues and for burying the L⁴ and L²⁰ residues (Fig. 4, c and d; see also Fig. 2, c and d, for the ρ-dependence of individual residues). Because in this case there are no additional anchoring groups, this orientation should be well defined around a relatively narrow free energy minimum. However, in WLP23 and WWALP23 the multiple pairs of residues that matter for adjustment to the membrane, including flanking and hydrophobic core residues, have their optimal Δ-height and/or individual height spread in a wide range of ρ values, leading to a fluctuating ρ in a wide and shallow free energy minimum (41).

It is remarkable to see how the various model TM helices have found distinct solutions for optimizing simultaneously their hydrophobic coupling as well as the specific anchoring requirements of either lysine or tryptophan. These complex adaptations appear to be possible simply by the interplay of τ and ρ, regardless of the conformational flexibility of the side chains, which is not considered here. This analysis is based on an intrinsic property of the helix geometry, plus a predictable positioning of flanking residues. Therefore, it should be possible to understand the orientation of TM helices in general on the same grounds. To this aim, we next analyze two additional examples, which suggest that the principles discussed previously apply even to dimeric TM helices and to TM segments of polytopic membrane proteins.

Azimuthal rotation in a helix-helix dimer

Helical TM model peptides with 26 residues and terminal lysines have been used to study systematically the relationship between the helix orientation and the position of the glycophorin A (GpA) dimerization motif (9) around the helix (25). Three peptide variants were designed (KLAm5, KLAm6, KLAm7) with successive 100° pitch rotations of the GpA motif, relative to the peptide termini, about the helix axis (Fig. 5, a–c). However, very similar ρ angles were measured for the three peptides in 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine, which was interpreted as a dominance of lysine-anchoring over helix-helix packing (25). Nevertheless, at the measured orientations (Fig. 5, a–c), only KLAm6 displays optimal access of the dimerization motif, as in the GpA dimer (9,43); i.e., roughly orthogonal with respect to the direction of the tilt. Additionally, KLAm6 exhibited unusually small fluctuations in ρ, and its tilt (τ ≈ 16°) (25) is almost half the value of the helix-helix crossing angle in the GpA dimer (35°–40°) (9,43).

Fig. 5, d–f, shows plots of the hydrophobic and flanking Δ-heights for the KLAm peptides as a function of ρ, in each case for the respective experimental τ (25). From these waves, and following the guidelines explained previously for KLP23, the three peptides are expected to orient with an azimuthal rotation of ρ ≈ 180°. This prediction is indeed very close to the reported experimental values: ρ ≈ 174°, 187°, and 188°, for KLAm5, KLAm6, and KLAm7, respectively (25). Such a rotation gives the largest Δ-height for the flanking residues K²–K²⁵, which approaches the essentially invariant K¹–K²⁶ Δ-height (Fig. 5, d–f). This way, all four lysines can reach anchoring in the three peptides, supporting that the outward position of these residues in the membrane interface is the main factor determining ρ. Additionally, the predicted/experimental ρ corresponds to a minimum in the hydrophobic L³–L²⁴ Δ-height, which is also favorable for the observed orientation. However, hydrophobic matching is apparently achieved only by KLAm5 (τ = 28°, Fig. 5 d) and KLAm7 (τ = 37°, Fig. 5 f), but not by KLAm6 (τ = 16°, Fig. 5 e). This observation implies, as already suggested (25) that the orientation of the latter peptide is additionally influenced by extra dimerization constraints. It is observed that in KLAm6 the dimerization motif and the first and last residues of the hydrophobic core (L³ and L²⁴) look to the same face of the helix (Fig. 5 b). As a consequence, helix-helix packing would hide these residues from the polar environment of the membrane interfaces, effectively reducing the exposed hydrophobic length in the peptide dimer, and in that way contributing to alleviate hydrophobic mismatch without a larger tilt. This is possible specifically for the KLAm6 variant, in which the position of the GpA motif around the helix is compatible with the preferred azimuthal rotation. Altogether, this suggests that the azimuthal rotation angle of TM helices is predictable even in the presence of dimeric interactions and despite the shallow ρ effects that accompany relatively small tilts.

Rotational orientation of natural TM helices in polytopic membrane proteins

Finally, we consider the orientation of TM helices in the tetrameric KcsA potassium channel, whose structure is well known from x-ray diffraction (Fig. 6 a) (36). To this aim, we choose helix H3 from any of the four subunits (equivalent by symmetry). This 30-residue helix, with a 21-residue hydrophobic core, has a complex anchoring pattern, compared to the model TM peptides discussed previously. It is flanked by one arginine toward the N-terminus and one polar threonine toward the C-terminus, plus an outer pair of tryptophan residues beyond (Fig. 6 a). To perform a rotational analysis of helix H3 we take it apart and keep it at the given tilt angle of the experimental structure (τ ≈ 33°), measured by assuming that the full tetrameric channel seats upright across the membrane with its axis of symmetry parallel to the bilayer normal. We find an optimal ρ (defined here with respect to C^α of G⁸⁸) of ∼230°, because this gives a minimum hydrophobic Δ-height (L⁹⁰–L¹¹⁰), a minimum W⁸⁷–W¹¹³ Δ-height, and maximum R⁸⁹–A¹¹¹ and G⁸⁸–T¹¹² Δ-heights (Fig. 6 b). This prediction agrees very well with the orientation of H3 in the crystal structure (ρ ≈ 231°), as depicted in Fig. 6 c. This example suggests that even in polytopic membrane proteins with natural complex sequences the rotational orientation optimizes not only hydrophobic matching, but also the specific anchoring interactions, in full agreement with our general rules deduced from individual model TM peptides. This should not be interpreted as a suggestion that the intramolecular forces play any minor role in determining the structure, but rather that evolution has designed TM helices for optimizing both helix-helix packing and interactions with the membrane, with agreement between the two types of forces.

Figure 6.

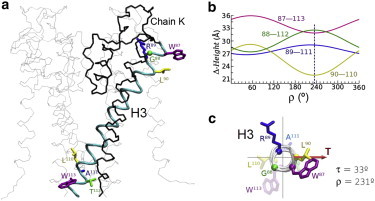
(a) The tetrameric KcsA potassium channel in its closed conformation (PDB ID 3eff) (36) with its symmetry axis aligned with the membrane normal. The backbone of chains L, M, and N is drawn with thin gray lines. Chain K is drawn in black, except for helix H3 (residues 86 to 115), which is highlighted and shows explicitly the side chains of the flanking residues and boundaries of the hydrophobic core. The reference for ρ (C^α of G⁸⁸) is indicated as a ball. (b) Height differences Δ as a function of ρ for the relevant hydrophobic core residues (L⁹⁰–L¹¹⁰) and the flanking residues (G⁸⁸–T¹¹², R⁸⁹–A¹¹¹, W⁸⁷–W¹¹³). The vertical dashed line marks the experimental value of ρ ≈ 231°. (c) Helix H3 viewed along its axis (from the N-terminus) at its given orientation in the crystal structure (36) with the relevant residues highlighted and marking the tilt vector (T) as in Figs. 4 and 5. The quoted values of τ and ρ are measured in the crystal structure as explained in the Methods section.

Conclusion

In summary, the geometry of tilted α-helices reveals a new, to our knowledge, contribution that determines their orientational adjustment in membranes. By optimizing the azimuthal angle, the height (or depth of insertion) of residues can change by several Å. These variations have to be considered when anchoring a TM helix at the hydrophilic-hydrophobic boundaries of the lipid bilayer. The adjustment of ρ serves to (i), minimize the effective hydrophobic height of the peptide in cases of positive mismatch, and at the same time to (ii), optimize the height difference between pairs of anchoring residues that are flanking the hydrophobic core of the helix. A maximum interanchor height is favorable for flanking lysines and other polar residues, whereas a minimum height is preferred for flanking tryptophans. These ρ-dependent effects, which had been overlooked so far, provide a straightforward mechanism to modulate the adaptation of TM helices to the membrane thickness, complementing the intuitively simple tilt-dependent response. Additionally, they provide a qualitative explanation to the large rotational dynamics that characterize monomeric peptide helices with various anchoring groups (17,41). They also have a strong predictive value, even for TM dimers and for helices of polytopic membrane proteins. It has been recently suggested (7) that the assembly of TM segments is driven predominantly by predetermined helix tilt angles imposed by the membrane thickness, rather than specific helix-helix packing. If this claim is correct, the ability to predict ρ angles would have a significant impact on the structure analysis of helix-helix bundles and even on the prediction of structures of multimembrane spanning proteins from their amino acid sequences.