Evanescent Excitation and Emission in Fluorescence Microscopy

Abstract

Evanescent light—light that does not propagate but instead decays in intensity over a subwavelength distance—appears in both excitation (as in total internal reflection) and emission (as in near-field imaging) forms in fluorescence microscopy. This review describes the physical connection between these two forms as a consequence of geometrical squeezing of wavefronts, and describes newly established or speculative applications and combinations of the two. In particular, each can be used in analogous ways to produce surface-selective images, to examine the thickness and refractive index of films (such as lipid multilayers or protein layers) on solid supports, and to measure the absolute distance of a fluorophore to a surface. In combination, the two forms can further increase selectivity and reduce background scattering in surface images. The polarization properties of each lead to more sensitive and accurate measures of fluorophore orientation and membrane micromorphology. The phase properties of the evanescent excitation lead to a method of creating a submicroscopic area of total internal reflection illumination or enhanced-resolution structured illumination. Analogously, the phase properties of evanescent emission lead to a method of producing a smaller point spread function, in a technique called virtual supercritical angle fluorescence.

Introduction

Total internal reflection fluorescence microscopy (TIRFM) (1), near-field scanning optical microscopy (NSOM) (2,3), and a newer technique, virtual supercritical angle fluorescence (vSAF) microscopy (4), all have something in common: they attempt to exceed the standard light microscope resolution limit by employing evanescent light that decays in at least one direction in a distance much shorter than the wavelength. In some cases, the evanescence is on the excitation side, in some it is on the emission side, and in some it is on both sides. Although it is not intended as an exhaustive summary of the published biological applications of evanescent wave optics, this review explores the physical concepts that these techniques share, discusses some fairly new experimentally confirmed applications, and points to some more speculative possible directions for future work in evanescence-based superresolution.

Evanescence in General

In conventional fluorescence microscopy, detection of both excitation and emission typically involves freely propagating light. The spacing λ_m between each traveling wavefront (i.e., the periodic locus of points of equal phase) for propagating light is simply given as λ_o/n_m, where λ_o is the light wavelength in vacuum, and n_m is the refractive index of the medium m (where m = 1,2,3 as used here). The wavefronts propagate through the medium m with a speed c/n_m.

However, light need not behave like this. Because of the geometry in special situations, the wavelength spacing can be forced to be smaller than λ_o/n_m. Such special geometrical situations include the lower refractive index side of an interface at which total internal reflection (TIR) occurs, and also include confinement of the light source to a region smaller than its wavelength, such as very near an excited molecule or the tip of a fine optical fiber. In these cases, light cannot freely propagate and instead becomes exponentially decaying in at least one dimension.

The physics of these situations are related and can be seen most easily by considering plane waves and then generalizing to other wavefront shapes. A plane wave propagating in a medium of refractive index n_m is characterized by a wavevector k_m pointing in the direction of its propagation:

$${\mathbf{k}}_m=k_{mx}\hat{\mathbf{x}}+k_{my}\hat{\mathbf{y}}+k_{mz}\hat{\mathbf{z}}$$ (1)

with a refractive index-dependent amplitude given by

$$k_m\equiv \frac{2\pi }{{\lambda }_m}=\frac{n_m\omega }{c}={\left(k_{mx}^2+k_{my}^2+k_{mz}^2\right)}^{\frac{1}{2}}$$ (2)

where c is the speed of light in vacuum and ω is the angular frequency of the color, which is the same everywhere in the optical system. The wavenumber k_m is fixed for any light in medium m, regardless of direction or proximity to interfaces. For freely propagating light, the spacing between wavefronts is 2π/k_m. The chosen orientation of the (x,y,z) axes depends on the geometry of optical surfaces nearby. The electric field along the x direction, at an instant in time, is described by the sinusoidal function exp(ik_mxx), and the spacing between wavefronts λ′_mx along the x direction is 2π/k_mx and likewise for the other components. The key point here is that the sum of the squares of the components k_mx, k_my, and k_mz in any medium must exactly equal k_m² for that medium.

But what happens if the geometry of the optical system somehow forces the sum of two of the components’ squares to be greater than k_m², for example, $\left(k_{mx}^2+k_{my}^2\right)>k_m^2$ ? This might happen if the wavefronts in the x-y direction are squeezed by geometry to become closer together. Equation 2 would then demand that $k_{mz}^2$ be negative and k_mz thus be imaginary. Then the electric field dependence in the z direction, exp(ik_mzz), becomes a real exponentially decaying function (an evanescent field).

This general mechanism of producing a spatial exponential decay in at least one dimension is shared in common by the otherwise very different optics of TIR, NSOM, and vSAF. The difference lies in how the geometry produces the excess $k_{mx}^2+k_{my}^2$ (or, equivalently, squeezed wavelength spacing). These shared mechanisms and individual differences will be examined more closely in the following sections.

Evanescence in Excitation: TIR

In TIR, the wavefront spacing squeeze is a direct consequence of the geometry of refraction at an interface. Plane wave light approaching a planar interface from a higher index n₃ dielectric toward a lower index n₁ (say, in the x-z plane; see Fig. 1) can create an exponentially decaying field (rather than a propagating field) in the lower index medium, provided the incidence angle θ (measured from the normal) is greater than the critical angle θ_c = sin⁻¹(n₁/n₃).

Figure 1.

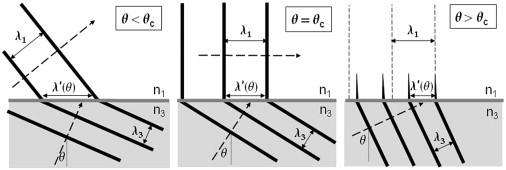
Wavefront spacing in TIR. Left panel: subcritical θ < θ_c; middle panel: critical θ = θ_c; right panel: supercritical θ > θ_c. Wavefronts are shown as heavy solid lines. The plane of incidence is the x-z plane as shown. The right panel shows that the wavefront spacing for a supercritical θ > θ_c is squeezed by geometry in the x direction to be smaller than the spacing demanded by freely propagating light in medium 1 (shown as light vertical dashed lines). This squeezing forces the electric field in the z direction to decay exponentially. The heavy dashed arrows indicate propagation direction. A phase shift exists between wavefronts in medium 3 versus medium 1 for the supercritical case, but to clarify the depiction of wavefront spacing, it is not shown here.

From the perspective of wavefronts, the spacing λ′_3x = 2π/(k₃sinθ) of wavefronts along the interface (the x direction) just inside medium 3 is always longer than the natural propagation wavelength λ₃ = 2π/k₃ in medium 3 because of the nonorthogonal angle with which the interface cuts the wavefronts. The wavefront spacing λ′_1x = 2π/k_1x in medium 1 on the other side of the interface is always forced to be exactly equal to λ′_3x because of the requirement to match the periodic boundary conditions as imposed by Maxwell’s equations. This common wavefront spacing is shown as λ′(θ) in Fig. 1. As long as the propagating light wavelength λ₁ = 2π/k₁ in medium 1 is shorter than λ′(θ), the periodicity at the interface can be matched if the light in medium 1 propagates away at some acute refraction angle (given by Snell’s law). But for a sufficiently large incidence angle θ, the wavelength spacing λ′(θ) along the x direction becomes smaller than the natural propagation wavelength λ₁ for medium 1. The corresponding k_1x = 2π/λ′(θ) thus becomes larger than k₁ = 2π/λ₁ permissable for propagating light in medium 1, thereby forcing k_1z to become imaginary.

The TIR evanescent field has four features of interest for experimental techniques: depth, intensity, polarization, and phase.

TIR depth

The exponential decay depth for the evanescent intensity (which is proportional to the square of the electric field strength) in medium 1 is

$$d=\frac{1}{2k_{3z}}=\frac{{\lambda }_o}{4\pi n_3}{\left({\text{sin}}^2\theta -{\text{sin}}^2{\theta }_c\right)}^{-\frac{1}{2}}$$ (3)

Depth d generally ranges from about λ_o at θ just slightly greater than θ_c, down to about λ_o/10 for easily attainable supercritical θ and typical refractive indices. This small d is the reason why TIR excitation of fluorescence (TIRF) is useful for selectively exciting surface-proximal molecules in medium 1, cell/substrate contact regions, and membrane-proximal cytoplasmic organelles while minimizing excitation of background fluorescence originating deeper within the sample. The fluorescence emission intensity versus θ profile has been used to deduce the concentration of a fluorophore as a function of distance from the substrate, because only the lower θ angles, with their deeper evanescent field depth, can reach out to fluorophores farther away from the interface (5,6).

TIR intensity and thin films

The intensity I_o of the evanescent field has a well-predicted monotonically decreasing shape versus θ for a simple interface (1). This shape becomes much richer if the substrate is coated with a thin film of refractive index n₂ (7,8). If the film is greater than ∼λ_o/2 in thickness and its refractive index is intermediate (n₃ > n₂ > n₁), the film can act as a lossy planar waveguide, complete with resonance modes that depend on θ. If θ is such that light propagates into the film from medium 3 but then totally reflects at the interface with medium 1, the totally reflected light will subsequently partially reflect at the n₃:n₂ interface, return to re-totally reflect at the n₂:n₁ interface (and so on), and thereby set up a pattern of destructive and constructive interference in the film.

Because the intensity of the light just inside the film in medium 2 immediately near the n₂:n₁ interface is proportional to the intensity of the evanescent field just inside medium 1, the resonance-like behavior in the film should be evident in the observed fluorescence intensity F versus θ excited by the evanescent field in medium 1. From the shape of F versus θ (perhaps even spatially resolved in a microscope), the thickness and refractive index and possible lateral heterogeneities of the film may be inferred. This phenomenon, as yet unapplied in biophysics, may have applications, for example, in characterizing a multilayer lipid coating supported on a surface. At particular incidence angles θ that produce a resonance in the film, the evanescent field in medium 1 can be enhanced in intensity by at least an order of magnitude over what it would be with no film.

TIR polarization

The polarization of the evanescent field in medium 1 depends on the incident polarization in medium 3. Say the incident beam lies in the x-z plane, with z normal to the interface. Incident light polarized along y (s-pol, perpendicular to the plane of incidence) will produce a purely y-polarized evanescent field. Incident light polarized in the x-z plane (p-pol) will produce an evanescent field mainly in the z direction with a small θ-dependent component in the x direction.

In polarized excitation TIRF, a p-polarized evanescent field can be uniquely utilized to highlight submicroscopic irregularities in the plasma membrane of living cells (9) and in supported lipid bilayers (10,11). The effect depends on the incorporation of fluorophore into the membrane with a high degree of orientational order.

The requirement for ensemble orientational order is eliminated in viewing singly labeled single molecules rather than membranes with highly oriented heavy labeling. Polarized excitation TIR has been used successfully to determine the orientation of single molecules of sparsely labeled F-actin (12).

TIRF evanescent field phase and interference

The evanescent field in medium 1 is sinusoidally periodic in the x-y plane (the plane of the interface supporting the TIR), with a slight phase shift relative to the incident propagating plane wave in medium 3 that is θ dependent. The evanescent field phase has no z dependence, so the wavefronts are perpendicular to the interface and the field can be represented simply as a 2D wave in x-y.

Because of the close spacing of wavefronts in the evanescent field, illumination by a pair of intersecting and mutually coherent TIR laser beams can produce a very closely spaced striped interference fringe pattern in the evanescent intensity (provided they have the same evanescent polarization). If the relative azimuthal angle ϕ between the two TIR beams is 180°, then the node-to-node spacing s of the evanescent fringes is given by

$$s=\frac{{\lambda }_0}{2n_3\sin \theta }$$ (4)

Spacing s is not dependent upon the refractive index n₁ of the medium (or cell) and can be smaller than the Raleigh resolution limit of the microscope. These fine stripes can be employed in structured illumination (13), thereby producing an even finer lateral resolution than what is standard for that already superresolution technique.

Interesting and potentially useful patterns can be produced by interfering more than one pair of TIR beams. Two orthogonal pairs of intersecting coherent TIR beams (i.e., four azimuthal angles spaced at 90°) will produce a checkerboard pattern in the evanescent intensity. In the limit of an infinite number of azimuthal angles (i.e., two-dimensional (2D) plane waves of equal strength all converging to a central spot where the phases are the same), evanescent 2D plane waves must be integrated from all angles ϕ (see Fig. 2, A and B). This produces a small, bright central spot of subwavelength dimension and with increasingly dimmer rings at larger radii, with an intensity pattern given by

$$I\left(r\right)={\left[E\int e^{i{\mathbf{k}}^{\prime }·\mathbf{r}}d\varphi \right]}^2={\left[E\int e^{i{k}^{\prime }r\cos \varphi }d\varphi \right]}^2=I\left(0\right){\left[J_0\left(k^{\prime }r\right)\right]}^2$$ (5)

where J₀ is a zero-order Bessel function. The intensity pattern is not an infinitesimal point, because although the integration is done over all of the 2D azimuthal directions given by angle ϕ, it is not done over all possible amplitudes of k′ (which would give a 2D δ function). Rather, the amplitude k′ is fixed and determined by the wavelength spacing in the evanescent field as set by the incidence angle θ, such that

$$k^{\prime }=\frac{2\pi n_3\sin \theta }{{\lambda }_o}$$ (6)

One can produce 2D plane waves converging from all azimuthal angles to a central spot by illuminating a ring at the objective back focal plane (BFP) of the microscope objective (for objective-based TIRF), which will produce a hollow cone of light of polar angle θ with an apex at the sample plane. Constructive interference creating the small TIR spot on the sample plane will occur only if all of the component 2D plane waves have the same evanescent polarization. The geometry requires that this evanescent polarization be in the z direction, which will occur only if the illumination ring at the BFP is radially polarized (Fig. 2 C).

Figure 2.

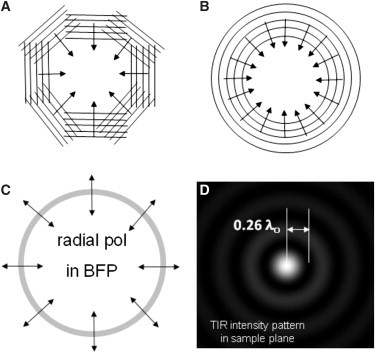
TIR from multiple directions. (A) Eight 2D plane waves in the evanescent field converging to an in-phase center. (B) An infinite number of such 2D plane waves, creating a converging circular wave. (C) This circular converging pattern can be produced by a thin annulus of illumination at the BFP of the microscope objective used for TIRF excitation. The polarization at the BFP must be radial so that all of the evanescent fields from each plane wave component will be predominantly in the z direction (normal to the TIR surface) and thus will mutually interfere. (D) The evanescent intensity theoretically predicted from such annular illumination according to Eq. 5. The width of the central maximum to the first minimum is ∼0.26 λ_o, assuming the annular ring at the BFP has a radius corresponding to NA = 1.45, which is easily accessible with a 1.49 NA objective.

The small central spot has a radius from the central maximum to the first minimum of only 0.26 λ_o, which is considerably less than the Raleigh resolution limit for a 1.49 NA objective (0.41 λ_o). Because all of the component plane waves have an incident angle of θ, the evanescent field depth of the small TIR spot is still given by Eq. 3. This spot is remarkable because standard single-direction coherent TIR illumination (e.g., a laser beam) or multidirection incoherent TIR illumination (e.g., a mercury arc) cannot produce such a small x-y area of illumination. The tiny size in all three dimensions achieved by radially polarized ring illumination at the BFP may be particular useful for defining a small fluorescence correlation spectroscopy (FCS) volume and possibly for stage-scanning-based image reconstruction.

Evanescence in Emission: The Fluorophore near Field

Apart from evanescence in excitation light, light emitted from a fluorophore can also show observable effects of evanescence. Even if there are no interfaces nearby, the spacing between wavefronts will be squeezed if the size of the source of light is very small, i.e., subwavelength. The result is that a portion of the light field will be evanescent in the direction away from the source. This portion is called the near field, and it has a number of practical consequences and analogies to excitation evanescence.

Near field of fluorophore emission: theory

A single fluorophore that is repeatedly excited and emitting can be modeled as a classical oscillating dipole, and the evanescence can be understood from classical electromagnetism theory. The electric field surrounding an oscillating dipole vector μ located at the origin in a medium with refractive index n₁ is directly derivable from Maxwell’s equations (in all standard electromagnetic theory texts) and can be written as follows:

$$\mathbf{E}\left(\mathbf{r}\right)=k_1^3\left[\left(\hat{\mathbf{r}}\times \mathbf{\mu }\right)\times \hat{\mathbf{r}}\left(\frac{1}{k_{1}r}\right)-\left(3\hat{\mathbf{r}}\left(\hat{\mathbf{r}}·\mathbf{\mu }\right)-\mathbf{\mu }\right)\left(\frac{i}{{\left(k_{1}r\right)}^2}\right)+\left(3\hat{\mathbf{r}}\left(\hat{\mathbf{r}}·\mathbf{\mu }\right)-\mathbf{\mu }\right)\left(\frac{1}{{\left(k_{1}r\right)}^3}\right)\right]e^{i\left(k_{1}r-\omega t\right)}$$ (7)

where E(r) is an outgoing spherical wave oscillating at angular frequency ω, but with amplitude and polarization dependent upon the direction and distance to the observation point at $\hat{\mathbf{r}}$. The three terms in the square brackets have increasingly rapid rates of drop-off with the distance k₁r to the observation point (measured in terms of the number of wavelengths × 2π). The first term, with the factor (k₁r)⁻¹, is the standard far-zone light that retains the same integrated energy through any sphere centered on the fluorophore and is responsible for all of the propagating emission seen from an isolated fluorophore far (i.e., k₁r ≫ 1) from any interface. The next two terms are called the near zone because they decay more rapidly with distance.

The behavior of the electric field generated by a fluorophore as it encounters a planar interface is governed by Snell’s law of refraction, the reflection law, and Fresnel coefficients. However, these optics laws are derived assuming that the incident light is a plane wave, not a spherical wave. Therefore, we express E(r) as an integral over plane waves with some weighting factors (shown explicitly in Hellen and Axelrod (14)). Each component plane wave interacts individually with the interface in a manner well predicted by the plane-wave optics laws, and we integrate the resulting reflected and transmitted plane waves with the original weighting factors to derive the behavior of E(r) as it interacts with the optical system.

The resolution of a curved wavefront field into component plane waves is called the angular spectrum of plane waves (15,16). The procedure is the theoretical justification for drawing rays from a point source and then treating each ray’s path through an optical system as if it were a plane wave. The angular spectrum of plane waves is a special case of expressing the original field as a 3D Fourier integral:

$$\mathbf{E}\left(\mathbf{r}\right)=\oint \mathbf{E}\left({\mathbf{k}}_1\right)e^{i{\mathbf{k}}_1·\mathbf{r}}{d}^3{\mathbf{k}}_1$$ (8)

In principle, the integration must be taken over all possible amplitudes and directions of wavevectors k₁. But recall that not all mathematically possible k₁ vectors can be used in optics: only those that also satisfy the optics requirement that the sum of the squares of the components k_1x,y,z equals k₁² can be used. Among these physically possible k₁ vectors, some may have, e.g., $\left(k_{1x}^2+k_{1y}^2\right)>k_1^2$, leading to an imaginary k_z and evanescence in the z direction, analogously to the situation in TIRF except with the decay starting at the z position of the fluorophore.

So the question is, are these squeezed plane wave components with $\left(k_{1x}^2+k_{1y}^2\right)>k_1^2$ really necessary to reconstruct the original field? The answer is yes. Consider, for example, standard plane waves propagating only in the x-y plane (say, defined as parallel to a nearby planar interface), such that $\left(k_{1x}^2+k_{1y}^2\right)=k_1^2$ and thus k_1z = 0. There is no way to add such waves together from all x-y directions simultaneously to produce a sharp singularity at r = 0 as required by Eq. 7. Even if the phases of all these propagating waves from all x-y directions are set to add constructively at the origin and given equal amplitudes, the sum near r = 0 will be a diffuse blur. (This is mathematically identical to the case discussed earlier for a coherent ring of TIR illumination, which gives the intensity pattern of Eq. 5.) To reconstruct the sharp r = 0 singularity resulting from any of the three terms in Eq. 7, plane waves that are evanescent in z and squeezed in their wavefront spacing in x and y are required. This is the origin of the evanescent near field near a fluorophore. The near-zone terms of Eq. 7 are not the sole source of the near field. Rather, all three terms, including the far-zone term, are responsible for setting up the near field because all three have infinite singularities at r = 0.

How can the near field be detected? If the fluorophore in medium 1 is close to an interface with a higher refractive index n₃, the tails of these evanescent components will interact with the interface. For x-y wavefront spacings that are not too small, the tails will convert into propagating light in the higher index material and travel away (possibly to a detector) at a large supercritical angle to the interface normal. The supercritical angle corresponds to the incidence angle that hypothetical TIR illumination would trace going in reverse and setting up an evanescent field with the same squeezed wavefront spacing. The smaller the x-y wavefront spacing of an evanescent emission component, the larger will be the supercritical angle of the propagation in the higher-index material. But for very small x-y spacing in medium 1, no propagating beam with matching spacing at the interface is possible. Such a field will remain evanescent even in the higher-index material and normally will not be detected. The higher the refractive index n₃, the more evanescent components of the fluorophore near field can be captured, converted into propagating light, and detected.

Near field of fluorophores: collection and imaging

Some of the near-field light emitted from a fluorophore converts into a hollow cone of propagating light in a nearby glass substrate. That hollow cone can then be captured by a high-aperture objective, as long as its NA is greater than the refractive index of the medium in which the fluorophore resides (e.g., 1.33 for water). Because the objective performs a one-to-one conversion of the polar angles at which light enters the objective into radial positions at the objective BFP, the hollow cone is converted into an annulus of illumination through the BFP, with radii corresponding to NA > 1.33 (see Fig. 3). None of the far-field propagating energy, for which $\left(k_{1x}^2+k_{1y}^2\right)\le k_1^2$, is cast into that high-angle hollow cone or BFP annulus; rather, it is all cast into subcritical angles and a central BFP disk corresponding to NA < 1.33. The light-collecting advantage of very-high-aperture objectives (NA > 1.33) resides purely in their ability to capture supercritical near-field light. The extra numerical aperture does not help in gathering far-field emission light because none of that light propagates in the glass at the supercritical angles.

Figure 3.

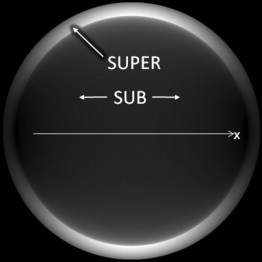
Theoretically computed intensity in the BFP of a 1.49 NA objective, as produced by a fluorophore modeled as a single oscillating dipole on a glass coverslip centered on the optical axis and oriented parallel to the coverslip surface in the x direction, calculated according to the methods Axelrod (8). The border between subcritical (radii corresponding to 0–1.33 NA) and supercritical (radii corresponding to 1.33–1.49 NA) emission features a sudden jump in intensity.

Each supercritical polar angle of emission (and radius in the BFP) corresponds to a particular near-field x-y wavefront spacing in the fluorophore near field and hence a particular z-direction exponential decay length. But since the BFP annulus has a finite thickness containing a range of supercritical angles up to the limiting aperture of the objective, the corresponding decay lengths in that annulus also cover a range of decay distances. Therefore, the total light power coming through the BFP supercritical annulus is not a single exponential. The association of a particular BFP radius with a particular decay length is completely analogous to the TIRF effect for light going the other way (excitation), whereby a particular angle of incidence gives rise to a particular TIR evanescent decay depth. Likewise, on the emission side, concentration profiles should also be deducible from the supercritical intensity versus BFP radius curve.

vSAF microscopy

Imaging of just the supercritical BFP annulus should select only those fluorophores that are close enough to the surface for it to capture their near fields. In previous works (17–19), investigators employed this system by physically blocking the subcritical light in the BFP with an opaque disk. The system does produce an image of exclusively surface-proximal fluorophores, even with standard nonTIR (i.e., EPI) illumination; however, the images obtained are not crisp. The point spread function (PSF) for light gathered only from the supercritical annulus in the BFP can be calculated (8,20) and it is not as sharp as light gathered from the entire objective aperture including the subcritical zone (Fig. 4, A–C).

Figure 4.

vSAF. The left column shows a schematic of the BFP with (A) no blockage; (B) only the supercritical zone physically blocked; or (C) only the subcritical zone physically blocked. The right column is the theoretical PSF for each case, assuming a dipole oriented along x (as in Fig. 3) and a 1.49 NA objective. Theoretical calculations were done according to the methods of Axelrod (8). Although surface-selective, the super-only PSF of panel C has rather bright large rings that decrement the image quality; these are much reduced by the image subtraction scheme shown in panel D.

To circumvent this problem, Barroca et al. (4) recently introduced an effective supercritical light method, called vSAF, that allows selective surface imaging while still preserving the sharpness of a standard image. Instead of directly imaging light from the supercritical zone (by physically blocking the subcritical zone in the BFP), a whole-aperture (super- and subcritical) image is taken, and from it is subtracted the image obtained from the subcritical zone (by physically blocking the supercritical zone in the BFP with a limiting aperture). The difference image is a virtual version of the direct supercritical image, but it is better in one important respect: the difference image preserves the coherent electric field interference between super- and subcritical light coming from each fluorophore in the sample. Interference between super- and subcritical light does not occur at the BFP, of course, but it does occur at the image plane, where light from the two zones from each fluorophore on the sample recombines. Preserving that information-containing interference in vSAF preserves the lateral resolution, whereas losing the interference in direct supercritical imaging decrements the lateral resolution. Theoretical reconstruction of the PSF according to the method of Axelrod (8) with a simulated vSAF procedure results in a much sharper PSF (Fig. 4 D) that still retains selectivity for surface-proximal fluorophores.

By combining the vSAF emission image protocol with standard TIRF excitation, one should be able to attain an even higher degree of surface selectivity than can be achieved with either method individually. There is an additional advantage to this combination: TIRF by itself has scattering artifacts, in part arising from the TIR evanescent field scattering at a heterogeneous sample (such as a layer of cells). This scattered light excites fluorophores farther away from the substrate than would normally be excited by a pure evanescent field. However, in combination with vSAF, these more-distant fluorophores are discriminated against, probably resulting in a significant reduction of scattering background intensity.

Emission polarization including supercritical light

The ability of a high-aperture objective to see an oriented fluorophore from a continuous range of angles tends to reduce the observed polarization of the emission, according to published formulas (21). However, these formulas are approximations because they assume that no interfaces are nearby. Neither refraction nor reflection, nor near-field capture at a nearby interface (such as a coverslip) are taken into account. A more complete calculation that does include these effects (8,14) shows that high-aperture objectives reduce polarization even more than predicted by the approximate formulas. Consider an excited single-molecule dipole residing in water immediately on a planar glass substrate and oriented parallel to the surface, say in the x direction, with the emission intensity F observed through a linear polarizer oriented to transmit in either the x or y direction. A low-aperture objective should see emission light almost entirely polarized in the x direction (i.e., F_y/F_x ∼ 0), and this is well predicted by both the approximate formulas and a complete calculation. However, for a 1.49 NA oil immersion objective that can gather a considerable amount of near-field light through the supercritical zone of the BFP, the approximate formulas (which neglect surfaces) predict F_y/F_x = 0.0394, whereas the complete calculation gives F_y/F_x = 0.135.

Supercritical emission: measurement of absolute distances of a fluorophore from a surface

Because the light passing through the supercritical zone of the BFP originates entirely from the fluorophore near field, the farther away from the interface the fluorophore resides, the dimmer will be the supercritical light. This suggests a direct experimental method to determine the absolute z position of a fluorophore from the substrate: take a ratio of the integrated supercritical to the integrated subcritical intensities (8) from direct images of the BFP. For a 1.49 NA objective and a dipole oriented parallel to the surface, the ratio starts at ∼1.4 for a fluorophore immediately on the surface (z/λ_o = 0.0), but rapidly drops to ∼0.85 at z/λ_o = 0.1. The ratio continues to decrease to 0.06 at z/λ_o = 1.0. Given any particular supercritical to subcritical ratio, the corresponding absolute z can be read. The key advantage to using this ratio to estimate z is that it does not depend on either calibration of the observed intensity or normalization by the total emitted power. The ratio is inherently normalized against changes in illumination power and emission and collection efficiencies.

For small z, most of the light gathered by a high-aperture objective comes through the supercritical zone. The extra aperture, say in going from NA = 1.33 (for which there is no supercritical zone) to 1.49 more than doubles the light-gathering ability, which is a strong reason for using the highest apertures available.

Characterization of films with supercritical emission light

The intensity of supercritical light captured from a fluorophore by a bare substrate and sent through supercritical radii in the BFP decreases monotonically with radius (8). However, the presence of a film of intermediate refractive index on the substrate can lead to multiple fluorescence peaks in the supercritical BFP zone. Fig. 5 shows a theoretical reconstruction of this effect. These supercritical emission peaks in the BFP are analogous to the TIR excitation evanescent field intensity peaks that can occur due to partial resonance in the film, as discussed earlier. For each film thickness h, the shape of the BFP intensity versus radius curve is qualitatively unique. Therefore, it should be possible to identify h (and also the refractive index of the film) by matching an experimentally observed curve shape to a theoretically predicted curve (8).

Figure 5.

Intensity of fluorescence emitted by a dipole oriented normal to the film-coated surface in the supercritical band of the BFP, for several different film thicknesses h. Each lower panel is a magnified view of the portion of the BFP indicated in the uppermost panel. These computer-generated images are based on the methods of Axelrod (8) and the following parameters are assumed: dipole oriented normal to the interface, positioned at z = 0, with NA = 1.49; n₁ = 1.33; n₂ = 1.42; n₃ = 1.52. The increasing number of sharp emission peaks in the supercritical zone with increasing h is analogous to the sharp resonances in intensity that are predicted for TIR excitation as a function of film thickness (8).

Evanescence from a Point Source: NSOM

NSOM includes many variants, all of which involve a submicroscopic-sized optical fiber tip in close apposition to a fluorescent sample. In the illumination aperture mode variant, excitation light is sent through the tip (assumed here to point downward along the z axis) and illuminates a submicroscopic region of the fluorescent sample. The emission is gathered by standard far-field detection. The output field of the tip is laterally confined to the tiny x-y size of the tip, which upon scanning is the feature that leads to superresolution in the x-y plane. As discussed above, such a small source can be expanded in terms of plane waves. However, to account for the severe x-y confinement of the field at the tip, one must include plane wave components with $\left(k_x^2+k_y^2\right)>k^2$, which necessarily leads to components with an evanescent decay in the z direction. Although this decay requires that the probe be positioned near the sample at all points in a lateral scan (which can be technically difficult in irregular surfaces), the extreme sensitivity to longitudinal position allows one to map the distances to fluorophores (22) and the surface topology.

Summary

Evanescence in both excitation and emission can be understood as a response to geometrical squeezing of wavefront spacing in at least one dimension. Evanescent light can be converted to or from propagating light traveling at supercritical angles by a nearby interface. Evanescence in fluorescence excitation and emission has numerous applications in fluorescence microscopy, ranging from already used to speculative ones. Here is a summary of those presented in this review:

On the excitation side

• •Supercritical excitation (TIRF) is commonly used for selective excitation of surface-proximal molecules in medium 1, cell/substrate contact regions, and membrane-proximal cytoplasmic organelles (1).
• •Variable-angle TIRF has been used to deduce the concentration of fluorophores as a function of distance from the substrate (5,6).
• •TIRF intensity versus incidence angle on film-coated surfaces should display a resonance behavior that allows one to measure the thickness, refractive index, and possible lateral heterogeneities of surface-supported multilayer lipid or protein coatings (7,8).
• •TIRF on film-coated surfaces can enhance the evanescent intensity by at least an order of magnitude (7,8).
• •Polarized excitation TIRF has been utilized to highlight submicroscopic irregularities in the plasma membrane of living cells and orientation of single molecules (9–12).
• •Intersecting TIRF beams can extend the superresolution of structured illumination (13).
• •Radially polarized ring TIR illumination at the BFP can produce a uniquely small illumination volume that may be useful for FCS and high-resolution scanning.
• •The evanescent field at an NSOM tip facilitates the mapping of distances to fluorophores (22) and surface topology (2,3).

On the emission side

• •The emission intensity pattern in the supercritical zone of the BFP reports the fluorophore concentration profile as a function of distance to the surface (8).
• •The ratio of emission power in the supercritical versus subcritical BFP zone can sensitively report the absolute distance of a fluorophore to the surface to an accuracy of tens of nanometers (8).
• •Taking into account the interaction of the fluorophore near field with a surface alters the predicted depolarization induced by high-aperture observation (8,14).
• •For a film-coated surface (such as a lipid multilayer), the emission intensity pattern in the supercritical zone of the BFP is uniquely sensitive to the film thickness (8).

On both excitation and emission sides

• •By combining the vSAF emission image protocol with standard TIRF excitation, one should be able to attain an even higher degree of surface selectivity than can be achieved with either method individually, with much less scattering background intensity (4).