Novel Role for Vinculin in Ventricular Myocyte Mechanics and Dysfunction

Abstract

Vinculin (Vcl) plays a key structural role in ventricular myocytes that, when disrupted, can lead to contractile dysfunction and dilated cardiomyopathy. To investigate the role of Vcl in myocyte and myocardial function, cardiomyocyte-specific Vcl knockout mice (cVclKO) and littermate control wild-type mice were studied with transmission electron microscopy (TEM) and in vivo magnetic resonance imaging (MRI) tagging before the onset of global ventricular dysfunction. MRI revealed significantly decreased systolic strains transverse to the myofiber axis in vivo, but no changes along the muscle fibers or in fiber tension in papillary muscles from heterozygous global Vcl null mice. Myofilament lattice spacing from TEM was significantly greater in cVclKO versus wild-type hearts fixed in the unloaded state. AFM in Vcl heterozygous null mouse myocytes showed a significant decrease in membrane cortical stiffness. A multiscale computational model of ventricular mechanics incorporating cross-bridge geometry and lattice mechanics showed that increased transverse systolic stiffness due to increased lattice spacing may explain the systolic wall strains associated with Vcl deficiency, before the onset of ventricular dysfunction. Loss of cardiac myocyte Vcl may decrease systolic transverse strains in vivo by decreasing membrane cortical tension, which decreases transverse compression of the lattice thereby increasing interfilament spacing and stress transverse to the myofibers.

Introduction

Vinculin (Vcl) is a 117-kDa membrane-associated protein expressed in all cell types. It localizes at both cell-matrix and cell-cell adhesion sites including costameres and intercalated disks in cardiomyocytes (1–3). Vcl is a key structural component in the formation of costamere protein complexes that link the actin cytoskeleton to integrins on the cell surface of muscle cells (4–7). Vcl mutations have been linked to both hypertrophic and dilated cardiomyopathies in humans (8). Previous studies have shown that suppression of Vcl expression by antisense oligonucleotide treatment of fetal cardiomyocytes causes a disturbance in normal myofibrillar arrangement (9). Additionally, investigation of heterozygous global Vcl knockout mice (VclKO) showed normal basal cardiac function, abnormal intercalated disks, and a predisposition toward stress-induced cardiomyopathy provoked by aortic constriction (5). The mouse model utilized in this study has cardiomyocyte-specific reduction of Vcl (cVclKO) and displays abnormal intercalated disks (4). Half of the cVclKO mice die suddenly, before the age of three months, and the remainder develop dilated cardiomyopathy (DCM) by 16 weeks of age (4). The normal expression of Vcl may allow cells to resist stresses that result from mechanical forces on the cell exterior (4), suggesting a structural role in force transmission between the exterior and interior of the myocyte. It has also been suggested that Vcl plays a significant role in mechanotransduction (5). Therefore Vcl deficiency may contribute to the development of ventricular remodeling leading to DCM, as was shown in the cVclKO mice. In addition to transducing mechanical signals, Vcl could directly affect mechanical function of the myocardium in a direction-dependent manner owing to its localization at the costamere, where it may contribute to the balance of myocyte forces between cortical membrane tension and transverse myocyte stresses.

To better understand the role of Vcl in regional cardiac function, the three-dimensional geometric structure of the heart and fiber architecture must be taken into account. Muscle fibers have a distinct helical pattern in the wall of the left ventricle (10). In addition to fiber orientation, endomysial collagen struts link costameres of adjacent cells in the transverse direction (11) forming a laminar sheet structure (10), and may be key to the transmission of forces transverse to the cells. Therefore, weakening of cell-extracellular matrix interactions or redistribution of intracellular forces, as could occur when cells have deficiencies in Vcl, may directly affect mechanics transverse to the myocyte fiber axis.

The goal of this study was to investigate the structural role of Vcl in cardiac myocytes, and to determine the implications for regional mechanics before the onset of global ventricular pump dysfunction in Vcl knockout mice. We hypothesized that altered cytoskeletal structure or force transmission may affect tissue mechanics relative to the muscle fiber structure. Studying these animals before they develop heart failure allows more direct examination of the role of the protein defect, before secondary effects of heart failure complicate the physiological response. Measurements of regional strains and isolated muscle mechanical properties may also reveal early contractile defects that are compensated at the scale of whole ventricular pump function. Three-dimensional cardiac strains were measured in vivo with magnetic resonance imaging (MRI) tagging in control and cVclKO mice at an age of 6–7 weeks before the onset of DCM in cVclKO. There were significant decreases in end-systolic transverse (radial and cross-fiber) strain components with no changes in fiber strains, and no changes in global systolic function. The structural basis of this dysfunction was examined with ultrastructural quantification of sarcomere lattice spacing and AFM measurements of myocyte membrane mechanics. A multiscale computational model showed that the measured increases in lattice spacing that occurred with Vcl deletion could explain the observed alterations in three-dimensional ventricular wall mechanics by increasing the angle between strongly bound crossbridges and the myofilaments thereby stiffening the lattice transversely during systole. The results suggest that the primary effect of Vcl deficiency on myocyte mechanics is not on axial shortening or force development. Rather, by decreasing membrane cortical tension, loss of Vcl increases lattice spacing and transverse force development by the sarcomeres, which in turn compromises regional myocardial strains in the cross-fiber and radial directions. These findings suggest a novel sarcomere-level structural mechanism for myocardial mechanical dysfunction that may also be important in the early pathogenesis of heart failure associated with cytoskeletal defects.

Materials and Methods

Mice

The cVclKO mice with cardiomyocyte-specific excision of the Vcl gene have been described previously (4). Cre-negative littermates (WT) with no Vcl excision were used as the controls. The mice used in this study were 6–7 weeks of age from strains that had been maintained in a mixed SV129/Black Swiss background and interbred for at least 10 generations. All protocols were performed according to the National Institute of Health’s Guide for the Care and Use of Laboratory Animals and was approved by the University of California-San Diego’s Animal Subjects Committee.

MRI and global function

MRI protocols for cine and tagging sequences were based on the methods in Chuang et al. (12) (see the Supporting Material for details). A sample tagged image at end-systole is shown in Fig. 1 A. In the cine images, the myocardium was segmented with a semiautomatic level set algorithm (13) to extract the endocardial and epicardial boundaries. A three-dimensional geometric model of the end-diastolic left ventricle (LV) was created (Fig. 1 B) by fitting high-order prolate spheroidal finite element meshes to the endocardial and epicardial points (12). Cavity and wall volumes were measured from the three-dimensional mesh, and wall mass was calculated by multiplying wall volume with myocardial density (1.05 g/mL) (11).

Figure 1.

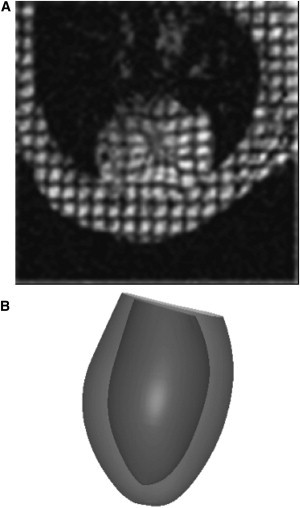
(A) MRI tagging of the mouse heart at end-systole showing deformed tag lines in a short-axis view predominantly of the LV wall (circular cross-section) and the nontagged (shaded) area of the LV chamber. (B) Three-dimensional geometric model of the mouse LV used for global parameter estimation.

Fiber strain analysis

Harmonic phase (HARP) analysis was used to automatically track myocardial material points in the SPAMM images (14). To calculate three-dimensional Lagrangian strains, a deformable model was created using material point displacements from the HARP analysis. The end-diastolic LV model was deformed to fit material point coordinates at end-systole. End-systolic strains with respect to the cardiac coordinates (circumferential, longitudinal, and radial) were calculated at the equator (midventricle) of the LV free wall, at five transmural locations (epicardial, subepicardial, midwall, subendocardial, and endocardial). Strains were then rotated about the radial axis through the measured fiber angle (see measurements below) to give regional strain in cardiac fiber coordinates (fiber, cross-fiber, and radial axes; as seen in Fig. S5 in the Supporting Material). Details of the implementation of the deformable model can be found in Chuang et al. (12).

Histology

After MRI, hearts were arrested and fixed for measurement of fiber and laminar sheet angles (see the Supporting Material for details).

Isolated muscle mechanics

Right ventricular papillary muscles were isolated from adult WT and heterozygous global Vcl null hearts, and mounted in a cardiac tissue culture chamber as previously described in Raskin et al. (15). After preconditioning, the muscles were stimulated at 1 Hz, and stretched from slack length to a passive muscle length with maximum developed systolic force. Peak isometric twitch force was recorded at several passive lengths along with muscle cross-sectional area to determine peak developed fiber stress as a function of passive length.

AFM for cell membrane stiffness and adhesion force

AFM was performed in cardiomyocytes isolated from adult WT and heterozygous global Vcl null hearts. In a third group vinculin gene transfer was performed in heterozygous null myocytes. The force contact mode of operation was used to measure adhesion force and cortical membrane stiffness (elastic modulus) from the retraction and approach curves, respectively (16–18) (see the Supporting Material for details).

Myofilament image analysis

Samples were prepared for transmission electron microscopy (TEM) using standard techniques (see the Supporting Material for details). Groups of cVclKO and WT hearts were fixed either in diastole (arrested) or in systole (barium contracture). Sarcomere length (SL) images and myofibril interfilament lattice spacing images were recorded with TEM, and a fast Fourier transform technique was used to measure lattice spacing from diffraction patterns (see the Supporting Material for details).

Myofilament lattice mechanics model

A micromechanical model of myofilament mechanics was used to derive transverse systolic sarcomere stiffness as a function of cross-bridge stiffness based on cross-bridge geometry and actomyosin lattice spacing (Fig. 2). Similar to the analysis by Schoenberg (19), transverse and axial cross-bridge forces were resolved using a simplified two-dimensional model where the S2 segment was modeled as a spring with a freely jointed hinge at the origination site on the thick filament backbone with an axial tilt angle at the attachment site (α, Fig. 2, A and B) of 45° (20,21). Because the S2 origin site was modeled as a freely rotating pivot point, the angle between the thick filament and the S2 region of myosin (θ in Fig. 2, E and F) is constrained by the other angles and varies as a function of actin-myosin lattice spacing (Δ). These assumptions are sufficient to allow the cross-bridge force F_S2 to be resolved into longitudinal (fiber) and cross-fiber (transverse) force components, F_f and F_t, respectively. An increase in lattice spacing increases the cross-bridge tension by increasing cross-bridge strain and increases the ratio of F_t to F_f by increasing θ (Fig. 2, A and B). The changes to F_t and F_f resulting from an incremental increase in Δ gives the transverse and fiber cross-bridge stiffnesses whose ratio is

$$\frac{K_{\text{t}}}{K_{\text{f}}}=\frac{l_{\text{S}2}-{\hat{l}}_{\text{S}2}{\text{cos}}^2\theta }{l_{\text{S}2}-{\hat{l}}_{\text{S}2}{\text{sin}}^2\theta },$$ (1)

where $l_{S2}$ and ${\hat{l}}_{S2}$ are the instantaneous and resting lengths of the S2 segment of myosin, respectively.

Figure 2.

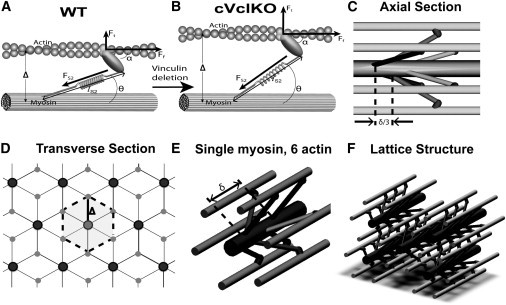
Micromechanical model for sarcomere lattice spacing and cross-bridge architecture. (A) Individual cross-bridge model consisting of a myosin stalk based on the geometry by Schoenberg (19). (B) As the lattice spacing (Δ) increases with Vcl deletion (transition from panels A to B), binding angles (θ) change and F_S2 increases, and attachment angle α remains constant. The result is an increase in the transverse force, but little change in the fiber force (F_t = transverse force, F_f = fiber force, F_S2 = force along S2 segment). (C and D) The unit cell of the lattice structure in the axial (C) and transverse (D) directions is marked (dotted outline, δ = 3 pairs of myosin heads spacing). (E) A single myosin filament is surrounded by six actin filaments. (F) Overall lattice structure. Details of this myofilament lattice model can be found in the Supporting Material.

To compute macroscopic three-dimensional transverse/fiber stiffness ratios, we next consider the myofilament lattice geometry in planes transverse and parallel to the myofilaments (Fig. 2, C and C) when all crossbridges are attached in the strongly bound state. By deriving the strain energy associated with equibiaxial transverse strain of the lattice and uniaxial fiber strain of the sarcomeres (see the Supporting Material for details), we obtain the following expression for the ratio of the transverse lattice stress (σ_tt) to the fiber lattice stress (σ_ff),

$$\frac{{\sigma }_{\text{tt}}}{{\sigma }_{\text{ff}}}=\frac{1}{2}\left(\frac{\text{Δ}}{\delta }\right)\frac{K_{\text{t}}}{K_{\text{f}}},$$ (2)

where δ is the distance along the thick filament between consecutive cross-bridge pairs in the same plane (Fig. 2 E) and also represents the length of a hexagonal unit element, with six crossbridges (three pairs) and a radius equal to the actin-myosin lattice spacing (Δ) (Fig. 2, C and D).

To use these expressions in a continuum constitutive model of systolic myocardial stress, the SL to be used is calculated from the macroscopic fiber strain using the unloaded reference sarcomere length (S₀) that was measured for each genotype from the electron micrographs of unloaded cardioplegia-arrested hearts. The time-varying myofilament lattice spacing was computed from the sarcomere length (S) using the assumption that sarcomere volume (V_S) remains constant during the cardiac cycle, i.e., S × Δ² = V_S. The volume constant V_S for each genotype was based directly on TEM measurements in the diastolic and systolic arrested preparations, which also supported the assumption that the lattice deformed isotropically during contraction (i.e., even though the ventricle thickened radially and shortened transverse to the fibers in the plane of the wall, the interfilament distances remained independent of orientation in the plane transverse to the filaments). V_S, derived from the electron micrographic measurements, was scaled up by 20% in both genotypes to account for the effects of lattice shrinkage due to dehydration and fixation previously reported by several groups using similar techniques, which only affects lattice spacing and not the SL (22–24).

In summary, by considering the mechanical equilibrium of the cross-bridge and myofilament lattice in three dimensions, we derived a micromechanical model for myocyte systolic stiffnesses in the fiber and transverse directions as a function of sarcomere length and lattice spacing. A kinematic model in turn enables the SL and lattice spacing to be determined from macroscopic fiber strains. The only parameters in this analysis that were varied between genotypes were the SL and V_s (calculated from SL and Δ) as measured directly from the electron micrographs.

Ventricular mechanics model

This microstructural model was included in a finite element model of ventricular mechanics to test whether measured alterations in sarcomere geometry were sufficient to explain observed mechanics in vivo in young WT and VclKO mice. The left ventricle was approximated by a truncated prolate spheroidal geometry and fiber orientations were included based on the histological measurements. Systolic active muscle stress was computed as a function of time and regional fiber strain using a previously published model (25) with parameters that were the same for both genotypes as given in the Supporting Material. Using measured SL and lattice spacing the dynamic transverse stiffness was computed from the model fiber stress using the ratio obtained above from the micromechanical model. The ventricular model was coupled to a Windkessel model of aortic impedance and used to compute regional wall stresses and strains and ejection fractions (see the Supporting Material for details).

Statistics

All measurements are presented as mean ± SD. End-systolic strains, sarcomere geometry measurements between cVclKO and WT mice, and fiber angles were compared by two-way repeated measures analysis of variance (ANOVA). P-values < 0.05 were considered significant. To identify the effects of genotype on Δ independent of differences in SL, the relationship was analyzed using analysis of covariance (ANCOVA) in which the regressor was $1/\sqrt{SL}$ based on the assumption of sarcomere volume conservation. To test the statistical significance of the results predicted by the model, z-scores were assigned to all the model strain results based on the experimental means and standard deviations, and used to determine if model results fall within the experimental variance.

Results

Global geometry and function

From the geometric models based on the cine MRI images of the myocardium, end-diastolic volume (EDV), end-systolic volume (ESV), ejection fraction (EF), and left-ventricular mass index (LVMI) were measured (n = 5 for both WT and knockout (KO)). EDV (48 ± 12 vs. 50 ± 11 μL) and ESV (20 ± 8 vs. 25 ± 6 μL) were slightly larger in cVclKO, but not significantly different. There were also no significant differences in EF (50 ± 4 vs. 58 ± 9%) and LVMI (4.2 ± 0.9 vs. 4.1 ± 0.7 mg/g) between cVclKO and WT mice, respectively. Mean lung/body weight ratios (0.60 ± 0.11%, WT and 0.64 ± 0.09%, KO) and liver/body weight ratios (3.73 ± 0.43%, WT and 4.05 ± 0.67%, KO) were not different between the groups. Peak systolic fiber stress was not different at any passive muscle length as determined from isolated papillary muscle studies (see the Supporting Material for data).

Fiber and sheet angles

Mean fiber angles at the equator of the LV free wall measured from histology displayed a linear transmural distribution between ∼−65° at the epicardium and +65° at the endocardium with no differences between cVclKO and WT hearts (n = 5 in each group). Sheet angles were on average negative throughout the wall, varying from −42° to −65° at the midventricle, similar to previously reported values (26). There were no significant differences in sheet angles between cVclKO and WT hearts. Both fiber and sheet angle measurement results can be seen in Fig. S1.

Regional strains

Regional midventricular strain tensors computed from the HARP analysis at three transmural locations and resolved with respect to local fiber coordinates (f = fiber, c = cross-fiber, r = radial), using the measured fiber angles, are shown in Fig. 3 at end-systole (referred to as an undeformed reference state at end-diastole). In WT mice, systolic fiber strain (E_ff) was negative (shortening) and uniform across the wall. Cross-fiber strain (E_cc) was also negative as expected and radial strain (E_rr) was positive, consistent with systolic wall thickening, and both of these components were largest at the endocardium and smallest at the epicardium, as seen previously in the mouse (12) and other species (27). In cVclKO hearts, two-way ANOVA analysis for the strain components (Table 1) showed that E_ff was not different from WT; however, the transverse components of strain (E_cc and E_rr) showed significant differences of interaction (n = 5, p = 0.010, and p = 0.001, respectively), implying a difference in the way the strains vary transmurally. E_rr in the cVclKO hearts decreased in magnitude with wall depth, opposite of the gradient observed in the WT hearts. There was also a significant difference (p < 0.001, n = 5) between genotypes regardless of transmural location for E_rr. All of the shear strains were relatively small in magnitude, but a genotype difference was observed for both E_fc and E_cr (n = 5, p = 0.002 and p = 0.015, respectively). Overall, Vcl deficiency significantly reduced myocardial systolic strains transverse to the myocytes but had no effect on systolic fiber shortening.

Figure 3.

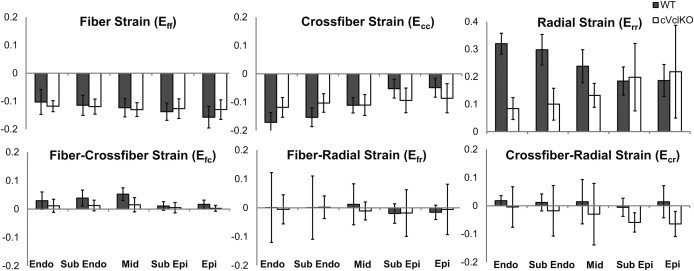
Regional end-systolic fiber strains found from MRI and three-dimensional model analysis at five transmural locations (n = 5). Six strain components are referenced to the local fiber coordinate system (f = fiber, c = cross-fiber, and r = radial axes). Values and gradients for WT are as expected, and statistical comparison between WT (solid) and cVclKO (open) shows decreases in strain magnitude predominately for the radial strains (E_rr). (Endo, endocardium; epi, epicardium; mid, midwall.)

Table 1.

Two-way ANOVA p-value results show the difference between WT and cVclKO strains based on the five locations through the wall and genotype

Strain component	Genotype	Wall location	Interaction
Eff	0.799	0.210	0.638
Ecc	0.618	<0.001a	0.010a
Err	<0.001a	0.976	0.001a
Efc	0.002a	0.053	0.548
Efr	0.879	0.965	0.990
Ecr	0.015a	0.629	0.871

^aStatistically significant values (p < 0.05).

Membrane stiffness and adhesion force with AFM

Cortical membrane stiffnesses were computed from force curve data (see Fig. S3, with more details in the Supporting Material). Stiffness in cardiomyocytes from Vcl heterozygous null mice (14.8 ± 0.6 kPa) decreased significantly by 55% compared with WT myocytes (32.5 ± 1.2 kPa, n = 10). Rescue of vinculin restored cell stiffness to control levels (34.5 ± 0.9 kPa, n = 10). There were no significant changes in the initial peak adhesion force among Vcl null (39.1 ± 0.2 pN, n = 10), vinculin rescued (39.9 ± 0.9 pN, n = 10), and WT myocytes (38.6 ± 1.6 pN, Fig. 4 B). The probability of adhesion to extracellular matrix protein fibronectin decreased significantly by 40% in Vcl heterozygous null myocytes compared with WT, and this difference was no longer significant in myocytes in which vinculin expression was rescued.

Figure 4.

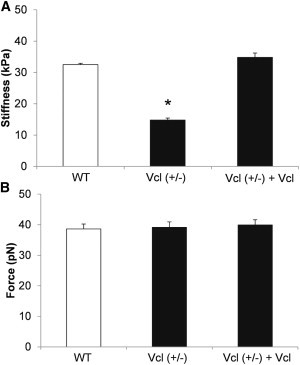
AFM measurements in cardiomyocytes from wild-type (WT), heterozygous null (Vcl+/−), and vinculin rescued (Vcl+/− + Vcl) groups. (A) Cell cortical stiffness was significantly decreased in Vcl+/− mouse cardiomyocytes. Rescue of vinculin expression in Vcl +/− cardiomyocytes restored stiffness to WT levels. (B) Adhesion force was not changed in the three groups. ^∗p < 0.05 vs. WT. n = 10 for each group.

Sarcomere geometry

Myofilament lattice dimensions measured from optical diffraction patterns computed from transmission electron micrographs (Fig. 5 A) are shown in Table 2 (n = 3 for both WT and KO). Actin-myosin lattice spacing obtained from the second-order diffraction distance and myosin-myosin lattice spacing (M-M Δ) from the first-order diffraction pattern were both larger for cVclKO mice than WT animals. The mean ratio of (M-M Δ)/Δ (1.70) was within 1.9% of $\sqrt{3}$, the ratio as derived for a hexagonal lattice. Sarcomere lengths were slightly lower (p = 0.051) in the KO mice, so to compare lattice dimensions independent of SL we plotted Δ vs. $1/\sqrt{SL}$ (Fig. 5 B). The slope of this relation is the sarcomere volume constant V_S (p = 0.59 between WT and cVclKO). There was no significant effect of genotype or contractile state on sarcomere volume. By ANCOVA there was a significant effect of genotype and a significant effect of contractile state on both myosin-myosin lattice spacing and Δ. Refer to Table 2 for all p-values.

Figure 5.

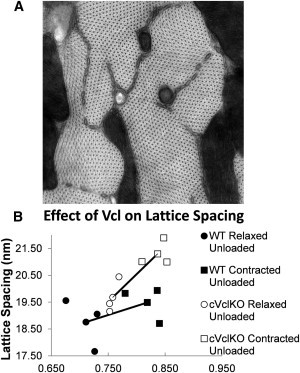
Lattice spacing image analysis. (A) Representative TEM image montage at ×47,000 magnification showing myofilament cross-sections of a relaxed unloaded cVclKO heart. The pixel size is 0.19 nm, and the image size is 2.3 μm × 2.3 μm. (B) Effect of Vcl deletion on actin-myosin filament spacing in mouse hearts arrested at end-diastolic (smaller $1/\sqrt{SL}$) and barium-contracted states (larger $1/\sqrt{SL}$). Assuming constant volume, Δ varies with $1/\sqrt{SL}$. (Line) Connection of average points.

Table 2.

Sarcomere length (SL), myosin-myosin lattice spacing (M-M Δ), and actin-myosin lattice spacing (Δ) raw measurements for cVclKO (n = 3) and WT (n = 3) hearts arrested at end-diastole, and hearts contracted with barium (Ba) against zero load (n = 3 each for WT and cVclKO)

		M-M Δ(nm)	Δ (nm)	SL (μm)
Relaxed unloaded hearts	VclKO (Avg ± SD)	33.47 ± 1.35	19.67 ± 0.68	1.74 ± 0.04
	WT (Avg ± SD)	30.83 ± 0.68	18.76 ± 0.98	1.99 ± 0.18
Ba-contracted unloaded hearts	VclKO (Avg ± SD)	37.61 ± 2.39	21.30 ± 0.52	1.43 ± 0.08
	WT (Avg ± SD)	32.90 ± 1.57	19.49 ± 0.68	1.50 ± 0.13
		M-M Δ	Δ
	Two-way ANCOVA (p-value)	0.0333	0.0446

The ANCOVA results show a significant genotype difference, for both M-M Δ and Δ.

Ventricular strains from model analysis

Table S1 in the Supporting Material summarizes all of the myofilament lattice mechanics as well as the finite element model parameters; the only parameters that were different between the models of the WT and cVclKO mice were those derived from the electron micrographs: unloaded reference SL (1.88 μm WT and 1.74 μm cVclKO), unloaded systolic SL (1.50 μm WT and 1.43 μm cVclKO), and volume constant V_S from which lattice spacing was computed (1620 nm²/μm WT and 2030 nm²/μm cVclKO). End-systolic strain components in fiber/cross-fiber coordinates referred to as end-diastole are shown in Fig. 6 for WT and cVclKO models and compared with experimental results from the MRI tagging experiments. Fiber strains computed with the models showed a slightly larger difference between WT and cVclKO than what was observed experimentally. The radial strain decreased substantially with the increased lattice spacing, but the reversal in the transmural gradient that was observed experimentally was not quite captured by the model. The cross-fiber strain decreased at the endocardium and midwall, but increased slightly at the epicardium with an increase in lattice spacing due to loss of Vcl, similar to the trend that was observed experimentally. In the simulation, end-systolic fiber stresses in the cVclKO model were 11% higher on average through the wall compared to WT, where the largest increase was seen at the epicardium (22%) and the smallest decrease was in the midwall (2%).

Figure 6.

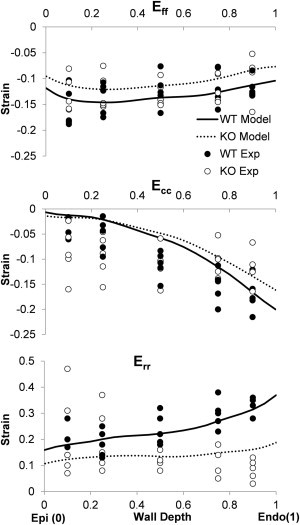
Model versus experiment comparison of fiber (E_ff), cross-fiber (E_cc), and radial (E_rr) systolic strains. Gradients and magnitudes are mostly similar, indicating general agreement between model and experiment.

Z-scores showed that model results were within two standard deviations of the mean experimental values for all six strain components at all transmural locations (z < 2) except for 1 of the 60 component/location combinations. In addition to the systolic strains, the model predicted an EF of 44% for WT and 35% for cVclKO. Statistical analysis of model-predicted values using the variance of the experimental EF showed no difference (p = 0.06), similar to the experimental finding (p = 0.08).

Discussion

In this study, we examined the effect of Vcl deletion and Vcl deficiency on myocyte and ventricular mechanics before the onset of global ventricular dysfunction in cVclKO mice. At this time we expected that Vcl deficiency is the main cause of the structural defects at the sarcomere level. The mechanistic multiscale model analysis and experimental results suggest that the observed early alterations in myocardial systolic wall strains transverse but not parallel to the myofibers can be explained by the observed increase in systolic and diastolic myofilament lattice spacing. As the angle between the thick filament and the S2 region increases with increased lateral myofilament spacing, the radial component of the force in the crossbridge increases with little change in the axial component. The lattice model suggests that this results in a comparable increase in transverse systolic stiffness relative to fiber stiffness at the level of the myocyte. The ventricular model suggests that these anisotropic changes in systolic stiffness due to Vcl deletion result in little change in systolic fiber shortening but a substantial decrease in radial wall thickening during systole—which is now being opposed by the higher radial stiffness of the lattice in the cVclKO mice. Changes in shear strains were small in the model and hence, owing to incompressibility, similar fiber shortening and decreased radial thickening resulted in decreased cross-fiber shortening in the cVclKO mouse model.

Consistent with this hypothesis, papillary muscle tests showed no changes in isometric tension in global Vcl heterozygous null mice compared with controls. Atomic force microscopy in global Vcl heterozygous null myocytes showed a decrease in the probability of binding to fibronectin-coated probe tips but no change in the force of adhesion, suggesting a decreased expression, availability, or affinity of integrin receptors. However, membrane cortical stiffness calculated from the AFM force curves showed a significant decrease in Vcl heterozygous null myocytes that was reversed when vinculin expression was rescued in vitro. We suggest here that this finding may be due to a decrease in membrane cortical tension that is in equilibrium with transverse compression of the myofilament lattice that is presumably transmitted via the Z-disk. The location of Vcl in relation to the Z-disk, myofilaments, and the cell membrane as well as its possible role in membrane tension can be seen in Fig. 7. When vinculin is deleted, there is a decrease in the stiffness of the protein complex at the costamere which causes a decrease in the cortical tension, allowing for Z-disk expansion (increasing the lattice spacing). By decreasing membrane cortical tension, the lattice compression is relieved, resulting in expansion that increases actin-myosin lattice spacing. Hence, we conclude that an early mechanism of ventricular mechanical dysfunction before the onset of heart failure in vinculin-deficient mice is an increase in systolic transverse myofiber stress development due to increased myofilament lattice spacing mediated by a decrease in membrane cortical tension. In the cVclKO model, the change in material properties led to a 13% increase in the subendocardial systolic fiber stress. Because increased wall stress is a known risk factor for hypertrophy and cardiac dilation, these structural changes could contribute to the subsequent development of heart failure in cVclKO mice.

Figure 7.

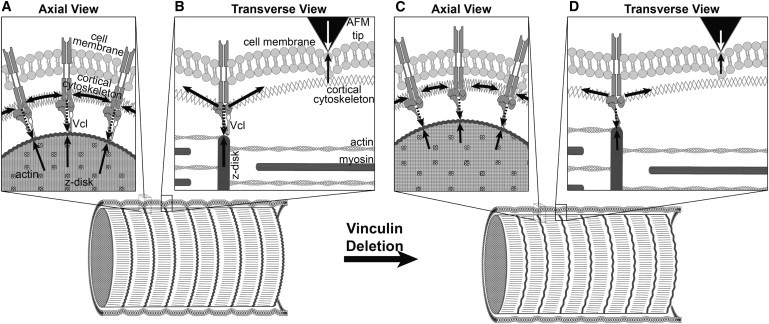
A hypothesized model of a possible role for vinculin in membrane cortical tension and compression of the Z-disk. In this model, vinculin maintains tension in the cortical cytoskeleton which compresses the Z-disk. When vinculin is deleted, the stiffness and force of the protein complex at the costamere (long dashed downwardarrows in panels A and B) is decreased (represented by shorter dashed arrows in panels C and D), which in turn leads to a decrease in the cortical tension (represented by shorter horizontal solid arrows in the cortical cytoskeleton in panels C and D), corresponding to lower AFM indentation force (open arrows). This decrease in cortical tension allows for the Z-disk to expand (owing to reduced compression of the Z-disk balanced by the reduced cortical tension). The expansion of the Z-disk leads to a larger lattice spacing.

Global cardiac function in 6–7-week-old WT mice, as shown by EDV and EF derived from MRI, were near the ranges reported in literature (28–30). Slight differences may be attributed to background strain, age, and anesthesia levels. On average, cVclKO hearts were slightly larger than WT hearts and EF was minimally lower, but there were no significant differences detected in any of the global parameters. Therefore, loss of Vcl did not significantly affect global systolic function or geometry in the animals studied here.

The measured three-dimensional end-systolic strains in the WT free wall agree well with previously published mouse data in terms of magnitude and sign (31,32). Our WT strains showed that E_rr is positive, indicating systolic wall thickening, and in general larger at the endocardium than the epicardium. In-plane strains were negative as expected, and torsional strain was also as seen before (30). Fiber architecture in the cVclKO hearts was not different from that found in control hearts, and was consistent with previously published mouse studies (26). Transforming strains into fiber coordinates provides insight into fiber and transverse-myocyte mechanics. The sign and magnitude of systolic fiber strain components in WT mice were similar to values measured in large animals such as the dog (27,33). In cVclKO mouse hearts, end-systolic E_ff strain was not significantly different from WT hearts, but E_rr and E_cc were decreased at several locations. This change in transverse function led to the hypothesis that sarcomere lattice spacing and myocyte force generation are altered by Vcl deficiency, and hence the histological and modeling studies.

Loss of normal Vcl expression led to increased myofilament lattice spacing that may be mediated by altered equilibrium of stresses in the cytoskeleton. On average, the myofilament lattice spacing in unloaded cVclKO hearts was larger than in the WT hearts at rest and in contracture, suggesting the presence of a cytoskeletal compressive prestress acting transverse to the filaments (tangentially to the Z-disk) that is partially released when Vcl is disrupted. Consistent with this hypothesis, membrane cortical stiffness measured by AFM was ∼55% lower in global heterozygous Vcl null cardiomyocytes than controls, and this difference was lost when vinculin expression was restored in these cells. Wang et al. (34) suggested that membrane stiffness is primarily a result of cortical pretension in adherent contractile cells. This idea is consistent with the tensegrity hypothesis of cell mechanics (35) the details of which are debated, but consistent with a growing number of cell mechanical studies. Thus we propose here that a decrease in membrane stiffness and expansion of the myofilament lattice can be mediated by a decrease in membrane pretension transmitted via the Z-disk.

Previously, x-ray diffraction studies in rat heart muscle (36) reported a 34-nm distance between the planes of the thick filaments (d₁₀ as described in Millman (24)) at a SL of 2.2 μm, which corresponds to a center-to-center distance between myosin filaments of 39 nm. Lattice spacing measurements from WT mice in this study were consistent (within 6%) with these values after accounting for expected lattice shrinkage due to TEM sample preparation methods (22–24). Although the WT TEM measurements were consistent with x-ray diffraction measurements, it should be noted that it is uncertain how lattice shrinkage due to TEM sample preparation might change with genotype or sarcomere length, which is a drawback to using TEM for this study. The lattice spacing in each mouse was also normalized by the inverse square-root of sarcomere length to exclude differences in lattice spacing due solely to differences in SL between preparations. Viewed this way, sarcomere volume was higher in cVclKO mouse cardiomyocytes irrespective of loading.

The micromechanical model used here assumed that the increased lattice spacing in the cVclKO hearts increases the cross-bridge angle, which would increase the transverse sarcomere stiffness and generated transverse force assuming no change in the location of the actin binding site. Because the location of the actin binding site was assumed to be the same between the two genotypes, the increased cross-bridge angle caused an increase in strain in the S2 segment of the myosin head. Owing to the fact that the S2 segment was modeled as a spring, the increased strain resulted in an increased force in this segment (as illustrated in Fig. 2). As a result, the cross-bridge active stress increased in the transverse direction but remained approximately constant along the fiber direction. This gave rise to a transverse stress on the lower end of the range recently determined by more complex models of the crossbridge (37). This analysis implies that a more sophisticated model could show an even more dramatic increase in the transverse component of force with an increase in lattice spacing, possibly increasing the difference in E_cc between WT and cVclKO hearts.

The analysis of cross-bridge mechanics was performed using angles and geometric lengths that were either previously referenced in literature or measured in this study. The only values that were changed between the WT and cVclKO simulations were differences that were directly measured experimentally. No free or adjustable parameters were used to model the effects of Vcl deficiency in the active contraction simulations. The two-dimensional myosin segment lengths were obtained via a projection of a three-dimensional model using parameters from literature, and are referenced in Table S1.

The altered sarcomere geometry of the cVclKO mice results in decreased radial strain as predicted in the stress analysis of the crossbridge. However, a limitation of the model is that it does not predict the minor change in transmural gradient of E_rr between WT and cVclKO as seen experimentally. Fiber strain in the model simulation changes more between WT and cVclKO than the experiments, but the magnitudes of strain match the experiments very closely. The larger difference in fiber strain in the model shows the limitations of the simple model that could possibly be improved in the future with a more complex model. The cross-fiber strain is decreased in the cVclKO model throughout the wall, which agrees very closely to experiments at the endocardium, but the agreement differs slightly at the midwall and epicardium. This disagreement is most likely due to the high levels of variability in the measured cross-fiber strains. Additionally, it was determined that the increase in transverse active stress decreases the amount of wall thickening at end-systole when Vcl function is altered, which is consistent with experimental observations. The magnitudes of the genotypic strain changes in the simulation were less than the measured values, suggesting that the measured changes in sarcomeric structure may not be the only mechanism responsible for the altered ventricular function associated with Vcl deletion.

There are several limitations in this study. In the active contraction simulation the fiber angles were only measured at the equator; these angles were then incorporated throughout the model. In addition, no transmural SL gradient was included in the model because no data have been collected to show that it exists in the mouse model being studied. However, if it was determined that this gradient did exist, it would affect the accuracy of the SL measurements as previously described, and its absence would alter the simulation results. Also, the simplifying assumptions of the model (i.e., ignoring the higher-order sheet structure; modeling the myocardium as a transversely isotropic material; no fiber dispersion, etc.) together with the simple axisymmetric geometry of the mesh result in a model that may not be capable of accurately depicting all of the mechanistic subtleties associated with Vcl deletion. It should also be noted that the AFM stiffness protocol could be measuring a decrease in lattice stiffness as opposed to cortical tension; however, our analysis of lattice stiffness suggests that there would be an increase in systolic lattice stiffness in the transverse direction.

The results of this study are an important step in understanding the mechanistic link between cellular structural alterations and contractile dysfunction associated with Vcl deletion and Vcl protein deficiency before the onset of DCM remodeling. MRI tagging studies defined a specific mechanical defect in ventricular wall function that precedes any decrease in fiber shortening or global chamber function. This defect in mechanical function can be explained by a specific and measurable direction-dependent ultrastructural change at the sarcomere level due to loss of costamere-associated Vcl. AFM measurements suggest a direct mechanical link between this alteration in sarcomere geometry and the loss of costameric Vcl. We describe and quantitatively tested what is to our knowledge, an entirely novel mechanism for contractile dysfunction that may also explain how other proteins in the costamere and dystrophin-glycoprotein complex might lead to contractile dysfunction and subsequent cardiomyopathy.