Abstract
As a model for understanding how molecular crowding influences diffusion and transport of proteins in cellular environments, we combined experimental and theoretical approaches to study the diffusion of proteins in highly concentrated protein solutions. Bovine serum albumin and γ-Globulin were chosen as molecular crowders and as tracers. These two proteins are representatives of the main types of plasma protein and have different shapes and sizes. Solutions consisting of one or both proteins were studied. The self-diffusion coefficients of the fluorescently labeled tracer proteins were measured by means of fluorescence correlation spectroscopy at a total protein concentration of up to 400 g/L. γ-Globulin is found to have a stronger influence as a crowder on the tracer self-diffusion coefficient than Bovine serum albumin. Brownian dynamics simulations show that the excluded volume and the shape of the crowding protein have a significantly stronger influence on translational and rotational diffusion coefficients, as well as transient oligomerization, than hydrodynamic or direct interactions. Anomalous subdiffusion, which is not observed at the experimental fluorescence correlation spectroscopy timescales (>100 μs), appears only at very short timescales (<1 μs) in the simulations due to steric effects of the proteins. We envision that the combined experimental and computational approach employed here can be developed to unravel the different biophysical contributions to protein motion and interaction in cellular environments by systematically varying protein properties such as molecular weight, size, shape, and electrostatic interactions.
Introduction
Molecular crowding is a fundamental aspect of protein diffusion and transport in cellular environments to which increasing attention is being paid (1–7). The aqueous compartments in living cells are packed with a high concentration of macromolecules such as proteins and nucleic acids, which strongly influence macromolecular diffusion (7,8). Subdiffusion, in which diffusion is hindered, and the mean-squared displacement (msd) does not increase linearly with time (9), is expected in highly crowded media such as the cytoplasm or cell membranes (6). This is because macromolecules are transiently confined to certain volumes due to molecular interactions with the surrounding crowders before they are, stochastically, allowed to diffuse further. Subdiffusion has been proposed to influence how proteins find partners for specific interactions in crowded environments (10).
To mimic physiological media in in vitro experiments, a total concentration of macromolecules of up to 400 g/L is commonly used (7,11). Frequently, random-coil polymers, such as polyethylene glycol, Ficoll, or dextran, are used as macromolecular crowding agents because of their ease of availability and experimental manipulation (12,13). However, these nonbiological crowding agents may not reveal physiologically relevant information (2,3). To obtain a more realistic description of physiological environments, biological macromolecules, such as globular proteins, can be used as crowding agents (3).
In this work, we have studied the effects of crowder and tracer size, shape, direct interactions, and hydrodynamic interactions on the translational diffusion coefficients of bovine serum albumin (BSA) and γ-Globulin (IgG) by means of fluorescence correlation spectroscopy (FCS) and Brownian dynamics (BD) simulation. BSA and IgG were used as tracers as well as crowding agents. The crystal structures of human and bovine serum albumin have a heart-shaped structure (14), whereas antibodies like IgG form a Y-shape. IgG has a much higher molecular mass (155 kDa) than BSA (66 kDa).
FCS is a highly sensitive optical method to measure the diffusion of fluorescently labeled molecules and their interactions in solution (15–19). FCS can be used to analyze fluorescence-intensity fluctuations arising from local concentration fluctuations of a low concentration solution (1 nM) of fluorescently labeled molecules. Because the measured correlation function reflects the kinetics of molecules diffusing in and out of the detection volume of a confocal microscope, it is an ideal analytical tool for studying molecular dynamics (20,21), concentration (15), chemical reaction kinetics (22), and the interactions of molecules at nanomolar concentrations (15,23–25). In the last decade, FCS has become a standard technique for studying diffusion, including anomalous diffusion and biomolecular interactions in crowded environments (12,26–29).
BD simulation is a computational technique that can be used to study the diffusion of macromolecules in solution on timescales from nanoseconds to hundreds of microseconds (30–32). In BD simulations, solvent molecules are treated implicitly. The inertia of the solute molecules is neglected under the assumption that the velocities of the diffusing solute particles relax much faster than the time interval used for the simulation analysis (33). In the model used here, the proteins are treated as atomically detailed rigid bodies moving in a continuum solvent.
Material and Methods
Sample preparation
Albumin from bovine serum (BSA), γ-Globulin (IgG) from bovine blood, and phosphate-buffered saline (PBS) were purchased from Sigma, Munich, Germany. γ-Globulin is referred to as IgG, because it is the main fraction (80%).
For titration experiments, the proteins were used without further purification and were dissolved in PBS to a wide range of concentrations (up to 400 g/L). The titration studies were performed with a small number of labeled proteins (tracer, ≪0.001 g/L) in a solution of unlabeled proteins (crowder, up to 400 g/L). For 0 g/L, the tracer proteins were dissolved in PBS. The final concentration of protein in 0g/L protein solution was <40 μg/L. Labeled proteins (BSA-633 and IgG-633) were prepared through covalent coupling of lysine residues with the amino-reactive n-hydroxysuccinimidyl ester derivative of the fluorescent dye Atto633 (see the Supporting Material).
Fluorescence correlation spectroscopy
The autocorrelation function describes the self-similarity of a measured signal within a certain time interval. The fluorescence fluctuation at time t is δF(t) = F(t) − 〈F(t)〉 and gives the deviation from the average fluorescence intensity (34). To analyze the fluorescence fluctuations δF(t), a normalized form of the autocorrelation function was used (22). The fluctuations of the fluorescence signal at time t were multiplied with the fluctuations of the signal shifted by a lag time τ. The correlation function G(τ) of the temporally changed fluorescence signal F(t) for a single species is defined as
| (1) |
The measured fluorescence autocorrelation functions G(τ) were fitted using the nonlinear least-squares method with a fitting program (OriginLab, Northampton, MA). The autocorrelation function G(τ) for a free three-dimensional diffusion single species with triplet state correction is given as (35)
| (2) |
with triplet state correction
| (3) |
and the translation diffusion-dependent term
| (4) |
In this equation, N is the total number of fluorescent particles in the detection volume element, which corresponds to 1/[G(0)−1]. The values z0 and w0 represent the radii of the axial and radial axis of the detection volume element.
is defined as the average lateral diffusion time, where Dt is the translational self-diffusion coefficient. The values T and τt are the fractional population and the relaxation time of the triplet state, respectively. The elongation and size of the volume were obtained by using the equation above. The calibration was done by measuring the diffusion time of Atto655-carboxylic acid in pure buffer and taking into account its translational diffusion coefficient (36).
Brownian dynamics simulations
BD simulations were performed with SDAMM (31), a parallelized program based on the SDA software (37) capable of handling many proteins treated as rigid bodies in atomic detail. The positions and orientations of the proteins were propagated using the Ermak-McCammon algorithm (33).
BD simulations were carried out using 250 protein molecules initially randomly positioned (avoiding overlaps) in a rectangular box with periodic boundary conditions. By using 250 proteins, each protein was surrounded by at least two nonperiodic proteins in each direction. The dimensions of the box were varied according to the concentration of the protein solution. Homogeneous solutions of BSA or IgG were simulated.
Each system was subjected to 6 μs of simulation at 300 K. Equilibration was assessed by monitoring the convergence of the radial distribution function and the stabilization of the energies. In all cases, 1 μs was sufficient to obtain an equilibrated system according to these criteria and the remaining 5 μs were used for the analysis. The integration timestep was 0.5 ps. The positions and orientations of the proteins were recorded along with energy values every 0.5 ns. Forces were computed as described below.
Interaction energies and forces
The forces between the proteins were computed as finite-difference derivatives of the pairwise free energies of interaction between the proteins. For each pair of proteins, the interaction free energy, ΔG1–2, was defined as
| (5) |
A detailed description and parameterization of Eq. 5 can be found in Mereghetti et al. (31) and Gabdoulline and Wade (38). In Eq. 5, Φel is the electrostatic potential computed by solution of the linearized Poisson-Boltzmann equation, Φedes is the electrostatic desolvation potential, Φnpdes is the nonpolar desolvation potential, and Esoftcore is the soft-core repulsion energies. The effective charges, q, are located on selected atoms in charged residues and derived from computation of the electrostatic potential with partial atomic charges assigned to all atoms (39), A are solvent-accessible surface areas, and the r notations are atomic coordinates. For computational efficiency, all interaction potentials, Φ, were mapped onto grids centered on the simulated proteins.
Hydrodynamic interactions
Hydrodynamic interactions (HI) are implemented in SDAMM using a mean field method (32,40–42). In this method, an isotropic short-time translational diffusion coefficient for a protein of a given type is assigned and rescaled based on the local volume fraction (ϕ) occupied by the proteins according to . The function f(ϕ), which describes the volume fraction-dependent, short-time translational diffusion coefficient, normalized by its infinite dilution value , is computed according to the model developed by Tokuyama and Oppenheim (43) which includes near-field as well as far-field hydrodynamic interactions (see Section S3 in the Supporting Material). Similarly, we took into account rotational HI by rescaling the short-time rotational diffusion coefficient using the model derived by Cichocki et al. (44), which includes lubrication forces as well as two- and three-body expansions of the mobility functions:
| (6) |
The rescaled values are then used in the Brownian dynamics simulations for updating the particle positions.
Protein preparation
Simulations of bovine serum albumin (BSA) solutions were performed using a three-dimensional structure of BSA obtained by homology modeling based on the crystal structure of human serum albumin (HSA) (14). The model was taken from MODBASE (45). Because of the high sequence identity (76%) between BSA and HSA, this model showed good quality as assessed using PROCHECK (46), ProQ (47), and AIDE (48). Further details about the model can be found in the Supporting Material. For the γ-Globulin simulations, we decided to consider only IgG as it represents the main fraction of the γ-Globulin in bovine blood (fraction 80%). Because the three-dimensional structure of bovine IgG is not available, we used the crystal structure of an intact mouse IgG (PDB:1IGT (49)) which has the highest resolution among the available intact IgG crystal structures.
Polar hydrogen atoms were added according to the specified pH and ionic strength using H++ (50). All simulations were performed at pH = 7 and ionic strength = 150 mM. At these conditions, the net charges of BSA and IgG are −16e and +3e, respectively. Partial atomic charges and radii were assigned to all atoms from the OPLS force field (51). Electrostatic potential grids Φ were computed by solving the linearized Poisson-Boltzmann equation using the UHBD software (52).
For BSA, nonpolar desolvation, electrostatic desolvation, and soft-core repulsion grids were set to 200 × 200 × 200 Å3 with a grid spacing of 1.0 Å, whereas the electrostatic potential grid size was set to 130 × 130 × 130 Å with a grid spacing of 1.0 Å. For the IgG, nonpolar desolvation, electrostatic desolvation, and soft-core repulsion grids were set to 190 × 190 × 190 Å3 with a grid spacing of 1.0 Å, whereas the electrostatic potential grid size was set to 200 × 200 × 200 Å3 with a grid spacing of 1.0 Å.
The infinite dilution values of the translational and rotational diffusion coefficients were computed using HYDROPRO from the protein atomic coordinates (53).
Analysis
Translational self-diffusion coefficient
The time-dependent, time ensemble-averaged, mean-squared translational displacement was computed using
| (7) |
where N′ is the number of proteins of the same type present in the simulation, τ is the time interval, tend is an integer multiple of τ, and ri(t) is the center of geometry of protein i at time t. In this article, will be simply denoted by msd.
A linear fit was performed on a closed interval [τ1, τ2], and the self-diffusion coefficient, Dt, was computed from the slope using the Einstein relation (see the Supporting Material). The results were compared with an analytical model developed by Tokuyama and Oppenheim (43) (see the Supporting Material) which describes the concentration dependence of the normalized long-time translational self-diffusion coefficient.
Computation of the anomalous exponent for translational diffusion
In complex media, the mean-square displacement of the protein position may deviate from the linear Stokes-Einstein relation, and obey a more general power-law behavior characterized by the exponent α (10). If α < 1, the dynamics is subdiffusive. On the other hand, when α > 1 the dynamics is superdiffusive. The exponent α was computed by a least-square fit of the curve log(msd/τ) versus log(τ). For details of the computation of the α-exponent, see the Supporting Material.
Rotational diffusion coefficient
The rotational diffusion coefficient was obtained by first computing the time-ensemble averaged autocorrelation function of the protein orientation vectors e(t) and then fitting it with a single exponential of the form (see the Supporting Material). Alternatively, as described in Mazza et al. (54), the long-time rotational diffusion coefficient was computed from the ensemble-averaged rotational mean-squared displacement (see the Supporting Material).
Oligomer analysis
The average fractions of oligomeric species were computed by recording the occurrence of the oligomeric states at each step of the simulation and then averaging over the total number of steps. The criteria used to define an oligomer and the details of the computation can be found in the Supporting Material.
Results and Discussion
Translational self-diffusion coefficient
The translational self-diffusion coefficients (Dt) of IgG and BSA were determined from FCS measurements and computed from BD simulations at several protein concentrations.
To exemplify the results of the FCS measurements, Fig. 1 (left panel) shows three measured normalized autocorrelation curves of BSA-633 in 0 g/L, 150 g/L, and 300 g/L BSA solution. The short-time fluctuations in the curve with 300 g/L BSA are within the standard deviation of the 10 repetitions. Moreover, the systematic measurement error, the optical aberration due to refractive index variation, is within the accuracy of the standard FCS technique (55). The diffusion coefficients determined from the FCS measurements are shown in Fig. 1. The normalized translational diffusion coefficients Dt/Dt0 of the tracer proteins, BSA-633 (solid symbols) and IgG-633 (open symbols), are plotted as a function of protein volume fraction. Plots are for crowder solutions of BSA with a maximum concentration of 400 g/L (black symbols) and IgG with a maximum concentration of 200 g/L (gray symbols). The tracer mobility was reduced by increasing the crowder concentration, resulting in a corresponding decrease in the translational diffusion coefficient. A distinctly faster decay was visible for the IgG crowder solution than for BSA solution.
Figure 1.
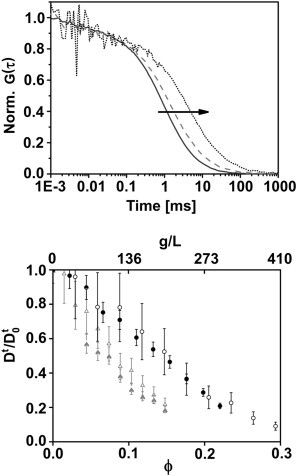
(Top) Exemplary normalized FCS curves. Each curve is an average of ten 60-s acquisitions of BSA-633 in BSA solution with increasing protein concentration shown without error bars for clarity. The average diffusion time increased with the BSA concentration: 0 g/L (solid line), 150 g/L (shaded dashed line), and 300 g/L (dotted line). (Bottom) Normalized translational diffusion coefficients of labeled BSA and IgG in the corresponding protein solutions measured with FCS by titration of BSA-633 (solid symbols) and IgG-633 (open symbols) in up to 400 g/L BSA solution (solid symbols) and up to 200 g/L IgG solution (shaded symbols).
Because the dependence on crowder type appears more important than the dependence on the tracer type, simulations were performed using homogeneous protein solutions, i.e., BSA in BSA and IgG in IgG. In Fig. 2, experimental and computed values of the concentration-dependent translational diffusion coefficients are compared to an analytical model derived by Tokuyama et al. (56) which considers spherical particles interacting by a soft-core potential as well as many body near-field and far-field hydrodynamic interactions. The comparison with the long-time self-diffusion coefficient obtained using the Tokuyama analytical model helps to explain what causes the reduction of the diffusion coefficient.
Figure 2.
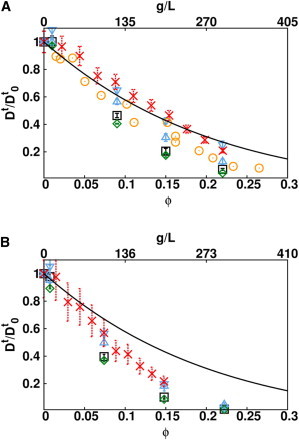
Normalized long-time translational self-diffusion coefficient of BSA (A) and IgG (B). Experimental values obtained in this work using FCS (red crosses) and, for BSA, by pulsed-gradient spin-echo NMR by Nesmelova et al. (57) (orange circles) are shown. The values computed from BD simulations with direct interactions and t-HI and r-HI (green diamonds), with direct interactions and t-HI (black squares), with soft-core and t-HI (blue up-triangles), and with soft-core interactions only (blue down-triangles) are shown. (Black continuous lines) Diffusion coefficient computed from the analytical model of Tokuyama et al. (56).
For BSA (Fig. 2 A), two sets of experimental data are shown, one obtained in this work using FCS (red crosses), the other (orange circles) obtained by pulsed-gradient spin-echo NMR by Nesmelova et al. (57). General agreement between the two experimental measurements is evident although a deviation appears at intermediate concentrations (0.1–0.15 ϕ). In BD simulations, the role of the different interaction terms can be revealed by including or omitting such terms in the simulations. We performed four sets of simulations: one including direct interactions, defined by Eq. 5, plus translational (t-HI) and rotational (r-HI) hydrodynamic interactions (the abbreviation HI means t-HI plus r-HI); a second set including direct and t-HI; a third set including soft-core interactions and t-HI; and finally, a set performed with the soft-core energy term only. As expected, on both BSA and IgG, rotational hydrodynamics have a negligible effect on the translational diffusion coefficient. Simulations with direct and HI give similar results to with soft-core and t-HI (within the error bars). On the other hand, when only the soft-core interactions are considered, the diffusion coefficients are overestimated. This suggests a minor role for direct interactions and HI in determining the translational diffusion coefficient. The values obtained from BD simulations, which include the direct and HI as well as the experimental values, deviate from the analytical model for concentrations above 0.15 volume fraction. When all but the soft-core terms are switched off, the diffusion coefficients are close to the analytical model curve, implying that the diffusion of BSA resembles that of a soft sphere.
More pronounced effects leading to similar conclusions are observed for IgG. In this case, a strong deviation from the analytical model is observed for experimental and computed diffusion coefficients, especially for concentrations above 0.1 ϕ. As can be seen in Fig. 2 B, very similar Dt values are obtained from the simulations with the soft-core only or including direct interactions and HI, which implies that the shape is the main factor responsible for the strong reduction of the translational diffusion coefficient. The HI tends to slightly lower the translational diffusion coefficients.
A significant improvement in the quality of fit of the experimental data by considering subdiffusion could not be observed for either of the proteins and would be small relative to the large systematic error (Fig. 1). Small deviations from normal diffusion measured by FCS could be explained by optical artifacts (28,58). To check for the possibility of subdiffusion, we computed the anomalous exponent, α, from the BD simulations.
Transient anomalous diffusion
The computed time-dependent diffusional properties were analyzed by examining plots of log(msd/τ) versus log(τ). By fitting these curves at given closed intervals, the anomalous exponent, α, was derived for different time regimes. Moreover, the crossover time, i.e., the time associated with a change from anomalous to normal diffusion (59), was obtained. A slope = 0, which corresponds to α = 1, reflects a normal diffusion process whereas a slope < 0 is associated with anomalous subdiffusive behavior. Significant deviation from normal diffusion appears for concentrations > 200 g/L (see Fig. 3 and Fig. S1 in the Supporting Material). For BSA, an appreciable deviation can be detected in the simulations at 300 g/L, whereas for IgG transient subdiffusive behavior was observed at 200 g/L as well.
Figure 3.
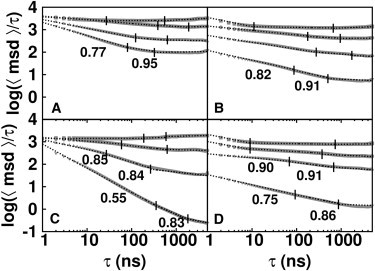
Computation of the anomalous diffusion exponent, α. Values computed from the BD simulations of log(msd/τ) are plotted against τ on a logarithmic scale for solutions at different concentrations. Concentration decreases from bottom to top (300, 203, 116, and 10 g/L for BSA and 300, 200, 100, and 10 g/L for IgG). The results for BD simulations with the soft-core interaction term only (A and C) and with the full interaction terms (B and D) are shown. Results of simulations of BSA are shown in panels A and B whereas those of IgG are shown in panels C and D. The α-exponent and the boundaries of the fitting intervals are shown on the plot.
Two diffusional regimes can be distinguished: an anomalous regime on the submicrosecond timescale and a normal diffusion regime on longer timescales. The crossover time (τc) varies depending on the concentration and it is in general longer for IgG compared to BSA, as indicated in Fig. 3. By comparing the simulations with direct interactions plus HI with the soft-core term only, we observe that the transient anomalous diffusion occurs in both cases (compare panels B and D with panels A and C in Fig. 3). Hence, we suggest that, for these systems, the subdiffusion is mainly determined by the steric effects of the crowder molecules. Moreover, we can observe that the presence of direct interactions increases the α-exponent resulting in less anomalous behavior. To explain this behavior, we should consider the formation of transient oligomers. When direct interactions are present, oligomers form in the solution in a concentration-dependent manner (see Transient Cluster Formation). Each monomer moves in a polydisperse medium where the oligomers can dynamically vary their size and the monomer itself can be transiently part of the oligomers. This implies that at short timescales on the order of the lifetime of the oligomers, diffusion is more strongly affected by increasing the concentration compared to simulations without direct interactions where no oligomers are formed. Indeed, comparison of panels B and D with panels A and C in Fig. 3 shows that the values of log(msd/τ) at short timescales are lower when direct interactions are computed. The formation of oligomers then leads to a faster convergence of the diffusion coefficient to its long-time value, explaining the less anomalous behavior in simulations with direct interactions.
Rotational diffusion coefficient
The simulations show that the short-time rotational diffusion coefficients of both BSA and IgG decrease markedly as protein concentration increases (see Fig. 4). For BSA, direct interactions have an important effect on the rotational diffusion coefficient. At the highest concentration, 300 g/L, the computed rotational diffusion coefficient is threefold lower in simulations with direct interactions compared to the simulations without direct interactions. Hydrodynamic interactions, when applied to the translational diffusion only, have an almost negligible effect on the rotational diffusion. However, the inclusion of rotational hydrodynamic interactions shows a modest effect, further reducing the rotational diffusion coefficient. For IgG, the concentration-dependent decrease in the rotational diffusion coefficient is even stronger than for BSA. But unlike BSA, the strong decrease in the rotational diffusion coefficient is almost completely due to the steric effects of the protein crowders. Indeed, simulations performed with the soft-core term only, show values of the rotational diffusion coefficients similar to those obtained including the direct plus rotational and translational HI. As for BSA, translational hydrodynamic interactions have a negligible effect. Very similar behavior is observed for the long-time rotational diffusion coefficient (see Fig. S2), implying that correlations are not seen beyond a few hundred nanoseconds.
Figure 4.
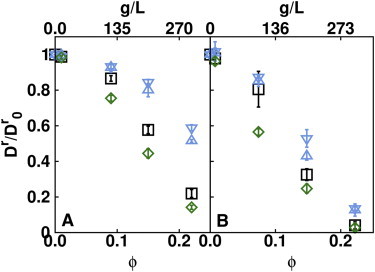
Normalized rotational diffusion coefficients of BSA (A) and IgG (B) estimated from the correlation function of protein orientations obtained in the BD simulations. The simulations were performed with direct interactions plus r-HI and t-HI (green diamonds), direct interactions with t-HI (black squares), soft-core plus t-HI (blue down-triangles), and soft-cores only (blue up-triangles).
Transient cluster formation
To further investigate the role of direct interactions (electrostatics and nonpolar desolvation) in determining the dynamics of the proteins in solution, we checked for the presence and formation of protein oligomers during the simulations. We restrict our discussion here to the analysis of oligomer formation in the IgG solutions; analogous conclusions can be drawn for BSA (see Fig. S3). As shown in Fig. 5 A, oligomer formation is observed to be concentration-dependent. The increase in the osmotic pressure, due to the increase in the concentration, allows the small electrostatic repulsion between the proteins to be overcome, resulting in short-range attractive interactions. From an analysis of oligomer formation in the simulations with only the soft-core repulsion term, using the same contact parameters as applied to the analysis of the simulations with direct interaction terms, we found that the simulations with the soft-core term only result in 99% of the proteins being in the monomer state at all concentrations. This observation indicates that the oligomers found in the simulations with direct interactions depend on the formation of true contacts (see Fig. S4). It should be noted that the oligomers formed in the simulations are diffusional encounter complexes. The absence of the treatment of internal flexibility and hydrogen bonds hinders the formation of fully bound oligomers. To characterize the oligomers found in the simulations, we computed their lifetimes (see Fig. 5 B). If the lifetime of an oligomer is much shorter than the time that it needs to diffuse one protein diameter, , the oligomer can be defined as transient and the dynamics will be essentially determined by the monomers (60). The diffusional relaxation time, , can be estimated as , where a is the hydrodynamic radius of a monomer and is its diffusion coefficient. For IgG, we assumed a hydrodynamic radius of 55.29 Å (estimated using HYDROPRO (53)), which gives a of 760 ns. The lifetimes of the oligomeric species shown in Fig. 5 B are at least one order of magnitude smaller than the diffusional time , indicating that oligomer formation is in the transient regime. Due to the rapid dissociation of the oligomers, the long-time dynamics are only slightly affected by oligomerization, as shown by the small reduction of the long-time diffusion coefficients that occurs when direct interactions are switched on (see Fig. 2).
Figure 5.
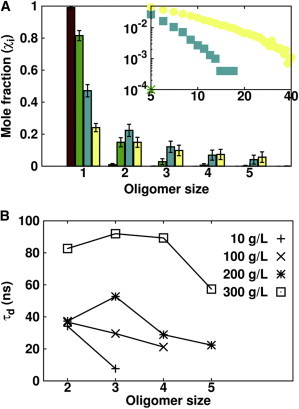
Transient oligomer formation in BD simulations of IgG solutions. (A) Average mole fractions of IgG oligomers up to pentamers observed in simulations at 10 g/L (dark red), 100 g/L (green), 200 g/L (blue), and 300 g/L (pale yellow) concentrations. Mole fractions of oligomers larger than or equal to pentamers are shown (inset) on a log-log scale (only present for concentrations ≥ to 200 g/L). (B) Oligomer dissociation times for IgG at different volume fractions. If a value is not plotted, e.g., the tetramers or pentamers at the lowest concentrations, it means that they form in too low a concentration to give reliable dissociation times.
Concluding Discussion
The measured and computed translational diffusion coefficients for systems with BSA and IgG as crowding solutions show good agreement. The simulations show that the strong concentration dependence of the translational diffusion coefficient observed experimentally for BSA and IgG solutions is mainly determined by the steric effect of the crowder proteins, which depends on both the excluded volume and the shape of the crowders. Indeed, the experimental translational diffusion coefficients can be quantitatively reproduced by means of BD simulations that only include the soft-core interaction term between the molecules. The concentration dependence of the translational diffusion coefficient of IgG could not be reproduced by an analytical model in which the protein is assumed to be spherical, underlining the important contribution of shape to translational diffusion. Given the good correspondence of the translational diffusion coefficients determined experimentally and computed from BD simulations, simulation data were analyzed to examine how the rotational diffusion coefficient and the transient oligomer formation depend on the properties of the crowder solution. We were not able to obtain rotational diffusion coefficients from time-resolved anisotropy measurements in the appropriate crowder concentration range for the proteins investigated here, possibly because different rotamer conformations of the Atto633 label lead to multiple lifetimes or because oligomer formation affects the lifetime of the fluorescence of the label.
The computed rotational diffusion coefficients also display a strong dependence on crowder concentration. However, whereas the rotational diffusion coefficient decreases strongly with increasing IgG crowder concentration because of the Y-shape of the molecule, for the more spherical BSA, the rotational diffusion coefficient is determined by both steric effects (excluded volume) and direct interactions. Moreover, for the systems studied, our results show that hydrodynamic interactions have a relatively minor role in determining diffusion properties. Oligomerization was dependent on the presence of direct interactions between the proteins. The extent of oligomerization was concentration-dependent but, at all concentrations studied, it was transient and therefore had little impact on the long-time translational diffusion. We conclude that the excluded volume and shape of crowder macromolecules are key determinants of the diffusional motion of (tracer) proteins.
Acknowledgments
This work was supported by the Klaus Tschira Foundation and the Center for Modelling and Simulation in the Biosciences in Heidelberg, and a grant for supercomputing time at the Environmental Molecular Science Laboratory (grant No. 30994). We also thank the Deutsche Forschungsgemeinschaft for financial support (DFG grants No. GRK 1114 and No. EXC 81).
We acknowledge M. Martinez (Heidelberg Institute for Theoretical Studies, Heidelberg), M. Weiss, and M. Hellmann (Center for Modelling and Simulation in the Biosciences, Heidelberg) for many valuable discussions. We are grateful to S.T. Schwaebel for assistance in the FCS data acquisition used in this article.
Supporting Material
References
- 1.Morelli M.J., Allen R.J., Wolde P.R.T. Effects of macromolecular crowding on genetic networks. Biophys. J. 2011;101:2882–2891. doi: 10.1016/j.bpj.2011.10.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Elcock A.H. Models of macromolecular crowding effects and the need for quantitative comparisons with experiment. Curr. Opin. Struct. Biol. 2010;20:196–206. doi: 10.1016/j.sbi.2010.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wang Y., Li C., Pielak G.J. Effects of proteins on protein diffusion. J. Am. Chem. Soc. 2010;132:9392–9397. doi: 10.1021/ja102296k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhou H.-X., Rivas G., Minton A.P. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Annu. Rev. Biophys. 2008;37:375–397. doi: 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Phillip Y., Sherman E., Schreiber G. Common crowding agents have only a small effect on protein-protein interactions. Biophys. J. 2009;97:875–885. doi: 10.1016/j.bpj.2009.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dix J.A., Verkman A.S. Crowding effects on diffusion in solutions and cells. Annu. Rev. Biophys. 2008;37:247–263. doi: 10.1146/annurev.biophys.37.032807.125824. [DOI] [PubMed] [Google Scholar]
- 7.Luby-Phelps K. Cytoarchitecture and physical properties of cytoplasm: volume, viscosity, diffusion, intracellular surface area. Int. Rev. Cytol. 2000;192:189–221. doi: 10.1016/s0074-7696(08)60527-6. [DOI] [PubMed] [Google Scholar]
- 8.Ellis R.J. Macromolecular crowding: obvious but underappreciated. Trends Biochem. Sci. 2001;26:597–604. doi: 10.1016/s0968-0004(01)01938-7. [DOI] [PubMed] [Google Scholar]
- 9.Geyer T. Mixing normal and anomalous diffusion. J. Chem. Phys. 2012;137:115101. doi: 10.1063/1.4753804. [DOI] [PubMed] [Google Scholar]
- 10.Guigas G., Weiss M. Sampling the cell with anomalous diffusion—the discovery of slowness. Biophys. J. 2008;94:90–94. doi: 10.1529/biophysj.107.117044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ellis R.J., Minton A.P. Cell biology: join the crowd. Nature. 2003;425:27–28. doi: 10.1038/425027a. [DOI] [PubMed] [Google Scholar]
- 12.Zorrilla S., Lillo M.P. Quantitative investigation of biomolecular interactions in crowded media by fluorescence spectroscopy, a good choice. Curr. Protein Pept. Sci. 2009;10:376–387. doi: 10.2174/138920309788922225. [DOI] [PubMed] [Google Scholar]
- 13.Zimmerman S.B., Minton A.P. Macromolecular crowding: biochemical, biophysical, and physiological consequences. Annu. Rev. Biophys. Biomol. Struct. 1993;22:27–65. doi: 10.1146/annurev.bb.22.060193.000331. [DOI] [PubMed] [Google Scholar]
- 14.Wardell M., Wang Z., Carter D.C. The atomic structure of human methemalbumin at 1.9 Å. Biochem. Biophys. Res. Commun. 2002;291:813–819. doi: 10.1006/bbrc.2002.6540. [DOI] [PubMed] [Google Scholar]
- 15.Elson E.L.L. Fluorescence correlation spectroscopy: past, present, future. Biophys. J. 2011;101:2855–2870. doi: 10.1016/j.bpj.2011.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Medina M.A., Schwille P. Fluorescence correlation spectroscopy for the detection and study of single molecules in biology. Bioessays. 2002;24:758–764. doi: 10.1002/bies.10118. [DOI] [PubMed] [Google Scholar]
- 17.Rigler R., Kask P. Fluorescence correlation spectroscopy with high count rate and low background: analysis of translational diffusion. Chem. Phys. 1993;22:169–175. [Google Scholar]
- 18.Jameson D.M., Ross J.A., Albanesi J.P. Fluorescence fluctuation spectroscopy: ushering in a new age of enlightenment for cellular dynamics. Biophys Rev. 2009;1:105–118. doi: 10.1007/s12551-009-0013-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zustiak S.P., Nossal R., Sackett D.L. Hindered diffusion in polymeric solutions studied by fluorescence correlation spectroscopy. Biophys. J. 2011;101:255–264. doi: 10.1016/j.bpj.2011.05.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Braeckmans K., Deschout H., Demeester J. Measuring molecular dynamics by FRAP, FCS, and SPT. In: Diaspro A., editor. Optical Fluorescence Microscopy. Springer; Berlin: 2011. pp. 153–163. [Google Scholar]
- 21.Krichevsky O., Bonnet G. Fluorescence correlation spectroscopy: the technique and its applications. Rep. Prog. Phys. 2002;65:251–297. [Google Scholar]
- 22.Magde D., Elson E.L., Webb W.W. Fluorescence correlation spectroscopy. II. An experimental realization. Biopolymers. 1974;13:29–61. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- 23.Kim S.A., Heinze K.G., Schwille P. Fluorescence correlation spectroscopy in living cells. Nat. Methods. 2007;4:963–973. doi: 10.1038/nmeth1104. [DOI] [PubMed] [Google Scholar]
- 24.Haustein E., Schwille P. Ultrasensitive investigations of biological systems by fluorescence correlation spectroscopy. Methods. 2003;29:153–166. doi: 10.1016/s1046-2023(02)00306-7. [DOI] [PubMed] [Google Scholar]
- 25.Wawrezinieck L., Lenne P.-F., Rigneault H. Fluorescence correlation spectroscopy to determine diffusion laws: application to live cell membranes. Proc. SPIE, Biophotonics Micro- and Nano-Imaging. 2004;5462:92–102. [Google Scholar]
- 26.Dauty E., Verkman A.S. Molecular crowding reduces to a similar extent the diffusion of small solutes and macromolecules: measurement by fluorescence correlation spectroscopy. J. Mol. Recognit. 2004;17:441–447. doi: 10.1002/jmr.709. [DOI] [PubMed] [Google Scholar]
- 27.Ushida K., Tokuyama M., Nishiyama H. Anomalous diffusion in polymer solution as probed by fluorescence correlation spectroscopy and its universal importance in biological systems. AIP Conf. Proc. 2008;982:464–469. [Google Scholar]
- 28.Malchus N., Weiss M. Elucidating anomalous protein diffusion in living cells with fluorescence correlation spectroscopy—facts and pitfalls. J. Fluoresc. 2010;20:19–26. doi: 10.1007/s10895-009-0517-4. [DOI] [PubMed] [Google Scholar]
- 29.Weiss M., Elsner M., Nilsson T. Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells. Biophys. J. 2004;87:3518–3524. doi: 10.1529/biophysj.104.044263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.McGuffee S.R., Elcock A.H. Atomically detailed simulations of concentrated protein solutions: the effects of salt, pH, point mutations, and protein concentration in simulations of 1000-molecule systems. J. Am. Chem. Soc. 2006;128:12098–12110. doi: 10.1021/ja0614058. [DOI] [PubMed] [Google Scholar]
- 31.Mereghetti P., Gabdoulline R.R., Wade R.C. Brownian dynamics simulation of protein solutions: structural and dynamical properties. Biophys. J. 2010;99:3782–3791. doi: 10.1016/j.bpj.2010.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mereghetti P., Wade R.C. Atomic detail Brownian dynamics simulations of concentrated protein solutions with a mean field treatment of hydrodynamic interactions. J. Phys. Chem. B. 2012;116:8523–8533. doi: 10.1021/jp212532h. [DOI] [PubMed] [Google Scholar]
- 33.Ermak D.L., McCammon J.A. Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 1978;69:1352–1360. [Google Scholar]
- 34.Magde D., Elson E., Webb W.W. Thermodynamic fluctuations in a reacting system - measurement by fluorescence correlation spectroscopy. Phys. Rev. Lett. 1972;29:705–708. [Google Scholar]
- 35.Widengren J., Rigler R., Mets U. Triplet-state monitoring by fluorescence correlation spectroscopy 1. J. Fluoresc. 1994;4:255–258. doi: 10.1007/BF01878460. [DOI] [PubMed] [Google Scholar]
- 36.Dertinger T., Pacheco V., Enderlein J. Two-focus fluorescence correlation spectroscopy: a new tool for accurate and absolute diffusion measurements. ChemPhysChem. 2007;8:433–443. doi: 10.1002/cphc.200600638. [DOI] [PubMed] [Google Scholar]
- 37.Gabdoulline R.R., Wade R.C. Simulation of the diffusional association of barnase and barstar. Biophys. J. 1997;72:1917–1929. doi: 10.1016/S0006-3495(97)78838-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gabdoulline R.R., Wade R.C. On the contributions of diffusion and thermal activation to electron transfer between Phormidium laminosum plastocyanin and cytochrome f: Brownian dynamics simulations with explicit modeling of nonpolar desolvation interactions and electron transfer events. J. Am. Chem. Soc. 2009;131:9230–9238. doi: 10.1021/ja809567k. [DOI] [PubMed] [Google Scholar]
- 39.Gabdoulline R.R., Wade R.C. Effective charges for macromolecules in solvent. J. Phys. Chem. 1996;100:3868–3878. [Google Scholar]
- 40.Heyes D. Mean-field hydrodynamics Brownian dynamics simulations of stabilized colloidal liquids under shear. J. Non-Newt. Fluid Mech. 1997;68:101–124. [Google Scholar]
- 41.Urbina-Villalba G., García-Sucre M., Toro-Mendoza J. Average hydrodynamic correction for the Brownian dynamics calculation of flocculation rates in concentrated dispersions. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2003;68:061408. doi: 10.1103/PhysRevE.68.061408. [DOI] [PubMed] [Google Scholar]
- 42.Sun J., Weinstein H. Toward realistic modeling of dynamic processes in cell signaling: quantification of macromolecular crowding effects. J. Chem. Phys. 2007;127:155105. doi: 10.1063/1.2789434. [DOI] [PubMed] [Google Scholar]
- 43.Tokuyama M., Oppenheim I. Dynamics of hard-sphere suspensions. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1994;50:R16–R19. doi: 10.1103/physreve.50.r16. [DOI] [PubMed] [Google Scholar]
- 44.Cichocki B., Ekiel-Jezewska M., Wajnryb E. Lubrication corrections for three-particle contribution to short-time self-diffusion coefficients in colloidal dispersions. J. Chem. Phys. 1999;111:3265–3273. [Google Scholar]
- 45.Pieper U., Eswar N., Sali A. MODBASE, a database of annotated comparative protein structure models and associated resources. Nucleic Acids Res. 2011;37:D347–D354. doi: 10.1093/nar/gkn791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Laskowski R.A., MacArthur M.W., Thornton J.M. PROCHECK: a program to check the stereochemical quality of protein structures. J. Appl. Cryst. 1993;26:283–291. [Google Scholar]
- 47.Wallner B., Elofsson A. Can correct protein models be identified? Protein Sci. 2003;12:1073–1086. doi: 10.1110/ps.0236803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Mereghetti P., Ganadu M.L., De Gioia L. Validation of protein models by a neural network approach. BMC Bioinformatics. 2008;9:66. doi: 10.1186/1471-2105-9-66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Harris L.J., Larson S.B., McPherson A. Refined structure of an intact IgG2a monoclonal antibody. Biochemistry. 1997;36:1581–1597. doi: 10.1021/bi962514+. [DOI] [PubMed] [Google Scholar]
- 50.Gordon J.C., Myers J.B., Onufriev A. H++: a server for estimating pKas and adding missing hydrogens to macromolecules. Nucleic Acids Res. 2005;33(Web Server issue):W368–W371. doi: 10.1093/nar/gki464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Jorgensen W.L., Tirado-Rives J. The OPLS (optimized potentials for liquid simulations) potential functions for proteins, energy minimizations for crystals of cyclic peptides and crambin. J. Am. Chem. Soc. 1988;110:1657–1666. doi: 10.1021/ja00214a001. [DOI] [PubMed] [Google Scholar]
- 52.Madura J.D., Briggs J.M., McCammon J.A. Electrostatics and diffusion of molecules in solution: simulations with the University of Houston Brownian dynamics program. Comput. Phys. Commun. 1995;91:57–95. [Google Scholar]
- 53.García De La Torre J., Huertas M.L., Carrasco B. Calculation of hydrodynamic properties of globular proteins from their atomic-level structure. Biophys. J. 2000;78:719–730. doi: 10.1016/S0006-3495(00)76630-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Mazza M.G., Giovambattista N., Starr F.W. Connection of translational and rotational dynamical heterogeneities with the breakdown of the Stokes-Einstein and Stokes-Einstein-Debye relations in water. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;76:031203. doi: 10.1103/PhysRevE.76.031203. [DOI] [PubMed] [Google Scholar]
- 55.von der Hocht I., Enderlein J. Fluorescence correlation spectroscopy in cells: confinement and excluded volume effects. Exp. Mol. Pathol. 2007;82:142–146. doi: 10.1016/j.yexmp.2006.12.009. [DOI] [PubMed] [Google Scholar]
- 56.Tokuyama M., Moriki T., Kimura Y. Self-diffusion of biomolecules in solution. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2011;83:051402. doi: 10.1103/PhysRevE.83.051402. [DOI] [PubMed] [Google Scholar]
- 57.Nesmelova I.V., Skirda V.D., Fedotov V.D. Generalized concentration dependence of globular protein self-diffusion coefficients in aqueous solutions. Biopolymers. 2002;63:132–140. doi: 10.1002/bip.10023. [DOI] [PubMed] [Google Scholar]
- 58.Hess S.T., Huang S., Webb W.W. Biological and chemical applications of fluorescence correlation spectroscopy: a review. Biochemistry. 2002;41:697–705. doi: 10.1021/bi0118512. [DOI] [PubMed] [Google Scholar]
- 59.Vilaseca E., Isvoran A., Mas F. New insights into diffusion in 3D crowded media by Monte Carlo simulations: effect of size, mobility and spatial distribution of obstacles. Phys. Chem. Chem. Phys. 2011;13:7396–7407. doi: 10.1039/c0cp01218a. [DOI] [PubMed] [Google Scholar]
- 60.Liu Y., Porcar L., Baglioni P. Lysozyme protein solution with an intermediate range order structure. J. Phys. Chem. B. 2011;115:7238–7247. doi: 10.1021/jp109333c. [DOI] [PubMed] [Google Scholar]
- 61.Zhang Y., Skolnick J. Scoring function for automated assessment of protein structure template quality. Proteins. 2004;57:702–710. doi: 10.1002/prot.20264. [DOI] [PubMed] [Google Scholar]
- 62.Levitt M., Gerstein M. A unified statistical framework for sequence comparison and structure comparison. Proc. Natl. Acad. Sci. USA. 1998;95:5913–5920. doi: 10.1073/pnas.95.11.5913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Majorek K.A., Porebski P.J., Minor W. Structural and immunologic characterization of bovine, horse, and rabbit serum albumins. Mol. Immunol. 2012;52:174–182. doi: 10.1016/j.molimm.2012.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Bujacz A. Structures of bovine, equine and leporine serum albumin. Acta Crystallogr. D Biol. Crystallogr. 2012;68:1278–1289. doi: 10.1107/S0907444912027047. [DOI] [PubMed] [Google Scholar]
- 65.Gabdoulline R.R., Wade R.C. Brownian dynamics simulation of protein-protein diffusional encounter. Methods. 1998;14:329–341. doi: 10.1006/meth.1998.0588. [DOI] [PubMed] [Google Scholar]
- 66.Pace C.N., Vajdos F., Gray T. How to measure and predict the molar absorption coefficient of a protein. Protein Sci. 1995;4:2411–2423. doi: 10.1002/pro.5560041120. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


