Abstract
Complex systems, arising in many contexts in the computer, life, social, and physical sciences, have not shared a generally-accepted complexity measure playing a fundamental role as the Shannon entropy H in statistical mechanics. Superficially-conflicting criteria of complexity measurement, i.e. complexity-randomness (C-R) relations, have given rise to a special measure intrinsically adaptable to more than one criterion. However, deep causes of the conflict and the adaptability are not much clear. Here I trace the root of each representative or adaptable measure to its particular universal data-generating or -regenerating model (UDGM or UDRM). A representative measure for deterministic dynamical systems is found as a counterpart of the H for random process, clearly redefining the boundary of different criteria. And a specific UDRM achieving the intrinsic adaptability enables a general information measure that ultimately solves all major disputes. This work encourages a single framework coving deterministic systems, statistical mechanics and real-world living organisms.
A widely-appropriate complexity measure is needed in numerous areas1,2,3,4, for directly applications or for a unified theoretical framework like statistical mechanics5. To date, except some special cases6,7,8, most calculable complexity measures are superficially classified into three types (I, II, and III) depending on three C-R relations: a monotonically ascending curve, a convex curve, and a monotonically descending curve, respectively8. Competition is mainly between the type-I and the type-II. According to many type-II supporters, highly complex systems like human brains evidently exist at a critical transition point between randomness (or deterministic chaos) and regularity called the edge of chaos or weak chaos9,10,11,12,13, and then an ideal type-II measure should regard an object of weak chaos as the most complex and low-periodic objects and completely-chaotic objects the simplest, despite most type-II measures, e.g. the logical depth14, do not suffice.
There is another deeper but perhaps not strictly accurate classification. Deterministic measures are usually estimations of the incomputable concept Kolmogorov complexity3 (KC), the uncompressible information account of individual object defined as the length of the minimal computer program that regenerates the object; while statistical measures are chiefly derived from H for systems describable in probabilistic language9,10. A quantity is called extensive if it scales (asymptotically) with the size rw of the random word (string) 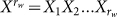 that describes the system under consideration15. In an isolated system, H is extensive, whereas even some statistical measures appear not9. Then disputes arise.
that describes the system under consideration15. In an isolated system, H is extensive, whereas even some statistical measures appear not9. Then disputes arise.
Amazingly, a recently-introduced deterministic measure lattice complexity CL exhibits intrinsic adaptability to various C-R relations6,7, even a degree of sensitivity to weak chaos, implying an ultimate solution of all above-mentioned disputes. For a deterministic α-nary symbol string s, intrinsic adaptability with a parameter r needs only treating all (overlapping) length-r words in s as αr-nary symbols for specific measures' calculation; while extrinsic adaptability needs extra variables and operations to show two existing different-type measures' behavior alone or jointly8. Traditionally, r is related to rw, because s is often considered a collection of outcomes of a length-r random word, and a statistical form of intrinsic adaptability may help to find the proper theoretic fundamental.
In this article, C2, a statistical measure previously known as of type II16,17, is found of somewhat intrinsic C-R adaptability. Further analysis reveals a contradiction between the adaptability and the random UDGM (r-UDGM), i.e. random process, in which entropies are exclusively rooted. With the nonlinear deterministic iterative system being identified as the deterministic UDGM (d-UDGM) that can generate any arbitrary symbol string as the traditional r-UDGM can, the C-R competition is clarified. A particular UDRM containing both r- and d-UDGM is shown to unit major competing ideas of complexity measurement naturally in an estimation of KC.
Results
Deterministic adaptable complexity
With its widely-used type-I estimation Lempel-Ziv complexity18 (CLZ), KC is traditionally considered a measure of randomness3,10,19. Although this judgment is valid for random objects, the adaptable estimation CL reveals more aspects of KC.
Both CLZ and CL simulate a machine reading the given string s over a finite alphabet  continuously into an unlimited memory. Alongside the reading procedure, both algorithms virtually separate s into uncompressible units and count the unit number as the complexity value of s. The present
unit is one such that has a present symbol just being read. It can still be compressible and then extendable.
continuously into an unlimited memory. Alongside the reading procedure, both algorithms virtually separate s into uncompressible units and count the unit number as the complexity value of s. The present
unit is one such that has a present symbol just being read. It can still be compressible and then extendable.
Compressibility is reduced to duplicability in CLZ. If the present unit can be duplicated from any section of the exhaustive memory including the already-read part of the unit itself, the duplication operation extends the unit simply symbol by symbol until no section of the memory equals the unit. At that time the present symbol is regarded as an insertion making the present unit uncompressible and the next unit, with its first symbol, will become the present (see the example below).
In CL, a present-unit-extending mechanism prior to the duplication is the deterministic iterative map on 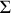 following either chaotic (no-symbol-repeating) rule or periodic rule. Iterations of such map are regarded as compressible as duplications, inspired by the fact that short-program-described iterative systems, e.g. logistic maps20, can produce any symbolic sequence out of chaotic or periodic orbits.
following either chaotic (no-symbol-repeating) rule or periodic rule. Iterations of such map are regarded as compressible as duplications, inspired by the fact that short-program-described iterative systems, e.g. logistic maps20, can produce any symbolic sequence out of chaotic or periodic orbits.
For example, let s = 0010001100 11010111 and the dot and the sign “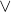 ” denote the insertion in CLZ and CL, respectively. The results are as follows:
” denote the insertion in CLZ and CL, respectively. The results are as follows:
According to CLZ, the first symbol is always an insertion without prefix. The second has a duplicable prototype in the memory, but the third makes the unit 01 does not match the exhaustive memory 00. The fourth and fifth symbols 00 together can be duplicated from the previous symbols 0010, while the sixth can not, because 000 has no prototype in 00100. Three following uncompressible units are 11, 001101 and 0111. Since there are 6 separated units, CL (s) = 6.
According to CL, the first two symbols 00 are generated by a 1-period iteration, but the third symbol 1 interrupts the iteration. Because 001 is not duplicable, it is an uncompressible unit. The next unit 0001 is identified similarly. Concerning the third unit 1001, since the first two symbols 1 and 0 are different from each other, they should be assumed following chaotic rule; the third symbol 0 implies that a periodic rule is employed with an initial state 1. After a periodic rule is broken, neither 1001 nor its follower unit 101011 is found duplicable. With the last unit 1 being separated, we see CL (s) = 5.
Let parameter r = 2, any two-symbol word in s compose a refined symbol and CL (s2) = 3. Let r ≥ 6, CL (sr) = 1. Indeed, as has been shown6,7, for a finite s, there is a critical order r* such that once r ≥ r*, sr can be regarded as a single iteration and then CL = 1. When r reaches the particular r* of a given “completely chaotic” object, with both the “completely chaotic” and the low-periodic object obtaining the minimal CL, CL achieves the transition from a type-I measure to a type-II. The objects of highest r*, with the most difficulty to obtain CL = 1, are strings of the period-doubling accumulating points known as weak chaos13.
Adaptable entropy
In classical information theory21, when the probability pi of any event xi is obtainable, with a random variable X representing all α possible events, the α-nary Shannon entropy is the mean of the information content −logαpi of X
If α = 2, the unit of S is just bit; and if not, since 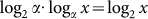 , one may time S by log2α to get the entropy H of bit. For an binary independent and identically distributed random word
, one may time S by log2α to get the entropy H of bit. For an binary independent and identically distributed random word 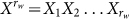 with
with 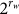 elemental events and any event
elemental events and any event 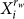 having the probability
having the probability 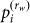 ,
, 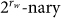 S becomes the entropy rate (entropy per symbol) of order rw
S becomes the entropy rate (entropy per symbol) of order rw
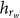 ,
,
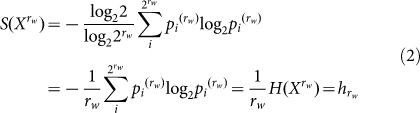 |
It is well-known that 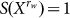 for uniformly distributed
for uniformly distributed 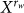 . Measuring the mean of bits needed for the shortest description of the random word's experimental outcome,
. Measuring the mean of bits needed for the shortest description of the random word's experimental outcome, 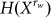 is extensive because in the limit
is extensive because in the limit 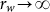 the entropy rate21
h is a constant.
the entropy rate21
h is a constant.
Accompanied by a type-I measure C1, C216,17 is derived from “a hierarchical approach to complexity of infinite stationary strings22.” By stationary, we see that statistical properties of the strings in consideration are fixed with time or space changing, a precondition for all statistical measures' application.
Given a binary string s of length n, there are totally 2r distinct words of length r (or r-words for short). Let Fa(r) denote the frequency of a distinct allowed r-words that really emerges in s and Ff(r) the frequency of a distinct forbidden r-words in s counted as follows: if in s (except its end) a (r − 1) -word  emerges x times, but no r-word
emerges x times, but no r-word 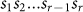 emerges, we account
emerges, we account 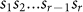 a forbidden r-word emerging x times. For example, when basic alphabet
a forbidden r-word emerging x times. For example, when basic alphabet 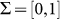 , if
, if 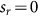 , then we regard the frequency of the allowed r-word
, then we regard the frequency of the allowed r-word 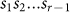 as that of the forbidden r-word
as that of the forbidden r-word 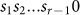 .
.
With the probability being replaced by relative frequency in s, C1 is the entropy rate of allowed r-words and C2 of forbidden r-words:
Here, i denotes each distinct r-word; 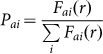 and
and 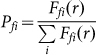 are relative frequencies.
are relative frequencies.
Given a finite r, if s containing all possible (including overlapping) 2r
r-words, no forbidden r-word occurs. For a completely chaotic (random) case, as 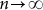 , the number of distinct forbidden r-words
, the number of distinct forbidden r-words 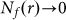 , then
, then 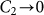 .
.
Since s is finite, C1 is a real-world estimate of hr, while C2 is roughly adaptable to type I and type II. First, the critical order r* still works. If s is of a level of randomness, every r*-word in s is distinct as well as every (r* + 1) -word is. So the number of distinct allowed (r* + 1)-word 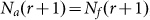 , thus
, thus 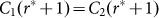 . Second, there may exist another critical word length
. Second, there may exist another critical word length 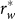 such that for
such that for 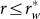 ,
, 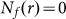 and then C2 = 0. By increasing r from the
and then C2 = 0. By increasing r from the 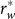 of a given completely chaotic object to the r* of the same object, C2 roughly achieves a transformation from a type-II measure to a type-I.
of a given completely chaotic object to the r* of the same object, C2 roughly achieves a transformation from a type-II measure to a type-I.
If s is a sequence of minimum period m, when r ≥ m, there are m different r-words of equal frequency, and then C2(r) can simply be predicted.
Functionally, C2 is composed of a type-I measure C1 and a type-II measure 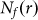 . As
. As 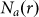 is a low-precision version of C2 and
is a low-precision version of C2 and 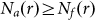 ,
, 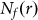 may cause a precision problem of C2 in showing type-II behavior.
may cause a precision problem of C2 in showing type-II behavior.
What is really involved in C2 calculation is the frequency of every distinct allowed r-word sharing length-(r − 1) prefix with a forbidden r-word. This means that C2 is actually applicable to α-nary strings. For convenience and without loss of generality, let us assume that the strings under consideration are binary hereafter.
Intrinsic adaptability
Let us use the logistic map 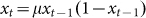 to exhibit the intrinsic adaptability. The case μ = 4 is known as the completely chaotic (pseudo-random) object and the case μ = 3.57 a representative sample of weak chaos. After 25000 times iteration deleted as transient, from a trajectory of xt we got a binary symbolic sequence of length 8204 by the partition 0.5. With different r, CLZ, CL, C1, and C2 for both μ = 4 and μ = 3.57 are calculated and shown in Fig. 1.
to exhibit the intrinsic adaptability. The case μ = 4 is known as the completely chaotic (pseudo-random) object and the case μ = 3.57 a representative sample of weak chaos. After 25000 times iteration deleted as transient, from a trajectory of xt we got a binary symbolic sequence of length 8204 by the partition 0.5. With different r, CLZ, CL, C1, and C2 for both μ = 4 and μ = 3.57 are calculated and shown in Fig. 1.
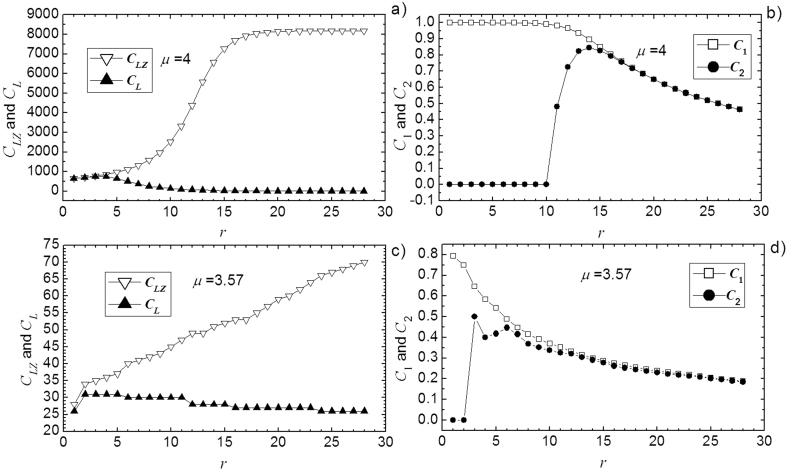
Figure 1. Complexity of logistic map.
(a) CLZ and CL for μ = 4; (b) C1 and C2 for μ = 4; (c) CLZ and CL for μ = 3.57; (d) C1 and C2 for μ = 3.57.
From Fig. 1, with r increasing remarkable symmetry can be found in behavior of the two pairs of measures, CLZ and CL, and C1 and C2. When μ = 4, 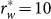 , and if we scale the ordinate logarithmically, we will find r* = 26. Although CLZ and CL of low r are almost equal, the difference between them increases with r until r ≥ r*. On the other hand, with
, and if we scale the ordinate logarithmically, we will find r* = 26. Although CLZ and CL of low r are almost equal, the difference between them increases with r until r ≥ r*. On the other hand, with 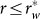 , C1 = 1 and C2 = 0. They rapidly converge when r approaching to r* and stay equal when
, C1 = 1 and C2 = 0. They rapidly converge when r approaching to r* and stay equal when 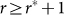 .
.
When μ = 3.57, 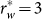 [Fig. 1(d)], and
[Fig. 1(d)], and 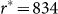 (not shown in Fig. 1). Actually, in a long range of r between about 26 and 834, C1 ≈ C2. To let C2 act as a type-II measure, r must be within the range from 4 to 10.
(not shown in Fig. 1). Actually, in a long range of r between about 26 and 834, C1 ≈ C2. To let C2 act as a type-II measure, r must be within the range from 4 to 10.
With r ≤ 3, the μ = 3.57 and the μ = 4 cases are not distinguishable by C2. When 26 > r > 10, CL and C2 are both in a type-transition state. The transition range is near the word length r = 13 [Fig. 1(b)], the solution of the equation 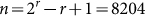 . It is easy to see that
. It is easy to see that 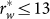 and
and  are valid for any length-n string and
are valid for any length-n string and 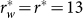 is valid only if in s each overlapping distinct possible r-word just appears once6.
is valid only if in s each overlapping distinct possible r-word just appears once6.
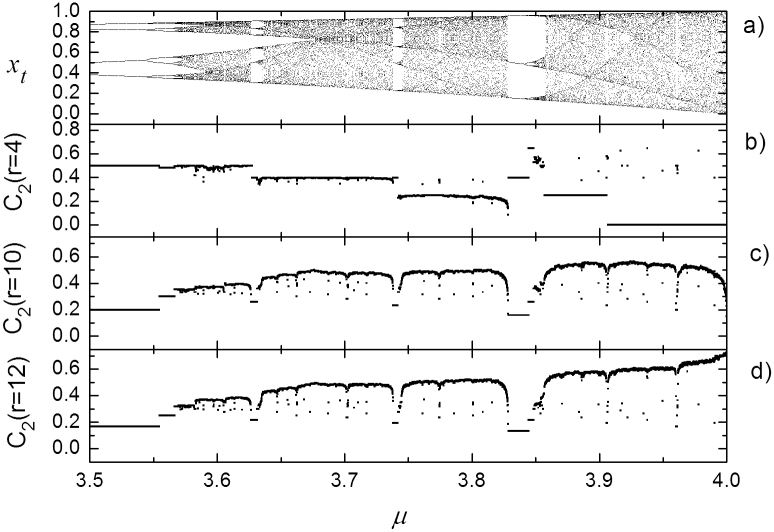
Fixing r but letting μ vary with Δμ = 0.0001 from 3.5 to 4, results are as shown in Fig. 2. When r = 3, almost all cases in the region about μ > 3.555 obtain C2 = 0 (not shown in Fig. 2); when r = 4, the zero-C2 region reduces to about μ > 3.907 [Fig. 2(b)]; and when r = 4 to about μ > 3.978 (not shown in Fig. 2). Since  is either 3 or 4 for most of chaotic cases, we see a serious precision problem of C2 of low r [Fig. 2(b)].
is either 3 or 4 for most of chaotic cases, we see a serious precision problem of C2 of low r [Fig. 2(b)].
Figure 2. The C2 of logistic map.
(a) Bifurcation diagram; (b) r = 4; (c) r = 10; (d) r = 12.
As C2(10) = 0 for μ = 4 [Fig. 2(c)], C2(10) is roughly type-II. For any chaotic s, C2 always rapidly converge to C1 once the 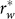 of s has been exceeded [Fig. 1]. Since 10 is certainly larger than 3 or 4, within most chaotic area except a small region very close to the point μ = 4, C1 and C2 act similarly.
of s has been exceeded [Fig. 1]. Since 10 is certainly larger than 3 or 4, within most chaotic area except a small region very close to the point μ = 4, C1 and C2 act similarly.
Highest C2 [as shown in Fig. 2 (c)] is not close to the edge of chaos as highest CL is [see Fig. 8 in Ref. 6]. When r is only a little higher than the 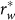 of μ = 4 case, e.g. r = 12, C2 becomes definitely a type-I measure [Fig. 2 (d)]. Thus, C2 has a significantly smaller range of choice of r for roughly type-II behavior than CL.
of μ = 4 case, e.g. r = 12, C2 becomes definitely a type-I measure [Fig. 2 (d)]. Thus, C2 has a significantly smaller range of choice of r for roughly type-II behavior than CL.
Symbolic dynamical analysis and UDGM
Symbolic dynamics for one-dimensional nonlinear iterative systems including logistic maps provides a one-to-one correspondence between any semi-infinite symbol string and the initial point of the trajectory producing the string20. A finite r-word represents a deterministic segment enclosing the initial point. Increments of r will rescale the segment into a shorter one. Therefore, the parameter r in CL is also called fine-graining order, while in entropy this name may not be appropriate, as discussed below.
Table 1 shows the distribution of all possible 4-bit words in μ = 3.645 case. If two adjacent 3-bit-prefix-sharing words both emerge or not emerge, they are ignored. Hence we get only three distinct 4-bit forbidden words 0110, 0100, and 1100, but ignore 1001, which is also adjacent to an allowed word. Moreover, since one r-word creates two prefix-sharing (r +1) -words, when r = 5, all (virtual) segments corresponding to 4-bit forbidden words are ignored. It makes 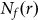 fluctuate irrelevantly to the real spatial structure in phase space. For instance, there always exist mid-position adjacent segments not being visited, but when r = 4, 5, and 6, the number of distinct forbidden words corresponding to such segments equals 2, 0, and 2, respectively. Thus the curves of C2 versus r can hardly be smooth except some cases of almost complete chaos [Fig. 1 (b) and (d)].
fluctuate irrelevantly to the real spatial structure in phase space. For instance, there always exist mid-position adjacent segments not being visited, but when r = 4, 5, and 6, the number of distinct forbidden words corresponding to such segments equals 2, 0, and 2, respectively. Thus the curves of C2 versus r can hardly be smooth except some cases of almost complete chaos [Fig. 1 (b) and (d)].
Table 1. Distribution of all possible 4-bit words in 8204-points μ = 3.645 case.
| 4-bit words | 0000 | 0001 | 0011 | 0010 | 0110 | 0111 | 0101 | 0100 | 1100 | 1101 | 1111 | 1110 | 1010 | 1011 | 1001 | 1000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fa(4) | 0 | 0 | 0 | 0 | 0 | 1349 | 977 | 0 | 0 | 1349 | 852 | 1348 | 977 | 1349 | 0 | 0 |
| Types | N | N | N | N | F | A | A | F | F | A | A | A | A | A | N | N |
From left to right, all words are enumerated according to their corresponding segments' positions in the phase space of logistic maps. The frequency of a distinct allowed 4-bit word Fa(4) equals the times the orbit visit the corresponding segment. In the third row, “F” means “forbidden word”, “A” means “allowed word”, and “N” means “neither forbidden word nor allowed word”.
Essentially, any entropy is only applicable for a random string emitting r-words with measureable stationary distribution, or the r-UDGM of arbitrary given deterministic string s. To apply the r-UDGM exclusively, one has to ignore all temporal or spatial information of s unrelated to the distribution, let alone nonstationary objects of no stable distribution. For instance, given r = 2, the 2-periodic infinite string 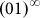 has C2 = 0.5 and be regarded as a medium complex case despite its simple temporal structure.
has C2 = 0.5 and be regarded as a medium complex case despite its simple temporal structure.
In contrast to the entropy, KC estimations CLZ and CL are in itself designed for single deterministic strings. The successive process in searching duplicable section ensures the low complexity value for simple regular strings, e.g. 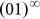 of CLZ = 3 and CL = 1.
of CLZ = 3 and CL = 1.
Due to the absence of a perspective of deterministic chaos in its process of dealing with irregular strings, CLZ is still type-I. Using the terminology of C1 and C2, we may say in s
CLZ successively counts up non-overlapping allowed words in assorted lengths, each of which is adaptively increased from 1 to such a value that the word is distinct from any part of the exhaustive memory. The word length adjusting mechanics makes CLZ be much more fine-grained than 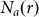 and let the parameter r become meaningless.
and let the parameter r become meaningless.
Deterministic iterative systems are considered in CL a sort of simple data-generating models. They can be regarded as logistic maps, in which fine-graining order r represents the size of the segments, or as equivalent one-bit-output binary recurrence equations, in which r represents the bit number of input. For any given s, when r < r*, this sort of models is non-universal data-generating model (NUDGM), and when r ≥ r*, become universal, i.e. the d-UDGM, and leave no space for others.
The d-UDGM can be used alone by regard s as a single trajectory of a simplest equation, whose operation assignment must be defined as regular as possible. Determining the exact optimal set of arithmetic operations and their assignment in the equation may need countless tentative calculations. What can absolutely not be reduced is the smallest bit number of input, the r* of s, representing the system's uncompressible information.
Henceforth let rw denote also the length of assumed random word in the r-UDGM of s to distinguish it from the fine-graining order r. For a length-n s, let CL(r, n) replace CL(sr) and let r = 0 mean that no segment involves iterative mappings, CLZ can be viewed as a special case of CL denoted by CL(0, n).
Discussion
Logically, a quantity designed for single deterministic strings is unconditionally suitable for stationary random strings because one can calculate the quantity's probabilistic mean, whereas the mean may not fit any individual string. The quantity's mean of a length-rw random string can be interpreted as the average of k individual results each computed from a length-rw string emitted by the random string with 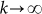 . To arrange such k emitted strings in a single sample
time series, we must assume that the random string, or equivalently the time series, is ergodic, i.e. the relative frequency of any distinct length-rw deterministic string in the time series equals the string's probability:
. To arrange such k emitted strings in a single sample
time series, we must assume that the random string, or equivalently the time series, is ergodic, i.e. the relative frequency of any distinct length-rw deterministic string in the time series equals the string's probability: 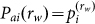 ,
, 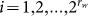 .
.
If every Pai(rw) is determined by previously known 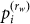 , in an ergodic time series the arrangement of all length-rw emitted strings can be overlapping or non-overlapping, in a certain order or disorder, which is pointless for calculating a quantity's mean: the mean can be theoretically obtained without numerical computation. A theorem of Brudno23 states that the KC per symbol of almost all emitted strings of infinite length is equal to the entropy rate h. Likewise, when fine-graining effect is absent or negligible (i.e. r = 0 or 1), maximum CL relates to emitted strings of maximum randomness and one can prove that6,18,21
, in an ergodic time series the arrangement of all length-rw emitted strings can be overlapping or non-overlapping, in a certain order or disorder, which is pointless for calculating a quantity's mean: the mean can be theoretically obtained without numerical computation. A theorem of Brudno23 states that the KC per symbol of almost all emitted strings of infinite length is equal to the entropy rate h. Likewise, when fine-graining effect is absent or negligible (i.e. r = 0 or 1), maximum CL relates to emitted strings of maximum randomness and one can prove that6,18,21
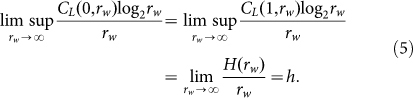 |
with probability 1. Hence, in traditional statistical-mechanics language 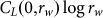 or
or 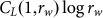 are not only extensive but also asymptotically equal to H.
are not only extensive but also asymptotically equal to H.
In order to apply entropy to a given length-n time series, we have to assume that s is ergodic despite its real generating mechanism. Without previously-known 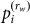 , from s only C1(rw) rather than h can be obtained. To make
, from s only C1(rw) rather than h can be obtained. To make 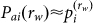 and
and 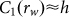 , we have to let
, we have to let 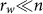 . For example, if s is a given completely random object without forbidden word, we must at least let
. For example, if s is a given completely random object without forbidden word, we must at least let 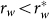 to ensure that no distinct rw-word has
to ensure that no distinct rw-word has 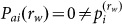 .
.
Here we encounter an unsolvable paradox: to show C2's type-I behavior, i.e. let 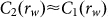 , it has to be valid that
, it has to be valid that 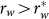 , or even
, or even 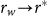 , for a given completely random object, thus the precondition
, for a given completely random object, thus the precondition 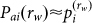 for any entropy's applications cannot be satisfied. Moreover, neither an r-UDGM-rooted measure nor a d-UDGM-rooted can embody the intrinsic adaptability, since in the r-UDGM fine-graining process is not only meaningless but also harmful, and in the d-UDGM r* of s is the ultimate point rather than an example of intrinsic adaptability.
for any entropy's applications cannot be satisfied. Moreover, neither an r-UDGM-rooted measure nor a d-UDGM-rooted can embody the intrinsic adaptability, since in the r-UDGM fine-graining process is not only meaningless but also harmful, and in the d-UDGM r* of s is the ultimate point rather than an example of intrinsic adaptability.
Independent of any specific data-generating model, the KC estimation concerns lossless regeneration of given data. The insertion operation in CL fills blanks left by any NUDGM with symbols already known from s and grants the UDRM containing this NUDGM universality. The duplication operation freely generates repeated words as the r-UDGM does, making the UDRM of CL(0, n) a sort of quasi-r-UDGM. Except for low-period objects, CL(0, n) shows no noticeable distinctness from C1 in its C-R behavior. Without needing to previously set a 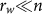 for calculating the average
for calculating the average 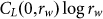 over all allowed rw-words in s, the whole s is treated as a single emitted object for CL, and then
over all allowed rw-words in s, the whole s is treated as a single emitted object for CL, and then 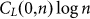 per symbol appear to be estimations of h even better than C124,25,26.
per symbol appear to be estimations of h even better than C124,25,26.
With r increasing, CL appears a simulator not only of H but also of r*. The intrinsic adaptability of CL embodies indeed a general information/complexity measure presenting a smooth transition from the r-UDGM-rooted (superficially type-I) information concept to the d-UDGM-rooted (ideally type-II) complexity concept, all consistent with the principle of KC.
The r-UDGM and the d-UDGM identified here enable us to succinctly redefine the C-R conflict and avoid unnecessary confusions caused by misuse of each UDGM, e.g. about randomness and chaos, not only in complexity measurement. Besides many well-defined deterministic dynamical systems, living organisms12,27,28,29, e.g. human brain, heart, and economic systems, appear nonstationary, edge-of-chaos, and, strictly speaking, beyond the scope of all types of r-UDGM-rooted statistical mechanics including generalised versions5. For these systems, a d-UDGM-rooted measure or framework is certainly an option and need further studies. However, in living organisms, randomness is not able to be excluded except that noise or free will30 is. Thus, a UDRM-rooted framework that proceeds from a KC-based general information measure, CL or its possible revised version, may have more adaptability to complicated real-world situations than a single-UDGM-rooted.
In brief, though we can separate complexity from information by using the d-UDGM and the r-UDGM alone, it would be more natural to accept a general measure encompassing H and its d-UDGM counterpart. The behavior of this measure should have been outlined by CL, since the d-UDGM always becomes more and more overwhelming with r increasing.
Acknowledgments
The author is grateful to Professor Qin-ye Tong for valuable discussion and to Professor Guo-zhao Wang for help in preparing the manuscript. This work was partly supported by National Natural Science Foundation of China (Grant No. 11005081) and Foundation of Wenzhou Medical College (Grant No. QTJ09003).
References
- Meyers R. A. (Ed.). Encyclopedia of Complexity and System Science. (Springer Science+Business Media, LLC., New York, 2009). [Google Scholar]
- Doebeli M. & Ispolatov I. Complexity and Diversity. Science 23, 494 (2010). [DOI] [PubMed] [Google Scholar]
- Li M. & Vitanyi P. An Introduction to Kolmogorov Complexity and Its Applications, third edition. (Springer-Verlag, New York, 2009). [Google Scholar]
- Spillman W. B. et al. Complexity, fractals, disease time, and cancer. Phys. Rev. E 70, 061911 (2004). [DOI] [PubMed] [Google Scholar]
- Beck C. Generalised information and entropy measures in physics. Contemporary Physics 50, 495 (2009). [Google Scholar]
- Ke D. G., Zhang H. & Tong Q. Y. Lattice complexity and fine-graining of symbolic sequence. ACTA Physica sinica 54, 534 (2005) (in Chinese, an English revised version is available at: http://arxiv.org/abs/nlin.CD/0603016). [Google Scholar]
- Ke D. G. & Tong Q. Y. Easily adaptable complexity measure for finite time series. Phys. Rev. E 77, 066215 (2008). [DOI] [PubMed] [Google Scholar]
- Shiner J. S., Davison M. & Landsberg P. T. Simple measure for complexity. Phys. Rev. E 59, 1459 (1999). [DOI] [PubMed] [Google Scholar]
- Crutchfield J. P. & Feldman D. P. Measures of Statistical Complexity: Why? Phys. Lett. A 238, 244 (1998). [Google Scholar]
- Crutchfield J. P. Between order and chaos. Nature Physics 8, 17 (2012). [Google Scholar]
- Langton C. G. Computation at the edge of Chaos: Phase-Transitions and Emergent Computation. Physica D 42, 12 (1990). [Google Scholar]
- Kitzbichler M. G., Smith M. L., Christensen S. R. & Bullmore E. Broadband Criticality of Human Brain Network Synchronization. PLoS Comput. Biol. 5, e1000314 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ananos G. F. J. & Tsallis C. Ensemble averages and nonextensivity at the edge of chaos of one-dimensional maps. Phys. Rev. Lett. 93, 020601 (2004). [DOI] [PubMed] [Google Scholar]
- Bennett C. H. Dissipation, information, computational complexity and the definition of organization. in Pines D. (ed.) Emerging Synthesis in Science (Addison-Wesley, Reading, MA, 1987). [Google Scholar]
- Touchette H. When is a quantity additive, and when is it extensive? Physica A 305, 84 (2002). [Google Scholar]
- Xu J. H., Liu Z. R. & Liu R. The Measures of sequence complexity for EEG studies. Chaos, Solitons & Fractals 4, 2111 (1994). [Google Scholar]
- Tong Q. Y., Kong J. & Xu J. H. A note on analysis schizophrenic EEG with complexity measure. Chaos, Solitons & Fractals 7, 371 (1996). [Google Scholar]
- Lempel A. & Ziv J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 22, 75 (1976). [Google Scholar]
- Boffetta G., Cencini M., Falcioni M. & Vulpiani A. Predictability: a way to characterize complexity. Physics Reports 356, 367 (2002). [Google Scholar]
- Hao B. L. Elementary Symbolic Dynamics and Chaos in Dissipative Systems. (World Scientific, Singapore, 1989). [Google Scholar]
- Cover T. & Thomas J. Elements of Information Theory second edition. (John Wiley&Sons, Hoboken, New Jersey, 2006). [Google Scholar]
- Alessandro G. D'. & Politi, A. A hierarchical approach to complexity with applications to dynamical systems. Phys. Rev. Lett. 64, 1609 (1990). [DOI] [PubMed] [Google Scholar]
- Brudno A. A. Entropy and the complexity of the trajectories of a dynamical system. Trans. Moscow Math. Soc. 44, 127 (1983). [Google Scholar]
- Amigó J. M., Szczepanski J., Wajnryb E. & Sanchez-Vives M. V. Estimating the Entropy Rate of Spike Trains via Lempel-Ziv Complexity. Neural Computation 16, 717 (2004). [DOI] [PubMed] [Google Scholar]
- Amigó J. M. & Kennel M. B. Variance estimators for the Lempel-Ziv entropy rate estimator. Chaos 16, 043102 (2006). [DOI] [PubMed] [Google Scholar]
- Kaltchenko A. & Timofeeva N. Rate of convergence of the nearest neighbor entropy estimator. Int. J. Electron. Commun. (AEÜ) 64, 75 (2010). [Google Scholar]
- Kaplana A. Y. et al. Nonstationary nature of the brain activity as revealed by EEG/MEG: Methodological, practical and conceptual challenges. Signal Process 85, 2190 (2005). [Google Scholar]
- Bernaola-Galván P. et al. Scale invariance in the nonstationarity of human heart rate. Phys. Rev. Lett. 87, 168105 (2001). [DOI] [PubMed] [Google Scholar]
- Hamilton J. D. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 57, 357 (1989). [Google Scholar]
- Hong F. T. Towards physical dynamic tolerance: an approach to resolve the conflict between free will and physical determinism. BioSystems 68, 85 (2003). [DOI] [PubMed] [Google Scholar]