Lateral Membrane Diffusion Modulated by a Minimal Actin Cortex

Abstract

Diffusion of lipids and proteins within the cell membrane is essential for numerous membrane-dependent processes including signaling and molecular interactions. It is assumed that the membrane-associated cytoskeleton modulates lateral diffusion. Here, we use a minimal actin cortex to directly study proposed effects of an actin meshwork on the diffusion in a well-defined system. The lateral diffusion of a lipid and a protein probe at varying densities of membrane-bound actin was characterized by fluorescence correlation spectroscopy (FCS). A clear correlation of actin density and reduction in mobility was observed for both the lipid and the protein probe. At high actin densities, the effect on the protein probe was ∼3.5-fold stronger compared to the lipid. Moreover, addition of myosin filaments, which contract the actin mesh, allowed switching between fast and slow diffusion in the minimal system. Spot variation FCS was in accordance with a model of fast microscopic diffusion and slower macroscopic diffusion. Complementing Monte Carlo simulations support the analysis of the experimental FCS data. Our results suggest a stronger interaction of the actin mesh with the larger protein probe compared to the lipid. This might point toward a mechanism where cortical actin controls membrane diffusion in a strong size-dependent manner.

Introduction

A pivotal property of cell membranes is their fluidity, which allows rapid lateral diffusion of lipids and proteins necessary for a continuous mixing of membrane components and diffusion-limited biochemical interactions. In 1972, the Singer-Nicholson fluid mosaic model described the plasma membrane as a rather simple two-dimensional (2D) lipid matrix in a fluid state with a mosaic of embedded proteins (1). Nowadays, this description of the plasma membrane has emerged to a more refined view (2), which includes proposed lipid nanodomains (rafts) (3), protein crowding (4), and interaction of the membrane with the cytoskeleton (5,6). As a possible consequence of this complexity, lateral diffusion coefficients in cell membranes are typically 5 to 50 times reduced, compared to diffusion coefficients determined in simple reconstituted membranes (6). In addition, strong heterogeneity of diffusion coefficients, generically often described as anomalous diffusion, can be observed for many species (7). However, the individual contribution of these factors to the decrease and variation in lateral diffusion is not well understood.

Actin (and spectrin) filaments bound to the inner cell membrane surface constitute the membrane skeleton (8) and have been suggested to influence the diffusion of lipids and proteins within the membrane (5,6,9–11). The actin meshwork is also supposed to prevent micrometer-scale phase separation, as indicated by recent experimental (12) and theoretical data (13,14).

The membrane skeleton mesh subdivides the plasma membrane into compartments. For two cell types the mesh was quantitatively characterized by electron microscopy, resulting in median mesh diameters of 50 and 200 nm (8). Based on single particle tracking experiments on membranes of living cells, it was reported that on small spatial scales, corresponding to the membrane skeleton mesh diameters, the diffusion was relatively rapid. On larger scales, the diffusion was reported to be greatly reduced. This led to the proposal of the hop-diffusion theory (6,8,15–17). In this model, diffusing species undergo fast diffusion (with similar diffusion coefficients to simple fluid-phase model membrane systems) confined within the areas defined by the actin mesh. Diffusing species could only occasionally escape an area delimited by actin, when thermal fluctuations would create a sufficiently large gap. As a consequence, the macroscopic diffusion coefficient would be reduced. A direct collision between the actin filaments and protruding headgroups of the diffusing molecule (i.e., a membrane protein) or a collision with membrane-bound actin anchors in the membrane plane were proposed as possible interaction mechanisms. A further in vivo study suggested that the actin mesh influences the probe mobility in a strong size-dependent manner (18). It was found that oligomers of a membrane protein diffuse much slower than the respective monomers. This differs from the conventional weak size dependency of membrane diffusion according to the Saffman and Delbrück model (19), which is valid for simple homogeneous membranes and thus, does not consider distortions such as interactions with the cytoskeleton. The aspect of size-dependent diffusion may be very important for signaling and cell polarization, where receptor proteins often oligomerize or bind a ligand at the cell membrane. For example, in an oligomerized (activated) state, receptors would be trapped by the actin mesh, resulting in signal localization on the cell membrane, whereas in a monomeric (inactive) state, the receptors would diffuse rather quickly in the membrane. However, it should be mentioned that due to the difficulty in observing the diffusion at the necessary high temporal and spatial resolution, which typically requires labeling of the molecules with colloidal gold, the evidence from particle tracking for hop diffusion is still under debate (17,20).

In a further in vivo study, the influence of cortical actin on the lateral diffusion was characterized by fluorescence correlation spectroscopy (FCS) with variable spot size (10,21). Depending on the diffusing probe, a different diffusion behavior was reported. For a transmembrane protein labeled with green fluorescent protein, the FCS data indicated a faster diffusion on a small scale and slower diffusion on a large scale in an actin-dependent manner corresponding to hop-diffusion. For putative raft markers, a model of trapping in regions of slow diffusion (i.e., lipid nanodomains) was reported. It was also discussed that for some probes, both mechanisms act simultaneously and may mask each other. Due to this simultaneous presence of several factors modulating the diffusion in vivo, it is challenging to characterize the effect of the membrane skeleton on the lateral diffusion of lipids and proteins independent of other factors. In addition to the structural complexity of cellular membranes, the cellular response to drugs modulating actin is also typically complex and can result in undesired and unknown side-effects.

Here, we used a minimal in vitro system of membrane-bound actin to directly study the isolated effect of actin on the lateral diffusion of a lipid and a membrane-binding protein by FCS. The presence of membrane-linked actin reduced the mobility of both probes in a concentration-dependent manner. We found that this reduction in mobility was much more pronounced for the larger protein, compared to the lipid. Comparison with the mobility reduction obtained by pure solvent viscosity supports the model that actin reduces the probe mobility strongly depending on the probe size. Spot variation FCS (sv-FCS) results were consistent with fast microscopic diffusion inside the actin mesh and slower macroscopic diffusion, with a stronger mesh confinement for the protein. Experiments using myosin-II filaments, which contract and condense the actin filaments, show the possibility to control the actin mesh to locally tune probe diffusion. These results suggest a modulating function of cortical actin in cells that might, for example, locally change signaling properties of the cell membrane. Monte Carlo simulations of diffusion in a partially reflective mesh complement our experimental data.

Materials and Methods

Actin preparation and labeling

Actin monomers (Molecular Probes/Life technologies, Paisley, UK) and biotinylated actin monomers (tebu-bio/Cytoskeleton, Denver, CO) were mixed in a 5:1 (actin: biotin-actin) ratio. Polymerization of the mixture (39.6 μM) was triggered in F-Buffer containing 50 mM KCl, 2 mM MgCl₂, 1 mM DTT, 1 mM ATP, 10 mM Tris-HCl buffer (pH 7.5). The biotinylated actin filaments were stabilized with Alexa-Fluor 488 Phalloidin (Molecular Probes). A final concentration of 2 μM (refers to monomers) Alexa-488-Phalloidin-labeled biotinylated actin filaments was obtained.

Myosin preparation

Myosin was purified as previously described (22) from rabbit skeletal muscle tissue. A classical motility assay where myosins bound to a nitrocellulose-coated glass surface of a perfusion chamber (tebu-bio/Cytoskeleton) propel actin filaments was used to test the activity of myosin. Myofilament assembly was triggered in reaction buffer containing 50 mM KCl, 2 mM MgCl₂, 1 mM DTT, and 10 mM Tris-HCl (pH 7.5).

Free-standing membranes

Free-standing membranes were prepared as described by Heinemann and Schwille (23) (for details see the Supporting Material). All experiments using the free-standing membranes were performed at 23.5 ± 1.5°C (measured in the solution over the objective).

Minimal actin cortex (MAC) preparation

2 μg of neutravidin (Molecular Probes) dissolved in 200 μl reaction buffer was added to the free-standing membranes and incubated at room temperature for 10 min. The sample was washed several times with >2 ml reaction buffer to remove unbound neutravidin. 50 μl of 2 μM (refers to monomers) Alexa-488-phalloidin-labeled biotinylated actin filaments were then added to the lipid bilayer and incubated for 1 h. The sample was carefully washed with ∼1–2 ml reaction buffer to remove unbound actin filaments (see also (24)).

Correlation of mobility reduction and actin density

Three consecutive FCS measurements were conducted at the center of the membrane spots: First, after generation of the free-standing membrane, second, after linking of neutravidin, and third, after linking of actin. The measurements at the different states were performed after the respective washing steps. Each measured spot was numbered (see Fig. 2 A) and changes in diffusion were related to changes in the same spot. The density of actin at each numbered spot was measured by acquisition of fluorescence images under standardized conditions (for details see the Supporting Material).

Figure 2.

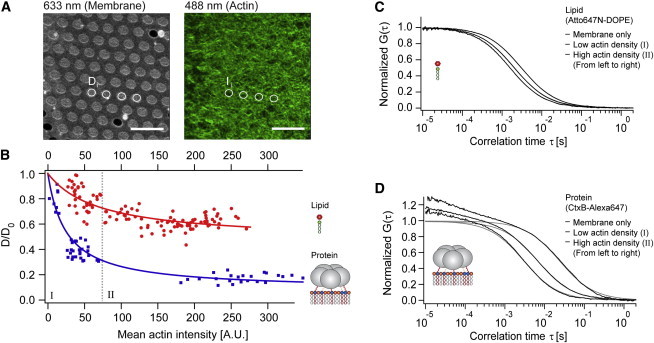
Correlation of the mean actin fluorescence (actin density) and the decrease in lateral membrane diffusion. (A) Confocal fluorescence images of free-standing membranes containing Atto647N-DOPE (left) and Alexa-488-phalloidin-labeled actin filaments (right) exhibiting a dense filamentous meshwork associated with the membrane. Diffusion coefficients D_i were determined by FCS in the center of numbered free-standing membrane spots i. The corresponding actin density I_i was determined from the average fluorescence intensity in a circular area of the respective spot i. Scale bars: 10 μm. (B) Relative change in diffusion coefficients plotted versus the mean actin intensity (measure of actin density) for the labeled lipid (red circles) and the membrane binding protein (blue squares). Each point represents a pair of measurements of D_i and I_i, the solid line is an empirical fit with an asymptotic function. Changes in diffusion are shown after normalization to D₀, the diffusion coefficient of the respective probe in the membrane after neutravidin addition but before actin coupling. The gray dotted line separates regime I (left) and regime II (right). (C and D) Potential effects on the shape of the FCS autocorrelation curves were investigated by classifying the data according to the actin density (I – low density, II – high density). FCS curves were class-averaged (black) and fitted with a model for 2D diffusion assuming single-component membrane diffusion (Eq. S2 or S3 in the Supporting Material, gray). At the timescales relevant for 2D diffusion, the theoretical models were a reasonable fit to the experimental data for the lipid (C) and the protein (D) independent of the actin density.

Point - FCS on membranes

The measurements were performed at the center of each membrane spot. Before each measurement, the focus was moved vertically in steps of 200 nm to determine the position of maximal fluorescence intensity. At this position, the fluorescence was recorded for 30–60 s. The vertical stability of the membrane was maintained by using a cast iron stage (JPK manual precision stage, JPK Instruments, Berlin, Germany). After each experiment, the vertical positioning was controlled, and experiments that showed vertical drift were rejected.

Decrease in lateral mobility induced by solvent viscosity

In a first set of experiments, the viscosity of the buffer surrounding both sides of the free-standing membranes was changed by preparing mixtures of the reaction buffer and sucrose. The change in diffusion coefficient was measured by line-scan FCS (LSFCS) (25). This method does not rely on the shape of the focal volume and therefore avoids artifacts induced by distortions of the focal volume due to changes in the refractive index (26). The mass ratios 0%, 10%, 20%, and 30% were used. Corresponding viscosity and refractive index values for water-sucrose mixtures were obtained from (27). A line with the center on a free-standing membrane patch with a length of 11.52 μm and 512 pixels was continuously scanned for 300 s and a constant scan speed of 768 μs/line on a LSM510 Meta setup (for details see the Supporting Material). Photon arrival times were recorded in the photon mode of a hardware correlator (Flex 02-01D, correlator.com, Bridgewater, VA). The spatio-temporal correlation was computed in MATLAB (The MathWorks, Natick, MA) and fitted to a model function as described by Ries, Chiantia, and Schwille (25). The diffusion coefficient D and the radial waist ω were directly obtained from the fit.

Supporting materials and methods

Details of the Free-Standing calibration of spot variation FCS, the fitting of the autocorrelation data, the alignment and calibration of the FCS setup, and the Monte Carlo simulations can be found in the Supporting Material.

Results and Discussion

Free-standing MAC

To investigate the effect of a membrane-bound actin cytoskeleton on the lateral diffusion of lipids and proteins in the membrane independent of other factors, we built a minimal system with membrane-bound actin filaments mimicking an actin cell cortex (24,28). We aimed to use a geometry of the membrane where both sides of the lipid bilayer were surrounded by buffer solution to avoid frictional coupling with a support as present in supported membranes (29). Additionally, the possibility to remove unbound proteins and to exchange buffer solutions by washing with buffer was desired. These requirements were met by a newly developed free-standing membrane system, where membranes were suspended over holes with 2.5 μm in diameter (23). Biotinylated actin filaments were coupled via neutravidin to both leaflets of the suspended membrane, which contains biotinylated lipids (24) (Fig. 1). The density of the actin meshwork can be controlled by varying the amount of biotinylated lipids present in the lipid bilayer (24). By this procedure, we obtained a dense filamentous actin meshwork associated with the membrane, which we refer to as the MAC (Fig. 2 A, right image).

Figure 1.

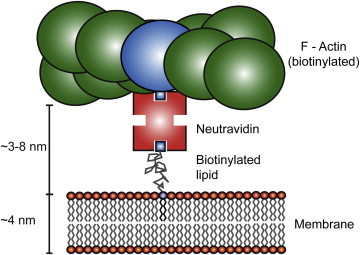
Scheme of the MAC. The filamentous biotinylated (blue) actin is coupled via neutravidin to the free-standing membrane (Egg PC) containing biotinylated lipids (DSPE-PEG(2000)-Biotin). For a more compact display the binding of actin is shown only to the upper leaflet of the membrane. In the experiments, actin presumably binds to both leaflets, because both membrane sides are accessible and contain biotinylated lipids.

Correlation of actin density and mobility

To characterize the effect of actin on the lateral diffusion of lipid and protein species, two different probes, the small labeled lipid Atto647N-DOPE and the larger membrane binding protein CtxB-Alexa647 were used. The density of actin varied on the different membrane spots and was quantified by acquisition of standardized confocal images of the fluorescently labeled actin, as shown in Fig. 2 A. This quantification allowed testing for a potential correlation between actin density and a change in probe mobility.

In Fig. 2 B, the change in the diffusion coefficient is plotted versus the actin density. Each symbol corresponds to a measurement on a single free-standing membrane spot. The values were normalized to the diffusion coefficient measured after the addition of neutravidin, i.e., directly before the addition of actin (typically the addition of neutravidin resulted in a slightly reduced mobility of up to 10% for both probes compared to the membrane alone, data not shown). For both probes, the graph shows a clear correlation between reduced mobility and increasing actin density. When comparing the normalized reductions in mobility at high actin densities (regime II in Fig. 2 B), the maximal effect was ∼3.5-fold stronger for the protein CtxB-Alexa647, compared to the lipid Atto647N-DOPE.

For a direct comparison of the results obtained using the two probes, the changes in the nonnormalized diffusion coefficients before and after actin coupling are helpful. Before addition of actin, the diffusion coefficients were D_lipid = 9.9 ± 0.6 μm² s⁻¹ and D_CtxB = 5.9 ± 0.9 μm² s⁻¹ (mean ± standard deviation). The ratio of the two diffusion coefficients corresponds to D_CtxB/D_lipid = 0.6. Comparable ratios for molecules of similar difference in size in a fluid membrane have previously been reported (30,31). It is important to mention that there is no general theory that describes both, the diffusion of the very small lipid and the larger protein, including the transition between the two size regimes. The diffusion of small molecules comparable to the size of the solvent is described by the free area theory (32) showing an exponential dependency on the size of the diffusant. For larger molecules, the Saffman-Delbrück equation becomes valid, showing a weaker logarithmic dependency of the lateral diffusion coefficients on the radius of the diffusing species (19). In the presence of the actin mesh, the diffusion of both probes is slowed down to D_lipid = 4.8 ± 0.4 μm² s⁻¹ and D_CtxB = 0.7 ± 0.1 μm² s⁻¹ (high actin density regime II in Fig. 2 B, mean ± standard deviation). The ratio decreases drastically from D_CtxB/D_lipid = 0.6 to D_CtxB/D_lipid = 0.15, indicating that upon presence of the actin mesh, the lateral diffusion of the larger protein is more strongly affected compared to the lipid.

A probable cause for the stronger effect of actin on the protein diffusion is a direct interaction of the part of the probe that protrudes from the membrane plane with the actin filaments. In the case of CtxB, the possible interaction might take place between the bulky protein and the actin. CtxB has a height of ∼3.5 nm (normal to the membrane plane) (33) and an attached Alexa647 with a size of ∼0.8 × 2.0 nm. For the labeled lipid Atto647N-DOPE, the major interaction with the actin could include the lipid headgroup and the attached fluorescent dye Atto647N with a size of 0.8 × 1.5 nm (structure from (34)). To compare these dimensions, we estimated the distance of actin to the membrane. Neutravidin has a diameter of ∼5.0 nm and four biotin-binding sites (35). Biotin at the biotinylated lipid is attached to a poly(ethylene glycol) (PEG) spacer with a molecular mass of 2 kDa. In the so-called mushroom configuration, which is predominant at low PEG lipid concentrations, a size of ∼2.8 nm is expected (half sphere radius of the PEG) (36). Hence, we roughly estimate an average distance of actin to the membrane in the range of 3–8 nm.

Another possible source for the reduction in mobility is the interaction with less mobile actin anchor points in the membrane plane (in our case, biotinylated lipids linked to actin), which might represent obstacles for the diffusion (16,17,37). A variation of anchor points by reducing the concentration of biotinylated actin monomers from 20% to 5% did not result in a difference in mobility reduction (Fig. S2), indicating that this may not be the dominant source of mobility reduction in our experiments. Nevertheless, the amount of 5% biotinylated actin monomers may still be too high to completely rule out a role of the anchoring lipids in mobility reduction. In addition, transmembrane proteins could be used as anchors in future experiments as they would couple the actin meshwork to both lipid leaflets and possibly enhance the potential inner membrane obstacle effect.

In summary, we assume that the major source of the mobility reduction is a direct interaction of the actin filaments and components of the diffusing species, which protrude from the membrane plane. This direct interaction also explains the observed large difference in mobility reduction for the two probes. For the bulky protein, it is much more likely to collide with the actin filaments, compared to the small lipid probe.

Our results are in agreement with previous in vivo experiments. Iino et al. (18) reported that the diffusion coefficient of the membrane protein E-cadherin in different oligomeric states decreases strongly with the size of the oligomers. It was suggested that this effect is caused by the interaction of the diffusing species with the membrane skeleton underneath the plasma membrane (6,18,37). For the larger oligomers, the probability to collide with the actin mesh would increase and result in a stronger confinement in the mesh and thus a stronger reduction of mobility.

Autocorrelation data correspond to single-component diffusion

According to the hop diffusion model (6,17,8,37), species such as membrane proteins or lipids diffuse relatively rapidly inside the compartments formed by the membrane skeleton but slow on a larger spatial scale, due to the barriers formed by the membrane skeleton. In FCS, the simultaneous presence of fast and slow diffusion can result in deviations from one-component diffusion. In particular, at actin mesh diameters comparable to the detection spot size, significant deviations from one-component diffusion may occur. In theory, this was demonstrated by previous Monte Carlo simulations (21) and further supported by the simulations shown here (cf. the corresponding section below).

To test, whether we see these potential deviations from single-component diffusion experimentally, we further analyzed the autocorrelation data of the experiments shown in Fig. 2. First, the experimental FCS data were classified according to the respective actin density (see Fig. 2 B). In the low actin density regime (I), the images showed a dense meshwork with filaments at the limit of optical resolution. Hence, at this low density, the FCS detection spot size was approximately comparable to the actin mesh diameter. For higher densities, the appearance became more homogeneous, indicating a distance of the filaments below the diffraction limit. FCS results obtained at low (I) and high actin densities (II) were normalized and averaged separately. This procedure should allow for the detection of smaller deviations from single-component diffusion, compared to the consideration of single autocorrelation curves.

The averaged FCS curves were then fitted with the single-component FCS models (Eqs. S2 and S3 in the Supporting Material) for the lipid and the protein, respectively (Fig. 2, C and D). For both probes and at low and high actin densities, the single-component fit models and the experimental FCS data coincided at timescales >1 ms, which are relevant for membrane diffusion. Thus, we do not directly observe proposed deviations from one-component diffusion.

However, the Monte Carlo simulations presented in the section below showed that for a rather weak interaction between the actin and the diffusing species, deviations from single-component diffusion are small, even in cases of comparable observation spot size and actin mesh diameter. Hence, from the constant spot FCS data alone, we can neither confirm nor exclude the presence of fast microscopic and slower macroscopic diffusion (hop diffusion) in our system.

Decrease in lateral mobility induced by solvent viscosity

Previous experimental data showed that solvent viscosity η affects lateral membrane diffusion (38–40), but so far, the effect of the viscosity on the lateral diffusion of a protein and a lipid has not been directly compared. Thus, we changed the viscosity of the surrounding solvent and measured the influence on the diffusion of the lipid and the protein. The aim of these experiments was to test whether solvent viscosity could also induce similar mobility differences for the two probes, as observed in the presence of actin.

Increasing the solvent viscosity with sucrose also increases the refractive index (27). Therefore, point-FCS is not well suited for measuring lateral diffusion coefficients in more viscous solutions, because for water immersion objectives, a defined shape of the observation volume is only guaranteed for solutions matching the refractive index of water. Already slightly higher refractive indexes result in an increased size and in a deformed shape of the observation volume (26). To avoid these potential pitfalls, LSFCS was used (Fig. 3 A), a technique belonging to the class of image correlation spectroscopy, and therefore not depending on a known size of the focal volume (25). In LSFCS, the diffusion coefficient D and the effective 2D waist ω are directly obtained from a fit. The effective waist indeed increases in size with increasing viscosity (Fig. 3 B).

Figure 3.

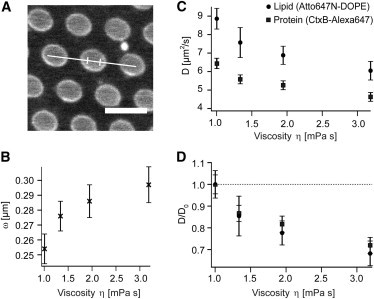
Effect of solution viscosity on the diffusion of the protein and the lipid (in the absence of actin). The viscosity of the solution was varied using different concentrations of sucrose. (A) Diffusion coefficients were determined by LSFCS, because compared to point FCS this method is less susceptible to distortions of the focal volume due to the use of a solution with a refractive index deviating from that of water. A line was continuously scanned and the spatio-temporal correlation in a free-standing part (indicated by the two strokes) was computed and fitted with a model function for 2D diffusion. Scale bar 5 μm. (B) Increase in focal waist depending on the viscosity of the buffer as determined by LSFCS. (C) Absolute changes in the lateral diffusion D of the labeled lipid (circle) and the protein (square). The mobility of both probes decreases with increasing viscosity. (D) Plotting the relative changes in mobility shows that, in contrast to the experiments in the presence of actin, the diffusion of both probes is affected to a comparable extent. The diffusion coefficients were normalized to the respective diffusion coefficient at 0% sucrose. All error bars are standard deviations.

In Fig. 3 C, the absolute changes in lateral diffusion coefficient in the presence of sucrose from 0% to 30% (m/m) are displayed. In agreement with our results from point FCS, the absolute diffusion coefficient at the viscosity of water is lower for the protein, compared to the lipid. With increasing viscosity, the diffusion of both probes is reduced, due to the increasing viscous drag. To compare the effect of solution viscosity on the lipid and the protein, the normalized changes are shown in Fig. 3 D. Comparing the normalized changes of the lipid and the protein in diffusion clearly reveals that the relative changes in mobility of both probes are similar, and therefore in contrast to the strong difference observed in the presence of the actin mesh (Fig. 2 B).

Confined diffusion in the actin mesh indicated by spot variation FCS

In recent years, it was shown that FCS with a variable size of the detection area is a useful tool to characterize diffusive processes in membranes, where the diffusion coefficient depends on the scale. In particular, Monte Carlo simulations (21,41), an analytical treatment (42), and in vivo experiments (10,34,43) demonstrated that sv-FCS can provide additional information about the mode of lateral membrane diffusion. In sv-FCS, autocorrelation curves are recorded at different sizes of the focal spot ω². For free diffusion, a plot of the diffusion time τ_d (ω²) versus the focal area ω² will yield a linear relationship τ_d (ω²) = 1/(4D)ω² where the slope is 1/(4D) (compare Eq. S4 in the Supporting Material). However, in many physiological cases, such as diffusion confined by the membrane skeleton or trapping by microdomains, the apparent diffusion coefficient D changes with the observation scale. For diffusion confined by a mesh, relatively fast diffusion D_micro inside the single mesh cells is expected at small scales, whereas at larger scales, the slow diffusion D_macro < D_micro in between different meshes dominates. Even if this transition cannot be observed directly, due to the diffraction limit of conventional confocal microscopes, extrapolation of the recorded relationship τ_d (ω²) to ω² = 0 allows to distinguish confined mesh diffusion from trapping. For confined mesh diffusion, the extrapolated intercept τ_d0=τ_d (0) will be at τ_d0 < 0, due to the intrinsic transition to fast diffusion at small scales (21). For trapping, in our experiments possibly induced by transient binding of the diffusing species to the actin filaments, an intercept τ_d0 > 0 is expected (21,41).

We used sv-FCS to characterize the predominant mode of diffusion for the two probes. Fig. 4, A and B, shows the measured diffusion times for the labeled lipid Atto647N-DOPE and the protein CtxB-Alexa647 for the free membrane (open symbols) and in the presence of actin (solid symbols). In both cases, Eq. S2 or S3 (see the Supporting Material) for the lipid and the protein, respectively, fit the autocorrelation data well at all spot sizes. For the free membranes, the linear extrapolation to τ_d0 intersects at the origin (Atto647N-DOPE: τ_d0 = 6 ± 209 μs, CtxB-Alexa647: τ_d0 = 62 ± 329 μs), as expected for free diffusion with a constant diffusion coefficient independent on the observation scale. In the presence of membrane linked actin, the extrapolation intersects at slightly negative τ_d0 values for the lipid (Atto647N-DOPE: τ_d0 = −501 ± 241 μs) and pronounced negative τ_d0 values for the protein (CtxB-Alexa647: τ_d0 = −7880 ± 2400 μs). This supports the interpretation that a confined mesh-like diffusion is present in both cases, and a transition from fast, free diffusion to slower macroscopic diffusion occurs at subdiffraction scales. In agreement with the results obtained with a constant detection spot size, the more pronounced negative intersection for the protein indicates a stronger confinement for the protein by the actin mesh compared to the lipid.

Figure 4.

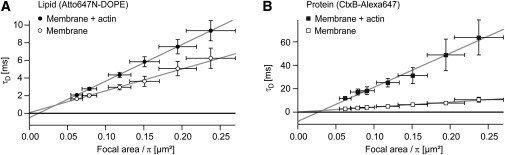
Spot variation FCS supports the view that upon presence of the actin mesh a transition from fast diffusion at a subdiffraction scale to slow macroscopic diffusion occurs. (A) Before actin linking, the diffusion time of the labeled lipid changes linearly with the spot size (open circles) and the extrapolation of the fitted line to zero spot size intersects at the origin (τ_d0 = 6 ± 209 μs). This is in agreement with a constant diffusion coefficient also at subdiffraction scales. In the presence of actin (solid circles), the extrapolation to the origin intersects at a slightly negative diffusion time (τ_d0 = −501 ± 241 μs). This could indicate a transition from fast diffusion (similar to the diffusion without actin) at a subdiffraction scale to slower diffusion on a larger scale (due to the presence of actin). (B) Furthermore, for the protein (open squares) the diffusion time in the membrane without actin scales linearly with the spot size and the fit intersects at the origin (τ_d0 = 62 ± 329 μs). In the presence of the actin mesh (solid squares) the extrapolated diffusion time at zero spot size is strongly negative (τ_d0 = −7880 ± 2400 μs), consistent with a transition from faster to slow diffusion at a subdiffraction scale, due to the presence of the actin mesh. All errors are standard deviations.

Monte Carlo simulations of diffusion in a mesh

To examine the possible influence of an actin mesh on the experimental FCS autocorrelation data, we performed Monte Carlo simulations of 2D diffusion in a meshwork, as illustrated in Fig. 5. The simulated mesh was partially reflective to model the difference in the confining effect of actin on different diffusing species. Previous simulations of similar type by Wawrezinieck et al. (21) already showed that different modes of diffusion can be distinguished by sv-FCS.

Figure 5.

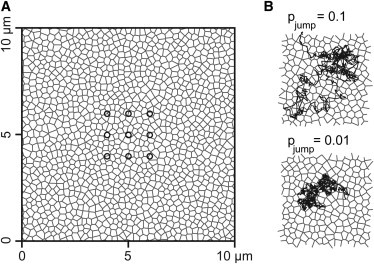
Scheme of the Monte Carlo simulations. (A) The actin membrane skeleton (gray) was modeled as a Voronoi mesh in an area of 10 μm edge length. Particles (not shown) performed a random walk and could cross the boundaries only with a certain probability p_jump and were reflected otherwise. Simulated fluorescence traces were acquired in the mesh with Gaussian-shaped detection spots with a waist of 250 nm (circles). Subsequently, the corresponding autocorrelation functions were computed. Each simulation was characterized by the average mesh size, the mesh distribution (either a narrow, homogeneous mesh size distribution, or a broad, heterogeneous mesh size distribution) and the confinement strength p_jump. (B) Example trajectories illustrating the influence of the parameter p_jump. At a low jump probability (bottom), the trajectory of the diffusing particle was strongly affected by the mesh, resulting in a strong confinement. For a higher jump probability (top), the confinement in the mesh is weaker and the trajectory expands over a larger spatial scale. Both trajectories represent a random walk over 5 s.

However, the availability of FCS instrumentation capable of sv-FCS is still limited and it is also insightful to study the effect of diffusion in a meshwork monitored by conventional FCS with a constant spot size. In particular, we aimed to elucidate three issues in more detail: First, we wanted to characterize the expected shape of the autocorrelation data and previously described deviations from a one-component model (21), depending on the mesh density in a quantitative manner. Second, we wanted to test whether a variable density of the simulated mesh could result in a comparable mobility reduction with one-component diffusion at all densities, as experimentally observed (Fig. 2). Third, we addressed the question of the impact on the mesh size distribution on the experimental results by comparing simulations performed on heterogeneously distributed meshes (wide distribution of mesh diameters) with simulations on homogeneous meshes (narrow distribution of mesh diameters), as illustrated in Fig. S3.

In Fig. 6, A and B, two sets of simulated autocorrelation curves for weaker confinement (probability to escape the mesh: p_jump = 0.1) and stronger confinement (p_jump = 0.01) are shown. Each set included different mesh diameters a (defined as the square root of the mesh area). With decreasing diameter of the mesh, the autocorrelation curves were in both cases shifted toward longer diffusion times. This effect was more pronounced for the stronger confining mesh (Fig. 6 B), because particles were on average in their respective cell for a longer time before they could pass a mesh-barrier. In the case of larger or smaller mesh diameters, compared to the detection spot, the shape of the autocorrelation functions resembled one-component diffusion. However, for the simulations where the mesh had a size comparable to the detection spot a ≈ ω, deviations from one-component diffusion were visible. For the stronger confining mesh (Fig. 6 B), these deviations were much more pronounced, compared to the mesh with weaker confinement (Fig. 6 A).

Figure 6.

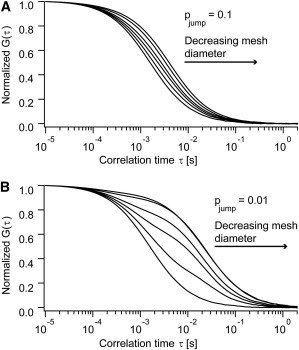
Simulated autocorrelation curves at varying mesh diameters a and constant FCS detection spot area of ω = 250 nm. (A and B) Two examples with difference in confinement are shown. In both plots the autocorrelation curves from left to right were simulated with decreasing mesh diameter and by using the same set of Voronoi meshes. The leftmost curves were obtained with a mesh larger than the FCS detection area, for the middle curves mesh and detection area were similar, and the right curves were simulated with a mesh smaller than the detection area (from left to right: ω/a = 0, 0.5, 0.9, 1.1, 2.1, 3.1). In both cases a transition from fast single-component microscopic diffusion (diffusion inside the mesh) over an intermediate regime to slower macroscopic diffusion (diffusion on scales larger than the mesh) occurs. (A) Autocorrelation curves simulated at comparably weak confinement (p_jump = 0.1). With decreasing mesh diameter the decay of the autocorrelation curve is shifted toward longer correlation times. (B) Autocorrelation curves simulated at stronger confinement (p_jump = 0.01). In this case, a clear deviation from single-component diffusion at mesh diameters comparable to the detection spot size is evident, due to the shape of the autocorrelation curves.

To quantify the observed deviations from one-component diffusion, the simulated autocorrelation curves were fitted with a one-component fit, and the error, represented by the standard deviation between fit and simulated curve, was calculated. In Fig. 7 A, the deviation from single-component diffusion is plotted against the ratio of focal spot size and mesh diameter. The dependency of the resulting autocorrelation data on ω/a, the spot size compared to the mesh size, is visible. The calculation of the error, allowed comparing the expected deviations from one-component diffusion for different confinement strengths. For large meshes compared to the detection spot, ω/a ≈ 0, the microscopic fast diffusion in the mesh dominates. At comparable sizes, ω/a ≈ 1, the microscopic diffusion will be simultaneously observed with slower macroscopic diffusion in between adjacent meshes. The stronger the confinement, the more dominant is the occurrence of two populations with a different diffusion coefficient. Thus, the confinement increases the observed deviations from one-component diffusion. On the other hand, for weak confinement, these deviations are marginal. Finally, if the mesh size becomes smaller than the detection spot, ω/a > 1, the macroscopic diffusion dominates and the FCS data approach again a single-component model.

Figure 7.

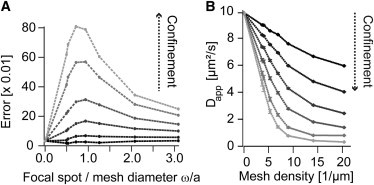
Analysis of the autocorrelation data from the Monte Carlo simulations obtained by variation of the mesh diameter and confinement strength. (A) Error of a single-component diffusion model fit to the autocorrelation data from the simulations plotted versus the focal spot size ω divided by the mesh diameter a. The error was defined as the standard deviation between the simulation result and a single component fit. Different shades of gray represent different strong confinement. From ω/a → 0 (large mesh) over ω/a ≈ 1 (mesh similar to detection spot) to ω/a ≫ 1 (small mesh) the transition from single-component diffusion over nonsingle-component diffusion to single-component diffusion is evident. For strong confinement the deviations to single-component diffusion are strong, when spot size and mesh diameter have similar dimensions. For weak confinement these deviations at ω/a ≈ 1 are weak or negligible. (B) Change in apparent diffusion coefficient D_app plotted versus the mesh density (see text for details). D_app decreases with mesh density. Stronger confinement led to a faster decrease in diffusion. However, also for weak confinement (topmost two curves), which showed no deviation from single-component diffusion in (A), a clear reduction in diffusion was obtained. D_app was calculated from a one-component fit to the simulation results. The data for (B) represent the same data set as used for (A).

In the membrane skeleton of cells, the actin meshwork does not have a single fixed mesh size, but the mesh sizes are rather broadly distributed (8). Therefore, when performing FCS measurements, it is conceivable that smaller and larger meshes simultaneously affect the FCS measurement. This could possibly result in a mixing of diffusing components and affect the shape of the autocorrelation curves compared to a homogeneous meshwork, where all meshes have an almost identical size (if not explicitly stated the homogeneous meshwork was used for the simulations). In Fig. S4 the deviation of a single-component model is shown in comparison for the homogeneous and the heterogeneous meshwork. Surprisingly, only minor differences were obtained. The maximal error of a one-component fit was slightly lower for the heterogeneous mesh, and the error of the heterogeneous mesh was distributed over a broader range of mesh sizes. Both results can be explained by the averaging over a wider range of mesh dimensions for the heterogeneous meshwork.

In our experiments with fluorescently labeled actin filaments, the density of actin was measured from the average fluorescence intensity I in an area A around the FCS detection spot (Fig. 2 A). Under the assumption that quenching and other processes, which reduce the observed fluorescence can be neglected, the average intensity I will be proportional to the sum of the individual filament lengths l_i in the detection area: $I=f{A}^{-1}\sum l_i$. The proportionality constant f is the average fluorescence emission per filament length. To compare the experimentally observed mobility reduction in the presence of an increasing actin density with the simulations, the mesh density ρ in the simulations was quantified by $\rho =A_{sim}^{-1}\sum l_i$, where A_sim represented the simulation area. The density ρ is directly proportional to the experimentally determined actin density I.

Fig. 7 B shows the apparent diffusion coefficient plotted versus the mesh density in the simulation. As expected, an increase in density resulted in a decreasing mobility. The result was practically identical for the homo- and the heterogeneously distributed mesh, as shown in Fig. S5. Initially, at low mesh densities, the decrease in mobility is rapid until the density of the mesh is such that ω/a ≈ 1 (corresponding to a density of ρ ≈ 7 μm⁻¹). Above this density, the decrease in mobility is less dramatic. For stronger confinement, the overall effect is generally stronger. However, most interestingly, even for the simulations with weak confinement, which showed no deviation from single-component diffusion, a distinct reduction in mobility could be obtained.

Qualitatively, the mesh size-dependent reduction in mobility in the simulations (Fig. 7 B) and the experiments (Fig. 2 B) agrees well. The experimental data show a fast initial decrease in mobility and then a slower decay with increasing actin density. Experimentally, at all actin densities, one-component autocorrelation curves were obtained. If the simulations adequately describe the in vitro experiments, they rule out the case of strong confinement, because in this case, clear deviations from one-component diffusion should have been observed. The simulations match well to the experimental data under the assumption of weak confinement, where one-component diffusion describes the data adequately at all actin densities.

Switching the diffusive membrane state by myosin II

An active regulation of the density of cortical actin is a possible mechanism to tune diffusion in the membrane. The actin density may be regulated in a myosin-dependent manner during cytokinesis (44,45), and also by the interaction with the manifold proteins modulating the actin mesh during other cell cycle phases (46). To demonstrate that tuning of the density of cortical actin is a possible way for cells to control diffusion in the membrane, we added myofilaments to membranes that were initially covered with actin, and measured the change in mobility of the labeled lipid. Before myosin addition and in presence of the actin mesh, the mobility of the lipid was reduced as already observed in the previously described experiments. After adding the myofilaments, the actin filaments typically condensed in a circular manner, exposing most of the free-standing membrane patches as shown in Fig. 8. We assume that the observed actin orientation along the support grid is induced by the higher membrane friction with the support. However, on a few free-standing patches, a concentration of actin was observed (Fig. 8, right image, central spot). The diffusion coefficients on the actin covered and the actin free spots were modified accordingly. On the free spots, the diffusion coefficients were close to the initial value before the addition of actin, whereas the areas covered with actin showed a reduced mobility.

Figure 8.

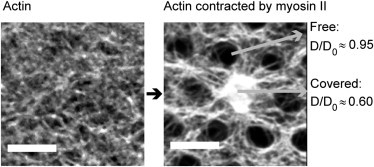
Addition of myosin II allows switching the diffusive state of the membrane. The left image shows the fluorescence of actin (labeled with phalloidin-Alexa488) linked to membranes. Upon addition of myosin II, the actin filaments retract from most of the free-standing membrane patches, but also condense on some spots as shown in the right image. The diffusive behavior is modified accordingly. On the spots where actin was removed, the diffusion is comparable to the diffusion in a membrane before actin coupling, whereas the diffusion is reduced at spots where actin was concentrated. Both measurements are for the labeled lipid (Atto647N-DOPE). Scale bars 5 μm.

Thus, a variation of the actin density might be a mechanism to efficiently control diffusion in the plasma membrane. A possible cellular function may be found in the spatial control of signaling events (6,47). In combination with a strong size-dependent lateral diffusion, as suggested by our data and reported previously (18), receptors with a bound cytoplasmic ligand or in an oligomeric state would be localized.

Conclusion

Although lateral membrane diffusion is an essential process for living cells, little is known about its regulation. The simultaneous interplay of several factors modulating lateral diffusion, including the interaction with the membrane skeleton, complicates an in-depth understanding. To this end, we developed a MAC to directly study the effect of a membrane-bound actin mesh on the lateral diffusion.

The lateral diffusion of a lipid and a membrane binding protein were both reduced in an actin density-dependent manner, and the maximal reductions in diffusion were much stronger for the protein, compared to the lipid. We showed that this was a specific feature of membrane-bound actin. This implies that membrane-bound cortical actin has a complex influence on the lateral diffusion, which depends on the type and/or size of the diffusing species. By using myofilaments to locally change the actin density, our experiments demonstrate a potential mechanism of how cells might vary the actin mesh density to control lateral diffusion. The proposed size dependency of lateral diffusion by the actin mesh implies that a control of the cortical actin density can help to localize cellular signals at certain areas of the membrane.