Magnetism and multiplets in metal-phthalocyanine molecules

Abstract

Magnetism and multiplets for metal-phthalocyanine (MPc) molecules with transition-metals (M) of Mn and Co were investigated based on the constraint density functional theory calculations by imposing density matrix constraint on the d-orbital occupation numbers. For the MnPc, the ground state is found to be the ⁴E_g state with the perpendicular magnetic anisotropy with respect to the molecular plane, while for the CoPc, the ground state is the ²A_1g state with a planar magnetic anisotropy.

INTRODUCTION

Transition-metal phthalocyanine (MPc), which forms a planar organic molecule with a transition-metal atom (M), is a promising material in applied and industrial fields, since a variety of electric, optical, and magnetic properties with the high chemical and physical stabilities can be designed by substituting the transition-metal in the MPc.^{1, 2, 3, 4, 5} Moreover, a challenge to miniaturize devices for novel magnetic applications now extends to treating an extreme limit of the single molecule. Importantly, the property of the MPc is governed by the electronic structure, so-called multiplet, which arises from the d-orbitals localized at the transition-metal atom. It is, thus, of importance to understand the multiplet structures of the MPc.

However, the ground state of the multiplets is still debated despite extensive experimental and theoretical investigations spanning decades. For examples, for the FePc, experiments^{6, 7, 8, 9} have individually proposed the ³E_g and either ³B_2g or ³A_2g state, and even the density functional theory (DFT) calculations have predicted contradictory.^{2, 10, 11, 12, 13, 14} For the MnPc, the multiplet for ground state has been suggested either ⁴E_g or ⁴B_2g state,^{11, 15, 16} and for the CoPc, the ²E_g or ²A_1g state.^{11, 13} For this, we previously proposed a constraint DFT approach, implemented in the full-potential linearized augmented plane-wave (FLAPW) method,¹⁷ by imposing density matrix constraints on the d-orbitals occupation numbers, and our total energy calculations demonstrate that for the FePc, there are three stationary states of the ³E_g, ³B_2g, and ³A_2g symmetries and that the ground state is the ³A_2g state with a planar magnetic anisotropy (MA). Here, we extend our DFT investigations for the MnPc and CoPc, and we demonstrate that for the MnPc (CoPc), the ground state is the ⁴E_g (²A_1g) state with the out-of-plane (planar) MA.

MODEL AND METHOD

An isolated molecule of the MPc has the simple planar structure shown in Fig. 1a, where the transition-metal (M) ion located at the center of the molecule has D_4h site symmetry. In the forms, as shown in Fig. 1b, a ligand-field splits the d-orbitals into three singlets (d_xy, d_z2, and d_x2-y2) and one doublet (d_xz+yz). Ignoring the high lying d_x2-y2 orbital that bonds to the four outer N ions, three multiplets ⁴A_1g (d_xy,↑, d_z2,↑, d_xz+yz,↑², d_z2,↓), ⁴B_2g (d_xy,↑, d_z2,↑, d_xz+yz,↑², d_xy,↓), and ⁴E_g (d_xy,↑, d_z2,↑, d_xz+yz,↑², d_xz+yz,↓) for MnPc, where the majority-spin states except the d_x2-y2 orbital are fully occupied, is approximately constructed, and two multiplets ²A_1g (d_xy,↑, d_z2,↑, d_xz+yz,↑², d_xy,↓, d_xz+yz,↓²) and ²E_g (d_xy,↑, d_z2,↑, d_xz+yz,↑², d_xy,↓, d_z2,↓, d_xz+yz,↓) for CoPc when no spin-orbit coupling (SOC) is considered.

Figure 1.

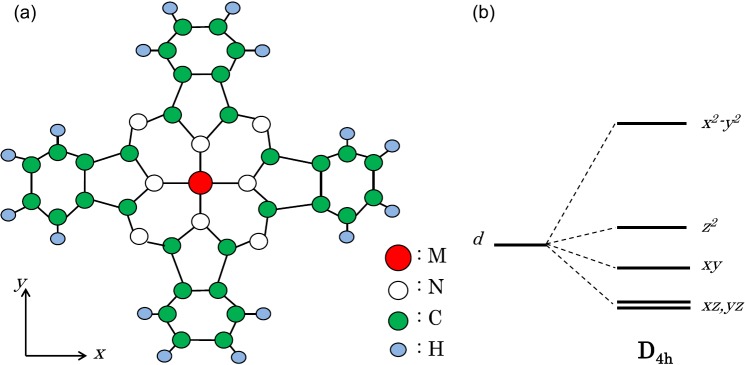
(a) Atomic structure of MPc molecule. Large closed circle (red) represents a transition-metal (M) ion located at the center of the molecule, which has D_4h site symmetry. (b) Energy level splitting for M²⁺ with a D_4h site symmetry in MPc.

As the model of the MPc, we adopted a monolayer slab with infinite vacuum on both sides, and a large in-plane lattice constant of 27 a.u. and atomic positions given by experiments^{18, 19} were employed.

Calculations were performed in the scalar relativistic approximation (SRA), i.e., excluding the SOC, based on the generalized gradient approximation (GGA)²⁰ for exchange-correlation, by using the FLAPW method with film geometries by including fully the additional vacuum regions outside of a single slab.^{21, 22} The LAPW basis with cutoffs of |k + G| ≤ 3.6 a.u.⁻¹ and muffin-tin (MT) sphere radii of 2.3 a.u. for transition metal (Mn and Co), 1.2 a.u. for N and C, and 0.8 a.u. for H were used. Lattice harmonics with angular momenta up to l = 8 for Mn and Co, 6 for N and C, and 4 for H are employed to expand the charge density, potential, and wave functions.

To constraint electronic configurations of multiplet structures in the MPc without a loss of the site symmetry, we introduce an appropriate total energy functional with constraint fields,

$$E\left[\rho \left(\mathbf{r}\right)\right]=E_{\text{GGA}}\left[\rho \left(\mathbf{r}\right)\right]+\sum _{mm\prime }{\mu }_{mm\prime }^{\alpha }\left(n_{mm\prime }^{\alpha }-N_{mm\prime }^{\alpha }\right),$$ (1)

where E_GGA[ρ(r)] is the usual total energy functional of the GGA, $n_{mm\prime }^{\alpha }$ is a density matrix of d-orbitals of an atom α, and $N_{mm\prime }^{\alpha }$ is an occupation number that should be constrained. In the LAPW basis, $n_{mm\prime }^{\alpha }$ is given by the projection of the wave function onto the Y_lm subspace²³ as

$$n_{mm\prime }^{\alpha }=\sum _{k,b}{f}_{k,b}\langle {\Phi }_{k,b}\left|{\widehat{P}}_{mm\prime }^{\alpha }\right|{\Phi }_{k,b}\rangle ,$$ (2)

$${\widehat{P}}_{mm\prime }^{\alpha }=|u_l^{\alpha }{Y}_{\mathit{l}\mathit{m}}\rangle \langle u_l^{\alpha }{Y}_{lm\prime }|+\frac{1}{{\dot{u}}_l{\dot{u}}_l}|{\dot{u}}_l^{\alpha }{Y}_{\mathit{l}\mathit{m}}\rangle \langle {\dot{u}}_l^{\alpha }{Y}_{lm\prime }|,$$ (3)

where k and b refer to a k-point in the Brillouin zone and a band index, respectively. The $f_{k,b}$ is electron occupation (Fermi) function, and $u_l^{\alpha }$ and ${\dot{u}}_l^{\alpha }$ are the radial wave function and its energy derivative in the basis function. The corresponding Kohn-Sham equation can be written as

$$\left[H_{\mathit{G}\mathit{G}\mathit{A}}+\sum _{mm\prime }{\mu }_{m\prime m}^{\alpha }{\widehat{P}}_{mm\prime }^{\alpha }\right]{\Phi }_{k,b}=\epsilon {\Phi }_{k,b},$$ (4)

where the constraint term in the Hamiltonian effectively projects out the chosen irreducible representation for the overall wave function, in which one can pick up an electronic configuration of corresponding multiplet. In practice, we specify a set of constraint fields, ${\mu }_n^{\alpha }$, along directions of the eigenvectors in the $n_{mm\prime }^{\alpha }$, consistent with the site symmetry. Then, the ${\mu }_{mm\prime }^{\alpha }$, which are rotated back from the ${\mu }_n^{\alpha }$, are introduced into Eq. 4, and the corresponding $n_{mm\prime }^{\alpha }$ are determined self-consistently. The self-consistent calculations were carried out using the second variation scheme, i.e., the diagonalization of Eq. 4 was carried out in a basis of the eigenfunctions, φ_k,b, of H_GGA. Full self-consistency was achieved for the density matrix as well as the charge and spin densities. The total energy is calculated using Eq. 1, with $N_{mm\prime }^{\alpha }$ = $n_{mm\prime }^{\alpha }$.

To determine the MA, the second variational method²⁴ for treating the SOC was performed by using the calculated eigenvectors in the SRA, and the MA energy, E_MA, was determined by the force theorem,^{25, 26, 27} which is defined as the eigenvalue difference for the magnetization oriented along the planar direction and the out-of-plane direction with respect to the molecule plane.

RESULTS AND DISCUSSION

Mn-phthalocyanine

Calculated total energy differences, ΔE, of the three multiplets of ⁴A_1g, ⁴B_2g, and ⁴E_g states for the MnPc with respect to a variation of the constraint field μ_xz(yz),↓ are shown in Fig. 2a, where the constraint is imposed in the occupation number of the d_xz(yz),↓ orbitals. First, we started self-consistent calculations by using an initial charge density superimposed by those of spherical atoms and with no constraint field, μ_xz(yz),↓ = 0, as carried out in the standard (usual) self-consistent calculations. We obtained the ⁴E_g solution [closed square in Fig. 2a], where the doublet d_xz+yz,↓ orbitals located at the top of the valence states are occupied by one electron, as shown in Fig. 2b. When the constraint field μ_xz(yz),↓ is introduced in the positive direction, the multiplet structure changes to the ⁴B_2g state [closed triangle in Fig. 2a]. However, as the μ_xz(yz),↓ sets to zero (zero constraint field), the system cannot remain in a stationary solution. Also, for ⁴A_1g state, no stationary solution is obtained at zero constraint field. Thus, the ground state may be concluded to the ⁴E_g state.

Figure 2.

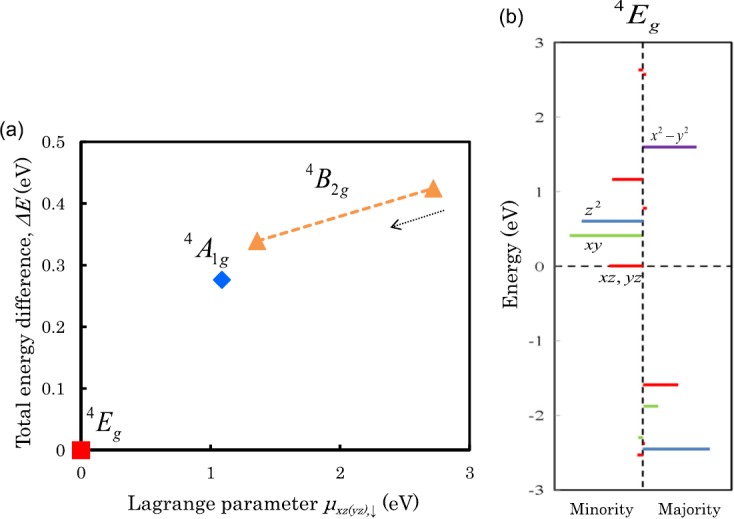
(a) Calculated total energy difference, ΔE, with respect to the constraint field, μ_xz(yz),↓, for MnPc, where the other μ_n's are set to zero. Closed square, rhombus, and triangle indicate solutions of ⁴E_g, ⁴A_1g, and ⁴B_2g states, respectively, obtained by self-consistent calculations. (b) Multiplet structures of the ⁴E_g state for the MnPc at zero constraint field. Bars (in color) represent weights of d-orbital contribution in muffin-tin Mn sphere. Negative and positive energies indicate occupied and unoccupied orbitals, respectively.

For the ⁴E_g ground state of the MnPc, the calculated E_MA has a positive value of 3.5 meV/molecule, indicating that the spin moments energetically favor pointing out-of-plane (out-of-plane MA). According to perturbation theory,²⁸ the SOC interaction between occupied and unoccupied d states with the same (different) m magnetic quantum number through the L_z (L_x, L_y) operator gives a positive (negative) contribution to the E_MA. Thus, for the ⁴E_g state, the half-occupied state (the occupied and unoccupied states) in the doublet d_xy+yz,↓ orbitals (m = ±1) yields a positive contribution to the E_MA.

Co-phthalocyanine

Calculated ΔE with respect to variations of μ_xz(yz),↓ for the CoPc are shown in Fig. 3a. Self-consisted calculations with an superimposed initial charge density and no constraints yield the ²A_1g state, where the singlet d_xy,↓ and doublet d_xz+yz,↓ orbitals are fully occupied, while the singlet d_z2,↓ orbital locates in energy above the valence top, as shown in Fig. 3b. When the negative μ_xz(yz),↓ is introduced, the stationary solution of the ²E_g state is obtained, where the two singlets d_xy,↓ and d_z2,↓ orbitals are fully occupied, and the doublet d_xz+yz,↓ orbitals are occupied by one electron. The total energy difference indicates that the ground state is the ²A_1g state, whose energy is lower than that of the ²E_g state by 150 meV/molecule.

Figure 3.

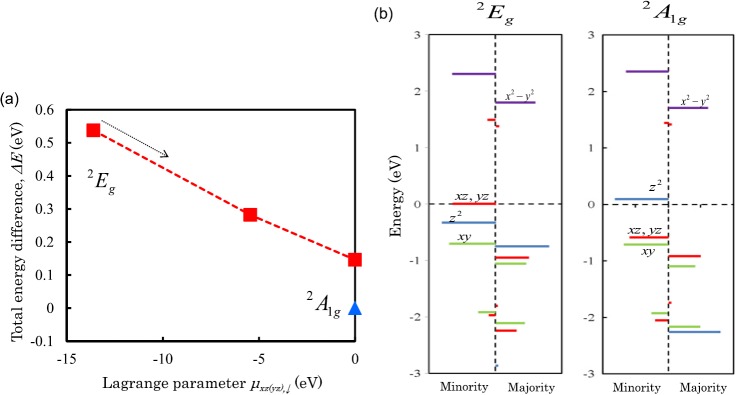
(a) Calculated total energy difference, ΔE, with respect to the constraint field, μ_xz(yz),↓, for CoPc, where the other μ_n's are set to zero. Closed triangle and square indicate solutions of ²A_1g and ²E_g states, respectively, obtained by self-consistent calculations. (b) Multiplet structures of the ²E_g and ²A_1g states for CoPc at zero constraint field. Notations are same as in Fig. 2.

The calculated E_MAs for the ²A_1g and ²E_g states result in −1.2 and 14.2 meV/molecule, which indicate the planar and out-of-plane MAs, respectively. The planar MA for ground state of the ²A_1g state arises from the SOC between the occupied d_xy+yz,↓ (m= ± 1) and unoccupied d_z2,↓ (m = 0) orbitals, while the out-of-plane MA for the ²E_g state is due to the SOC in the half-occupied state in the doublet d_xy+yz,↓ orbitals (m = ±1).

SUMMARY

We carried out the first principles calculations with the FLAPW method, based on constraint DFT, to investigate the electronic structures and MA of the multiplets for the MnPc and CoPc. Results predicted that for the MnPc, the ground state is the ⁴E_g state, in which the easy axis of magnetization favors pointing out of-plane, while there are no stationary solutions of the ⁴B_2g and ⁴A_1g states. For the CoPc, the ²A_1g state with the planar MA is the ground state, whose total energy is lower than that of the ²E_g state.