Abstract
We describe techniques for the robust detection of community structure in some classes of time-dependent networks. Specifically, we consider the use of statistical null models for facilitating the principled identification of structural modules in semi-decomposable systems. Null models play an important role both in the optimization of quality functions such as modularity and in the subsequent assessment of the statistical validity of identified community structure. We examine the sensitivity of such methods to model parameters and show how comparisons to null models can help identify system scales. By considering a large number of optimizations, we quantify the variance of network diagnostics over optimizations (“optimization variance”) and over randomizations of network structure (“randomization variance”). Because the modularity quality function typically has a large number of nearly degenerate local optima for networks constructed using real data, we develop a method to construct representative partitions that uses a null model to correct for statistical noise in sets of partitions. To illustrate our results, we employ ensembles of time-dependent networks extracted from both nonlinear oscillators and empirical neuroscience data.
Many social, physical, technological, and biological systems can be modeled as networks composed of numerous interacting parts.1 As an increasing amount of time-resolved data has become available, it has become increasingly important to develop methods to quantify and characterize dynamic properties of temporal networks.2 Generalizing the study of static networks, which are typically represented using graphs, to temporal networks entails the consideration of nodes (representing entities) and/or edges (representing ties between entities) that vary in time. As one considers data with more complicated structures, the appropriate network analyses must become increasingly nuanced. In the present paper, we discuss methods for algorithmic detection of dense clusters of nodes (i.e., communities) by optimizing quality functions on multilayer network representations of temporal networks.3, 4 We emphasize the development and analysis of different types of null-model networks, whose appropriateness depends on the structure of the networks one is studying as well as the construction of representative partitions that take advantage of a multilayer network framework. To illustrate our ideas, we use ensembles of time-dependent networks from the human brain and human behavior.
INTRODUCTION
Myriad systems have components whose interactions (or the components themselves) change as a function of time. Many of these systems can be investigated using the framework of temporal networks, which consist of sets of nodes and/or edges that vary in time.2 The formalism of temporal networks is convenient for studying data drawn from areas such as person-to-person communication (e.g., via mobile phones5, 6), one-to-many information dissemination (such as Twitter networks7), cell biology, distributed computing, infrastructure networks, neural and brain networks, and ecological networks.2 Important phenomena that can be studied in this framework include network constraints on gang and criminal activity,8, 9 political processes,10, 11 human brain function,4, 12 human behavior,13 and financial structures.14, 15
Time-dependent complex systems can have densely connected components in the form of cohesive groups of nodes known as “communities” (see Fig. 1), which can be related to a system's functional modules.16, 17 A wide variety of clustering techniques have been developed to identify communities, and they have yielded insights in the study of the committee structure in the United States Congress,18 functional groups in protein interaction networks,19 functional modules in brain networks,4 and more. A particularly successful technique for identifying communities in networks16, 20 is optimization of a quality function known as “modularity,”21 which recently has been generalized for detecting communities in time-dependent and multiplex networks.3
Figure 1.
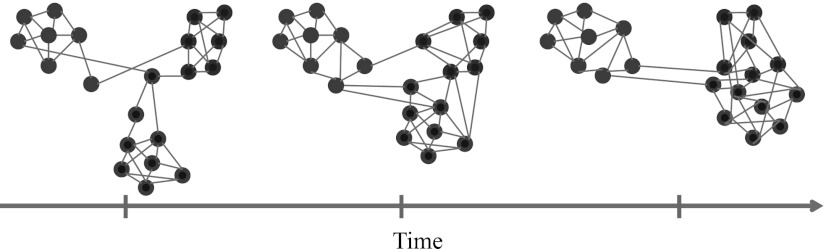
An important property of many real-world networks is community structure, in which there exist cohesive groups of nodes such that a network has stronger connections within such groups than it does between such groups. Community structure often changes in time, which can lead to the rearrangement of cohesive groups, the formation of new groups, and the fragmentation of existing groups.
Modularity optimization allows one to algorithmically partition a network's nodes into communities such that the total connection strength within groups of the partition is more than would be expected in some null model. However, modularity optimization always yields a network partition (into a set of communities) as an output whether or not a given network truly contains modular structure. Therefore, application of subsequent diagnostics to a network partition is potentially meaningless without some comparison to benchmark or null-model networks. That is, it is important to establish whether the partition(s) obtained appear to represent meaningful community structures within the network data or whether they might have reasonably arisen at random. Moreover, robust assessment of network organization depends fundamentally on the development of statistical techniques to compare structures in a network derived from real data to those in appropriate models (see, e.g., Ref. 22). Indeed, as the constraints in null models and network benchmarks become more stringent, it can become possible to make stronger claims when interpreting organizational structures such as community structure.
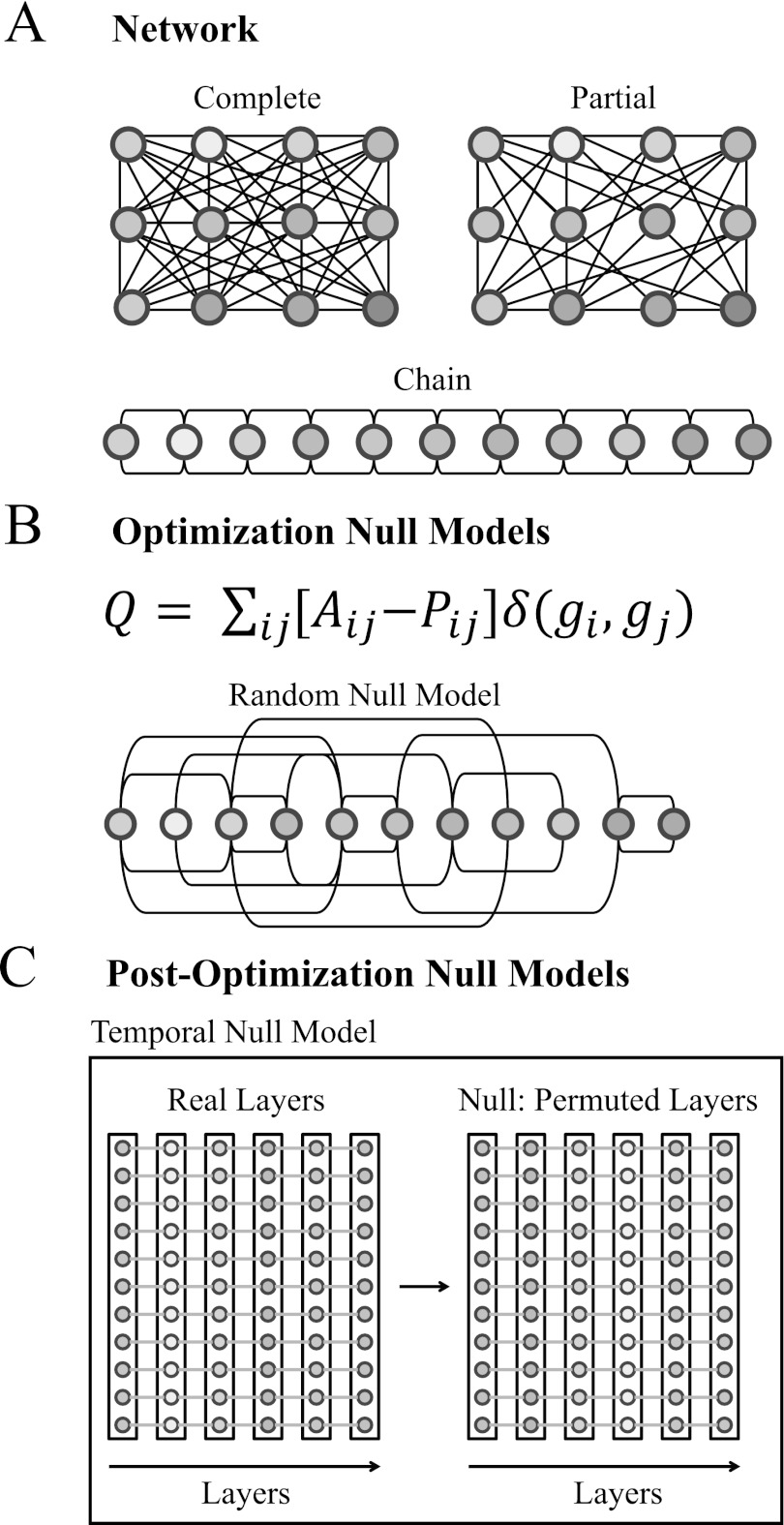
In the present paper, we examine null models in time-dependent networks and investigate their use in the algorithmic detection of cohesive, dynamic communities in such networks (see Fig. 2). Indeed, community detection in temporal networks necessitates the development of null models that are appropriate for such networks. Such null models can help provide bases of comparison at various stages of the community-detection process, and they can thereby facilitate the principled identification of dynamic structure in networks. Indeed, the importance of developing null models extends beyond community detection, as such models make it possible to obtain statistically significant estimates of network diagnostics.
Figure 2.
Methodological considerations important in the investigation of dynamic community structure in temporal networks. (A) Depending on the system under study, a single network layer (which is represented using an ordinary adjacency matrix with an extra index to indicate the layer) might by definition only allow edges from some subset of the complete set of node pairs, as is the case in the depicted chain-like graph. We call such a situation partial connectivity. (B) Although the most common optimization null model employs random graphs (e.g., the Newman-Girvan null model, which is closely related to the configuration model1, 16), other models can also provide important insights into network community structure. (C) After determining a set of partitions that maximize the modularity Q (or a similar quality function), it is interesting to test whether the community structure is different from, for example, what would be expected with a scrambling of time layers (i.e., a temporal null model) or node identities (i.e., a nodal null model).4
Our dynamic network null models fall into two categories: optimization null models, which we use in the identification of community structure; and post-optimization null models, which we use to examine the identified community structure. We describe how these null models can be selected in a manner appropriate to known features of a network's construction, identify potentially interesting network scales by determining values of interest for structural and temporal resolution parameters, and inform the choice of representative partitions of a network into communities.
METHODS
Community detection
Community-detection algorithms provide ways to decompose a network into dense groups of nodes called “modules” or “communities.” Intuitively, a community consists of a set of nodes that are connected among one another more densely than they are to nodes in other communities. A popular way to identify community structure is to optimize a quality function, which can be used to measure the relative densities of intra-community connections versus inter-community connections. See Refs. 16, 20, 23 for recent reviews on network community structure and Refs. 24, 25, 26, 27 for discussions of various caveats that should be considered when optimizing quality functions to detect communities.
One begins with a network of N nodes and a given set of connections between those nodes. In the usual case of single-layer networks (e.g., static networks with only one type of edge), one represents a network using an adjacency matrix A. The element Aij of the adjacency matrix indicates a direct connection or “edge” from node i to node j, and its value indicates the weight of that connection. The quality of a hard partition of A into communities (whereby each node is assigned to exactly one community) can be quantified using a quality function. The most popular choice is modularity16, 20, 21, 28, 29
| (1) |
where node i is assigned to community gi, node j is assigned to community gj, the Kronecker delta if and it equals 0 otherwise, γ is a resolution parameter (which we will call a structural resolution parameter), and Pij is the expected weight of the edge connecting node i to node j under a specified null model. The choice is very common, but it is important to consider multiple values of γ to examine groups at multiple scales.16, 30, 31 Maximization of Q0 yields a hard partition of a network into communities such that the total edge weight inside of modules is as large as possible (relative to the null model and subject to the limitations of the employed computational heuristics, as optimizing Q0 is NP-hard16, 20, 32).
Recently, the null model in the quality function 1 has been generalized so that one can consider sets of L adjacency matrices, which are combined to form a rank-3 adjacency tensor A that can be used to represent time-dependent or multiplex networks. One can thereby define a multilayer modularity (also called “multislice modularity”)3
| (2) |
where the adjacency matrix of layer l has components Aijl, the element Pijl gives the components of the corresponding layer-l matrix for the optimization null model, is the structural resolution parameter of layer l, the quantity gil gives the community assignment of node i in layer l, the quantity gjr gives the community assignment of node j in layer r, the element gives the connection strength (i.e., an “interlayer coupling parameter,” which one can call a temporal resolution parameter if one is using the adjacency tensor to represent a time-dependent network) from node j in layer r to node j in layer l, the total edge weight in the network is , the strength (i.e., weighted degree) of node j in layer l is , the intra-layer strength of node j in layer l is , and the inter-layer strength of node j in layer l is .
Equivalent representations that use other notation can, of course, be useful. For example, multilayer modularity can be recast as a set of rank-2 matrices describing connections between the set of all nodes across layers [e.g., for spectral partitioning29, 33, 34]. One can similarly generalize Q for higher-rank tensors, which one can use when studying community structure in networks that are both time-dependent and multiplex, through appropriate specification of inter-layer coupling tensors.
Network diagnostics
To characterize multilayer community structure, we compute four example diagnostics for each hard partition: the modularity Q, the number of modules n, the mean community size s (which is equal to the number of nodes in the community and is proportional to 1/n), and the stationarity ζ.35 To compute ζ, we calculate the autocorrelation function U(t, t + m) of two states of the same community G(t) at m time steps (i.e., m network layers) apart
| (3) |
where is the number of nodes that are members of both G(t) and G(t + m), and is the number of nodes in the union of the community at times t and t + m. Defining t0 to be the first time step in which the community exists and to be the last time in which it exists, the stationarity of a community is35
| (4) |
This gives the mean autocorrelation over consecutive time steps.36
In addition to these diagnostics, which are defined using the entire multilayer community structure, we also compute two example diagnostics on the community structures of the component layers: the mean single-layer modularity and the variance of the single-layer modularity over all layers. The single-layer modularity Qs is defined as the static modularity quality function, , computed for the partition g that we obtained via optimization of the multilayer modularity function Q. We have chosen to use a few simple ways to help characterize the time series for Qs, though of course other diagnostics can also be informative.
Data sets
We illustrate dynamic network null models using two example network ensembles: (1) 75-time-layer brain networks drawn from each of 20 human subjects and (2) behavioral networks with about 150 time layers drawn from each of 22 human subjects. Importantly, the use of network ensembles makes it possible to examine robust structure (and also its variance) over multiple network instantiations. We have previously examined both data sets in the context of neuroscientific questions.4, 13 In this paper, we use them as illustrative examples for the consideration of methodological issues in the detection of dynamic communities in temporal networks.
These two data sets, which provide examples of different types of network data, illustrate a variety of issues in network construction: (1) node and edge definitions, (2) complete versus partial connectivity, (3) ordered versus categorical nodes, and (4) confidence in edge weights. In many fields, determining the definition of nodes and edges is itself an active area of investigation.37 See, for example, several recent papers that address such questions in the context of large-scale human brain networks38, 39, 40, 41, 42, 43 and in networks more generally.44 Another important issue is whether to examine a given adjacency matrix in an exploratory manner or to impose structure on it based on a priori knowledge. For example, when nodes are categorical, one might represent their relations using a fully connected network and then identify communities of any group of nodes. However, when nodes are ordered—and particularly when they are in a chain of weighted nearest-neighbor connections—one expects communities to group neighboring nodes in sequence, as typical community-detection methods are unlikely to yield many out-of-sequence jumps in community assignment. The issue of confidence in the estimation of edge weights is also very important, as it can prompt an investigator to delete edges from a network when their statistical validity is questionable. A closely related issue is how to deal with known or expected missing data, which can affect either the presence or absence of nodes themselves or the weights of edges.45, 46, 47, 48
Data set 1: Brain networks
Our first data set contains categorical nodes with partial connectivity and variable confidence in edge weights. The nodes remain unchanged in time, and edge weights are based on covariance of node properties. This covariance structure is non-local in the sense that weights exist between both topologically neighboring nodes and topologically distant nodes.49, 50 This property has been linked in other dynamical systems to behaviors such as chimera states, in which coherent and incoherent regions coexist.51, 52, 53 Another interesting feature of this data set is that it is drawn from an experimental measurement with high spatial resolution (on the order of centimeters) but relatively poor temporal resolution (on the order of seconds).
As described in more detail in Ref. 4, we construct an ensemble of networks (20 individuals over 3 experiments, which yields 60 multilayer networks) that represent the functional connectivity between large regions of the human brain. In these networks, N = 112 centimeter-scale, anatomically distinct brain regions are our (categorical) network nodes. We study the temporal interaction of these nodes—such interactions are thought to underly cognitive function—by first measuring their activity every 2 s during simple finger movements using functional magnetic resonance imaging (fMRI). We cut these regional time series into time slices (which yield layers in the multilayer network) of roughly 3-min duration. Each such layer corresponds to a time series whose length is 80 units.
To estimate the interactions (i.e., edge weights) between nodes, we calculate a measure of statistical similarity between regional activity profiles.54 Using a wavelet transform, we extract frequency-specific activity from each time series in the range 0.06–0.12 Hz. For each time layer l and each pair of regions i and j, we define the weight of an edge connecting region i to region j using the coherence between the wavelet-coefficient time series in each region, and these weights form the elements of a weighted, undirected temporal network W with components . The magnitude-squared coherence Gij between time series i and j is a function of frequency. It is defined by the equation
| (5) |
where and are the power spectral density functions of i and j, respectively, and is the cross-power spectral density function of i and j. We let Hij denote the mean of over the frequency band of interest, and the weight of edge Wijl is equal to Hij computed for layer l.
We use a false-discovery rate correction55 to threshold connections whose coherence values are not significantly greater than that expected at random. This yields a multilayer network A with components Aijl (i.e., a rank-3 adjacency tensor). The nonzero entries in A retain their weights. We couple the layers of A to one another with temporal resolution parameters of weight between node j in layer r and node j in layer l. In this paper, we let be identical between each node j in a given layer and itself in nearest-neighbor layers. (In all other cases, .)
In Fig. 3a, we show an example time layer from A for a single subject in this experimental data. In this example, the statistical threshold is evinced by the set of matrix elements set to 0. Because brain network nodes are categorical, one can apply community detection algorithms in these situations to identify communities composed of any set of nodes. (Note that the same node from different times can be assigned to the same community even if the node is assigned to other communities at intervening times.) One biological interpretation of network communities in brain networks is that they represent groups of nodes that serve distinct cognitive functions (e.g., vision, memory, etc.) that can vary in time.12, 56
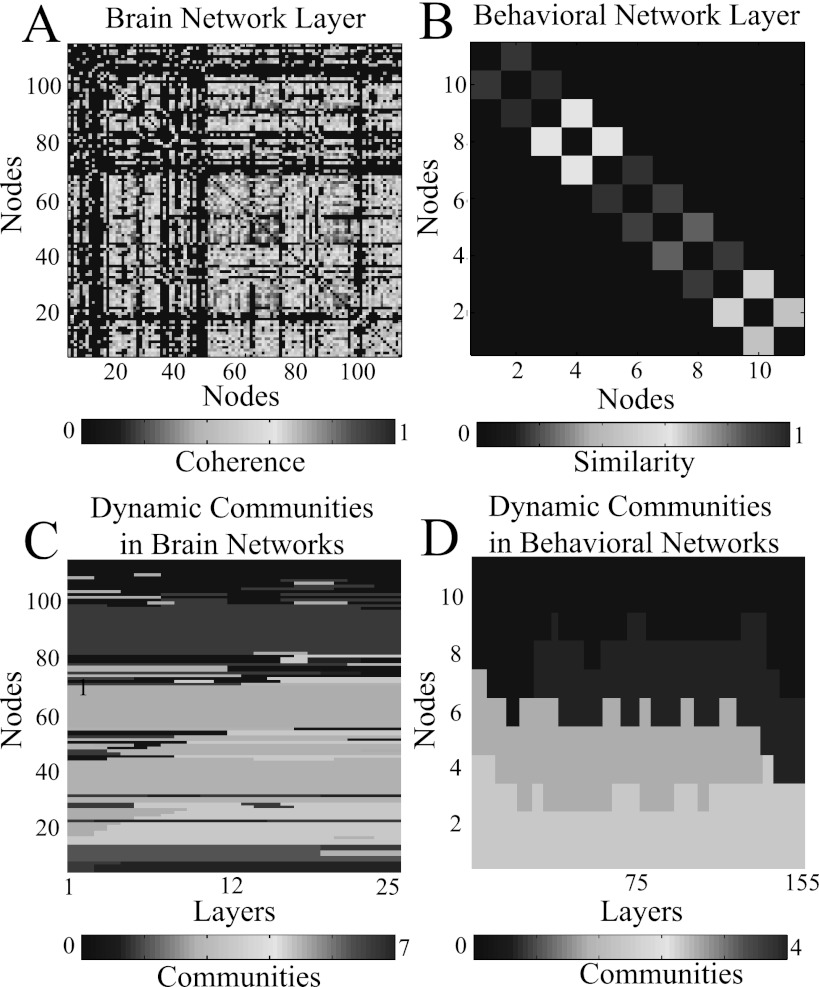
Figure 3.
Network layers and community assignments from two example data sets: (A) a brain network based on correlations between blood-oxygen-level-dependent (BOLD) signals4 and (B) a behavioral network based on similarities in movement times during a simple motor learning experiment.13 We use these data sets to illustrate situations with categorical nodes and ordered nodes, respectively. In the bottom panels, we show community assignments obtained using multilayer community detection for (C) the brain networks and (D) the behavioral networks.
Data set 2: Behavioral networks
Our second data set contains ordered nodes that remain unchanged in time. The network topology in this case is highly constrained, as edges are only present between consecutive nodes. (We call this “nearest-neighbor” coupling.) Another interesting feature of this data set is that the number of time slices is an order of magnitude larger than the number of nodes in a slice.
As described in more detail in Ref. 13, we construct an ensemble of 66 behavioral networks from 22 individuals and 3 experimental conditions. These networks represent a set of finger movements in the same simple motor learning experiment from which we constructed the brain networks in data set 1. Subjects were instructed to press a sequence of buttons corresponding to a sequence of 12 pseudo-musical notes shown to them on a screen.
Each node represents an interval between consecutive button presses. A single network layer consists of N = 11 nodes (i.e., there is one interval between each pair of notes), which are connected in a chain via weighted, undirected edges. In Ref. 13, we examined the phenomenon of motor “chunking,” which is a fascinating but poorly understood phenomenon in which groups of movements are made with similar inter-movement durations. (This is similar to remembering a phone number in groups of a few digits or grouping notes together as one masters how to play a song.) For each experimental trial l and each pair of inter-movement intervals i and j, we define the weight of an edge connecting inter-movement i to inter-movement j as the normalized similarity in inter-movement durations. The normalized similarity between nodes i and j is defined as
| (6) |
where dijl is the absolute value of the difference of lengths of the ith and jth inter-movement time intervals in trial l and is the maximum value of dijl in trial l. These weights yield the elements Wijl of a weighted, undirected multilayer network W. Because finger movements occur in series, inter-movement i is connected in time to inter-movement i ± 1 but not to any other inter-movements i + n for .
To encode this conceptual relationship as a network, we set all non-contiguous connections in W to 0 and thereby construct a weighted, undirected chain networkA. In Fig. 3b, we show an example trial layer from A for a single subject in this experimental data. We couple layers of A to one another with weight , which gives the connection strength between node j in experimental trial r and node j in trial l. In a given instantiation of the network, we again let be identical for all nodes j for all connections between nearest-neighbor layers. (Again, in all other cases.) Because inter-movement nodes are ordered, one can apply community-detection algorithms to identify communities of nodes in sequence. Each community represents a motor “chunk.”
RESULTS
Modularity-optimization null models
After constructing a multilayer network A with elements Aijl, it is necessary to select an optimization null model P in Eq. 2. The most common modularity-optimization null model used in undirected, single-layer networks is the Newman-Girvan null model16, 20, 21, 28, 29
| (7) |
where is the strength of node i and . The definition 7 can be extended to multilayer networks using
| (8) |
where is the strength of node i in layer l and . Optimization of Q using the null model 8 identifies partitions of a network into groups that have more connections (in the case of binary networks) or higher connection densities (in the case of weighted networks) than would be expected for the distribution of connections (or connection densities) expected in a null model. We use the notation for the layer-l adjacency matrix composed of elements Aijl and the notation to denote the layer-l null-model matrix with elements Pijl. See Fig. 4a for an example layer from a multilayer behavioral network and Fig. 4b for an example instantiation of the Newman-Girvan null model .
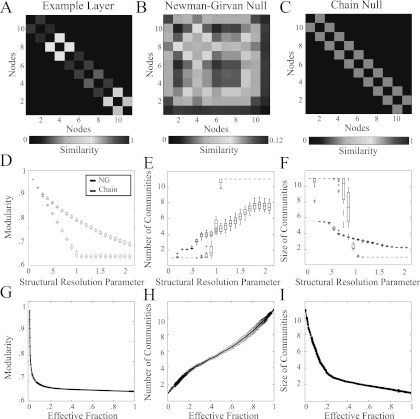
Figure 4.
Modularity-optimization null models. (A) Example layer from a behavioral network. (B) Newman-Girvan and (C) chain null models for the layer shown in panel (A). (D) Optimized multilayer modularity value Q, (E) number of communities n, and (F) mean community size s for the complete multilayer behavioral network employing the Newman-Girvan (black) and chain (red) optimization null models as a function of the structural resolution parameter γ. (G)Optimized modularity value Q, (H) number of communities n, and (I) mean community size s for the multilayer behavioral network employing chain optimization null models as a function of the effective fraction of edges that have larger weights than their null-model counterparts. We averaged the values of Q, n, and s over the 3 different 12-note sequences and C = 100 optimizations. Box plots in (D-F) indicate quartiles and 95% confidence intervals over the 22 individuals in the study. The error bars in panels (G-I) indicate a standard deviation from the mean. In some instances, this is smaller than the line width. The temporal resolution-parameter value is .
Optimization null models for ordered node networks
The Newman-Girvan null model is particularly useful for networks with categorical nodes, in which a connection between any pair of nodes can occur in theory. However, when using a chain network of ordered nodes, it is useful to consider alternative null models. For example, in a network represented by an adjacency matrix A′, one can define
| (9) |
where ρ is the mean edge weight of the chain network and A′ is the binarized version of A, in which nonzero elements of A are set to 1 and zero-valued elements remain unaltered. Such a null model can also be defined for a multilayer network that is represented by a rank-3 adjacency tensor A. One can construct a null model P with components
| (10) |
where is the mean edge weight in layer l and A′ is the binarized version of A. The optimization of Q using this null model identifies partitions of a network whose communities have a larger strength than the mean. See Fig. 4c for an example of this chain null model for the behavioral network layer shown in Fig. 4a.
In Fig. 4d, we illustrate the effect that the choice of optimization null model has on the modularity values Q of the behavioral networks as a function of the structural resolution parameter. (Throughout the manuscript, we use a Louvain-like locally greedy algorithm to maximize the multilayer modularity quality function.57, 58) The Newman-Girvan null model gives decreasing values of Q for , whereas the chain null model produces lower values of Q, which behaves in a qualitatively different manner for versus . To help understand this feature, we plot the number and mean size of communities as a function of γ in Figs. 4e, 4f. As γ is increased, the Newman-Girvan null model yields network partitions that contain progressively more communities (with progressively smaller mean size). The number of communities that we obtain in partitions using the chain null model also increases with γ, but it does so less gradually. For , one obtains a network partition consisting of a single community of size ; for , each node is instead placed in its own community. For , nodes are assigned to several communities whose constituents vary with time (see, for example, Fig. 3d).
The above results highlight the sensitivity of network diagnostics such as Q, n, and s to the choice of an optimization null model. It is important to consider this type of sensitivity in the light of other known issues, such as the extreme near-degeneracy of quality functions like modularity.24 Importantly, the use of the chain null model provides a clear delineation of network behavior in this example into three regimes as a function of γ: a single community with variable Q (low γ), a variable number of communities as Q reaches a minimum value (), and a set of singleton communities with minimum Q (high γ). This illustrates that it is crucial to consider a null model appropriate for a given network, as it can provide more interpretable results than just using the usual choices (such as the Newman-Girvan null model).
The structural resolution parameter γ can be transformed so that it measures the effective fraction of edges that have larger weights than their null-model counterparts.31 One can define a generalization of ξ to multilayer networks, which allows one to examine the behavior of the chain null model near in more detail. For each layer l, we define a matrix with elements , and we then define to be the number of elements of that are less than 0. We sum over layers in the multilayer network to construct . The transformed structural resolution parameter is then given by
| (11) |
where is the value of γ for which the network still forms a single community in the multilayer optimization, and is the value of γ for which the network still forms N singleton communities in the multilayer optimization. (We use Roman typeface in the subscripts in and to emphasize that we are describing multilayer objects and, in particular, that the subscripts do not represent indices.) In Figs. 4g, 4h, 4i, we report the optimized (i.e., maximized) modularity value, the number of communities, and the mean community size as functions of the transformed structural resolution parameter . (Compare these plots to Figs. 4d, 4e, 4f.) For all three diagnostics, the apparent transition points seem to be more gradual as a function of than they are as a function of γ. For systems like the present one that do not exhibit a pronounced, nontrivial plateau in these diagnostics as a function of a structural resolution parameter, it might be helpful to have a priori knowledge about the expected number or sizes of communities (see, e.g., Ref. 13) to help guide further investigation.
Optimization null models for networks derived from time series
Although the Newman-Girvan null model can be used in networks with categorical nodes, such as the brain networks in data set 1 (see Fig. 5a), it does not take advantage of the fact that these networks are derived from similarities in time series. Accordingly, we generate surrogate data to construct two dynamic network null models for community detection that might be particularly appropriate for networks derived from time-series data.
Figure 5.
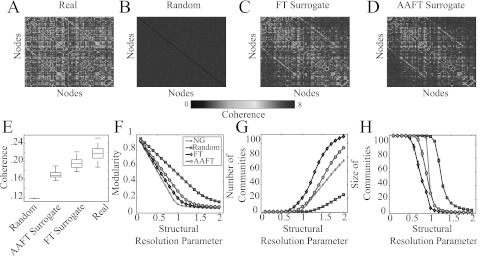
Modularity-optimization null models for time series. (A) Example coherence matrix averaged over layers from a brain network. (B) Random time shuffle, (C) FT surrogate, and (D) AAFT surrogate null models averaged over layers. (E) Coherence of each matrix type averaged over subjects, scans, and layers. We note that the apparent lack of structure in (B) is partially related to its significantly decreased coherence in comparison to the other models. (F) Optimized modularity values Q, (G) number of communities n, and (H) mean community size s for the multilayer brain network employing the Newman-Girvan (black), random time-shuffle (blue), FT surrogate (gray), and AAFT surrogate (red) optimization null models as functions of the structural resolution parameter γ. We averaged the values of these diagnostics over 3 different scanning sessions and C = 100 optimizations. Box plots indicate quartiles and 95% confidence intervals over the 20 individuals in the study. The temporal resolution parameter is .
First, we note that a simple null model (which we call “Random”) for time series is to randomize the elements of the time-series vector for each node before computing the similarity matrix (see Fig. 5b).59 However, the resulting time series do not have the mean or variance of the original time series, and this yields a correlation- or coherence-based network with very low edge weights. To preserve the mean, variance, and autocorrelation function of the original time series, we employ a surrogate-data generation method that scrambles the phase of time series in Fourier space.60 Specifically, we assume that the linear properties of the time series are specified by the squared amplitudes of the discrete Fourier transform (FT)
| (12) |
where sv denotes an element in a time series of length V. (That is, V is the number of elements in the time-series vector.) We construct surrogate data by multiplying the Fourier transform by phases chosen uniformly at random and transforming back to the time domain
| (13) |
where are chosen independently and uniformly at random.61 This method, which we call the FT surrogate (see Fig. 5c), has been used previously to construct covariance matrices62 and to characterize networks.63 A modification of this method, which we call the amplitude-adjusted Fourier transform (AAFT) surrogate, allows one to also retain the amplitude distribution of the original signal64 (see Fig. 5d). One can alter nonlinear relationships between time series while preserving linear relationships between time series by applying an identical shuffling to both time series; one can alter both linear and nonlinear relationships between time series by applying independent shufflings to each time series.60
We demonstrate in Fig. 5e that, among the four null models that we consider, the mean coherence of pairs of FT surrogate series match that of the original data most closely. Pairs of Random time series have the smallest mean coherence, and pairs of AAFT surrogate series have the next smallest. The fact that the AAFT surrogate is less like the real data (in terms of mean coherence) than the simpler FT surrogate might stem from a rescaling step62 that causes the power spectrum to whiten (i.e., the step flattens the power spectral density).65, 83, 84 In Figs. 5f, 5g, 5h, we show three diagnostics (optimized modularity, mean community size, and number of communities) as a function of the structural resolution parameter γ for the various optimization null models. We note that the Newman-Girvan null model produces the smallest Q value and a middling community size, whereas the surrogate time series models produce higher Q values and more communities of smaller mean size. The Random null model produces the largest value of Q and the fewest communities, which is consistent with the fact that it contains the smallest amount of shared information (i.e., mean coherence) with the real network.
Post-optimization null models
After identifying the partition(s) that maximize modularity, one might wish to determine whether the identified community structure is significantly different from that expected under other null hypotheses. For example, one might wish to know whether any temporal evolution is evident in the dynamic community structure (see Fig. 2c). To do this, one can employ post-optimization null models, in which a multilayer network is scrambled in some way to produce a new multilayer network. One can then maximize the modularity of the new network and compare the resulting community structure to that obtained using the original network. Unsurprisingly, one's choice of post-optimization null model should be influenced by the question of interest, and it should also be constrained by properties of the network under examination. We explore such influences and constraints using our example networks.
Intra-layer and inter-layer null models
There are various ways to construct connectional null models (i.e., intra-layer null models), which randomize the connectivity structure within a network layer ().4, 66 For binary networks, one can obtain ensembles of random graphs with the same mean degree as that of a real network using Erdős-Rényi random graphs,1 and ensembles of weighted random networks can similarly be constructed from weighted random graph models.67 To retain both the mean and distribution of edge weights, one can employ a permutation-based connectional null model that randomly rewires network edges with no additional constraints by reassigning uniformly at random the entire set of matrix elements Aijl in the lth layer (i.e., the matrix ). Other viable connectional null models include ones that preserve degree21, 68 or strength69 distributions, or—for networks based on time-series data—preserve length, frequency content, and amplitude distribution of the original time series.70 In this section, we present results for a few null models that are applicable to a variety of temporal networks. We note, however, that this is a fruitful area of further investigation.
We employ two connectional null models specific for the broad classes of networks represented by the brain and behavioral networks that we use as examples in this paper. The brain networks provide an example of time-dependent similarity networks, which are weighted and either fully connected or almost fully connected.31 (The brain networks have some 0 entries in their corresponding adjacency tensors because we have removed edges with weights that are not statistically significant.4) We, therefore, employ a constrained null model that is constructed by randomly rewiring edges while maintaining the empirical degree distribution.68 In Fig. 6a1, we demonstrate the use of this null model to assess dynamic community structure. Importantly, this constrained null model can be used in principle for any binary or weighted network, though it does not take advantage of specific structure (aside from strength distribution) that one might want to exploit. For example, the behavioral networks have chain-like topologies, and it is desirable to develop models that are specifically appropriate for such situations. (One can obviously make the same argument for other specific topologies.) We, therefore, introduce a highly constrained connectional null model that is constructed by reassigning edge weights uniformly at random to existing edges. This does not change the underlying binary topology. (That is, we preserve network topology but scramble network geometry.) We demonstrate the use of this null model in Fig. 6b1.
Figure 6.
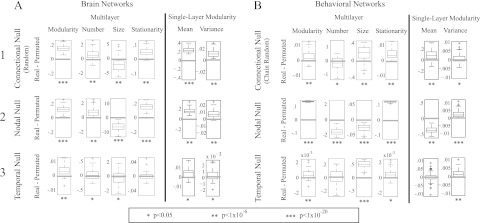
Post-optimization null models. We compare four multilayer diagnostics (optimized modularity, number of communities, mean community size, and stationarity) and two single-layer diagnostics (mean and variance of Qs) for (A) brain and (B) behavioral networks with the connectional (row 1), nodal (row 2), and temporal (row 3) null-model networks. Box plots indicate quartiles and 95% confidence intervals over the individuals and experimental conditions. The structural resolution parameter is , and the temporal resolution parameter is .
In addition to intra-layer null models, one can also employ inter-layer null models—such as ones that scramble time or node identities.4 For example, we construct a temporal null model by randomly permuting the order of the network layers. This temporal null model can be used to probe the existence of significant temporal evolution of community structure. One can also construct a nodal null model by randomly permuting the inter-layer edges that connect nodes in one layer to nodes in another. After the permutation is applied, an inter-layer edge can, for example, connect node i in layer t with node in layer t + 1 rather than being constrained to connect each node i in layer t with itself in layer t + 1. One can use this null model to probe the importance of node identity in network organization. We demonstrate the use of our temporal null model in row 2 of Fig. 6, and we demonstrate the use of our nodal null model in row 3 of Fig. 6.
Calculation of diagnostics on real versus null-model networks
We characterize the effects of post-optimization null models using four diagnostics: maximized modularity Q, the number of communities n, the mean community size s, and the stationarity ζ (see Sec. 2B for definitions). Due to the possibly large number of partitions with nearly optimal Q,24 the values of such diagnostics vary over realizations of a computational heuristic for both the real and null-model networks. (We call this optimization variance.) The null-model networks also have a second source of variance (which we call randomization variance) from the myriad possible network configurations that can be constructed from a randomization procedure. We note that a third type of variance—ensemble variance—can also be present in systems containing multiple networks. In the example data sets that we discuss, this represents variability among experimental subjects.
We test for statistical differences between the real and null-model networks as follows. We first compute C = 100 optimizations of the modularity quality function for a network constructed from real data and then compute the mean of each of the four diagnostics over these C samples. This yields representative values of the diagnostics. We then maximize modularity for C different randomizations of a given null model (i.e., 1 optimization per randomization) and then compute the mean of each of the four diagnostics over these C samples. For both of our example data sets, we perform this two-step procedure for each network in the ensemble (60 brain networks and 66 behavioral networks; see “Sec. 2”). We then investigate whether the set of representative diagnostics for the networks constructed from real data are different from those of appropriate ensembles of null-model networks. To address this issue, we subtract the diagnostic value for the null model from that of the real network for each subject and experimental session. We then use one-sample t-tests to determine whether the resulting distribution differs significantly from 0. We show our results in Fig. 6.
Results depend on all three factors (the data set, the null model, and the diagnostic), but there do seem to be some general patterns. For example, the real networks exhibit the most consistent differences from the nodal null model for all diagnostics and both data sets (see row 2 of Fig. 6). For both data sets, the variance of single-layer modularity in the real networks is consistently greater than those for all three null models, irrespective of the mean (see the final two columns of Figs. 6a, 6b); this is a potential indication of the statistical significance of the temporal evolution. However, although optimized modularity is higher in the real network for both data sets, the number of communities is higher in the set of brain networks and lower in the set of behavioral networks. Similarly, in comparison to the connectional null model, higher modularity is associated with a smaller mean community size in the brain networks but a larger mean size in the behavioral networks (see row 1 of Fig. 6). These results demonstrate that the three post-optimization null models provide different information about the network structure of the two systems and thereby underscores the critical need for further investigations of null-model construction.
Structural and temporal resolution parameters
When optimizing multilayer modularity, we must choose (or otherwise derive) values for the structural resolution parameter γ and the temporal resolution parameter ω. By varying γ, one can tune the size of communities within a given layer: large values of γ yield more communities, and small values yield fewer communities. A systematic method for how to determine values of has not yet been discussed in the literature. In principle, one could choose different values for different nodes, but we focus on the simplest scenario in which the value of is identical for all nodes j and all contiguous pairs of layers l and r (and is otherwise 0). In this framework, the temporal resolution parameter ω provides a means of tuning the number of communities discovered across layers: high values of ω yield fewer communities, and low values yield more communities. It is beneficial to study a range of parameter values to examine the breadth of structural (i.e., intra-layer24, 25, 71) and temporal (i.e., inter-layer) resolutions of community structure, and some papers have begun to make progress in this direction.3, 4, 13, 31, 72
To characterize community structure as a function of resolution-parameter values (and hence of system scales), we quantify the quality of partitions using the mean value of optimized Q. To do this, we examine the constitution of the partitions using the mean similarity over C optimizations, and we compute partition similarities using the z-score of the Rand coefficient.73 For comparing two partitions α and β, we calculate the Rand z-score in terms of the network's total number of pairs of nodes M, the number of pairs that are in the same community in partition α, the number of pairs that are in the same community in partition β, and the number of pairs that are assigned to the same community both in partition α and in partition β. The z-score of the Rand coefficient comparing these two partitions is
| (14) |
where is the standard deviation of (as in Ref. 73). Let the mean partition similarity z denote the mean value of over all possible partition pairs for .
In Fig. 7, we show both z and optimized Q as a function of γ and ω in both brain and behavioral networks. The highest modularity values occur for low γ and high ω. The mean partition similarity is high for large γ in the brain networks, and it is high for both small and large γ in the behavioral networks. Interestingly, in both systems, the partition similarity when is lower than it is elsewhere in the parameter plane, so the variability in partitions tends to be large at this point. Indeed, as shown in the second row of Fig. 7, modularity exhibits significant variability for compared to other resolution-parameter values.
Figure 7.
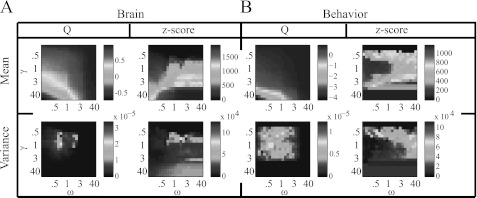
Optimized modularity Q and Rand z-score as functions of the resolution parameters γ and ω for the (A) brain and (B) behavioral networks. The top row shows the mean value of maximized Q over C = 100 optimizations and the mean partition similarity z over all possible pairs of the C partitions. The bottom row shows the variance of maximized Q over the optimizations and the variance of the partition similarity over all possible pairs of partitions. The results shown in this figure come from a single individual and experimental scan, but we obtain qualitatively similar results for other individuals and scans. Note that the axis scalings are nonlinear.
It is useful to be able to determine the ranges of γ and ω that produce community structure that is significantly different from a particular null model. One can thereby use null models to probe resolution-parameter values at which a network displays interesting structures. This could be especially useful in systems for which one wishes to identify length scales (such as a characteristic mean community size) or time scales4, 35, 74, 75 directly from data.
In Fig. 8, we show examples of how the difference between diagnostic values for real and null-model networks varies as a function of γ and ω. As illustrated in panels (A) and (B), the brain and behavioral networks both exhibit a distinctly higher mean optimized modularity than the associated nodal null-model network for . Interestingly, this roundly peaked difference in Q is not evident in comparisons of the real networks to temporal null-model networks (see Figs. 8c, 8d), so resolution-parameter values (and hence system scales) of potential interest might be more identifiable by comparison to nodal than to temporal null models in these examples. It is possible, however, that defining temporal layers over a longer or shorter duration would yield identifiable peaks in the difference in Q.
Figure 8.
Differences, as a function of γ and ω, between the real networks and the (A,B) nodal and (C,D) temporal null models for maximized modularity Q and partition similarity z for the (A,C) brain and (B,D) behavioral networks. The first row in each panel gives the difference in the mean values of the diagnostic variables between the real and null-model networks. Panels (A,B) show the results for and , and panels (C,D) show the results for and . The quantities Q and z again denote the modularity and partition similarity of the real network, Qn and zn denote the modularity and partition similarity of the nodal null-model network, and Qt and zt denote the modularity and partition similarity of the temporal null-model network. The second row in each panel gives the difference between the optimization variance of the real network and the randomization variance of the null-model network for the same diagnostic variable pairs. The third row in each panel gives the difference in the optimization variance of the real network and the optimization variance of the null-model network for the same diagnostic variable pairs. We show results for a single individual and scan in the experiment, but results are qualitatively similar for other individuals and scans. Note that the axis scalings are nonlinear.
The differences in the Rand z-score landscapes are more difficult to interpret, as the values of mean partition similarity z are much larger in the real networks for some resolution-parameter values (positive differences; red) but are much larger in the null-model networks for other resolution-parameter values (negative differences; blue). The clearest situation occurs when comparing the brain's real and temporal null-model networks (see Fig. 8c), as the network built from real data exhibits a much larger value of z (and hence much more consistent optimization solutions) than the temporal null-model networks for high values of γ (i.e., when there are many communities) and low ω (i.e., when there is weak temporal coupling). These results are consistent with the fact that weak temporal coupling in a multilayer network facilitates greater temporal variability in network partitions across time. Such variability appears to be significantly different than the noise induced by scrambling time layers. These results suggest potential resolution values of interest for the brain system, as partitions are very consistent across many optimizations. For example, it would be interesting to investigate community structure in these networks for high γ (e.g., ) and low ω (e.g., ). At these resolution values, one can identify smaller communities with greater temporal variability than the communities identified for the case of .4
The optimization and randomization variances appear to be similar in the brain and behavioral networks (see rows 2–3 in every panel of Fig. 8) not only in terms of their mean values but also in terms of their distribution in the part of the parameter plane that we examined. In particular, the variance in Q is larger in the real networks precisely where the mean is also larger, so mean and variance are likely either dependent on one another or on some common source. Importantly, such dependence influences the ability to draw statistical conclusions because it is possible that the points in the plane with the largest differences in mean are not necessarily the points with the most significant differences in mean.
We also find that the dependencies of the diagnostics on γ and ω are consistent across subjects and scans, suggesting that our results are ensemble-specific rather than individual-specific.
Examination of data generated from a dynamical system
Real-world data are often clouded by unknown or mathematically undefinable sources of variance, so it is also important to examine data sets generated from dynamical systems (or other models). Because we are concerned with time-dependent networks, we consider an example consisting of time-dependent data generated by a well-known dynamical system.
We construct a network of Kuramoto oscillators, in which the phase of the oscillator evolves in time according to
| (15) |
where is the natural frequency of oscillator i, the matrix A gives the binary coupling between each pair of oscillators, and κ is a positive real constant that indicates the strength of the coupling. We draw the frequencies from a Gaussian distribution with mean 0 and standard deviation 1. In our simulations, we use a time step of , a constant of , and a network size of N = 128.
Kuramoto oscillators have been studied in the context of various network topologies and geometries51, 52, 53, 76, 77, 78 and from both the component and ensemble perspectives.79 We are interested in networks with dynamic community structure. Following Refs. 77, 80, we impose a well-defined community structure in which each community is composed of 16 nodes. In each time step, each node has 13 connections with nodes in its own community and 1 connection with nodes outside of its community (see Fig. 9a).
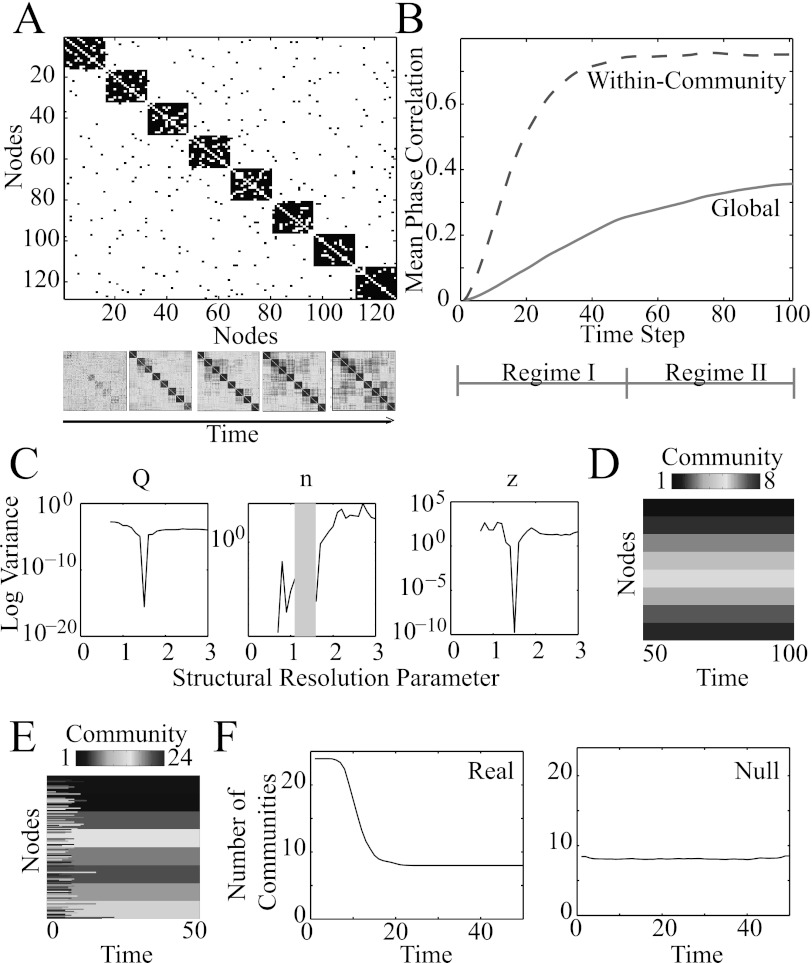
Figure 9.
Dynamic community detection in a network of Kuramoto oscillators. (A, top) The coupling matrix between N = 128 phase oscillators contains 8 communities, each of which has 16 nodes. (A, bottom) Over time, oscillators synchronize with one another. Color indicates the mean phase correlation between oscillators, where hotter (darker gray) colors indicate stronger correlations. (B) Phase correlation between oscillators as a function of time. The mean phase correlation between oscillators in the same community (dashed red curve) increases faster than the mean phase correlation between all oscillators in the system (solid gray curve). Regime I encompasses the first 50 time steps, and regime II emcompasses the subsequent 50 time steps. (C) Variance of maximized multilayer modularity (left), number of communities (middle), and partition similarity z (right) over 100 optimizations of the multilayer modularity quality function for the temporal network in regime II as a function of the structural resolution parameter for . The shaded gray area indicates values of the structural resolution parameter that provide 0 variance in the number of communities. (D) Example partition of the temporal network in regime II at , which occurs near the troughs in panel (C). (E) Example partition of the temporal network in regime I at . (F) Number of communities as a function of time for (left) the temporal network in regime I and (right) its corresponding temporal null model. We averaged values over C = 100 optimizations of multilayer modularity.
To quantify the temporal evolution of synchronization patterns, we define a set of temporal networks given by the time-dependent correlation between pairs of oscillators
| (16) |
where the angular brackets indicate an average over 20 simulations. As time evolves from time step t = 0 to t = 100, oscillators tend to synchronize with other oscillators in their same community more quickly than with oscillators in other communities (see Fig. 9b).
To examine the performance of our multilayer community-detection techniques in this example, we compute and using the multilayer extension of the Newman-Girvan null model Pijl given in Eq. 8. We separately optimize Q for two temporal regimes: (1) regime I (with ), for which the synchronization within communities increases rapidly; and (2) regime II (with ), for which the within-community synchronization level is roughly constant but the global synchronization still increases gradually. We set and probe the effects of the structural resolution parameter γ in regime II. In Figs. 9c, 9d, we illustrate that one can identify the value of γ that best uncovers the underlying hard-wired connectivity using troughs in the optimization variance of several diagnostics (e.g., maximized modularity, number of communities, and mean partition similarity).
We probe the community structure in regime I using the value of γ that best uncovered the underlying hard-wired connectivity in regime II. We observe temporal changes of community structure at early time points, as evidenced by the large number of communities for (see Figs. 9e, 9f). Importantly, the temporal dependence of community number on t is not expected from a post-optimization temporal null model (see the right panel of Fig. 9f). We obtain qualitatively similar results when we optimize the multilayer modularity quality function over the entire temporal network without separating the data into two regimes.
Our results illustrate that one can use dynamic community detection to uncover the resolution of inherent hard-wired structure in a data set extracted from the temporal evolution of a dynamical system and that post-optimization null models can be used to identify regimes of unexpected temporal dependence in network structure.
Dealing with degeneracy: Constructing representative partitions
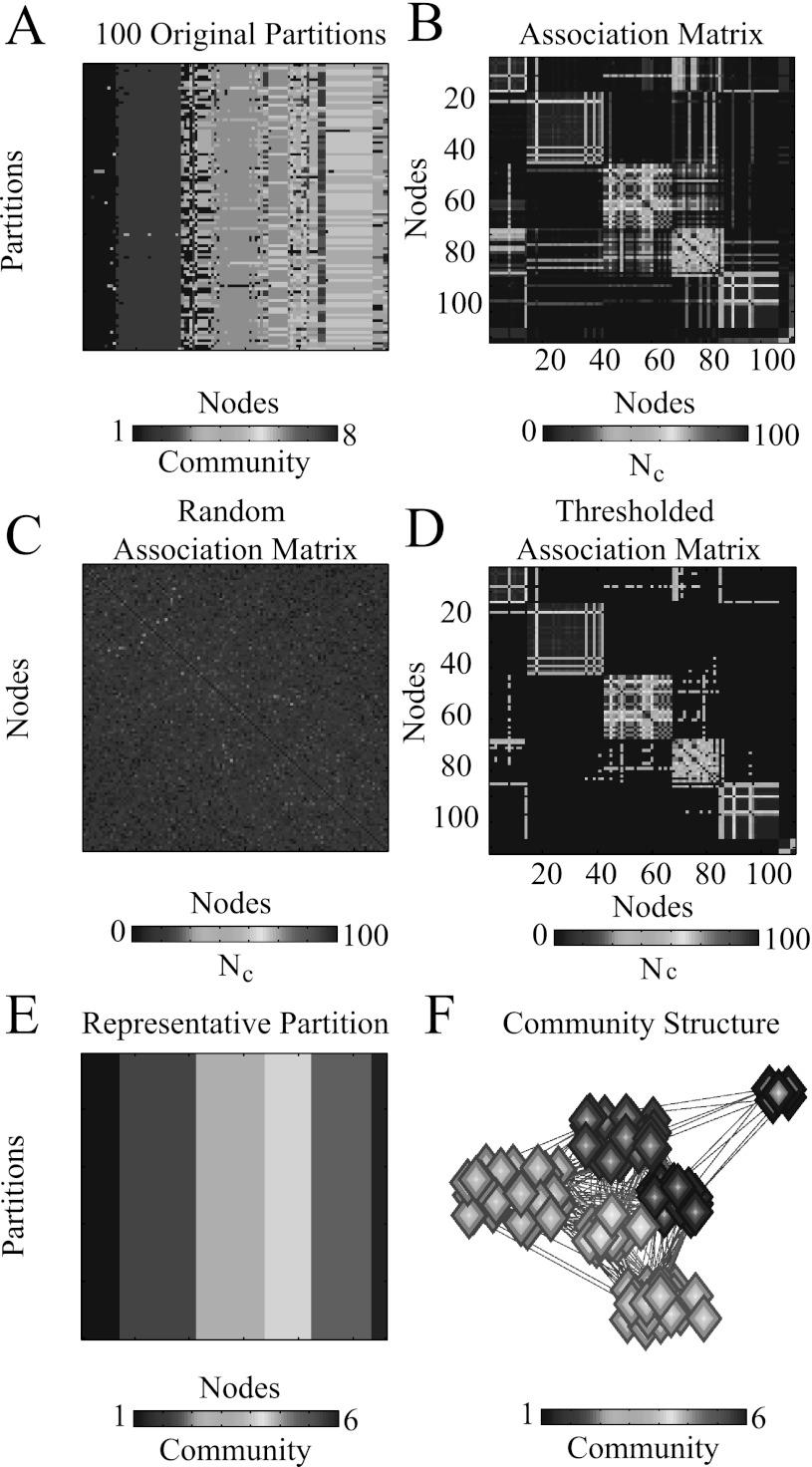
The multilayer modularity quality function has numerous near-degeneracies, so it is important to collect many instantiations when using a non-deterministic computational heuristic to optimize modularity.24 In doing this, an important issue is how (and whether) to distill a single representative partition from a (possibly very large) set of C partitions.81 In Fig. 10, we illustrate a new method for constructing a representative partition based on statistical testing in comparison to null models.
Figure 10.
Constructing representative partitions for an example brain network layer. (A) Partitions extracted during C optimizations of the quality function Q. (B) The N × N nodal association matrix T, whose elements indicate the number of times node i and node j have been assigned to the same community. (C) The N × N random nodal association matrix , whose elements indicate the number of times node i and node j are expected to be assigned to the same community by chance. (D) The thresholded nodal association matrix , where elements with values less than those expected by chance have been set to 0. (E) Partitions extracted during C = 100 optimizations of the single-layer modularity quality function Qs for the matrix T from panel (D). Note that each of the C optimizations yields the same partition. (F) Visualization of the representative partition given in (E).82 We have reordered the nodes in the matrices in panels (A-E) for better visualization of community structure.
Consider C partitions from a single layer of an example multilayer brain network (see Fig. 10a). We construct a nodal association matrix T, where the element Tij indicates how many times nodes i and j have been assigned to the same community (see Fig. 10b). We then construct a null-model association matrix based on random permutations of the original partitions (see Fig. 10c). That is, for each of the C partitions, we reassign nodes uniformly at random to the n communities of mean size s that are present in the selected partition. For every pair of nodes i and j, we let be the number of times these two nodes have been assigned to the same community in this permuted situation (see Fig. 10c). The values then form a distribution for the expected number of times two nodes are assigned to the same partition. Using an example with C = 100, we observe that two nodes can be assigned to the same community up to about 30 times out of the C partitions purely by chance. To be conservative, we remove such “noise” from the original nodal association matrix T by setting any element Tij whose value is less than the maximum entry of the random association matrix to 0 (see Fig. 10d). This yields the thresholded matrix , which retains statistically significant relationships between nodes.
We use a Louvain-like algorithm to perform C optimizations of the single-layer modularity Q0 for the thresholded matrix . Interestingly, this procedure typically extracts identical partitions for each of these optimizations in our examples (see Fig. 10e). This method, therefore, allows one to deal with the inherent near-degeneracy of the modularity quality function and provides a robust, representative partition of the original example brain network layer (see Fig. 10f).
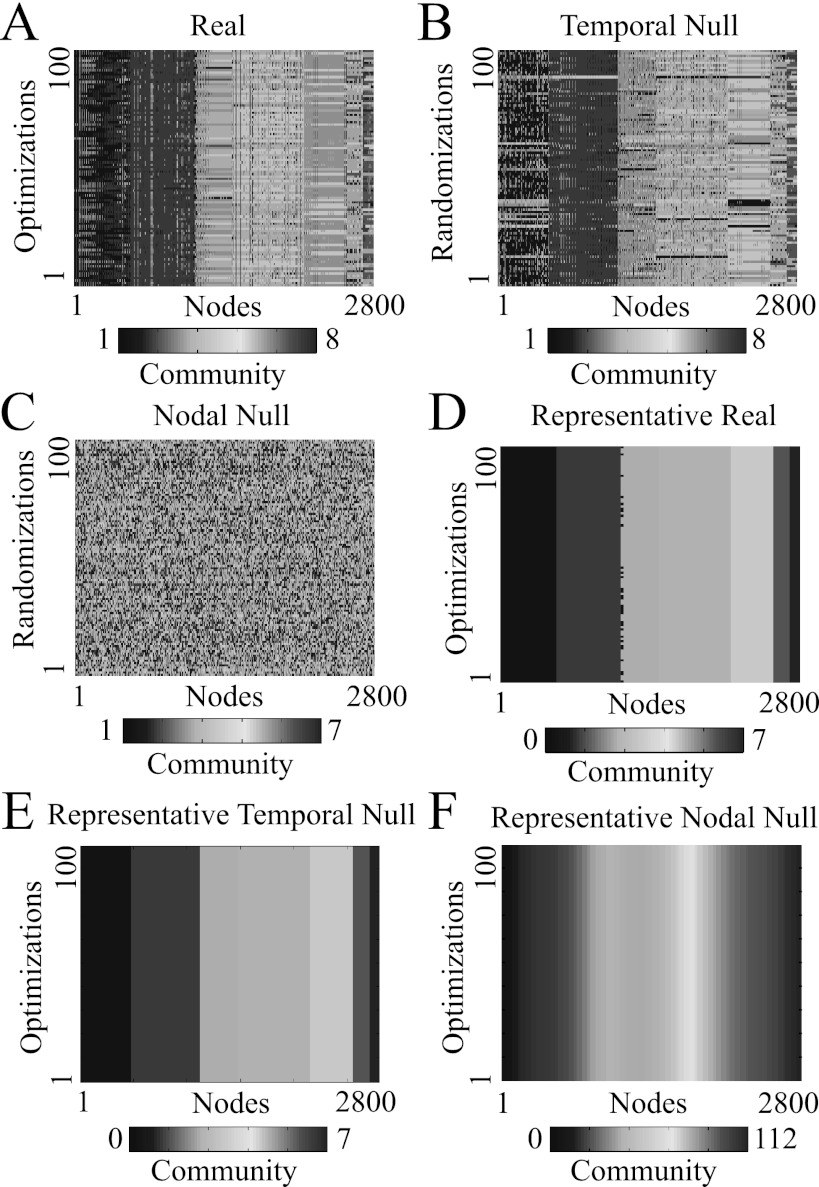
We apply the same method to multilayer networks (see Fig. 11) to find a representative partition of (1) a real network over C optimizations, (2) a temporal null-model network over C randomizations, and (3) a nodal null-model network over C randomizations. Using these examples, we have successfully uncovered representative partitions when they appear to exist (e.g., in the real networks and the temporal null-model networks) and have not been able to uncover a representative partition when one does not appear to exist (e.g., in the nodal null-model network, for which each of the 112 brain regions is placed in its own community in the representative partition). We also note that the representative partitions in the temporal null-model and real networks largely match the original data in terms of both sizes and number of communities. These results indicate the potential of this method to uncover meaningful representative partitions over optimizations or randomizations in multilayer networks.
Figure 11.
Representative partitions of multilayer brain networks for an example subject and scan. (A) Partitions extracted for C = 100 optimizations of the quality function Q on the real multilayer network (112 nodes × 25 time windows, which yields 2800 nodes in total). Partitions extracted for C randomizations for the (B) temporal and (C) nodal null-model networks. (D) Partitions extracted for C optimizations of the quality function Q of the thresholded nodal association matrix for the (D) real, (E) temporal null-model, and (F) nodal null-model networks. Note that the partitioning is robust to multiple optimizations. We have reordered the nodes in each column for better visualization of community structure. The structural resolution parameter is , and the temporal resolution parameter is .
CONCLUSIONS
In this paper, we discussed methodological issues in the determination and interpretation of dynamic community structure in multilayer networks. We also analyzed the behavior of several null models used for optimizing quality functions (such as modularity) in multilayer networks.
We described the construction of networks and the effects that certain choices can have on the use of both optimization and post-optimization null models. We introduce novel modularity-optimization null models for two cases: (1) networks composed of ordered nodes (a “chain null model”) and (2) networks constructed from time-series similarities (FT and AAFT surrogates). We studied “connectional,” “temporal,” and “nodal” post-optimization null models using several multilayer diagnostics (optimized modularity, number of communities, mean community size, and stationarity) as well as novel single-layer diagnostics (in the form of measures based on time series for optimized modularity). To investigate the utility of such considerations for model-generated data, we also applied our methodology to time-series data generated from coupled Kuramoto oscillators.
We examined the dependence of optimized modularity and partition similarity on structural and temporal resolution parameters as well as the influence of their variances on putative statistical conclusions. Finally, we described a simple method to address the issue of near-degeneracy in the landscapes of modularity and similar quality functions using a method to construct a robust, representative partition from a network layer.
The present paper illustrates what we feel are important considerations in the detection of dynamic communities. As one considers data with increasingly complicated structures, network analyses of such data must become increasingly nuanced, and the purpose of this paper has been to discuss and provide some potential starting points for how to try to address some of these nuances.
ACKNOWLEDGMENTS
We thank L. C. Bassett, M. Bazzi, K. Doron, L. Jeub, S. H. Lee, D. Malinow, and the anonymous referees for useful discussions. This work was supported by the Errett Fisher Foundation, the Templeton Foundation, David and Lucile Packard Foundation, PHS Grant NS44393, Sage Center for the Study of the Mind, and the Institute for Collaborative Biotechnologies through Contract No. W911NF-09-D-0001 from the U.S. Army Research Office. M.A.P. was supported by the James S. McDonnell Foundation (Research Award #220020177), the EPSRC (EP/J001759/1), and the FET-Proactive Project PLEXMATH (FP7-ICT-2011-8; Grant #317614) funded by the European Commission. He also acknowledges SAMSI and KITP for supporting his visits to them. P.J.M. acknowledges support from Award No. R21GM099493 from the National Institute of General Medical Sciences; the content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of General Medical Sciences or the National Institutes of Health.
References
- Newman M. E. J., Networks: An Introduction (Oxford University Press, 2010). [Google Scholar]
- Holme P. and Saramäki J., Phys. Rep. 519, 97 (2012). 10.1016/j.physrep.2012.03.001 [DOI] [Google Scholar]
- Mucha P. J., Richardson T., Macon K., Porter M. A., and Onnela J.-P., Science 328, 876 (2010). 10.1126/science.1184819 [DOI] [PubMed] [Google Scholar]
- Bassett D. S., Wymbs N. F., Porter M. A., Mucha P. J., Carlson J. M., and Grafton S. T., Proc. Natl. Acad. Sci. U.S.A. 108, 7641 (2011). 10.1073/pnas.1018985108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onnela J.-P., Saramäki J., Hyvönen J., Szabó G., Lazer D., Kaski K., Kertész J., and Barabási A. L., Proc. Natl. Acad. Sci. U.S.A. 104, 7332 (2007). 10.1073/pnas.0610245104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Y., Zhou C., Xiao J., Kurths J., and Schellnhuber H. J., Proc. Natl. Acad. Sci. U.S.A. 107, 18803 (2010). 10.1073/pnas.1013140107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzaález-Bailón S., Borge-Holthoefer J., Rivero A., and Moreno Y., Sci. Rep. 1, 197 (2011). 10.1038/srep00197 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fararo T. J. and Skvoretz J., in Status, Network, and Structure: Theory Development in Group Processes (Stanford University Press, 1997), pp. 362–386. [Google Scholar]
- Stomakhin A., Short M. B., and Bertozzi A. L., Inverse Probl. 27, 115013 (2011). 10.1088/0266-5611/27/11/115013 [DOI] [Google Scholar]
- Mucha P. J. and Porter M. A., Chaos 20, 041108 (2010). 10.1063/1.3518696 [DOI] [PubMed] [Google Scholar]
- Waugh A. S., Pei L., Fowler J. H., Mucha P. J., and Porter M. A., “ Party polarization in Congress: A network science approach,” arXiv:0907.3509 (2011).
- Doron K. W., Bassett D. S., and Gazzaniga M. S., Proc. Natl. Acad. Sci. U.S.A. 109, 18661 (2012). 10.1073/pnas.1216402109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wymbs N. F., Bassett D. S., Mucha P. J., Porter M. A., and Grafton S. T., Neuron 74, 936 (2012). 10.1016/j.neuron.2012.03.038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fenn D. J., Porter M. A., McDonald M., Williams S., Johnson N. F., and Jones N. S., Chaos 19, 033119 (2009). 10.1063/1.3184538 [DOI] [PubMed] [Google Scholar]
- Fenn D. J., Porter M. A., Williams S., McDonald M., Johnson N. F., and Jones N. S., Phys. Rev. E 84, 026109 (2011). 10.1103/PhysRevE.84.026109 [DOI] [PubMed] [Google Scholar]
- Porter M. A., Onnela J.-P., and Mucha P. J., Not. Am. Math. Soc. 56, 1082 (2009). [Google Scholar]
- Simon H., Proc. Am. Philos. Soc. 106, 467 (1962). [Google Scholar]
- Porter M. A., Mucha P. J., Newman M., and Warmbrand C. M., Proc. Natl. Acad. Sci. U.S.A. 102, 7057 (2005). 10.1073/pnas.0500191102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis A. C. F., Jones N. S., Porter M. A., and Deane C. M., BMC Syst. Biol. 4, 100 (2010). 10.1186/1752-0509-4-100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fortunato S., Phys. Rep. 486, 75 (2010). 10.1016/j.physrep.2009.11.002 [DOI] [Google Scholar]
- Newman M. E. J. and Girvan M., Phys. Rev. E 69, 026113 (2004). 10.1103/PhysRevE.69.026113 [DOI] [Google Scholar]
- Lancichinetti A., Radicchi F., and Ramasco J. J., Phys. Rev. E 81, 046110 (2010). 10.1103/PhysRevE.81.046110 [DOI] [PubMed] [Google Scholar]
- Newman M. E. J., Nat. Phys. 8, 25 (2012). 10.1038/nphys2162 [DOI] [Google Scholar]
- Good B. H., de Montjoye Y. A., and Clauset A., Phys. Rev. E 81, 046106 (2010). 10.1103/PhysRevE.81.046106 [DOI] [PubMed] [Google Scholar]
- Fortunato S. and Barthélemy M., Proc. Natl. Acad. Sci. U.S.A. 104, 36 (2007). 10.1073/pnas.0605965104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bickel P. J. and Chen A., Proc. Natl. Acad. Sci. U.S.A. 106, 21068 (2009). 10.1073/pnas.0907096106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchings S., “ The behavior of modularity-optimizing community detection algorithms,” M.Sc. Thesis (University of Oxford, 2011). [Google Scholar]
- Newman M. E. J., Phys. Rev. E 69, 066133 (2004). 10.1103/PhysRevE.69.066133 [DOI] [Google Scholar]
- Newman M. E. J., Proc. Natl. Acad. Sci. U.S.A. 103, 8577 (2006). 10.1073/pnas.0601602103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reichardt J. and Bornholdt S., Phys. Rev. E 74, 016110 (2006). 10.1103/PhysRevE.74.016110 [DOI] [PubMed] [Google Scholar]
- Onnela J.-P., Fenn D. J., Reid S., Porter M. A., Mucha P. J., Fricker M. D., and Jones N. S., Phys. Rev. E. 86, 036104 (2012). 10.1103/PhysRevE.86.036104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandes U., Delling D., Gaertler M., Görke R., Hoefer M., Nikoloski Z., and Wagner D., IEEE Trans. Knowl. Data Eng. 20, 172 (2008). 10.1109/TKDE.2007.190689 [DOI] [Google Scholar]
- Newman M. E. J., Phys. Rev. E 74, 036104 (2006). 10.1103/PhysRevE.74.036104 [DOI] [Google Scholar]
- Richardson T., Mucha P. J., and Porter M. A., Phys. Rev. E 80, 036111 (2009). 10.1103/PhysRevE.80.036111 [DOI] [PubMed] [Google Scholar]
- Palla G., Barabási A., and Vicsek T., Nature 446, 664 (2007). 10.1038/nature05670 [DOI] [PubMed] [Google Scholar]
- Equation 4 gives the definition for the notion of stationarity that we used in Ref. 4. The equation for this quantity in Ref. 4 has a typo in the denominator. We wrote incorrectly in that paper that the denominator was , whereas the numerical computations in that paper used .
- In other areas of investigation, it probably should be.
- Bullmore E. T. and Bassett D. S., Ann. Rev. Clin. Psych. 7, 113 (2011). 10.1146/annurev-clinpsy-040510-143934 [DOI] [PubMed] [Google Scholar]
- Bassett D. S., Brown J. A., Deshpande V., Carlson J. M., and Grafton S. T., Neuroimage 54, 1262 (2011). 10.1016/j.neuroimage.2010.09.006 [DOI] [PubMed] [Google Scholar]
- Zalesky A., Fornito A., Harding I. H., Cocchi L., Yucel M., Pantelis C., and Bullmore E. T., Neuroimage 50, 970 (2010). 10.1016/j.neuroimage.2009.12.027 [DOI] [PubMed] [Google Scholar]
- Wang J., Wang L., Zang Y., Yang H., Tang H., Gong Q., Chen Z., Zhu C., and He Y., Hum. Brain Mapp 30, 1511 (2009). 10.1002/hbm.20623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bialonski S., Horstmann M. T., and Lehnertz K., Chaos 20, 013134 (2010). 10.1063/1.3360561 [DOI] [PubMed] [Google Scholar]
- Ioannides A. A., Curr. Opin. Neurobiol. 17, 161 (2007). 10.1016/j.conb.2007.03.008 [DOI] [PubMed] [Google Scholar]
- Butts C. T., Science 325, 414 (2009). 10.1126/science.1171022 [DOI] [PubMed] [Google Scholar]
- Kossinets G., Soc. Networks 28, 247 (2006). 10.1016/j.socnet.2005.07.002 [DOI] [Google Scholar]
- Clauset A., Moore C., and Newman M. E. J., Nature 453, 98 (2008). 10.1038/nature06830 [DOI] [PubMed] [Google Scholar]
- Guimerá R. and Sales-Pardo M., Proc. Natl. Acad. Sci. U.S.A. 106, 22073 (2009). 10.1073/pnas.0908366106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim M. and Leskovec J., SIAM International Conference on Data Mining (2011).
- Sporns O., Networks of the Brain (MIT, 2010). [Google Scholar]
- Bullmore E. and Sporns O., Nat. Rev. Neurosci. 10, 186 (2009). 10.1038/nrn2575 [DOI] [PubMed] [Google Scholar]
- Abrams D. M. and Strogatz S. H., Phys. Rev. Lett. 93, 174102 (2004). 10.1103/PhysRevLett.93.174102 [DOI] [PubMed] [Google Scholar]
- Kuramoto Y. and Battogtokh D., Nonlinear Phenom. Complex Syst. 5, 380 (2002). [Google Scholar]
- Shima S. I. and Kuramoto Y., Phys. Rev. E 69, 036213 (2004). 10.1103/PhysRevE.69.036213 [DOI] [PubMed] [Google Scholar]
- Friston K. J., Hum. Brain Mapp 2, 56 (1994). 10.1002/hbm.460020107 [DOI] [PubMed] [Google Scholar]
- Benjamini Y. and Yekutieli Y., Ann. Stat. 29, 1165 (2001). 10.1214/aos/1013699998 [DOI] [Google Scholar]
- Bullmore E. and Sporns O., Nat. Rev. Neurosci. 13, 336 (2012). 10.1038/nrn3214 [DOI] [PubMed] [Google Scholar]
- Blondel V. D., Guillaume J. L., Lambiotte R., and Lefebvre E., J. Stat. Mech. 10, P10008 (2008). [Google Scholar]
- Jutla I. S., Jeub L. G. S., and Mucha P. J., “ A generalized Louvain method for community detection implemented in matlab,” (2011–2012); http://netwiki.amath.unc.edu/GenLouvain.
- A discrete time series can be represented as a vector. A continuous time series would first need to be discretized.
- Prichard D. and Theiler J., Phys. Rev. Lett. 73, 951 (1994). 10.1103/PhysRevLett.73.951 [DOI] [PubMed] [Google Scholar]
- The code used for this computation actually operates on [0,2π]. However, this should be an equivalent mathematical estimate to the same computation on [0,2π), which is the same except for a set of measure zero.
- Nakatani H., Khalilov I., Gong P., and van Leeuwen C., Phys. Lett. A 319, 167 (2003). 10.1016/j.physleta.2003.09.082 [DOI] [Google Scholar]
- Zalesky A., Fornito A., and Bullmore E., Neuroimage 60, 2096 (2012). 10.1016/j.neuroimage.2012.02.001 [DOI] [PubMed] [Google Scholar]
- Theiler J., Eubank S., Longtin A., Galdrikian B., and Farmer J. D., Physica D 58, 77 (1992). 10.1016/0167-2789(92)90102-S [DOI] [Google Scholar]
- It is also important to note that the AAFT method can allow nonlinear correlations to remain in the surrogate data. Therefore, the development of alternative surrogate data generation methods might be necessary (Refs. ).
- In the descriptions below, we use terms like “random” rewiring to refer to a process that we are applying uniformly at random aside from specified constraints.
- Garlaschelli D., New J. Phys. 11, 073005 (2009). 10.1088/1367-2630/11/7/073005 [DOI] [Google Scholar]
- Maslov S. and Sneppen K., Science 296, 910 (2002). 10.1126/science.1065103 [DOI] [PubMed] [Google Scholar]
- Ansmann G. and Lehnertz K., Phys. Rev. E 84, 026103 (2011). 10.1103/PhysRevE.84.026103 [DOI] [PubMed] [Google Scholar]
- Bialonski S., Wendler M., and Lehnertz K., PLoS ONE 6, e22826 (2011). 10.1371/journal.pone.0022826 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traag V. A., Van Dooren P., and Nesterov Y., Phys. Rev. E 84, 016114 (2011). 10.1103/PhysRevE.84.016114 [DOI] [PubMed] [Google Scholar]
- Macon K. T., Mucha P. J., and Porter M. A., Physica A 391, 343 (2012). 10.1016/j.physa.2011.06.030 [DOI] [Google Scholar]
- Traud A. L., Kelsic E. D., Mucha P. J., and Porter M. A., SIAM Rev. 53, 526 (2011). 10.1137/080734315 [DOI] [Google Scholar]
- Bassett D. S., Owens E. T., Daniels K. E., and Porter M. A., Phys. Rev. E 86, 041306 (2012). 10.1103/PhysRevE.86.041306 [DOI] [PubMed] [Google Scholar]
- Lou X. and Suykens J. A., Chaos 21, 043116 (2011). 10.1063/1.3655371 [DOI] [PubMed] [Google Scholar]
- Arenas A., Díaz-Guilera A., Kurths J., Moreno Y., and Zhou C., Phys. Rep. 469, 93 (2008). 10.1016/j.physrep.2008.09.002 [DOI] [Google Scholar]
- Arenas A., Díaz-Guilera A., and Pérez-Vicente C. J., Phys. Rev. Lett. 96, 114102 (2006). 10.1103/PhysRevLett.96.114102 [DOI] [PubMed] [Google Scholar]
- Stout J., Whiteway M., Ott E., Girvan M., and Antonsen T. M., Chaos 21, 025109 (2011). 10.1063/1.3581168 [DOI] [PubMed] [Google Scholar]
- Barlev G., Antonsen T. M., and Ott E., Chaos 21, 025103 (2011). 10.1063/1.3596711 [DOI] [PubMed] [Google Scholar]
- Arenas A., Díaz-Guilera A., and Pérez-Vicente C. J., Physica D 224, 27 (2006). 10.1016/j.physd.2006.09.029 [DOI] [Google Scholar]
- Lancichinetti A. and Fortunato S., Sci. Rep. 2, 336 (2012). 10.1038/srep00336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traud A. L., Frost C., Mucha P. J., and Porter M. A., Chaos 19, 041104 (2009). 10.1063/1.3194108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Räth C., Gliozzi M., Papadakis I. E., and Brinkmann W., Phys. Rev. Lett. 109, 144101 (2012). 10.1103/PhysRevLett.109.144101 [DOI] [PubMed] [Google Scholar]
- Rossmanith G., Modest H., Räth C., Banday A. J., Gorski K. M., and Morfill G., Phys. Rev. D 86, 083005 (2012). 10.1103/PhysRevD.86.083005 [DOI] [Google Scholar]