Abstract
The myocardial ischemic border zone is associated with the initiation and sustenance of arrhythmias. The profile of ionic concentrations across the border zone play a significant role in determining cellular electrophysiology and conductivity, yet their spatial-temporal evolution and regulation are not well understood. To investigate the changes in ion concentrations that regulate cellular electrophysiology, a mathematical model of ion movement in the intra and extracellular space in the presence of ionic, potential and material property heterogeneities was developed. The model simulates the spatial and temporal evolution of concentrations of potassium, sodium, chloride, calcium, hydrogen and bicarbonate ions and carbon dioxide across an ischemic border zone. Ischemia was simulated by sodium-potassium pump inhibition, potassium channel activation and respiratory and metabolic acidosis. The model predicted significant disparities in the width of the border zone for each ionic species, with intracellular sodium and extracellular potassium having discordant gradients, facilitating multiple gradients in cellular properties across the border zone. Extracellular potassium was found to have the largest border zone and this was attributed to the voltage dependence of the potassium channels. The model also predicted the efflux of  from the ischemic region due to electrogenic drift and diffusion within the intra and extracellular space, respectively, which contributed to
from the ischemic region due to electrogenic drift and diffusion within the intra and extracellular space, respectively, which contributed to  depletion in the ischemic region.
depletion in the ischemic region.
Introduction
Myocardial ischemia is caused by reduced perfusion to regions of the heart leading to a localised reduction in supply of metabolites, limited waste removal and compromised ionic homeostasis. The first 10 minutes of ischemia are associated with an increased risk of arrhythmias peaking after 5–6 minutes [1]. During this period arrhythmias are commonly initiated within the border zone (BZ) separating viable, well perfused, tissue and the ischemic, underperfused, region [2]–[4]. Ischemia causes an increase in extracellular potassium ( ), intra and extracellular proton concentrations (
), intra and extracellular proton concentrations ( and
and  , respectively), intracellular sodium (
, respectively), intracellular sodium ( ) and intracellular calcium (
) and intracellular calcium ( ) concentrations [5]. The dominant mechanisms for these changes have been attributed to a shift in the ATP/ADP ratio, which inhibits the Sodium-Potassium ATPase pump (
) concentrations [5]. The dominant mechanisms for these changes have been attributed to a shift in the ATP/ADP ratio, which inhibits the Sodium-Potassium ATPase pump ( ) and increases the conductance of ATP-inactivated
) and increases the conductance of ATP-inactivated  channels; respiratory acidosis causing an increase in
channels; respiratory acidosis causing an increase in  ; and metabolic acidosis, where a shift towards anaerobic respiration increases the production of
; and metabolic acidosis, where a shift towards anaerobic respiration increases the production of  in the cell [5]. Inherently, these changes in ionic concentrations in the ischemic region lead to gradients in properties across the BZ, creating electrophysiological heterogeneities that are thought to favour the occurrence of arrhythmias [6]–[8].
in the cell [5]. Inherently, these changes in ionic concentrations in the ischemic region lead to gradients in properties across the BZ, creating electrophysiological heterogeneities that are thought to favour the occurrence of arrhythmias [6]–[8].
Experimentally, the development of gradients of extracellular pH ( ) and
) and  [9], [10] have been well characterised using ion sensitive electrodes. Intracellular metabolite gradients have been characterised by fluorescent NADH [11] and biopsy [12] measurements. However, less is known on the gradients of intracellular ions, in particular
[9], [10] have been well characterised using ion sensitive electrodes. Intracellular metabolite gradients have been characterised by fluorescent NADH [11] and biopsy [12] measurements. However, less is known on the gradients of intracellular ions, in particular  ,
,  and
and  , nor are the mechanisms that underpin the spatial and temporal evolution of these ion concentration gradients well characterised or understood. This study aims to investigate the spatial-temporal evolution of ion gradients across ischemic BZ and the primary regulators of the BZ size and rate of development.
, nor are the mechanisms that underpin the spatial and temporal evolution of these ion concentration gradients well characterised or understood. This study aims to investigate the spatial-temporal evolution of ion gradients across ischemic BZ and the primary regulators of the BZ size and rate of development.
Previous measurements of ion concentrations and metabolites across the BZ have either been performed at multiple locations but at a limited number of time points [10], [12] or have tracked the time evolution of ion concentrations but only from a limited number of locations [13], [14]. Furthermore, these measurements have only been able to characterise a subset of ions of interest across the BZ. The need to track the evolution of multiple ionic species in space and time to understand the gradients of cellular electrophysiology across the BZ motivates the use of biophysical computational modelling. Previous models of electrophysiology during acute regional ischemia have simulated the effects of these spatial gradients but have not simulated their time evolution [15]–[17]. More recent work has simulated the time evolution of  gradients [18], but have not considered other ionic gradients, the effects of nonlinear interactions between
gradients [18], but have not considered other ionic gradients, the effects of nonlinear interactions between  and other ions, the effect of
and other ions, the effect of  diffusion in the intracellular space or the effects of potential gradients on ion diffusion.
diffusion in the intracellular space or the effects of potential gradients on ion diffusion.
In this study a new model of cardiac tissue electrophysiology is developed to investigate the spatial-temporal evolution of ionic concentrations across the ischemic BZ, during the first 5 minutes of reduced perfusion. The proposed model extends the conventional bidomain equations to explicitly link membrane potential to ionic concentrations and enforces ionic species conservation. A model of ion regulation across the cell membrane is then developed, parameterized, validated and coupled to the tissue model. This combined model is then used to investigate the spatial and temporal dispersion of ions across the BZ.
Methods
To model the evolution of ionic concentrations in the presence of multiple ionic gradients, electric gradients and heterogeneous tissue properties requires the development of a new set of equations for modelling the myocardium. In the next section the equations to model the BZ are derived and a model of passive cell membrane ion regulation is developed and validated. The changes to the cell membrane model to simulate  inhibition,
inhibition,  channel activation, respiratory acidosis and metabolic acidosis are then described.
channel activation, respiratory acidosis and metabolic acidosis are then described.
Tissue Model Derivation
Consistent with previous models of cardiac tissue electrophysiology the myocardium is represented as a two phase medium, with each point in the domain containing a fraction of intra and extracellular space. This gives rise to the scaling variables.
| (1) |
where  is the volume of the
is the volume of the  space in a unit of
space in a unit of  myocardium volume,
myocardium volume,  is the volume fraction of space
is the volume fraction of space  (with
(with  corresponding to the extra (
corresponding to the extra ( ) or intra (
) or intra ( ) cellular space),
) cellular space),  is the interspace surface area per unit volume myocardium and
is the interspace surface area per unit volume myocardium and 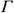 is area of the interspace surface. The intracellular volume fraction (
is area of the interspace surface. The intracellular volume fraction ( ) can be separated into sub volume fractions representing the cytosol (
) can be separated into sub volume fractions representing the cytosol ( ), mitochondria (
), mitochondria ( ) or the sarcoplasmic reticulum (
) or the sarcoplasmic reticulum ( ) to model distinct subcellular spaces, as described below. At each point in space there exists an intracellular potential (
) to model distinct subcellular spaces, as described below. At each point in space there exists an intracellular potential ( ), an extracellular potential (
), an extracellular potential ( ), a transmembrane potential (
), a transmembrane potential ( ) and an intra and extracellular ion concentration for each of the ion species in the model. The movement of each ion species in each domain is driven by diffusion, due to a gradient in ion concentration, and drift, due to a gradient in the electric field. This movement is described by the Nernst-Plank equations
) and an intra and extracellular ion concentration for each of the ion species in the model. The movement of each ion species in each domain is driven by diffusion, due to a gradient in ion concentration, and drift, due to a gradient in the electric field. This movement is described by the Nernst-Plank equations
| (2) |
where  is the concentration of unbound ion
is the concentration of unbound ion  in space
in space  ,
,  is the charge of ion
is the charge of ion  ,
,  is the effective diffusion of ion
is the effective diffusion of ion  in space
in space  ,
,  is Faraday's constant,
is Faraday's constant,  is the gas constant,
is the gas constant,  is the absolute temperature and
is the absolute temperature and  is the potential in the space
is the potential in the space  . The conventional Nernst-Plank equations are adapted to represent the movement of ions across the cell membrane between the intra and extracellular spaces. This gives
. The conventional Nernst-Plank equations are adapted to represent the movement of ions across the cell membrane between the intra and extracellular spaces. This gives
| (3) |
where  is the flux of ion
is the flux of ion  across the cell membrane.
across the cell membrane.  is defined in units of mM ms
is defined in units of mM ms mm. The surface separating the two regions is modelled as a simple capacitor and defining the transmembrane potential to scale with intracellular charge gives
mm. The surface separating the two regions is modelled as a simple capacitor and defining the transmembrane potential to scale with intracellular charge gives
| (4) |
where  is the intracellular charge per unit cell membrane area and
is the intracellular charge per unit cell membrane area and  is the membrane capacitance per unit cell membrane area. The charge on either side of the membrane is assumed to be equal but opposite, giving
is the membrane capacitance per unit cell membrane area. The charge on either side of the membrane is assumed to be equal but opposite, giving
| (5) |
Separating the concentration of each ion species in the intra and extracellular space into ions that are membrane bound and make up the membrane charge ( ) and those that are in solution gives.
) and those that are in solution gives.
| (6) |
where  and
and  are the ions in solution and membrane bound ions, respectively. By assuming charge neutrality for the ions within the solute gives:
are the ions in solution and membrane bound ions, respectively. By assuming charge neutrality for the ions within the solute gives:
| (7) |
Multiplying Eqn 6 by the ion species charge and Faraday's constant, then summing over all ion species in space  gives.
gives.
| (8) |
Converting the concentration of ions per unit volume in domain  to charge per unit cell membrane area and introducing a static charge term (
to charge per unit cell membrane area and introducing a static charge term ( ) that characterises all charge not attributable to
) that characterises all charge not attributable to  , gives
, gives
| (9) |
Combining with Eqn 8 gives
| (10) |
This defines the charge on the membrane as equal to the unbalanced charge in space  . Using the charge balance Eqn 5, gives
. Using the charge balance Eqn 5, gives
| (11) |
Differentiating Eqn 11 with respect to time, substituting in Eqn 3 and recognising that all transmembrane fluxes are balanced, provides
 |
(12) |
this ensures that there is no net charge accumulation in any unit volume of myocardium. Defining the relationship between the intra and extracellular potentials gives
| (13) |
Using Eqn 4 and the definition of charge (Eqn 10), then gives the algebraic definition of the transmembrane potential:
| (14) |
Rearranging Eqn 13 and substituting in the definition of  from Eqn 14 allows
from Eqn 14 allows  to be defined in terms of
to be defined in terms of  and
and  . Combining this definition of
. Combining this definition of  with Eqns 14, 13, 12, 3 and 2 then represents a closed set of equations. These equations are equivalent to the bidomain equations in the case of a single charge carrier and no gradient in ion concentrations, as shown below.
with Eqns 14, 13, 12, 3 and 2 then represents a closed set of equations. These equations are equivalent to the bidomain equations in the case of a single charge carrier and no gradient in ion concentrations, as shown below.
In cardiac myocytes many important ions, including  and
and  are heavily buffered, both within the cell and the extracellular space. To account for buffering the free and buffer bound fraction of
are heavily buffered, both within the cell and the extracellular space. To account for buffering the free and buffer bound fraction of  are calculated. In general, as
are calculated. In general, as  the effect of ions bound to the cell membrane will not be included in the buffering equations for simplicity. This gives
the effect of ions bound to the cell membrane will not be included in the buffering equations for simplicity. This gives
| (15) |
where  are the unbound ions and
are the unbound ions and  are the ions bound to buffers. At this time all buffers will be treated as rapid and to a single representative buffer species, giving
are the ions bound to buffers. At this time all buffers will be treated as rapid and to a single representative buffer species, giving
 |
(16) |
where  ,
,  and
and  are the concentration, binding affinity and Hill coefficient, respectively, for the buffer of ion
are the concentration, binding affinity and Hill coefficient, respectively, for the buffer of ion  in space
in space  . Assuming that ions bound to buffers are immobile, only
. Assuming that ions bound to buffers are immobile, only  is used to calculate the diffusion and drift of ions in Eqn 3, and similarly in Eqn 12. As binding of ions to a buffer implicitly removes a charged binding site located on a static protein, Eqn 14 remains unchanged.
is used to calculate the diffusion and drift of ions in Eqn 3, and similarly in Eqn 12. As binding of ions to a buffer implicitly removes a charged binding site located on a static protein, Eqn 14 remains unchanged.
Due to the complex anatomy of the cardiac myocyte many sub volumes exist within the cell that affect ionic concentrations. The sum of the volume fraction ( ) values must be less than, but do not have to be equal to, one, allowing the model to represent any volume fractions that are not directly accessible by ions. In particular the
) values must be less than, but do not have to be equal to, one, allowing the model to represent any volume fractions that are not directly accessible by ions. In particular the  variable can represent all space in the cell or can be substituted for
variable can represent all space in the cell or can be substituted for  representing the volume fraction of the cytosol (a sub volume of
representing the volume fraction of the cytosol (a sub volume of 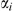 ). This allows the effects of SR, mitochondrial or other subcellular structure volumes on intracellular ionic concentrations to be accounted for in the model.
). This allows the effects of SR, mitochondrial or other subcellular structure volumes on intracellular ionic concentrations to be accounted for in the model.
Equation summary
The modelled equations are given by
| (17) |
 |
 |
where it is important to note that for non buffered ions  and
and  .
.
Consistency with bidomain equations
Imposing the implicit assumptions of the bidomain equations that charge carriers are not buffered, ion concentrations are homogenous and charge is carried by a single carrier to Eqn 18, the bidomain equations can be derived. Assuming homogenous ion concentrations and considering the case of the intracellular space reduces Eqn 18 to
| (18) |
Differentiating Eqn 14 for the intracellular space gives
 |
(19) |
substituting Eqn 18 into Eqn 19 gives
| (20) |
As ion concentrations are homogenous conductivity is defined as
| (21) |
Then Eqn 20 reduces to
| (22) |
Applying the single charge carrier assumption and converting from ionic flux to current gives the first bidomain equation
| (23) |
The second bidomain equation is readily derived from applying the homogenous ion concentration assumption to Eqn 12 and multiplying by Faraday's constant (to convert from conserving ion flux to current) giving
| (24) |
Substituting in the definition of conductivity from Eqn 21 then gives the second bidomain equation
| (25) |
Modelling the Membrane Fluxes
Cardiac electrophysiology is predominantly determined by the movement of  ,
,  and
and  . For charge neutrality
. For charge neutrality  must also be included in the model. To simulate the evolution of acidosis requires the inclusion of
must also be included in the model. To simulate the evolution of acidosis requires the inclusion of  ,
,  and
and  in the model. All of these ions (and
in the model. All of these ions (and  ) were modelled in the intra and extracellular space, with
) were modelled in the intra and extracellular space, with  and
and  being buffered. The goal of the model, in this study, was not to track the propagation of the action potential but to simulate the gradients of ions that exist over the BZ. These ion gradients were modelled based on the diastolic properties of the cell. This assumption was also a requirement to enable the simulation of minutes, while remaining computationally tractable.
being buffered. The goal of the model, in this study, was not to track the propagation of the action potential but to simulate the gradients of ions that exist over the BZ. These ion gradients were modelled based on the diastolic properties of the cell. This assumption was also a requirement to enable the simulation of minutes, while remaining computationally tractable.
The membrane ion transport pathways are described first for  ,
,  and
and  . Ion specific channels are then described that balance the flux of each ion species. The channel and transporter densities were determined by imposing zero net flux for each ion species, using the relative densities of
. Ion specific channels are then described that balance the flux of each ion species. The channel and transporter densities were determined by imposing zero net flux for each ion species, using the relative densities of  and
and  transporters recorded experimentally, and intra and extracellular ionic concentrations and membrane potential values derived from the literature. Where possible experimental data was taken preferentially from rabbit or guinea pig data at body temperature. This limited number of constraints then allowed the model transporters and channel densities to be uniquely determined.
transporters recorded experimentally, and intra and extracellular ionic concentrations and membrane potential values derived from the literature. Where possible experimental data was taken preferentially from rabbit or guinea pig data at body temperature. This limited number of constraints then allowed the model transporters and channel densities to be uniquely determined.
Sodium regulation
The model of  regulation included representations of the
regulation included representations of the  , sodium calcium exchanger (
, sodium calcium exchanger ( ), sodium hydrogen exchanger (
), sodium hydrogen exchanger ( ), sodium bicarbonate co-transporter (
), sodium bicarbonate co-transporter ( ) and a lumped sodium channel (
) and a lumped sodium channel ( ).
).  was modelled using the thermodynamically consistent equation set proposed by Smith and Crampin [19]. This model was subsequently revised by Terkildsen et al., [20] and this parameter set that was used here. The model for
was modelled using the thermodynamically consistent equation set proposed by Smith and Crampin [19]. This model was subsequently revised by Terkildsen et al., [20] and this parameter set that was used here. The model for  was fitted to guinea pig data as limited rabbit data was available. However, the maximum flux was rescaled to match rabbit data, as described below.
was fitted to guinea pig data as limited rabbit data was available. However, the maximum flux was rescaled to match rabbit data, as described below.
The  model was taken from Weber et al., [21]. The model has been fitted to rabbit experimental data at 37°C. The
model was taken from Weber et al., [21]. The model has been fitted to rabbit experimental data at 37°C. The  model was based on the model developed by Crampin and Smith [22] and reparameterized by Niederer and Smith [23]. In this study extracellular
model was based on the model developed by Crampin and Smith [22] and reparameterized by Niederer and Smith [23]. In this study extracellular  and
and  regulation of
regulation of  were included. This model was fitted predominantly to sheep Purkinje data [24], although the
were included. This model was fitted predominantly to sheep Purkinje data [24], although the  dependence of
dependence of  remains relatively consistent between species [25]. The
remains relatively consistent between species [25]. The  model was taken from Crampin and Smith [22]. The model assumes
model was taken from Crampin and Smith [22]. The model assumes  is electro neutral, which is true for only part of the
is electro neutral, which is true for only part of the  population [25]. There was not sufficient data to fully characterise the electrogenic and electro neutral forms of
population [25]. There was not sufficient data to fully characterise the electrogenic and electro neutral forms of  , hence the electro neutral model was used. Background
, hence the electro neutral model was used. Background  flux across residual open fast
flux across residual open fast  and persistent
and persistent  channels is limited when the cell is quiescent. However, some flux is still present [26] and a simple lumped background ionic flux equation was used, given by
channels is limited when the cell is quiescent. However, some flux is still present [26] and a simple lumped background ionic flux equation was used, given by
| (26) |
to model the residual  flux across any open
flux across any open  channels. The same equation form was used for modelling all background ion channels.
channels. The same equation form was used for modelling all background ion channels.
Proton regulation
In the proposed model  was regulated by
was regulated by  , described above, chloride-hydroxide exchanger (
, described above, chloride-hydroxide exchanger ( ), hydrolysis and buffering. Background
), hydrolysis and buffering. Background  leak or other
leak or other  exchangers were not considered in the general model of
exchangers were not considered in the general model of  regulation, described here, but do include models of
regulation, described here, but do include models of  -lactate exchange and intracellular metabolism derived
-lactate exchange and intracellular metabolism derived 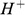 sources in the model of ischemia, described below. The
sources in the model of ischemia, described below. The  model comes from Niederer et al., [27] and was fitted to guinea pig data at 37
model comes from Niederer et al., [27] and was fitted to guinea pig data at 37 C. The hydrolysis of
C. The hydrolysis of  into
into  and
and  was governed by
was governed by
| (27) |
where  and
and  are the forward and reverse rates of hydrolysis. Hydrolysis occurs in both the intra and extracellular space and the rate constants were assumed to be the same in both domains.
are the forward and reverse rates of hydrolysis. Hydrolysis occurs in both the intra and extracellular space and the rate constants were assumed to be the same in both domains.  buffering in the intra and extracellular space is due to mobile and static
buffering in the intra and extracellular space is due to mobile and static  buffers and
buffers and  [28]. The intra and extracellular buffering of
[28]. The intra and extracellular buffering of  were assumed to be instantaneous and represented by a single population of buffers. To reduce the model size, partial differential equations were only solved for the total concentration of
were assumed to be instantaneous and represented by a single population of buffers. To reduce the model size, partial differential equations were only solved for the total concentration of  or
or  . The concentration of free ions were then calculated by
. The concentration of free ions were then calculated by
 |
(28) |
where  and
and  represent the concentration of the buffer and the binding affinity, respectively. This buffer model was used for both intra and extracellular
represent the concentration of the buffer and the binding affinity, respectively. This buffer model was used for both intra and extracellular  , with a separate set of parameters for each ion.
, with a separate set of parameters for each ion.
Calcium regulation
A simplified model of intracellular cardiac  was developed assuming that
was developed assuming that  in the intracellular space reaches an approximate equilibrium over the time scales of interest. Furthermore, SERCA ATPase function was modelled with a Hill coefficient of one as opposed to two, to allow the definition of
in the intracellular space reaches an approximate equilibrium over the time scales of interest. Furthermore, SERCA ATPase function was modelled with a Hill coefficient of one as opposed to two, to allow the definition of  to remain deterministic. The intracellular space was assumed to consist of a sarcoplasmic reticulum (SR) and a cytosolic space. The subsarcolemmal and dyadic space are small and are also likely to be in equilibrium with the cytosolic
to remain deterministic. The intracellular space was assumed to consist of a sarcoplasmic reticulum (SR) and a cytosolic space. The subsarcolemmal and dyadic space are small and are also likely to be in equilibrium with the cytosolic  , so were not included in the model. The
, so were not included in the model. The  dynamics were described by
dynamics were described by
| (29) |
| (30) |
| (31) |
| (32) |
| (33) |
where  is the SR
is the SR  ,
,  is the flux of calcium out of the SR,
is the flux of calcium out of the SR,  is the uptake of
is the uptake of  by SERCA,
by SERCA,  is the maximum SERCA flux,
is the maximum SERCA flux,  is the diffusion permeability of the SR membrane,
is the diffusion permeability of the SR membrane,  is the binding coefficient of
is the binding coefficient of  to SERCA,
to SERCA, 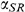 and
and  are the volume fractions of the SR and cytosol, respectively,
are the volume fractions of the SR and cytosol, respectively,  is the L-type calcium channel and
is the L-type calcium channel and  is the background
is the background  channel. In this model the background and L-type
channel. In this model the background and L-type  channels were modelled as a single lumped generic
channels were modelled as a single lumped generic  channel. Introducing cytosolic buffering, ignoring the effects of SR buffering and setting
channel. Introducing cytosolic buffering, ignoring the effects of SR buffering and setting  as one and assuming that the cytosol and the SR are in equilibrium then gives
as one and assuming that the cytosol and the SR are in equilibrium then gives
| (34) |
 |
defining
| (35) |
| (36) |
and collecting terms gives
| (37) |
 |
(38) |
| (39) |
| (40) |
As  is always negative the cubic always has at least one positive real root for possible values of
is always negative the cubic always has at least one positive real root for possible values of  . The value of
. The value of  was then found using the root finding method first proposed by Francois Viete in 1600 and reused more recently by Faber and Rudy [29]:
was then found using the root finding method first proposed by Francois Viete in 1600 and reused more recently by Faber and Rudy [29]:
 |
(41) |
The model of  dynamics assumes that all
dynamics assumes that all  buffers were static and that the transport of ions via mobile buffers was accounted for in the effective diffusion parameters of free
buffers were static and that the transport of ions via mobile buffers was accounted for in the effective diffusion parameters of free  . It is possible to extend the proposed model to include mobile buffers but they were assumed to play a secondary role in the current model.
. It is possible to extend the proposed model to include mobile buffers but they were assumed to play a secondary role in the current model.  was assumed to be buffered by a single species and was modelled using the same framework described above for
was assumed to be buffered by a single species and was modelled using the same framework described above for  (Eqn 28).
(Eqn 28).
Chloride regulation
In this model  homeostasis was maintained by the
homeostasis was maintained by the  and the
and the  -
- exchanger (
exchanger ( ), which bring
), which bring  into the cell, and a
into the cell, and a  channel that allows
channel that allows  to flow out of the cell. The
to flow out of the cell. The  model is described above. The
model is described above. The  model was taken from Crampin and Smith [22] and was developed using guinea pig data at 37
model was taken from Crampin and Smith [22] and was developed using guinea pig data at 37 C. The
C. The  channel uses the conventional background channel formulation. A linear
channel uses the conventional background channel formulation. A linear  dependence of the background
dependence of the background  current was added to the model based on observations from Komukai et al., [30].
current was added to the model based on observations from Komukai et al., [30].
Potassium regulation
In dynamic action potential models of cardiac electrophysiology there are a large number of  channels [31] that bring
channels [31] that bring 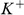 into the cell. This influx was balanced by the
into the cell. This influx was balanced by the  pump, described above, that extrudes
pump, described above, that extrudes  . For the passive membrane model, all of the
. For the passive membrane model, all of the  channels were lumped into a single background current (
channels were lumped into a single background current ( ) formulation that was set to balance the flux of
) formulation that was set to balance the flux of  on
on  . It was assumed that the membrane potential and
. It was assumed that the membrane potential and  reversal potential are the dominant factors affecting this channel and other forms of regulation have not been considered.
reversal potential are the dominant factors affecting this channel and other forms of regulation have not been considered.
Bicarbonate regulation
 was assumed to be regulated principally by hydrolysis and through
was assumed to be regulated principally by hydrolysis and through  and
and  . All of these components have been described above and it was assumed that there are no other
. All of these components have been described above and it was assumed that there are no other  pathways across the membrane.
pathways across the membrane.
Carbon Dioxide
 is regulated primarily through hydrolysis and can diffuse relatively freely across the membrane. The model of hydrolysis is described above and
is regulated primarily through hydrolysis and can diffuse relatively freely across the membrane. The model of hydrolysis is described above and  diffusion was assumed to obey Fick's law.
diffusion was assumed to obey Fick's law.
Model Parameters
For each transmembrane ion pathway described above, all kinetic, binding affinity and membrane potential dependencies were taken from the original models. Here the definition of geometrical parameters, ionic concentrations, buffering parameters and the density/scaling of each transmembrane pathway are motivated from data in the literature.
Geometrical parameters
The extracellular space is estimated to be between  [32]–[35],
[32]–[35],  and
and  [33], [36] of the volume of the heart in rabbit, cat, and rat hearts, respectively. This gave an
[33], [36] of the volume of the heart in rabbit, cat, and rat hearts, respectively. This gave an  value of
value of  leading to an
leading to an  value of
value of  . The surface to volume ratio of a cell is reported as
. The surface to volume ratio of a cell is reported as  m
m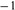 [37], [38] in rat and rabbit myocytes, corresponding to a
[37], [38] in rat and rabbit myocytes, corresponding to a  value of
value of  mm
mm . The relative SR volume was set to
. The relative SR volume was set to  of intracellular volume, giving an
of intracellular volume, giving an  value of
value of  , based on reported values of
, based on reported values of  of cell volume [37], [39], [40] in mouse, rat and swine. The relative mitochondrial volume (
of cell volume [37], [39], [40] in mouse, rat and swine. The relative mitochondrial volume ( ) was set to
) was set to  based on an estimated mitochondrial cell volume fraction of
based on an estimated mitochondrial cell volume fraction of  [37], [40]. The cytosol volume fraction was set to
[37], [40]. The cytosol volume fraction was set to  of the intracellular space, resulting in an
of the intracellular space, resulting in an  value of
value of  . To account for the effects of subscellular domains on intracellular ionic concentrations in the model, all references to
. To account for the effects of subscellular domains on intracellular ionic concentrations in the model, all references to 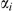 in Eqn 18 were replaced by
in Eqn 18 were replaced by  . A summary of geometrical parameters is given in Table 1.
. A summary of geometrical parameters is given in Table 1.
Table 1. Geometric variables.
| Variable | Value |

|
0.8 |

|
0.2 |

|
264 mm
|

|
0.536 |

|
0.24 |

|
0.024 |
Intracellular ionic concentrations
 has been measured using SBF1 fluorescence and
has been measured using SBF1 fluorescence and  sensitive electrodes. A significant range of values have been reported from
sensitive electrodes. A significant range of values have been reported from  mM [26], [41]–[44] to
mM [26], [41]–[44] to  mM [34], [45], [46]. Early measurements of intracellular ionic concentrations were performed using ion sensitive electrodes. These experiments measure ion activity and not ionic concentration and are often performed in multi-cellular preparations, confounding measurements. For these reasons
mM [34], [45], [46]. Early measurements of intracellular ionic concentrations were performed using ion sensitive electrodes. These experiments measure ion activity and not ionic concentration and are often performed in multi-cellular preparations, confounding measurements. For these reasons  in quiescent myocytes was set to
in quiescent myocytes was set to  mM, consistent with recent calibrated fluorescent measurements in isolated rabbit myocytes [26], [44].
mM, consistent with recent calibrated fluorescent measurements in isolated rabbit myocytes [26], [44].
No fluorescence dye is routinely used for measuring  . Using ion sensitive electrodes Lee et al., [45] were able to calibrate their measurements of ion activity in rabbit myocytes using an estimated
. Using ion sensitive electrodes Lee et al., [45] were able to calibrate their measurements of ion activity in rabbit myocytes using an estimated  activity coefficient of
activity coefficient of  , giving a value of
, giving a value of  mM. This compares with a range of
mM. This compares with a range of  mM calculated by applying the Lee et al.,
mM calculated by applying the Lee et al.,  ion activity coefficient to ion activity measurements in rabbit, cat and guinea pig [34], [43], [47], [48]. Alternate measurement using flame emission spectrometry by Powell et al., [49] measured
ion activity coefficient to ion activity measurements in rabbit, cat and guinea pig [34], [43], [47], [48]. Alternate measurement using flame emission spectrometry by Powell et al., [49] measured  in rat myocytes, giving a concentration of
in rat myocytes, giving a concentration of  mM. Given the lower values of the two calibrated measurements,
mM. Given the lower values of the two calibrated measurements,  was set to
was set to  mM.
mM.
No dye is routinely used for measuring  concentration in cardiac cells, however,
concentration in cardiac cells, however,  can be measured using ion sensitive electrodes.
can be measured using ion sensitive electrodes.  activity has been reported as
activity has been reported as  mM [35], [48], [50], [51] in sheep, rabbit and guinea pig heart cells. Estimations of
mM [35], [48], [50], [51] in sheep, rabbit and guinea pig heart cells. Estimations of  from total tissue
from total tissue  concentrations have resulted in values of
concentrations have resulted in values of  mM [35] and
mM [35] and  mM [34] in rabbit cells and
mM [34] in rabbit cells and  mol/g dry wt (or
mol/g dry wt (or  mM using the
mM using the  mM per
mM per  mol/g dry wt scaling factor from Bers [52]) in rat. The higher value of
mol/g dry wt scaling factor from Bers [52]) in rat. The higher value of  mM may be attributed to the higher extracellular space used in these calculations (
mM may be attributed to the higher extracellular space used in these calculations ( as compared to
as compared to  ). Considering the relative convergence of values
). Considering the relative convergence of values  was set to
was set to  mM.
mM.
Resting free  is measured using calibrated fluorescence measurements. These measurements range from
is measured using calibrated fluorescence measurements. These measurements range from  nM in rabbit and guinea pig preparations [53]–[57]. Given this consistency the
nM in rabbit and guinea pig preparations [53]–[57]. Given this consistency the  will be set to
will be set to  nM. SR
nM. SR  concentration is calculated from integrating the current across the cell membrane following the release of
concentration is calculated from integrating the current across the cell membrane following the release of  from the SR in response to caffeine. These measurements show two populations with high values in rat (
from the SR in response to caffeine. These measurements show two populations with high values in rat ( M [58]–[61]), canine (
M [58]–[61]), canine ( M [62]), rabbit (87–106
M [62]), rabbit (87–106  M [60], [61]) and ferret (
M [60], [61]) and ferret ( M [63]), compared to lower measurements in guinea pig (
M [63]), compared to lower measurements in guinea pig ( M [58], [64]). Given that the majority of species have a higher reported concentration, including rabbit, simulations were run with SR
M [58], [64]). Given that the majority of species have a higher reported concentration, including rabbit, simulations were run with SR  load set to
load set to  M. The buffering of
M. The buffering of  can be described by Hill equation(s), mass action equation(s) or a constant buffering power. To compromise between biophysics and complexity, buffering was modelled by a single Hill equation. Hove-Madsen and Bers [65] fitted
can be described by Hill equation(s), mass action equation(s) or a constant buffering power. To compromise between biophysics and complexity, buffering was modelled by a single Hill equation. Hove-Madsen and Bers [65] fitted  buffering in rabbit myocytes using two Hill curves; however, the lower affinity buffer will not play a significant role at passive diastolic
buffering in rabbit myocytes using two Hill curves; however, the lower affinity buffer will not play a significant role at passive diastolic  concentrations. For this reason the high affinity site, with cooperativity reduced from
concentrations. For this reason the high affinity site, with cooperativity reduced from  to unity, was used to model
to unity, was used to model  buffering, giving a buffer concentration of 208.98
buffering, giving a buffer concentration of 208.98  M (converted using a scaling factor of
M (converted using a scaling factor of  from Bers [52]) and an affinity of
from Bers [52]) and an affinity of  M. This model of
M. This model of  buffering in rabbit is similar to the concentration/affinity values of
buffering in rabbit is similar to the concentration/affinity values of  M [66],
M [66],  M [67] and
M [67] and  M [68] values measured in other species.
M [68] values measured in other species.
 has been measured using
has been measured using  sensitive electrodes and fluorescence dyes. Measurement of
sensitive electrodes and fluorescence dyes. Measurement of  consistently falls within the range of
consistently falls within the range of  [57], [69]–[71] in either HEPES or
[57], [69]–[71] in either HEPES or  buffered solutions. In the model
buffered solutions. In the model  was set to 7.1.
was set to 7.1.  are heavily buffered in the cytosol by intrinsic buffers and
are heavily buffered in the cytosol by intrinsic buffers and  . Here the buffering of
. Here the buffering of  by
by  was modelled explicitly and the intrinsic buffers were assumed to be in rapid equilibrium. Leem et al., [70] measured (and modelled)
was modelled explicitly and the intrinsic buffers were assumed to be in rapid equilibrium. Leem et al., [70] measured (and modelled)  buffering by two populations of buffers with binding affinity pK values of
buffering by two populations of buffers with binding affinity pK values of  and
and  and concentrations of
and concentrations of  mM and
mM and  mM. Zanbioni et al., [25] differentiated between mobile and fixed buffers and found that the fixed buffers had a consistent concentration of
mM. Zanbioni et al., [25] differentiated between mobile and fixed buffers and found that the fixed buffers had a consistent concentration of  mM and binding affinity (pK) value of
mM and binding affinity (pK) value of  across rat, rabbit and guinea pig, while the mobile buffers had a constant
across rat, rabbit and guinea pig, while the mobile buffers had a constant  value of
value of  . Fitting a single buffering curve to these two models over a pH range of
. Fitting a single buffering curve to these two models over a pH range of  gives concentrations of
gives concentrations of  mM and pK values of
mM and pK values of  , which gave a value of
, which gave a value of  mM and pK value of
mM and pK value of  for this model.
for this model.
Extracellular ionic concentrations
The concentration of the majority of ions in the extracellular space have been measured in canine [46], [72], rat [36], [73] and cat [74] hearts. These measurements provide a consistent range of ion concentrations for  ,
,  and
and  , giving
, giving  as
as  mM,
mM,  as
as  mM and
mM and  as
as  mM. In the model
mM. In the model 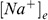 was set to
was set to  mM,
mM,  was set to
was set to 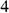 mM, consistent with measurements in guinea pig hearts [75] and rabbit atrium [76] and
mM, consistent with measurements in guinea pig hearts [75] and rabbit atrium [76] and  was set to
was set to  mM. The
mM. The  values reported range from
values reported range from  mM, however, these values do not differentiate between buffered and ionized
mM, however, these values do not differentiate between buffered and ionized  . The properties of
. The properties of  buffering in the extracellular space are not well characterised and are generally ignored in previous cardiac cell models. To approximate the buffering properties of extracellular
buffering in the extracellular space are not well characterised and are generally ignored in previous cardiac cell models. To approximate the buffering properties of extracellular  using a simple single species steady state mass action model, with no cooperative binding, requires two parameters, the concentration of the buffer and the binding affinity. Assuming the ratio of free
using a simple single species steady state mass action model, with no cooperative binding, requires two parameters, the concentration of the buffer and the binding affinity. Assuming the ratio of free  in the extracellular space to bound ions is similar to serum [77] and assuming that the primary buffer of
in the extracellular space to bound ions is similar to serum [77] and assuming that the primary buffer of  in the extracellular space are phospholipids, then extracellular
in the extracellular space are phospholipids, then extracellular  buffering will have a binding affinity of
buffering will have a binding affinity of  mM [78], within the range observed across multiple species [79], and a buffer concentration of
mM [78], within the range observed across multiple species [79], and a buffer concentration of  mM based on a free
mM based on a free  concentration of
concentration of  mM and assuming
mM and assuming  of
of  are bound to buffers [77].
are bound to buffers [77].  was set to
was set to  , to be consistent with the majority of experimental studies [57], [69]–[71] and measurements across a range of species [80]. Limited measurements were available to model
, to be consistent with the majority of experimental studies [57], [69]–[71] and measurements across a range of species [80]. Limited measurements were available to model  buffering, however, Yan and Kleber [81] reported 39 mM of buffered
buffering, however, Yan and Kleber [81] reported 39 mM of buffered  in the extracellular space. By assuming similar binding affinities for the intra and extracellular buffers and that
in the extracellular space. By assuming similar binding affinities for the intra and extracellular buffers and that  is
is  , then gave a concentration of extracellular proton buffers of
, then gave a concentration of extracellular proton buffers of  mM. A summary of ion concentrations and buffering parameters are given in Table 2 and Table 3, respectively.
mM. A summary of ion concentrations and buffering parameters are given in Table 2 and Table 3, respectively.
Table 2. Intra and extracellular free ion concentrations.
| Ion | Concentration (mM) | |
| Intracellular | Extracellular | |

|
4.0 | 140 |

|
135 | 4.0 |

|
18 | 110 |

|

|
1.2 |
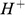
|

|

|

|
1.17 | 1.17 |
Table 3. Buffering Parameters.
| Parameter | Value (mM) | |
| Intracellular | Extracellular | |

|
65 | 350 |

|

|

|

|
0.209 | 2.3 |

|

|
1.1 |
The concentration of  was calculated using the parameters proposed and measured for guinea pig ventricular myocytes at
was calculated using the parameters proposed and measured for guinea pig ventricular myocytes at  C by Leem and Vaughan-Jones [82]. The concentration of
C by Leem and Vaughan-Jones [82]. The concentration of  in the extracellular solution was calculated using
in the extracellular solution was calculated using
| (42) |
where  is the solubility of
is the solubility of  , set to
, set to  mM mmHg
mM mmHg from human measurements at pH
from human measurements at pH  and
and  C [83],
C [83],  is the fraction of air that is
is the fraction of air that is  , set to
, set to  at baseline and
at baseline and  is atmospheric pressure, set to
is atmospheric pressure, set to  mmHg
mmHg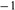 . This gives a partial pressure of
. This gives a partial pressure of  (
( ) of
) of  mmHg, consistent with although slightly higher than the
mmHg, consistent with although slightly higher than the  3 mmHg measured in rabbit hearts [84]. The hydration of
3 mmHg measured in rabbit hearts [84]. The hydration of  was modelled by a mass action reaction (Eqn 27). The
was modelled by a mass action reaction (Eqn 27). The  and
and  values were measured and modelled by Leem and Vaughan-Jones in guinea pig myocytes at
values were measured and modelled by Leem and Vaughan-Jones in guinea pig myocytes at  C [82], giving values of
C [82], giving values of  s
s and
and  s
s , respectively, resulting in an equilibrium constant of
, respectively, resulting in an equilibrium constant of  . The rate of hydration of
. The rate of hydration of  was assumed to be similar in both the intra and extracellular space. The movement of
was assumed to be similar in both the intra and extracellular space. The movement of  across the cell membrane was modelled by Fick's law. Previous models have used permittivity values of
across the cell membrane was modelled by Fick's law. Previous models have used permittivity values of  mms
mms [82], based on measurements in red blood cells. This value was reused despite its lack of species and cell type consistency, as there were no recent studies characterising the permeability in cardiac myocytes and the high permeability leads
[82], based on measurements in red blood cells. This value was reused despite its lack of species and cell type consistency, as there were no recent studies characterising the permeability in cardiac myocytes and the high permeability leads  to be close to equilibrium between the intra and extracellular spaces.
to be close to equilibrium between the intra and extracellular spaces.
Current, exchanger and pump densities
The model of each transmembrane ion pathway ( ) was separated into a kinetic regulatory component (
) was separated into a kinetic regulatory component ( ) dependent on transmembrane potential and ionic concentrations, and a scalar (
) dependent on transmembrane potential and ionic concentrations, and a scalar ( ) representing either the maximum flux or channel conduction of the pathway. The flux across a pathway (
) representing either the maximum flux or channel conduction of the pathway. The flux across a pathway ( ) is then given by
) is then given by
| (43) |
The  values were determind by calculating all of the
values were determind by calculating all of the  values (excluding
values (excluding  ,
,  and
and  as
as  and
and  were unknown) using the ionic concentrations in Table 2 and assuming a membrane potential of −80 mV. The remaining unknown
were unknown) using the ionic concentrations in Table 2 and assuming a membrane potential of −80 mV. The remaining unknown  and ionic concentrations were then determined from a limited number of measurements and by enforcing a zero net flux condition described by
and ionic concentrations were then determined from a limited number of measurements and by enforcing a zero net flux condition described by
 |
(44) |
As the parameters for hydrolysis and permeability of the cell membrane to  (
( ,
,  and
and  ) were derived from the literature, the constraints on
) were derived from the literature, the constraints on  and
and  were used to determine the concentrations of
were used to determine the concentrations of  and
and  , respectively. Measurements of transmembrane
, respectively. Measurements of transmembrane  influx gave
influx gave  as
as  mM ms
mM ms ,
,  as
as  mM ms
mM ms ,
,  as
as  mM ms
mM ms and
and  as
as  mM ms
mM ms [85]. The
[85]. The 
 flux was assumed to be equal to the sum of all
flux was assumed to be equal to the sum of all  influx. As the model does not include
influx. As the model does not include  -
-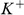 -2-
-2- co-transporter (NaK2Cl) or
co-transporter (NaK2Cl) or  -
- exchanger (NaMg), primarily due to the limited data to constrain the kinetics,
exchanger (NaMg), primarily due to the limited data to constrain the kinetics,  was reduced from the flux measured by Despa et al., [85] to 1.13
was reduced from the flux measured by Despa et al., [85] to 1.13 mM ms
mM ms . Setting these
. Setting these  values defines
values defines  ,
,  ,
,  ,
,  ,
,  and
and  . In the experimental and modelling work by the Vaughan-Jones group [70], [86] the relative size of
. In the experimental and modelling work by the Vaughan-Jones group [70], [86] the relative size of  to
to 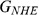 is
is  at
at  , this gave an estimated ratio of
, this gave an estimated ratio of  . Scaling
. Scaling  determined from [85] by 0.16 provided an estimate of
determined from [85] by 0.16 provided an estimate of  of
of  mM ms
mM ms . This allows
. This allows  and
and  to be defined.
to be defined.  must be balanced by
must be balanced by  and as
and as  and
and  were known, this flux was used to set
were known, this flux was used to set  . Combining the
. Combining the  and
and 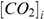 concentrations with the defined hydrolysis parameters and the known value of
concentrations with the defined hydrolysis parameters and the known value of  then gave
then gave  . Knowing
. Knowing  and
and  gave
gave  and hence
and hence  . Similarly,
. Similarly,  was calculated from
was calculated from  and
and  ,which gave
,which gave  . Finally,
. Finally,  was calculated using
was calculated using  and
and  , calculated using the derived
, calculated using the derived  value. By automating this parameter derivation process the model parameters could be updated to ensure static ion concentrations, and hence membrane potential, for any perturbation in model parameters or ionic concentrations. Parameters for all simulations in this study were derived following this process.
value. By automating this parameter derivation process the model parameters could be updated to ensure static ion concentrations, and hence membrane potential, for any perturbation in model parameters or ionic concentrations. Parameters for all simulations in this study were derived following this process.
Intracellular calcium dynamics
The intracellular regulation of  was treated as an equilibrium system. This resulted in the SR effectively acting as an additional buffer on
was treated as an equilibrium system. This resulted in the SR effectively acting as an additional buffer on 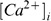 . The parameters
. The parameters  ,
,  ,
,  ,
,  and
and  were defined from enforcing a zero net flux constraint and experimental measurements. Measurements of
were defined from enforcing a zero net flux constraint and experimental measurements. Measurements of  are similar in rat and rabbit [65] and have been reported as 0.260–0.350
are similar in rat and rabbit [65] and have been reported as 0.260–0.350 M in rabbit [65], [87] and 250–280
M in rabbit [65], [87] and 250–280 M in rat [65], [87], [88]. A value of 0.3
M in rat [65], [87], [88]. A value of 0.3 M was used in the model.
M was used in the model.  is reported as 0.001–0.012
is reported as 0.001–0.012  Mms
Mms in rabbit, mouse and rat [54], [89]–[91]. A value of 0.01
in rabbit, mouse and rat [54], [89]–[91]. A value of 0.01 Mms
Mms was used in the model. Enforcing a zero net flux constraint on the SR gave
was used in the model. Enforcing a zero net flux constraint on the SR gave  as 0.038
as 0.038  Mms
Mms , comparable with values of 0.03–0.08
, comparable with values of 0.03–0.08 Mms
Mms measured in rabbit [65], [87], [92] with units converted using scale factors from Bers [52].
measured in rabbit [65], [87], [92] with units converted using scale factors from Bers [52].
Membrane Model Validation
To validate the passive membrane model, a series of tests based on the response of the cell models intracellular ionic concentrations and transmembrane potential to changes in extracellular ionic concentrations or inhibition of major ion transporters was performed. In order to maximise the number of tests the model was compared against data from cardiac cells, regardless of temperature, species or preparation type. This maximised the number of tests but meant that a quantitative comparison was not valid and so only a qualitative comparison was performed. A summary of experimental data used in the validation is provided in Table 4. Fig. 1 shows the comparison between the model and data. From the 72 simulations performed 43 matched the experimental data, data was not available or was inconsistent for 19, changes were too small to be measured in 5 and the model did not match experiments in 5 cases.
Table 4. Qualitative changes in intracellular ionic concentrations or membrane potential in response to changes in extracellular ionic concentration or inhibition of membrane transporters.
| Protocol | Change in Concentration or Potential | Reference | ||||||
| Variable | Change |

|
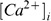
|

|

|

|

|
|
1-24-9 
|
||||||||
| Decrease |

|

|

|

|
 x2 x2  x4 x4 |
[160]–[163] | ||
| [164]–[166] | ||||||||
| Increase |


|

|

|
[167], [168] | ||||

| ||||||||
| Decrease |

|

|

|

|


|
[163], [169], [170] | ||
| Increase |

|

|

|
[171], [172] | ||||

| ||||||||
| Decrease |


|

|

|

|

|

|
[160], [161], [173], [174] | |
| [71], [162], [175], [176] | ||||||||
| Increase |


|


|

|


|

|

|
[50], [161], [175], [177], [178] | |
| [131], [173], [176], [179], [180] | ||||||||

|
||||||||
| Increase |

|

|

|

|
[71], [166], [181]–[183] | |||

| ||||||||
| Decrease |

|

|

|

|

|
[184]–[186] | ||
| [50], [71], [187] | ||||||||
| Increase |

|

|

|

|
[50], [184], [187] | |||

|
||||||||
| Increase |

|

|



|

|
[161], [165], [166], [188] | |||

|
||||||||
| Inhibition |

|

|

|

|

|


|
[43], [170], [175] | |
| [35], [160], [177], [189] | ||||||||

|
||||||||
| Inhibition |

|

|

|

|
[44], [166] | |||
Figure 1. Cell membrane model validation.
Arrow direction shows model prediction for the change in intracellular concentrations and membrane potential for a change in extracellular ion concentrations or inhibition of membrane transporter as indicated by the panel label. The color of the arrow indicates how the model compares with experimental data, summarised in Table 4. Black arrows indicate where the model matches experimental data, white arrows indicate where there is no or inconsistent data, gray arrows indicate where no change was observed experimentally and striped arrows indicate where the model does not match experimental data. Data was considered inconsistent if different studies reported opposite changes in intracellular ion concentration or membrane potential in response to a change in extracellular ionic concentrations (for example the change in membrane potential following a decrease in  ). In cases where one study reported no change in intracellular ion concentration or membrane potential and another found a change, it was assumed that the change was correct (for example the change in
). In cases where one study reported no change in intracellular ion concentration or membrane potential and another found a change, it was assumed that the change was correct (for example the change in  in response to an increase or a decrease in
in response to an increase or a decrease in  ). For example in panel A) corresponding to a decrease in
). For example in panel A) corresponding to a decrease in  (as indicated by the panel label), the experimental data comes from row 1 of Table? 4. The model predicts that
(as indicated by the panel label), the experimental data comes from row 1 of Table? 4. The model predicts that  decreases and that
decreases and that  and
and  increase, consistent with experimental measurements and the arrows are shaded black. There is no consistent observed change in the transmembrane potential so the
increase, consistent with experimental measurements and the arrows are shaded black. There is no consistent observed change in the transmembrane potential so the  arrow remains white. No data is available for the change in
arrow remains white. No data is available for the change in  in response to a decrease in
in response to a decrease in  so the
so the  arrow remains white. The model predicts a decrease in
arrow remains white. The model predicts a decrease in  yet experimental measurements found an increase, hence the
yet experimental measurements found an increase, hence the  arrow is striped.
arrow is striped.
Diffusion Parameters
The tissue model required the definition of diffusion parameters for each of the ionic species in the intra and extracellular space. The diffusion parameters used in the model were all for the apparent diffusivity of free ions, lumping the effects of any mobile buffers, tortuosity and gap junctions into a single diffusion parameter. Using Eqn 21 the conductivity parameters were shown to be directly related to the conductivity parameters in the bidomain equations. From the review of bidomain conductivities and relative values in the intra and extracellular space by Roth [93] a conductivity value of 0.25 Sm was taken for both the intra and extracellular space. This conductivity, along with the ionic concentrations from Table 2, were used to derive the diffusion parameters. The apparent diffusion of
was taken for both the intra and extracellular space. This conductivity, along with the ionic concentrations from Table 2, were used to derive the diffusion parameters. The apparent diffusion of  and
and 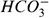 are
are  mm
mm ms
ms and
and  mm
mm ms
ms in the >intracellular space [86] and were assumed to be similar in the extracellular space. The apparent diffusion constant of
in the >intracellular space [86] and were assumed to be similar in the extracellular space. The apparent diffusion constant of  (including the effects of mobile buffers) has been estimated from experimental measurements in previous modelling studies as
(including the effects of mobile buffers) has been estimated from experimental measurements in previous modelling studies as  mm
mm ms
ms [94]–[96]. Here a value of
[94]–[96]. Here a value of  mm
mm ms
ms [94] was used and the effect of diffusion in the SR was not included, as it was assumed to be non contiguous between cells. It was assumed that
[94] was used and the effect of diffusion in the SR was not included, as it was assumed to be non contiguous between cells. It was assumed that  diffusion is limited by buffering, resulting in the same value in the intra and extracellular space.
diffusion is limited by buffering, resulting in the same value in the intra and extracellular space.  ,
,  and
and  were all assumed to have a common diffusion coefficient in either the intra or extracellular space as these ions are only nominally buffered and are only affected by gap junctions and tortuosity. Diffusion of
were all assumed to have a common diffusion coefficient in either the intra or extracellular space as these ions are only nominally buffered and are only affected by gap junctions and tortuosity. Diffusion of  was estimated from previous modelling/experimental studies of
was estimated from previous modelling/experimental studies of  in tissue as
in tissue as  mm
mm ms
ms [97], and was assumed to be the same in the intra and extracellular space. Solving Eqn 21 for the diffusion of intra and extracellular
[97], and was assumed to be the same in the intra and extracellular space. Solving Eqn 21 for the diffusion of intra and extracellular  ,
,  and
and  gives the diffusion parameters summarised in Table 5.
gives the diffusion parameters summarised in Table 5.
Table 5. Effective ion diffusion parameters.
| Ion | Diffusion Constant (10 mm mm ms ms ) ) |
|
| Intracellular | Extracellular | |

|
7.7 | 12.9 |
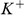
|
7.7 | 12.9 |

|
7.7 | 12.9 |

|
1.5 | 1.5 |

|
1.52 | 1.52 |

|
7.7 | 7.70 |

|
11.3 | 11.3 |
Finally, the effects of  on gap junction conductivity were included. Measurements in cell pairs by Swietach et al., [98] have demonstrated that the permeability of gap junctions has a biphasic dependence on the
on gap junction conductivity were included. Measurements in cell pairs by Swietach et al., [98] have demonstrated that the permeability of gap junctions has a biphasic dependence on the  concentration. To introduce these effects into the model the intracellular diffusion constants were scaled by
concentration. To introduce these effects into the model the intracellular diffusion constants were scaled by
| (45) |
where  /
/ and
and  /
/ are the cooperativity and binding affinity for the activation and deactivation of gap junctions by protons, respectively and
are the cooperativity and binding affinity for the activation and deactivation of gap junctions by protons, respectively and  scales all intracellular diffusion constants. Using the measured parameters from end-to-end cell pairs in Swietach et al., [98]
scales all intracellular diffusion constants. Using the measured parameters from end-to-end cell pairs in Swietach et al., [98]
 ,
,  ,
,  mM and
mM and  mM. In this model of proton effects on gap junction permeability there is an implicit assumption that the gap junction permeability plays a dominant role in defining diffusion. At this stage no other regulators of permeability were included in the model, notably
mM. In this model of proton effects on gap junction permeability there is an implicit assumption that the gap junction permeability plays a dominant role in defining diffusion. At this stage no other regulators of permeability were included in the model, notably  regulation is absent but this can readily be included in the modelling framework as required.
regulation is absent but this can readily be included in the modelling framework as required.
Simulating Ischemia
In this study the effect of  inhibition,
inhibition,  activation and respiratory and metabolic acidosis during ischemia on cell ionic homeostasis were considered. This list is not exhaustive and absent factors are discussed below. Ischemia was modelled by respiratory acidosis, metabolic acidosis, increased
activation and respiratory and metabolic acidosis during ischemia on cell ionic homeostasis were considered. This list is not exhaustive and absent factors are discussed below. Ischemia was modelled by respiratory acidosis, metabolic acidosis, increased  channel conductance and decreased
channel conductance and decreased  function. The specific time course of each of these changes is poorly characterised. Previous modelling studies have assumed that changes in cell function with ischemia have evolved linearly [99] or as a nonlinear function of prescribed metabolite concentrations [20]. To avoid any undue bias from the arbitrary selection of a time course, all changes are initially considered instantaneous.
function. The specific time course of each of these changes is poorly characterised. Previous modelling studies have assumed that changes in cell function with ischemia have evolved linearly [99] or as a nonlinear function of prescribed metabolite concentrations [20]. To avoid any undue bias from the arbitrary selection of a time course, all changes are initially considered instantaneous.
NaK inhibition and  channel activation were modelled by scaling the respective fluxes. Respiratory acidosis was assumed to result from an imbalance of production and washout of
channel activation were modelled by scaling the respective fluxes. Respiratory acidosis was assumed to result from an imbalance of production and washout of  . To simulate this, an (implicitly electro neutral) intracellular source of
. To simulate this, an (implicitly electro neutral) intracellular source of  was introduced into the ischemic region. There was no flux of
was introduced into the ischemic region. There was no flux of  out of the extracellular space and this resulted in a build up of
out of the extracellular space and this resulted in a build up of  in both the intra and extracellular space in the ischemic region.
in both the intra and extracellular space in the ischemic region.
To model metabolic acidosis required the introduction of an additional intracellular  source. However, introducing a source of cations into the cell compromised the conservation of charge constraint. To provide an electro neutral source of
source. However, introducing a source of cations into the cell compromised the conservation of charge constraint. To provide an electro neutral source of  required the concurrent introduction of a source of anions that match the production of
required the concurrent introduction of a source of anions that match the production of  inside the cell. It was implicitly assumed that the anions entered the cell in an electro neutral form with an
inside the cell. It was implicitly assumed that the anions entered the cell in an electro neutral form with an  bound, and the anions and
bound, and the anions and  separate within the cell due to metabolic processes. The source of
separate within the cell due to metabolic processes. The source of  in ischemia is likely to be due to increased ATP production through glycolysis [100]; in the absence of oxygen this also results in increased lactate production. As lactate readily dissociates from
in ischemia is likely to be due to increased ATP production through glycolysis [100]; in the absence of oxygen this also results in increased lactate production. As lactate readily dissociates from  it was assumed that the anion source that matches
it was assumed that the anion source that matches  flux has similar characteristics to lactate including transmembrane regulation via the lactate-
flux has similar characteristics to lactate including transmembrane regulation via the lactate- membrane exchanger MCT1 [101]. Given the ambiguity in structure, MCT1 was modelled as an ordered exchanger, using the kinetic parameters from Vinnakota and Beard [102] and the maximum influx value of
membrane exchanger MCT1 [101]. Given the ambiguity in structure, MCT1 was modelled as an ordered exchanger, using the kinetic parameters from Vinnakota and Beard [102] and the maximum influx value of  mMms
mMms recorded in guinea pig myocytes [103]. In the absence of metabolic acidosis, lactate concentration was assumed to be nominal, consistent with the small flux of lactate observed in rabbit hearts under normal conditions [104]. Model simulations were performed on a 1D strand with length 32 mm, oriented in the preferred conduction or fibre direction, with a transition between ischemic and viable tissue at 16 mm to ensure the simulation captured the BZ width with nominal boundary condition artefacts. The transition between viable tissue and ischemic tissue was approximated by a Hill equation with a Hill coefficient set to ensure a steep transition between the ischemic region and viable tissue over
recorded in guinea pig myocytes [103]. In the absence of metabolic acidosis, lactate concentration was assumed to be nominal, consistent with the small flux of lactate observed in rabbit hearts under normal conditions [104]. Model simulations were performed on a 1D strand with length 32 mm, oriented in the preferred conduction or fibre direction, with a transition between ischemic and viable tissue at 16 mm to ensure the simulation captured the BZ width with nominal boundary condition artefacts. The transition between viable tissue and ischemic tissue was approximated by a Hill equation with a Hill coefficient set to ensure a steep transition between the ischemic region and viable tissue over  m, consistent with the rapid drop in oxygen pressure across the BZ in swine [105].
m, consistent with the rapid drop in oxygen pressure across the BZ in swine [105].
Numerical Methods for Tissue Model
The nonlinear equations were solved using a fully implicit finite difference scheme with a line search Newton-Raphson method. The transmembrane flux component of the Jacobian was calculated using finite differencing with the remainder calculated analytically. The Jacobian was inverted directly using MatLab and was only recalculated if the residual fails to decrease or convergence was not reached within  Newton-Raphson iterations.
Newton-Raphson iterations.
The dependence of the BZ width on the spatial and temporal discretizations was determined to test for numerical convergence. The width of the transition for each ion concentration between the viable and ischemic region, referred to as the BZ width for each ion, was calculated by fitting a Hill curve to each ionic profile. The width of the BZ for each ion was then calculated as the distance between  and
and  of the change in concentration.
of the change in concentration.
A convergence analysis was performed and a mesh discretization of  m and a time step of
m and a time step of  ms was used. Increasing the spatial discretization by a factor of
ms was used. Increasing the spatial discretization by a factor of  results in a maximum change in BZ width of any ion of
results in a maximum change in BZ width of any ion of  mm. Decreasing the time step to
mm. Decreasing the time step to  ms increases the maximum BZ width of any ion by
ms increases the maximum BZ width of any ion by  mm.
mm.
Results
The individual effects of each of the four components of ischemia were first demonstrated. A combined model of ischemia was then developed and the width and magnitude of the changes in ionic concentrations across the ischemic BZ were predicted. The effect of movement of  ,
,  and
and  within and between intra and extracellular spaces across the BZ were calculated to show the net movement of ions across the BZ.
within and between intra and extracellular spaces across the BZ were calculated to show the net movement of ions across the BZ.
Simulating Individual Components of Ischemia
The level of inhibition of  , the activation of
, the activation of  and the level of
and the level of  and
and  production in the cell during ischemia is not known. To investigate the effects of each of these aspects of ischemia, they were each individually introduced into the model at five levels of severity, for x
production in the cell during ischemia is not known. To investigate the effects of each of these aspects of ischemia, they were each individually introduced into the model at five levels of severity, for x mm along a
mm along a  mm strand. Fig. 2 shows the effect of each component on the change in
mm strand. Fig. 2 shows the effect of each component on the change in  ,
,  ,
,  and
and  across the ischemic BZ. The range of alterations in ion concentrations is shown by the shaded regions. The minimum and maximum changes in each component are shown by dashed lines and the mid change is shown by the solid line.
across the ischemic BZ. The range of alterations in ion concentrations is shown by the shaded regions. The minimum and maximum changes in each component are shown by dashed lines and the mid change is shown by the solid line.  (yellow) was inhibited by up to 100% (no flux) in
(yellow) was inhibited by up to 100% (no flux) in  increments,
increments,  (red) was scaled by up to
(red) was scaled by up to  in
in  increments, metabolic acidosis was simulated by introducing an
increments, metabolic acidosis was simulated by introducing an  flux in five increments up to a maximum value of
flux in five increments up to a maximum value of  Mms
Mms and respiratory acidosis (blue) was simulated by a intracellular
and respiratory acidosis (blue) was simulated by a intracellular  flux increased in five increments up to a maximum value of
flux increased in five increments up to a maximum value of  Mms
Mms .
.
Figure 2. Effect of individual components of ischemia on the change in  (column 1),
(column 1),  (column 2),
(column 2),  (column 3) and
(column 3) and  (column 4).
(column 4).
Effect of 50–250% increase in  (red shaded region enclosed by dashed line) and a 150% increase in
(red shaded region enclosed by dashed line) and a 150% increase in  (red line) on A)
(red line) on A)  , B)
, B)  , C)
, C)  and D)
and D)  . Effect of 20–100% maximum
. Effect of 20–100% maximum  flux (purple shaded region enclosed by dashed line) and 60% maximum
flux (purple shaded region enclosed by dashed line) and 60% maximum  flux (purple line) on E)
flux (purple line) on E)  , F)
, F)  , G)
, G)  and H)
and H)  . Effect of 20–100% NaK inhibition (yellow shaded region enclosed by dashed line) and a 60% NaK inhibition (yellow line) on I)
. Effect of 20–100% NaK inhibition (yellow shaded region enclosed by dashed line) and a 60% NaK inhibition (yellow line) on I)  , J)
, J)  , K)
, K)  and L)
and L)  . Effect of 20–100% maximum
. Effect of 20–100% maximum  flux (blue shaded region enclosed by dashed line) and a 60% maximum
flux (blue shaded region enclosed by dashed line) and a 60% maximum  flux (blue line) on M)
flux (blue line) on M)  , N)
, N)  , O)
, O)  and P)
and P)  .
.
Modelling Ischemia
Inherently, there is no single mode of ischemia and the relative contribution of acidosis,  inhibition or
inhibition or 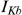 activation will depend on the residual flow, age, gender, disease state, location of ischemic region and species under study. To provide a representative case to study, 5 minutes of ischemia were simulated in the presence of all four ischemic mechanisms that match representative results from the literature.
activation will depend on the residual flow, age, gender, disease state, location of ischemic region and species under study. To provide a representative case to study, 5 minutes of ischemia were simulated in the presence of all four ischemic mechanisms that match representative results from the literature.
Partial pressure measurements of  in canine ischemic models show a
in canine ischemic models show a  increase in
increase in  partial pressure following occlusion, depending on the level of flow inhibition, after
partial pressure following occlusion, depending on the level of flow inhibition, after  minutes. The elevation in
minutes. The elevation in  was approximately linear over time and hence in the model it was assumed
was approximately linear over time and hence in the model it was assumed  concentration increases by
concentration increases by  increase in the first
increase in the first  minutes of ischemia [106], [107]. This corresponded to an increase in the concentration of
minutes of ischemia [106], [107]. This corresponded to an increase in the concentration of  in the model from
in the model from  mM to
mM to  mM. In the model respiratory acidosis was caused by an increase in
mM. In the model respiratory acidosis was caused by an increase in  flux that cannot be vented from the extracellular space. Although it is recognised that the decrease in
flux that cannot be vented from the extracellular space. Although it is recognised that the decrease in  due to metabolic acidosis will also contribute to elevated
due to metabolic acidosis will also contribute to elevated  , initially the
, initially the  flux was set at a
flux was set at a  level to achieve an increase in
level to achieve an increase in  concentration to
concentration to  mM, which resulted in a decrease of
mM, which resulted in a decrease of  to
to  . During ischemia
. During ischemia  decreases rapidly before plateauing after approximately
decreases rapidly before plateauing after approximately  minutes. The decrease in the initial
minutes. The decrease in the initial  minutes has been reported to fall between
minutes has been reported to fall between  to
to  pH units in rat [108], ferret, [109] and guinea pig [110] preparations. Respiratory and metabolic acidosis will both contribute to this drop in
pH units in rat [108], ferret, [109] and guinea pig [110] preparations. Respiratory and metabolic acidosis will both contribute to this drop in  . In the model setting the level of intracellular
. In the model setting the level of intracellular  flux to
flux to  caused a
caused a  pH unit drop and an increase in
pH unit drop and an increase in  to
to  mM. Combined metabolic and respiratory acidosis caused a
mM. Combined metabolic and respiratory acidosis caused a  unit drop in pH and an increase in
unit drop in pH and an increase in  to
to  mM.
mM.
In studies of ischemia  tends to increase linearly with time. In the rat heart ischemia caused an increase in
tends to increase linearly with time. In the rat heart ischemia caused an increase in  by
by  over
over  minutes [111], by
minutes [111], by  after
after  minutes [112], from
minutes [112], from  mM to
mM to  mM during
mM during  minutes ischemia [113], by
minutes ischemia [113], by  ,
,  ,
,  and
and  after 9,
after 9,  ,
,  and
and  minutes, respectively [114], by two fold over
minutes, respectively [114], by two fold over  minutes [115], from
minutes [115], from  mM to
mM to  mM over
mM over  minutes [116], by
minutes [116], by  over
over 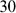 minutes [117], by
minutes [117], by  over
over  minutes [118], no change over
minutes [118], no change over  minutes [108] and by
minutes [108] and by  over
over  minutes [119]. Changes in
minutes [119]. Changes in  in guinea pig hearts during ischemia is controversial with reports of a decrease from
in guinea pig hearts during ischemia is controversial with reports of a decrease from  mM to
mM to  mM over
mM over  minutes [120] and of an increase of
minutes [120] and of an increase of  over
over  minutes [121]. Only considering the cases where
minutes [121]. Only considering the cases where  increases, as these represent a repeatable consensus result, the range of expected increases in
increases, as these represent a repeatable consensus result, the range of expected increases in  over a
over a  minute period is
minute period is  , assuming a linear increase with time. These cluster into two groups with ranges
, assuming a linear increase with time. These cluster into two groups with ranges  and
and  . In the model reducing the maximum flux of
. In the model reducing the maximum flux of  by
by  caused an increase in
caused an increase in  to
to  mM (
mM ( ) in the absence of acidosis or
) in the absence of acidosis or  mM (
mM ( ) in the presence of the acidotic components of ischemia, described above.
) in the presence of the acidotic components of ischemia, described above.
Given the inhibition of  and levels of respiratory and metabolic acidosis a sweep of
and levels of respiratory and metabolic acidosis a sweep of  activation values was performed in the presence of these changes to achieve the desired level of extracellular
activation values was performed in the presence of these changes to achieve the desired level of extracellular 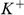 accumulation. During ischemia,
accumulation. During ischemia,  increases over three characteristic phases, with the first phase occurring during the initial
increases over three characteristic phases, with the first phase occurring during the initial  minutes of ischemia prior to reaching a plateau from minutes
minutes of ischemia prior to reaching a plateau from minutes  to
to  , before increasing again. In guinea pigs, ischemia caused
, before increasing again. In guinea pigs, ischemia caused  to increase from
to increase from  to
to  mM over
mM over  minutes [122] or
minutes [122] or  to
to  mM over
mM over  minutes [123]. In swine, ischemia caused
minutes [123]. In swine, ischemia caused  to increase from
to increase from  mM to
mM to  mM after
mM after  minutes [124], [125]. In rat, ischemia caused an increase from
minutes [124], [125]. In rat, ischemia caused an increase from  mM to 8mM over
mM to 8mM over  minutes [110], although other groups have seen a biphasic change in
minutes [110], although other groups have seen a biphasic change in  in rat with an increase from
in rat with an increase from  mM to
mM to  mM before falling back to
mM before falling back to  mM then continuing to rise again, observed over the first
mM then continuing to rise again, observed over the first  minutes [126]. In rabbit, ischemia caused
minutes [126]. In rabbit, ischemia caused  to increase from
to increase from  mM to
mM to  mM over
mM over  minutes [10], [110], [125]. In canine,
minutes [10], [110], [125]. In canine,  increases from
increases from  mM to
mM to  mM after
mM after  minutes [127], [128]. These results indicate an increase in
minutes [127], [128]. These results indicate an increase in  from
from  mM to
mM to  mM after
mM after  minutes and assuming
minutes and assuming  of this rise occurs in the first
of this rise occurs in the first  minutes [127], and combined with the 5 minute data gives an estimate of
minutes [127], and combined with the 5 minute data gives an estimate of  after 5 minutes of ischemia as
after 5 minutes of ischemia as  mM. In the model an increase in
mM. In the model an increase in  of
of  was used to achieve an elevation of
was used to achieve an elevation of  to
to  mM, resulting in an increase in the membrane potential of
mM, resulting in an increase in the membrane potential of  mV to
mV to  mV. This is consistent with measurements in cat (
mV. This is consistent with measurements in cat ( mV over
mV over  minutes) [129], [130], sheep (
minutes) [129], [130], sheep ( mV over
mV over  minutes) [131], guinea pigs (
minutes) [131], guinea pigs ( mV over
mV over  minutes) [132] and mice (
minutes) [132] and mice ( mV over
mV over  minutes) [133], but less than measurements in rabbit (
minutes) [133], but less than measurements in rabbit ( mV over
mV over  minutes [10]) and guinea pig (
minutes [10]) and guinea pig ( mV over
mV over  minutes [120] or
minutes [120] or  mV over
mV over  minutes [134]–[136]). The broad variation in membrane potential changes was not unexpected given the range of changes in
minutes [134]–[136]). The broad variation in membrane potential changes was not unexpected given the range of changes in  and
and  reported and in simulations an intermediate value has been achieved.
reported and in simulations an intermediate value has been achieved.
The individual and combined effects of the four components of ischemia on the temporal evolution of the maximum change in ionic concentrations and the spatial concentration and potential distribution profile after  minutes of simulated ischemia are shown in Fig. 3. As ischemia progressed,
minutes of simulated ischemia are shown in Fig. 3. As ischemia progressed,  continued to increase. The early rise was attributed to
continued to increase. The early rise was attributed to  inhibition; the later increases were due to metabolic and respiratory acidosis. The early rise in
inhibition; the later increases were due to metabolic and respiratory acidosis. The early rise in  was significantly affected by
was significantly affected by  inhibition with
inhibition with  activation playing a greater role as ischemia progresses and the membrane potential diverges from the
activation playing a greater role as ischemia progresses and the membrane potential diverges from the  reversal potential. The decrease in
reversal potential. The decrease in  was solely due to acidosis with no impact from
was solely due to acidosis with no impact from  activation or
activation or  inhibition.
inhibition.  elevation was contributed to principally by
elevation was contributed to principally by  inhibition, while increased
inhibition, while increased  decreased
decreased  . Ischemia caused an initial drop followed by a sustained rise in
. Ischemia caused an initial drop followed by a sustained rise in  .
.  activation caused an early hyperpolarisation of the membrane potential, which was subsequently countered by the depolarising effects of
activation caused an early hyperpolarisation of the membrane potential, which was subsequently countered by the depolarising effects of  inhibition, with acidosis having a limited effect.
inhibition, with acidosis having a limited effect.
Figure 3. Evolution and profile of A-B)  , C-D)
, C-D)  , E-F)
, E-F)  , G-H)
, G-H)  and I-J) membrane potential across the BZ due to each component of ischemia.
and I-J) membrane potential across the BZ due to each component of ischemia.
Complete ischemia,  inhibition,
inhibition,  inhibition, respiratory acidosis and metabolic acidosis are represented by black, yellow, red, blue and purple lines, respectively. Column 1 shows the profile of ionic concentrations and membrane potential after 5 minutes and column 2 shows the evolution of the change in magnitude in ionic concentrations and potential across the border zone with time.
inhibition, respiratory acidosis and metabolic acidosis are represented by black, yellow, red, blue and purple lines, respectively. Column 1 shows the profile of ionic concentrations and membrane potential after 5 minutes and column 2 shows the evolution of the change in magnitude in ionic concentrations and potential across the border zone with time.
Figure 4 plots the width of the BZ for each ion with striped bars corresponding to extracellular space and the darker the bar the more significant the concentration gradient relative to the initial concentration. This plot shows that  had a significantly wider BZ with greater magnitude than
had a significantly wider BZ with greater magnitude than  . For pH regulation,
. For pH regulation,  had a narrower BZ compared to the significantly wider
had a narrower BZ compared to the significantly wider  BZ, which may indicate the facilitation of proton transport via
BZ, which may indicate the facilitation of proton transport via  diffusion.
diffusion.
Figure 4. Width of ionic BZ. Gray scale represents magnitude of gradient with white indicating no gradient.

Solid bars indicate intracellular gradient and striped bars indicate extracellular gradient.
Extracellular Potassium Gradients
The  BZ width was significantly wider than other BZ ion widths and notably larger than the
BZ width was significantly wider than other BZ ion widths and notably larger than the  BZ width. To determine the cause of this extended
BZ width. To determine the cause of this extended  BZ the source of the cumulative changes in
BZ the source of the cumulative changes in  due to transmembrane flux, drift or diffusion over the 5 minutes of ischemia were calculated and plotted in Fig. 5. This showed that only the transmembrane flux had a significant gradient across the ischemic region. Separating the transmembrane flux into the
due to transmembrane flux, drift or diffusion over the 5 minutes of ischemia were calculated and plotted in Fig. 5. This showed that only the transmembrane flux had a significant gradient across the ischemic region. Separating the transmembrane flux into the  and
and  components then identified the
components then identified the  channel, which includes the ATP-inactivated
channel, which includes the ATP-inactivated  current, as the cause of this gradient. The gradient of IKb was due to the extensive membrane potential gradient into the ischemic region (see Fig. 3). To confirm that this was the cause of the
current, as the cause of this gradient. The gradient of IKb was due to the extensive membrane potential gradient into the ischemic region (see Fig. 3). To confirm that this was the cause of the  BZ width, the membrane potential was calculated as normal, but an additional clamped membrane potential was calculated at each time step. The clamped membrane potential had the same maximum and minimum values as the correct membrane potential but instead of a smooth gradient across the BZ it had a sharp transition over the BZ. A comparison of this clamped and the control membrane potentials is shown in the Fig. 5C. The effects of using a clamped membrane potential to calculate the
BZ width, the membrane potential was calculated as normal, but an additional clamped membrane potential was calculated at each time step. The clamped membrane potential had the same maximum and minimum values as the correct membrane potential but instead of a smooth gradient across the BZ it had a sharp transition over the BZ. A comparison of this clamped and the control membrane potentials is shown in the Fig. 5C. The effects of using a clamped membrane potential to calculate the  flux or the
flux or the  current on the cumulative changes in
current on the cumulative changes in  after 5 minutes of simulated ischemia are plotted in Fig. 5B, demonstrating that by removing the gradient in the membrane potential experienced by
after 5 minutes of simulated ischemia are plotted in Fig. 5B, demonstrating that by removing the gradient in the membrane potential experienced by 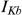 there is a significant narrowing in the
there is a significant narrowing in the  BZ.
BZ.
Figure 5. Mechanisms underpinning .

 BZ width. A) Reference change in
BZ width. A) Reference change in  after 5 minutes of simulated ischemia caused by transmembrane flux (blue dashed line), diffusion (purple line), drift (red line) and the total change due to all causes (yellow line). The BZ is indicated by the yellow shaded region. B) Change in
after 5 minutes of simulated ischemia caused by transmembrane flux (blue dashed line), diffusion (purple line), drift (red line) and the total change due to all causes (yellow line). The BZ is indicated by the yellow shaded region. B) Change in  in the reference model (yellow line) compared with change in
in the reference model (yellow line) compared with change in  when
when  (purple dashed line) or
(purple dashed line) or 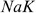 (blue dashed line) are exposed to a clamped membrane potential. The reference BZ and BZ when
(blue dashed line) are exposed to a clamped membrane potential. The reference BZ and BZ when  is exposed to a clamped membrane potential are indicated by the yellow and purple shaded regions, respectively.
is exposed to a clamped membrane potential are indicated by the yellow and purple shaded regions, respectively.
Drift and Diffusion
To investigate the relative contribution of drift and diffusion to intra region fluxes (inter or extracellular) the drift and diffusion fluxes in each region were plotted, alongside the transmembrane flux, over the length of the strand after  minutes of ischemia. Fig. 6 shows the differences in drift and diffusion between
minutes of ischemia. Fig. 6 shows the differences in drift and diffusion between  ,
,  and
and  . As expected from the intra and extracellular gradients, intracellular
. As expected from the intra and extracellular gradients, intracellular  and
and  diffused into and out of the ischemic region in the intra and extracellular space, respectively. The converse was the case for
diffused into and out of the ischemic region in the intra and extracellular space, respectively. The converse was the case for  . Due to the decrease in transmembrane potential, characteristic of ischemic regions, there was a convergence of intra and extracellular potentials with the extracellular potential decreasing in the ischemic region and the intracellular potential increasing. This gradient caused positive ions to drift into the ischemic region in the extracellular space and drift out of the ischemic region in the intracellular space. The converse was true for negatively charged ions. As drift is proportional to the ionic concentration,
. Due to the decrease in transmembrane potential, characteristic of ischemic regions, there was a convergence of intra and extracellular potentials with the extracellular potential decreasing in the ischemic region and the intracellular potential increasing. This gradient caused positive ions to drift into the ischemic region in the extracellular space and drift out of the ischemic region in the intracellular space. The converse was true for negatively charged ions. As drift is proportional to the ionic concentration,  drift was significant in the extracellular space and
drift was significant in the extracellular space and  drift was significant in the intracellular space. For
drift was significant in the intracellular space. For  , drift and diffusion operated in the same direction in the intra and extracellular space. The result was a cyclical movement of
, drift and diffusion operated in the same direction in the intra and extracellular space. The result was a cyclical movement of  moving into the ischemic region in the extracellular space, while moving out of the ischemic region in the intracellular space. The
moving into the ischemic region in the extracellular space, while moving out of the ischemic region in the intracellular space. The  movement was also circular but in the opposite direction (Fig. 6P). However, for
movement was also circular but in the opposite direction (Fig. 6P). However, for  drift and diffusion were in opposite directions. In the extracellular space where the
drift and diffusion were in opposite directions. In the extracellular space where the  concentration was low, diffusion dominated and
concentration was low, diffusion dominated and  moved out of the ischemic region. In the intracellular space, where there was a higher concentration of
moved out of the ischemic region. In the intracellular space, where there was a higher concentration of  , drift dominated, also causing
, drift dominated, also causing  ions to move out of the ischemic region. Thus ischemia caused a depletion of
ions to move out of the ischemic region. Thus ischemia caused a depletion of  in the ischemic region through both the intra and extracellular space and, contrary to previous hypothesis [13], the model suggests that intracellular
in the ischemic region through both the intra and extracellular space and, contrary to previous hypothesis [13], the model suggests that intracellular  movement is the dominant path for
movement is the dominant path for  to leave the ischemic region.
to leave the ischemic region.
Figure 6. Regulation of  ,
,  and
and  ionic concentrations across the border zone after 5 minutes of ischemia.
ionic concentrations across the border zone after 5 minutes of ischemia.
Intra and extracellular A)  , B)
, B)  and C)
and C)  ionic concentrations. D) Intra and extracellular potential. Intracellular drift and diffusion flux of E)
ionic concentrations. D) Intra and extracellular potential. Intracellular drift and diffusion flux of E) 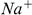 , F)
, F)  and G)
and G)  . Extracellular drift and diffusion of H)
. Extracellular drift and diffusion of H)  , I)
, I)  and J)
and J)  . Transmembrane flux of K)
. Transmembrane flux of K)  , L)
, L)  and M)
and M)  . Schematics showing the general direction of ion movement within and between the intra and extracellular space for N)
. Schematics showing the general direction of ion movement within and between the intra and extracellular space for N)  , O)
, O)  and P)
and P)  .
.
Discussion
In this study a new model of cardiac tissue electrophysiology was developed. The model predicted that the width of the  gradient across an ischemic BZ would be significantly wider the
gradient across an ischemic BZ would be significantly wider the  BZ. The cause of this difference was attributed to the voltage dependence of the
BZ. The cause of this difference was attributed to the voltage dependence of the  channel. The model also demonstrated that, due to electrogenic drift,
channel. The model also demonstrated that, due to electrogenic drift,  moved out of the ischemic region in both the intra and extracellular space which will lead to
moved out of the ischemic region in both the intra and extracellular space which will lead to  depletion.
depletion.
The model of ionic movement and tissue electrophysiology was developed by combining the Nernst-Plank equations with the bidomain framework. No attempt was made to explicitly validate the proposed tissue model equations due to the paucity of experimental data. However, applying simplifying assumptions with regards to ionic or voltage gradients reduces the proposed equations to the well validated bidomain equations [137], [138] or coupled reaction-diffusion equations [28], [86], respectively, providing support for the validity of the proposed modelling framework. The limited attempts at simulating the spatial temporal evolution of ionic gradients across the ischemic BZ have largely uncoupled the movement of ions and the electric field. Potse et al., [18] demonstrated that measured 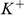 gradients across an ischemic BZ could be simulated using a model of
gradients across an ischemic BZ could be simulated using a model of  diffusion coupled to a source term. The spatially varying
diffusion coupled to a source term. The spatially varying  gradient could then be included as a boundary condition to models of transmembrane current in the bidomain equations. This model did not include any effect of electric gradients on
gradient could then be included as a boundary condition to models of transmembrane current in the bidomain equations. This model did not include any effect of electric gradients on  movement,
movement,  movement, inter ionic species interactions or the effect of the ischemic region on any other ion gradient. Similar sets of equations to those proposed here have been used for simulating the potential gradient surrounding cells, including the Debye layer [139], electrical propagation along strands of cardiac cells [140], [141] and for modelling ion diffusion in the cable equation [142]. These previous models have either explicitly represented the intra and extracellular domains or only considered the intracellular domain but have not modelled the tissue within the bidomain framework, as derived and implemented here.
movement, inter ionic species interactions or the effect of the ischemic region on any other ion gradient. Similar sets of equations to those proposed here have been used for simulating the potential gradient surrounding cells, including the Debye layer [139], electrical propagation along strands of cardiac cells [140], [141] and for modelling ion diffusion in the cable equation [142]. These previous models have either explicitly represented the intra and extracellular domains or only considered the intracellular domain but have not modelled the tissue within the bidomain framework, as derived and implemented here.
The proposed equations can be applied generally in three dimensions as opposed to the one dimensional simulations presented here. The current study does not consider the effects of anisotropy on ion or membrane potential gradients across the BZ, however, if implemented in two or three dimensions the model is capable of representing tissue anisotropy and any effects this may have on BZ gradients. By conserving ionic species the proposed equations provide a more biophysical representation of cardiac electrophysiology than the bidomain equations and can appropriately be applied to simulate a broader range of conditions. However, these benefits come at a cost. Unlike the bidomain equations, with two partial differential equations that can readily be uncoupled and solved as two sets of linear equations [143], the proposed model is nonlinear and contains two parabolic partial differential equations for each ionic species and one elliptic partial differential equation to model the electric potential. This results in a significant increase both in the complexity and number of equations that must be solved and hence comes at a significant increase in computational cost. The proposed framework can be used to simulate electrically active tissue by introducing a full action potential cell model [31]. This would require identifying and separating out the transmembrane pathways for each ionic species present in the cell model to calculate the net transmebrane flux for each ion or  in Eqn 18. The internal cell model state variables, including gating variables, Markov states and intracellular
in Eqn 18. The internal cell model state variables, including gating variables, Markov states and intracellular  dynamics would also need to be solved, introducing a system of nonlinear ordinary differential equations at each grid point. The small time steps and increased number of degrees of freedom required to simulate electrically active tissue would further increase the computational cost of the proposed model.
dynamics would also need to be solved, introducing a system of nonlinear ordinary differential equations at each grid point. The small time steps and increased number of degrees of freedom required to simulate electrically active tissue would further increase the computational cost of the proposed model.
A new model of ion movement across the un-stimulated cell membrane was developed. This model has been published online and is available at cellml.org. The model creation approach demonstrated two novel methods. Firstly, the ion transporter densities were uniquely constrained by a small number of experimental data sets and a zero net flux constraint. This provided a repeatable and unique method for determining model parameters under quiescent conditions and could readily be applied to any cardiac electrophysiology model to constrain model parameters. Secondly, in the development of this model a grid of  experimental observations were created to provide a comprehensive validation of the model response to changes in ion concentrations and in the presence of blockers of major transporters. Although these observations only provide a qualitative comparison, they do provide a benchmark for quantifying the generality of models. Furthermore, Table 4 identified
experimental observations were created to provide a comprehensive validation of the model response to changes in ion concentrations and in the presence of blockers of major transporters. Although these observations only provide a qualitative comparison, they do provide a benchmark for quantifying the generality of models. Furthermore, Table 4 identified  experiments that do not appear to have been performed or remain controversial, highlighting the potential for additional experiments.
experiments that do not appear to have been performed or remain controversial, highlighting the potential for additional experiments.
In this study the process of validating the model against  experimental observations demonstrated the general capacity of the model to replicate the majority of experimental results. However, the model was unable to match ten of the
experimental observations demonstrated the general capacity of the model to replicate the majority of experimental results. However, the model was unable to match ten of the  observations. Five of the experimental observations found no change in a measurement. Due to the numerical nature of the model, even very small changes in a concentration can be observed and without adding in a semi arbitrary threshold that should reflect the variability and confidence of each experimental measurement it was not possible for the model to return no change in a value. In general the five remaining failed observations can be attributed to absent mechanisms in the model or inconsistencies with the model and specific experimental setups. The model did not predict the
observations. Five of the experimental observations found no change in a measurement. Due to the numerical nature of the model, even very small changes in a concentration can be observed and without adding in a semi arbitrary threshold that should reflect the variability and confidence of each experimental measurement it was not possible for the model to return no change in a value. In general the five remaining failed observations can be attributed to absent mechanisms in the model or inconsistencies with the model and specific experimental setups. The model did not predict the  response to depressed
response to depressed  and the
and the  response to depressed
response to depressed  . This is potentially due to the absence of NaK2Cl from the model, largely due to the lack of data characterising the transporter. The model was unable to replicate the decrease in
. This is potentially due to the absence of NaK2Cl from the model, largely due to the lack of data characterising the transporter. The model was unable to replicate the decrease in  due to elevated
due to elevated  . This may be due to the specifics of the experimental protocol. Decreasing
. This may be due to the specifics of the experimental protocol. Decreasing  , which should have the opposite effect on
, which should have the opposite effect on  , caused both increases and decreases in
, caused both increases and decreases in  in different studies indicating that the
in different studies indicating that the  dependence on
dependence on  is sensitive to the specifics of the experimental setup. The model did not predict the change in
is sensitive to the specifics of the experimental setup. The model did not predict the change in  or
or  with a decrease in
with a decrease in  . Experimental observations report an increase in
. Experimental observations report an increase in  with both a decrease or an increase in
with both a decrease or an increase in  . This may indicate that the
. This may indicate that the  is at some minima with respect to
is at some minima with respect to  , although this seems unlikely. It more likely reflects inconsistent data due to differences in experimental setups that were impossible for the model to replicate. In cardiac myocytes it is postulated that
, although this seems unlikely. It more likely reflects inconsistent data due to differences in experimental setups that were impossible for the model to replicate. In cardiac myocytes it is postulated that  and
and  compete for common buffering sites [144], [145]. The decrease in
compete for common buffering sites [144], [145]. The decrease in  may drain the cell of
may drain the cell of  , reducing the
, reducing the  bound to buffers that could then be occupied by
bound to buffers that could then be occupied by  , resulting in a decrease in
, resulting in a decrease in  . A common pool of
. A common pool of  and
and  buffering was not present in the model and this may explain the disparity between model predictions and experimental results. Despite the inability of the model to replicate
buffering was not present in the model and this may explain the disparity between model predictions and experimental results. Despite the inability of the model to replicate  of the
of the  observations, the majority of the absent mechanisms are expected to play a secondary role during ischemia. NaK2Cl is a potential contributor to the elevation in
observations, the majority of the absent mechanisms are expected to play a secondary role during ischemia. NaK2Cl is a potential contributor to the elevation in  [146], although this has been questioned [131], and its absence is unlikely to affect the general model conclusions.
[146], although this has been questioned [131], and its absence is unlikely to affect the general model conclusions.
Models simulations found a BZ width for the different ions of between  mm (
mm ( ) and
) and  mm (
mm ( ). The variation in the width of each ion across the BZ means that there was no single BZ width predicted by the model. The majority of ions transitioned from viable to ischemic concentrations over
). The variation in the width of each ion across the BZ means that there was no single BZ width predicted by the model. The majority of ions transitioned from viable to ischemic concentrations over  mm, with
mm, with  and
and  notable outliers. The model predictions are consistent with previous measurements of the BZ between
notable outliers. The model predictions are consistent with previous measurements of the BZ between  and
and  mm [10], [11], [147]–[149]. However, the model did not include the sharp gradients in metabolites over
mm [10], [11], [147]–[149]. However, the model did not include the sharp gradients in metabolites over  mm [11] or the effects of regions of reduced perfusion affecting mechanics over 20 mm distance from the ischemic region [150].
mm [11] or the effects of regions of reduced perfusion affecting mechanics over 20 mm distance from the ischemic region [150].
The model predicted that  and
and  have significantly different BZ widths (Fig. 4). It was expected that the coupling of
have significantly different BZ widths (Fig. 4). It was expected that the coupling of 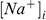 and
and  via
via  would result in concordant gradients in these two ions across the BZ. The extended
would result in concordant gradients in these two ions across the BZ. The extended  gradient was attributed to the voltage dependence of the
gradient was attributed to the voltage dependence of the  (Fig 5). Unlike
(Fig 5). Unlike  ,
,  is regulated by two electrogenic transmembrane pathways
is regulated by two electrogenic transmembrane pathways  and
and  , whereas
, whereas  is regulated by multiple exchangers that are electro neutral, or have attenuated voltage dependence, compared to ion channels. This discordance in
is regulated by multiple exchangers that are electro neutral, or have attenuated voltage dependence, compared to ion channels. This discordance in  and
and  gradients will have a significant effect on the gradient of action potential morphology across the BZ. Elevation of
gradients will have a significant effect on the gradient of action potential morphology across the BZ. Elevation of  depolarises the cell and shortens the action potential duration, whereas elevation of
depolarises the cell and shortens the action potential duration, whereas elevation of  causes a reduction in action potential duration [151], [152]. The combined effect of the two gradients will be a slower change in resting membrane potential on the length scale of the
causes a reduction in action potential duration [151], [152]. The combined effect of the two gradients will be a slower change in resting membrane potential on the length scale of the  gradient and a much more rapid transition in action potential duration due to the faster change in
gradient and a much more rapid transition in action potential duration due to the faster change in  in conjunction with the change in
in conjunction with the change in  over the BZ. The temporal evolution of the two gradients are also distinct, with a sustained constant increase in
over the BZ. The temporal evolution of the two gradients are also distinct, with a sustained constant increase in  over the first
over the first  minutes, while
minutes, while  increases rapidly for
increases rapidly for  minutes before plateauing (Fig. 3). These simulation results are consistent with experimental measurements of ionic concentrations [111], [152] and changes in ECG morphology, which report an early elevation of resting membrane potential, followed by a decrease in action potential duration [153] during early ischemia. These spatial-temporal increases in ion concentrations and secondary effects on electrophysiology will increase tissue heterogeneity and have the capacity to play an important role in the BZ arrhythmogenic substrate.
minutes before plateauing (Fig. 3). These simulation results are consistent with experimental measurements of ionic concentrations [111], [152] and changes in ECG morphology, which report an early elevation of resting membrane potential, followed by a decrease in action potential duration [153] during early ischemia. These spatial-temporal increases in ion concentrations and secondary effects on electrophysiology will increase tissue heterogeneity and have the capacity to play an important role in the BZ arrhythmogenic substrate.
Experimental measurements have reported a decrease in  during ischemia [152]. Loss of
during ischemia [152]. Loss of  has been attributed to a combination of increased
has been attributed to a combination of increased  conduction and
conduction and  inhibition [152], [154]. However, depletion of
inhibition [152], [154]. However, depletion of  due to transmembrane
due to transmembrane  movement, in the absence of a potential gradient, would cause an intracellular flux of
movement, in the absence of a potential gradient, would cause an intracellular flux of  into the ischemic zone, due to diffusion, to replenish
into the ischemic zone, due to diffusion, to replenish  , mitigating the effects of changes of
, mitigating the effects of changes of  transmembrane flux on
transmembrane flux on  . The model proposed here demonstrated that this is not necessarily the case. The model predicted a significant electrogenic
. The model proposed here demonstrated that this is not necessarily the case. The model predicted a significant electrogenic  flux in the intracellular space out of the ischemic zone (Fig. 6), resulting in a net efflux of
flux in the intracellular space out of the ischemic zone (Fig. 6), resulting in a net efflux of  out of the ischemic zone both in the intra and extracellular space. The movement of
out of the ischemic zone both in the intra and extracellular space. The movement of  in the intracellular space out of the ischemic zone would further deplete
in the intracellular space out of the ischemic zone would further deplete  in the ischemic region and exacerbate
in the ischemic region and exacerbate  loss, but may limit
loss, but may limit  accumulation in the extracellular space.
accumulation in the extracellular space.
Limitations
The model is inherently an approximation and hence represents a finite set of known cellular properties and changes that occur during ischemia. In particular, the model treated all buffers as static and rapid, the effects of protons on channel, exchanger and co-transports were not considered, ischemic changes were instantaneous and the model did not include all possible changes or pathways that may affect ionic homeostasis during ischemia.
The tissue model assumed that  and
and  buffers are static, rapid and made up of a single population of binding sites. It is known that some of the buffers for both
buffers are static, rapid and made up of a single population of binding sites. It is known that some of the buffers for both  and
and  are mobile, these could be introduced into the model framework as an additional concentration but these effects were approximated, without the additional computational cost of adding a additional ionic concentration, by using effective diffusion constants. The equilibrium assumption was likely to be valid in the current model due to the long time scales of interest; however, simulation of cardiac action potentials would require the re-evaluation of this assumption. It is also known that
are mobile, these could be introduced into the model framework as an additional concentration but these effects were approximated, without the additional computational cost of adding a additional ionic concentration, by using effective diffusion constants. The equilibrium assumption was likely to be valid in the current model due to the long time scales of interest; however, simulation of cardiac action potentials would require the re-evaluation of this assumption. It is also known that  [28] and
[28] and  [155] are buffered by multiple proteins with distinct binding kinetics but over the range of concentrations simulated these multiple buffer species were unlikely to have significant effects.
[155] are buffered by multiple proteins with distinct binding kinetics but over the range of concentrations simulated these multiple buffer species were unlikely to have significant effects.
The model of intracellular  dynamics assumes that the SR and cytosolic
dynamics assumes that the SR and cytosolic  concentrations remain in equilibrium, which is clearly not the case during an action potential. The model of intracellular
concentrations remain in equilibrium, which is clearly not the case during an action potential. The model of intracellular  dynamics provided a numerically efficient representation of intracellular
dynamics provided a numerically efficient representation of intracellular  buffering and SR
buffering and SR  uptake. The use of a Hill coefficient of one for SERCA as opposed to the more common and biophysical value of two removed the need for an additional differential equation to model
uptake. The use of a Hill coefficient of one for SERCA as opposed to the more common and biophysical value of two removed the need for an additional differential equation to model  or the solution of a set of nonlinear equations to model
or the solution of a set of nonlinear equations to model  regulation. Furthermore, over the range of
regulation. Furthermore, over the range of  values studied it was possible to adjust the maximum SERCA flux to minimize discrepancies between a model with a Hill coefficient of one or two.
values studied it was possible to adjust the maximum SERCA flux to minimize discrepancies between a model with a Hill coefficient of one or two.
It is well recognised that  play an important role in regulating cellular electrophysiology [156]. Experimental and modelling studies have demonstrated the effects of
play an important role in regulating cellular electrophysiology [156]. Experimental and modelling studies have demonstrated the effects of  on ryanodine receptor opening probabilities,
on ryanodine receptor opening probabilities,  ,
,  channels,
channels,  buffering and SERCA [22], [157]. The majority of the effects of
buffering and SERCA [22], [157]. The majority of the effects of  on
on  regulation are unlikely to play a significant role in determining the spatial and temporal
regulation are unlikely to play a significant role in determining the spatial and temporal  and
and  . However, inhibition of
. However, inhibition of  potentially contributes to
potentially contributes to  gradients but this will be secondary to the effects of
gradients but this will be secondary to the effects of  inhibition.
inhibition.
The model treats all changes for ischemia as instantaneous. The time dependence of inhibition of  , activation of
, activation of  , increased
, increased  flux or increased
flux or increased  flux are not known and can only be approximated. A linear ramp in ischemic changes has been used previously, but this fails to consider the possibility that changes occur over different time scales. In order to minimise ambiguity in model simulations an instantaneous change in
flux are not known and can only be approximated. A linear ramp in ischemic changes has been used previously, but this fails to consider the possibility that changes occur over different time scales. In order to minimise ambiguity in model simulations an instantaneous change in  ,
,  ,
,  flux and
flux and  flux was chosen.
flux was chosen.
To limit the scope of this study, the effects of cell swelling and the effects of this on changes in ion concentrations [122] were not included in the model. However, previous, modelling studies have found these effects to not significantly alter  accumulation and may not fundamentally alter the study conclusions [20]. Mitani and Shattock [146] identified the Na dependent potassium channel as a potential contributor to the elevation of
accumulation and may not fundamentally alter the study conclusions [20]. Mitani and Shattock [146] identified the Na dependent potassium channel as a potential contributor to the elevation of  . However, the effects of an increase in any
. However, the effects of an increase in any  current are captured by the elevation in
current are captured by the elevation in  that does not necessarily need to be the sole result of an increase in conduction in the ATP inactivated
that does not necessarily need to be the sole result of an increase in conduction in the ATP inactivated  channel. Furthermore, the model does not include an increased
channel. Furthermore, the model does not include an increased  channel conductance during ischemia. This has been reported during ischemia in the form of increased permeability of
channel conductance during ischemia. This has been reported during ischemia in the form of increased permeability of  through the persistent
through the persistent  current [116] and the ATP activated
current [116] and the ATP activated  channel [158]. However, other groups have found a limited impact of the persistent
channel [158]. However, other groups have found a limited impact of the persistent  channel in
channel in  accumulation during ischemia [159] and previous modelling studies have shown that its inclusion is not required to capture the salient features of ischemia in the single cell [20]. For these reasons a potential increase in the
accumulation during ischemia [159] and previous modelling studies have shown that its inclusion is not required to capture the salient features of ischemia in the single cell [20]. For these reasons a potential increase in the  channel conductance was not included in this study.
channel conductance was not included in this study.
Summary
A new mathematical framework was derived for simulating cardiac tissue electrophysiology with ion species conservation. The model was used to simulate the movement of ions due to transmembrane channels, pumps and transporters, diffusion and drift in the intra and extracellular space. The model predicted that 1) the sodium BZ is approximately a quarter of the length of the potassium BZ and this is due to the effects of the membrane potential gradient on  and 2) that during ischemia there is a gross movement of potassium ions out of the ischemic region in both the intra and extracellular space due to the effects of drift, which will lead to a depletion of
and 2) that during ischemia there is a gross movement of potassium ions out of the ischemic region in both the intra and extracellular space due to the effects of drift, which will lead to a depletion of  from the ischemic region.
from the ischemic region.
Funding Statement
The work was supported by UK Engineering and Physical Sciences Research Council EP/F043929/1, British Heart Foundation (PG/11/101/29212) and Boston Scientific. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Kaplinsky E, Ogawa S, Balke CW, Dreifus LS (1979) Two periods of early ventricular arrhythmia in the canine acute myocardial infarction model. Circulation 60: 397–403. [DOI] [PubMed] [Google Scholar]
- 2. Janse MJ, Cinca J, Morena H, Fiolet JW, Kleber AG, et al. (1979) The “border zone” in myocardial ischemia. an electrophysiological, metabolic, and histochemical correlation in the pig heart. Circulation Research 44: 576–588. [DOI] [PubMed] [Google Scholar]
- 3. Cascio WE (2001) Myocardial ischemia: What factors determine arrhythmogenesis? Journal of Cardiovascular Electrophysiology 12: 726–729. [DOI] [PubMed] [Google Scholar]
- 4. Zaitsev AV, Guha PK, Sarmast F, Kolli A, Berenfeld O, et al. (2003) Wavebreak formation during ventricular fibrillation in the isolated, regionally ischemic pig heart. Circulation Research 92: 546–553. [DOI] [PubMed] [Google Scholar]
- 5. Carmeliet E (1999) Cardiac ionic currents and acute ischemia: From channels to arrhythmias. physiological reviews 73: 917–1017. [DOI] [PubMed] [Google Scholar]
- 6. Sidorov VY, Uzelac I, Wikswo JP (2011) Regional increase of extracellular potassium leads to electrical instability and reentry occurrence through the spatial heterogeneity of apd restitution. American Journal of Physiology - Heart and Circulatory Physiology 301: H209–H220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Weiss JN, Chen PS, Qu Z, Karagueuzian HS, Garfinkel A (2000) Ventricular fibrillation. Circulation Research 87: 1103–1107. [DOI] [PubMed] [Google Scholar]
- 8. Horacek T, Neumann M, von Mutius S, Budden M, Meesmann W (1984) Nonhomogeneous electrophysiological changes and the bimodal distribution of early ventricular arrhythmias during acute coronary artery occlusion. Basic Research in Cardiology 79: 649–667. [DOI] [PubMed] [Google Scholar]
- 9. Klber AG (1984) Extracellular potassium accumulation in acute myocardial ischemia. Journal of Molecular and Cellular Cardiology 16: 389–394. [DOI] [PubMed] [Google Scholar]
- 10. Wilensky RL, Tranum-Jensen J, Coronel R, Wilde AA, Fiolet JW, et al. (1986) The subendocardial border zone during acute ischemia of the rabbit heart: an electrophysiologic, metabolic, and morphologic correlative study. Circulation 74: 1137–1146. [DOI] [PubMed] [Google Scholar]
- 11. Harken AH, Barlow CH, Harden Iii WR, Chance B (1978) Two and three dimensional display of myocardial ischemic border zone in dogs. The American Journal of Cardiology 42: 954–959. [DOI] [PubMed] [Google Scholar]
- 12. Yellon DM, Hearse DJ, Crome R, Grannell J, Wyse RKH (1981) Characterization of the lateral interface between normal and ischemic tissue in the canine heart during evolving myocardial infarction. The American Journal of Cardiology 47: 1233–1239. [DOI] [PubMed] [Google Scholar]
- 13. Coronel R, Fiolet JW, Wilms-Schopman FJ, Schaapherder AF, Johnson TA, et al. (1988) Distribution of extracellular potassium and its relation to electrophysiologic changes during acute myocardial ischemia in the isolated perfused porcine heart. Circulation 77: 1125–1138. [DOI] [PubMed] [Google Scholar]
- 14. Coronel R, Wilms-Schopman FJG, Fiolet JWT, Opthof T, Janse MJ (1995) The relation between extracellular potassium concentration and ph in the border zone during regional ischemia in isolated porcine hearts. Journal of Molecular and Cellular Cardiology 27: 2069–2073. [DOI] [PubMed] [Google Scholar]
- 15. Tice BM, Rodrguez B, Eason J, Trayanova N (2007) Mechanistic investigation into the arrhythmogenic role of transmural heterogeneities in regional ischaemia phase 1a. Europace 9: vi46–vi58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Trnor B, Ferrero JM, Rodrguez B, Montilla F (2005) Effects of pinacidil on reentrant arrhythmias generated during acute regional ischemia: A simulation study. Annals of Biomedical Engineering 33: 897–906. [DOI] [PubMed] [Google Scholar]
- 17. Potse M, Coronel R, Falcao S, LeBlanc AR, Vinet A (2007) The effect of lesion size and tissue remodeling on ST deviation in partial-thickness ischemia. Heart Rhythm 4: 200–206. [DOI] [PubMed] [Google Scholar]
- 18. Potse M, Coronel R, LeBlanc AR, Vinet A (2007) The role of extracellular potassium transport in computer models of the ischemic zone. Medical and Biological Engineering and Computing 45: 1187–1199. [DOI] [PubMed] [Google Scholar]
- 19. Smith NP, Crampin EJ (2004) Development of models of active ion transport for whole-cell modelling: cardiac sodium-potassium pump as a case study. Progress in Biophysics & Molecular Biology 85: 387–405. [DOI] [PubMed] [Google Scholar]
- 20. Terkildsen JR, Crampin EJ, Smith NP (2007) The balance between inactivation and activation of the Na+-K+ pump underlies the triphasic accumulation of extracellular K+ during myocardial ischemia. Am J Physiol Heart Circ Physiol 293: H3036–3045. [DOI] [PubMed] [Google Scholar]
- 21. Weber CR, Piacentino I Valentino, Ginsburg KS, Houser SR, Bers DM (2002) Na+-Ca2+ exchange current and submembrane [Ca2+]. during the cardiac action potential. Circulation Research 90: 182–189. [DOI] [PubMed] [Google Scholar]
- 22. Crampin EJ, Smith NP (2006) A dynamic model of excitation-contraction coupling during acidosis in cardiac ventricular myocytes. Biophysical Journal 90: 3074–3090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Niederer SA, Smith NP (2007) A mathematical model of the slow force response to stretch in rat ventricular myocytes. Biophysical Journal 92: 4030–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Wu ML, Vaughan-Jones RD (1997) Interaction between Na+ and H+ ions on Na-H exchange in sheep cardiac purkinje fibers. Journal of Molecular and Cellular Cardiology 29: 1131–1140. [DOI] [PubMed] [Google Scholar]
- 25. Zaniboni M, Swietach P, Rossini A, Yamamoto T, Spitzer KW, et al. (2003) Intracellular proton mobility and buffering power in cardiac ventricular myocytes from rat, rabbit, and guinea pig. American Journal of Physiology 285: H1236–H1246. [DOI] [PubMed] [Google Scholar]
- 26. Despa S, Islam MA, Pogwizd SM, Bers DM (2002) Intracellular Na+. and Na+ pump rate in rat and rabbit ventricular myocytes. J Physiol (Lond) 539: 133–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Niederer SA, Swietach P, Wilson DA, Smith NP, Vaughan-Jones RD (2008) Measuring and modeling chloride-hydroxyl exchange in the guinea-pig ventricular myocyte. Biophysical Journal 94: 2385–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Zaniboni M, Rossini A, Swietach P, Banger N, Spitzer KW, et al. (2003) Proton permeation through the myocardial gap junction. Circulation Research 93: 726–735. [DOI] [PubMed] [Google Scholar]
- 29. Faber GM, Rudy Y (2000) Action potential and contractility changes in Na+ (i) overloaded cardiac myocytes: A simulation study. Biophysical Journal 78: 2392–2404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Komukai K, Brette F, Pascarel C, Orchard CH (2002) Electrophysiological response of rat ventricular myocytes to acidosis. American Journal of Physiology - Heart and Circulatory Physiology 283: H412–H422. [DOI] [PubMed] [Google Scholar]
- 31. Fink M, Niederer SA, Cherry EM, Fenton FH, Koivumki JT, et al. (2011) Cardiac cell modelling: Observations from the heart of the cardiac physiome project. Progress in Biophysics and Molecular Biology 104: 2–21. [DOI] [PubMed] [Google Scholar]
- 32. Monnereau-Soustre H, Revial MF, Leoty C, Pager J (1969) evaluation of extracellular space of the rat heart: effect of adrenalectomy; electrophysiological implications. C R Seances Soc Biol Fil 163: 1419–22. [PubMed] [Google Scholar]
- 33. Polimeni P (1974) Extracellular space and ionic distribution in rat ventricle. American Journal of Physiology – Legacy Content 227: 676–683. [DOI] [PubMed] [Google Scholar]
- 34. Poole-Wilson P, Cameron I (1975) ECS, intracellular pH, and electrolytes of cardiac and skeletal muscle. American Journal of Physiology – Legacy Content 229: 1299–1304. [DOI] [PubMed] [Google Scholar]
- 35. Caille JP, Ruiz-Ceretti E, Schanne OF (1981) Intracellular chloride activity in rabbit papillary muscle: effect of ouabain. American Journal of Physiology - Cell Physiology 240: C183–C188. [DOI] [PubMed] [Google Scholar]
- 36. Polimeni PI (1974) Cardiac electrolytes and water in thyroparathyroidectomized rat. Journal of Molecular and Cellular Cardiology 6: 531–541. [DOI] [PubMed] [Google Scholar]
- 37. Page E (1978) Quantitative ultrastructural analysis in cardiac membrane physiology. American Journal of Physiology - Cell Physiology 235: C147–C158. [DOI] [PubMed] [Google Scholar]
- 38. Page E, Surdyk-Droske M (1979) Distribution, surface density, and membrane area of diadic junctional contacts between plasma membrane and terminal cisterns in mammalian ventricle. Circulation Research 45: 260–267. [DOI] [PubMed] [Google Scholar]
- 39. Chopra N, Kannankeril PJ, Yang T, Hlaing T, Holinstat I, et al. (2007) Modest reductions of cardiac calsequestrin increase sarcoplasmic reticulum Ca2+ leak independent of luminal Ca2+ and trigger ventricular arrhythmias in mice. Circulation Research 101: 617–626. [DOI] [PubMed] [Google Scholar]
- 40. Singh S, White F, Bloor C (1981) Myocardial morphometric characteristics in swine. Circulation Research 49: 434–441. [DOI] [PubMed] [Google Scholar]
- 41. Abete P, Vassalle M (1988) Relation between Na+-K+ pump, Na+ activity and force in strophanthidin inotropy in sheep cardiac purkinje fibres. The Journal of Physiology 404: 275–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Sossalla S, Wagner S, Rasenack ECL, Ruff H, Weber SL, et al. (2008) Ranolazine improves diastolic dysfunction in isolated myocardium from failing human hearts – role of late sodium current and intracellular ion accumulation. Journal of Molecular and Cellular Cardiology 45: 32–43. [DOI] [PubMed] [Google Scholar]
- 43. Kimura S, Bassett AL, Gaide MS, Kozlovskis PL, Myerburg RJ (1986) Regional changes in intracellular potassium and sodium activity after healing of experimental myocardial infarction in cats. Circulation Research 58: 202–208. [DOI] [PubMed] [Google Scholar]
- 44. Baartscheer A, Hardziyenka M, Schumacher CA, Belterman CNW, Borren MMGJv, et al. (2008) Chronic inhibition of the Na-H exchanger causes regression of hypertrophy, heart failure, and ionic and electrophysiological remodelling. British Journal of Pharmacology 154: 1266–1275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Lee CO, Fozzard HA (1975) Activities of potassium and sodium ions in rabbit heart muscle. The Journal of General Physiology 65: 695–708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Prasad K, Khatter JC, Bharadwaj B (1979) Intra- and extracellular electrolytes and sarcolemmal ATPase in the failing heart due to pressure overload in dogs. Cardiovascular Research 13: 95–104. [DOI] [PubMed] [Google Scholar]
- 47. Cohen C, Fozzard H, Sheu S (1982) Increase in intracellular sodium ion activity during stimulation in mammalian cardiac muscle. Circulation Research 50: 651–662. [DOI] [PubMed] [Google Scholar]
- 48. Baumgarten CM, Fozzard HA (1981) Intracellular chloride activity in mammalian ventricular muscle. American Journal of Physiology - Cell Physiology 241: C121–C129. [DOI] [PubMed] [Google Scholar]
- 49. Powell T, Terrar DA, Twist VW (1980) Electrical properties of individual cells isolated from adult rat ventricular myocardium. The Journal of Physiology 302: 131–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Vaughan-Jones RD (1979) Non-passive chloride distribution in mammalian heart muscle: micro-electrode measurement of the intracellular chloride activity. The Journal of Physiology 295: 83–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Lai ZF, Nishi K (1998) Intracellular chloride activity increases in guinea pig ventricular muscle during simulated ischemia. American Journal of Physiology - Heart and Circulatory Physiology 275: H1613–H1619. [DOI] [PubMed] [Google Scholar]
- 52.Bers DM (2001) excitation-contraction coupling and cardiac contractile force. Dordrecht: Kluwer Academic Publishers, first edition.
- 53. Baartscheer A, Schumacher CA, Belterman CN, Coronel R, Fiolet JW (2003) SR calcium handling and calcium after-transients in a rabbit model of heart failure. Cardiovascular Research 58: 99–108. [DOI] [PubMed] [Google Scholar]
- 54. Bassani JW, Bassani RA, Bers DM (1995) Calibration of indo-1 and resting intracellular [Ca]i in intact rabbit cardiac myocytes. Biophysical Journal 68: 1453–1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Siri FM, Krueger J, Nordin C, Ming Z, Aronson RS (1991) Depressed intracellular calcium transients and contraction in myocytes from hypertrophied and failing guinea pig hearts. American Journal of Physiology - Heart and Circulatory Physiology 261: H514–H530. [DOI] [PubMed] [Google Scholar]
- 56. Han S (1994) Schiefer A, Isenberg G (1994) Ca2+ load of guinea-pig ventricular myocytes determines efficacy of brief Ca2+ currents as trigger for Ca2+ release. The Journal of Physiology 480: 411–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Nakanishi T, Seguchi M, Tsuchiya T, Yasukouchi S, Takao A (1990) Effect of acidosis on intracellular ph and calcium concentration in the newborn and adult rabbit myocardium. Circulation Research 67: 111–123. [DOI] [PubMed] [Google Scholar]
- 58. Terracciano CM, MacLeod KT (1997) Measurements of Ca2+ entry and sarcoplasmic reticulum Ca2+ content during the cardiac cycle in guinea pig and rat ventricular myocytes. Biophysical journal 72: 1319–1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Varro A, Negretti N, Hester SB, Eisner DA (1993) An estimate of the calcium content of the sarcoplasmic reticulum in rat ventricular myocytes. Pflügers Archiv European Journal of Physiology 423: 158–160. [DOI] [PubMed] [Google Scholar]
- 60. Bassani RA, Bers DM (1995) Rate of diastolic Ca release from the sarcoplasmic reticulum of intact rabbit and rat ventricular myocytes. Biophysical Journal 68: 2015–2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Delbridge LM, Satoh H, Yuan W, Bassani JW, Qi M, et al. (1997) Cardiac myocyte volume, Ca2+ fluxes, and sarcoplasmic reticulum loading in pressure-overload hypertrophy. American Journal of Physiology - Heart and Circulatory Physiology 272: H2425–H2435. [DOI] [PubMed] [Google Scholar]
- 62. Hobai IA, ORourke B (2001) Decreased sarcoplasmic reticulum calcium content is responsible for defective excitation-contraction coupling in canine heart failure. Circulation 103: 1577–1584. [DOI] [PubMed] [Google Scholar]
- 63. Trafford AW, Daz ME, Eisner DA (1999) A novel, rapid and reversible method to measure ca buffering and time-course of total sarcoplasmic reticulum ca content in cardiac ventricular myocytes. Pflgers Archiv European Journal of Physiology 437: 501–503. [DOI] [PubMed] [Google Scholar]
- 64. Bennett DL, ONeill SC, Eisner DA (1999) Strophanthidin-induced gain of Ca2+ occurs during diastole and not systole in guinea-pig ventricular myocytes. Pflugers Archiv European Journal of Physiology 437: 731–736. [DOI] [PubMed] [Google Scholar]
- 65. Hove-Madsen L, Bers D (1993) Sarcoplasmic reticulum Ca2+ uptake and thapsigargin sensitivity in permeabilized rabbit and rat ventricular myocytes. Circulation Research 73: 820–828. [DOI] [PubMed] [Google Scholar]
- 66. Berlin JR, Bassani JW, Bers DM (1994) Intrinsic cytosolic calcium buffering properties of single rat cardiac myocytes. Biophysical Journal 67: 1775–1787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Walden AP, Dibb KM, Trafford AW (2009) Differences in intracellular calcium homeostasis between atrial and ventricular myocytes. Journal of Molecular and Cellular Cardiology 46: 463–473. [DOI] [PubMed] [Google Scholar]
- 68. Díaz ME, Trafford AW, Eisner DA (2001) The effects of exogenous calcium buffers on the systolic calcium transient in rat ventricular myocytes. Biophysical Journal 80: 1915–1925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Gottlieb RA, Gruol DL, Zhu JY, Engler RL (1996) Preconditioning rabbit cardiomyocytes: role of ph, vacuolar proton atpase, and apoptosis. J Clin Invest 97: 2391–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Leem CH, Lagadic-Gossmann D, Vaughan-Jones RD (1999) Characterization of intracellular pH regulation in the guinea-pig ventricular myocyte. Journal of Physiology 517: 159–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Lagadic-Gossmann D, Buckler KJ, Vaughan-Jones RD (1992) Role of bicarbonate in pH recovery from intracellular acidosis in the guinea-pig ventricular myocyte. Journal of Physiology 458: 361–384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Cummings JR (1960) Electrolyte changes in heart tissue and coronary arterial and venous plasma following coronary occlusion. Circulation Research 8: 865–870. [DOI] [PubMed] [Google Scholar]
- 73. Polimeni P, Al-Sadir J (1975) Expansion of extracellular space in the nonischemic zone of the infarcted heart and concomitant changes in tissue electrolyte contents in the rat. Circulation Research 37: 725–732. [DOI] [PubMed] [Google Scholar]
- 74. Boyer PK, Poindexter CA (1940) The influence of digitalis on the electrolyte and water balance of heart muscle. American Heart Journal 20: 586–591. [Google Scholar]
- 75. Erdmann E, Bolte HD, Lderitz B (1971) The (Na++K+)-atpase activity of guinea pig heart muscle in potassium deficiency. Archives of Biochemistry and Biophysics 145: 121–125. [DOI] [PubMed] [Google Scholar]
- 76. Kunze D (1977) Rate-dependent changes in extracellular potassium in the rabbit atrium. Circulation Research 41: 122–127. [DOI] [PubMed] [Google Scholar]
- 77. Moore EW (1970) Ionized calcium in normal serum, ultrafiltrates, and whole blood determined by ion-exchange electrodes. J Clin Invest 49: 318–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Post JA, Langer GA (1992) Sarcolemmal calcium binding sites in heart: I. molecular origin in “gas-dissected” sarcolemma. Journal of Membrane Biology 129: 49–57. [DOI] [PubMed] [Google Scholar]
- 79. Bers DM, Philipson KD, Langer GA (1981) Cardiac contractility and sarcolemmal calcium binding in several cardiac muscle preparations. American Journal of Physiology - Heart and Circulatory Physiology 240: H576–H583. [DOI] [PubMed] [Google Scholar]
- 80. Gayeski TE, Honig CR (1991) Intracellular PO2 in individual cardiac myocytes in dogs, cats, rabbits, ferrets, and rats. American Journal of Physiology - Heart and Circulatory Physiology 260: H522–H531. [DOI] [PubMed] [Google Scholar]
- 81. Yan G, Kleber A (1992) Changes in extracellular and intracellular ph in ischemic rabbit papillary muscle. Circulation Research 71: 460–470. [DOI] [PubMed] [Google Scholar]
- 82. Leem CH, Vaughan-Jones RD (1998) Sarcolemmal mechanisms for pH(i) recovery from alkalosis in the guinea-pig ventricular myocyte. Journal of Physiology 509: 487–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Austin WH, Lacombe E, Rand PW, Chatterjee M (1963) Solubility of carbon dioxide in serum from 15 to 38 c. Journal of Applied Physiology 18: 301–304. [DOI] [PubMed] [Google Scholar]
- 84. Conway RS, Weiss HR (1985) Dependence of spatial heterogeneity of myocardial blood flow on mean blood flow rate in the rabbit heart. Cardiovascular Research 19: 160–168. [DOI] [PubMed] [Google Scholar]
- 85. Despa S, Bers DM (2003) Na/K pump current and Na.i in rabbit ventricular myocytes: Local Na.i depletion and Na buffering. Biophysical Journal 84: 4157–4166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86. Swietach P, Zaniboni M, Stewart AK, Rossini A, Spitzer KW, et al. (2003) Modelling intracellular H+ ion diffusion. Progress in Biophysics and Molecular Biology 83: 69–100. [DOI] [PubMed] [Google Scholar]
- 87. Bassani JW, Bassani RA, Bers DM (1994) Relaxation in rabbit and rat cardiac cells: species-dependent differences in cellular mechanisms. The Journal of Physiology 476: 279–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. Balke CW, Egan TM, Wier WG (1994) Processes that remove calcium from the cytoplasm during excitation-contraction coupling in intact rat heart cells. The Journal of Physiology 474: 447–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89. Shannon TR, Ginsburg KS, Bers DM (2002) Quantitative assessment of the SR Ca2+ leak-load relationship. Circulation Research 91: 594–600. [DOI] [PubMed] [Google Scholar]
- 90. Zima AV, Bovo E, Bers DM, Blatter LA (2010) Ca2+ spark-dependent and -independent sarcoplasmic reticulum Ca2+ leak in normal and failing rabbit ventricular myocytes. The Journal of Physiology 588: 4743–4757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91. Li L, Niederer SA, Idigo W, Zhang YH, Swietach P, et al. (2010) A mathematical model of the murine ventricular myocyte: a data-driven biophysically based approach applied to mice overexpressing the canine NCX isoform. Am J Physiol Heart Circ Physiol 299: H1045–63. [DOI] [PubMed] [Google Scholar]
- 92. Mattiazzi A, Hove-Madsen L, Bers DM (1994) Protein kinase inhibitors reduce SR Ca transport in permeabilized cardiac myocytes. American Journal of Physiology - Heart and Circulatory Physiology 267: H812–H820. [DOI] [PubMed] [Google Scholar]
- 93. Roth BJ (1997) Electrical conductivity values used with the bidomain model of cardiac tissue. Biomedical Engineering, IEEE Transactions on 44: 326–328. [DOI] [PubMed] [Google Scholar]
- 94. Cordeiro JM, Spitzer KW, Giles WR, Ershler PE, Cannell MB, et al. (2001) Location of the initiation site of calcium transients and sparks in rabbit heart purkinje cells. The Journal of Physiology 531: 301–314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95. Kitazawa T (1984) Effect of extracellular calcium on contractile activation in guinea-pig ventricular muscle. The Journal of Physiology 355: 635–659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96. Backx PH, de Tombe PP, Van Deen JH, Mulder BJ, ter Keurs HE (1989) A model of propagating calcium-induced calcium release mediated by calcium diffusion. The Journal of General Physiology 93: 963–977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97. Cascio W, Yan G, Kleber A (1992) Early changes in extracellular potassium in ischemic rabbit myocardium. the role of extracellular carbon dioxide accumulation and diffusion. Circulation Research 70: 409–422. [DOI] [PubMed] [Google Scholar]
- 98. Swietach P, Rossini A, Spitzer KW, Vaughan-Jones RD (2007) H+ ion activation and inactivation of the ventricular gap junction: A basis for spatial regulation of intracellular pH. Circulation Research 100: 1045–1054. [DOI] [PubMed] [Google Scholar]
- 99. Rodriguez B, Tice BM, Eason JC, Aguel F, Ferrero J Jose M, et al. (2004) Effect of acute global ischemia on the upper limit of vulnerability: a simulation study. Am J Physiol Heart Circ Physiol 286: H2078–2088. [DOI] [PubMed] [Google Scholar]
- 100. Dennis SC, Gevers W, Opie LH (1991) Protons in ischemia: Where do they come from; where do they go to? Journal of Molecular and Cellular Cardiology 23: 1077–1086. [DOI] [PubMed] [Google Scholar]
- 101. Bonen A (2001) The expression of lactate transporters (MCT1 and MCT4) in heart and muscle. European Journal of Applied Physiology 86: 6–11. [DOI] [PubMed] [Google Scholar]
- 102. Vinnakota KC, Beard DA (2011) Kinetic analysis and design of experiments to identify the catalytic mechanism of the monocarboxylate transporter isoforms 4 and 1. Biophysical Journal 100: 369–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103. Wang YP, Fuchs F (1994) Length, force, and Ca2+-troponin-C affinity in cardiac and slow skeletal-muscle. American Journal of Physiology 266: C1077–C1082. [DOI] [PubMed] [Google Scholar]
- 104. Hak JB, van Beek JH, van Wijhe MH, Westerhof N (1993) Dynamics of myocardial lactate efflux after a step in heart rate in isolated rabbit hearts. American Journal of Physiology - Heart and Circulatory Physiology 265: H2081–H2085. [DOI] [PubMed] [Google Scholar]
- 105. Rumsey WL, Pawlowski M, Lejavardi N, Wilson DF (1994) Oxygen pressure distribution in the heart in vivo and evaluation of the ischemic “border zone”. Am J Physiol Heart Circ Physiol 266: H1676–1680. [DOI] [PubMed] [Google Scholar]
- 106. Khuri SF, Flaherty JT, O'Riordan JB, Pitt B, Brawley RK, et al. (1975) Changes in intramyocardial st segment voltage and gas tensions with regional myocardial ischemia in the dog. Circulation Research 37: 455–63. [DOI] [PubMed] [Google Scholar]
- 107. Hillis LD, Khuri SF, Braunwald E, Kloner RA, Tow D, et al. (1979) Assessment of the efficacy of interventions to limit ischemic injury by direct measurement of intramural carbon dioxide tension after coronary artery occlusion in the dog. The Journal of Clinical Investigation 63: 99–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108. Park CO, Xiao XH, Allen DG (1999) Changes in intracellular Na+ and pH in rat heart during ischemia: role of Na+/H+ exchanger. Am J Physiol Heart Circ Physiol 276: H1581–1590. [DOI] [PubMed] [Google Scholar]
- 109. Elliott AC, Smith GL, Eisner DA, Allen DG (1992) Metabolic changes during ischaemia and their role in contractile failure in isolated ferret hearts. The Journal of Physiology 454: 467–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110. Wilde AA, Escande D, Schumacher CA, Thuringer D, Mestre M, et al. (1990) Potassium accumulation in the globally ischemic mammalian heart. a role for the atp-sensitive potassium channel. Circulation Research 67: 835–43. [DOI] [PubMed] [Google Scholar]
- 111. Pike MM, Luo CS, Clark MD, Kirk KA, Kitakaze M, et al. (1993) NMR measurements of Na+ and cellular energy in ischemic rat heart: role of Na+-H+ exchange. Am J Physiol Heart Circ Physiol 265: H2017–2026. [DOI] [PubMed] [Google Scholar]
- 112. Ten Hove M, Nederhoff MGJ, Van Echteld CJA (2005) Relative contributions of Na+/H+ exchange and Na+/HCO3 − cotransport to ischemic Nai + overload in isolated rat hearts. Am J Physiol Heart Circ Physiol 288: H287–292. [DOI] [PubMed] [Google Scholar]
- 113. van Echteld CJA, Kirkels JH, Eijgelshoven MHJ, van der Meer P, Ruigrok TJC (1991) Intracellular sodium during ischemia and calcium-free perfusion: A 23Na NMR study. Journal of Molecular and Cellular Cardiology 23: 297–307. [DOI] [PubMed] [Google Scholar]
- 114. Imahashi K, Kusuoka H, Hashimoto K, Yoshioka J, Yamaguchi H, et al. (1999) Intracellular sodium accumulation during ischemia as the substrate for reperfusion injury. Circulation Research 84: 1401–1406. [DOI] [PubMed] [Google Scholar]
- 115. Van Emous JG, Vleggeert-Lankamp CLAM, Nederhoff MGJ, Ruigrok TJC, Van Echteld CJA (2001) Postischemic Na+-K+-ATPase reactivation is delayed in the absence of glycolytic ATP in isolated rat hearts. Am J Physiol Heart Circ Physiol 280: H2189–2195. [DOI] [PubMed] [Google Scholar]
- 116. Xiao XH, Allen DG (1999) Role of Na+/H+ exchanger during ischemia and preconditioning in the isolated rat heart. Circulation Research 85: 723–730. [DOI] [PubMed] [Google Scholar]
- 117. El Banani H, Bernard M, Baetz D, Cabanes E, Cozzone P, et al. (2000) Changes in intracellular sodium and ph during ischaemia–reperfusion are attenuated by trimetazidine. Cardiovascular Research 47: 688–696. [DOI] [PubMed] [Google Scholar]
- 118. Imahashi K, Nishimura T, Yoshioka J, Kusuoka H (2001) Role of intracellular Na+ kinetics in preconditioned rat heart. Circulation Research 88: 1176–1182. [DOI] [PubMed] [Google Scholar]
- 119. Baetz D, Bernard M, Pinet C, Tamareille S, Chattou S, et al. (2003) Different pathways for sodium entry in cardiac cells during ischemia and early reperfusion. Molecular and Cellular Biochemistry 242: 115–120. [PubMed] [Google Scholar]
- 120. Kleber A (1983) Resting membrane potential, extracellular potassium activity, and intracellular sodium activity during acute global ischemia in isolated perfused guinea pig hearts. Circulation Research 52: 442–450. [DOI] [PubMed] [Google Scholar]
- 121. Hartmann M, Decking UKM (1999) Blocking Na+-H+ exchange by cariporide reduces Na+-overload in ischemia and is cardioprotective. Journal of Molecular and Cellular Cardiology 31: 1985–1995. [DOI] [PubMed] [Google Scholar]
- 122. Yan GX, Chen J, Yamada KA, Klber AG, Corr PB (1996) Contribution of shrinkage of extracellular space to extracellular K+ accumulation in myocardial ischaemia of the rabbit. The Journal of Physiology 490: 215–228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123. Vanheel B, Hemptinne Ad (1992) Influence of KATP channel modulation on net potassium efflux from ischaemic mammalian cardiac tissue. Cardiovascular Research 26: 1030–1039. [DOI] [PubMed] [Google Scholar]
- 124. Hill J, Gettes L (1980) Effect of acute coronary artery occlusion on local myocardial extracellular K+ activity in swine. Circulation 61: 768–778. [DOI] [PubMed] [Google Scholar]
- 125. Kanda A, Watanabe I, Williams ML, Engle CL, Li S, et al. (1997) Unanticipated lessening of the rise in extracellular potassium during ischemia by pinacidil. Circulation 95: 1937–1944. [DOI] [PubMed] [Google Scholar]
- 126. Mitani A, Kinoshita K, Fukamachi K, Sakamoto M, Kurisu K, et al. (1991) Effects of glibenclamide and nicorandil on cardiac function during ischemia and reperfusion in isolated perfused rat hearts. Am J Physiol Heart Circ Physiol 261: H1864–1871. [DOI] [PubMed] [Google Scholar]
- 127. Wiegand V, Guggi M, Meesmann W, Kessler M, Greitschus F (1979) Extracellular potassium activity changes in the canine myocardium after acute coronary occlusion and the influence of beta-blockade. Cardiovascular Research 13: 297–302. [DOI] [PubMed] [Google Scholar]
- 128. Yan GX, Joshi A, Guo D, Hlaing T, Martin J, et al. (2004) Phase 2 reentry as a trigger to initiate ventricular fibrillation during early acute myocardial ischemia. Circulation 110: 1036–1041. [DOI] [PubMed] [Google Scholar]
- 129. Kimura J, Miyamae S, Noma A (1987) Identification of sodium calcium exchange current in single ventricular cells of guinea-pig. Journal of Physiology-London 384: 199–222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130. Kimura S, Bassett AL, Kohya T, Kozlovskis PL, Myerburg RJ (1986) Simultaneous recording of action potentials from endocardium and epicardium during ischemia in the isolated cat ventricle: relation of temporal electrophysiologic heterogeneities to arrhythmias. Circulation 74: 401–409. [DOI] [PubMed] [Google Scholar]
- 131. Gasser RN, Vaughan-Jones RD (1990) Mechanism of potassium efflux and action potential shortening during ischaemia in isolated mammalian cardiac muscle. The Journal of Physiology 431: 713–741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132. Cole WC, McPherson CD, Sontag D (1991) ATP-regulated K+ channels protect the myocardium against ischemia/reperfusion damage. Circulation Research 69: 571–81. [DOI] [PubMed] [Google Scholar]
- 133. Saito T, Sato T, Miki T, Seino S, Nakaya H (2005) Role of ATP-sensitive K+ channels in electrophysiological alterations during myocardial ischemia: a study using kir6.2-null mice. American Journal of Physiology - Heart and Circulatory Physiology 288: H352–H357. [DOI] [PubMed] [Google Scholar]
- 134. Rouet R, Picard S, Libersa C, Ghadanfar M, Alabaster C, et al. (2000) Electrophysiological effects of dofetilide in an in vitro model of “border zone” between normal and ischemic/reperfused myocardium. Circulation 101: 86–93. [DOI] [PubMed] [Google Scholar]
- 135. Yvon A, Hanouz J, Terrien X, Ducouret P, Rouet R, et al. (2002) Electrophysiological effects of morphine in an in vitro model of the ‘border zone’ between normal and ischaemic–reperfused guinea-pig myocardium. British Journal of Anaesthesia 89: 888–895. [DOI] [PubMed] [Google Scholar]
- 136. Ducroq J, Rouet R, Puddu PE, Sall L, Tabourel C, et al. (2005) Electrophysiological effects of azimilide in an in vitro model of simulated-ischemia and reperfusion in guinea-pig ventricular myocardium. European Journal of Pharmacology 518: 165–174. [DOI] [PubMed] [Google Scholar]
- 137. Wikswo Jr JP, Lin SF, Abbas RA (1995) Virtual electrodes in cardiac tissue: a common mechanism for anodal and cathodal stimulation. Biophysical Journal 69: 2195–2210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138. Muzikant AL, Henriquez CS (1998) Validation of three-dimensional conduction models using experimental mapping: are we getting closer? Progress in Biophysics & Molecular Biology 69: 205–223. [DOI] [PubMed] [Google Scholar]
- 139.Richardson G (2009) A multiscale approach to modelling electrochemical processes occurring across the cell membrane with application to transmission of action potentials. Mathematical Medicine and Biology. [DOI] [PubMed]
- 140. Mori Y, Fishman GI, Peskin CS (2008) Ephaptic conduction in a cardiac strand model with 3D electrodiffusion. Proceedings of the National Academy of Sciences 105: 6463–6468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141. Hand P, Peskin C (2010) Homogenization of an electrophysiological model for a strand of cardiac myocytes with gap-junctional and electric-field coupling. Bulletin of Mathematical Biology 72: 1408–1424. [DOI] [PubMed] [Google Scholar]
- 142. Nygren A, Halter JA (1999) A general approach to modeling conduction and concentration dynamics in excitable cells of concentric cylindrical geometry. Journal of Theoretical Biology 199: 329–358. [DOI] [PubMed] [Google Scholar]
- 143. Vigmond EJ, Aguel F, Trayanova NA (2002) Computational techniques for solving the bidomain equations in three dimensions. Biomedical Engineering, IEEE Transactions on 49: 1260–1269. [DOI] [PubMed] [Google Scholar]
- 144. Blanchard E, Solaro R (1984) Inhibition of the activation and troponin calcium binding of dog cardiac myofibrils by acidic ph. Circulation Research 55: 382–391. [DOI] [PubMed] [Google Scholar]
- 145. Orchard CH, Kentish JC (1990) Effects of changes of pH on the contractile function of cardiac-muscle. American Journal of Physiology 258: C967–C981. [DOI] [PubMed] [Google Scholar]
- 146. Mitani A, Shattock MJ (1992) Role of Na-activated K channel, Na-K-Cl cotransport, and Na-K pump in [K]e changes during ischemia in rat heart. Am J Physiol Heart Circ Physiol 263: H333–340. [DOI] [PubMed] [Google Scholar]
- 147. Coronel R, Wilms-Schopman FJ, Opthof T, van Capelle FJ, Janse MJ (1991) Injury current and gradients of diastolic stimulation threshold, TQ potential, and extracellular potassium concentration during acute regional ischemia in the isolated perfused pig heart. Circulation Research 68: 1241–9. [DOI] [PubMed] [Google Scholar]
- 148. Hearse DJ, Yellon DM (1981) The border zone in evolving myocardial infarction: Controversy or confusion? The American Journal of Cardiology 47: 1321–1334. [DOI] [PubMed] [Google Scholar]
- 149. Schaapherder AFM, Schumacher CA, Coronel R, Fiolet JWT (1990) Transmural inhomogeneity of extracellular K. and pH and myocardial energy metabolism in the isolated rat heart during acute global ischemia; dependence on gaseous environment. Basic Research in Cardiology 85: 33–44. [DOI] [PubMed] [Google Scholar]
- 150. Prinzen FW, Arts T, Hoeks APG, Reneman RS (1989) Discrepancies between myocardial blood flow and fiber shortening in the ischemic border zone as assessed with video mapping of epicardial deformation. Pflügers Archiv European Journal of Physiology 415: 220–229. [DOI] [PubMed] [Google Scholar]
- 151. Carmeliet E (2006) Action potential duration, rate of stimulation, and intracellular sodium. Journal of Cardiovascular Electrophysiology 17: S2–S7. [DOI] [PubMed] [Google Scholar]
- 152. Wilde AA, Aksnes G (1995) Myocardial potassium loss and cell depolarisation in ischaemia and hypoxia. Cardiovascular Research 29: 1–15. [PubMed] [Google Scholar]
- 153. Kleber AG, Janse MJ, van Capelle FJ, Durrer D (1978) Mechanism and time course of S-T and T-Q segment changes during acute regional myocardial ischemia in the pig heart determined by extracellular and intracellular recordings. Circulation Research 42: 603–613. [DOI] [PubMed] [Google Scholar]
- 154. Kantor PF, Coetzee WA, Carmeliet EE, Dennis SC, Opie LH (1990) Reduction of ischemic K+ loss and arrhythmias in rat hearts. effect of glibenclamide, a sulfonylurea. Circulation Research 66: 478–85. [DOI] [PubMed] [Google Scholar]
- 155. Robertson SP, Johnson JD, Potter JD (1981) The time-course of Ca2+ exchange with calmodulin, troponin, parvalbumin, and myosin in response to transient increases in Ca2+ . Biophysical Journal 34: 559–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156. Allen DG, Orchard CH (1983) The effects of changes of pH on intracellular calcium transients in mammalian cardiac-muscle. Journal of Physiology 335: 555–567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157. Vaughan-Jones RD, Spitzer KW, Swietach P (2009) Intracellular pH regulation in heart. Journal of Molecular and Cellular Cardiology 46: 318–331. [DOI] [PubMed] [Google Scholar]
- 158. Bollensdorff C, Knopp A, Biskup C, Zimmer T, Benndorf K (2004) Na+ current through katp channels: consequences for Na+ and K+ fluxes during early myocardial ischemia. Am J Physiol Heart Circ Physiol 286: H283–295. [DOI] [PubMed] [Google Scholar]
- 159. Eigel BN, Hadley RW (1999) Contribution of the Na+ channel and Na+/H+ exchanger to the anoxic rise of Na+. in ventricular myocytes. American Journal of Physiology 277: H1817–1822. [DOI] [PubMed] [Google Scholar]
- 160. Ellis D (1977) Effects of external cations and ouabain on intracellular sodium activity of sheep heart purkinje-fibers. Journal of Physiology-London 273: 211–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161. Deitmer JW, Ellis D (1980) Interactions between the regulation of the intracellular pH and sodium activity of sheep cardiac purkinje fibres. The Journal of Physiology 304: 471–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162. Bers DM, Ellis D (1982) Intracellular calcium and sodium activity in sheep heart purkinje-fibers - effect of changes of external sodium and intracellular pH. Pfluegers Archiv European Journal of Physiology 393: 171–178. [DOI] [PubMed] [Google Scholar]
- 163. Katzung B (1975) Effects of extracellular calcium and sodium on depolarization-induced automaticity in guinea pig papillary muscle. Circulation Research 37: 118–127. [DOI] [PubMed] [Google Scholar]
- 164. Baartscheer A, Schumacher CA, Fiolet JWT (1997) Small changes of cytosolic sodium in rat ventricular myocytes measured with SBFI in emission ratio mode. Journal of Molecular and Cellular Cardiology 29: 3375–3383. [DOI] [PubMed] [Google Scholar]
- 165. Vaughan-Jones RD, Wu ML (1990) Extracellular H+ inactivation of Na+-H+ exchange in the sheep cardiac purkinje fibre. Journal of Physiology 428: 441–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166. Ellis D, MacLeod KT (1985) Sodium-dependent control of intracellular pH in purkinje fibres of sheep heart. The Journal of Physiology 359: 81–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167. Kusuoka H, de Hurtado MCC, Marban E (1993) Role of sodium/calcium exchange in the mechanism of myocardial stunning: Protective effect of reperfusion with high sodium solution. Journal of the American College of Cardiology 21: 240–248. [DOI] [PubMed] [Google Scholar]
- 168. Sasyniuk BI, Jhamandas V (1984) Mechanism of reversal of toxic effects of amitriptyline on cardiac purkinje fibers by sodium bicarbonate. Journal of Pharmacology and Experimental Therapeutics 231: 387–394. [PubMed] [Google Scholar]
- 169. Cheung JY, Thompson IG, Bonventre JV (1982) Effects of extracellular calcium removal and anoxia on isolated rat myocytes. American Journal of Physiology - Cell Physiology 243: C184–C190. [DOI] [PubMed] [Google Scholar]
- 170. Kaila K, Vaughan-Jones RD (1987) Influence of sodium-hydrogen exchange on intracellular pH, sodium and tension in sheep cardiac purkinje fibres. The Journal of Physiology 390: 93–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171. Deitmer JW, Ellis D (1978) Changes in the intracellular sodium activity of sheep heart purkinje fibres produced by calcium and other divalent cations. The Journal of Physiology 277: 437–453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172. Allen DG, Eisner DA, Orchard CH (1984) Factors influencing free intracellular calcium concentration in quiescent ferret ventricular muscle. The Journal of Physiology 350: 615–630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173. Sheu S, Korth M, Lathrop D, Fozzard H (1980) Intra- and extracellular K+ and Na+ activities and resting membrane potential in sheep cardiac purkinje strands. Circulation Research 47: 692–700. [DOI] [PubMed] [Google Scholar]
- 174. Spitzer KW, Walker JL (1980) Intracellular chloride activity in quiescent cat papillary muscle. American Journal of Physiology - Heart and Circulatory Physiology 238: H487–H493. [DOI] [PubMed] [Google Scholar]
- 175. Deitmer JW, Ellis D (1980) The intracellular sodium activity of sheep heart purkinje fibres: effects of local anaesthetics and tetrodotoxin. The Journal of Physiology 300: 269–282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176. Miura DS, Hoffman BF, Rosen MR (1977) The effect of extracellular potassium on the intracellular potassium ion activity and transmembrane potentials of beating canine cardiac purkinje fibers. The Journal of General Physiology 69: 463–474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 177. Abete P, Vassalle M (1992) Role of intracellular Na+ activity in the negative inotropy of strophanthidin in cardiac purkinje fibers. European Journal of Pharmacology 211: 399–409. [DOI] [PubMed] [Google Scholar]
- 178. Vaughan-Jones RD (1979) Regulation of chloride in quiescent sheep-heart purkinje fibres studied using intracellular chloride and pH-sensitive micro-electrodes. J Physiol (Lond) 295: 111–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 179. Cyran SE, Phillips J, Ditty S, Baylen BG, Cheung J, et al. (1993) Developmental differences in cardiac myocyte calcium homeostasis after steady-state potassium depolarization: Mechanisms and implications for cardioplegia. The Journal of Pediatrics 122: S77–S83. [DOI] [PubMed] [Google Scholar]
- 180. Chapman RA (1986) Sodium/calcium exchange and intracellular calcium buffering in ferret myocardium: an ion-sensitive micro-electrode study. The Journal of Physiology 373: 163–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181. Vaughan-Jones RD (1986) An investigation of chloride-bicarbonate exchange in the sheep cardiac purkinje fibre. Journal of Physiology 379: 377–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 182. Bountra C, Powell T, Vaughan-Jones RD (1990) Comparison of intracellular pH transients in single ventricular myocytes and isolated ventricular muscle of guinea-pig. The Journal of Physiology 424: 343–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 183. Gambassi G, Hansford RG, Sollott SJ, Hogue BA, Lakatta EG, et al. (1993) Effects of acidosis on resting cytosolic and mitochondrial Ca2+ in mammalian myocardium. The Journal of General Physiology 102: 575–597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 184. Fozzard HA, Lee CO (1976) Influence of changes in external potassium and chloride ions on membrane potential and intracellular potassium ion activity in rabbit ventricular muscle. J Physiol 256: 663–689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185. Carmeliet E, Verdonck F (1977) Reduction of potassium permeability by chloride substitution in cardiac cells. The Journal of Physiology 265: 193–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 186. Wu M, Tsai M, Tseng Y (1994) DIDS-sensitive pHi regulation in single rat cardiac myocytes in nominally HCO3 − free conditions. Circulation Research 75: 123–132. [DOI] [PubMed] [Google Scholar]
- 187. Bolton TB, Vaughan-Jones RD (1977) Continuous direct measurement of intracellular chloride and ph in frog skeletal muscle. The Journal of Physiology 270: 801–833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 188. Bountra C, Vaughan-Jones RD (1989) Effect of intracellular and extracellular pH on contraction in isolated, mammalian cardiac muscle. The Journal of Physiology 418: 163–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 189. Miura D, Rosen M (1978) The effects of ouabain on the transmembrane potentials and intracellular potassium activity of canine cardiac purkinje fibers. Circulation Research 42: 333–338. [DOI] [PubMed] [Google Scholar]






