Complex trait divergence contributes to environmental niche differentiation in ecological speciation of Boechera stricta

Abstract

Ecological factors may contribute to reproductive isolation if differential local adaptation causes immigrant or hybrid fitness reduction. Since local adaptation results from the interaction between natural selection and adaptive traits, it is crucial to investigate both in order to understand ecological speciation. Previously, we used niche modeling to identify local water availability as an environmental correlate of incipient ecological speciation between two subspecies in Boechera stricta, a close relative of Arabidopsis. Here, we performed several large-scale greenhouse experiments to investigate the divergence of various physiological, phenological, and morphological traits. Although we found no significant difference in physiological traits, the Western subspecies has significantly faster growth rate, larger leaf area, less succulent leaves, delayed reproductive time, and longer flowering duration. These trait differences are concordant with previous results that habitats of the Western genotypes have more consistent water availability, while Eastern genotypes inhabit locations with more ephemeral water supplies. In addition, by comparing univariate and multivariate divergence of complex traits (Q_ST) to the genome-wide distribution of SNP F_ST, we conclude that aspects of phenology and morphology (but not physiology) are under divergent selection. In addition, we also identified several highly diverged traits without obvious water-related functions.

Introduction

Natural selection and neutral processes are two major forces contributing to genetic differentiation and reproductive isolation among lineages (Slatkin 1987). Ecological factors may contribute to genetic divergence via differential local adaptation, which reduces immigrant or hybrid fitness and causes reproductive isolation. This process, termed ‘ecological speciation’ (Sobel et al. 2010) or ‘isolation by adaptation’ (Nosil et al. 2008), is an area of active research. If the trait under selection or the source of selection is clear, this may provide starting points for investigation; examples include salt tolerance in Mimulus guttatus (Lowry et al. 2008) and host plant adaptation in insects (Funk et al. 2011; Via et al. 2000), among others. However, in many species the trait under selection or the source of selection is unclear.

One possible solution comes from niche modeling and landscape genetics (Manel et al. 2003; Storfer et al. 2010), which allows the identification of specific environmental factors correlated with genetic differentiation. Often, however, investigations do not advance beyond correlational inference, and the traits under selection remain ambiguous even after possible environmental causes of natural selection are identified statistically. The scarcity of empirical tests of niche modeling predictions may in part reflect the difficulty of conducting manipulative experiments in many species. Nevertheless, verification of correlational inferences requires empirical evidence.

Boechera stricta is a short-lived perennial mustard native to the Rocky Mountains in North America and is an emerging model for ecological genetics (Prasad et al. 2012; Rushworth et al. 2011). In a previous study (Lee & Mitchell-Olds 2011), we identified two subspecies of B. stricta (“East” versus “West”), which show clear differentiation for neutral molecular markers, as well as for ecologically important traits (below). Crosses between these subspecies generate fertile recombinant inbred lines, which sometimes show subtle hybrid breakdown (Anderson et al. 2011). Among B. stricta populations in the western United States, the primary axis of genetic differentiation is between these Eastern versus Western subspecies, and the Eastern subspecies can be subdivided along a Northern to Southern continuum. While the genetic differentiation between Northern and Southern groups primarily reflects isolation by distance, the divergence between Eastern and Western subspecies suggests environmental adaptation, independently from the effects of geographic distance (Lee & Mitchell-Olds 2011). Further analysis showed that local water availability is the most important factor explaining the habitat segregation between the two groups, and Western genotypes mostly inhabit environments with more constant and abundant water supply. Given that fertile hybrid genotypes exist in the field and can be generated in the greenhouse, intrinsic hybrid inviability or infertility may not be the main form of reproductive isolation between these two subspecies. Therefore, the East-West divergence pattern may represent a case of incipient ecological speciation (isolation by adaptation), where the amount of gene flow in the secondary contact zone is reduced by differential local adaptation. We hypothesized that local water availability may be an important selective agent decreasing the fitness of immigrants or hybrids, causing reproductive isolation and genetic differentiation (Lee & Mitchell-Olds 2011).

In this study, we test the prediction that Eastern and Western genotypes are diverged in some traits associated with local water availability. Specifically, the Eastern subspecies should exhibit phenotypes adaptive in their drier native environments, while the Western subspecies should have phenotypes conferring higher fitness in wet riparian environments. By estimating the trait divergence from 24 accessions in the greenhouse and comparing their univariate and multivariate Q_ST to the empirical distribution of SNP F_ST, we show that the two genetic groups mainly utilize morphology and phenology, but not physiology, for their adaptation to differential water availability.

Materials and Methods

Plant material

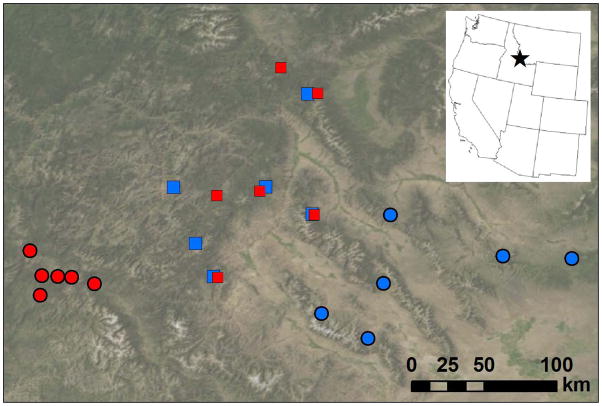
Throughout this study we will use the terms East and Eastern interchangeably, and likewise for West and Western. We focus our study on the vicinity of the East-West contact zone in Idaho, USA (Lee & Mitchell-Olds 2011) because this is the region where differential local adaptation is most likely to oppose gene flow. We chose 24 core populations representing the four combinations of ‘East vs. West subspecies’ and ‘allopatric vs. sympatric geographical zones’ (Figure 1, Table S1). We randomly sampled one genotype from each population because Boechera stricta has low genetic variation within local populations (Song et al. 2006). The 24 genotypes incorporate most of the genetic and geographical variation around the contact zone (Figure S1).

Figure 1.

Collection sites of 24 genotypes used in this study. The region is denoted as a black star on the state boundary map. Blue circles – allopatric East. Blue squares – sympatric East. Red circles – allopatric West. Red squares – sympatric West.

Each genotype was grown in the greenhouse for at least one generation to reduce maternal effects. Because Boechera stricta has a high self-fertilization rate in natural environments (Song et al. 2006), selfed seeds obtained from each genotype can be used as replicates in the three following independent experiments. In addition, this selfed family design has been shown to be better than a half-sib crossing design when estimating trait Q_ST in highly selfing species (Goudet & Buchi 2006). Seeds in all experiments were stratified in 4 degrees C for four weeks and planted in Ray Leach SC10 ‘Cone-tainers’ (21 cm in depth and 3.8 cm in diameter, Stuewe & Sons Inc., Tangent, OR, USA). Following our standard procedures for growing B. stricta in the greenhouse, the lower 80% of each Cone-tainer was filled with Fafard 4P Mix soil (Conrad Fafard, Agawam, MA, USA), and the top 20% was filled with Sunshine MVP soil (Sun Gro Horticulture, Vancouver, BC, Canada). All experiments were conducted in the same room of the Duke University Greenhouse, with 16-hour day length (6 am to 10 pm), daytime temperature of 65 to 70 degrees F, and nighttime temperature of 55 to 60 degrees F. Because most traits were non-normally distributed, measured traits (Table 2) were log transformed and standardized to improve normality and provide a more accurate estimate of variance components.

Table 2.

Trait divergence between subspecies. For all traits in 24 genotypes, shown are trait, category, P-value for subspecies in ANOVA, the subspecies with higher trait value, Q_ST, P-value of Q_ST compared to empirical F_ST distribution (Figure 4), and the correlation with discriminant function analysis (DFA) score from each trait category.

Trait	Category	P-value a	Higher b	QST	QST P c	DFA-cor d
Instantaneous WUE dry	Physiology	0.256	East	-	-	-
Instantaneous WUE wet	Physiology	0.429	West	0.00	1.000	-
Long-term Δ13C dry	Physiology	0.050	West	0.22	0.358	-
Long-term Δ13C wet	Physiology	0.202	West	0.05	0.616	-
Bolting time	Phenology	< 0.001	West	0.66	0.129	0.85
Flowering time	Phenology	0.008	West	0.42	0.217	0.60
Flowering duration	Phenology	< 0.001	West	0.63	0.142	0.68
Flowering rosette width	Phenology	0.591	East	0.00	1.000	−0.04
Flowering height	Phenology	< 0.001	East	0.78	0.076	−0.85
Flowering leaf number	Phenology	0.032	West	0.29	0.290	0.35
Flowering rosette number	Phenology	0.040	East	0.27	0.309	−0.38
Flowering stalk number	Phenology	0.006	East	0.48	0.195	−0.43
Main stalk diameter	Morph-stalk	< 0.001	West	0.71	0.110	0.73
Reproductive branch number	Morph-stalk	0.020	West	0.21	0.369	0.23
Main stalk height	Morph-stalk	< 0.001	East	0.84	0.061	−0.82
Stalk height containing branch	Morph-stalk	< 0.001	East	0.68	0.120	−0.61
Internode between branch	Morph-stalk	< 0.001	East	0.87	0.061	−0.91
Rosette width	Morph-rosette	0.189	West	0.08	0.570	0.23
Rosette height	Morph-rosette	0.901	East	0.00	1.000	−0.02
Rosette volume	Morph-rosette	0.369	West	0.00	1.000	0.17
Rosette leaf number	Morph-rosette	0.117	East	0.21	0.369	−0.23
Rosette fresh weight	Morph-rosette	0.001	West	0.64	0.138	0.47
Rosette dry weight	Morph-rosette	0.001	West	0.67	0.123	0.46
Rosette water weight	Morph-rosette	0.002	West	0.63	0.142	0.47
Rosette water proportion	Morph-rosette	0.475	East	0.00	1.000	−0.13
Rosette leaf area	Morph-rosette	< 0.001	West	0.73	0.107	0.56
Rosette leaf packing	Morph-rosette	0.002	West	0.50	0.185	0.54
Rosette fresh weight/area	Morph-rosette	0.002	East	0.53	0.174	−0.47
Rosette dry weight/area	Morph-rosette	0.282	East	0.02	0.718	−0.17
Rosette water weight/area	Morph-rosette	0.001	East	0.53	0.175	−0.49
Leaf shape Y1	Morph-leaf	0.492	West	0.00	1.000	0.07
Leaf shape Y2	Morph-leaf	0.025	West	0.59	0.158	0.26
Leaf shape Y3	Morph-leaf	< 0.001	West	0.92	0.029	0.54
Leaf shape Y4	Morph-leaf	< 0.001	West	0.94	0.029	0.80
Leaf shape Y5	Morph-leaf	< 0.001	West	0.93	0.029	0.87
Leaf shape Y6	Morph-leaf	< 0.001	West	0.93	0.029	0.90
Leaf shape Y7	Morph-leaf	< 0.001	West	0.94	0.029	0.94
Leaf shape Y8	Morph-leaf	< 0.001	West	0.94	0.029	0.95
Leaf shape Y9	Morph-leaf	< 0.001	West	0.90	0.036	0.92

^aBoldface denotes significant P-values after sequential Bonferroni correction within each trait category.

^bThis column denotes which subspecies has the higher trait value.

^cEmpirical P-values, based on the proportion of SNPs with F_ST higher than or equal to Q_ST for this trait. Boldface denotes values less than 0.05.

^dPearson’s correlation coefficient between trait value and the DFA score of each trait category. DFA is not available for physiology traits.

Experiment 1. Short-term drought manipulation and phenology

A total of 576 individuals were arranged into 12 randomized complete blocks. The 48 individuals within each block were composed of the 24 core genotypes, with two individuals from each genotype subjected to different water regime treatments (well-watered or drought). Our planting approach imposed water-regime treatments within each block, thereby avoiding a split-plot design. A one-week short-term drought treatment was imposed on three-month-old rosettes. During the treatment period, roots of well-watered plants were flooded with four inches of water for 30 minutes every day, and drought-treated plants remained un-watered for the week. Instantaneous water-use efficiency (WUE), calculated by dividing carbon fixation rate by water transpiration rate, was recorded on whole plants using a modified system and protocol (Tonsor & Scheiner 2007) based on a Li-Cor LI-6400 apparatus (Li-Cor, Lincoln, Nebraska, USA). At the end of the one-week treatment, each plant was put in a separate cuvette, and from each cuvette, five measurements were taken with a 10-second interval once the concentration of CO₂ had stabilized. The mean of five measurements from each plant was used in further analysis. Measurements were made between 9 am to 5 pm with about 400 μmol mol⁻¹ CO₂ and 26% relative humidity in the surrounding environment. We are able to process all plants within each block in the same day, and the seven-day drought treatment for each block was initiated in different dates. Therefore, plants in the drought treatment had experienced dry conditions for exactly seven days at the time of WUE measurement. In addition, the light intensity (photosynthetically active radiation, PAR) was recorded real-time in each cuvette as a covariate for photosynthetic rate.

Statistical analyses were performed with mixed model ANOVA fitted by REML in JMP 8 (SAS, Cary, NC). Subspecies (East/West), treatment (water/drought), geography (allopatric/sympatric), and their two-way (subspecies-by-geography, subspecies-by-treatment, geography-by-treatment) and three-way (subspecies-by-geography-by-treatment) interactions were used as fixed effects. Random effects include blocks and genotypes (nested within subspecies-by-geography). The interaction effect between treatment and genotype explained virtually no variance and was therefore not included in the model. In addition, the log-transformed light intensity in each Li-Cor chamber and the time of day were used as fixed effect covariates. To investigate the trait divergence between subspecies under a specific water regime, we also performed statistical analyses separately for the drought and watering treatment, with all factors involving treatment removed. If instantaneous WUE has diverged in response to different local water availability between habitats of the two subspecies, we predict that Eastern genotypes should have higher overall or treatment-specific WUE.

After Li-Cor measurement, all plants were returned to normal watering for two additional weeks before vernalization. Plants were vernalized in 4 degree C for six weeks under short day condition (12 hour daylight). All plants remained in normal watering conditions after vernalization. We monitored the plants every day and recorded bolting time and the starting and ending dates of flowering. The end of the flowering period is defined as the day after which no flower appeared for ten days. On the day of first flowering, width, height, leaf number, rosette number (total number of main and side rosettes), and stalk number were also recorded. After flowering finished, we also measured the diameter of the main flowering stalk, height of the stalk, and average reproductive internode length (stalk length containing reproductive branches/[number of reproductive branches − 1]).

Statistical models for phenology and morphological traits were similar to the model for physiology traits, except that light and time-of-day covariates were not used. Because prior analyses found no effect of the short-term water-regime treatment on phenology and morphology traits, the effects involving water regime treatment were also excluded from the statistical model. Adapted to their native montane environment with ephemeral water supply, we predicted that Eastern genotypes should show typical traits of drought escape (Mckay et al. 2003), including faster bolting and flowering time, shorter flowering duration, and smaller plant size when flowering. On the other hand, the Western subspecies should have overall delayed phenology and larger size at reproduction to maximize the reproductive output in their native environment with abundant and persistent water supply. Since the relationship between stalk morphology and local water availability is not yet clear, we make no prediction for this trait.

Experiment 2. Long-term drought manipulation

In this experiment, another 1152 individuals were planted in 24 randomized blocks. Individuals within each block were arranged in the same way as Experiment 1, allowing a within-block watering treatment. The well-watered treatment was the same as experiment 1, but the plants under drought were watered once per week. The treatment was imposed on one-month-old rosettes, and one leaf from each individual was collected after eight weeks of drought treatment. For each genotype in a treatment, leaves from four blocks were pooled together, resulting in 288 samples for carbon stable isotope analysis, with 6 replicates of 24 genotypes and 2 treatments. Leaves were dried in 37 degrees C for one week and homogenized into powder in liquid nitrogen. Δ¹³C, the parameter associated with long-term water use efficiency (Farquhar et al. 1989), was measured in the Duke Environmental Stable Isotope Laboratory.

The statistical model was similar to the model for instantaneous water use efficiency in experiment 1, except that block, light intensity, and time-of-day effects were not included. The leaf samples were submitted for carbon isotope analyses in three batches of 96-well plates, and therefore batch was used as a random effect in the model (following the recommendation of Bolker et al. 2009). As in experiment 1, we predict that Eastern genotypes should have higher overall or treatment-specific WUE if this trait has responded to different local environments.

Experiment 3. Vegetative-phase morphology without drought treatment

In this experiment, five plants from each of the 24 genotypes were grown in a completely randomized design under well-watered conditions for two months. By modeling a rosette as a cone, we calculated rosette volume (cm³) as:

$$\pi r^{2}h/3,$$

where r is the radius and h is the height of the rosette. Alternatively, rosette volume could be modeled as a cylinder (π r² h), which would not affect our estimation of P-value or Q_ST since the volume of a cone and a cylinder only differ by a constant. All leaves were collected from each plant and scanned on a white background. Total leaf area (cm²) was estimated by calculating the number of non-white pixels in the picture (with a resolution of 200 dpi, or 40,000 pixels per square inch). Rosette leaf packing was calculated as total leaf area divided by rosette volume. In addition, leaf fresh weight was measured at the time of harvest, and dry weight was measured after drying leaves at 65 degree C for one week. Rosette water content and water proportion were also calculated, along with unit-leaf-area fresh weight, dry weight, and water weight. Since all plants were harvested at the same age, the measured whole-rosette dry weight is proportional to the growth rate of each plant. Throughout this study we will use the terms whole-rosette dry weight and plant growth rate interchangeably.

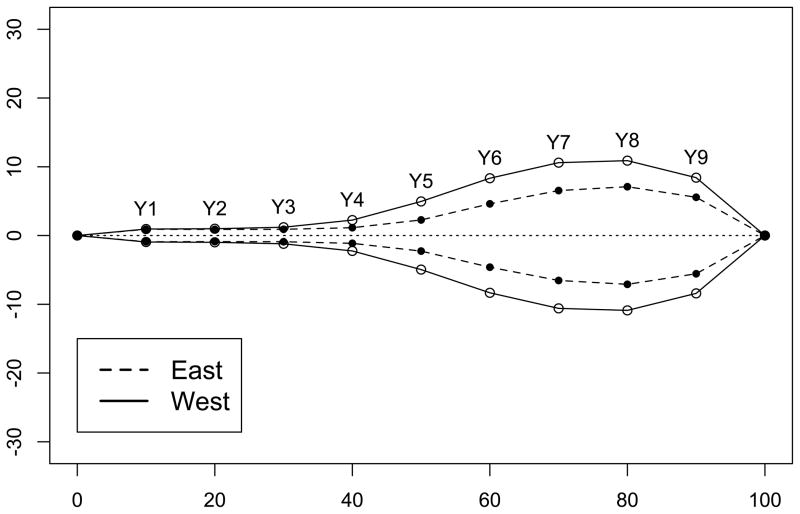
From the scanned image we chose one fully developed leaf from each individual for leaf shape analysis. A custom Perl script was used to generate lines separating the longer axis of a leaf into ten sections of equal length. Twenty landmarks were picked in ImageJ (Abramoff et al. 2004) from the intersection between these lines and the leaf perimeter. Another custom Perl script was used to rotate and scale the landmark points to a standardized length for each leaf. Half of the width across the nine line-boundary intersections of a standardized leaf was used for the final analysis. Therefore, the nine leaf shape parameters (Y1 to Y9, Figure 5) represent the width/length ratio across nine internal segments of a leaf. The statistical model was identical to the model for morphological traits (without treatment) in experiment 1, except that there is no block random effect in this experiment.

Figure 5.

Average leaf shape of East and West genotypes (n = 60 from each subspecies). Eastern leaf - closed circles connected by dashed line. Western leaf -open circles connected by solid line. For every leaf, landscape points were rotated and scaled to obtain equal length among all leaves (a standardized length of 100 units across the horizontal axis), and points Y1 to Y9 separate the central leaf axis (dotted line) into ten sections of equal length. The Y coordinates of Y1 to Y9 were used in the statistical analyses.

For rosette morphology, we predict that Western genotypes would have higher rosette fresh weight, dry weight, and total leaf area, reflecting a non-conservative water use strategy to obtain maximum biomass before reproduction. On the other hand, the Eastern subspecies may have higher leaf water content and lower overall growth rate, reflecting a life history strategy for water conservation. In addition, the Eastern subspecies may have higher leaf packing (total leaf area per unit rosette volume) to reduce leaf water loss (McKay et al. 2001). Finally, the thermoregulation of leaves is critical to plants. During exposure to sunlight leaves may decrease their temperature via convection and transpiration. Small and narrow leaves have small boundary layers and are more efficient in heat convection, while large and wide leaves are more efficient in thermoregulation via transpiration (Nicotra et al. 2011). Therefore, we expect that genotypes from water-limited environments (East) would have narrow leaves, while the riparian Western genotypes would have wider leaves, reflecting different strategies of foliar thermoregulation in response to different local water availability. In addition, wider leaves of Western genotypes may also contribute to rapid biomass accumulation before reproduction.

Principal component analysis

To summarize and visualize the trait differentiation among genotypes, we performed principal component analysis (PCA) with function prcomp in R (http://www.r-project.org/), using least square means of the 24 genotypes from the univariate mixed model ANOVA described above. We further separated all measured traits into five categories (physiology, phenology, morphology-stalk, morphology-rosette, and morphology-leaf) and performed PCA within each category. Notice that PCA was calculated from genotypic means rather than individual-level data because micro-environmental effects may influence the pattern of major PC axes in individual-level PCA.

Calculation of univariate and multivariate Q_ST

Q_ST calculates the proportion of heritable trait variation that exists among populations. If a trait is under divergent selection, Q_ST may be higher than F_ST, the proportion of neutral molecular variation among populations (Whitlock 2008). To calculate the variance components of subspecies and genotypes, we used subspecies and genotype nested within subspecies as random effects. For traits measured in experiment 1, block was also used as a random effect. Geographical effects were not included in this model because they lack significant effects for nearly all traits. Q_ST was calculated as:

$$V_{\mathit{Subsp}}/(V_{\mathit{Subsp}}+V_{\mathit{Genotype}}),$$

where V_Subsp and V_Genotype are the variance components of subspecies and genotype-within-subspecies, respectively. Notice this differs from the typical Q_ST formula in that we did not multiply the within-subspecies variance component (V_Genotype) by two in the denominator. Like Arabidopsis thaliana, Boechera stricta is a highly selfing species and therefore can be modeled as haploid for these calculations (Whitlock 2008). In addition, since B. stricta has low genetic variation within local populations, our experimental design does not involve multiple genotypes from the same local population. The trait ‘instantaneous water use efficiency under drought’ had zero heritability, and therefore we do not calculate its Q_ST.

The multivariate trait Q_ST was calculated separately for four trait categories (phenology, morphology-stalk, morphology-rosette, and morphology-leaf). Within each trait category, the individual-level phenotypes of multiple traits were first scaled to zero mean and unit variance and then analyzed in a discriminant function analysis (DFA), with subspecies as the grouping variable. DFA identifies a linear combination of traits that maximizes the variation between and minimizes the variation within subspecies, providing a rotation of axes to the direction of greatest divergence between groups. The DFA score of each individual was then considered as a new univariate trait, and the Q_ST of this ‘composite trait’ was calculated with the same random effects model above (refer to Figure S2 for a detailed explanation of composite trait). We did not calculate the multivariate Q_ST of physiological traits under dry and wet treatments because the calculation requires traits from the same individual plants within the same experiment. To investigate the relationship between univariate traits and the composite traits, we estimated Pearson’s correlation coefficient between each univariate trait and the DFA score from the same trait category.

Empirical SNP F_ST distribution

When comparing Q_ST with F_ST, recent opinion has called for the use of SNPs rather than microsatellite markers, because the high mutation rate of microsatellites may increase the within-population molecular variation and thus falsely decrease F_ST (Edelaar & Björklund 2011; Edelaar et al. 2011). In addition, Whitlock (2008) emphasized that Q_ST should be compared to genome-wide F_ST distribution, not to mean F_ST. To generate the empirical distribution of SNP F_ST, we used the method developed by Andolfatto et al. (2011). Genomic DNA of 18 genotypes (a subset of the core 24 in this study) was digested using the Sau3AI restriction enzyme, and a barcoded library was prepared with modified Illumina adaptors (Andolfatto et al. 2011). The library was sequenced in one lane of HiSeq 2000 (Illumina, San Diego, CA, USA) with paired-end 100 bp reads. This was the first trial of this method for Boechera stricta, and we only obtained ~33 million read-pairs, which proved sufficient for the current study. We applied a stringent quality filtering, retaining a sequence pair only if all bases in both reads have sequencing error rate <= 10⁻⁵. Among the 33 million pairs, 26.6 million passed the quality filtering and had unambiguous barcode sequences.

The LTM genotype, one of the 24 core genotypes used in this study, has been sequenced with the Roche 454 platform by the Department of Energy Joint Genome Institute and with Sanger BAC end-sequences by HudsonAlpha Institute for Biotechnology. From these data, we assembled a draft genome with Newbler software (454 Life Sciences, Branford, CT, USA) using default parameters. The draft genome after length filtering is about 170 Mb, ~80% of the estimated B. stricta 216 Mb genome. About 21 million Illumina HiSeq read-pairs from the 18 B. stricta accessions were successfully mapped to the LTM draft genome with BWA (Li & Durbin 2009) using default parameters, and genotypes were called with SAMtools (Li et al. 2009) with default parameters. In every SNP, the genotype of a plant accession was considered missing if the sequencing depth is less than 6x, and a SNP was retained only when the proportion of missing plant accessions is < 25%. Together with the LTM reference genome, this data set contains 23,379 SNP from 11 West and 8 East genotypes. The F_ST of each SNP was estimated with the package HIERFSTAT (Goudet 2005) in R. With about 23.5 thousand SNPs, the expected distance between neighboring SNPs is roughly 9 kb. Since SNPs in close linkage may not evolve independently and the linkage disequilibrium (LD) in B. stricta decays in about 10 kb (Song et al. 2009), we compared the F_ST distribution from all 23.5 thousand SNPs to the average distribution from 1,000 re-sampled data sets where SNPs have lower LD due to their wider separation in the genome. Each data set contains 5,000 randomly re-sampled SNPs, with the expected mean distance between SNPs as 43 kb. We then obtained the average distribution from those 1,000 distributions and obtained the 101 percentiles (0% to 100% with 1% intervals) from this average distribution. There is a strong correlation (Pearson’s correlation coefficient r ≈1.0) between the percentiles from the average 5,000-SNP distribution and the percentiles from the 23.5-thousand-SNP distribution. Therefore in this study we used the original F_ST distribution with all SNPs for F_ST-Q_ST comparison.

Since B. stricta is a primarily self-fertilizing species and has high microsatellite homozygosity (Lee & Mitchell-Olds 2011; Song et al. 2006), some SNPs with apparently high heterozygosity may represent duplicated genomic regions. Indeed, the distribution of SNP heterozygosity is highly skewed, with the median at zero (all homozygous) and upper 5% tail at about 0.5 (half of the accessions are heterozygous). Excluding SNPs with heterozygosity > 0.5 only slightly increases the mean F_ST from 0.237 to 0.245, but the upper 5% or 10% F_ST tail used for F_ST-Q_ST comparison remains unchanged.

Results

No significant divergence in eco-physiological traits between subspecies

In this study, we performed two differential watering treatment experiments, one with one-week (experiment 1) and the other with eight-week (experiment 2) drought treatments. Although we found significant effects for genotype under long-term drought, for light intensity under short-term drought, and for drought treatment in both experiments, we did not observe any significant effects involving subspecies, geography, or their interaction effects with treatment (Table 1).

Table 1.

Mixed model ANOVA results of water use efficiency in short-term and long-term drought experiment.

Factor1	Effect type2	Instantaneous WUE		Long-term Δ13C
		F-value	P-value	F-value	P-value
Subsp	Fixed	0.32	0.580	3.13	0.092
Geo	Fixed	1.23	0.281	1.75	0.201
Trt	Fixed	13.21	< 0.001*	101.24	< 0.001*
Subsp*Geo	Fixed	2.10	0.163	2.73	0.114
Subsp*Trt	Fixed	2.03	0.155	1.11	0.292
Geo*Trt	Fixed	0.80	0.371	0.41	0.521
Subsp*Geo*Trt	Fixed	1.79	0.181	0.05	0.821
Time of day	Fixed	0.49	0.482	-	-
Light intensity	Fixed	11.56	< 0.001*	-	-
Geno(Subsp, Geo)	Random	-	0.556	-	< 0.001*
Block or batch	Random	-	< 0.001*	-	0.009*

¹Subsp – subspecies; Geo – geography; Trt – treatment; Geno(Subsp, Geo) – genotype nested within subspecies and geography.

²The degree of freedom is 1 for all effects

Trait divergence betweenEAST and WEST subspecies

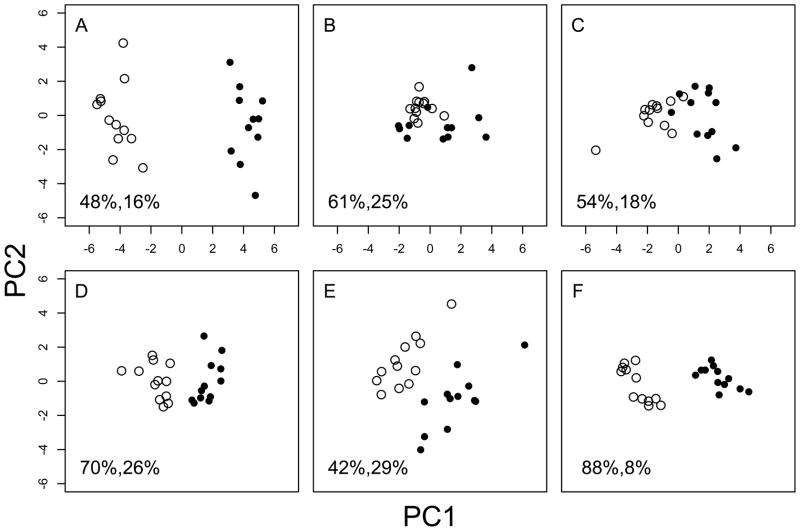
Figure 2 shows the PCA result of all traits together and for five subsets of traits (physiology, phenology, morphology-stalk, morphology-rosette, and morphology-leaf). In all trait categories except physiology (Figure 2B), PC1 separates the two subspecies, signifying the substantial trait divergence between subspecies.

Figure 2.

Principal components of genotype-level trait values. East genotypes - closed circles. West genotypes - open circles. A - all traits. B – four physiology traits. C – eight phenology traits. D – five stalk morphology traits. E – thirteen rosette morphology traits. F – nine leaf shape traits. Refer to Table 2 for the traits within each category.

To specifically examine which traits show significant East-West divergence, we performed mixed model ANOVA for each trait. Consistent with the trend from PCA, many non-physiological traits show significant divergence between subspecies after sequential Bonferroni correction within each trait category (Table 2 and Figure 3A). In addition, the direction of trait divergence is mostly consistent with our previous niche modeling prediction. Specifically, the Western subspecies has faster growth rate (higher biomass and larger total leaf area at the time of leaf harvest), overall delayed phenology (slower bolting time, delayed flowering time, and longer flowering duration), and larger photosynthetic organ size (larger total leaf area and broader leaves), allowing them to attain higher overall biomass and reproductive output in their native riparian habitat. On the other hand, the Eastern subspecies has a slower growth rate, overall accelerated phenology, and narrower and more succulent leaves (higher water weight but not dry weight per unit leaf area), consistent with the escape from late-summer drought in their native montane habitat. Results from the 19 genotypes with SNP data (Table S2 and Figure S3) are highly consistent with the results from all 24 genotypes. Table S1 shows the least square means of all traits.

Figure 3.

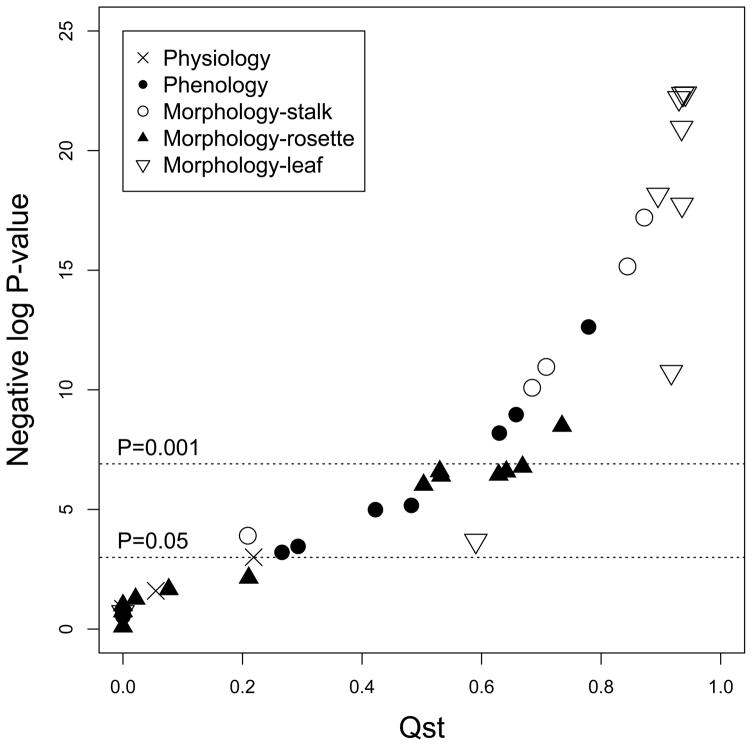
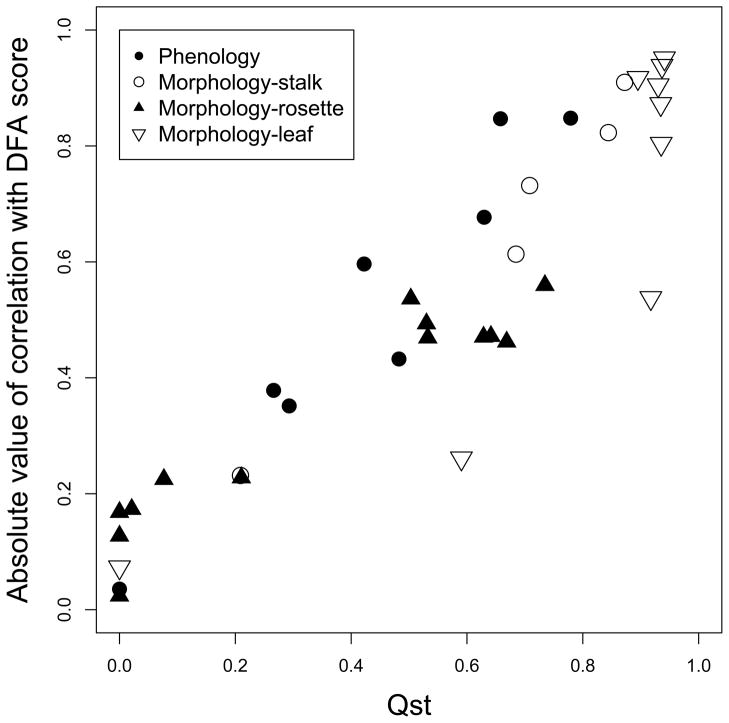
Relationship between trait Q_ST and (A) negative log P-value of subspecies effect in ANOVA (B) absolute value of correlation with discriminant function analysis (DFA) score from each trait category. Traits with high Q_ST generally have low P-values (high negative log P) and high correlation with DFA score. Consistent with Figure 2, many morphological and phenological traits are highly diverged. Shown are data from all 24 genotypes.

Comparing F_ST to univariate and multivariate Q_ST

In general, Q_ST of most traits corresponds to the P-values for subspecies divergence in ANOVA (Figure 3A), and traits with small P-values also have large Q_ST values. Because many traits were chosen to test divergent selection between the two subspecies, we only compared trait Q_ST to the upper tail of genome-wide distribution of SNP F_ST.

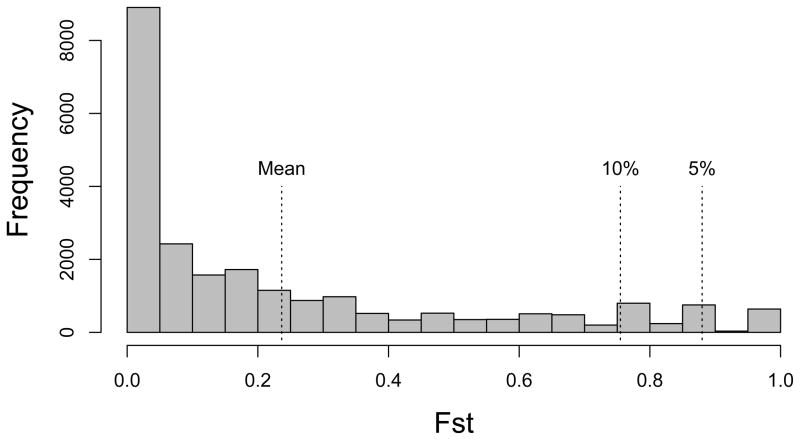
Figure 4 shows the F_ST distribution from 23,379 SNPs across the B. stricta genome, with the 5% cutoff at 0.88. Leaf shape parameters Y3 to Y9 have higher Q_ST than this F_ST cutoff, suggesting divergent selection on leaf shape between the two subspecies (Table 2 and Figure 3A). Figure 5 shows the average leaf shape of the two subspecies from all samples standardized for leaf length. Given the high amount of variation explained by PC1 of these leaf shape parameters (88%, Figure 2F), these parameters mostly represent the width/length ratio of a leaf. Clearly, the width/length ratio of the blade portion of a leaf is highly diverged between the two subspecies. In addition, some other traits have higher Q_ST than the 10% F_ST tail (0.75), including flowering height, main stalk height, and internode length between reproductive branches (Table 2). The adaptive significance of the three height-related traits, however, is not yet clear. Q_ST values obtained from the 19 genotypes with SNP data have only minor numerical difference from the 24 genotypes (Table S2). Specifically, in the 19-genotype data set two additional traits (rosette dry weight and rosette leaf area) have higher Q_ST than the 10% F_ST tail. Together with the higher leaf width/length ratio, this higher growth rate and larger photosynthetic organ size of the West subspecies may contribute to enhanced biomass accumulation before reproduction, which may be adaptive in its native environment with abundant water supply. On the other hand, the slower growth rate and narrower leaves of East subspecies may facilitate more water conservation.

Figure 4.

Empirical SNP F_ST distribution between 11 WEST and 8 EAST genotypes.

Because traits within each category may be correlated, and natural selection may simultaneously act on multiple traits, we employed a multivariate version of Q_ST, looking at the divergence of all traits within each category. Within each trait category, the use of discriminant function analysis (DFA) between two subspecies generates a ‘composite trait’ with highest degree of between-subspecies divergence. This approach asks: what combination of traits shows greatest divergence between subspecies, and what is the Q_ST for this direction of maximum genetic divergence? The biological meaning of each composite trait can be inferred by examining the direction of individual trait divergence (‘Higher’ column in Table 2) and the sign of their correlation to DFA score (‘DFA-cor’ column in Table 2). In each trait category, small DFA values represent typical Eastern traits (Phenology: accelerated reproductive time, smaller reproductive size, and more branches when flowering. Stalk morphology: thinner and taller flowering stalk with longer internodes. Rosette morphology: less rosette weight and total leaf area, but higher unit-leaf-area fresh weight and water weight. Leaf morphology: smaller width/length ratio.)

As shown in Table 3, all four categories have their composite trait Q_ST near or above the 5% F_ST cutoff of 0.88. The marginally significant (P = 0.061, Table 3) phenological multivariate Q_ST, for example, may reflect simultaneous natural selection on multiple phenological traits to accelerate reproduction of Eastern genotypes. Similar pattern exists when only 19 genotypes were analyzed (Table S3). In addition, univariate traits with high Q_ST generally show higher correlations with the composite trait (Table 2 and Figure 3B). These data suggest that aspects of phenology as a whole may be under divergent selection, although to a lesser extent than morphological traits.

Table 3.

Divergence of the ‘composite trait’ for each trait category. For DFA scores from each trait category, this table shows the P-value of the subspecies effect in univariate ANOVA, the Q_ST, and the empirical P-value of Q_ST compared to genome-wide distribution of SNP F_ST (Figure 4). Data are from all 24 genotypes.

Trait category	ANOVA P	QST	P vs. FST
Phenology	< 0.001	0.87	0.061
Morphology – stalk	< 0.001	0.89	0.042
Morphology – rosette	< 0.001	0.97	0.027
Morphology – leaf	< 0.001	0.96	0.027

Discussion

Isolation by adaptation and ecological speciation result from differential local adaptation, where natural selection in distinct environments favors different organismal phenotypes. Reproductive isolation among populations may result from natural selection against immigrants or hybrids with deleterious phenotypes in local environments. Therefore, to understand how ecological factors affect genetic differentiation, one must investigate 1) the source of natural selection, 2) the traits under disruptive selection, and 3) whether the direction of trait divergence is concordant with local environments (Kawecki & Ebert 2004). However, few studies have investigated all three aspects of differential local adaptation. On one hand, many famous examples in ecological and evolutionary genetics investigated traits or genes under selection (Barrett & Hoekstra 2011; Mitchell-Olds et al. 2007), but sometimes little is known about the ecological causes of phenotypic change. For example, despite more than 80 years of study and clear empirical evidence of strong selection, the cause of natural selection on bony armor plates in three-spined sticklebacks remains ambiguous (MacColl 2011). On the other hand, the source of selection can be inferred via niche modeling in landscape genetics, but subsequent experimental verification is still needed.

Our previous landscape genetics study (Lee & Mitchell-Olds 2011) suggested that local water availability may be an important selection force underlying ecological speciation between East and West subspecies of Boechera stricta. Using 24 genotypes in several large-scale greenhouse experiments, in this study we investigate: 1) whether water-regime associated traits have diverged between the two subspecies, and 2) whether the direction of trait divergence corresponds to their native environments. As in other studies, we employed Q_ST-F_ST comparison in controlled environments to identify possible traits under divergent selection. The alternative approach would be estimating the correlation between traits and fitness in the native environments. However, ideally such an experiment would be performed with a cross (instead of natural accessions) to minimize historical linkage disequilibrium among traits. These efforts are ongoing in our laboratory.

Trait divergence corresponds to niche modeling predictions

Many traits have diverged significantly between these subspecies, especially for phenological and morphological traits (Table 2). Although there is significant variation among genotypes for water use efficiency estimated from Δ¹³C, the lack of subspecies or subspecies-by-treatment effect suggests that local adaptation between the two subspecies is not based on physiological traits for differential water usage (Table 1). Alternatively, this phenotype might be significantly different in the field environment, given the possibility of genotype-by-environment interaction.

Most of the significantly diverged traits show a direction of divergence conforming to our previous predictions (Table 2). In phenology, Eastern genotypes flower significantly faster and for shorter duration, which are typical traits of drought escape (Mckay et al. 2003). Escaping from drought during the reproductive stage is probably important for this species, since our preliminary greenhouse observations show that reproductive organs (flowers and fruits) are more susceptible to drought stress than vegetative organs, as is commonly found in crop plants (Bernier et al. 2008; Messmer et al. 2011). Although we did not identify univariate phenological traits with high Q_ST, the high multivariate Q_ST suggests divergent selection on overall phenology. In addition, the divergence in phenology may further decrease gene flow between subspecies. Since the decreased gene flow would increase genome-wide genetic divergence, this effect may make the F_ST-Q_ST comparison conservative for moderately diverged traits (such as phenology itself), but has little effect on the identification of highly diverged ecologically important traits (such as vegetative morphology, below).

In vegetative morphology, the leaves of Western genotypes are more mesophytic (broader, thinner, and with larger surface area), which may facilitate the higher growth rate and higher biomass observed in our controlled environment. On the other hand, leaves of Eastern genotypes are narrower, smaller, and more succulent (with higher water content per unit leaf area), reflecting a more xerophytic morphology which may enable water conservation. Western genotypes’ faster growth rate and delayed phenology result in higher biomass accumulation before the onset of reproduction, which may be advantageous in their native riparian habitats where the length of growing season is not strongly constrained by water availability. In addition, the high Q_ST of leaf shape parameters (width/length ratio) may be caused by their dual functions in photosynthesis and thermoregulation, both of which are related to local water availability.

The significant divergence and high Q_ST of some stalk morphology traits, however, may not reflect natural selection from local water availability. For example, Eastern genotypes have taller central reproductive stalks and longer reproductive internodes. We hypothesize that taller fruiting structures enable seeds to disperse further (which may be adaptive in complex or successional environments) and that longer internodes between fruits might reduce the risk that multiple fruits be attacked by an insect herbivore. However, detailed studies are needed to identify the real agent of selection on these traits.

At first glance, our results may seem mixed: some water-related traits (physiology) do not diverge significantly, and some traits (stalk morphology) diverge without obvious reason. The strong divergence in stalk morphology may indicate that our previous niche modeling study did not identify all factors contributing to the East-West divergence. On the other hand, for water availability to cause ecological speciation, not all water-related traits have to diverge significantly, and ecological speciation could be caused by divergent selection on a few traits (Sobel et al. 2010). Indeed, among all traits that are predicted to be water-related and observed to be significantly divergent, all but one trait show the direction of divergence conforming to our prediction. This exception is leaf packing (leaf area per unit rosette volume). In theory, leaf packing should be higher in drought-adapted genotypes, where similar amounts of total leaf area are packed into smaller rosette volume to minimize leaf water loss. Given the similar rosette volume between the two subspecies, we think the high leaf packing in the West subspecies may be a by-product of its larger total leaf area, a water-related trait under strong divergent selection.

Lack of physiological differentiation

Previous studies have shown that leaf morphology, such as specific leaf area (leaf area per unit dry weight) and leaf water content, can influence water use efficiency (Condon et al. 2004; Hoffmann et al. 2005; Nautiyal et al. 2002). In this study we found significant subspecies differentiation in some leaf morphology traits, but physiological traits (instantaneous and long-term water use efficiency) did not differ significantly between subspecies. At first glance our result may seem contradictory to previous studies. However, our results show that the two subspecies lack significant differentiation in the two important morphological traits that influence water use efficiency (rosette water proportion and rosette dry weight/area, Table 2), and this is consistent with the lack of physiological differentiation between subspecies. In addition, the whole-rosette-level physiology is a balance between individual-leaf-level physiology and rosette structure. As discussed above, rosette leaf packing is the only significantly diverged trait that contradicts our prediction. The higher leaf packing in Western genotypes may decrease rosette water loss from convection and offset the higher evaporation rate from the mesophytic Western leaves (and vice versa for Eastern genotypes), leading to non-significant East-West physiological differentiation. Another influencing factor may be that our experimental conditions are imperfect models of natural environments.

In addition to rosette-level water use efficiency, a recent study has shown that inflorescences have higher water use efficiency than rosettes in A. thaliana (Earley et al. 2009). It is possible that similar patterns may exist in B. stricta, and there may be different water use efficiency between Eastern and Western inflorescences given our observed difference in stalk morphology. Future experiments are needed to examine this possibility.

Lack of geographic effects

Previous analysis of molecular polymorphism suggests that the current geographical distribution of these subspecies represents secondary contact after historical allopatry (Lee & Mitchell-Olds 2011). From the previous niche modeling result, we proposed a possible relationship between trait divergence and reproductive isolation: during the allopatric phase, the two subspecies diverged in traits associated with local water regime. After secondary contact, these diverged traits caused differential local adaptation in distinct environments, and therefore immigrants or hybrids had reduced fitness, contributing to reproductive isolation. This hypothesis predicts that, within each subspecies, the traits associated with local water regime would not differ between sympatric and allopatric regions. Consistent with this hypothesis, we found no evidence for water-regime-associated traits with significant geography or geography-by-subspecies interaction effects.

Between two taxa, reinforcement in speciation refers to the situation where sympatric populations have higher pre-mating reproductive isolation than allopatric populations (Coyne & Orr 2004), which avoids the costs of producing unfit hybrids. For a reproductive trait, reinforcement is inferred when the trait divergence is higher in sympatric than in allopatric regions. We do not observe this pattern in phenology traits, and this is consistent with the observed high hybrid viability from artificial crosses and the highly-selfing reproductive system in this species. On the other hand, if hybridization homogenized trait distributions, then trait divergence would be lower in sympatric than in allopatric regions. We find no evidence for this pattern, either. In fact, the observation that some traits have higher Q_ST than neutral F_ST shows that, instead of being reduced by hybridization, the trait divergence has been maintained by divergent selection between heterogeneous environments.

Comparing F_ST with multivariate Q_ST

Three methods could be used to analyze trait divergence among genetic groups: 1) estimating subspecies effects (P-value) in ANOVA, 2) comparing Q_ST to the confidence interval of mean F_ST, and 3) comparing Q_ST with the genome-wide distribution of F_ST. Although the second method is the most widely used for F_ST-Q_ST comparison, recent opinions advise against this practice (Whitlock 2008). In accordance with recent suggestions (Edelaar & Björklund 2011; Edelaar et al. 2011; Whitlock 2008), we compared trait Q_ST to the genome-wide distribution of SNP F_ST.

The high divergence (mean F_ST = 0.24) between EAST and WEST subspecies, however, sets a high threshold for detecting significant Q_ST, and we only find a few univariate traits (leaf shape parameters, in particular) with Q_ST above the 5% F_ST cutoff (Table 2). In addition, judging from the frequency of SNPs with F_ST higher than 0.75 (Figure 4) and field evidence that many traits and QTL experience natural selection in this species (Anderson et al. 2011; Anderson et al. 2013; Anderson et al. 2012; Prasad et al. 2012), our genome-wide F_ST distribution also may contain SNPs linked with genomic regions under divergent selection. Since Q_ST should be compared to the distribution of neutral F_ST (Whitlock 2008), our results are likely conservative. We therefore designed a measure of multivariate Q_ST to investigate the joint divergence of multiple traits. Q_ST allows researchers to search for signatures of natural selection on individual traits, while its population genetics analogs (F_ST and related parameters) facilitate the search for single target genes under selection. Recently, population geneticists have emphasized that adaptation may occur by slight allele frequency changes at many genes (polygenic adaptation), and each locus may show little signature of natural selection (Pritchard et al. 2010). Similarly, natural selection often acts on combinations of traits (Blows 2007), causing only moderate increase in the Q_ST of univariate traits. Thus, we present a simple measure of selection on multiple traits, using the Q_ST of a new composite trait from discriminant function analyses (DFA) between these subspecies. This composite trait represents the axis of maximum divergence in the multivariate trait space (Figure S2). Indeed, our results show that the multivariate Q_ST is close to the 5% tail of F_ST distribution, as expected when multiple traits are simultaneous targets of divergent selection (Chenoweth et al. 2008).

Because the DFA approach (by definition) maximizes the among-group variation and minimizes the within-group variation, is this multivariate Q_ST somehow unrepresentative or biased? This is not a concern for several reasons. First, most quantitative traits are multivariate, embedded in combinations of other traits (Houle et al. 2010). Therefore, a DFA composite trait is biologically meaningful – the trait (which we are unable to identify a priori, such as overall phenology) that is under the strongest divergent selection (Figure S2). Second, this procedure is simply a rotation of axes, hence the statistical concept of bias does not apply. Identifying this direction of greatest divergence is an important evolutionary question, which is not related to statistical bias. Third, DFA is closely related to MANOVA. Although MANOVA may give lower P-values than univariate ANOVA, this does not imply that MANOVA has biased the P-value downwards, and MANOVA is still a standard practice in biology. Similarly, there is no reason to think that Q_ST of DFA score would be biased upwards. Fourth, similar concepts have been proposed by several authors. Lande (1979), when regressing fitness onto multiple traits, suggested ‘… constructing a selection index or discriminant function where each character is weighted by the force of directional selection on it…’, and therefore ‘Calculation of the minimum selective mortality is thus reduced to a consideration of truncation selection on the index, a one-dimensional problem…’ Blows (2007) proposed a similar idea: ‘This immediately suggests that the presence of linear selection can be most effectively tested for by considering the significance of selection on the univariate discriminant function…’ Both suggestions by definition maximize the variation of fitness explained by traits, but this does not introduce bias. Finally, although one might apply DFA to SNP polymorphisms, this approach would be unlikely to represent the neutral null distribution needed for F_ST-Q_ST comparison.

Although other measures of multivariate Q_ST has been proposed based on decomposing covariance matrices (Kremer et al. 1997; Martin et al. 2008; Ovaskainen et al. 2011), our method has two differences: 1) Estimating the covariance component matrix may be time-consuming and unstable when the number of groups or subspecies is low. Our composite-trait method avoids this complication. 2) The DFA composite trait is biologically meaningful – it is analogous to the most diverged combination of traits between two subspecies (Blows 2007; Lande 1979).

Conclusion

Differential local adaptation forms the basis of ecological speciation and isolation by adaptation. To understand the process of ecological speciation, one must investigate the source of natural selection and the traits under selection, whose interactions shape the patterns of differential local adaptation. In a previous study (Lee & Mitchell-Olds 2011), we showed that local water regime may be the selective force underlying ecological speciation between two genetically diverged subspecies of Boechera stricta. In this study we have identified possible traits experiencing this disruptive selection, and the direction of trait divergence mostly corresponds to niche modeling predictions. On the other hand, we have also identified several traits that are highly diverged without obvious water-related functionality. This suggests that some important selection forces were not identified in our previous niche modeling study (Lee & Mitchell-Olds 2011). In summary, this study identifies traits contributing to incipient ecological speciation in B. stricta and demonstrates the importance of experimental verification of inferences from niche modeling approaches. Furthermore, this evidence for differentiation of ecologically important traits provides the starting point for genetic dissection and evolutionary interpretation of trait variation contributing to ecological speciation.