Abstract
When we make hand movements to visual targets, gaze usually leads hand position by a series of saccades to task-relevant locations. Recent research suggests that the slow smooth pursuit eye movement system may interact with the saccadic system in complex tasks, suggesting that the smooth pursuit system can receive non-retinal input. We hypothesize that a combination of saccades and smooth pursuit guides the hand movements toward a goal in a complex environment, using an internal representation of future trajectories as input to the visuomotor system. This would imply that smooth pursuit leads hand position, which is remarkable since the general idea is that smooth pursuit is driven by retinal slip. To test this hypothesis, we designed a video-game task in which human subjects used their thumbs to move two cursors to a common goal position while avoiding stationary obstacles. We found that gaze led the cursors by a series of saccades interleaved with ocular fixation or pursuit. Smooth pursuit was neither correlated with cursor position nor cursor velocity. We conclude that a combination of fast and slow eye-movements, driven by an internal goal instead of a retinal goal, led the cursor movements and that both saccades and pursuit are driven by an internal representation of future trajectories of the hand. The lead distance of gaze relative to the hand may reflect a compromise between exploring future hand (cursor) paths and verifying that the cursors move along the desired paths.
Keywords: eye-hand coordination, smooth pursuit, saccades, oculomotor neurophysiology, human
Introduction
When subjects make hand movements to visual targets, gaze usually leads hand position by a series of saccades to task-relevant locations (Flanagan & Johansson, 2003; Hayhoe et al., 2003; Land et al., 1999; Neggers & Bekkering, 2001). In addition to saccades, smooth pursuit eye movements also contribute to these gaze changes to targets of interest. Smooth pursuit is classically regarded as an automatic feedback system, driven by retinal slip (Lisberger, 2010). However, increasing evidence suggests that the input to the smooth pursuit system is not just retinal slip. For example, anticipatory smooth eye movements can be cued in the direction of an upcoming stationary target (Blohm et al. 2005; Kowler & Steinman, 1979a,b) or moving target (see Barnes, 2008; de Hemptinne, 2008). Moreover, pursuit is maintained when the target is temporarily occluded (Becker and Fuchs, 1985; Mrotek & Soechting, 2007), suggesting input from a short-term velocity memory to smooth pursuit (Orban de Xivry et al., 2008). In a study of Vercher et al. (1995) subjects had to track a visual target that was moved by their own, unseen arm. When the target unexpectedly moved opposite to the arm, smooth pursuit initially followed the direction of the arm rather than the visual target, suggesting that the initial pursuit could be driven by an efference copy related to the arm movement (Lazzari et al., 1997; Scarchilli et al. 1999). Gardner & Lisberger (2001) showed that the choice of which moving target to follow in smooth pursuit is coupled to the choice of the saccadic system. This raises the possibility of a cognitive input to the smooth pursuit system, in a situation where pursuit is interleaved with a series of saccades.
Recently, we showed that subjects fixate at a particular distance ahead of the hand when they move the hand along a well-defined path (Tramper & Gielen, 2011). This lead distance might reflect a compromise between exploring the future path and verifying that the hand moves along the path. We hypothesized that a similar mechanism might be active when subjects use a combination of saccades and smooth pursuit to guide their hands toward a goal in a complex environment. To investigate the role of saccades and smooth pursuit when subjects create their own internal representation of a future trajectory, we designed a video-game task in which subjects used their thumbs to move two cursors through two gates toward a final goal. The two cursors may facilitate a target selection mechanism for the smooth pursuit system. The stationary visual targets (gates and goal) served as possible targets for the saccadic system. As expected, this task elicited a series of saccades to sequentially fixate the stationary visual targets. In addition, we discovered a range of smooth eye velocities between saccades, when gaze was well ahead of the cursor positions. Gaze velocities during these segments were unrelated to the velocities of the cursors, suggesting that smooth pursuit was driven by some internal representation of the future cursor paths.
Materials and methods
Subjects
Six subjects (labeled S1–S6) with ages between 22 and 27 years participated in this study. S3, S4 and S6 were male. All subjects were right-handed and none of them had any known neurological disorder. S1–S6 took part in experiment 1 and S1–S4 also participated in experiment 2 (see below). One subject (S4) was aware of the purpose of the experiment, whereas the others were naive. S3 and S6 had extensive experience with video games that use a game controller (S3 (age 22): 1–2 hours a day since age 20; S6 (age 24): 1–2 hours from childhood to age 17); the other subjects had no substantial experience. the study was in conformity with The Code of Ethics of the World Medical Association (Declaration of Helsinki), printed in the British Medical Journal (18 July 1964). All subjects gave written informed consent prior to the start of the experiment according to institutional guidelines of the local ethics committee (CMO Committee on Research Involving Human Subjects, region Arnhem-Nijmegen, the Netherlands).
Experimental setup
Subjects were seated in a chair with a high backrest in front of a 1.5 × 1.1-m2 rear-projection screen in a completely darkened room. The subject's eyes were positioned at a distance of approximately 90 cm to the screen. The height of the chair was adjusted to align the subject's cyclopean eye with the center of the projection area. Head movements were restrained by a chin rest fixed to the chair.
Two-dimensional visual scenes were rear projected on the screen with a 3D-ILA SXGA projector (JVC DLA-S15U) with a refresh rate of 75 Hz. The scenes were generated by Open Graphics Library (OpenGL) using the Psychophysics Toolbox for Matlab. The exact distance between the subject's cyclopean eye and the screen was measured before each experiment to adjust the size of the computer generated scene to a field-of-view of 45 deg in both the azimuth φ (horizontal) and elevation θ (vertical) direction.
Eye movements were recorded using the double magnetic induction (DMI) method (Bour et al., 1984; Bremen et al., 2007) and sampled at 1000 Hz using an NI PCI-6220 (National Instruments) data acquisition card. To use the DMI method, the subject was seated in the center of a primary oscillating magnetic field with three orthogonal components with different oscillation frequencies, generated by a 3 × 3 × 3-m3 cubic frame A gold-plated copper ring was placed on the subject's eye. A pick-up coil was placed in front of the eye in the frontal plane and an “anticoil” was connected antiparallel to the pick-up coil to cancel the contribution of the primary field. In this way, the pick-up coil only detected the secondary magnetic field generated by eye-orientation dependent currents in the copper ring. The DMI method was chosen over the scleral search coil technique because subjects experience less discomfort wearing the ring instead of a scleral coil that needs a wire to connect with the recording apparatus. After calibration a precision of approximately 0.2 deg was achieved for both azimuth and elevation over a range of 45 deg.
Each subject held a wireless game controller (Microsoft XBOX 360 Wireless Controller for Windows) consisting of two thumb sticks to move two cursors in the scene by making thumb movements. The velocity of each of the cursors was proportional to the excursion of the corresponding thumb stick that could be moved in all directions. The maximum cursor velocity in both the azimuth and elevation direction was 39.7 deg/s.
Experiment
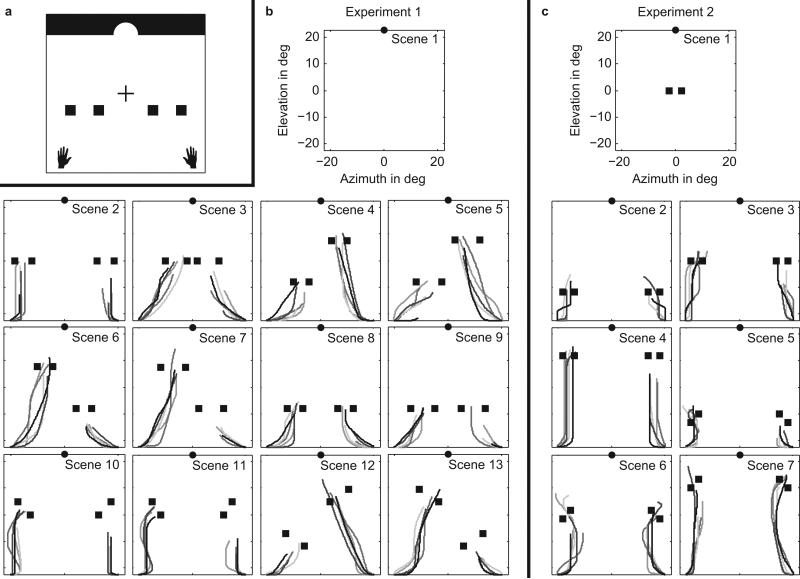
In experiment 1, S1–S6 were asked to move the left and right cursors, displayed as left and right hand icons, through two gates toward a final common goal, using the two thumb sticks on the game controller. Figure 1a gives a rough schematic of the game, with black and white reversed and objects not drawn to scale. We call the geometric arrangement of the gates and the goal the “scene”. To successfully complete a trial, subjects had to reach the goal within three seconds while moving the left and right cursor through the left and right gate, respectively. In this way, we created a highly demanding visuomotor task, since vision had to be allocated carefully to observe the scene and guide both cursors through the gates within a very short time.
Figure 1.
(a) Schematic of the video-game display with left and right gates represented by pairs of squares and a final common goal represented by an opening in a virtual wall at the top of the display. The black hand icons represent the initial position of the left and right cursor, respectively. The cross represents the location of initial gaze fixation. Icons are not to scale and the screen background was black, not white, with gray objects. (b) Location of gates and goal of each scene for experiment 1. Each scene had a field-of-view of 45 deg, with azimuth and elevation running from –22.5 to 22.5 deg and consisting of one final goal (circle). Scenes 2-13 included two gates (squares) located at various positions. In scene 1 no gates were present. The size of the gate openings was 4.2 deg (scene 2), 6.2 deg (scene 3), 3.8 deg (scenes 4, 6, 8, 11), 7.2 deg (scenes 5, 7, 9), 4.6 deg (scene 10), and 6.6 deg (scenes 12, 13). Icons are not on scale. Each pair of lines with the same grayscale represents the left and right cursor trajectories of a single trial, for S2. Traces only show the trajectory between movement onset of the left (right) cursor until the time when gaze moved away from the left (right) gate. (c) Same as (b) for experiment 2. In scene 1, only one gate was present; scenes 2-7 included two gates. The size of the gate openings was 2.5 deg in all scenes.
We presented thirteen different scenes: twelve gate scenes and one no-gate scene (Fig. 1b). Each scene had a black background and consisted of a goal represented by an opening in a virtual white wall with a width of 7.5 deg and located at (φ, θ) = (0, 22.5) deg. Each gate was formed by a pair of gray squares and the size of each square was 1.9 × 1.9 deg. The size of the gate openings was 4.2 deg (scene 2), 6.2 deg (scene 3), 3.8 deg (scenes 4, 6, 8, 11), 7.2 deg (scenes 5, 7, 9), 4.6 deg (scene 10), and 6.6 deg (scenes 12, 13).
Each trial started with a white fixation cross (size 0.4 deg) displayed at the center of the black screen, and the gates were invisible. The cursors had the shape of a left and right hand icon (size 2.1 × 2.5 deg and gray color) and were displayed at (–20.5, –22.5) deg and (20.5, –22.5) deg, respectively. Subjects were asked to fixate the cross until they moved one of the cursors, which caused the fixation cross to disappear and the gates to appear. No instructions on eye movements were given for the remaining part of the trial. When either cursor hit a gate obstacle (displayed as a square on the screen) or the upper boundary of the scene (θ = 22.5 deg), the cursor stopped moving.
The experiment was divided into six blocks with 65 trials each. The position of the two gates changed on every trial, randomly selected from the set of thirteen different scenes, yielding 30 repetitions for each scene. To calibrate the eye movement signals, each block was preceded by a calibration trial in which subjects fixated on 36 calibration points, sequentially presented in a grid. The experiment started with instructions and one block of 65 practice trials to get familiar with the controller and the task (duration 5 minutes), followed by the application of the DMI equipment (eye ring and pickup-coil, 3 minutes), the first calibration trial (1 minute), the first block of trials (3.5 minutes), until all six blocks were completed. Each experiment took approximately 30 minutes in total.
In experiment 2, we tested S1–S4 in a different set of seven scenes (Fig. 1c). One scene consisted of a single gate located at (φ, θ) = (0, 0) deg, and both cursors had to pass through that gate. The size of the gate openings was 2.5 deg. This experiment was divided into six blocks with 70 trials each. The position of the two gates changed on every trial, randomly selected from the set of seven different scenes, yielding 60 repetitions for each scene. All other experimental conditions were exactly the same as for experiment 1. The purpose of experiment 2 was to create a more difficult task by making smaller gate openings, thereby increasing the visual demand and requiring more accurate maneuvering of the cursors. This allowed us to investigate to what extent the results were influenced by the difficulty of the task.
Data preprocessing
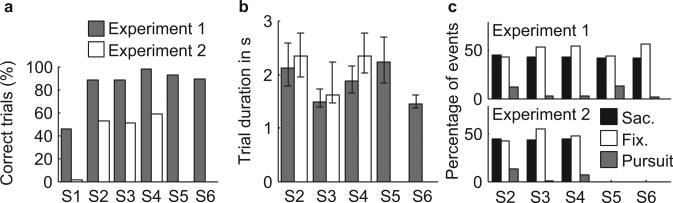
Eye position was calibrated using a parameterized self-organizing map (PSOM) (Essig et al., 2006). We adapted this method to make it suitable for calibration of gaze position in the two dimensional plane. The 36 calibration points were arranged in a Chebyshev-spaced grid to increase the calibration performance (Walter and Ritter, 1995). A trial was completed correctly if each of the following three criteria was met: (1) each cursor was navigated through its corresponding gate; (2) each cursor reached the goal before the deadline of three seconds; (3) the vertical cursor velocity was always positive (moving upward) and larger than zero except for the beginning and end of the trial. The latter criterion was included to ensure that subjects moved each cursor in a smooth fashion without hitting one of the gate obstacles or going backwards. Figure 2a shows the percentage of correctly completed trials. Only correctly completed trials were used for further analyses.
Figure 2.
Task performance and classification of eye movements. (a) Percentage of trials completed correctly for S1–S6 for experiment 1 (gray) and S1–S4 for experiment 2 (white). (b) Median trial duration for S2–S6 for experiment 1 (gray) and S2–S4 for experiment 2 (white). Lower and upper error bars indicate the 5% and 95% percentiles, respectively. (c) Total percentage of saccades (black), fixations (white) and smooth pursuit segments (gray) in all scenes for S2–S6 in experiment 1 (top panel) and S2–S4 in experiment 2 (bottom panel).
Event detection
We used an adaptive algorithm developed by Nyström & Holmqvist (2010) to classify gaze epochs as a fixation or a saccade. This algorithm uses a data-driven approach based on the signal-to-noise ratio to find the saccade onset and end thresholds, instead of predetermined parameters set by the user. Since the noise in the raw voltage signals differed among subjects due to the exact placement of the DMI equipment, this method improved the event detection. We made the following adjustments to the algorithm. We set the initial peak velocity threshold for saccade onset to 80 deg/s, the minimum saccade duration to 10 ms and the minimum fixation duration to 50 ms. The maximum saccade velocity and maximum saccade acceleration were excluded as selection criteria. We extended the algorithm to also detect smooth pursuit. Therefore, we took all epochs which were initially classified as a fixation and for each epoch, we smoothed gaze velocity using a Savitzky-Golay filter with a span of 100 ms and order 2. Within that epoch, a series of subsequent data points was labeled as a smooth pursuit epoch if (1) the gaze velocity in the elevation direction exceeded 3 deg/s, (2) the gaze displacement was larger than 1 deg of visual angle, and (3) the duration was larger than 50 ms. The remaining data points in the epoch were labeled as a fixation if the duration exceeded the minimum fixation duration. Otherwise, the remaining data points were merged with the smooth pursuit epoch.
Results
Overall performance
Since subjects had to maneuver two cursors via two gates to a final common goal at the top of the screen within three seconds and without hitting the gates, success rates varied across subjects. As indicated in Figure 2a, S1 had great difficulty in both experiments, with only about 40% of trials successfully completed in experiment 1 and almost no successful trials in experiment 2. This subject was therefore excluded from further analysis. The values for successful completion for the other subjects were on average 92% (range 89–98%) for experiment 1 and 54% (51–59%) for experiment 2, which confirmed that experiment 2 was more difficult. S2 and S5 tended to use more time to complete each trial (more than 2 s), especially compared with S3 and S6, who had an average trial duration of about 1.5 s (Fig. 2b).
Gaze data were analyzed by detecting saccades (black bars in Fig. 2c) and then classifying non-saccade segments as fixation (white bars) or smooth pursuit (gray bars). The subjects with longer trial durations generally had a larger number of smooth pursuit events, which comprised about 23% of all non-saccadic segments in S2 and S5, compared to about 5% in the other subjects (Fig. 2c).
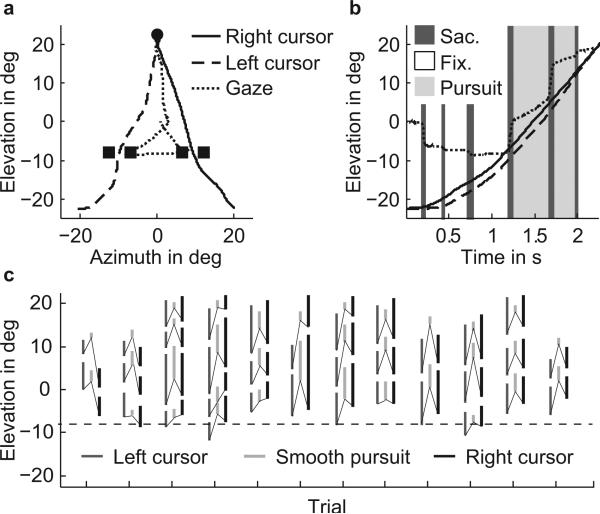
Figure 3a,b shows an example of a single trial where the first four non-saccade segments were classified as fixation, the next two segments were classified as smooth pursuit (light gray shaded areas in Fig. 3b), and the last segment was classified as a fixation. In the last phase of the trial, after passing through the gates (after about 1.2 s), each cursor (dashed and solid black lines) moved at a more or less constant velocity. In contrast, the smooth pursuit velocity (dotted line) was higher in the first smooth pursuit segment (between 1.3 and 1.7 s) than in the second (1.7–2.0 s; Fig. 3b, light gray shaded epochs), and in both segments considerably smaller than the velocity of the cursors. In general, gaze position was leading the position of the cursors throughout the entire movement (Fig 3b). This is illustrated in another way in Fig. 3c, which shows the vertical position between onset and offset of pursuit (light grey bars) and the corresponding position of the cursors during the same time intervals (dark grey and black solid lines, representing the left and right cursor positions, respectively). Smooth pursuit eye movements virtually always occurred between the gates and the target, as indicated by the vertical light gray bars that are located above the dashed line in Figure 3c, which represents the position of the gates. The thin solid lines in Fig. 3c connect the corresponding positions of left and right cursor at the time of onset of pursuit. The segment of pursuit is always smaller than the segments of corresponding cursor movements, since pursuit velocity was much smaller than cursor velocity (as illustrated in Fig. 3b). At the onset of pursuit, the cursor positions were lagging behind the smooth eye movement. These observations are representative for all subjects and we will elaborate on each of these aspects in the next sections.
Figure 3.
(a) Left cursor (dashed line), right cursor (solid line) and gaze (dotted line) paths for a single trial (S2, scene 8, experiment 1). The goal and gates are represented by the circle and squares, respectively. (b) Corresponding time traces in the elevation direction for gaze (dotted line), left cursor (dashed line) and right cursor (solid line). Shaded areas indicate either fixations (white), saccades (dark gray) or smooth pursuit (light gray). (c) Elevation position of smooth pursuit paths for trials of scene 8, experiment 1, shown as light gray lines (S2). The dark gray and black lines show the elevation position of the left and right cursor, respectively, in the same time frame as the corresponding smooth eye movement (light gray bar). For clarity. The thin lines connect position of pursuit at onset of pursuit with the corresponding position of the left and right cursor at that onset time. The dashed line indicates the elevation position of the gates.
Saccade metrics
In this section we will investigate the extent to which saccadic eye movements and cursor movements are coupled. In Figure 1b and c, showing trial data from S2, each pair of lines with the same gray scale represents the left and right cursor paths of a single trial. The traces only show the paths between movement onset of the left (right) cursor until the time when gaze moved away from the left (right) gate. For asymmetric scenes, like scenes 6 and 7 of experiment 1 (Fig. 1b), gaze visited the lower gate first, and then moved away well before the cursor reached it. Thus the right cursor paths in scenes 6 and 7 are truncated well beneath the right gate. However, gaze generally departed from the second gate around the time the cursor reached the gate. The same was true for symmetric scenes except in this case, since there was no lower gate, the eye may have visited either the left or the right gate first. This behavior was consistent across the original experiment (experiment 1) and the more difficult experiment (experiment 2), and this strategy was similar across subjects.
For all scenes, the time when the cursor entered the gate and the time when gaze left that gate was correlated (Pearson's correlation coefficient r = 0.68, SD 0.17, P < 0.03 for each scene). To investigate whether gaze was leading or lagging behind the cursors, we computed the time difference between the time when gaze left the gate and the time when the cursor entered the gate. A positive value means that gaze left the gate before the cursor entered the gate. Pooled over all subjects, scenes, and experiments we found an average time difference of 122 ms (SD 235 ms). We then subdivided the scenes of experiment 1 according to the arrangement of the gates. For symmetric scenes, we found a time difference of 336 ms (SD 240 ms) for the gate that gaze visited first and a time difference of 42 ms (SD 138 ms) for the second gate. The values for experiment 2 were 203 ms (SD 236 ms) and –11 ms (SD 145 ms) for the first and second gate, respectively. The time differences for experiment 2 were significantly different from experiment 1 (two-tailed two-sample t test, first gate: P < 10–18, second gate: P < 10–8), which shows that the lead time between gaze and cursors decreased in the more difficult situation when the cursors had to pass smaller gates.
For the asymmetric scenes in experiment 1, we found a time difference of 125 ms (SD 166 ms) for the first gate and a time difference of 27 ms (SD 139 ms) for the second gate. The difference between symmetric and asymmetric scenes from experiment 1 was significant for the first gate (two-tailed two-sample t test, P < 10–51) but was not significant for the second gate (P = 0.09). Thus, the relative timing between gaze and cursors was dictated by scene geometry (symmetric versus asymmetric arrangements of the gates) as well as gate geometry (small versus large gate openings).
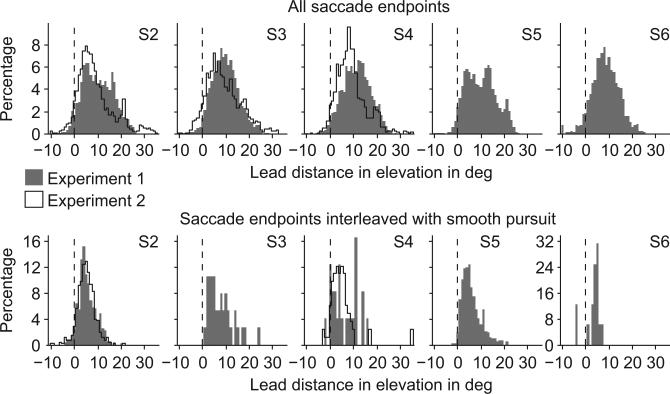
Saccade endpoints were generally ahead (positive elevation) of cursor location. This was true for all subjects, both cursors, and both experiments (Fig. 4, top row). We also considered separately the saccade endpoints that were interleaved between gaze segments classified as smooth pursuit (Fig. 4, bottom row). S3 and S6 (the subjects with short trial durations) had relatively few of these events, but it is still clear that the endpoints of these saccades were generally about 5 deg above cursor location. This result corresponds to our previous observations on pursuit location in Figure 3c.
Figure 4.
Saccade endpoints are ahead of cursor location. Histograms of lead distances in the elevation direction for S2–S6 in experiment 1 (gray bars) and for S2–S4 in experiment 2 (black line). For each saccade, the lead distance was calculated as the elevation of gaze position minus the elevation of cursor position at the end of a saccade. Data for left and right cursors were pooled. The dashed lines mark the lead distance of 0 deg. The top row shows data for all saccade endpoints. The bottom row shows data for saccade endpoints for saccades that were interleaved with smooth pursuit eye movements. S3 did not show saccades interleaved with smooth pursuit in experiment 2.
Smooth pursuit
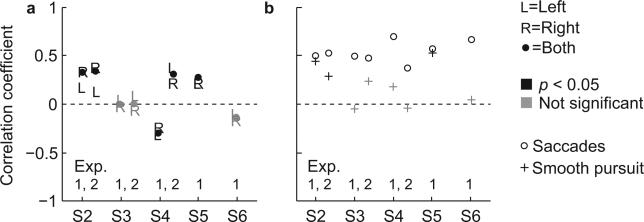
Since the endpoints of saccades that were interleaved with smooth pursuit (Fig. 4, bottom row) correspond to the location of smooth pursuit onset, the results in Figure 4 demonstrate that not only the saccades, but also the segments of smooth pursuit started ahead of the cursor location. Thus, gaze position during smooth pursuit did not match the location of one of the cursors. This raised the question whether smooth pursuit velocity was related to the cursor velocity, as predicted by the retinal-slip model. This velocity could either be the velocity of the left or right cursor, depending on which one was being pursued, or the average velocity of both cursors. To test this hypothesis, we took the average velocity in the elevation direction of each of the gaze segments that were classified as smooth pursuit and did the same for the corresponding left and right cursor segments. As shown for all subjects in Figure 5a, we used these velocities to compute the Pearson's correlation between smooth pursuit velocity and the velocity of the left (‘L’) and right (‘R’) cursor, and the average velocity of both cursors (filled circles). When considering all r-values together, we found a significant correlation between smooth pursuit velocity and cursor velocity in 60% of the cases. For these cases, the correlation was weak, and could be either positive or negative, ranging from –0.3 to 0.4, where a negative correlation corresponds to a situation where pursuit velocity decreased when cursor velocity increased.
Figure 5.
Smooth pursuit velocity correlates with distance-to-goal and not with cursor velocity. Pearson's correlation coefficients (r-values) are represented by bold (experiment 1) or regular symbols (experiment 2). Significant (P < 0.05) and non-significant values are shown in black and gray, respectively. (a) Correlation between smooth pursuit velocity and the velocity of the left (‘L’) and right (‘R’) cursor, and the average velocity of both cursors (solid dot), computed by taking the average velocity in elevation direction of each of the gaze segments that were classified as smooth pursuit and the average velocity in elevation direction for the corresponding left and right cursor segments. (b) Correlation between smooth pursuit velocity (same segments as in (a)) and the average distance between gaze and the final goal (+). Same for saccade peak velocity (o).
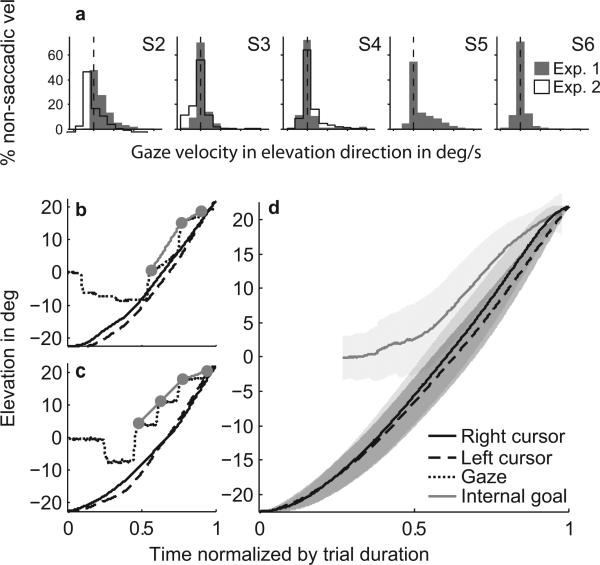
Thus the lack of correlation indicates that smooth pursuit velocity was not related to cursor velocity (Fig. 5a) and non-saccadic events always exhibited a unimodal continuum of cursor velocity. To further explore this finding, we performed an additional analysis in which we took all non-saccade epochs (smooth pursuit and fixations) and focused on the elevation component of gaze. If smooth pursuit velocity was indeed related to cursor velocity, we would expect the gaze velocity in these non-saccade epochs to exhibit a bimodal distribution, with one peak centered around zero velocity (fixation) and a second, smaller peak centered around 30 deg/s, which would approach the speed of the cursors (average of both cursors across subjects in the second half of trials was 34.7 deg/s (SD 4.7 deg/s)). Our data did not show this. Instead, the velocities of all non- saccade segments followed a distribution with a single peak (Fig. 6a). Pooling all scenes, most subjects showed a peak centered at zero velocity (fixation) and a tail in the positive (upward) direction. In one special scene where the gates were absent (experiment 1, scene 1), subjects showed fewer fixations and more smooth pursuit segments. In this case, all subjects had a distribution of gaze velocities with a tail in the positive direction and showed a positive drift in the unimodal gaze velocity distributions. We repeated this analysis using two-dimensional gaze velocities and found similar results.
Figure 6.
Gaze follows a goal trajectory ahead of the cursors with a unimodal distribution of non-saccadic gaze velocities, which argues against ocular following of the cursors. (a) Histograms of gaze velocities during fixations and smooth pursuit for S2–S6 in experiment 1 (gray) and S2–S4 experiment 2 (white). For each non-saccadic segment (i.e., fixations and smooth pursuit), we calculated the mean gaze velocity in elevation direction. The dashed lines mark the gaze velocity of 0 deg/s as would be expected for steady fixation. The top row shows data from all scenes.(b) left cursor (dashed line), right cursor (solid black line) and gaze (dotted line) position in the elevation direction as a function of time (normalized by trial duration) for a single trial of S2, scene 8, experiment 1. Gray line illustrates the linear interpolation of saccade endpoints (gray dots) occurring beyond the final gate. (c) Same as (b) for S4. (d) Left (dashed line) and right (solid black line) cursor position in the elevation direction averaged over all subjects, scenes, and experiments. Gray line shows the average over all interpolated gaze epochs (see gray lines in (b) and (c)), representing the internal goal trajectory. Shaded areas represent the standard deviation. Trial durations were between 1.5–3 s (see Fig. 2b).
The lack of correlation indicates that smooth pursuit velocity was not related to cursor velocity (Fig. 5a) and that non-saccadic events always exhibited a unimodal continuum of gaze velocities (Fig. 6a). In addition, smooth pursuit was interleaved with saccades which took gaze well ahead of cursor location (Fig. 4). This behavior is different from regular “catch-up” saccades that bring the fovea back onto a retinal target during fast or unpredictable target motion. This led us to hypothesize that the slow eye movements were not simply an ocular following of the moving cursors. Instead we considered that smooth pursuit might work in conjunction with the saccades, to drive the control of the movements of the cursors, upward toward the final goal.
To test this hypothesis, we calculated for each smooth pursuit segment the average distance between gaze and the final goal of the cursors, and correlated this distance with the average smooth pursuit velocity of that segment (r-values marked with ‘+’ in Fig. 5b). For the subjects with a high portion of smooth pursuit eye movements (S2 and S5, see Fig. 2c), we found that smooth pursuit velocity was positively correlated (r = 0.45, P < 10–24, S2, experiment 1; r = 0.29, P < 10–7, S2, experiment 2; r = 0.52, P < 10–33, S5) with the distance to the goal. Thus, gaze appeared to slow down when approaching the final goal by slowing down pursuit. This result explains the range in correlations found between pursuit and cursor velocity (Fig. 5a). The degree with which subjects accelerated the cursors to the maximum velocity differed among subjects. Subjects that quickly accelerated the cursors had a constant cursor velocity (equal to the maximum velocity) during the second part of the movement where the smooth pursuit events occurred. This yielded a correlation coefficient around zero. Subjects that accelerated the cursor more gradually had an increasing cursor velocity during the second part of the movement, resulting in a negative correlation since the pursuit velocity decreased towards the end of the movement. In some cases, subjects decelerated the cursors when they approached the final goal, resulting in a positive correlation.
An interesting question arises as whether saccades also become slower (and therefore smaller) when approaching the final common goal of the cursors. To answer this question, for each trial we took the series of saccades between the gates and the final goal and we correlated the peak velocity of each saccade (except the last one, see below) with distance-to-goal measured as the Euclidean distance between saccade onset and goal (r-values marked with ‘o’ in Fig. 5b). Notice that for the last saccade in each series, the saccade endpoint is equal (or close) to the final goal. Thus, for these saccades it is trivial that saccade velocity is correlated with distance-to-goal since smaller saccades have lower peak velocities. For the other saccades, the endpoint could be anywhere between the gates and the goal. For all subjects we found significant correlations between 0.37 (P < 10–5) and 0.69 (P < 10–33), confirming that also the saccades that brought the eye via intermediate locations on the screen to the goal slowed down as they approached the goal.
In summary, we found that gaze followed a goal trajectory that consisted of a series of saccades interleaved with smooth pursuit (Fig. 6b) or fixations (Fig. 6c). This goal trajectory, revealed by performing a linear interpolation of the saccade endpoints and averaging the outcome over all trials (Fig. 6d), was always ahead of the movement of the cursors and slowed down in the final stretch, while the cursors maintained a more or less constant velocity. Pursuit velocity was not related to velocity of one of the cursors, but was often related to distance of gaze relative to the final goal with a positive correlation between pursuit velocity and distance-to-goal. The same was true of saccade velocity. Thus a combination of fast and slow eye-movements, driven by an internal goal trajectory, seems to guide the cursor movements.
Discussion
In this study we investigated the role of saccades and smooth pursuit when subjects created their own internal representation of a future trajectory to guide two cursors in a video game. We found that gaze led the cursors toward the final common goal in a series of saccades as illustrated in Figure 6, and especially for two slower subjects, also segments of slow goal-directed eye movements. Surprisingly, these segments of smooth pursuit did not correlate with the position and velocity of the moving cursors on the screen, but seemed to follow an internal trajectory ahead of the cursor movements. To our knowledge, this study is the first to demonstrate that gaze can lead self-generated movements in a visuomotor task by a combination of saccades and smooth pursuit, and that smooth pursuit can be used proactively to plan and guide a future movement.
When executing visually-guided hand movements, saccades often lead the hand to spatial target locations (Sailer et al., 2005; Land, 2006). In a reaching task in which the demand for vision was manipulated, it was shown that gaze moved to the next location as the demand at the previous location decreased (Sims et al., 2011). Our study shows that, in addition, the relative timing between gaze and cursor movements depends on the demand for vision at the next event. For asymmetric scenes, we found that gaze was directed toward the first (lower) gate and moved on to the next (upper) gate about 125 ms before the cursor entered the first gate. However, for the symmetric scenes, this strategy could become problematic since each cursor enters its respective gate nearly simultaneously, while gaze cannot be directed to both gates simultaneously. In these cases, subjects directed their gaze toward the second gate about 336 ms before the cursor entered the first gate, which was more than 2.5 times earlier than for the asymmetric scenes. However, at the second gate there was no urge for gaze to quickly move on to the next event—the distance between the second gate and the final goal was more than 10 deg of visual angle for all scenes. Therefore, lead times at the second gate were much smaller than at the first gate. This result implies a flexible coupling between gaze and the thumb movements depending on scene geometry, which is different from previous studies that suggest a fixed “yoking” of eye and hand (Neggers & Bekkering, 2000, 2001).
In a previous study, eye and hand movements were measured during tracking of a target that made an unpredictable change in direction. The investigators incorporated conditions where the hand and eye tracked the target separately, as well as in combination (Engel & Soechting, 2003). They found that for combined eye-hand tracking, the latency for a change in direction of the eye movement increased to approach the latency of the hand movement, compared to the latency in the eye-alone tracking. The hand did exactly the opposite, that is, it decreased its latency with respect to hand-alone tracking. In our study, both smooth pursuit and saccade velocity decreased over time during the second part of the movement. This is nicely illustrated by Figure 6, which shows that the deceleration of gaze during the second part of the trial reduced the distance between gaze and the cursors and thus improved the visual guidance of the cursors to the final common goal. Taken together, these observations demonstrate a flexible coupling between gaze and cursors in which gaze tends to join the cursors and vice versa.
This hypothetical compromise between eye and cursor trajectories might reflect a compromise between exploring the future path and verifying that the cursors move along the path. Recently, we suggested that such a strategy could explain why the eye leads the fingertip by a fixed distance, using a series of fixations interleaved with saccades, when the finger traces a fully visible target path (Tramper & Gielen, 2011). We also showed that interpolating the saccade endpoints revealed the goal trajectory of the eye along the path, which leads the hand position along the path. In the present study, we used the same analysis which revealed an internal goal trajectory for gaze that was not following the moving cursors visible on the screen (Fig. 6). Instead, gaze was leading the cursors.
It is possible to generate pursuit in absence of a foveal stimulus (see Introduction), for example when subjects were instructed to pursue the mid-point between two peripherally located targets that moved sinusoidally (Barnes & Hill, 1984). In these cases, smooth eye velocity is highly correlated with the movement of peripheral targets. We found that smooth pursuit velocity slowed down when the eyes approached the final goal of the cursors whereas the cursor velocity remained rather constant. This explains why smooth pursuit velocity was correlated with the distance remaining between gaze location and the goal but was not well correlated with hand velocity. Thus, during smooth pursuit, gaze did not follow the average movement of the extra-foveal cursors but followed a different, self-generated target trajectory. To distinguish this target from imaginary moving targets or occluded targets, we call this an internal target.
The observation of pursuit eye movements in the absence of a moving target is not new. First of all, there are glissades at the end of saccades. However, since the duration of glissades is short (about 24 ms, see Nystrom & Holmqvist, 2010), they cannot explain the pursuit of inter-saccadic intervals of several hundred of milliseconds as in our study. Moreover, Frens & van der Geest (2002) demonstrated that glissades are absent when using scleral search coils. Therefore, they may also be absent with the DMI-methods used in this study where subjects use a ring on the sclera. Post-saccadic enhancement (Lisberger, 1998) just after saccades may well contribute to our inter-saccade pursuit, but this is consistent with our interpretation. Moreover, anticipatory pursuit has been reported when the subject expects the target to move and pursuit is subject to modulation by attention (Kowler, 1990). Our data reveal a new type of pursuit in the absence of a physically moving target, which was not reported before. All these findings together indicate that pursuit is much more flexible than previously thought and our study shows a clear functional role for such flexibility in a natural task involving hand-eye coordination.
Recently, scientists debated the traditional view that the smooth pursuit and saccadic system are two distinct neural systems (Keller & Missal, 2003; Krauzlis, 2004). In this study, we found that both smooth pursuit as well as saccadic eye movements slowed down when approaching the common target for the two hands. This result provides behavioral evidence that both systems can work together to follow the same, internal trajectory in complex visuomotor tasks. It is known that saccades anticipate the future location of gaze before the actual eye movement is made (Duhamel et al., 1992). Recently, it has been shown that the same holds for smooth pursuit where attention is allocated ahead of the pursuit eye movement (Khan et al., 2010). Our result perfectly fits with the idea that both visual attention and gaze are biased in the direction of the goal to plan and guide upcoming movement.
Acknowledgements
This work was supported by US National Institutes of Health (NIH) Grant R01 NS027484 (M.F.). The authors declare no competing financial interests.
Footnotes
Author contributions: J.T., A.L. and S.G. designed the study. J.T. and A.L. performed the experiments. J.T. and M.F. analyzed the data. J.T., M.F. and S.G. wrote the paper.
References
- Barnes GR. Cognitive processes involved in smooth pursuit eye movements. Brain Cognition. 2008;68:309–326. doi: 10.1016/j.bandc.2008.08.020. [DOI] [PubMed] [Google Scholar]
- Barnes GR, Hill T. The influence of display characteristics on active pursuit and passively induced eye movements. Exp. Brain Res. 1984;56:438–447. doi: 10.1007/BF00237984. [DOI] [PubMed] [Google Scholar]
- Becker W, Fuchs AF. Further properties of the human saccadic system: eye movements and correction saccades with and without visual fixation points. Vision Res. 1969;9:1247–125. doi: 10.1016/0042-6989(69)90112-6. [DOI] [PubMed] [Google Scholar]
- Blohm G, Missal M, Lefèvre P. Direct evidence for a position input to the smooth pursuit system. J. Neurophysiol. 2005;94:712–721. doi: 10.1152/jn.00093.2005. [DOI] [PubMed] [Google Scholar]
- Bour LJ, Van Gisbergen JAM, Bruijns J, Ottes FP. The double magnetic induction method for measuring eye movement-results in monkey and man. IEEE T. Biomed. Eng. 1984;31:419–427. doi: 10.1109/TBME.1984.325281. [DOI] [PubMed] [Google Scholar]
- Bremen P, Van der Willigen RF, Van Opstal AJ. Applying double magnetic induction to measure two-dimensional head-unrestrained gaze shifts in human subjects. J. Neurophysiol. 2007;98:3759. doi: 10.1152/jn.00886.2007. [DOI] [PubMed] [Google Scholar]
- Carpenter RHS. Movements of the eyes. 2nd rev Pion Limited; 1988. [Google Scholar]
- De Hemptinne C, Lefèvre P, Missal M. Neuronal bases of directional expectation and anticipatory pursuit. J. Neurosci. 2008;28:4298–4310. doi: 10.1523/JNEUROSCI.5678-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duhamel JR, Colby CL, Goldberg ME. The updating of the representation of visual space in parietal cortex by intended eye movements. Science. 1992;255:90–92. doi: 10.1126/science.1553535. [DOI] [PubMed] [Google Scholar]
- Engel KC, Soechting JF. Interactions between ocular motor and manual responses during two-dimensional tracking. Prog. Brain Res. 2003;142:141–153. doi: 10.1016/S0079-6123(03)42011-6. [DOI] [PubMed] [Google Scholar]
- Essig K, Pomplun M, Ritter H. A neural network for 3D gaze recording with binocular eye trackers. Int. J. Parallel Emergent Distributed Syst. 2006;21:79–95. [Google Scholar]
- Flanagan JR, Johansson RS. Action plans used in action observation. Nature. 2003;424:769–771. doi: 10.1038/nature01861. [DOI] [PubMed] [Google Scholar]
- Frens MA, van der Geest JN. Scleral search coils influence saccade dynamics. J. Neurophysiol. 2002;88:692–698. doi: 10.1152/jn.00457.2001. [DOI] [PubMed] [Google Scholar]
- Gardner JL, Lisberger SG. Linked target selection for saccadic and smooth pursuit eye movements. J. Neurosci. 2001;21:2075–2084. doi: 10.1523/JNEUROSCI.21-06-02075.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayhoe MM, Shrivastava A, Mruczek R, Pelz JB. Visual memory and motor planning in a natural task. J. Vision. 2003;3:49–63. doi: 10.1167/3.1.6. [DOI] [PubMed] [Google Scholar]
- Hochberg Y, Tamhane AC. Multiple comparison procedures. Vol. 82. Wiley Online Library; 1987. [Google Scholar]
- Johansson RS, Westling G, Bäckström A, Flanagan JR. Eye-hand coordination in object manipulation. J. Neurosci. 2001;21:6917–6932. doi: 10.1523/JNEUROSCI.21-17-06917.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller EL, Missal M. Shared brainstem pathways for saccades and smooth-pursuit eye movements. Ann. N. Y. Acad. Sci. 2003;1004:29–39. doi: 10.1196/annals.1303.004. [DOI] [PubMed] [Google Scholar]
- Khan AZ, Lefèvre P, Heinen SJ, Blohm G. The default allocation of attention is broadly ahead of smooth pursuit. J. Vision. 2010;10 doi: 10.1167/10.13.7. [DOI] [PubMed] [Google Scholar]
- Kowler E, Steinman RM. The effect of expectations on slow oculomotor control–I. Periodic target steps. Vision Res. 1979a;19:619–632. doi: 10.1016/0042-6989(79)90238-4. [DOI] [PubMed] [Google Scholar]
- Kowler E, Steinman RM. The effect of expectations on slow oculomotor control–II. Single target displacements. Vision Res. 1979b;19:633–646. doi: 10.1016/0042-6989(79)90239-6. [DOI] [PubMed] [Google Scholar]
- Kowler E. The role of visual and cognitive processes in the control of eye movements. In: Kowler E, editor. Eye movements and Their Role in Visual and Cognitive Processes. Elsevier; Amsterdam: 1990. pp. 1–70. [Google Scholar]
- Krauzlis RJ. Recasting the smooth pursuit eye movement system. J. Neurophysiol. 2004;91:591–603. doi: 10.1152/jn.00801.2003. [DOI] [PubMed] [Google Scholar]
- Land M, Mennie N, Rusted J. The roles of vision and eye movements in the control of activities of daily living. Perception. 1999;28:1311–1328. doi: 10.1068/p2935. [DOI] [PubMed] [Google Scholar]
- Land MF. Eye movements and the control of actions in everyday life. Prog. Retin. Eye. Res. 2006;25:296–324. doi: 10.1016/j.preteyeres.2006.01.002. [DOI] [PubMed] [Google Scholar]
- Lazzari S, Vercher JL, Buizza A. Manuo-ocular coordination in target tracking. I. A model simulating human performance. Biol. Cybern. 1997;77:257–266. doi: 10.1007/s004220050386. [DOI] [PubMed] [Google Scholar]
- Lisberger SG. Postsaccadic enhancement of initiation of smooth pursuit eye movements in monkeys. J. Neurophysiol. 1998;79:1918–1930. doi: 10.1152/jn.1998.79.4.1918. [DOI] [PubMed] [Google Scholar]
- Lisberger SG. Visual guidance of smooth-pursuit eye movements: sensation, action, and what happens in between. Neuron. 2010;66:477–491. doi: 10.1016/j.neuron.2010.03.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masson GS, Stone LS. From following edges to pursuing objects. J. Neurophysiol. 2002;88:2869–2873. doi: 10.1152/jn.00987.2001. [DOI] [PubMed] [Google Scholar]
- Movshon JA, Adelson EH, Gizzi MS, Newsome WT. The analysis of moving visual patterns. Pattern Recogn. 1985;54:117–151. [Google Scholar]
- Mrotek LA, Soechting JF. Predicting curvilinear target motion through an occlusion. Exp. Brain. Res. 2007;178:99–114. doi: 10.1007/s00221-006-0717-y. [DOI] [PubMed] [Google Scholar]
- Neggers SFW, Bekkering H. Ocular gaze is anchored to the target of an ongoing pointing movement. J. Neurophysiol. 2000;83:639–651. doi: 10.1152/jn.2000.83.2.639. [DOI] [PubMed] [Google Scholar]
- Neggers SFW, Bekkering H. Gaze anchoring to a pointing target is present during the entire pointing movement and is driven by a non-visual signal. J. Neurophysiol. 2001;86:961–970. doi: 10.1152/jn.2001.86.2.961. [DOI] [PubMed] [Google Scholar]
- Nyström M, Holmqvist K. An adaptive algorithm for fixation, saccade, and glissade detection in eyetracking data. Behav. Res. Methods. 2010;42:188–204. doi: 10.3758/BRM.42.1.188. [DOI] [PubMed] [Google Scholar]
- Orban de Xivry JJ, Missal M, Lefèvre P. A dynamic representation of target motion drives predictive smooth pursuit during target blanking. J. Vision. 2008;8:6, 1–13. doi: 10.1167/8.15.6. [DOI] [PubMed] [Google Scholar]
- Pack CC, Born RT. Temporal dynamics of a neural solution to the aperture problem in visual area MT of macaque brain. Nature. 2001;409:1040–1042. doi: 10.1038/35059085. [DOI] [PubMed] [Google Scholar]
- Sailer U, Flanagan JR, Johansson RS. Eye-hand coordination during learning of a novel visuomotor task. J. Neurosci. 2005;25:8833–8842. doi: 10.1523/JNEUROSCI.2658-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scarchilli K, Vercher JL, Gauthier GM, Cole J. Does the oculo-manual coordination control system use an internal model of the arm dynamics? Neurosci. Lett. 1999;265:139–142. doi: 10.1016/s0304-3940(99)00224-4. [DOI] [PubMed] [Google Scholar]
- Sims CR, Jacobs RA, Knill DC. Adaptive allocation of vision under competing task demands. J. Neurosci. 2011;31:928–943. doi: 10.1523/JNEUROSCI.4240-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, Majaj NJ, Movshon JA. Dynamics of motion signaling by neurons in macaque area MT. Nat. Neurosci. 2005;8:220–228. doi: 10.1038/nn1382. [DOI] [PubMed] [Google Scholar]
- Tramper JJ, Gielen CCAM. Visuomotor coordination is different for different directions in three-dimensional space. J. Neurosci. 2011;31:7857–7866. doi: 10.1523/JNEUROSCI.0486-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vercher JL, Quaccia D, Gauthier GM. Oculo-manual coordination control: respective role of visual and non-visual information in ocular tracking of self-moved targets. Exp. Brain. Res. 1995;103:311–322. doi: 10.1007/BF00231717. [DOI] [PubMed] [Google Scholar]
- Walter J, Ritter H. Local PSOMs and Chebyshev PSOMs—improving the parametrised self-organizing maps. Proc. Int. Conf. Artificia. Neural Networks (ICANN-95), Paris. 1995;1:95–102. [Google Scholar]
- Zambarbieri D, Schmid R, Magenes G, Prablanc C. Saccadic responses evoked by presentation of visual and auditory targets. Exp. Brain Res. 1982;47:417–427. doi: 10.1007/BF00239359. [DOI] [PubMed] [Google Scholar]