Abstract
Neuroimaging methods with enhanced spatial resolution such as functional magnetic resonance imaging (FMRI) suggest that the subcortical striatum plays a critical role in human reward processing. Analysis of FMRI data requires several preprocessing steps, some of which entail tradeoffs. For instance, while spatial smoothing can enhance statistical power, it may also bias localization towards regions that contain more gray than white matter. In a meta-analysis and reanalysis of an existing dataset, we sought to determine whether spatial smoothing could systematically bias the spatial localization of foci related to reward anticipation in the nucleus accumbens (NAcc). An Activation Likelihood Estimate (ALE) meta-analysis revealed that peak ventral striatal ALE foci for studies that used smaller spatial smoothing kernels (i.e. < 6 mm FWHM) were more anterior than those identified for studies that used larger kernels (i.e. > 7 mm FWHM). Additionally, subtraction analysis of findings for studies that used smaller versus larger smoothing kernels revealed a significant cluster of differential activity in the left relatively anterior NAcc (Talairach coordinates: −10, 9, −1). A second meta-analysis revealed that larger smoothing kernels were correlated with more posterior localizations of NAcc activation foci (p < 0.015), but revealed no significant associations with other potentially relevant parameters (including voxel volume, magnet strength, and publication date). Finally, repeated analysis of a representative dataset processed at different smoothing kernels (i.e., 0–12 mm) also indicated that smoothing systematically yielded more posterior activation foci in the NAcc (p < 0.005). Taken together, these findings indicate that spatial smoothing can systematically bias the spatial localization of striatal activity. These findings have implications both for historical interpretation of past findings related to reward processing and for the analysis of future studies.
Keywords: Nucleus Accumbens (NAcc), ventral striatum (VS), spatial smoothing, functional magnetic resonance imaging (fMRI), reward, monetary incentive delay (MID) task
1. Introduction
With the improved spatiotemporal resolution of neuroimaging methods such as functional magnetic resonance imaging or FMRI, researchers have become increasingly interested in visualizing activity in subcortical circuits related to reward processing (O’Doherty, 2004; Knutson and Cooper, 2005). Reward processing critically recruits a group of subcortical nuclei called the “striatum” (Haber & Knutson, 2010). The striatum is comprised of distinct components, which can be differentiated based on their structural, connectional, chemical, and functional properties. Ventromedial regions of the striatum, notably the nucleus accumbens (NAcc), receive dopaminergic projections from the ventral tegmental area of the midbrain and have been particularly implicated in reward processing (Kelley and Berridge, 2002; Wise, 2002; Robbins and Everitt, 1996). Both animal and human studies imply a functional gradient in the NAcc running from anterior to posterior, with anterior components involved specifically in reward processing and posterior components involved in more general motivational processing (Reynolds and Berridge, 2002; Seymour et al., 2007; Berns and Bell, 2012). With increasing spatial resolution afforded by FMRI, the potential for more specific functional localization grows.
While statistical techniques for analyzing FMRI data are designed to optimize statistical power, this may come at the cost of anatomical specificity. One such technique involves spatial smoothing, in which voxel activation values are integrated with neighboring voxel values through convolution with a spatial kernel (e.g., with a Gaussian profile). Investigators typically use spatial smoothing to reduce high-frequency and increase low-frequency activity components, so as to increase signal to noise ratio and compensate for functional and anatomical variation across subjects. In advocating these techniques, however, theorists have acknowledged potential trade-offs: “One knows from standard filtering theory that the ‘best’ smoothing filter or kernel is one that matches the objects to be identified…however…the theory of Gaussian random fields…only holds when the voxel size is appreciably smaller than smoothness.” (Worsley and Friston, 1995). By implication, if an investigator has no prior expectation that they will observe activity in small brain regions, then they may adopt larger spatial smoothing kernels in order to minimize the number of statistical tests applied to their data. However, if small regions are activated, large smoothing kernels may systematically bias or even obscure evidence of underlying activation (Friston et al., 1994).
Particularly in the case of subcortical nuclei implicated in reward processing, spatial smoothing could systematically alter the localization of activation foci. Specifically, the NAcc comprises a small tubelike structure that bilaterally extends from the sides to the center of the brain. While the anterior section of the NAcc is surrounded by white matter, the posterior section is surrounded by the gray matter of the neighboring striatal structures called the putamen and caudate. Gray matter content contributes significantly more to blood oxygen level dependent FMRI activity, since gray matter uses four times as much energy and contains considerably more veins than white matter (Logothetis and Wandell, 1994). Thus, given the greater proportion of gray to white matter in anterior versus posterior regions of the striatum (and surrounding the NAcc in particular), increased spatial smoothing might have the appearance of “moving” anterior activation foci into more posterior regions.
The goal of the current study was to determine whether differences in spatial smoothing could systematically bias the localization of reward related activity in the ventral striatum (and particularly the NAcc). Based on the greater contribution of white matter to voxel content in the anterior versus posterior NAcc, we predicted that spatial smoothing would “shift” activation foci from anterior to posterior in the striatum. To address this issue, we used two meta-analytic techniques to examine foci reported in several studies of reward processing. These studies were designed to elicit anticipation of monetary rewards and have been shown to robustly elicit NAcc activity several different laboratories, as exemplified by the monetary incentive delay or “MID” task (Knutson et al., 2000) and similar paradigms. To establish the specificity of the smoothing kernel’s influence on the localization of activation foci, we further reanalyzed an existing MID task dataset after systematically preprocessing that data with different smoothing kernels.
2. Materials and methods
2.1 Meta-analytic analyses
2.1.1 Study selection
For meta-analysis, we explored the BrainMap database using the Sleuth interface (v2.0, http://www.brainmap.org; Laird et al, 2005; Fox and Lancaster 2002; Fox et al, 2005; search date: 16 April 2012). Relevant FMRI studies were identified using the following search criteria: context “normal mapping” and paradigm class “reward task” (n = 160). From this set, a subset was identified that implemented the MID task or similar experimental manipulations that specifically elicited anticipation of financial reward. Studies were excluded if they did not list foci or isolate a contrast as “anticipation of monetary gain vs. anticipation of no gain” or use a similar label. To maintain homogeneity, contrasts of “anticipation of monetary gain vs. anticipation of monetary loss” were not included. Contrasts in studies of aging or psychiatric patients were only included for younger or control groups, respectively. One additional eligible study not in the BrainMap database but recommended by a reviewer was also included (Simon et al, 2010).
Data from the 23 studies that fit these criteria were subsequently submitted to meta-analyses (Table 1). Since the current comparison primarily focused on spatial smoothing, kernels were identified for each study (magnet strength and acquisition voxel volume were also identified). If a given study spatially smoothed both raw functional data and statistical maps (i.e. t or z maps), then an aggregate smoothing kernel was estimated with the following formula: Se = sqrt(Sa2 + Sb2), where Sa and Sb are the implicated smoothing kernels and Se is the aggregate smoothing kernel estimate. 22 of the 23 studies reported using Gaussian smoothing kernels specified in terms of mm of full width at half maximum (FWHM). One study (Knutson et al, 2001a) used root-mean square (RMS) smoothing, which was converted to FWHM using the following formula: FWHM = 1.359556*RMS (Analysis of Functional Neuroimages (AFNI) documentation: http://www.afni.nimh.nih.gov/).
Table 1.
Meta-analysis study data.
| Study | Subjects | Smoothing (FWHM mm) | Magnet strength (T) | Voxel Size (mm3) | Region Label | R/L coord (Tal mm) | A/P coord (Tal mm) | I/S coord (Tal mm) | Peak z-score |
|---|---|---|---|---|---|---|---|---|---|
| Abler et al. (2006) | 11 | 8.0 | 3 | 33.8 | VS | 9.3 | 8.7 | −7.4 | 4.12 |
| Abler et al. (2007) | 8 | 8.0 | 3 | 33.8 | VS | 7.3 | 12.5 | 5.6 | 3.74 |
| Adcock et al. (2006) | 12 | 4.0 | 3 | 59.2 | NAcc | 12.0 | 4.0 | 0.0 | 8.26 |
| Beck et al. (2009) | 19 | 8.0 | 1.5 | 52.8 | VS | 14.9 | 9.9 | 1.7 | 4.01 |
| Bjork et al. (2004) | 12 | 4.5 (4, 2) | 3 | 28.1 | NAcc | 12.0 | 19.0 | −1.0 | 7.75 |
| Bjork et al. (2008) | 13 | 4.0 | 3 | 28.2 | NAcc | 10.0 | 8.0 | −5.0 | 3.63 |
| Breiter et al. (2001) | 12 | 6.3 | 3 | 28.8 | VS/NAcc | 12.0 | 9.0 | 0.0 | 4.35 |
| Juckel et al. (2006) | 10 | 8.0 | 1.5 | 52.8 | VS/NAcc | 20.6 | 4.7 | 1.5 | 3.89 |
| Kirsch et al. (2003) | 27 | 6.0 | 1.5 | 45.0 | NAcc | 11.1 | 6.2 | 1.4 | 6.25 |
| Knutson et al. (2001a) | 8 | 5.4 | 1.5 | 53.4 | NAcc | 12.0 | 19.0 | −1 | 2.20 |
| Knutson et al. (2001b) | 9 | 5.7 (4, 4) | 1.5 | 98.4 | NAcc | 11.0 | 12.0 | 0.0 | 5.69 |
| Knutson et al. (2003) | 12 | 4.0 | 1.5 | 52.7 | NAcc | 11.0 | 12.0 | 0.0 | 5.11 |
| Knutson et al. (2004) | 8 | 4.5 (4, 2) | 3 | 28.1 | NAcc | 15.0 | 19.0 | 0.0 | 7.52 |
| Knutson et al. (2008) | 14 | 5.7 (4, 4) | 1.5 | 56.3 | NAcc | 10.0 | 11.0 | −1.0 | 5.89 |
| Preuschoff et al. (2006) | 19 | 8.0 | 3 | 32.3 | VS | 12.0 | 5.0 | −3.0 | 5.34 |
| Ramnani and Miall (2003) | 8 | 10.0 | 3 | 80.0 | Ventral pallidum | 13.7 | −0.3 | 8.1 | 3.31 |
| Samanez-Larkin et al. (2007) | 12 | 4.0 | 1.5 | 56.3 | VS/putamen | 13.0 | 11.0 | −3.0 | 3.63 |
| Simon et al. (2010) | 24 | 8.0 | 3 | 27.0 | VS | 13.0 | 1.6 | 1.3 | 4.54 |
| Schlagenhauf et al. (2008) | 10 | 8.9 (8, 4) | 1.5 | 52.8 | VS | 17.6 | 4.7 | 2.2 | 3.53 |
| Spreckelmeyer et al. (2009) | 32 | 6.0 | 1.5 | 53.4 | NAcc | 9.0 | 15 | 0.0 | 7.01 |
| Strohle et al. (2008) | 10 | 8.0 | 1.5 | 52.8 | VS | 17.7 | 9.7 | −0.9 | 3.52 |
| Wrase et al. (2007a) | 16 | 4.0 | 1.5 | 52.8 | VS | 15.7 | 9.2 | 1.4 | 4.80 |
| Wrase et al (2007b) | 14 | 6.0 | 1.5 | 52.8 | VS | 15.7 | 3.9 | 4.9 | 5.99 |
| Total studies: 23, total subjs: | 320 | Avg: 6.3 |
FWHM: Full width at half maximum; T: Tesla; VS: Ventral Striatum; NAcc: Nucleus Accumbens; R/L: Right/Left; A/P: Anterior/Posterior; I/S: Inferior/Superior; Tal: Talairach. In smoothing column, parenthetical numbers indicate distinct kernels used for data and statistical maps.
2.1.2 Activation Likelihood Estimate (ALE) meta-analysis
ALE meta-analysis was conducted using the BrainMap GingerALE software suite (v2.1, http://www.brainmap.org; Eickhoff et al. 2009; Turkeltaub et al, 2012; Eickhoff et al, 2012a; Eickhoff et al, 2011). ALE analysis represents foci from included contrasts as peaks of Gaussian functions, and models the probability of activation over all studies at each spatial point in the brain, returning localized “activation likelihood estimates” or ALE values. The number of subjects in a given study dictates the spatial extent of the Gaussian function used. ALE values are computed for each voxel by computing the likelihood that an activation focus lies in that voxel. The ALE values are then compared against a null distribution created from simulated datasets with randomly placed foci, and significantly activated clusters are identified. All analyses were conducted in the Talairach coordinate system. Foci originally reported in Montreal Neurological Institute coordinates were transformed into the Talairach coordinate system with the icbm2tal algorithm (Lancaster et al, 2007; Laird et al, 2010).
To compare the effects of smaller versus larger spatial smoothing kernels on foci localization, studies selected from the BrainMap database were separated into two groups: (1) those in which the spatial smoothing kernel used was less than 6 mm FWHM (i.e., “smaller;” n = 10); and (2) those in which the spatial smoothing kernel used was greater than 7 mm FWHM (i.e., “larger;” n = 9). Statistically thresholded ALE maps for each group were computed (FDR (q) = 0.001, minimum cluster size = 200 mm3), and peak NAcc foci were compared. ALE subtraction analysis was then conducted to directly compare localization of foci in smaller versus larger kernel groups (with FDR (q) = 0.01, minimum cluster size = 64 mm3; Eickhoff et al, 2012b). We then conducted a t-test to estimate the effect size of the difference between the anterior coordinates of foci for smaller versus larger groups.
2.1.3 Correlation analyses
From each of the 23 studies previously identified, peak foci coordinates associated with the NAcc were identified, and, if necessary, converted to Talairach coordinates (using icbm2tal). Magnet strength and acquisition voxel volume were also noted. In each study of interest, foci and z-scores were included if labeled as ventral striatum (VS), NAcc, VS/NAcc, VS/putamen, or ventral pallidum. In order to assess relationships between smoothing, peak z-score, magnet strength and foci coordinates, Pearson linear correlation coefficients were calculated. Bonferroni correction was used to correct for multiple comparisons across three spatial dimensions (i.e. critical alpha = 0.05/3 = 0.0167). If bilateral regions were identified in a given study, the largest absolute x coordinate, largest y coordinate, and largest z coordinate were included in the analyses. This procedure includes all identified studies in all analyses (i.e., each study reported at least one NAcc activation focus, though not every study reported bilateral NAcc activation foci). If a peak statistical value was originally reported as a t score, then it was converted to z-score by first assessing the p-value associated with the given t score using the degrees-of-freedom of the statistic (1 less than the number of subjects in the contrast) and the Student’s t probability function (function tpdf(); MATLAB, the Mathworks Inc.). Next, corresponding z-scores were identified using the normal probability density function (function normpdf();MATLAB, the Mathworks Inc.). Errors between t-value and z-score p-values were no greater than 0.00001.
2.2 Reanalysis of a common dataset
2.2.1 Subjects
Subjects consisted of a community sample of 22 healthy young adults (right-handed, English speaking, 16 female, age range = 21–45, age mean = 33.4 years, age SD =7.0). The data from these subjects was collected previously for a study of reward processing across the lifespan (Samanez-Larkin et al., 2010). Subjects were healthy (no self-reported history of psychiatric or neurological disorders, no current psychiatric or cardiac medication). Informed consent was obtained from all subjects, under approval by the Stanford University School of Medicine IRB. In addition to receiving $20/hour reimbursement, subjects received additional payment dependent on their performance on the Monetary Incentive Delay (MID) task.
2.2.2 Monetary incentive delay task
Subjects completed a version of the MID task (E-Prime, Pittsburgh PA) during fMRI acquisition (Knutson et al., 2000; Samanez-Larkin et al., 2007). After spoken and written instruction, subjects completed one practice session before experimental sessions were conducted in the scanner. Each trial consisted of viewing cues (2000 ms) first, which indicated incentive valence and magnitude (gain/loss, ±$0/0.5/5). Next a fixation cross appeared (“anticipation” phase; 2000–2500 ms), followed by a centrally presented target (150–500 ms). If the subject pressed a button before the target’s offset, then they either gained or avoided losing the cued monetary amount. The trial’s outcome then appeared (“outcome” phase; 2000 ms). Inter-trial intervals pseudorandomly varied from 2000–6000 ms. In total, subjects completed 180 fully randomized trials, including 30 repetitions of each of the 6 trial types. Subject performance was maintained by adaptively changing target durations within condition (performance goal = 66% correct). FMRI data acquisition was time-locked to cue and outcome presentation using a real-time drift correction algorithm.
2.2.3 MRI acquisition and analysis
FMRI data was collected with a 1.5T General Electric MRI scanner with quadrature head coil (General Electric, Milwaukee, WI). High-resolution structural scans were collected for spatial localization and co-registration of functional data (T1-weighted, spoiled gradient recalled acquisition in steady sequence; TR = 100 ms, TE = 7 ms, flip angle = 90°). Functional data was acquired with 24, 4 mm thick slices (in-plane resolution = 3.75 X 3.75 mm; no gap). The volume extended from midpons to the top of the skull, thus fully including the striatum. A T2*-sensitive in-out spiral pulse sequence that specifically reduced signal dropout at the base of the brain was used (TR = 2 s, TE = 40 ms, flip angle = 90°; Glover et al., 2001).
2.2.4 fMRI analysis
Analyses focused on the anticipation period (2000–2500 ms period post-cue and pre-target in which a fixation cross appeared) for gain trials (i.e. button press during the target period resulted in monetary reward). Analysis of Functional Neuroimages software (AFNI; http://afni.nimh.nih.gov/) was used for all fMRI analyses. Preprocessing included concatenation of runs, refitting and slice-timing correction, motion correction (using Fourier interpolation), spatial smoothing using a variable Gaussian kernel (variable -- see below), raw signal normalization to percent change (with reference to mean activation across the entire run), and high-pass filtering at 0.011 Hz. Seven different analyses were conducted at variable FWHM values of 0, 2, 4, 6, 8, 10, and 12 mm.
Preprocessed data from each subject were analyzed using a multiple regression model (Neter et al., 1996), which included fully orthogonal regressors contrasting gain (+$0.5/5) vs. non-gain (+$0) anticipation, loss (−$0.5/5) vs. non-loss (−$0) anticipation, gain (hit: +$0.5/5) vs. non-gain (miss: +$0.5/5) outcomes, and nonloss (hit: −$0.5/5) vs. loss (miss: −$0.5/5) outcomes. 2 additional orthogonal regressors highlighted periods of interest (anticipation/outcome), 6 described residual motion and 6 modeled baseline, linear, and quadratic trends. Regressors modeled activity during 2 s periods convolved with a prototypical hemodynamic response function (Cohen, 1997). Individual coefficient maps were warped to Talairach space and group level-t-tests were conducted voxel-by-voxel on gain vs. non-gain anticipation coefficients. Resulting t-statistic maps were then transformed to z-scores.
Relative maximum activation foci were manually identified. Relative maximum voxels exhibited larger z-scores than each facing voxel (i.e. not including cornering voxels). Selected voxels were constrained either to lie within, or to border the NAcc. The NAcc was defined superiorly by drawing a line from the tip of the internal capsule medially to the ventricle, laterally by drawing a line from the tip of the internal capsule inferiorly to the white matter, and posteriorly by the anterior commissure. All other edges were defined by white matter boundaries (Breiter et al., 1997; Knutson et al., 2008; see Figure 4, Panel H). The maximum value in the anterior/posterior (A/P) dimension was selected from either the left or right side for each analysis (n = 7). After the maximum A/P focus was identified, the slope of the line of best fit (least-squares) was calculated across their coordinates. This slope was compared in a permutation test to similar slopes calculated from 100,000 permuted datasets in which previously selected A/P coordinates were randomly assigned to a smoothing kernel. The proportion of slopes equally as large or larger was computed, resulting in an index of statistical significance (p-value).
Figure 4. Activation as a function of smoothing kernel.
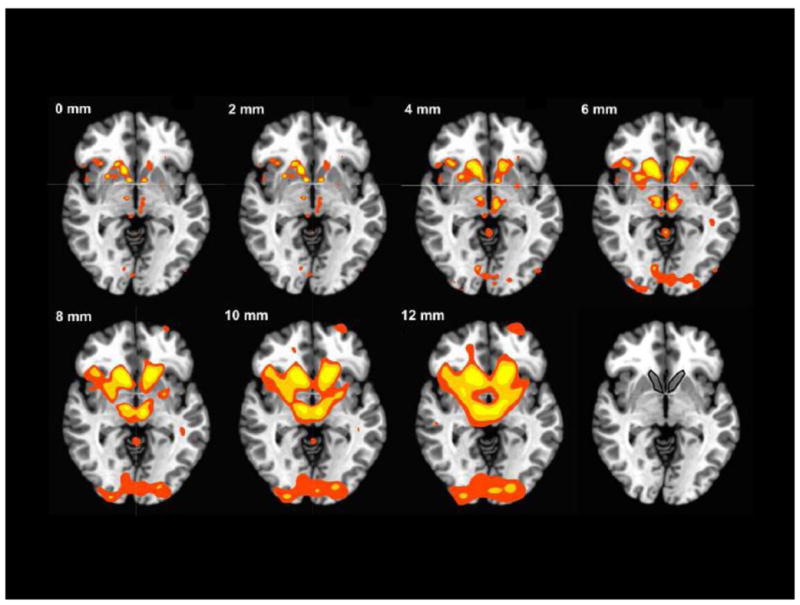
Axial slices at Z=−2; red: p < 0.001; orange: p < 0.0001; yellow: p < .00001, uncorrected; Numbers describe FWHM of smoothing kernels; NAcc volume of interest outlined in bottom right panel.
3. Results
3.1 ALE meta-analysis
ALE analysis of reward versus nonreward anticipation activity in the “smaller” smoothing kernel group (< 6 mm; foci = 103, experiments = 10, number of subjects = 116) revealed two significant activation likelihood clusters, the larger with relative maxima in left NAcc, right NAcc, and right thalamus (Table 2). ALE analysis of reward versus nonreward anticipation activity in the “larger” smoothing kernel group (> 7 mm;” foci = 86, experiments = 9, subjects = 119) revealed significant activation likelihood clusters in right NAcc and left putamen (Table 2). Both right and left NAcc foci in the smaller group were anterior to corresponding right NAcc and left putamen foci in the larger group (right Talairach anterior coordinate: 8 mm vs. 4 mm, left Talairach anterior coordinate: 10 mm vs. 6 mm).
Table 2.
Activation Likelihood Estimate clusters and corresponding foci for smaller and larger smoothing kernel studies.
| Region | ALE (X10−3) | R/L (Tal mm) | A/P (Tal mm) | S/I (Tal mm) |
|---|---|---|---|---|
| < 6 mm FWHM | ||||
| Left NAcc* | 56.3 | −12 | 10 | −2 |
| Right NAcc* | 52.6 | 10 | 8 | 2 |
| Right Thalamus* | 22.4 | 2 | −8 | 12 |
| Right Anterior Insula | 20.8 | 32 | 18 | 0 |
| > 7 mm FWHM | ||||
| Right NAcc | 27.9 | 12 | 4 | 0 |
| Left Putamen | 23.7 | −16 | 6 | 0 |
| < 6 mm FWHM minus > 7 mm FWHM | ||||
| Left NAcc | 354.0 | −10 | 9 | −1 |
FWHM: Full width at half maximum; NAcc: Nucleus Accumbens; ALE: Activation Likelihood Estimate; R/L: Right/Left; A/P: Anterior/Posterior; S/I: Superior/Inferior; Tal: Talairach coordinate;
focus is a relative maximum in a single cluster.
Further, an ALE subtraction analysis comparing activity in the smaller versus the larger group revealed one significant cluster in left NAcc (Table 2). This cluster appeared anterior and medial to the left putamen activation focus identified in the larger group (Figure 1; larger cluster focus at Talairach coordinates −10, 9 −1). Additionally, a t-test of the most anterior foci in the smaller group versus the larger group indicated a significant difference in anterior localization (t(17)=2.87; p<.02), with a large effect size (Cohen’s d = 1.31). Significant violations of normality were not apparent, and nonparametric tests revealed similar significant associations.
Figure 1. ALE meta-analytic comparison.
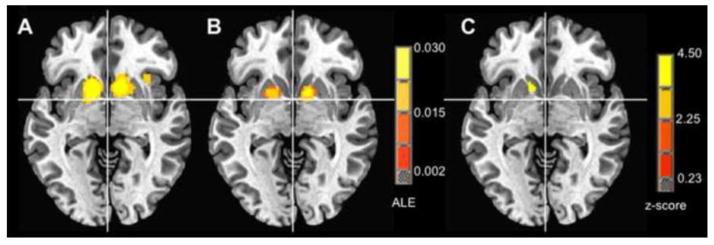
Ventral striatum (z = −3): A) < 6 mm spatial smoothing, B) > 7 mm spatial smoothing, C) ALE subtraction analysis, < 6 mm minus > 7 mm spatial smoothing.
3.2 Anterior foci identification
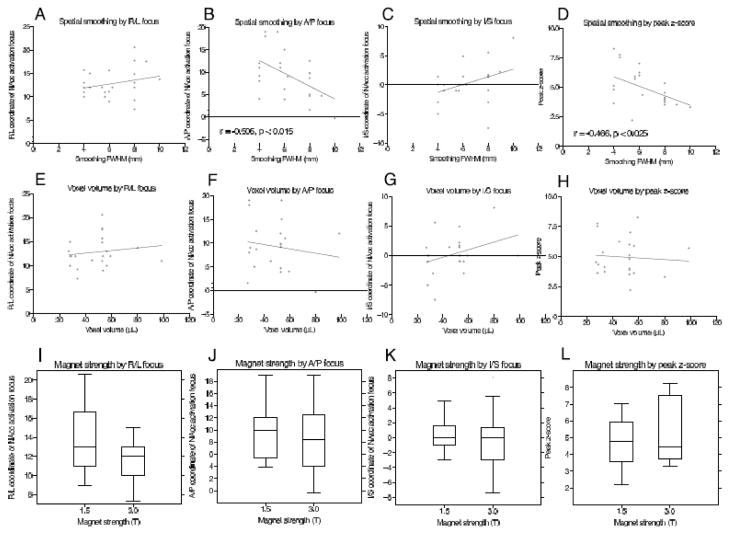
Of the 23 studies identified, 9 labeled activation foci in the ventral striatum (VS), with 10 labeled in the nucleus accumbens (NAcc), 2 in ventral striatum/nucleus accumbens (VS/NAcc), 1 in ventral striatum/putamen (VS/putamen), and 1 in ventral pallidum (Table 1). These studies included a combined total of 320 subjects, and utilized smoothing kernels ranging from 4 to 10 mm FWHM. Correlation analyses revealed significant negative associations of spatial smoothing kernel with the anterior localization of ventral striatal activation foci (Pearson’s r = −0.51, p < 0.015; Figure 2B) and peak voxel z-score (Pearson’s r = −0.47, p < 0.025; Figure 2D). In contrast, voxel volume at acquisition, magnet strength and publication date were not associated with any localization parameters (Figure 2E–L).
Figure 2. Meta-analytic association of ventral striatal activation foci characteristics with preprocessing and experimental parameters.
Significant values indicate univariate correlations (Pearson r; Panels A–H) or two sample t-tests (Panels I–L).
3.3 Data reprocessing at different smoothing kernels
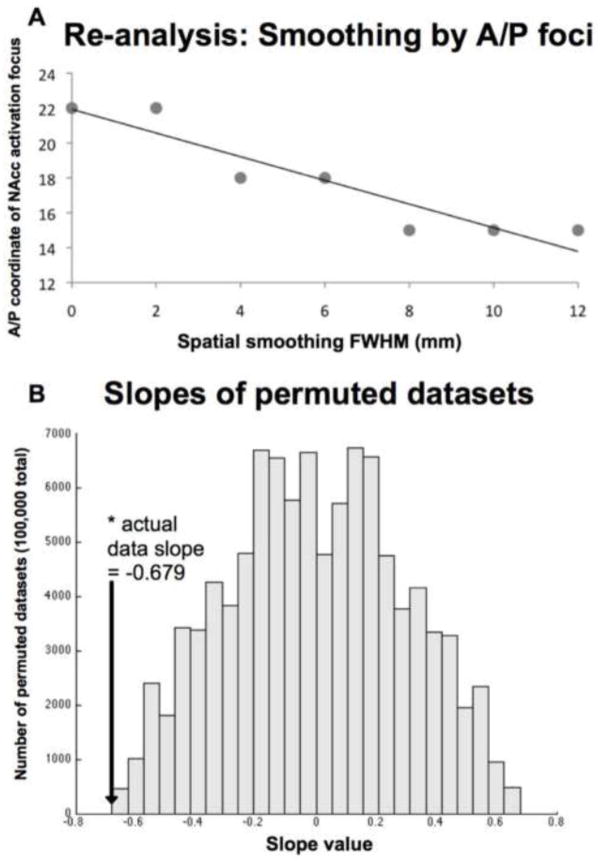
Activation foci were identified from datasets that were preprocessed using 0, 2, 4, 6, 8, 10, and 12 mm FWHM smoothing kernels (Supplementary Table 1). The non-parametric permutation test revealed a significant negative association of spatial smoothing kernel size with the anterior versus posterior localization of the most anterior activation foci (p < 0.005). Horizontal slice images at z = −2 suggested that increasingly large smoothing kernels reduced spatial resolution and merged activation foci (but also increased peak z-scores in some cases; Figure 4).
4. Discussion
We investigated whether spatial smoothing could systematically bias the localization of subcortical activation during reward anticipation. In both analyses of existing reports in the literature and in a single reprocessed dataset, increasing spatial smoothing “shifted” activation foci posteriorly in the ventral striatum (particularly in the NAcc). Specifically, an ALE meta-analysis of FMRI studies of reward anticipation indicated that increasing the smoothing kernel shifted peak ALE foci back in the striatum. Specifically, smoothing kernel size was significantly associated with posterior displacement of activation foci, and direct comparison of studies involving smaller (< 6 mm) versus larger (> 7 mm) smoothing kernels verified this posterior displacement. Notably, foci in the left of the striatum not only shifted posteriorly, but also across regions from the nucleus accumbens to the putamen. Further, repeated analysis of the same dataset reprocessed at increasing levels of smoothing also indicated a posterior shift in activation foci.
These findings are consistent with the prediction that increasing smoothing kernel size can shift apparent activation foci from regions including minimal gray matter to those with denser gray matter composition. By comparison, shifts in other directions (e.g., superior-inferior or right-left) were not significant. Other potentially relevant parameters showed no significant association with localization (e.g., voxel size, magnet strength, year of publication). An additional variable that might significantly influence investigators’ ability to detect activation in small subcortical regions involves the choice of a cluster criterion for significance. For instance, as defined in this study, the NAcc in a standard Talairach-warped brain encompasses approximately 600 mm3 (i.e., approximately nine four-mm cubic voxels; see also Neto et al., 2008). By definition, any cluster criterion that exceeds approximately 600 mm3 should preclude detection of localized activity in the NAcc. All of the studies reviewed in this meta-analysis used smaller (or no) cluster criteria, but larger cluster criteria are commonly adopted in the literature. Together, these meta-analytic findings suggest a potential for bias in the literature related to emotion and incentive processing, particularly in reviews that do not statistically account for spatial preprocessing parameters (e.g., Lindquist et al., 2012; Chase et al., 2011; Liu et al., 2011; Knutson and Greer, 2008).
Other untested parameters, however, might also contribute to the observed meta-analytic association of smoothing kernel size with posterior localization. To control for potential confounds, we repeatedly analyzed an existing dataset with known activation during reward versus nonreward anticipation after preprocessing it with different degrees of spatial smoothing. Consistent with meta-analytic findings, increasing the smoothing kernel moved apparent activation foci posterior in the NAcc, and even outside that structure into the neighboring putamen. Visual inspection of activation foci suggested that this “shift” may be more attributable to omitting anterior foci than to perturbing the locale of more posterior foci. Fortunately, these collected findings suggest a simple solution -- using smaller smoothing kernels (e.g., 4 mm FWHM or less) should minimize displacement in studies of reward processing. Future statistical methods might provide more sophisticated smoothing algorithms that can account for variable gray and white matter composition in different voxels, as well as for edges between gray and white matter (Walker et al., 2006; Yue et al., 2010).
Since the genesis of fMRI, investigators have cautioned investigators about the necessary trade-off between spatial smoothing and statistical power (Friston et al., 1994). Over the past decade, however, most investigators have opted for statistical power over spatial localization, perhaps due to the default settings of many statistical analysis packages. Other early reviews have theoretically considered the influence of spatial smoothing on cortical localization (Worsely and Friston 1995; Aguirre et al., 1997). Subcortical structures, however, have distinct idiosyncrasies, including small and irregular gray matter structure as well as variable white matter boundaries. Consistent with animal studies, these subcortical regions have increasingly been implicated in incentive processing, which holds potential relevance for the diagnosis and treatment of psychiatric disorders (e.g., Schumann et al., 2010). Thus, a combination of technological advances and health relevance has increased the need for more accurate localization of subcortical activity, and calls for a reevaluation of the tradeoff between spatial localization and statistical power.
While we have focused on spatial smoothing, other parameters related to localization deserve further scrutiny (e.g., cluster size, temporal resolution). Although understandable based on purely statistical considerations, the current meta-analytic findings suggest that use of large spatial smoothing kernels both persists in the literature and can bias localization. Consistent with the predicted trade-off, spatial smoothing increased the strength of activation foci in regions dense with gray matter in the meta-analytic results, and possibly in the reanalyzed dataset (if one includes foci outside the NAcc). However, the increasing strength and homogeneity of scanning techniques may eventually obviate the need to boost power with statistical techniques, preserving spatial localization without sacrificing detectability. Since we focused on circuits relevant to incentive processing, the present findings may apply more to subcortical than cortical regions. By extension, other subcortical circuits (e.g., the hippocampus or ventral tegmental area) may also be subject to these types of biases and thus deserve similar consideration.
5. Conclusions
These findings indicate that spatial smoothing may systematically bias the localization of subcortical activity related to incentive processing. They suggest caution in interpreting past literature (based on preprocessing parameters) and imply that investigators should apply minimal smoothing in future studies of incentive processing.
Supplementary Material
Figure 3. Re-analyses of dataset indicating relationship of anterior coordinate to spatial smoothing kernel.
Most anterior NAcc activation foci by smoothing kernel, with line of best fit (Panel A); Significance of slope plotted against distribution of permuted slopes (Panel B).
Acknowledgments
We thank Travis Alvarez and Kiefer Katovich for help with data acquisition and analysis, as well as Charlene Wu and Katja Spreckelmeyer for feedback on earlier drafts. This research was supported by NSF: GRFP DGE-1147470 to MS, and NSF Grant 0748915 to BK.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Matthew D. Sacchet, Email: msacchet@stanford.edu.
Brian Knutson, Email: knutson@psych.stanford.edu.
References
- Abler B, Walter H, Erk S, Kammerer H, Spitzer M. Prediction error as a linear function of reward probability is coded in human nucleus accumbens. Neuroimage. 2006;31:790–795. doi: 10.1016/j.neuroimage.2006.01.001. [DOI] [PubMed] [Google Scholar]
- Abler B, Erk S, Walter H. Human reward system activation is modulated by a single dose of olanzapine in healthy subjects in an event-related, double-blind placebo-controlled fMRI study. Psychopharmacology. 2007;191:823–933. doi: 10.1007/s00213-006-0690-y. [DOI] [PubMed] [Google Scholar]
- Adcock RA, Thangavel A, Whitfield-Gabrieli S, Knutson B, Gabrieli JDE. Reward-motivated learning: mesolimbic activation precedes memory formation. Neuron. 2006;50:507–517. doi: 10.1016/j.neuron.2006.03.036. [DOI] [PubMed] [Google Scholar]
- Aguirre GK, Zarahn E, D’Esposito M. Empirical analyses of BOLD fMRI statistics: II. Spatially smoothed data collected under null-hypothesis and experimental conditions. Neuroimage. 1997;5:199–212. doi: 10.1006/nimg.1997.0264. [DOI] [PubMed] [Google Scholar]
- Beck A, Schlagenhauf F, Wustenberg T, Hein J, Kienast T, Kahnt T, Schmack K, Hagele C, Knutson B, Heinz A, Wrase J. Ventral striatal activation during reward anticipation correlates with impulsivity in alcoholics. Biol Psychiatry. 2009;66:734–742. doi: 10.1016/j.biopsych.2009.04.035. [DOI] [PubMed] [Google Scholar]
- Berns GS, Bell E. Striatal topography of probability and magnitude for decisions under uncertainty. Neuroimage. 2012;59:3166–3172. doi: 10.1016/j.neuroimage.2011.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bjork JM, Knutson B, Font GW, Caggiano DM, Bennett SM, Hommer DW. Incentive-elicited brain activation in adolescents: Similarities and differences from young adults. J Neurosci. 2004;24:1793–1802. doi: 10.1523/JNEUROSCI.4862-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bjork JM, Knutson B, Hommer DW. Incentive-elicited striatal activation in adolescent children of alcoholics. Addiction. 2008;103:1308–1319. doi: 10.1111/j.1360-0443.2008.02250.x. [DOI] [PubMed] [Google Scholar]
- Breiter HC, Aharon I, Kahneman D, Dale AM, Shizgal P. Functional imaging of neural responses to expectancy and experience of monetary gains and losses. Neuron. 2001;30:619–639. doi: 10.1016/s0896-6273(01)00303-8. [DOI] [PubMed] [Google Scholar]
- Breiter HC, Gollub RL, Weisskoff RM, Kneedey DN, Berke JD, Goodman JM, Kantor HL, Gastfriend DR, Riorden JP, Mathew RT, Rosen BR, Hyman SE. Acute effects of cocaine on human brain activity and emotion. Neuron. 1997;19:591–611. doi: 10.1016/s0896-6273(00)80374-8. [DOI] [PubMed] [Google Scholar]
- Chase HW, Eickhoff SB, Laird AR, Hogarth L. The neural basis of drug stimulus processing and craving: An activation likelihood estimation meta-analysis. Biol Psychiatry. 2011;70:785–793. doi: 10.1016/j.biopsych.2011.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MS. Parametric analysis of fMRI data using linear systems methods. Neuroimage. 1997;6:93–103. doi: 10.1006/nimg.1997.0278. [DOI] [PubMed] [Google Scholar]
- Eickhoff SB, Laird AR, Grefkes C, Wang LE, Zilles K, Fox PT. Coordinate-based activation likelihood estimation meta-analysis of neuorimaging data: A random-effects approach based on empirical estimates of spatial uncertainty. Hum Brain Mapp. 2009;30:2907–2926. doi: 10.1002/hbm.20718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickhoff SB, Bzdok D, Laird AR, Roski C, Caspers S, Zilles K, Fox PT. Co-activation patterns distinguish cortical modules, their connectivity and functional differentiaion. Neuroimage. 2011;57:938–949. doi: 10.1016/j.neuroimage.2011.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickhoff SB, Bzdok D, Laird AR, Kurth F, Fox PT. Activation likelihood estimation revisited. Neuroimage. 2012a;59:2349–2361. doi: 10.1016/j.neuroimage.2011.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickhoff SB, Bzdok D, Laird AR, Kurth F, Fox PT. Co-activation patterns distinguish cortical modules, their connectivity and functional differentiation. Neuroimage. 2012b;57:938–949. doi: 10.1016/j.neuroimage.2011.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox PT, Lancaster JL. Mapping context and content: The BrainMap model. Nat Rev Neurosci. 2002;3:319–321. doi: 10.1038/nrn789. [DOI] [PubMed] [Google Scholar]
- Fox PT, Laird AR, Fox SP, Fox M, Uecker AM, Crank M, Koenig SF, Lancaster JL. BrainMap taxonomy of experimental design: Description and evaluation. Hum Brain Mapp. 2005;25:185–198. doi: 10.1002/hbm.20141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Worsley KJ, Frackowiak RSJ, Mazziotta JC, Evans AC. Assessing the significance of focal activations using their spatial extent. Hum Brain Mapp. 1994;1:214–220. doi: 10.1002/hbm.460010306. [DOI] [PubMed] [Google Scholar]
- Glover GH, Law CS. Spiral-in/out BOLD fMRI for increased SNR and reduced susceptibility artifacts. Magn Reson Med. 2001;46:515–522. doi: 10.1002/mrm.1222. [DOI] [PubMed] [Google Scholar]
- Haber S, Knutson B. The reward circuit: Linking primate anatomy and human imaging. Neuropsychopharmacology. 2010;35:4–26. doi: 10.1038/npp.2009.129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Juckel G, Schlagenhauf F, Koslowski M, Wustenberg W, Villringer A, Knutson B, Wrase J, Heinz A. Dysfunction of ventral striatal reward prediction in schizophrenia. Neuroimage. 2006;29:409–416. doi: 10.1016/j.neuroimage.2005.07.051. [DOI] [PubMed] [Google Scholar]
- Kelley AE, Berridge KC. The neuroscience of natural rewards: Relevance to addictive drugs. J Neurosci. 2002;22(9):3306–3311. doi: 10.1523/JNEUROSCI.22-09-03306.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirsch P, Schienle A, Stark R, Sammer G, Blecker C, Walter B, Ott U, Burkart J, Vaitl D. Anticipation of reward in a noninvasive differential conditioning paradigm and the brain reward system: An event-related fMRI study. Neuroimage. 2003;20:1086–1095. doi: 10.1016/S1053-8119(03)00381-1. [DOI] [PubMed] [Google Scholar]
- Knutson B, Westdorp A, Kaiser E, Hommer D. FMRI visualization of brain activity during a monetary incentive delay task. Neuroimage. 2000;12:20–27. doi: 10.1006/nimg.2000.0593. [DOI] [PubMed] [Google Scholar]
- Knutson B, Adams CM, Fong GW, Hommer D. Anticipation of increasing monetary reward selectivity recruits nucleus accumbens. J Neurosci. 2001a;21:1–5. doi: 10.1523/JNEUROSCI.21-16-j0002.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knutson B, Fong GW, Adams CM, Varner JL, Hommer D. Dissociation of reward anticipation and outcome with event-related fMRI. Neuroreport. 2001b;12:3683–3687. doi: 10.1097/00001756-200112040-00016. [DOI] [PubMed] [Google Scholar]
- Knutson B, Fong GW, Bennett SM, Adams CM, Hommer D. A region of the mesial prefrontal cortex tracks monetarily rewarding outcomes: Characterization with rapid event-related fMRI. Neuroimage. 2003;18:263–272. doi: 10.1016/s1053-8119(02)00057-5. [DOI] [PubMed] [Google Scholar]
- Knutson B, Bjork JM, Fong GW, Hommer D, Mattay VS, Weinberger DR. Amphetamine modulates human incentive processing. Neuron. 2004;43:261–269. doi: 10.1016/j.neuron.2004.06.030. [DOI] [PubMed] [Google Scholar]
- Knutson B, Cooper JC. Functional magnetic resonance imaging of reward prediction. Curr Opin Neurobiol. 2005;18:411–417. doi: 10.1097/01.wco.0000173463.24758.f6. [DOI] [PubMed] [Google Scholar]
- Knutson B, Bhanji JP, Cooney RE, Atlas LY, Gotlib IH. Neural responses to monetary incentives in major depression. Biol Psychiatry. 2008;63:686–692. doi: 10.1016/j.biopsych.2007.07.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knutson B, Delgado MR, Phillips PEM. Representation of subjective value in the striatum. In: Glimcher PW, Camerer CF, Fehr E, Poldrack RA, editors. Neuroeconomics: Decision making and the brain. Oxford: Oxford University Press; 2008. pp. 389–406. [Google Scholar]
- Knutson B, Greer SM. Anticipatory affect: Neural correlates and consequences for choice. Philos Trans R Soc Lond B. 2008;363:3771–3786. doi: 10.1098/rstb.2008.0155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird AR, Lancaster JL, Fox PT. BrainMap: The social evolution of a functional neuorimaging database. Neuroinformatics. 2005;3:65–78. doi: 10.1385/ni:3:1:065. [DOI] [PubMed] [Google Scholar]
- Laird AR, Robinson JL, McMillan KM, Tordesillas-Gutierrez D, Moran ST, Gonzales SM, Ray KL, Franklin C, Glahn DC, Fox PT. Comparison of the disparity between Talairach and MNI coordinates in functional neuorimaging data: Validation of the Lancaster transform. Neuroimage. 2010;51:677–683. doi: 10.1016/j.neuroimage.2010.02.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lancaster JL, Tordesillas-Gutierrez D, Martinez M, Salinas F, Evans A, Zilles K, Mazziotta JC, Fox PT. Bias between MNI and Talairach coordinates analyzed using the ICBM-152 brain template. Hum Brain Mapp. 2007;28:1194–1205. doi: 10.1002/hbm.20345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindquist KA, Wager TD, Kober H, Bliss-Moreau E, Barrett LF. Behav Brain Sci. 2012;35:121–202. doi: 10.1017/S0140525X11000446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Hairston J, Schreir M, Fan J. Common and distinct networks underlying reward valence and processing stages: A meta-analysis of functional neuorimaging studies. Neurosci Biobehav Rev. 2011;35:1219–1236. doi: 10.1016/j.neubiorev.2010.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK, Wandell BA. Interpreting the BOLD signal. Annu Rev Phsiol. 1994;66:735–769. doi: 10.1146/annurev.physiol.66.082602.092845. [DOI] [PubMed] [Google Scholar]
- Neter J, Kutner MH, Nachtsheim CJ, Wasserman W. Applied linear statistical models. Irwin; Chicago, USA: 1996. [Google Scholar]
- Neto LL, Oliveira E, Correia F, Ferreira AG. The human nucleus accumbens: Where is it? A stereotactic, anatomical, and magnetic resonance imaging study. Neuromodulation. 2008;11(1):13–22. doi: 10.1111/j.1525-1403.2007.00138.x. [DOI] [PubMed] [Google Scholar]
- O’Doherty JP. Reward representations and reward-related learning in the human brain: Insights from neuorimaging. Curr Opin Neurobiol. 2004;14(6):769–776. doi: 10.1016/j.conb.2004.10.016. [DOI] [PubMed] [Google Scholar]
- Preuschoff K, Bossaerts P, Quartz SR. Neural differentiation of expected reward and risk in human subcortical structures. Neuron. 2006;51:381–390. doi: 10.1016/j.neuron.2006.06.024. [DOI] [PubMed] [Google Scholar]
- Ramnani N, Miall RC. Instructed delay activity in the human prefrontal cortex is modulated by monetary reward expectation. Cereb Cortex. 2003;13:318–327. doi: 10.1093/cercor/13.3.318. [DOI] [PubMed] [Google Scholar]
- Reynolds SM, Berridge KC. Positive and negative motivation in nucleus accumbens shell: Bivalent rostrocaudal gradients for GABA-elicited, taste “liking”/“disliking” reactions, place preference/avoidance, and fear. J Neurosci. 2002;22(16):7308–7320. doi: 10.1523/JNEUROSCI.22-16-07308.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robbins TW, Everitt BJ. Neurobehavioural mechanisms of reward and motivation. Curr Opin Neurobiol. 1996;6(2):228–236. doi: 10.1016/s0959-4388(96)80077-8. [DOI] [PubMed] [Google Scholar]
- Samanez-Larkin GR, Gibbs SEB, Khanna K, Nielsen L, Carstensen LL, Knutson B. Anticipation of monetary gain but not loss in healthy older adults. Nat Neurosci. 2007;10:787–791. doi: 10.1038/nn1894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samanez-Larkin GR, Kuhnen CM, Yoo DJ, Knutson B. Variability in nucleus accumbens activity mediates age-related suboptimal financial risk taking. J Neurosci. 2010;30:1426–1434. doi: 10.1523/JNEUROSCI.4902-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlagenhauf F, Juckel G, Koslowski M, Kahnt T, Knutson B, Dembler T, Kienast T, Gallinat J, Wrase J, Heinz A. Reward system activation in schizophrenic patients switched from typical neuroleptics to olanzapine. Psychopharmacology. 2008;196:673–684. doi: 10.1007/s00213-007-1016-4. [DOI] [PubMed] [Google Scholar]
- Schumann G, Loth E, Banaschewski T, Barbot A, Barker G, Buchel C, Conrad PJ, Dalley JW, Flor H, Gallinat J, Garavan H, Heinz A, Itterman B, Lathrop M, Mallik C, Mann K, Martinot JL, Paus T, Poline JB, Robbins TW, Rietschel M, Reed L, Smolka M, Spanagel R, Speiser C, Stephens DN, Strohle A, Struve M IMAGEN consortium. The IMAGEN study: reinforcement-related behaviour in normal brain function and psychopathology. Mol Psychiatry. 2010;15:1128–1139. doi: 10.1038/mp.2010.4. [DOI] [PubMed] [Google Scholar]
- Seymour B, Daw N, Dayan P, Singer T, Dolan R. Differential encoding of losses and gains in the human striatum. J Neurosci. 2007;27(18):4826–4831. doi: 10.1523/JNEUROSCI.0400-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon JJ, Walther S, Fiebach CJ, Friederich HC, Stippich C, Weisbrod M, Kaiser S. Neural reward processing is modulated by approach- and avoidance-realted personality traits. Neuroimage. 2010;49:18688–1874. doi: 10.1016/j.neuroimage.2009.09.016. [DOI] [PubMed] [Google Scholar]
- Spreckelmeyer KN, Krach S, Kohls G, Rademacher L, Irmak A, Konrad K, Kircher T, Grunder G. Anticipation of monetary and social reward differently activates mesolimbic brain structures in men and women. Soc Cogn Affect Neurosci. 2009;4:158–165. doi: 10.1093/scan/nsn051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strohle A, Stoy M, Wrase J, Schwarzer S, Schlagenhauf F, Huss M, Hein J, Nedderhut A, Neumann B, Gregor A, Juckel G, Knutson B, Lehmkuhl U, Bauer M, Heinz A. Reward anticipation and outcomes in males with attention-deficit/hyperactivity disorder. Neuroimage. 2008;39:966–972. doi: 10.1016/j.neuroimage.2007.09.044. [DOI] [PubMed] [Google Scholar]
- Turkeltaub PE, Eichhoff SB, Laird AR, Fox M, Wiener M, Fox P. Minimizing within-experiment and within-group effects in activation likelihood estimation meta-analyses. Hum Brain Mapp. 2012;33:1–13. doi: 10.1002/hbm.21186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker SA, Miller D, Tanabe J. Bilateral spatial filtering: Refining methods for localizing brain activation in the presence of parenchymal abnormalities. Neuroimage. 2006;33:564–569. doi: 10.1016/j.neuroimage.2006.06.051. [DOI] [PubMed] [Google Scholar]
- Wise RA. Brain reward circuity: Insights from unsensed incentives. Neuron. 2002;36:229–240. doi: 10.1016/s0896-6273(02)00965-0. [DOI] [PubMed] [Google Scholar]
- Worsley KJ, Friston KJ. Analysis of fMRI time-series revisited—again. Neuroimage. 1995;2(3):173–181. doi: 10.1006/nimg.1995.1023. [DOI] [PubMed] [Google Scholar]
- Wrase J, Schlagenhauf F, Kienast T, Wustenberg T, Bermpohl F, Kahnt T, Beck A, Strohle A, Juckel G, Knutson B, Heinz A. Dysfunction of reward processing correlates with alcohol craving in detoxified alcoholics. Neuroimage. 2007a;35:787–794. doi: 10.1016/j.neuroimage.2006.11.043. [DOI] [PubMed] [Google Scholar]
- Wrase J, Kahnt T, Schlagenhauf F, Beck A, Cohen MX, Knutson B, Heinz A. Different neural systems adjust motor behavior in response to reward and punishment. Neuroimage. 2007b;36:1253–1262. doi: 10.1016/j.neuroimage.2007.04.001. [DOI] [PubMed] [Google Scholar]
- Yue Y, Loh JM, Lindquiest MA. Adaptive spatial smoothing of fMRI images. Stat Interface. 2010;3:3–13. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.