Accurate SHAPE-directed RNA secondary structure modeling, including pseudoknots

Abstract

A pseudoknot forms in an RNA when nucleotides in a loop pair with a region outside the helices that close the loop. Pseudoknots occur relatively rarely in RNA but are highly overrepresented in functionally critical motifs in large catalytic RNAs, in riboswitches, and in regulatory elements of viruses. Pseudoknots are usually excluded from RNA structure prediction algorithms. When included, these pairings are difficult to model accurately, especially in large RNAs, because allowing this structure dramatically increases the number of possible incorrect folds and because it is difficult to search the fold space for an optimal structure. We have developed a concise secondary structure modeling approach that combines SHAPE (selective 2′-hydroxyl acylation analyzed by primer extension) experimental chemical probing information and a simple, but robust, energy model for the entropic cost of single pseudoknot formation. Structures are predicted with iterative refinement, using a dynamic programming algorithm. This melded experimental and thermodynamic energy function predicted the secondary structures and the pseudoknots for a set of 21 challenging RNAs of known structure ranging in size from 34 to 530 nt. On average, 93% of known base pairs were predicted, and all pseudoknots in well-folded RNAs were identified.

RNA constitutes the central information conduit in biology (1). Information is encoded in an RNA molecule at two levels: in its primary sequence and in its ability to form higher-order secondary and tertiary structures. Nearly all RNAs can fold to form some secondary structure and, in many RNAs, highly structured regions encode important regulatory motifs. Such structured regulatory elements can be composed of canonical base pairs but may also feature specialized and distinctive RNA structures. Among the best characterized of these specialized structures are RNA pseudoknots. Pseudoknots are relatively rare but occur overwhelmingly in functionally important regions of RNA (2–4). For example, all of the large catalytic RNAs contain pseudoknots (5, 6); roughly two-thirds of the known classes of riboswitches contain pseudoknots that appear to be essential for ligand binding and gene regulatory functions (7); and pseudoknots occur prominently in the regulatory elements that viruses use to usurp cellular metabolism (3). Pseudoknots are thus harbingers of biological function. An important and challenging goal is to identify these structures reliably.

Pseudoknots are excluded from the most widely used algorithms that model RNA secondary structure (8). This exclusion is based on the challenge of incorporating the pseudoknot structure into the efficient dynamic programming algorithm used in the most popular secondary structure prediction approaches and because of the additional computational effort required. The prediction of lowest free energy structures with pseudoknots is NP-complete (9), which means that lowest free energy structure cannot be solved as a function of sequence length in polynomial time. In addition, allowing pseudoknots greatly increases the number of (incorrect) helices possible and tends to reduce secondary structure prediction accuracies, even for RNAs that include pseudoknots. Current algorithms also have high false-positive rates for pseudoknot prediction, necessitating extensive follow-up testing and analysis of proposed structures.

Pseudoknot prediction is challenging, in part, for the same reasons that RNA secondary structure prediction is difficult. First, energy models for loops are incomplete because they extrapolate from a limited set of experiments. Second, folding can be affected by kinetic, ligand-mediated, tertiary, and transient interactions that are difficult or impossible to glean from the sequence. Prediction is also difficult for a third reason unique to pseudoknots: Energy models for pseudoknot formation are generally incomplete because the factors governing their stability are not fully understood (10–12). The result is that current algorithms that model pseudoknots predict the base pairs in the simplest pseudoknots (termed H-type, formed when bases in a loop region bind to a single-stranded region), when the beginning and end of the pseudoknotted structure are known, with accuracies of only about 75% (10). Secondary structure prediction is much less accurate for full-length biological RNA sequences, with as few as 5% of known pseudoknotted pairs predicted correctly and with more false-positive than correct pseudoknot predictions in some benchmarks (13).

The accuracy of secondary structure prediction is improved dramatically by including experimental information as restraints (14, 15). Selective 2′-hydroxyl acylation analyzed by primer extension (SHAPE) probing data have proved especially useful in yielding robust working models for RNA secondary structure (15, 16). In essence, inclusion of SHAPE information provides an experimental adjustment to the well-established, nearest-neighbor model parameters (17) for RNA folding. This adjustment is implemented as a simple pseudo-free energy change term, ∆G°_SHAPE. SHAPE reactivities are approximately inversely proportional to the probability that a given nucleotide is base paired (high reactivities correspond to a low likelihood of being paired and vice versa) and the logarithm of a probability corresponds to an energy, in this case ∆G°_SHAPE, which has the form

The slope, m, corresponds to a penalty for base pairing that increases with the experimental SHAPE reactivity, and the intercept, b, reflects a favorable pseudo-free energy change term for base pairing at nucleotides with low SHAPE reactivities. These two parameters must be determined empirically. This pseudo-free energy change approach yields high-quality secondary structure models for both short RNAs and those that are kilobases long (15, 16).

Our original SHAPE-directed algorithm did not allow for pseudoknotted base pairs (15). Given the strong relationship between pseudoknots and functionally critical regions in RNA and the fact that it is impossible to know a priori whether an RNA contains a pseudoknot, this limitation severely restricts the accuracy and generality of experimentally directed RNA structure analysis. Here, we describe a concise approach for applying SHAPE-directed RNA secondary structure modeling to include pseudoknots, in an algorithm we call ShapeKnots, and we show that the algorithm yields high-quality structures for diverse RNA sequences.

Results

Challenging RNA Test Set.

We developed the ShapeKnots algorithm, using a test set of 16 nonpseudoknotted and pseudoknot-containing RNAs that were selected for their complex, and generally difficult to predict, structures (Table 1, Top). These RNAs included (i) 5 RNAs with lengths >300 nt, both with and without pseudoknots; (ii) 5 riboswitch RNAs whose structures form only upon binding by specific ligands, for which thermodynamic rules are obligatorily incomplete; (iii) 4 RNAs with structures that are predicted especially poorly, with accuracies <60% using nearest-neighbor thermodynamic parameters; and (iv) 3 RNAs whose structures are probably modulated by protein binding. SHAPE experiments were performed on each of the RNAs in the presence of ligand if applicable but in the absence of any protein. Each of the training set RNAs had SHAPE probing patterns that suggested these RNAs folded in solution into structures generally consistent with accepted secondary structure models based on either X-ray crystallography or comparative sequence analyses. The structures of the 16 RNAs in the test set are predicted poorly by a conventional algorithm based on their sequences alone: The average sensitivity (sens, fraction of base pairs in the accepted structure predicted correctly), positive predictive value (ppv, the fraction of predicted pairs that occur in the accepted structure), and geometric average of these metrics are 72%, 78%, and 74%, respectively (Table 1).

Table 1.

Prediction accuracies as a function of algorithm and SHAPE information

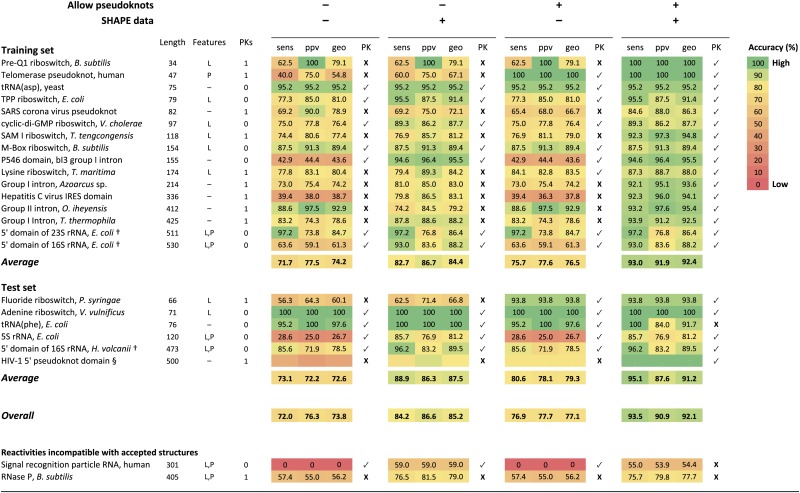Sensitivities (sens), positive predictive value (ppv), and their geometric average (geo) are shown for four test cases: no pseudoknots allowed and no SHAPE data, no pseudoknots allowed and with SHAPE data (both by free energy minimization), pseudoknots allowed and no SHAPE data, and pseudoknots allowed and with SHAPE data (both using ShapeKnots). Complicating features are ligand (L) binding and protein (P) binding that are not accounted for in nearest-neighbor thermodynamic parameters. Pseudoknot (PK) predictions are indicated with a checkmark (✓) or an X; a checkmark indicates that pseudoknots were predicted correctly and that there were no false-positive pseudoknot predictions. For the ribosomal RNAs (†), regions in which the SHAPE reactivities were clearly incompatible with the accepted structure, as described in ref. 15, were omitted from the sensitivity and ppv calculations; for the E. coli 16 rRNA, this included nucleotides 143–220. The HIV-1 5′ leader domain (§) was included as an example of pseudoknot prediction in a large RNA. Because the accepted structure for this RNA is based on SHAPE-directed prediction (24), we did not include sensitivity and ppv for this RNA in the overall average values; however, the pseudoknot was proved independently (23) and is included.

In the process of developing this training set, we also analyzed two RNAs—RNase P RNA and the human signal recognition particle RNA—whose in vitro SHAPE reactivities were incompatible with the accepted structures for these RNAs. We include prediction statistics for these RNAs (Table 1, Bottom) but did not use these to evaluate our SHAPE-directed modeling algorithm.

Simple, Robust Model for Pseudoknot Formation.

The favorable energetic contributions for forming the helices that comprise a pseudoknot are likely to be predicted accurately by the Turner nearest-neighbor model (17, 18) when modified by the experimental ∆G°_SHAPE term (Eq. 1). In addition, pseudoknot formation must overcome an entropic penalty; these energetics are difficult to estimate. The most widely used models are complex and include a large number of constituent parameters (11, 12). We adopted a simple approach to estimate the entropies on the basis of three primary insights. First, any secondary structure prediction must ultimately be compatible with a specific, energetically favorable, fold in the RNA in which nucleotides that base pair in the pseudoknot are close in three-dimensional space. This fundamental close-in-space feature must also be recapitulated in secondary structure prediction.

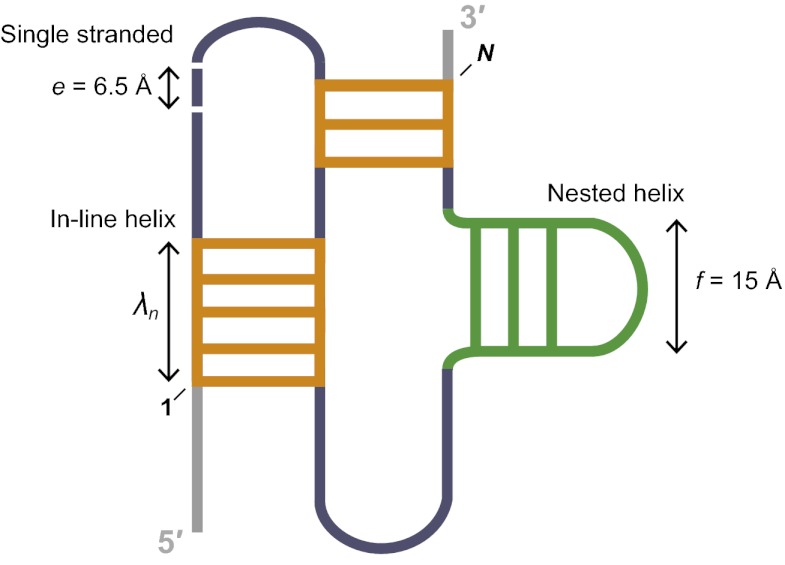
We modeled RNA pseudoknots as the sum of simple distance features or beads. There are exactly three possibilities for the structures that compose a pseudoknot: single-stranded nucleotides, nested helices, and in-line helices (Fig. 1). Duplexes containing single-nucleotide bulges are counted as a single helix. This model emphasizes structures rather than topologies and appears to be compatible with the vast majority of known pseudoknots. In essence, energetically favorable pseudoknots feature a small number of the single-stranded, nested helix, and in-line helix “beads”. Second, to account for the number of constituent single-stranded (SS) nucleotides and nested (NE) helices (Fig. 1), we adopted a simple polymer physics-based model (19). The energetic penalty associated with each of these features is weighted by distances of e = 6.5 Å and f = 15 Å, the mean lengths of a single-stranded nucleotide and a nested helix element, respectively (19) (Fig. 1). Finally, we created a penalty for in-line (IL) helices (Fig. 1). The potential to form these structures is weighted by their end-to-end length (n) in the context of A-form helix geometry and the distribution of in-line helices in RNAs of known structure. The model for the entropic cost of pseudoknot formation, ∆G°_PK, has two adjustable parameters, P1 and P2,

where λ_n is the penalty constant for in-line helices of length n (Table S1). The first term penalizes formation of pseudoknots with long single-stranded regions and many nested helices, whereas the second term enforces an optimal geometry for in-line helices.

Fig. 1.

Overview of pseudoknot structure model and entropic penalty terms. Length features are incorporated into ∆G°_PK as described in Eq. 2. Energy penalties for single-stranded nucleotides and nested helices are based on a previously developed model (19); the penalty for in-line helices was developed in this work.

RNA Structure Interrogation by SHAPE.

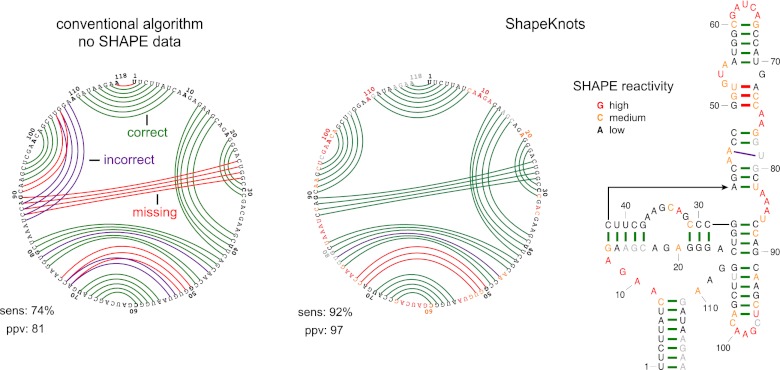
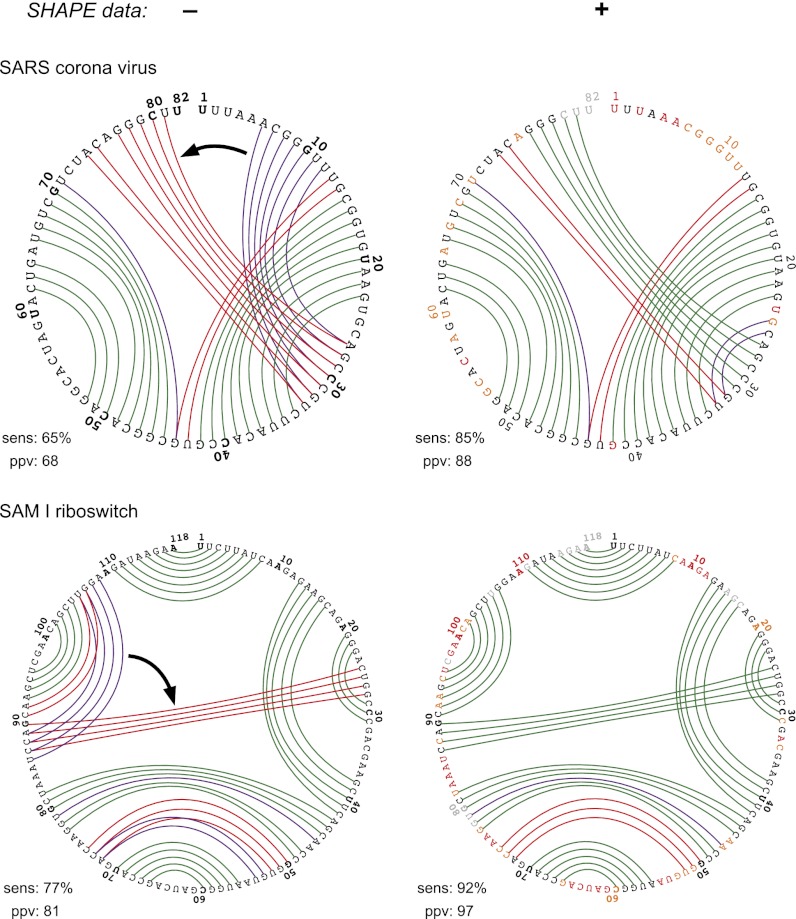
Most RNAs were transcribed in vitro and contained short hairpin-containing structure cassettes at their 5′ and 3′ ends (20). The 16S and 23S ribosomal RNAs were isolated from total Escherichia coli or Haloferax volcanii RNA (15). The transcribed RNAs were folded in a standard buffer with physiologically relevant ion concentrations (and saturating ligand concentrations for riboswitches) and treated with 1-methyl-7-nitroisatoic anhydride (1M7) (21). Sites of 2′-O-adduct formation were detected by primer extension, using a previously described high-throughput SHAPE approach (20). SHAPE reactivities were normalized to place them on a scale from zero (unreactive) to ∼1.5 (highly reactive). In this work, we illustrate modeling results in the form of circle plots, which provide an unbiased way to visualize correct and incorrect base pairs (Fig. 2). The nucleotide sequence is arrayed on the outer circle: Unreactive nucleotides (SHAPE reactivities <0.4) are colored black, moderately reactive nucleotides (0.4–0.85) are yellow, and highly reactive nucleotides (>0.85) are red. Base pairs are shown as arcs, colored by whether they are predicted correctly or not (Fig. 2, Left). Pseudoknots correspond to helices whose arcs cross in the circle plot. In general, there was a strong correspondence between SHAPE reactivities and the pattern of base pairing in the accepted structures. Nucleotides that participate in canonical base pairs were generally unreactive; whereas nucleotides in loops, bulges, and other connecting regions were reactive (Fig. 2, Center and Right).

Fig. 2.

Representative ShapeKnots structure prediction for the SAM I riboswitch. Base pair predictions are illustrated with colored lines: green, correctly predicted; red, missed base pair relative to the accepted (29) structure; and purple, prediction of a pair not in the accepted structure. (Left) Predictions without SHAPE data. (Center and Right) Predictions made when SHAPE data were included, using circle plot and conventional representations, respectively. Sensitivity (sens) and ppv are listed for each structure. SHAPE data are shown as colored nucleotide letters on a black, yellow, and red scale for low, medium, and high SHAPE reactivities, respectively. Plots were generated using the CircleCompare program in the RNAstructure package.

Algorithm and Parameter Determination.

Our ShapeKnots algorithm has four underlying parameters: m and b used in calculation of ΔG°_SHAPE and P1 and P2 used to calculate ΔG°_PK from Eqs. 1 and 2, respectively. The ΔG°_SHAPE parameters, m and b, penalize or favor base pairs with high and low SHAPE reactivities, respectively, are universal to all RNAs, and do not directly contribute to the entropic penalty for pseudoknot formation. These parameters can thus be fit independently of the ΔG°_PK terms, P1 and P2. m and b were optimized using the seven RNAs in our training dataset that do not contain pseudoknots. To reduce overoptimization of these parameters, we used a leave-one-out jackknife approach (22) to assess prediction sensitivities, ppv, and the geometric mean of these parameters at each grid point for seven quasi-independent data sets, each containing six of the seven RNAs.

Our algorithm for identification of pseudoknots follows the approach implemented in HotKnots (10). A two-stage refinement first finds stable helices, using a dynamic programming algorithm that does not allow pseudoknots. The second stage uses the same dynamic programming algorithm to predict structures for each stable helix found in stage one. In stage two, structures are predicted such that nucleotides in the stable helix are forced to not pair. These pairs are subsequently added back to the structure, and these helices can therefore be pseudoknotted. This allows the prediction of up to one pseudoknot per run. Run times for the final ShapeKnots algorithm were less than 1 min for RNAs of fewer than 150 nt and ∼90 min for the longest (530 nt) RNA (Table S2).

The pseudoknot-specific parameters, P1 and P2, were fit using a jackknife approach incorporating data from all 16 RNAs in the training set. Parameters were optimized in three stages (Methods). In this analysis, m = 1.8 and b = −0.6 kcal/mol yielded the most accurate secondary structure predictions (Fig. S1). These parameters differ slightly from the values (m = 2.6 and b = −0.8 kcal/mol) determined previously using only E. coli 23S rRNA (15). We recommend use of these new values for RNA structure prediction both with and without pseudoknots. Applying ShapeKnots using these ∆G°_SHAPE and ∆G°_PK parameters yielded an average sensitivity for secondary structure prediction of 93% for the 16 RNAs in the test set (Table 1, Top).

Extension to Additional RNAs.

We used ShapeKnots to model secondary structures for six RNAs that were not used to optimize the final algorithm. Three RNAs—the adenine riboswitch, tRNA^Phe, and E. coli 5S rRNA—were chosen because prior approaches using nonstandard data analysis suggested that they folded poorly with SHAPE data (16). The other three RNAs—the fluoride riboswitch pseudoknot, the 5′ domain of the H. volcanii 16S rRNA, and the 5′ pseudoknot leader of the HIV-1 RNA genome—adopt structures that are predicted poorly by conventional approaches. Overall prediction sensitivities for these six RNAs were ∼95% (Table 1, Middle), and the pseudoknots in the HIV-1 and fluoride riboswitch RNAs (23–25) were identified correctly.

Discussion

Pseudoknots are relatively rare in large RNAs but are highly overrepresented in important functional regions (2, 3, 6, 7). Despite their importance, the most commonly used RNA structure prediction algorithms do not permit pseudoknots because allowing pseudoknots increases both algorithmic complexity and the number of possible structures. Current algorithms that allow pseudoknots recover only ∼70% of the total accepted base pairs. The prediction sensitivity for base pairs that specifically form pseudoknots varies by algorithm and benchmark RNAs but averages only 5–40%, with many false-positive predictions (ref. 13 and Tables S3 and S4). Thus, the current generation of pseudoknot prediction algorithms is poorly suited for designing testable biological hypotheses.

ShapeKnots combines an iterative pseudoknot discovery algorithm with experimental SHAPE information and a simple energy model for the entropic cost of pseudoknot formation. The pseudoknot penalty in ShapeKnots has only two adjustable parameters (Fig. 1 and Eq. 2) that limit formation of pseudoknots with long single-stranded regions and many nested helices and that enforce an optimal geometry for in-line helices. ShapeKnots also allows incorporation of an experimental correction to standard free energy terms. Including SHAPE data both limits the number of possible structures and provides information that accounts for hidden features that stabilize RNA folding, including the significant effects of metal ion and ligand binding.

Our set of training structures was composed of 16 RNAs of known structure that ranged in length from 34 to 530 nt; pseudoknots occur in 9 of the 16 RNAs. Prediction accuracies were consistently high (Table 1 and Dataset S1). ShapeKnots significantly outperformed currently available pseudoknot prediction algorithms and is the only algorithm to achieve >90% overall and pseudoknot-specific sensitivities with this test set (Tables S3 and S4; see Methods for additional discussion). Both the specific pseudoknot energy penalty and use of SHAPE data contribute to the accuracy of the ShapeKnots approach. It is likely that inclusion of SHAPE data will generally improve accuracies for pseudoknot prediction algorithms.

We summarize our modeling results by emphasizing four classes of RNA: (i) short pseudoknotted RNAs with structures that ShapeKnots predicts very accurately; (ii) large, challenging RNAs that ShapeKnots predicts with good accuracy; (iii) RNAs with high likelihood of being mischaracterized with false-positive or missed pseudoknots that ShapeKnots predicts accurately; and (iv) RNAs that interact with other molecules such as ligands, proteins, and metal ions that pose unique challenges. For most RNAs analyzed here, differences between models generated by ShapeKnots and currently accepted structures were minor and typically involved short-range interactions or base pairs at the ends of helices. In some cases, differences likely reflect thermodynamically accessible states at equilibrium in solution.

Short Pseudoknotted RNAs.

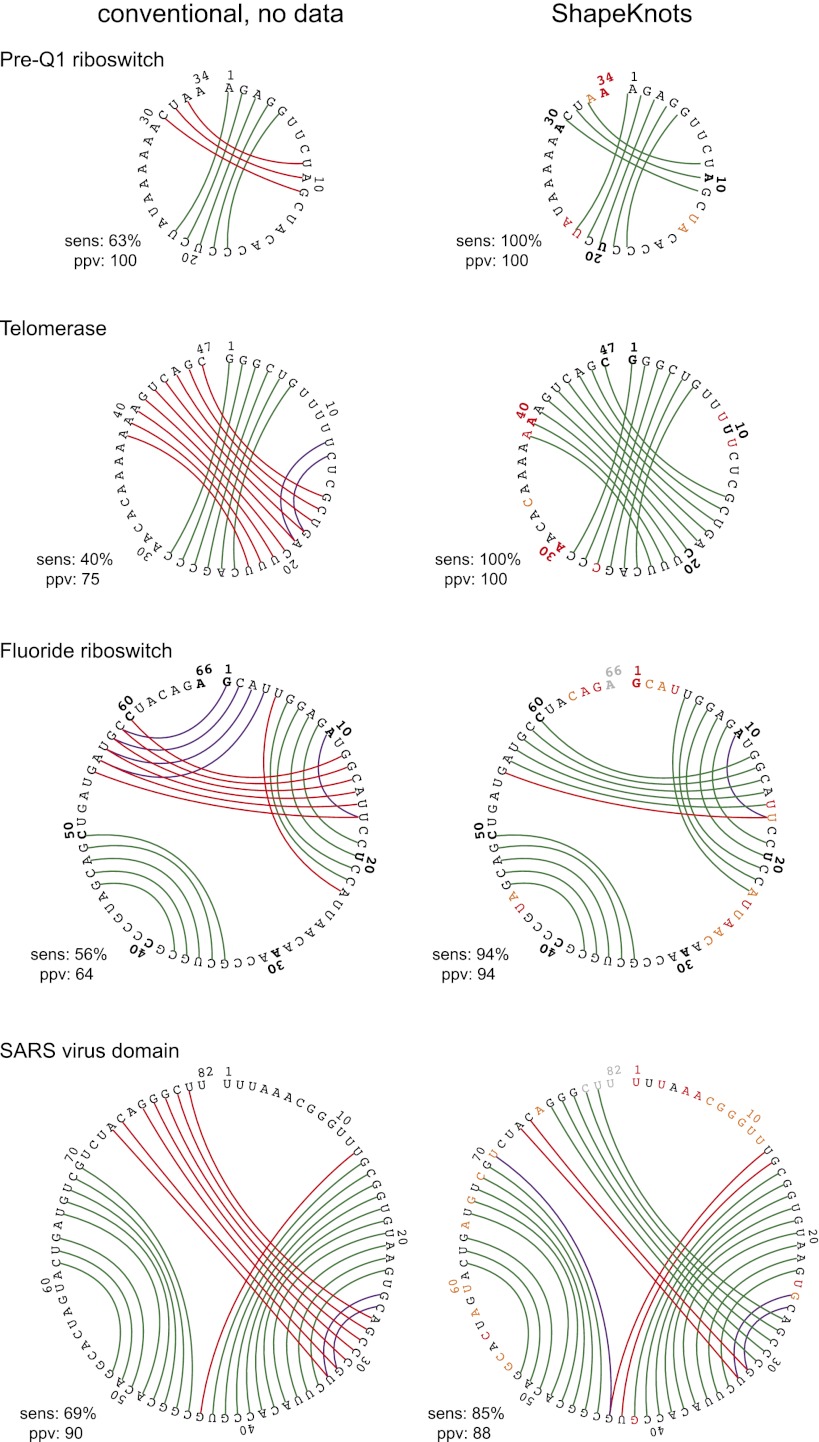
The first class includes small RNAs that contain H-type pseudoknots: the pre-Q1 riboswitch, human telomerase, the fluoride riboswitch, and a severe acute respiratory syndrome (SARS) corona virus domain. Because the most commonly used dynamic programming algorithms cannot predict base pairs in an H-type pseudoknot, prediction sensitivities using a conventional algorithm (14) were quite poor; in contrast, ShapeKnots yielded perfect or near-perfect predictions in each case (Fig. 3, compare Left and Right columns). The only ShapeKnots-predicted base pairs that do not occur in the accepted structures involve sets of 2 or fewer bp located at the ends of individual helices in the fluoride riboswitch and the SARS domain. These results suggest that ShapeKnots prediction of H-type pseudoknots in short RNAs is robust.

Fig. 3.

Summary of predictions for four H-type pseudoknots. Base pair predictions are illustrated as outlined in Fig. 2; sensitivity (sens) and ppv are listed for each structure. Left and Right columns show predictions for a conventional mfold-class algorithm vs. ShapeKnots (with experimental SHAPE restraints).

Large, Complex RNAs.

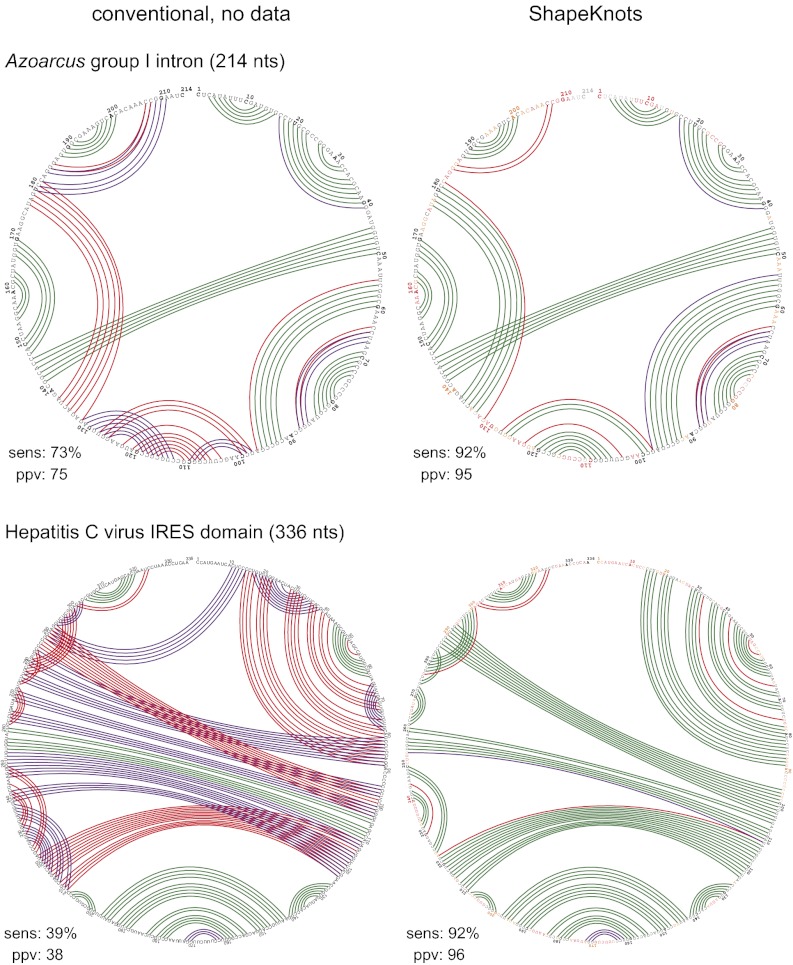
The second class includes large RNAs that do not require ligands or protein cofactors for correct folding. Large RNAs pose a challenge to modeling algorithms due to the vast number of possible structures and due to the large number of structures with similar folding free energies changes. For example, in the absence of experimental structure probing data, two representative RNAs, the Azoarcus group I intron and the hepatitis C virus internal ribosome entry sequence (IRES) domain, are predicted with sensitivities of 73% and 39%, respectively. Mispredictions occur primarily in two hairpin motifs in the Azoarcus RNA but span essentially the entire hepatitis C virus (HCV) IRES RNA (Fig. 4). Inclusion of SHAPE data yielded near-perfect predictions in each case, including correct identification of the pseudoknot in each RNA (Fig. 4, compare Left and Right columns).

Fig. 4.

Prediction summaries for two large, pseudoknot-containing RNAs. Structural annotations are as described in Fig. 2.

RNAs with Difficult to Predict Pseudoknots.

Within a given RNA sequence, several physically reasonable pseudoknots are often possible, for example, in the SARS virus domain (Fig. 5, Upper Left, arrow linking purple and red helices). Conversely, as exemplified by the SAM I riboswitch, pseudoknots can be missed because the energy function does not distinguish small differences in stabilities of a pseudoknot-forming vs. a more local helix (Fig. 5, Lower Left, arrow). The experimental SHAPE-based correction correctly reranked the stabilities for the two possible helices located close to one another in topological space in the SARS and riboswitch RNAs, ultimately avoiding both false-positive and false-negative pseudoknot predictions (Fig. 5, Right column).

Fig. 5.

Representative examples in which ShapeKnots avoids false-positive (Upper) or false-negative (Lower) pseudoknot predictions. Left and Right columns show the results of ShapeKnots predictions without and with SHAPE data, respectively. Arrows in the Left column emphasize the replacement of an accepted (red) helix with an incorrect (purple) helix in the absence of data. Other structural annotations are as described in Fig. 2.

RNAs That Do Not Adopt Their Accepted Structures.

During our analysis of experimentally directed structure modeling, we examined two RNAs for which the in vitro SHAPE data were clearly incompatible with the accepted structure. These RNAs were the signal recognition particle RNA and RNase P. In each case, the SHAPE-directed model using ShapeKnots provided a significant improvement relative to the pseudoknot-free lowest free energy predicted structure (Table 1, Bottom). Nonetheless, a large part of each structure was mispredicted relative to the accepted structure. In each case, nucleotides in some helices in the accepted structural model were reactive by SHAPE, suggesting that these helices do not form under the solution conditions used here for in vitro structure probing (Fig. S2). There are several possible explanations for the observed discrepancies. First, the conditions under which these RNAs were crystallized are different from the roughly physiological ion conditions used in SHAPE probing experiments. The differences in conditions could cause the crystallographic structure to be different from that in solution or there may be structural inhomogeneity in solution. Second, both the RNase P and signal recognition particle RNAs function as RNA–protein complexes. These proteins were not present during in vitro SHAPE experiments.

Perspective.

It is difficult to account for many factors that impact RNA secondary structure—including effects of metal ions, ligands, and protein binding—using a system based on thermodynamic or structural parameters. For example, the M-Box and fluoride riboswitch RNAs undergo large conformational changes upon binding by Mg²⁺ or F^– ions, respectively (25, 26), and binding of ligands to the pre-Q1, TPP, cyclic-di-GMP, SAM, and adenine riboswitches provides a large fraction of the total interactions that ultimately stabilize the accepted structure (7). In addition, many of the RNAs in our dataset contain base triple interactions, which are common in pseudoknots (27). With the inclusion of SHAPE data, the ShapeKnots approach does a good job of modeling these interactions (Table 1).

Other challenges to structure prediction are that some base pairs may be stable only in the presence of bound proteins and some RNAs, especially as exemplified by riboswitches (7), sample multiple conformations. Finally, in vitro refolding and probing protocols may not fully recapitulate the functional or in vivo structure. Our analyses of the signal recognition particle RNA and RNase P illustrate these challenges: Neither of these RNAs appears to fold stably to the accepted structure under solution conditions used in this work (Fig. S2). These two RNAs are widely used to benchmark folding algorithms, even though they may fold robustly to their accepted structures only in the context of their native RNA–protein complexes. In this case, for the specific solution environment used here, the SHAPE-directed structures appear to be roughly “correct” but just not the expected ones.

In the context of the diverse RNAs examined in this work, the ShapeKnots algorithm recovered 93% of accepted base pairs in well-folded RNAs (Table 1), significantly outperforming current algorithms. Nonetheless, evaluation of ShapeKnots is currently restricted by challenges that impact the entire RNA structure modeling field (16). Relatively few RNAs with nontrivial structures exist that are known at a high level of confidence. The ShapeKnots energy penalty and search algorithm may require adjustment as new pseudoknot topologies are discovered. RNAs that have been solved by crystallography have features that make them simultaneously both more and less difficult to predict than more typical structures: They tend to contain a relatively high level of noncanonical and complex tertiary interactions (difficult to predict features), and they fold into structures with many stable base-paired regions (more readily predicted using thermodynamics-based algorithms). In addition, the structures inferred from high-resolution data may not represent the solution conformation of the purified RNAs. For RNAs in which the accepted structure is based on phylogenetic and in-solution evidence—as exemplified by the SARS virus and HCV IRES domains—ShapeKnots predictions may identify correct features missed in current accepted structures. The approaches outlined in this work—use of simple models for base pairing and pseudoknot formation, including experimental corrections to thermodynamic parameters, and nuanced interpretation of differences between current accepted and modeled structures—represent a critical departure point for future accurate RNA secondary structure modeling.

Methods

Detailed descriptions of the ShapeKnots algorithm, parameterization of ∆G°_SHAPE and ∆G°_PK, and SHAPE probing experiments are provided in SI Methods. For the general user community, the current best parameters for SHAPE-directed structure modeling (for algorithms that both do and do not allow pseudoknots) are m = 1.8, b = −0.6, P1 = 0.35, and P2 = 0.65 kcal/mol (Eqs. 1 and 2). It is critical that SHAPE experiments be processed accurately to obtain highest-quality structure models (16). We recommend normalizing SHAPE data by a model-free box-plot (15) approach and defining the borders for low, medium, and high SHAPE reactivities (Fig. 2, black, yellow, and red) at 0.40 and 0.85 (see SI Methods for additional details). All SHAPE data used in this work are available at www.chem.unc.edu/rna and at the SNRNASM community structure probing database (28). ShapeKnots is freely available as part of the RNAstructure software package at http://rna.urmc.rochester.edu.