Stacking nonenzymatic circuits for high signal gain

Abstract

Signal amplification schemes that do not rely on protein enzymes show great potential in areas as abstruse as DNA computation and as applied as point-of-care molecular diagnostics. Toehold-mediated strand displacement, a programmable form of dynamic DNA hybridization, can be used to design powerful amplification cascades that can achieve polynomial or exponential amplification of input signals. However, experimental implementation of such amplification cascades has been severely hindered by circuit leakage due to catalyst-independent side reactions. In this study, we systematically analyzed the origins, characteristics, and outcomes of circuit leakage in amplification cascades and devised unique methods to obtain high-quality DNA circuits that exhibit minimal leakage. We successfully implemented a two-layer cascade that yielded 7,000-fold signal amplification and a two-stage, four-layer cascade that yielded upward of 600,000-fold signal amplification. Implementation of these unique methods and design principles should greatly empower molecular programming in general and DNA-based molecular diagnostics in particular.

Signal amplification is a ubiquitous theme in biology and engineering, and the ability to amplify signals at the molecular level in large measure determines the complexity and robustness of the molecular devices and systems that can be built. Over the past decade, DNA has been established as the ultimate “intelligent material” to build complex structures, circuits, and devices. DNA circuits have been integrated to form complex Boolean networks (1) and molecular neural networks (2). Such programmed circuits have begun to have applications in ordered chemical synthesis (3, 4), multiplexed labeling of biomolecules for fluorescent microscopy (5, 6), and detection of both nucleic acid and nonnucleic acid analytes (7–9). The combination of DNA circuitry and DNA nanotechnology (10, 11) has given rise to DNA robotics (12) and assembly lines (13).

The signal amplifiers underlying many of these advances are metastable DNA substrates whose conformational transformations can be catalytically triggered by strand displacement. The first amplifier of this class was designed by Turberfield et al. (14) and was later modified by Seelig et al. by using metastable kissing-loop structures (15). Since then, many hybridization-based catalytic systems have been developed, including ones based on topologically constrained interactions (16), entropy-driven strand exchange (17), and catalyzed hairpin assembly (CHA) (18). Some of these schemes allow cascading of catalysis wherein the product of one reaction serves as the catalyst of another reaction. Autocatalytic reactions (17, 19) and cross-catalytic reactions (18) may also be constructed and programmed. Such molecular amplifiers can guard against signal damping during serial signal transductions in nucleic acid circuits and are easily adapted to the integration of logical operations (20).

Whereas the outcome of these amplifiers, the amplification of nucleic acid signals, is functionally similar to enzyme-based methods such as PCR, current implementations of these hybridization-based signal amplifiers are far inferior at least in terms of fold amplification. Although PCR routinely amplifies signals by 10⁸- to 10¹⁰-fold, DNA circuits typically amplify signals by less than 1,000-fold. Here, the term “fold amplification” is defined as the number of product molecules that each molecule of input (template or catalyst) is responsible for. In a constant-volume, single-tube reaction, fold amplification can be calculated by the concentration of the input-dependent final product (signal) divided by the concentration of the input. In a more complex protocol where immobilization and/or dilution is involved, it is also appropriate to compare the quantity (rather than the concentration) of the final product and the input.

A major barrier to implementation of these enzyme-free amplifiers involves mistriggering of the amplification cascade (also known as circuit leakage) in the absence of the analyte nucleic acid. Such leakage usually leads to substantial background that masks signal gain and is especially detrimental in cascaded reactions. Although it is widely believed that leakage is primarily caused by defects of oligonucleotides that occur during DNA synthesis, direct evidence has been lacking, and methods to effectively eliminate circuit leakage have not yet been developed. Moreover, it is not clear how the level and kinetics of circuit leakage affect design of amplification cascades.

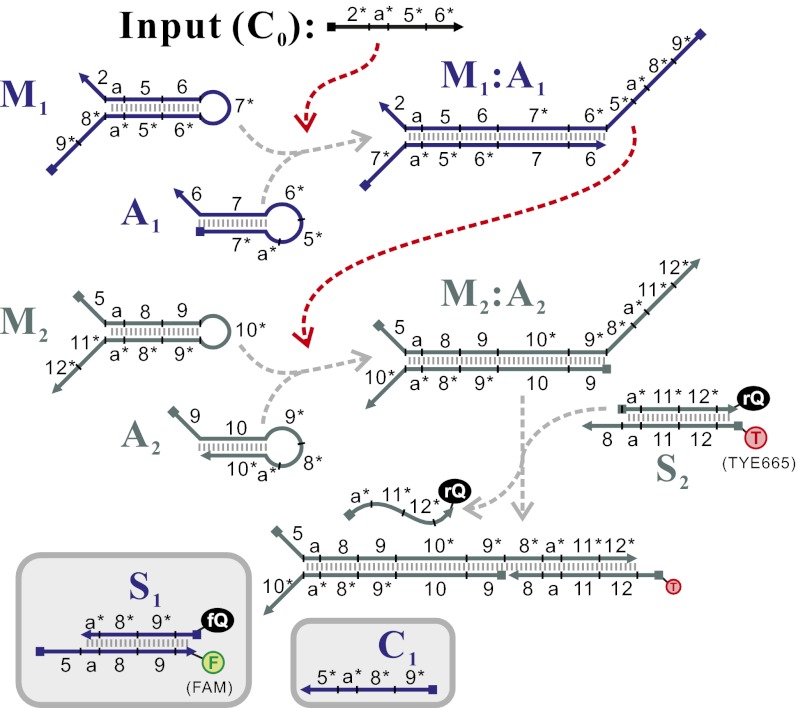
We have now systematically studied and optimized the cascading of the CHA reaction. In a simple CHA reaction (such as M₁ + A₁ → M₁:A₁ shown in Fig. 1 and Fig. S1), the catalyst strand (C₀) first hybridizes to an ∼8-nt overhang [known as the toehold (21)] of one hairpin (M₁) and subsequently hybridizes to the entire arm of the hairpin through branch migration. This reaction causes the hairpin to open and exposes another toehold that can bind the overhang of a second hairpin (A₁). Subsequent branch migrations result in the full hybridization of the two hairpins and the recycling of the catalyst strand. CHA reactions can be cascaded using the design shown in Fig. 1 (7, 18). Here, we designed two-layer and four-layer amplification cascades based on a particular type of CHA reaction we have optimized before (7). We analyzed the origin and profile of circuit leakage and used a combination of modeling and experiments to reveal that the performance of the CHA cascade, in terms of both fold amplification and sensitivity, depends on the leakage profiles of individual CHA reactions. Theoretically, we formulated a simulation-based guideline to determine optimal cascade architecture based on the leakage profile, and we analyzed the sequence–function relationship that may govern the speed of individual CHA reactions. Experimentally, we developed a method to obtain a large quantity of DNA substrates of extremely high quality through enzymatic synthesis and showed record-high 600,000-fold signal amplification with the help of these high-quality DNA substrates. We believe these discoveries and achievements not only set a milestone in the development of in vitro DNA circuitry but also provide roadmaps for the future development of this area.

Fig. 1.

Cascading of the CHA reaction. In the first-layer reaction C₀ catalyzes the formation of M₁:A₁ from substrate hairpins M₁ and A₁. (See Fig. S1 for the detailed pathway of this reaction.) The formation of M₁:A₁ exposes the 5* toehold domain of M₁, enabling M₁:A₁ to catalyze the formation of M₂:A₂ in the second-layer reaction. The formation of M₂:A₂ can be sensed by using a fluorescent reporter S₂. Hairpins of the same layer are shown in the same color. (Insets in gray) Additional reagents that are useful in testing individual CHA reactions (such as C₁ and S₂). Gray dashed arrows connect reactants and products, whereas red dashed arrows connect catalysts and catalyzed reactions. This two-layer cascade can be abbreviated using the presentation shown in the second row of Fig. 2A.

Results

Leakage Profile Dictates Optimal Circuit Architecture.

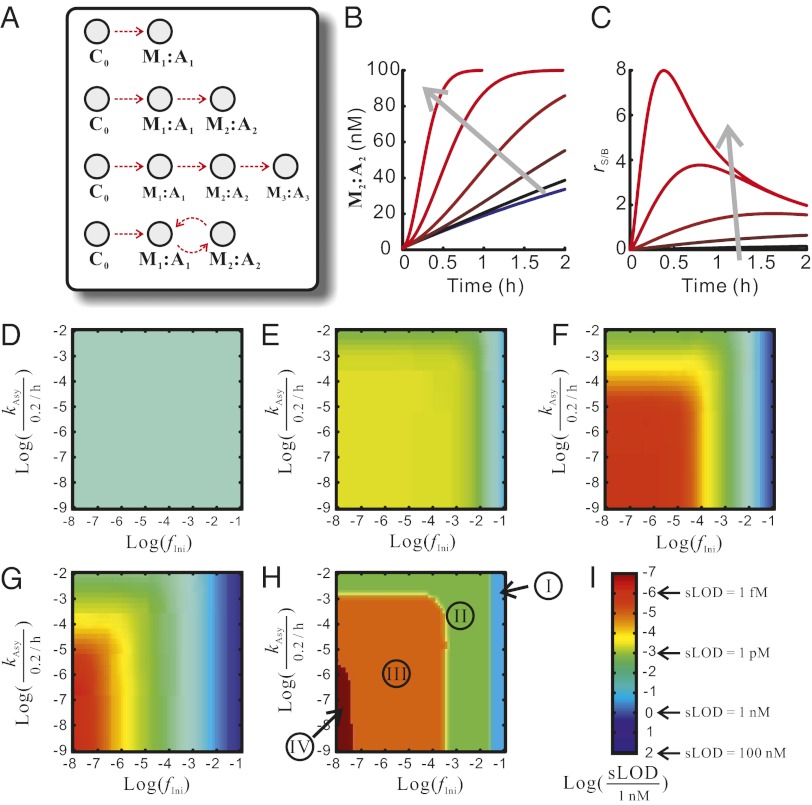
Because nucleic acid circuits are amenable to rational design at the sequence level, they can be cascaded so that the product of one reaction acts as the catalyst of another reaction. In theory, many cascade architectures can be constructed, including linear multilayer cascades and circular (i.e., self-catalytic or cross-catalytic) cascades (Fig. 2A). Unlike a single amplification reaction where the concentration of the final product increases linearly with time, these cascades potentially allow for polynomial and exponential amplification. However, they are at the same time more susceptible to background because mistriggered hybridization products might also be amplified.

Fig. 2.

Leakage profile dictates optimal cascade architecture. (A) Four cascade architectures studied in the simulation. From top to bottom: single-layer CHA reaction, two-layer linear cascade, three-layer linear cascade, and two-layer circular cascade. (B) An example of the kinetics of product (M₂:A₂) formation in a two-layer linear cascade. The leakage profile used in this simulation is f_Ini = 10⁻², k_Asy = 2 × 10⁻⁵⋅h⁻¹. Kinetics of background formation (formation of M₂:A₂ in the absence of initial trigger) are shown in the blue trace. The kinetics of M₂:A₂ formation in the presence of various concentrations of initial trigger are shown in traces with red hues. In the direction of the gray arrow, the concentrations of initial trigger were 10 pM, 50 pM, 200 pM, 1 nM, and 5 nM. (C) Signal-to-background ratio as a function of time and initial trigger concentration, calculated from the simulation shown in B. (D–G) Simulated limits of detection (sLOD, shown in colors according to the scale in I) as a function of f_Ini and k_Asy (shown on the x and y axes, respectively) for different cascade architectures. (D) Single-layer CHA reaction. (E) Two-layer linear cascade. (F) Three-layer linear cascade. (G) Two-layer circular cascade. (H) The optimal cascade architecture, as defined by the architecture that attains the lowest sLOD, as a function of leakage profile. In zones I, II, III, and IV, the optimal architectures are single-layer reaction, two-layer linear cascade, three-layer linear cascade, and two-layer circular cascade, respectively.

Intuitively, the more layers a linear cascade has, the greater both the amplification and the background will be; circular cascades offer the fastest amplification but are most susceptible to leakage. This leads to an operational question regarding which cascade architecture is optimal for amplifying signals while keeping the background at a manageable level.

To answer this question, we dissected the kinetics of circuit leakage both theoretically and experimentally, using CHA circuits as an example. To facilitate understanding, we introduce the following notation. A single-layer CHA reaction, where strand C₀ catalyzes the reaction (hybridization) of hairpins M₁ and A₁ (Fig. 2A, top), can be written as

Therefore, a three-layer linear cascade (Fig. 2A, third from top) can be written as

whereas a two-layer circular (i.e., cross-catalytic) cascade (Fig. 2A, bottom) can be written as

In all instances C₀ serves as the initial trigger.

The kinetics of such amplifiers can be followed with a fluorescent reporter (S_i as shown in Fig. 1), such that only M_i:A_i (but not correctly folded M_i or A_i alone) can displace the quencher-bearing strand of S_i, resulting in increased fluorescence. On the basis of our and others’ observation of the kinetics of CHA and other catalytic nucleic acid circuits, circuit leakage can be roughly categorized into initial leakage and asymptotic leakage. Initial leakage is likely due to the small fraction (usually <10%) of malformed (missynthesized and/or misfolded) M_i and A_i that quickly hybridize to form M_i:A_i in the absence of C_i−1 or M_i−1:A_i−1. Asymptotic leakage represents the slow, uncatalyzed hybridization of M_i and A_i due to conformational fluctuations (Sources of Circuit Leakage).

We set out to determine how the levels of different types of leakage influence optimum cascade architecture. To this end, we initially carried out a simulation of four different circuit architectures: (i) a single-layer CHA reaction, (ii) a two-layer linear cascade, (iii) a three-layer linear cascade, and (iv) a two-layer circular (i.e., cross-catalytic) cascade (Fig. 2A).

We can model the rate of designed reactions, using the equation

where k_app is the apparent second-order catalytic efficiency of M_i−1:A_i−1. For the three linear cascades, [M₀:A₀] = [C₀]. For the cross-catalytic cascade, [M₀:A₀] = [C₀] + [M₂:A₂]. We also assume A_i is in large excess and its contribution to the rate of reaction is reflected by k_app. We choose 0.2⋅nM⁻¹⋅h⁻¹, a typical value based on our (Fig. S2; see Fig. S6) and others’ (18) data, as the value of k_app for all layers. We use 100 nM as the total concentration of each M_i.

To take leakage into account, we introduce the parameter f_Ini to express initial leakage. f_Ini is defined as the fraction of M_i that is transformed into M_i:A_i upon mixing. Therefore, the initial concentration of M_i:A_i equals f_Ini × 100 nM. Accordingly, the initial concentration of M_i is (1 − f_Ini) × 100 nM.

We can also model asymptotic leakage by the equation

where k_Asy is the apparent first-order rate constant of the reaction and takes [A_i] into account.

Therefore, the complete ordinary differential equation (ODE) set for each layer is

Given f_Ini, k_Asy, and [C₀], one can simulate the kinetics of a cascade, using this ODE set. Throughout, we define the term background as the concentration of the final product in the absence of the initial trigger (i.e., caused by circuit leakage), and we define the term signal as the difference between the concentrations of the final product with and without the initial trigger. In general, both signal and background increase over time. Once signal saturates, background continues to rise, causing a decrease in the signal-to-background ratio. The dependence of the signal-to-background ratio on time and initial trigger concentration can be seen in Fig. 2 B and C.

To evaluate a cascade architecture given the leakage profile (f_Ini and k_Asy) of its CHA reactions, we computed the lowest concentration of C₀ that would lead to a discernable signal within the first 12 h. More precisely, we define “discernable signal” as (i) the signal is at least 10 nM (a number based on the sensitivities of many fluorescence readers) and (ii) the signal-to-background ratio is at least 0.15 (that is, assuming a combined 5% relative error in cascade preparation and reading, a signal-to-background ratio of 0.15 implies the signal is 3 standard deviations higher than background). This concentration is similar to the limit of detection (LOD) and is thus termed “simulated limit of detection” (sLOD). Indeed, the sLOD varies as a function of f_Ini and k_Asy as shown in Fig. 2 D–G, where f_Ini and k_Asy are shown on the x and y axes in log scale, respectively, and sLOD is shown by color (see Fig. 2I for color scale). It can be seen that although the sLOD is fairly independent of circuit leakage for the single-layer amplifier, it is highly dependent upon leakage in the cross-catalytic cascade. Interestingly, in low-leakage regimes the cross-catalytic cascade and the three-layer cascade exhibit low sLOD due to faster catalysis, whereas in high-leakage regimes these circuits are actually less sensitive than their simpler counterparts due to a faster accumulation of leakage. As a result, the optimum architecture to achieve the lowest sLOD varies as the level of leakage changes (Fig. 2H).

Design of a Two-Layer Amplification Cascade.

On the basis of the analysis above and our experience with the leakage of single-layer CHA circuits (f_Ini typically ≤10% without optimization; k_Asy typically ≤10⁻⁴⋅h⁻¹), we decided to implement stacked, linear CHA cascades. To begin to establish design principles at the level of DNA sequence, we first designed a two-layer CHA cascade (Fig. 1). The initial trigger C₀ catalyzes the kinetically trapped M₁ to open and hybridize to A₁, forming M₁:A₁, which in turn catalyzes the formation of M₂:A₂ from hairpins M₂ and A₂. Each layer used design principles we have previously formalized (7). In particular, all toeholds are 8 nt long and have a 50% GC content. In addition, the catalyst dissociates passively [rather than actively, as in previous circuits (18)] from the product at the conclusion of each cycle of reaction, because we found designs with active product dissociation usually led to higher asymptotic leakage. The only exception is that buffer domains (domains a and a*) were introduced to “pad” hairpins M_i and reduce background leakage (see type IV leakage in Sources of Circuit Leakage).

We first characterized the performance of each layer, using hairpins purified by denaturing PAGE (named “D-pure” hairpins). The catalysts for the first- and second-layer reactions were C₀ and C₁, respectively. C₁ (Fig. 1, Inset) is a mimic of the portion of the M₁:A₁ duplex (domains 9*-8*-a*-5*) that catalyzes the second-layer CHA reaction. Fluorescent reporters S₁ and S₂ (Fig. 1) were used to monitor the formation of the product of the two CHA reactions, respectively. The performance of each layer was qualitatively similar to that of similar single-layer amplifiers (7), in that it showed robust signal amplification and low leakage (Fig. S2). In the presence of 100 nM M_i, 200 nM A_i, and 5 nM catalyst C_i−1, a theoretical maximum of 20-fold amplification was obtained after 3–6 h, whereas the amount of M_i:A_i formed due to circuit leakage (in the absence of C_i−1) was generally lower than 5 nM (5% of total M_i concentration). The apparent second-order catalytic efficiency values (k_app, equivalent to k_cat/K_m of an enzyme; SI Methods, section 1) for the first- and second-layer CHA reactions were estimated to be 0.1⋅nM⁻¹⋅h⁻¹ and 0.2⋅nM⁻¹⋅h⁻¹, respectively.

We next attempted to combine the two layers into a cascaded reaction. Consistent with the simulation, whereas leakage was low in each single-layer reaction, when the two layers were joined, the small leakage in the upstream layer was amplified by the downstream layer, creating substantial background (M₂:A₂ formed in the absence of C₀). When 100 nM M₁, 200 nM A₁, 100 nM M₂, 200 A₂, and 150 nM S₂ were mixed at 37 °C in the absence of C₀, ∼70 nM M₂:A₂ was formed within 1.5 h (red trace in Fig. 3A). Even in the presence of high concentrations (5 nM) of C₀, the maximum signal (difference in [M₂:A₂] accumulation with and without C₀) was ∼45 nM, whereas the maximum signal-to-background ratio was only ∼2 (compare green and red traces in Fig. 3A). The best fold amplification was therefore (45 nM/5 nM =) ∼9. It should be noted that signal-to-background ratio is a more intrinsic parameter that reflects the performance of the molecular signal amplifier. In contrast, signal-to-noise ratio, which determines the limit of detection, is more influenced by extrinsic factors such as idiosyncracies of instrumentation and experimental variation (e.g., precision of pipetting). Because the aim of this work is to develop a more powerful amplifier, we focus mainly on the variables signal-to-background ratio and fold amplification (Discussion). It was clear from these experiments that the fast-rising background masked the C₀-dependent signal.

Fig. 3.

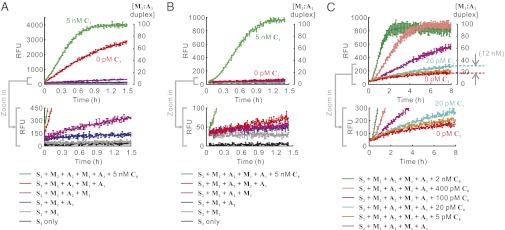
Performance of a two-layer linear CHA cascade composed of chemically synthesized hairpins from different purification processes. (A) Experiments with D-pure hairpins. (B and C) Experiments with DNB-pure M₁ and DN-pure A₁, M₂, and A₂. (A–C, Bottom) The combinations of reaction components are shown. A and B focus on the dissection of circuit leakage by incrementally adding reactants. C shows the response of the two-layer cascade to different concentrations of the initial trigger (C₀).

Sources of Circuit Leakage.

To reduce leakage, it was important to analyze its origin. On the basis of empirical observations gained during the construction of single-layer CHA circuits, we hypothesized three sources of circuit leakage: (i) the presence of a small population of malformed M_i that could inadvertently activate the reporter S_i or catalyze the formation of M_i+1:A_i+1, (ii) the presence of a small population of malformed M_i and/or A_i that resulted in the formation of M_i:A_i duplexes in the absence of the corresponding catalyst, and (iii) the formation of M_i:A_i duplexes from perfectly formed M_i and A_i in the absence of a corresponding catalyst. We term these three types of leakage type I, type II, and type III, respectively. The three types of leakage should have distinct kinetic profiles and may thereby be differentiated from one another, using different combinations of reagents (schematically shown in Fig. S3A). In particular, type I leakage is indicated by mixing M_i and S_i and observing a burst of fluorescent signal above the background fluorescence exhibited by S_i only (Fig. S3A, compare green and black lines). Type II leakage can be detected by mixing M_i and A_i together with S_i (Fig. S3A, solid blue line). On top of type I or type II leakage, a slower steady increase in fluorescent signal that asymptotically approaches the full conversion to M_i:A_i is sometimes observed (Fig. S3A, dashed blue line), representing type III leakage. (In theory this steady increase might also be caused by malformed M_i or A_i that somehow catalyzes the formation of M_i:A_i. However, this possibility seems unlikely in our particular design.) An additional type of leakage can happen in CHA cascades. That is, perfectly formed M_i−1 may also catalyze the formation of M_i:A_i. We term this process type IV leakage. Phenomenologically, type I leakage and type II leakage constitute “initial leakage”; whereas type III leakage and type IV leakage together constitute “asymptotic leakage.”

Type I leakage and type II leakage are caused by impurities and can potentially be minimized by making higher-quality oligonucleotides or by purifying correctly synthesized or folded substrates. In contrast, type III leakage and type IV leakage are inherent to a particular design. Fortunately, we have found in the course of this and a previous study (7) that our design principle yielded many robust CHA designs that led to undetectable type III and type IV leakage. Thus, if malformed M_i and A_i molecules can be removed, background can be drastically reduced.

Purification Methods to Remove Type I and Type II Leakage.

We first attempted to eliminate type II leakage by incubating D-pure M_i and A_i overnight in the absence of the catalyst, allowing malformed M_i and A_i to form an M_i:A_i duplex, and then isolating remaining unreacted M_i and A_i, using native PAGE. We call this purification method native (N) purification and the resultant DNA hairpins “DN-pure” hairpins.

To reduce type I leakage, we used a biotinylated “capture construct” analogous to the fluorescent reporter S_i (Fig. S3B). This capture construct was immobilized on a streptavidin-coated resin and incubated with DN-pure M_i. Most of the M_i that underwent type I leakage was captured on the resin whereas unreacted M_i was collected from the flow-through and concentrated. We call this purification method biotin (B) purification and the resultant M_i is dubbed “DNB-pure” M_i.

We prepared DN-pure A₁, M₂, and A₂ and DNB-pure M₁ and repeated the experiment shown in Fig. 3A, using these hairpins. As shown in Fig. 3B, these purification methods significantly reduced the overall leakage: Only ∼5 nM background was observed over 1.5 h, a 9-fold reduction over using D-pure hairpins alone. When 5 nM of C₀ was added, the maximum signal was ∼100 nM (a 2-fold improvement), and the maximum signal-to-background ratio was ∼20 (a 10-fold improvement).

We next tested the signals elicited by various concentrations of C₀ in longer reactions. As low as 20 pM of C₀ elicited significant signal above background (∼12 nM) with a signal-to-background ratio of 0.5 (Fig. 3C). In other words, this two-layer cascade resulted in a 600-fold signal amplification in ∼8 h, similar to the performance of the previously reported two-layer cascade based on entropy-driven catalysis (17).

Improved Performance with Enzymatically Synthesized CHA Hairpins.

Another factor that limited the fold amplification was the turnover number of the catalyst. Zhang and Winfree proposed that some malformed DNA substrates may lead to the formation of “dead-end” intermediates that irreversibly consume the catalyst (22). Unfortunately, it is very challenging to remove these types of malformed substrates through conventional purification strategies. Instead, we hoped to generate higher-quality DNA hairpins at the outset via enzymatic synthesis.

Several methods to obtain enzymatically synthesized ssDNA have been developed (see ref. 23 for a recent review). However, there are special needs for DNA nanotechnology or circuitry that few existing methods meet. We therefore decided to use a modified version of strand displacement amplification (SDA) (24, 25). SDA is an amplification method based on continuous nicking of a dsDNA (by a sequence-specific nicking enzyme) and primer extension from the nicked site (by a DNA polymerase with strong strand-displacement activity). However, because SDA tends to produce nonspecific artifacts (26), we separated nicking (using enzyme Nt.BstBNI) and strand displacement into two reactions. Although this procedure introduced some sequence constraints, they were minimal and could be readily adapted to our design method. The synthesis strategy is shown in Fig. S4 and a detailed description of the process can be found in SI Methods, section 2. We found that up to 1 nmol extremely pure ssDNA could be produced via this method.

To test whether enzymatic synthesis enhanced apparent reactivity, we designed a new two-layer cascade, where the first layer was produced enzymatically and the second layer was produced chemically followed by D and N purification. We named these hairpins eM₁, eA₁, eM₂, and eA₂. The secondary structure and the position of the CAG (or complementary CTG, both due to the introduction of the PvuII site) trinucleotides of the newly designed structure are shown in Fig. S5.

We first confirmed the functionality of each layer (Fig. S6 A and B). Strikingly, even though we did not apply N or B purification to eM₁ and eA₁, the leakage from this layer was undetectable (red trace in Fig. S6A). The extremely low leakage also translated into very low background in a two-layer cascade that contained 50 nM eM₁, 100 nM eA₁, 100 nM eM₂, 200 nM eA₂, and 150 nM eS₂. After 1.5 h and 12 h of reaction in the absence of the initial catalyst eC₀, only ∼5 nM and ∼20 nM eM₂:eA₂ were formed, respectively (Fig. 4A, red trace). This is comparable to results obtained with freshly prepared, DNB-pure M₁ and DN-pure A₁, M₂, and A₂ (Fig. 3A, red trace). In other words, enzymatic production of strands for CHA indeed resulted in lower background while requiring less purification.

Fig. 4.

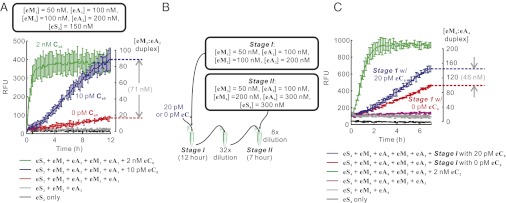
Performance of two-layer and four-layer linear CHA cascades that contain enzymatically synthesized substrate hairpins. (A) The performance of the two-layer linear cascade consisting of enzymatically synthesized eM₁ and eA₁ and chemically synthesized DN-pure eM₂ and eA₂. (B and C) Scheme and performance of the two-stage reaction of the four-layer linear cascade consisting of eM₁, eA₁, eM₂, eA₂, eM₃, eA₃, eM₄, and eA₄. Note that the two stages of reaction were carried out sequentially in different test tubes (main text).

Most importantly, in the presence of 10 pM eC₀, robust amplification was observed: At the end of the 12-h reaction, 71 nM of eM₂:eA₂ duplex above background was formed, marking a (71 nM/10 pM =) ∼7,000-fold signal amplification and a signal-to-background ratio at this low concentration of ∼4 (Fig. 4A, compare blue and red traces). Each of these factors represents an ∼10-fold improvement over our earlier data that relied on chemically synthesized hairpins (Fig. 3C) and the previous reports that relied on chemically synthesized substrates in entropy-driven cascades (17). This dramatically improved signal-to-background ratio should potentially allow the detection of much less initial trigger (eC₀) especially in an integrated detection system that strives to minimize noise levels. Moreover, we did not observe any background leakage of enzymatically prepared DNA hairpins in the single-layer assays, even when the hairpins had been stored at 4 °C for months. This is in distinct contrast to chemically synthesized, DN(B)-purified hairpins, which exhibited substantial leakage after storage at 4 °C for a similar period, to the point that they behaved similarly to D-pure hairpins.

Two-Stage, Four-Layer CHA Cascade for over 10⁵-Fold Signal Amplification.

To achieve even higher fold amplification, we designed two additional layers of CHA comprising hairpins eM₃, eA₃, eM₄, and eA₄ (see Fig. S6 C and D for their characterization in single-layer reactions) and coupled them with the first two layers. As before, eM₃ and eA₃ were enzymatically synthesized, whereas eM₄ and eA₄ were chemically synthesized followed by D purification. This two-layer cascade yielded ∼500-fold signal amplification after a 12-h reaction (Fig. S7). The low fold amplification obtained (only 7% as much as the ∼7,000-fold obtained with the first two layers) can be attributed to slow reaction within the fourth layer (eM₄ + eA₄), which had a k_app value of only 0.028⋅nM⁻¹⋅h⁻¹, 7% as fast as the second layer (eM₂ + eA₂, k_app = 0.37⋅nM⁻¹⋅h⁻¹; Fig. S2B). Notably, these reactions bookend other CHA reactions that we have designed in this work, all of which routinely exhibited k_app values between 0.1⋅nM⁻¹⋅h⁻¹ and 0.2⋅nM⁻¹⋅h⁻¹. Interestingly, the rate of CHA seemed to be negatively correlated with the strength of toehold binding (Fig. S8). The requirement for precise energy balancing is surprising, given that we had already designed all toeholds to be 50% GC. Mechanistically, these finding suggest that the rate of most reactions, especially the fourth-layer reaction, could be limited by product dissociation.

To test the four-layer cascade, we stacked the previously constructed two-layer cascades in sequence such that the second set of CHA reactions started only upon addition of finished reaction from the first set (Fig. 4B). In this way we could maximize signal while avoiding parallel development of background. First, two 20-µL, two-layer reactions (consisting of layers 1 and 2, i.e., 50 nM eM₁, 100 nM eA₁, 100 nM eM₂, and 200 nM eA₂) were initially executed with and without 20 pM initial catalyst eC₀. These reactions were incubated at 37 °C for 12 h, after which 1 µL of each reaction was diluted by 32-fold. A 2.5-µL aliquot of the diluted reaction was then added to a 17.5-µL mixture containing layers 3 and 4 (final concentrations: [eM₃] = 50 nM, [eA₃] = 100 nM, [eM₄] = 200 nM, [eA₄] = 300 nM, and [eS₄] = 300 nM). After ∼7 h, the reaction with 20 pM initial catalyst eC₀ resulted in ∼46 nM more final product than the reaction without initial catalyst (Fig. 4C, compare blue and red traces). The fold amplification can therefore be calculated to be (46 nM × 20 µL)/[20 pM × (2.5 µL/32)] = ∼600,000. That said, the signal-to-background ratio at this level of amplification was ∼0.3, similar to that seen with less layered, chemically synthesized CHA reactions. This ratio can likely be further improved by optimizing individual CHA reactions, using the sequence–activity relationships revealed in Fig. S8. Nevertheless, we have reported a uniquely high fold amplification with engineered enzyme-free, isothermal DNA circuits.

Discussion

There are several parameters that should be considered when describing the performance of an amplifier. Beyond fold amplification, which we defined in the introductory section, the sensitivity of an amplifier is also influenced by its signal-to-background ratio. The background, caused by leakage of the circuit, has a strong impact on background noise that determines the sensitivity of nucleic acid detection. In most cases background noise is positively correlated, and sometimes proportional, to background. Therefore, reduction of background usually results in increase of sensitivity (decrease of limit of detection). However, background is not the only determinant of background noise. Errors in liquid handling and quality of the final detector (e.g., the fluorometer) also determine the background noise. Therefore, the limit of detection is more useful in comparing entire detection systems, but can be misleading in comparing amplifiers. More informative and intrinsic parameters to compare are fold amplification and signal-to-background ratio at the same concentration of trigger. With ∼10 pM initial trigger (eC₀), the two-layer amplifier (composed of eM₁, eA₁, eM₂, and eA₂) yielded 7,000-fold signal amplification and 4-fold signal-to-background ratio, each parameter representing ∼10-fold improvement over our and previously reported (17) two-layer amplifiers based solely on chemically synthesized substrates. If such a circuit were to be integrated into a detection system that limited the combined error (including liquid handling and readout) to 5%, the 4-fold signal-to-background ratio would translate into an 80-fold signal-to-noise ratio, which would certainly allow the detection of much lower amounts of the initial trigger.

The potential impact of improved signal amplifiers and of technologies for limiting error accumulation on the development of molecular programming should be transformative. Because of the ease of designing circuits on the basis of the simple rules that govern base pairing, even the limited (∼10-fold) signal amplification achieved with entropy-driven circuits [such as Seesaw Gates (27)] has paved the way to substantial scaling up of DNA computations (1, 2). The 10³- to 10⁵-fold signal amplification achieved in this work and the new methods to generate ultrapure DNA substrates with more uniform conformations should now allow even more substantive advances to be made in DNA-based molecular programming.

Methods

All chemicals were purchased from Sigma-Aldrich or Fisher Scientific at analytical grade. All unlabeled oligonucleotides and fluorophore-labeled oligonucleotides were ordered from Integrated DNA Technologies (IDT) at desalted grade and other fluorophore- or quencher-labeled oligonucleotides were ordered from IDT at HPLC-purified grade. TOP10 chemically competent cells used for plasmid construction and propagation were purchased from Invitrogen. Procedures to purify chemically synthesized DNA hairpins and the method to obtain high-quality DNA hairpins through enzymatic synthesis are detailed in SI Methods, sections 1 and 2, respectively. Protocols to carry out kinetic measurements can be found in SI Methods, section 3. Domain sequences and oligonucleotide sequences are summarized in Tables S1 and S2, respectively.