Activationless charge transport across 4.5 to 22 nm in molecular electronic junctions

Abstract

In this work, we bridge the gap between short-range tunneling in molecular junctions and activated hopping in bulk organic films, and greatly extend the distance range of charge transport in molecular electronic devices. Three distinct transport mechanisms were observed for 4.5–22-nm-thick oligo(thiophene) layers between carbon contacts, with tunneling operative when d < 8 nm, activated hopping when d > 16 nm for high temperatures and low bias, and a third mechanism consistent with field-induced ionization of highest occupied molecular orbitals or interface states to generate charge carriers when d = 8–22 nm. Transport in the 8–22-nm range is weakly temperature dependent, with a field-dependent activation barrier that becomes negligible at moderate bias. We thus report here a unique, activationless transport mechanism, operative over 8–22-nm distances without involving hopping, which severely limits carrier mobility and device lifetime in organic semiconductors. Charge transport in molecular electronic junctions can thus be effective for transport distances significantly greater than the 1–5 nm associated with quantum-mechanical tunneling.

Charge transport mechanisms in organic and molecular electronics underlie the ultimate functionality of a new generation of electronic devices. Understanding, controlling, and designing molecular devices for use as practical components requires an intimate knowledge of the system energy levels and operative transport mechanisms, and how key variables such as molecule length, identity, temperature, etc., affect device performance parameters. Especially interesting in this context is the relationship between organic electronic devices, which typically have active layer thicknesses of tens to hundreds of nanometers, and molecular electronic devices reported to date, in which at least one dimension for charge propagation is below 10 nm. Indeed, many types of functional organic electronic devices have been demonstrated, including thin-film transistors, organic light-emitting diodes, and memory cells (1, 2). Bridging the gap between organic and molecular devices may therefore reveal pathways for improving the performance of such devices, or even lead to new types of devices based on alternative transport mechanisms.

The great majority of molecular electronic devices investigated to date have transport distances of <5 nm between the contacts, where the prevalent transport mechanism is quantum-mechanical tunneling. For this distance range, there is general agreement that the conductance scales exponentially with length, with an attenuation coefficient (β), defined as the slope of ln J vs. thickness (d), equal to 8 to 9 nm⁻¹ for aliphatic molecules (3–6) and 2–3 nm⁻¹ for aromatic molecules (7–14). A few molecular electronic systems have been investigated beyond 5 nm (15, 16), some of which exhibit a decrease in β to less than 1 nm⁻¹. Such small values of β are significant both practically (17, 18) and fundamentally (19–22), because they imply transport across distances much greater than the dimensions of single molecules and may enable complex molecular circuits. These low β-values are often dependent on temperature and have been attributed to activated hopping by a redox exchange mechanism (10, 23). However, phase-coherent tunneling has also been proposed for cases where the molecules have orbitals close in energy to the contact Fermi level (15, 24), resulting in minimal temperature dependence.

In this paper, we investigate the frontier between molecular and organic electronics by describing the electrical characteristics of conjugated molecular junctions of the structure carbon/molecule/carbon/Au over a wide range of thickness (from 4.5 to 22 nm). Reduction of a diazonium reagent of bis-thienylbenzene (BTB) (25–29) on carbon surfaces permits formation of molecular films of controlled thickness consisting of conjugated oligomers, and the electronic junction is completed by electron-beam deposition of carbon and gold (30). Such grafted oligo(BTB) layers can be easily p-doped and switched from insulating to conductive states in electrochemical conditions (25–28). Previous transport measurements in planar Au junctions containing a 7-nm–thick BTB molecular layer were explained with a mixed-transport mechanism combining a conducting molecular region with a tunnel barrier (31). In the present work, temperature and electrical field dependence of transport were analyzed to determine the likely transport mechanisms in three thickness regions: less than 8 nm, 8–16 nm, and greater than 16 nm. The results indicate three distinct transport mechanisms: coherent tunneling for d < 8 nm, activated hopping similar to that observed in bulk organic semiconductors for d > 16 nm, and a third mechanism which occurs over a broad range of temperature and electric field for molecular layer thicknesses of 8–22 nm.

Results and Discussion

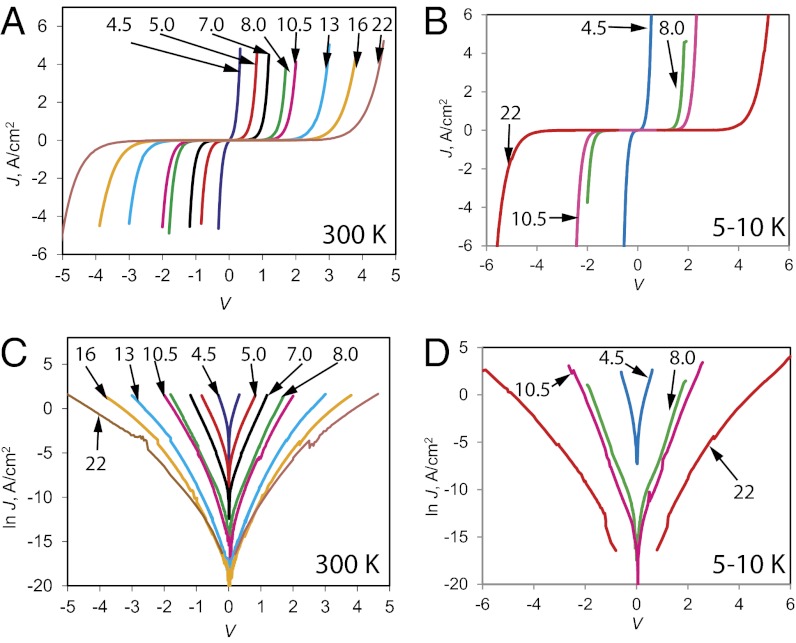
Molecular junctions (area = 0.0013 cm²) were constructed (9, 30, 32, 33) on pyrolyzed photoresist film (PPF), which is a flat, conducting sp² hybridized carbon surface described in detail previously (34). SI Appendix, Fig. S1 shows a junction schematic and the four-wire electronic apparatus used for device characterization; SI Appendix, sections 2 and 3 detail the fabrication procedure and thickness determination. Current density vs. voltage (JV) curves obtained for PPF/BTB/e-C/Au junctions with BTB thickness from 4.5 to 22 nm are shown in Fig. 1 A and C for linear and semilog J scales, respectively. Fig. 1 B and D shows a selection of the same devices collected at temperature (T) <10 K on linear (Fig. 1B) and semilog (Fig. 1D) scales. It is clear from analysis of these curves that: (i) J is nonlinear in V, but nearly symmetric with respect to polarity; (ii) the slope of ln J vs. ln V approaches 1.0 at low V, but increases to 13–15 at high V (SI Appendix, Fig. S5 and Table S2); (iii) there is a strong dependence on thickness of the BTB layer; and (iv) there are no major changes in appearance or symmetry of the JV curves between high and low T.

Fig. 1.

Current density vs. voltage (JV) curves for PPF/BTB/e-C/Au molecular junctions with BTB layer thickness indicated on each curve in nanometers. In all cases, the top contact consisted of 10 nm of carbon (e-C) and 15 nm of Au deposited by electron-beam evaporation at ∼5 × 10⁻⁷ torr. PPF is pyrolyzed photoresist film with covalent bonding to BTB layer, described previously (14, 34) (SI Appendix, section 2). JV curves were obtained with a four-wire geometry to correct for lead resistance. A and C were obtained at 300 K in air, whereas B and D were obtained at <10 K in vacuum.

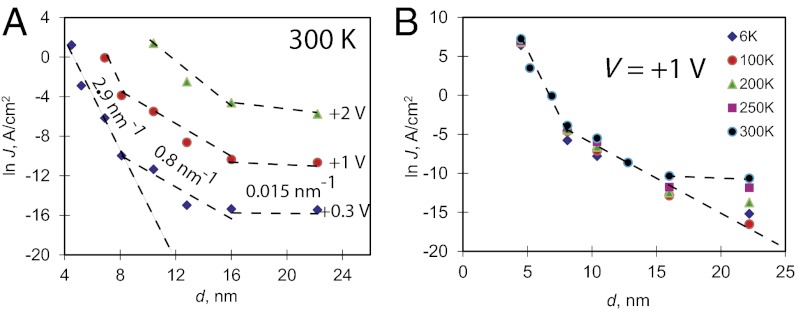
To visualize the strong effect of thickness more directly, Fig. 2A displays room temperature attenuation plots (ln J vs. d) at three different bias voltages for all of the data in Fig. 1. The slope of the attenuation plot gives the value for β, a characteristic transport parameter that has been tied to transport mechanism, molecule identity, and other electronically relevant parameters such as conjugation length. There are three statistically distinguishable β-values identified from Fig. 2A (listed in SI Appendix, Table S3): β = 3.0 ± 0.3 nm⁻¹ (mean ± SD for n = 8) for d = 4–8 nm; β = 1.0 ± 0.2 nm⁻¹ (n = 19) for d = 8–16 nm; and β < 0.2 nm⁻¹ (n = 6) for d = 15–22. The values of β for d < 8 nm agree well with the 2–4 nm⁻¹ values reported for other aromatic molecules for this range of thickness (13, 14). Note that extrapolation of the ln J vs. d plot in the β = 3 nm⁻¹ region to d >8 nm (shown by the dashed line in Fig. 2A) predicts current densities that are well below the observed values for d >8 nm, and J is predicted to decay below the detection limit at 0.3 V for d > 15 nm. This result clearly demonstrates that additional mechanisms must contribute for d > 8 nm. Previous studies using aromatic molecules have reported a transition from β ∼ 3 nm⁻¹ to ∼1 nm⁻¹ when d exceeds 4–5 nm (10, 23) This transition was attributed to a change in mechanism, with tunneling current dominant for the <4–5-nm region and thermally activated hopping for thicker layers. In these cases, the transition was accompanied by a change from temperature-independent current to measured activation barriers of 0.3–0.5 eV (10, 23, 35).

Fig. 2.

(A) Attenuation plots (ln J vs. d) at three bias values indicated, obtained at 300 K in air. (B) Attenuation plots obtained at V = +1 V at the indicated temperatures between 6 and 300 K, all in vacuum. Linear regions with three different slopes are indicated by dashed lines. In two instances (4.5 and 5.2 nm at 300 K) in B, the current was too high to be measured at 1 V; these data points were obtained by extrapolating curves obtained at 0.5 to 1 V. SDs for similar devices are <25% in J and ±0.6 nm in thickness (9, 14, 30).

Fig. 2B shows an overlay of attenuation plots for BTB with a bias of +1 V obtained at five temperatures from 6 to 300 K. Importantly, for d < 8 nm both the value of β and the current magnitude are weakly dependent on temperature, consistent with transport controlled by quantum-mechanical tunneling, as previously reported for similar junctions (9, 30, 31). However, for the intermediate thickness range (8–12 nm), the current density decreases slowly with lower temperature, whereas β itself does not change significantly. This result indicates a low activation energy (described below), but also that the dominant transport mechanism in the β = 1.0 nm⁻¹ region is not strongly temperature dependent. For the thickness range of 16–22 nm, the attenuation factor β undergoes a shift from nearly zero to higher values at lower temperatures, approaching the β = 1 nm⁻¹ line extrapolated from d = 8–16 nm (Fig. 2B). Thus, for the thickest layers (>16 nm), there is an additional thermally activated transport mechanism with β < 0.2 nm⁻¹. SI Appendix, Fig. S4B shows direct overlap of the JV curves for 16 and 22 nm for low V and 300 K, confirming the small value of β. As discussed below, this additional current observed for d > 16 nm has characteristics of hopping, i.e., significant activation energy and weak distance dependence.

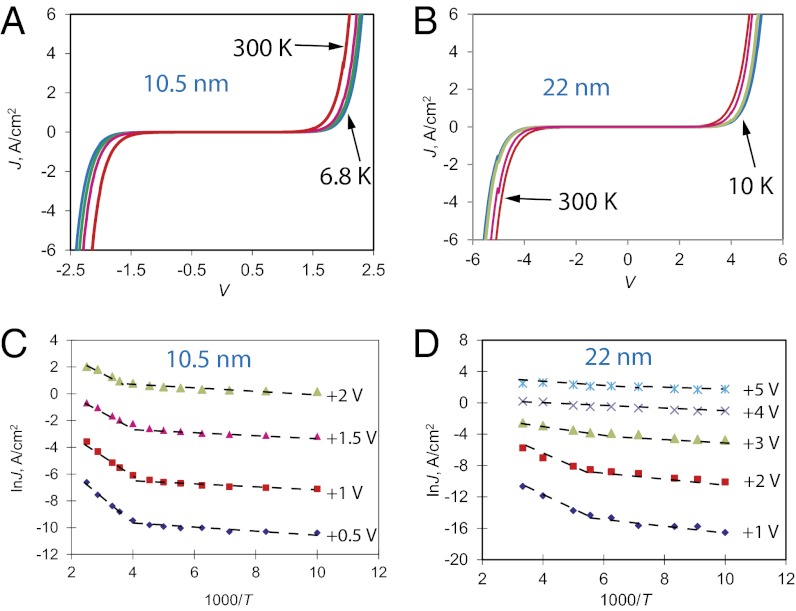
Fig. 3 A and B shows JV curves obtained from <10–300 K for 10.5- and 22-nm BTB junctions (d = 4.5 and 8.0 nm are shown in SI Appendix, Fig. S6). Arrhenius plots derived from JV curves at several bias values are shown in Fig. 3 C and D, and Table 1 provides activation barrier energies (E_a) derived from Arrhenius slopes as a function of bias, temperature range, and BTB thickness. In most cases, there are two linear sections: a high-temperature region with E_a > 100 meV and a low-temperature region with much smaller E_a, usually <25 meV. Several observations, which bear directly on the transport mechanism(s), are possible by analyzing data in Table 1 and Fig. 3. First, E_a is <0.5 meV for all thicknesses and voltages in the temperature range from 5 to 50 K. Second, the higher E_a values (150–300 meV) are observed in the high-thickness regime (d = 16–22 nm) for T = 200–300 K and low V where β ∼ 0. Moreover, for this regime the E_a decreases sharply with increasing bias voltage. Third, E_a values of 26–85 meV with weaker T dependence are observed in the same temperature range for d = 8.0 and 10.5 nm.

Fig. 3.

JV curves at <10, 100, 200, and 300 K for (A) 10.5- and (B) 22-nm junctions. Arrhenius plots of ln J vs. 1000/T for (C) 10.5- and (D) 22.2-nm BTB junctions, obtained at the indicated bias values. Linear portions are identified by dashed lines, and a complete listing of E_a appears in Table 1. SI Appendix, Fig. S8A shows the dependence of E_a on bias.

Table 1.

Arrhenius slopes for varying thickness and bias

		Ea, meV
d, nm	V	5–50 K	100–200 K	200–300 K
	0.1	0.16	9	30
4.5	0.2	0.12	6	24
	0.5	0.1
8.0	0.2	0.28	5	26
	0.5	0.12	4	39
	1.0	0.04	4	48
	1.5	0.08	3	43
10.5	0.2	0.15	13	85
	0.5	0.43	8	79
	1.0	0.01	8	75
	1.5	0.1	8	54
	2.0	0.08	6	36
16	0.2			291
	0.5		10	209
	1.0		5	175
	1.5		2	130
	2.0		2	99
	3.0		1	60
22	1.0	0.26	43	160
	2.0	0.43	33	119
	3.0	0.34	22	47
	4.0	0.09	13	28
	5.0	0.03	10	9

We now consider the electrical characteristics of the thicker junctions (d = 8–22 nm) in conditions where β ∼ 0 or 1 nm⁻¹ to assess possible transport mechanisms. Temperature-dependent transport with a small β-value has been associated with activated hopping between sites in both single molecules (35, 36) and ensemble junctions (16, 23), presumably governed by Marcus–Levich kinetics. The low-V, high-T Arrhenius slopes of 150–300 meV listed in Table 1 are comparable to those reported for bulk polythiophene, e.g., 128–143 meV (37) and 280 meV (38), in which interchain charge transfer dominates transport (39, 40). The additional thermally activated transport mechanism that provides an extra current contribution and yields the β = 0 nm⁻¹ values seen in BTB devices at room temperature can thus be attributed to redox hopping, and represents the bulk limit commonly observed in organic semiconductors. However, for either high V or low T, the activated character of transport is diminished, indicating a change in mechanism. Regardless of the origin of such behavior, an important and exciting consequence is the possibility of long distance, activationless charge transport across distances not possible with coherent tunneling.

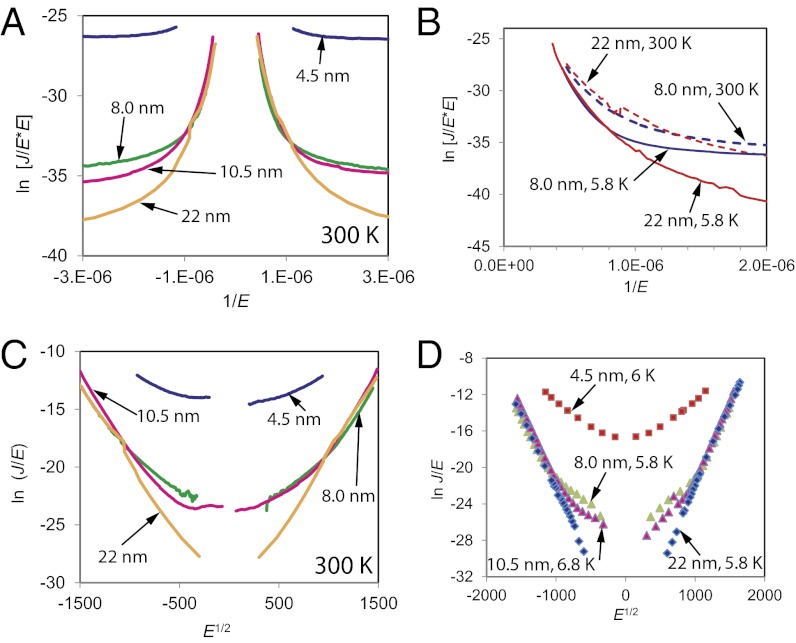
Several classical mechanisms possible in molecular junctions in addition to tunneling and hopping include thermionic (i.e., Schottky) emission, field ionization (i.e., Fowler–Nordheim, or FN, tunneling), Poole–Frenkel (PF) transport between Coulombic traps, and variable range hopping (VRH). Of these, FN tunneling is independent of temperature, and is predicted to yield a linear plot of ln (J/E²) vs. 1/E (i.e., an FN plot), where E is the electric field (41, 42). Fig. 4A shows an overlay of FN plots of BTB junctions as a function of BTB thickness at 300 K. Note that the curves for d = 8.0, 10.5, and 22 nm converge at high field, implying that transport is controlled by electric field above E = 1 MV/cm. Fig. 4B shows the same plot for the 8.0- and 22-nm thicknesses at 6 and 300 K. It is clear that the curves converge at high E for both temperatures, but do not exhibit the linear region predicted from FN theory. VRH is characterized by a linear plot of ln J vs. T^-1/4 for three-dimensional Mott VRH or ln J vs. or T^-1/2 for one-dimensional Mott VRH or Efros–Shklovskii VRH (43–45). Several such plots are shown in SI Appendix, Fig. S7, and exhibit no linear regions for the temperature dependence shown in Fig. 3. We conclude that neither VRH nor FN mechanisms are consistent with the JV results over the entire temperature and bias ranges examined. PF and Schottky mechanisms predict linearity of ln (J/E) vs. E^1/2, and such plots are shown in Fig. 4C at 300 K and Fig. 4D for < 10 K. The curves for d = 8.0–22 nm converge at high E at both temperatures, and the low-T case shows excellent linearity of ln (J/E) vs. E^1/2, especially for d = 22 nm for which R² = 0.9989 over 8 orders of magnitude of J/E. Both mechanisms also predict linearity of E_a vs. E^1/2 with intercepts at zero field equal to the barrier height. Such plots are shown in SI Appendix, Fig. S8A, exhibiting reasonable linearity for 16- and 22-nm junctions for the 200- to 300-K Arrhenius slopes, and intercepts at zero field indicating barrier heights of ∼350 meV (16 nm) and ∼300 meV (22 nm). These results indicate that PF or Schottky mechanisms may be valid above 200 K for d ≥ 16 nm, where a voltage-dependent E_a is observed (Table 1). PF transport has been proposed for organic semiconductors across distances greater than studied here, and is consistent with observed E dependence (46–49).

Fig. 4.

(A) FN plot of ln (J/E²) vs. 1/E, where E = electric field (V/cm) at 300 K for the indicated BTB thicknesses. (B) FN plot for 8.0- and 22-nm BTB devices at <5.8 and 300 K. (C and D) PF plots of ln (J/E) vs. E^1/2 for the same four BTB thicknesses at (C) 300 and (D) <10 K.

However, PF and Schottky mechanisms are not consistent with the weak temperature dependence below 200 K. Comparing Fig. 4 C and D, the experimental curves are very similar for 300 K and <10 K, contrary to the predictions of Schottky and PF equations for ∼300-meV barriers. As shown in SI Appendix, Fig. S8B, the slope of the experimental ln (J/E) vs. E^1/2 plot increases by a factor of 1.32 between 300 and 6 K for d = 22 nm, although theory predicts it should increase by a factor of >50 (300/6) for either PF or Schottky mechanisms. We conclude that classical Schottky or PF transport cannot explain transport in BTB junctions, nor can the FN or VRH models discussed above. Therefore, there must be another mechanism operative below 200 K which becomes dominant at moderate and high electric field. This mechanism has not been reported previously for molecular junctions, and is temperature independent with a β of ∼1.0 nm⁻¹ for BTB junctions with d = 8–22 nm, as shown in Fig. 2.

Given that classical mechanisms are not consistent with the BTB JV behavior, we note a few recent observations of field-driven mechanisms for transport in much thicker organic films (>100 nm) (46–49). Whereas transport dimensions and bias voltages were much larger than the 4.5–22-nm range studied here, a linear dependence of ln J vs. E^1/2 was observed, as was T-independent conductance at low T. Although the mechanism is controversial, these observations were attributed to field-assisted hopping (46, 48), field-assisted tunneling (47, 48), multistep tunneling (47), or behavior similar to a Luttinger liquid (49). For the case of polythiophene thin-film transistors, a transition from PF-like behavior at room temperature to temperature-independent field-emission hopping with an E^1/2 dependence at low temperature was reported (48).

In the present case, to explain transport in the region where β ∼ 1.0 nm⁻¹, we propose that field ionization occurs when the stabilization energy of an electron in the applied field exceeds the trap depth, similar to PF transport. The “trap” could be a localized state such as the highest occupied molecular orbital (HOMO) of oligo(BTB) or a hybrid orbital that has density on both the molecule and the contact, such as a “gap state” (50). Such hybrid states are likely in a system with a covalently bonded molecular layer, which is known to induce Fermi-level pinning and strong electronic coupling (14, 50). The distinction between classical PF behavior and the proposed field ionization mechanism lies in the events following ionization. Conventional activated PF transport involves thermal carrier generation assisted by the applied field, and subsequent transport characterized by the mobility of the carriers. The very short transport distances in the BTB junctions may permit ballistic carrier transport following ionization, such that ionization and transport are concerted. Rapid refilling of the field-ionized orbital from one electrode would permit further ionization and current flow with no need for reorganization, thus maintaining activationless transport. An additional possibility after the initial field-ionization event is relaxation of the ionized centers to form polarons, resulting in new conduction channels with high conductivity. Such polarons are expected to be 5–10 nm long, and are therefore comparable to the thickness of several of the BTB junctions studied, so that a single intrachain transfer is sufficient for charge transport within the molecular layer (51, 52). Such intrachain transport is expected to have activation energies in the 40–80-meV range (51), consistent with some of the low observed E_a values.

Conclusions

Charge transport in 4.5–22-nm BTB molecular junctions is characterized by three attenuation factors and three distinct mechanisms. For d < 8 nm, current is controlled by coherent tunneling, with minimal temperature dependence and β = 3 nm⁻¹, as described previously for conjugated molecular junctions (9, 14, 30). For low field and high T, the thickest devices (d > 16 nm) exhibit hopping transport with β < 0.1 nm⁻¹ and strong T dependence, similar to that observed for bulk organic semiconductors. For a wide range of thickness (8–22 nm) and T (6–300 K), a third, nearly activationless mechanism with β ∼ 1 nm⁻¹ and E_a between 0 and 80 meV is observed, for which the current is controlled mainly by the electric field. This mechanism is consistent with field-induced ionization of molecular HOMOs or interface states to generate charge carriers. The field required for onset of ionization is presumably dependent on the energy of the orbital to be ionized relative to the system Fermi level. Following ionization, the empty state may be rapidly refilled from the negatively biased electrode, or may reorganize to form a polaron and a new conducting channel. Activated hopping is important for thicker films at high T and low electric field, whereas field ionization becomes dominant at high electric field and all temperatures examined. In addition to identifying an additional transport mechanism for molecular junctions, the current report unifies the fields of molecular and organic electronics by covering distances from short-range tunneling to activated, long-range hopping which underlies transport in bulk organic semiconductors.