Wing flexibility enhances load-lifting capacity in bumblebees

Abstract

The effect of wing flexibility on aerodynamic force production has emerged as a central question in insect flight research. However, physical and computational models have yielded conflicting results regarding whether wing deformations enhance or diminish flight forces. By experimentally stiffening the wings of live bumblebees, we demonstrate that wing flexibility affects aerodynamic force production in a natural behavioural context. Bumblebee wings were artificially stiffened in vivo by applying a micro-splint to a single flexible vein joint, and the bees were subjected to load-lifting tests. Bees with stiffened wings showed an 8.6 per cent reduction in maximum vertical aerodynamic force production, which cannot be accounted for by changes in gross wing kinematics, as stroke amplitude and flapping frequency were unchanged. Our results reveal that flexible wing design and the resulting passive deformations enhance vertical force production and load-lifting capacity in bumblebees, locomotory traits with important ecological implications.

1. Introduction

Insect wings are flexible structures that passively bend and twist during flight. Although our understanding of the mechanisms by which insects produce aerodynamic force has increased dramatically over the last several decades [1–3], nearly all of this research has ignored flexible wing deformations by modelling wings as simplified rigid plates. Recently, a new wave of research has focused on uncovering the aerodynamic effects of wing deformations, both to understand the implications of diverse insect wing designs and to maximize performance of bioinspired micro air vehicles. Most of these studies have employed either computational fluid dynamics simulations [4–8], where wing flexibility or emergent deformations are numerically manipulated to probe their aerodynamic contributions, or robotic flapping devices [9–11], where flows and forces produced by wings of varying stiffness are measured. Results from these studies are not always in agreement, however, raising uncertainty about the aerodynamic consequences of wing deformation in insect flight and the adaptive significance of flexible wings.

Recent computational models have shown that realistic wing kinematics of deforming locust [4] and hoverfly [5] wings generate greater stroke-averaged lift and power economy than simplified flat-plate aerofoils oscillating at the same instantaneous angle of attack (AoA; defined at either the mid-wing; [4], or the radius of second moment of area; [5]). In another recent computational analysis, Nakata & Liu [6] built a fluid–structure interaction-based model of hawkmoth wing kinematics, and found that wing flexibility increases stroke-averaged vertical aerodynamic force production and efficiency, compared with rigid wings that are flapped with the same wing base kinematics. By contrast, recent physical modelling studies using robotic flapping devices have revealed that rigid wings can produce greater lift than flexible ones [10,11]. Zhao et al. [10] used a dynamically scaled mechanical model of low-Reynolds number (approx. 2000) flapping flight to measure the aerodynamic forces produced by homogeneous wings with a range of flexural stiffnesses, and found that a rigid wing produced the greatest stroke-averaged lift at angles of attack up to 50°, beyond which flexible wings began to dominate. Tanaka et al. [11] used a piezoelectric flapping mechanism to directly measure forces on an at-scale model of a hoverfly wing, and found that a model wing mimicking the average flexural stiffness of a natural wing generated lower mean lift than a rigid carbon fibre wing flapped with the same actuation pattern. Despite this convergence of research using both computational and robotic approaches, the aerodynamic consequences of flexible wing deformations has never been directly tested in live insects.

Wing flexibility results from the structural and material properties of the hollow supporting veins and thin membranes making up a wing [12]. In some insects, wing flexibility may be enhanced by embedded resilin structures [13–15]. Resilin is a flexible, rubber-like protein with an extremely high elastic efficiency that appears in the locomotory structures of many insects [16–18]. The few studies that have mapped the distribution of resilin in insect wings report that the protein is typically found in joints between veins, where wings either fold at rest or are likely to flex during flight [13–15,19], although a recent study found that resilin is also present in some proximal areas of wing membrane in blowfly wings [20]. However, the effect of resilin on overall wing stiffness and the extent to which it influences patterns of wing deformation during flight has not been explored.

We mapped the distribution of embedded resilin structures in the bumblebee wing and developed a technique to splint a particular resilin vein joint with a small piece of glitter, substantially increasing wing stiffness with minimal addition of mass. This novel wing stiffening method presented us with a unique opportunity to directly explore the effects of wing flexibility on aerodynamic force production in a live insect. No study to date has tested the aerodynamic effects of wing flexibility in live insects owing to the technical challenges associated with experimentally manipulating wing stiffness in vivo. Insect wings are small, extremely lightweight structures (estimated to be 0.4–6.0% of body mass; [21]), and in many insects, the wings and thorax form a resonant system that is highly sensitive to changes in wing mass. Methods designed to increase wing stiffness by coating all or part of the wing with a stiffening agent thus risk increasing wing mass to the point of dramatically altering wing dynamics or preventing natural flight behaviour entirely. Motivated by our finding that bumblebee wing stiffness can be altered by splinting just one vein joint with minimal addition of mass, we applied this technique to live bees, and used a load-lifting test to directly measure the contribution of wing flexibility to maximum vertical aerodynamic force production and load-carrying capacity.

Load-lifting experiments have been used to quantify maximum vertical aerodynamic force production and maximum power output in insects [22–25], birds [25–27] and bats [25] and have been shown to reliably predict insect load-carrying capacity in nature [28,29]. Load-lifting tests typically involve attaching supplemental mass to the animal and recording the maximum load it can lift off the floor, either by incremental addition of mass [22,23,28], or by attaching a weighted string that applies an asymptotically increasing load as the animal ascends [23,24,26,27].

These load-lifting studies are based on the assumption that the animal is acting to maximize vertical aerodynamic force production, within its anatomical and physiological limits, in response to a progressively increasing load. It does so by increasing wing velocity—through changes in stroke amplitude, wingbeat frequency or both—until it reaches its maximum flight muscle power output, and hence its maximum vertical aerodynamic force and load-carrying capacity. Beyond altering wingbeat frequency and/or amplitude, little is known about potential modulation of more subtle kinematic features, as AoA, to maximize vertical aerodynamic force [23,26,30]. This is due in part to the technical difficulties involved in imaging extremely rapid, subtle kinematic features of freely flying animals, and in part due to the fact that most techniques for measuring AoA rely on a rigid-wing assumption, making this a difficult parameter to define precisely in flexible wings, particularly during stroke reversals, when wings undergo significant deformations.

In this study, we artificially stiffened bumblebee wings by splinting a centrally located resilin joint with a small piece of glitter. We measured the effect of this joint splint, as well as a control splint applied to an adjacent location containing no resilin, on overall wing flexural stiffness (EI) in the chordwise direction. We then tested the effects of wing stiffening on vertical aerodynamic force production by performing a series of load-lifting tests with both control and experimental splints applied to each bee. Our results show that a single resilin vein joint plays an important role in overall wing flexibility and vertical aerodynamic force production in bumblebees.

2. Material and methods

Bumblebee hives of Bombus impatiens were purchased from International Technology Services and stored in a 0.6 × 0.6 × 1.8 m netting enclosure in the laboratory. The bees had access to a reservoir of BIOGLUC artificial nectar (approx. 50% sugar solution) within the hive, and could enter and leave the hive freely to explore the surrounding enclosure.

(a). Artificial wing stiffening

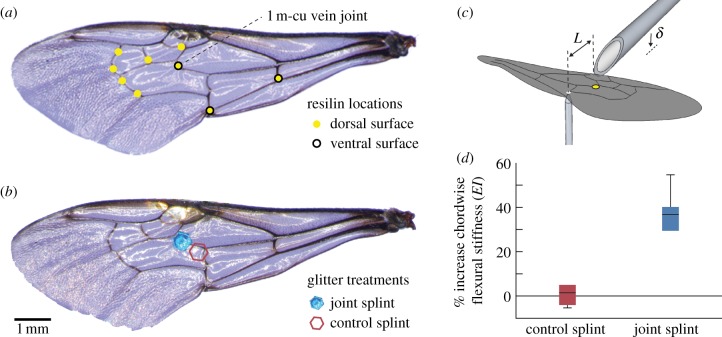
We mapped the distribution of resilin in the bumblebee wing using fluorescent microscopy (340–380 nm excitation, 420 nm emission filter, figure 1a) [15]. Among the nine patches of resilin discovered, three contained resilin on both the dorsal and ventral sides of the wing, and we hypothesized that the most centrally located of these (along the first medio-cubital cross-vein; 1 m-cu [31]) plays a particularly important role in chordwise wing flexibility. We immobilized the 1 m-cu joint with a micro-splint, consisting of a single piece of extra-fine polyester glitter glued across the joint with cyanoacrylate (figure 1b; electronic supplementary material, movie S1). The mass of the glitter and glue together was approximately 5 per cent of the total forewing mass. Because even this small addition of mass may affect wing dynamics, we also developed a control treatment, in which we affixed a piece of glitter immediately adjacent to the resilin joint, still overlapping the 1 m-cu vein but not interfering with the joint (figure 1b).

Figure 1.

Experimental manipulation of wing stiffness in bumblebees. (a) Resilin structures mapped on the forewing of a bumblebee, Bombus impatiens, using fluorescent microscopy. (b) A piece of extra-fine polyester glitter (0.4 mm diameter, 20 µg) was affixed to the dorsal wing surface with cyanoacrylate, either splinting the 1 m-cu joint (experimental treatment, blue), or positioned adjacent to the joint (control treatment, red). (c) Method used to measure wing flexural stiffness. Each forewing was affixed at the leading edge to the tip of a syringe needle, and positioned above a pin attached to a micro force sensor. The wing was lowered a small distance (δ, 5% chord length) onto the pin head, applying a point force along the second branch of the cubitus vein at 85% chord length from the leading edge (L). The yellow dot marks the location of the 1 m-cu vein joint. (d) Percent increase in chordwise flexural stiffness (EI) caused by the control splint (Wilcoxon signed-rank test: p = 0.844) and joint splint (p = 0.031).

To quantify the effect of joint immobilization on overall wing flexibility, we measured flexural stiffness before and after splint application in a total of 12 freshly extracted bumblebee wings; six wings received a joint splint and another six received a control splint. We determined chordwise flexural stiffness by immobilizing the wing at the leading edge and measuring the force required to deflect the trailing edge by a small, known distance (figure 1c) [9,32] The wing was attached at its leading edge to the tip of a syringe needle using Crystalbond adhesive. The syringe needle was fastened to a three-axis manual translation stage, and the wing was positioned dorsal-side-up above a vertically oriented pin attached to a micro force sensor (Femtotools FT-S540), to measure force applied to the ventral surface of the wing. The force sensor signal was captured by a data acquisition board (NI USB-6229 BNC) and recorded to a computer at 1 kS s⁻¹. The head of the pin was precisely aligned to contact the second branch of the cubitus vein at 85 per cent chord length from the leading edge.

During each trial, the wing was slowly depressed onto the pin head until its deflection reached 5 per cent of chord length, held in place for 5 s, and then quickly lifted off the pin. From the resulting force trace, we calculated the mean force between (t₀−4) and (t₀−1) seconds, where t₀ marked the instant the wing was completely lifted off the pin (easily identifiable on the force trace). Thus, the representative force was a 3 s average of the applied load during full wing deflection. We then calculated wing chordwise flexural stiffness (EI) as

where F is force, L is beam length from the leading edge of the wing to the point of force application and δ is deflection (figure 1c) [9,32]. For each wing, we performed five consecutive stiffness measurements in the un-manipulated state, and another five measurements immediately following splint application (either the joint splint or control splint treatment). All stiffness measurements were completed within 30 min of wing removal, to minimize the gradual effects of wing stiffening caused by desiccation [33]. We used the median EI value from each set of pre- and post-manipulation measurements to calculate percent increase in chordwise flexural stiffness.

(b). Load-lifting trials

To quantify maximum vertical aerodynamic force production, we measured bee load-lifting capacity by attaching a beaded string that applied an asymptotically increasing load as the bee ascended. We tested the effects of both the joint splint and control splint treatments (applied symmetrically to both wings) on the aerodynamic force capacity of each bee using a randomized, repeated measures design. The experimental protocol consisted of two rounds of splint applications (one experimental and one control splint treatment) and flight trials per bee. We tested a total of 17 bees; seven bees received the joint splint treatment first, another seven received the control splint treatment first, and three bees were subject to sham treatments. The sham-treated bees underwent the same experimental protocol as the others, but splints were never attached to the wings.

To ensure that bees carried sufficient energy reserves to undergo two rounds of wing treatments and multiple flight trials at maximum power output, they were initially deprived of food in order to motivate ingestion of artificial nectar. We placed each bee in a separate cage without food for 3–4 h, measured its body mass after food deprivation, and then allowed it to feed on nectar for 10–15 min. Most bees ingested a large quantity of nectar, sometimes gaining so much mass that they struggled to get airborne with the additional load. Therefore, each bee was returned to a separate cage without food for another 30 min prior to testing, allowing it reduce some of its water content.

Each bee was cold-anaesthetized at −15°C for 5–10 min until the first signs of quiescence, then promptly removed from the freezer and outfitted with a beaded string and the first set of wing splints. A noose of braided monofilament thread was tightened around the bee's petiole, near the centre of body mass [23], and the free end was tied to a fine polyester thread (approx. 35 cm in length) with groups of two beads attached every 3–4 cm. Although the distance of the applied weight from the bee's centre of mass may induce a pitching moment [23], it has previously been shown that maximum lift production in dragonflies is not affected by the location of weight attachment, despite large variation in applied pitching moments [25]. Furthermore, natural body pitching moments in honeybee foragers caused by large exogenous loads of pollen (stored on the hind legs) and nectar (stored in the abdominal honey crop) have no effect on wingbeat frequency, stroke amplitude, body angle or the inclination of the stroke plane [34].

Following anaesthetization, the bee was placed in a custom brace designed to splay its wings apart, allowing us to precisely apply wing splints under a high-powered dissecting scope without harming the individual or its wings. The bee was allowed to recover at room temperature for 10–20 min before flight trials began.

Bees were placed in a 60 × 30 × 40 cm glass flight chamber in a dark room. Three of the interior chamber walls were coated with fluon to discourage the bee from climbing, while the fourth wall was left clear for filming. A UV lamp was suspended above the chamber to attract the bees upwards, and the chamber was illuminated from the sides with two red lamps (invisible to the bees; [35]) to enable video imaging of load-lifting trials. Flight trials were recorded from the side and top with two high-speed cameras (Photron SA-3) filming at 1500 frames/second. We recorded three to six load-lifting trials for each wing treatment. During each trial, the bee would ascend from the bottom of the chamber, progressively lifting more beads off the ground until it reached its load-carrying capacity, transiently hover at constant height and then descend (see the electronic supplementary material, movie S2).

In each of the first 6 bees tested, we measured body mass before and after all load-lifting trials within a given treatment (i.e. three to six lifting flights), and found that body mass was substantially reduced over even this short period, presumably due to evaporation and excretion of metabolic water [36]. We therefore modified our experimental protocol for the remaining 11 bees (including the three sham-treated bees) to measure body mass after each load-lifting trial, in order to reduce uncertainty in our subsequent calculations of aerodynamic force capacity (see below). Following the load-lifting test for the first wing splint treatment, we re-anaesthetized the bee, peeled off the first set of wing splints with tweezers, attached new splints for the second treatment and performed another load-lifting test.

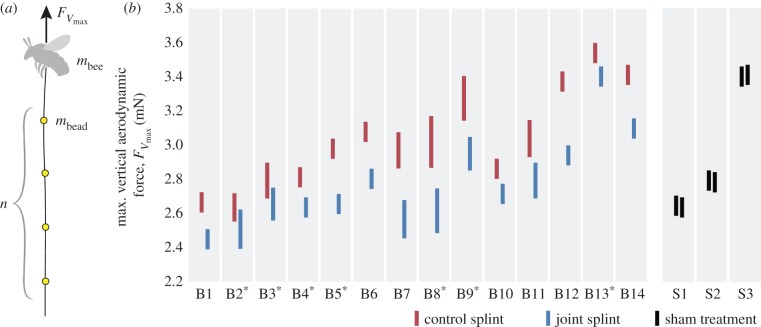
We calculated maximum vertical aerodynamic force produced during each load-lifting trial based on the maximum load carried, including both body mass and total bead/string mass (figure 2a). The mass of each bead group was estimated by dividing the total mass of the beaded string by the number of attached bead groups. We examined the flight videos to determine the total number of bead groups lifted in each trial, which we multiplied by the mass per bead group to find the total bead and string mass lifted. Body mass was approximated as the average of the two body mass measurements recorded before and after all load-lifting trials in the six bees for which we did not have inter-trial body mass measurements, or before and after each load-lifting trial in the remaining 11 bees. We calculated maximum vertical aerodynamic force, 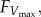for each trial as the product of total mass lifted (body plus bead/string) and gravitational acceleration (9.81m s⁻²). We report the highest maximum vertical aerodynamic force value calculated for each set of load-lifting trials for each treatment, although maximum force measurements were generally quite consistent within the three to six trials performed following each treatment.

Figure 2.

Results of load-lifting tests in bees with experimentally manipulated wing stiffness. (a) A string with evenly spaced, uniform bead groups was attached to a bee's petiole, applying an asymptotically increasing load as the bee ascended. Three to six load-lifting trials per bee were captured on video, and maximum vertical aerodynamic force was calculated as 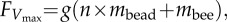where g is the earth's gravity, n the maximum number of bead groups lifted, and m_bead and m_bee are mass per bead group and bee body mass. (b) Maximum vertical aerodynamic force produced by 14 bees (B1–B14, arranged by increasing wing span) subject to both the control splint (red) and joint splint (blue) treatments and three bees (S1–S3) subject to sham treatments. Bees that received the joint splint treatment first are indicated with an asterisk. Bar height encompasses measurement uncertainty, owing to both the mass of an individual bead group (measurement resolution is limited by the discrete n × m_bead term) and any decrease in body mass between the beginning and end of a flight trial.

We analysed the load-lifting videos to measure wingbeat frequency and stroke amplitude during maximal load lifting for each treatment. Since stroke planes of hovering bumblebees are close to horizontal [37,38], we quantified stroke amplitude in the top-view video by digitizing extreme anterior and posterior wing positions in the flapping cycle using Matlab digitization software [39]. We digitized two points along the leading edge of each forewing, one near the wing base and the other at mid-wing, at 10 consecutive stroke reversals, and calculated stroke amplitude as the mean swept angle of both wings across five strokes. Mean wingbeat frequency was calculated over 40 complete strokes during peak load lifting.

3. Results

Splinting the 1 m-cu joint caused a significant increase in chordwise flexural stiffness (Wilcoxon signed-rank test: p = 0.031), whereas the control splint had no effect on EI (Wilcoxon signed-rank test: p = 0.844). The joint splint increased flexural stiffness by an average of 37.6 ± 9.37% (N = 6, figure 1d). Most of the wings exhibited moderate viscoelastic relaxation under load, with an average relaxation rate of −3.71 ± 4.55 × 10^–11 (kg m³ s⁻²) s^–1 (N = 24, based on results of a least-squares linear regression on EI values of all wings in both treatments during the 3-s period of maximal stress).

Artificial wing stiffening caused a significant reduction in maximum vertical aerodynamic force production (figure 2b). When the joint splint was applied, bees produced a maximum vertical force that was 8.55 ± 3.27% lower on average (N = 14) than the same bees with the control splint applied (paired t-test: t = 9.08, d.f. = 13, p < 0.0001). The mean maximum vertical aerodynamic force in the control treatment was 3.03 ± 0.28 mN (N = 14), compared with 2.77 ± 0.26 mN in the joint splint treatment. By contrast, there was no significant difference in maximum vertical force production between the two sham treatments in the three bees (Wilcoxon signed-rank test: p = 1).

There was no significant difference in wingbeat frequency (paired t-test: t = 0.799, d.f. = 13, p = 0.439) or stroke amplitude (paired t-test: t = −0.228, d.f. = 13, p = 0.824) between the control splint and joint splint treatments (figure 3). The mean wingbeat frequency for all bees in both treatments was 173 ± 4.3 Hz (N = 28), and the mean stroke amplitude was 140° ± 2.6°.

Figure 3.

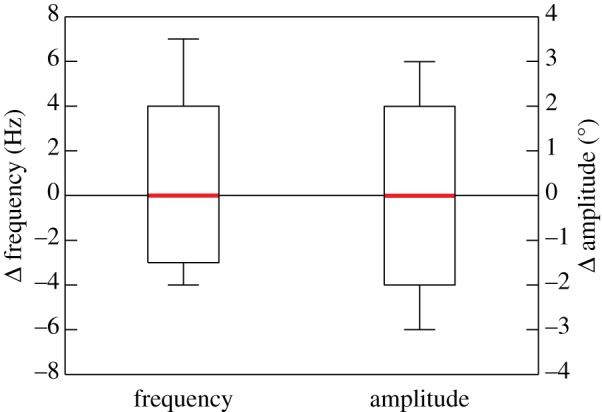
Differences in wingbeat frequency (paired t-test: t = 0.799, d.f. = 13, p = 0.439) and stroke amplitude (paired t-test: t = −0.228, d.f. = 13, p = 0.824) between the joint splint treatment and control splint treatment during maximum vertical force production (N = 14).

Finally, we evaluated the effect of the joint splint on two independent samples consisting of bees tested with the control splint first (N = 7), and those tested with the joint splint first (N = 7). There was no significant difference between these two groups in the fractional change (from control splint values to joint splint values) of maximum vertical force (Wilcoxon signed-rank test: p = 0.469), wingbeat frequency (p = 0.094) or stroke amplitude (p = 0.578). These results, together with the non-significant difference in maximum vertical force between the two sham treatments (above), indicate that our results are independent of testing order.

4. Discussion

Our flexural stiffness tests of splinted wings demonstrate that a single resilin joint in the bumblebee wing contributes significantly to overall chordwise wing flexibility. These results, together with resilin's known material properties (low stiffness, high strain and high elastic efficiency [40]) and the fact that it is often associated with flexible wing joints [13–15,19], suggest that resilin may play an important role in determining overall wing stiffness and shaping wing deformations during flapping flight.

Bumblebees with artificially stiffened wings produced less maximum vertical aerodynamic force than they did with un-manipulated flexible wings. However, a comparison of aerodynamic performance between flexible and stiff wings is only informative if wing kinematics, including wingbeat frequency, stroke amplitude and AoA, are otherwise similar between the two treatments. We found no significant difference in wingbeat frequency or stroke amplitude between bees with artificially stiffened wings and those receiving the control splint. A direct comparison of AoA between flexible and stiff wings is inherently ill-defined, since wing flexion yields a spatially varying AoA along the wing span (torsion) and chord (camber), and because established methods of measuring AoA typically involve fitting a rigid model wing to high-speed video frames, which would introduce error and bias into the comparison. Prior computational and robotic studies have typically either matched AoA of a rigid wing with AoA of a flexible wing at a defined spanwise location (i.e. mid-span) [4,5], or actuated wings with the same wing base kinematics [6,9–11].

Although we are unable to directly compare AoA in our load-lifting experiments, we can infer that it was similar in the two treatments. Load-lifting tests are designed to elicit maximum vertical aerodynamic force production, which is ultimately constrained by flight muscle power output [23–25]. A moderate change in AoA would cause a pronounced change in the drag coefficient of a flapping aerofoil [5,41], which would lead to a corresponding change in wing velocity if power output were unchanged (e.g. maximized). Since we found no change in either wingbeat frequency or stroke amplitude, which would accompany a change in wing velocity, we can conclude that AoA could not have been substantially different between the two treatments. At a more detailed level, it remains unclear whether the bumblebees were actuating stiffened and flexible wings with identical driving kinematics, or whether they were actively tuning AoA to maximize the lift coefficient for each unique wing state separately. Thus, while our results do not unequivocally demonstrate that the optimal lift coefficient (across all potential AoAs) of a flexible bumblebee wing is greater than that of an artificially stiffened wing, they do demonstrate that bumblebees rely on wing flexibility at the 1 m-cu joint to enhance vertical force production during maximum power output.

Buchwald & Dudley [23] performed similar asymptotic load-lifting trials on Bombus impatiens bumblebees (with un-manipulated wings), and reported a mean maximum body mass-specific vertical force production of 1.53 ± 0.24 (N = 24). A direct comparison of our results with theirs is obscured by a difference in experimental methodologies. Immediately prior to testing, Buchwald & Dudley squeezed each bee's abdomen with forceps to empty any nectar stored in the honey crop, and calculated mass-specific force based on final body mass measurements taken after all load-lifting trials [23]. By contrast, we fed our bees prior to testing to ensure that they had enough caloric reserve to last the duration of the load-lifting trials, which also meant that their post-trial body mass was inflated by whatever nectar load remained in their crop. Using body mass measurements after all load-lifting trials, the maximum body mass-specific vertical force of our bees was 1.24 ± 0.09 (N = 14) for the joint splint treatment and 1.36 ± 0.10 for the control treatment. These values are slightly lower than those reported by Buchwald & Dudley, potentially because the inflated body mass measurements of our bees lowered the mass-specific force estimates. Alternatively, using body mass measurements recorded after the initial 3–4 h of food deprivation (prior to feeding), our mass-specific force was 1.67 ± 0.12 (N = 14) for the joint splint treatment and 1.83 ± 0.15 for the control treatment. These values are somewhat higher than those reported by Buchwald & Dudley, possibly because starvation more thoroughly depletes overall water content from the body than squeezing the honeycrop does, yielding relatively lower body mass measurements. However, in general, the mass-specific vertical forces of bees in this study were in close agreement with previously published values.

Buchwald & Dudley also measured a mean wingbeat frequency of 181 Hz and mean stroke amplitude of 144° in their bumblebee load-lifting tests [23], compared with our measured values of 173 Hz and 140°, respectively. The small discrepancy in wingbeat frequency (8 Hz) is likely due to the effects of the glitter splint on wing inertia. Laboratory experiments show that decreasing wing inertia in bumblebees (by wing clipping) causes an increase in wingbeat frequency [42]. It follows that increasing wing inertia by adding a small splint mass would cause a corresponding decrease in wingbeat frequency, as seen here. Importantly, however, splint application did not differentially affect wing inertia in the control versus joint splint treatments, as demonstrated by the fact that we found no significant difference in either wingbeat frequency or stroke amplitude, and consistent with the close proximity of the control splint and joint splint locations on the wing surface.

To qualitatively explore how joint splinting affects patterns of passive deformation in a flapping wing, we captured high-speed video of wing flapping in a tethered bee, both before and after application of a joint splint (see the electronic supplementary material, movie S3). It is important to note that a rigidly tethered insect displays flapping wing kinematics that can differ from those observed during natural free flight, and that flapping kinematics during tethered flight can vary even from trial to trial on the same insect, including unpredictable changes in variables such as stroke amplitude, frequency, AoA and stroke plane. Thus, we avoid interpreting kinematic differences in tethered flapping that do not directly involve flexion at the 1 m-cu joint, because these differences are not necessarily owing to the joint splint. The un-manipulated wing in the electronic supplementary material, movie S3 shows flexion occurring at the 1 m-cu joint during ventral stroke reversal, with the wing transiently adopting a dorsally concave (cambered) shape that is most extreme during supination; this shape persists, although it is less pronounced, as the wing moves into the upstroke. While not apparent in the electronic supplementary material, movie S3, our analysis of wing flapping from different camera views indicates that joint flexion is not as prominent at dorsal stroke reversal (pronation) or during the downstroke. In the second sequence of the electronic supplementary material, movie S3, the glitter splint completely prevents flexion at the 1 m-cu joint, eliminating camber deformation during supination and into the upstroke.

A large body of experimental and computational work over the past several decades has shown that aerodynamic force production in insects is often enhanced by unsteady, separated flow that leads to the formation of a leading edge vortex (LEV) over the wing [1,2,43–46]. LEVs form when flow separates from the wing as it crosses the leading edge and reattaches somewhere along the wing chord before reaching the trailing edge, creating a vortex that enhances wing circulation and thus lift (for a review, see [47]). Bomphrey et al. [43] used smoke visualization to analyse aerodynamic mechanisms of free-flying bumblebees (Bombus terrestris), and identified an LEV that appeared on the wing during supination at the end of the downstroke and persisted into the upstroke, coinciding with the period of prominent wing flexion that we observed at the 1 m-cu joint. This suggests that the reduced force capacity of artificially stiffened wings may be linked to the effects of wing stiffening on the production and/or maintenance of this LEV. The cambered wing shape associated with chordwise flexion at the 1 m-cu joint during supination may initially promote or stabilize the production of an LEV. As the wing then transitions into the upstroke, the persisting joint flexion creates a positively cambered profile during early translation. In the absence of an LEV, a cambered wing in translation is known to generate greater lift than a flat wing at a similar AoA. In the presence of an LEV, wing camber may support a larger vortex than a rigid wing, thereby further enhancing lift production [5,10].

Our aerodynamic force estimates are also consistent with recent computational models of hoverflies [5], which display wing kinematics similar to bumblebees. Du & Sun [5] studied the effects of wing deformation on the aerodynamic forces produced by hoverfly wings using the detailed kinematic measurements of Walker et al. [48]. Hoverflies have wingbeat frequencies (150–180 Hz) and stroke amplitudes (70°–130°) that are similar to those of bumblebees, and also display similar wing camber deformations, especially during supination and into the upstroke [48]. Du & Sun found that camber deformations increased lift by about 10 per cent (compared with an un-cambered wing at a similar AoA), which they attributed to the effects of camber on LEV production [5]. The LEV of the cambered wing was more concentrated and was located closer to the wing surface than that of the simplified, flat-plate wing, which they argued would increase the time rate of change of the vorticity moment, and hence aerodynamic force, according to vortex theory [5,49]. The LEV is thought to be the single most important lift enhancing mechanism in insect flight [47]. Thus our results, together with recent flow visualization and computational findings, suggest that the role of wing flexibility in promoting and controlling LEV structures warrants further investigation.

Flight force capacity in insects represents a locomotory constraint with potentially far-reaching ecological implications, owing to its effects on manoeuverability, predator escape and resource acquisition. Aerodynamic force capacity has been linked to aerial manoeuverability and acceleration in dragonflies [50,51] and butterflies [52,53]. In bumblebees, experimental reduction of wing area simulating natural wing damage results in less direct flight paths between flowers [54], reduces maximum vertical aerodynamic force production [23], and causes an increase in mortality in both bumblebees [55] and honeybees [56]. Because these manipulations do not increase metabolic flight costs (despite causing an increase in flapping frequency [42]), it has been hypothesized that wing area loss increases susceptibility to predators by constraining flight force capacity and reducing aerial manoeuverability [42,56].

Moreover, load carrying is integral to resource acquisition in many insects, including predators and scavengers [29], as well as colony-based social insects, such as bumblebees. Worker bees forage for floral nectar and pollen and must continually transport food resources back to the hive to meet the perpetual nutritional and energetic demands of the colony [57]. A bee's load-carrying capacity restricts its net rate of food delivery [56]—a limitation that, when scaled up, is thought to constrain foraging efficiency at the colony level [29,56]. Thus, colony fitness may be sensitive to even subtle changes in individual load-lifting capacity, underscoring the potential adaptive significance of flexible wings and their effect on aerodynamic force production.

The constraints imposed by aerodynamic force capacity on a number of ecologically relevant flight behaviours implies that force capacity is subject to strong evolutionary selective pressure in bumblebees and probably in many flying insects. Our results suggest that passive wing deformations, and the localized resilin joints that promote these deformations in many species, play an important role in maximizing aerodynamic force production in flying insects.