Markov Chain Monte Carlo: an introduction for epidemiologists

Abstract

Markov Chain Monte Carlo (MCMC) methods are increasingly popular among epidemiologists. The reason for this may in part be that MCMC offers an appealing approach to handling some difficult types of analyses. Additionally, MCMC methods are those most commonly used for Bayesian analysis. However, epidemiologists are still largely unfamiliar with MCMC. They may lack familiarity either with he implementation of MCMC or with interpretation of the resultant output. As with tutorials outlining the calculus behind maximum likelihood in previous decades, a simple description of the machinery of MCMC is needed. We provide an introduction to conducting analyses with MCMC, and show that, given the same data and under certain model specifications, the results of an MCMC simulation match those of methods based on standard maximum-likelihood estimation (MLE). In addition, we highlight examples of instances in which MCMC approaches to data analysis provide a clear advantage over MLE. We hope that this brief tutorial will encourage epidemiologists to consider MCMC approaches as part of their analytic tool-kit.

Introduction

Markov Chain Monte Carlo (MCMC) methods are increasingly popular for estimating effects in epidemiological analysis.^1–8 These methods have become popular because they provide a manageable route by which to obtain estimates of parameters for large classes of complicated models for which more standard estimation is extremely difficult if not impossible. Despite their accessibility in many software packages,⁹ the use of MCMC methods requires basic understanding of these methods and knowledge of how to determine whether they have functioned appropriately in a particular application. Simulation-based methods, such as MCMC methods, offer a fundamentally different approach from maximum-likelihood–based methods for obtaining the distribution of parameters of interest. Transitioning from maximum-likelihood to simulation-based methods requires some explanation of their similarities and differences. Additionally, determining whether an MCMC algorithm has converged to the ‘correct answer’ is quite different than determining whether standard algorithms used in maximum-likelihood estimation have converged. The use of MCMC methods requires that researchers be comfortable in reading visual output that suggests whether or not MCMC results can be considered reliable.

In this paper we address both of these issues. First, we offer a brief overview of Monte Carlo integration and Markov Chains. Next, we provide a simple example to illustrate that, in some model specifications, MCMC and asymptotic maximum-likelihood approaches can return similar results for samples of moderate size. Through this example, we explain how to set up an MCMC analysis and recognize convergence in an MCMC model; we focus on 3 visual plots that are standard for assessing convergence with MCMC models, and offer guidance on how to read these plots. Markov Chain Monte Carlo methods are a potentially useful complement to the standard tools used by epidemiologists for estimating associations, albeit a complement that is often more computationally intensive than maximum-likelihood approaches. We hope that this brief tutorial will ease the path to simulation-based MCMC approaches to data analysis.

Markov Chain Monte Carlo: more than a tool for Bayesians

Markov Chain Monte Carlo is commonly associated with Bayesian analysis, in which a researcher has some prior knowledge about the relationship of an exposure to a disease and wants to quantitatively integrate this information. The task of incorporating this prior knowledge can yield a suitably complex model in which the exact distribution of one or more variables is unknown and estimators that rely on assumptions of normality may perform poorly. This limitation often leads researchers to implement their Bayesian models with MCMC, because it is quite effective at handling complex models; however, this does not mean that MCMC is equivalent to Bayesian analysis. Rather, MCMC is simply a tool for estimating model parameters that has been proven to be effective for handling complex problems. Even though MCMC is often treated as a synonym for ‘Bayesian,’ it can just as readily be used in frequentist analyses.¹⁰ Similarly, although asymptotic maximization techniques are often considered akin to frequentist analysis, these methods are used in Bayesian analysis as well.^11,12 The appeal of MCMC is that it can handle more complex models by design, whereas maximization techniques can be more limited in their ability to do so. This is shown in recent work by Cole et al., who utilize a technique for obtaining Bayesian posterior distributions without Markov chains, but conclude that when models become more complex, MCMC procedures provide a clear benefit over approximation techniques for Bayesian analysis.¹³

Recent papers offer a number of compelling examples of regression models implemented in an MCMC framework. For example, Hamra et al. use MCMC to formally integrate evidence from experimental animal and cellular research into an epidemiologic analysis with a constraint of order.¹⁴ MacLehose et al. used MCMC to inform the estimation of multiple, highly correlated exposures using semiparametric priors and a Dirichlet process before the clustering of effects into groups for more efficient estimation¹⁵; Richardson et al. used MCMC to conduct time-window analyses of the relationship between occupational exposures and lung-cancer risk when a second-stage was specified as a parametric latency model⁸; and the MCMC framework has proven useful for estimating the excess relative risk created by interaction and estimation in log-binomial models.^2,3 This is not to say that asymptotic estimators are not useful. In fact, when the available data are large and the models less complex, MCMC may provide little or no benefit relative to standard estimating procedures. However, when faced with complex models, which are increasingly common in epidemiologic inquiry, the researcher may find benefit in MCMC.

Markov Chains and Monte Carlo integration

Unlike deterministic maximum-likelihood algorithms, MCMC is a stochastic procedure that repeatedly generates random samples that characterize the distribution of parameters of interest. This is distinct from commonly practiced asymptotic maximum-likelihood techniques, which are typically used to characterize the sampling distribution of an estimator. The process of generating the random samples in MCMC is the role of the Markov chain. The process of generating summary statistics from those random samples is the role of Monte Carlo integration.

A Markov chain can be thought of as a directed random walk through the parameter space that describes all the possible values of the parameter of interest. A directed random walk implies that although the next value drawn in the Markov chain is random, some values are more likely to be drawn than others; a well-constructed Markov chain will sample from these more likely regions of the sample space. The sampling of parameter values proportionally to their probability (which is determined by the information in the data and, in the case of a Bayesian analysis, by any informative prior information the user provides) allows the user to reconstruct the parameter’s entire distribution. This is one of the more remarkable results of modern statistics: although this distribution of the estimator might not be available in a form that can be easily written, random samples can still be drawn from it. There are many algorithms that produce these random walks through the parameter space, including the widely used Gibbs sampler and the Metropolis–Hastings algorithm. The finding by the algorithm of this distribution (known as the stationary distribution of the chain) is referred to as convergence of the MCMC procedure. We can then draw as many samples from it as we like and summarize them via Monte Carlo integration to obtain the desired description of the distribution of the parameter of interest.

We can create a histogram of the random samples produced from the Markov chain to characterize the posterior distribution. However, we might also be interested in the mean of the random variable X or the mean of a function of the random variables E[f(X)]. The random variable and function could be the probability of the outcome and a logarithm, respectively, of an odds ratio. There are two main ways to find E[f(X)]. The first solution requires detailed algebra and calculus: we could derive the distribution of f(X) and then integrate f(X) over that distribution to obtain the expectation. The second solution dispenses with the difficult mathematics and focuses on summarizing random samples of X. If we draw x₁ … x_n from this distribution and then apply the function to each of these values, we obtain f(x₁) … f(x_n); we can then simply calculate the mean of these values to obtain our expectation. More formally, this can be written as

This solution is known as Monte Carlo integration and can be extremely powerful whenever deriving the distribution of f(X) proves too cumbersome. Combining Markov chains and Monte Carlo integration, we arrive at a process by which Markov chains are used to draw random samples from a distribution and Monte Carlo integration is used to generate summary estimates from those random samples. The technical details of Markov chain theory can be daunting; however, there are many algorithms that produce these ‘random walks’ through the parameter space. For further detail, we recommend the seminal paper by Gelfand and Smith, as well as the texts by Carlin and by Louis, Gilks, and Richardson, or Gill.^16–18

Use of Monte Carlo integration does not necessitate a major departure from the evaluation of parameter estimates with which epidemiologists are most familiar. In a frequentist analysis, if we know that a parameter is normally distributed, with a mean µ and variance σ², we can easily compute a 95% confidence interval (CI) around the effect estimate of interest. The same calculation can be done with Monte Carlo integration, with the bonus of interpreting the distribution in an intuitive way as discussed above. If, for example, we draw 1000 random samples from the normal distribution, the 2.5th and 97.5th percentile values will correspond to the limits of a 95% CI; additionally, we obtain the mean, median, and mode, which paint a clearer picture of the parameter’s distribution. In fact, in finite samples, the mean has been shown to be more stable than the median or mode.¹⁹ Markov Chain Monte Carlo will provide this information by design.

Markov Chain Monte Carlo is not magic: a simple example

To illustrate specification with an MCMC procedure and the diagnosis of convergence of a model, we use a simple example drawn from work by Savitz et al. regarding a case–control study of the association between residential exposure to a magnetic field (where X = 1 for exposure and X = 0 for non-exposure) and childhood leukemia (where Y = 1 for cases and Y = 0 for controls).^11,12,20 The data were presented as a simple two-way table in which n_xy was the number of individuals in each cell, with n₁₁ = 3, n₁₀ = 5, n₀₁ = 33, and n₀₀ = 193. These data could be analyzed with a logistic-regression model of the form: Logit(Pr(D = 1)) = β₀ + β₁x, where x identifies residential magnetic-field exposure.

This simple regression model could be estimated through MCMC methods. When we implement an MCMC simulation, the process must begin at some value for the parameter of interest. This starting point, which can be user specified, should not contribute to summarizing the posterior distribution of interest. Thus, we specify a ‘burn-in’, which is a grace period during which the Markov Chain wanders to the most probable region of the sample space; in fact, the samples obtained during the burn-in are ultimately discarded. After the burn-in, the simulation will continue to generate samples from the distributions of the parameters of interest for as long as we specify, which is the total number of iterations specified. If, for example, we run an MCMC model with 100 000 iterations and a burn-in of 10 000 samples, we are specifying 110 000 iterations, but we throw out the first 10 000. A challenge of using MCMC is specifying an appropriate number of iterations and appropriate burn-in. In practice, there are no hard and fast rules for this process. Instead, the researcher uses a trial-and-error process to determine that the number of iterations and burn-in are adequate. In our own work, we often specify a starting point of 10 000 iterations with a burn-in of 1000 iterations, and increase the values from these as necessary. Evaluating diagnostic plots, discussed below, will help indicate whether the Markov chain has run long enough. It is also worth noting that increasing the number of iterations and burn-in iterations will not solve an inherently intractable problem, such as estimating a non-identified parameter. For instance, if we have run MCMC simulations for 1 000 000 iterations with a burn-in of 100 000 and have seen little or no sign of convergence in a model, we may question whether or not the parameter can be estimated. Although MCMC is a very powerful tool, it is of little use if asked to answer an unanswerable question.

Markov Chain Monte Carlo models are often used in Bayesian analyses in which a prior is specified. Suppose that we specify a very ‘diffse’ or non-informative prior, such as β₁, N ∼ (µ = 0, σ² = 100 000). The goal of such a ‘diffuse’ prior is to allow the likelihood to overwhelm, and thus fully characterize, the posterior distribution of the parameter of interest. Indeed, this model yields a posterior OR (the median of the posterior distribution) and 95% posterior interval of 3.37 (0.67, 16.08). Throughout this paper we present 95% highest posterior density intervals, which are helpful for describing the posterior density when it is non-symmetrical. The geometric mean in the model being discussed is 3.30, indicating slight skewness in the distribution of the parameter of interest. If in contrast we specify a more informative prior, as in Greenland’s example, such that β₁, N ∼ (µ = 0, σ² = 0.5), we obtain a posterior OR (95% posterior interval) of 1.71 (0.57, 4.97). Greenland’s original analyses yield an OR (95% CI) of 3.51 (0.80, 15.4) with no prior information included and a posterior OR (95% posterior limits) of 1.80 (0.65, 4.94) when he integrates, via data augmentation, the null-centered prior mentioned above (details of this calculation are provided elsewhere ¹¹). We describe Greenland’s results here to point out that although MCMC returns an exact distribution for the parameter of interest, previous methods can in some cases provide good approximations.²¹

The next step in an MCMC analysis is to assess model convergence. Unlike MCMC, convergence of likelihood estimators happens in the background through the use of a pre-specified optimization algorithm (such as the Newton–Raphson algorithm). However, judgments about the convergence of an MCMC procedure require the user to evaluate several diagnostics, the most common of which are visual summaries. Three visual plots are routinely used to assess model convergence:

1. Trace plots. These document the magnitude of the sample drawn (y-axis) at each iteration (x-axis) of the MCMC procedure. Once the chain has identified the stationary distribution of samples, the samples that are drawn will appear to have been randomly sampled from the same region of the y-axis.

2. Autocorrelation plots. These document the correlation (y-axis) of samples at each step of the chain with previous estimates of that same variable, lagged by some number of iterations (x-axis). Ideally, the autocorrelation declines rapidly, so that it is eventually possible to be confident that the samples from the stationary distribution can be thought of as random, and not reliant on initial values in the chain. If the autocorrelation fails to diminish, a pattern in the sample draws in the trace plot will become more discernible, suggesting that at the very least, the posterior distribution has not been well characterized by the drawn samples.

3. Density plot. As its name implies, this plot is a summary of the sampled values that define the stationary distribution of values, which approximates the posterior distribution of interest. The peak of the density (the maximum a posteriori, or MAP, estimate) is the mode of the distribution, which is the value with the most support from the data and the specified prior. Other posterior summaries, such as the posterior mean or posterior median, are also easily obtained. Kernel density estimation is used to smooth over the samples and produce an estimate of the posterior distribution. It should be noted that the density plot is not a formal means of diagnosing model convergence, as are the autocorrelation and trace plots. However, unexpected peaks or strange shapes in the posterior density can be a sign of poor model convergence.

In addition to the visual plots discussed above, a Gelman–Rubin diagnostic check is often used to assess model convergence. This diagnostic involves running multiple MCMC procedures, specifying the same model and prior information, from different starting values and comparing the variance within each chain with the variance between chains. Lack of model convergence is indicated when the variance between chains is larger than the variance within chains. This can result from multimodal problems in which a chain has identified two or more distinct parameter distributions, or from a high degree of correlation in the observed data. Although there are no rules for how many different chains to run, researchers often run the Gelman–Rubin diagnostic for 3 chains.

It should be noted that there is no formal method by which to diagnose that a chain has converged. The plots and tests we describe here can only aid in detecting lack of convergence. We conduct analyses in SAS version 9.2 (SAS Institute, Cary, NC) with the GENMOD procedure and using a BAYES statement.⁹ It is worth noting that MCMC has its own procedure in SAS and can also be called upon in the PHREG procedure. Additionally, software is available in the free WinBUGS and R statistical packages. We provide an eSupplement with a code for implementing this example as a Bayesian analysis in GENMOD. This example code will produce both frequentist and Bayesian results, with the associated diagnostic plots we describe above.

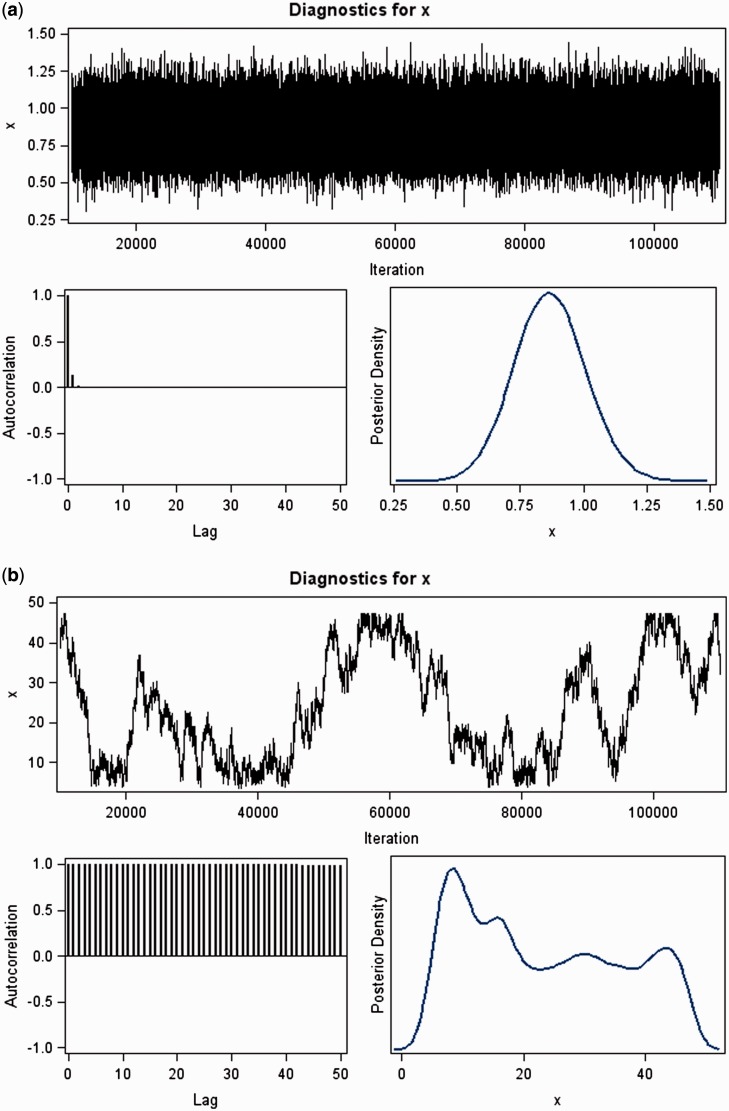
Figure 1a illustrates the result of Greenland’s example with the use of a diffuse prior. An MCMC algorithm that has converged will tend to quickly wander randomly around the same area, rarely venturing outside that area. The trace plot in Figure 1a suggests that the chain is wandering through the same region of the parameter space and has found the stationary distribution, but it is not guaranteed that this is so. For this reason we must use the trace plot in conjunction with the autocorrelation and density plots as well as the Gelman–Rubin statistic to assess model convergence. The autocorrelation drops precipitously, from lag 0 to lag 50, which tells us that each sample in the chain is only slightly correlated with the previous draw, and suggests no reason for concern. These plots suggest that the samples are approximately independent, random draws from a parameter distribution. Lastly, the density plot allows assessment of the posterior distribution of the parameter of interest. In this case we see a symmetric distribution for the parameter estimate. The density plot is also useful when assessing whether or not chains started from different values converge to the same distribution.

Figure 1.

Diagnostic plots illustrating convergence (top) and non-convergence (bottom) of an MCMC procedure

Figure 1b provides an example of non-convergence of an MCMC procedure. This was achieved by replacing the n₀₁ cell in our example with a value of 0, creating quasi-complete separation.²² The trace and autocorrelation plots are particularly informative here. The Markov chain wanders slowly through the parameter space, attempting to find a stationary distribution, but never settles into an area from which it can yield independent samples. It appears as though estimates are serially correlated with previous estimates in the chain. This is confirmed by the autocorrelation plot, in which the draws are almost perfectly correlated with draws made 50 iterations prior. The samples may be from a distribution of the parameter of interest, but they are not independent random samples. The kernel density plot reflects the lack of convergence seen in the trace and autocorrelation plots, showing that the chain was unable to find a smooth distribution with a single point estimate with more support than any other point estimate (as will often be the case in simple models).

An example of hierarchical modeling

The nicest feature of MCMC is its ability to handle otherwise complex model specifications. An example of this is specification of a hierarchical model. Breslow and Day present an example of this from the Ille-et-Villaine study of the relationship between alcohol and tobacco consumption and risk of esophageal cancer.²³ Data are available for five forms of alcohol: wine, beer, cider, digestifs, and apertifs. A researcher might model each individually, combine them into a single term, or choose a subset. An appealing alternative to these options is to specify a hierarchical model in which the first-stage model contains a term for each form of alcohol consumed, e.g. β₁–β₅, and the second-stage model contains a single term representing the common mean of alcohol consumption, e.g. µ. By modeling alcohol consumption in this way, we are saying that we believe, a priori, that the distinct types of alcohol are exchangeable, as represented in this case by the expression β_j ∼ N(µ, τ²). These data are analyzed with a first-stage logistic-regression model of the form: Logit(Pr(D = 1)) =α + β_ix_i, where x indexes each form of alcohol (0 = no alcohol consumption, 1 = any alcohol consumption) as well as age (centered at the mean of 52 years). Analyses are restricted to non-smokers, to aid in illustrating how the grand mean can influence the individual parameter estimates in the presence of sub-optimal data. The second stage, or prior, is specified such that the model shrinks the coefficients (β_1-5) of alcohol consumption toward their grouped mean (µ) weighted by the inverse variances (τ). The priors specified for µ and τ are N ∼ (mean = 0, var = 100 000) and γ ∼ (0.01, 0.01), where the parameters correspond to the shape and inverse-scale parameters of the gamma distribution, respectively. The latter will be unfamiliar to many, but it is simply another way of specifying a very weak prior so that the weight of information in the data supporting the grand mean, µ, define its strength. Additionally, the prior for age is specified as diffuse, with N ∼ (mean = 0, var = 100 000).

The data in Table 1 show that in the absence of a hierarchical structure to the model, the individual estimates for some forms of alcohol are quite imprecise, although all of the forms of alcohol produce positive-effect estimates. When shrinkage of their grouped mean is induced through a Bayesian hierarchical model, all of the effect estimates are within a similar range of values, extending from an OR of 2.11 for aperitif consumption to an OR of 2.36 for beer consumption. Effect estimates from the hierarchical regression are noticeably more precise, which is expected, because the formulation of this model allows regression estimates to borrow strength through the prior.²⁴

Table 1.

Odds ratios of esophageal cancer associated with consumption of distinct forms of alcohol in the Ille-et-Villaine study^a

	Model
	Logistic		Hierarchical model results
Alcohol type	OR	95% CI	OR	95% HPD
Beer	3.41	0.71–16.31	2.36	0.71–5.55
Cider	2.68	0.49–14.60	2.29	0.63–5.45
Wine	1.44	0.15–14.14	2.15	0.38–5.16
Apertif	1.57	0.35–7.09	2.11	0.56–4.58
Digestif	1.86	0.36–9.47	2.18	0.64–4.73

^aAll models are adjusted for age (centered at 52 years).

In executing this analysis, we began with 10 000 iterations and a burn-in of 1000. This was inadequate to produce reliable estimates, as indicated by a high autocorrelation for the parameters of interest, resembling what is seen in Figure 1b. We increased the number of iterations to 500 000 with a burn-in of 50 000. At this point we introduced thinning, which is a procedure that may be used to reduce autocorrelation. Thinning is the act of discarding some samples from the simulation. For instance, if we specify ‘thin = 2’ or ‘thin = 3’, the procedure will retain only every second or third parameter value, respectively. We settled on retaining every fourth parameter value (thin = 4) and increased the MCMC procedure to 2-million iterations with a burn-in of 100 000 iterations, which left 500 000 iterations to summarize the posterior distribution of each parameter (since, again, we kept only every fourth sample of a total of 2 million samples). Although this may seem like a lengthy procedure, the final models ran in just under 22 minutes on a common laptop computer.

Discussion

In this paper we have provided a basic introduction to Markov Chain Monte Carlo methods. Drawing on Greenland’s example from his Bayesian series, we illustrate the basic tools needed for executing a basic MCMC analysis with a weak and non-informative Bayesian prior.¹¹ We emphasize that results of MCMC simulation need not produce different estimates than those provided by standard frequentist regression techniques currently used by epidemiologists.

Despite the practical similarities between a Bayesian analysis with a non-informative prior in MCMC and a frequentist analysis with maximum-likelihood estimators, there are conceptual differences in the two techniques. Thus, for example, frequentist theory treats parameters as fixed values with an associated random error, whereas Bayesian analysis treats all parameters as random values. Further, from a theoretical point of view, the two procedures are attempting to solve different problems. Frequentist theory is concerned with long-run properties (bias, mean squared error) of estimators with repeated sampling, whereas Bayesian theory is concerned with computing a posterior distribution from a single analysis sample and prior. However, in the absence of an informative prior, the two techniques will often return similar if not identical point and interval estimates for the parameters of interest. When the sample size becomes small, or a regression model becomes sufficiently complex, traditional asymptotic maximum-likelihood estimation may poorly estimate the parameter of interest; alternately, MCMC is capable of returning an exact distribution of the parameter of interest. It should be noted that the poor performance of traditional likelihood methods comes from their reliance on asymptotic normality. Alternative likelihood methods are available to provide more accurate parameter estimates that do not rely on assumptions of normality. Two common examples of these alternative methods are profile-likelihood estimation and bootstrapping. As with MCMC, either of these approaches allows users to improve on asymptotic maximum-likelihood techniques.

As with other methods, MCMC methods have limitations, most notably the computational power required for some models. However, computational obstacles are increasingly overcome with improvements in computer technology, although this may still be off-putting to some. In addition, choosing an MCMC approach to data analysis will not remedy the problems of bias (confounding, information, and selection) that plague many epidemiological studies. However, it does ease the inclusion of information to correct for these biases.^25,26 Doing this does make the form of a model more complex, but handling challenging models is the reason for which MCMC was designed.

As with any valid epidemiologic inquiry, MCMC relies on proper model specification to yield valid results. If a model is not properly specified, the results may be incorrect even if a Markov chain converges, as is the case for any frequentist approach. The more complex the model, the more difficult it becomes to diagnose proper model convergence. Thus, care must be taken in developing a correct model. Care must also be given to specifying a prior, because not every prior distribution can be used in every situation. A poorly specified prior can result in a greater mean squared error than with frequentist estimators. For example, a prior distribution that designates the most likely relative risk for the smoking–lung cancer relationship to be 0.5 is likely to result in poorly performing estimators.^17,27 In practice, what constitutes the mis-specification of a prior is difficult to quantify, and many users of Bayesian techniques tend to err on the side of specifying more diffuse prior distributions to diminish their risk of error and help ensure they have not grossly mis-specified their prior. In addition, there is no established method for determining an appropriate number of iterations and burn-in size. Rather, we use a trial-and-error process in which the ultimate goal is to obtain stable parameter estimates that minimize simulation error. As with the computational intensity discussed above, these steps require more time on the part of the researcher. However, MCMC estimation is indispensable as a tool for handling intractable epidemiological inquiries.

Markov Chain Monte Carlo methods are not limited to use in obtaining Bayesian posterior distributions. Proponents of frequentist statistics can just as easily use the machinery of MCMC to obtain parameter estimates of interest.¹⁰ Advances in statistical software packages have provided easier approaches to the specification of a model and of priors for individual parameters. In our view, epidemiologists would not need to seek out the guidance of biostatisticians for conducting simple Bayesian analysis, such as with generalized linear models. With more complicated models, expert advice may be required. Lastly, the act of recklessly applying a “Bayes” stamp to an analysis may lead to dubious results.^1,28 Thus, careful consideration should be given when applying a Bayesian method to data analysis. We hope that readers will find MCMC methods less daunting, and we look forward to their increased use by epidemiologists in future studies.

Funding

Dr Hamra was supported by the U.S. Centers for Disease Control and Prevention (grant 1R03OH009800-01) and U.S. National institute of Environmental Health Sciences (training grant ES07018). Dr MacLehose was supported by the U.S. National Institute of Health (grant 1U01-HD061940).