Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Apr 9;3:1633. doi: 10.1038/srep01633

Full spatial characterization of a nanofocused x-ray free-electron laser beam by ptychographic imaging

Andreas Schropp 1,2,a, Robert Hoppe 1, Vivienne Meier 1, Jens Patommel 1, Frank Seiboth 1, Hae Ja Lee 2, Bob Nagler 2, Eric C Galtier 2, Brice Arnold 2, Ulf Zastrau 2, Jerome B Hastings 2, Daniel Nilsson 3, Fredrik Uhlén 3, Ulrich Vogt 3, Hans M Hertz 3, Christian G Schroer 1
PMCID: PMC3620670  PMID: 23567281

Abstract

The emergence of hard X-ray free electron lasers (XFELs) enables new insights into many fields of science. These new sources provide short, highly intense, and coherent X-ray pulses. In a variety of scientific applications these pulses need to be strongly focused. In this article, we demonstrate focusing of hard X-ray FEL pulses to 125 nm using refractive x-ray optics. For a quantitative analysis of most experiments, the wave field or at least the intensity distribution illuminating the sample is needed. We report on the full characterization of a nanofocused XFEL beam by ptychographic imaging, giving access to the complex wave field in the nanofocus. From these data, we obtain the full caustic of the beam, identify the aberrations of the optic, and determine the wave field for individual pulses. This information is for example crucial for high-resolution imaging, creating matter in extreme conditions, and nonlinear x-ray optics.

The capability of hard X-ray free-electron lasers (XFELs) to probe matter on the atomic length scale and femtosecond time scale opens a window into broad scientific areas ranging from single shot images of biological structures1,2, to imaging the dynamics of matter3, to creating matter in extreme conditions4, and observing nonlinear optical effects in the hard X-ray range5. E. g., the availability of these short x-ray pulses of 50 fs and below holds open the possibility for structure determination of single molecules with atomic resolution by outrunning structural damage6,7,8, which continues to be the most important limitation in x-ray protein crystallography9. Nevertheless, these experiments often still require a strongly focused beam in order to increase the fluence on the sample.

Over the last few years, a variety of X-ray optics10,11,12 has been developed to cope with the high peak brilliance of XFEL radiation and to generate nanofocused XFEL beams. They have been shown to efficiently concentrate the XFEL pulse into a small area, thus increasing the fluence on the sample by many orders of magnitude. All those experiments that require high fluence greatly benefit from using a nanofocused beam. For instance, in coherent X-ray diffraction microscopy13,14,15 the spatial resolution is limited by the fluence on the sample16, in the creation of extreme states of matter using absorption of the XFEL pulse, the energy density transferred to a sample is determined by the fluence4, and nonlinear processes depend strongly on peak intensities5,17. Especially, since nonlinear effects play a crucial role in experimental scenarios involving a tightly focused XFEL beam18, the detailed modeling of these experiments requires — ideally — the exact knowledge of the wave front or at least of the intensity distribution on the sample.

The characterization of nanofocused X-ray pulses is particularly challenging, due to pulse-to-pulse fluctuations of the XFEL beam and a focused peak intensity well above the damage threshold of any material. To date, imprint techniques have predominantly been used by evaluating the damage in a flat surface caused by the intense X-rays11,19. With this technique, the focus size can be estimated from the size of the crater. However, it does not reveal the intensity distribution with high spatial resolution. Another proposed method, which is based on phase retrieval applied to single far-field diffraction patterns20, has not found a practical implementation until now.

In recent years, scanning coherent diffraction microscopy, also known as ptychography, has revolutionized nanobeam characterization at synchrotron radiation sources. In this X-ray microscopy technique, a sample is scanned through a confined coherent beam, recording at each position of the scan a far-field diffraction pattern21. From these data, the complex transmission function, describing both the attenuation and phase shift by the object, and the complex illuminating wave field can be reconstructed quantitatively by iterative phase retrieval algorithms22,23. Besides hard X-ray micrographs of highest spatial resolution22,24,25,26 the method gives full access to the spatial component of the complex wave field in the object plane and thus to the full caustic of the beam and to potential aberrations caused by the focusing optics27,28,29,30,31.

Results

We applied the method of ptychography to the characterization of a nanofocused XFEL beam at the Linac Coherent Light Source (LCLS)32. The experiment was carried out at the Matter in Extreme Conditions (MEC) instrument located in the far hall of the LCLS, 464 m from the XFEL undulator. Fig. 1 (a) is a schematic of the experimental setup. A set of parabolic refractive X-ray lenses made of beryllium33,34 was used to focus the XFEL pulses to a nominal full width at half maximum (FWHM) spot size of 115 nm about 250 mm behind the optic (see nanofocusing by beryllium CRL optics in the Methods). In order to avoid chromatic aberration and to stabilize the focus position along the optical axis, we fixed the photon energy of the XFEL beam to E = 8.2 keV by a four bounce (Bartels type) monochromator positioned at a distance of 376.4 m upstream the sample.

Figure 1. Description of setup and sample.

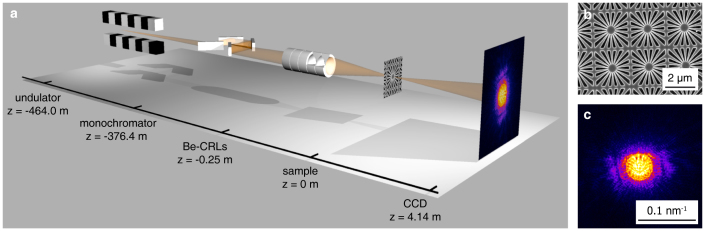
Figure 1

Open in a new tab

(a) Schematic outline of the experimental setup. Optical axis is not to scale. (b) Scanning electron microscope (SEM) image of a high-resolution test chart made of a 40 by 40 array of starlike structures, patterned into a tungsten layer (thickness 1 μm) on a diamond substrate (thickness 100 μm). Its smallest features have a size of about 50 nm. (c) Single-pulse far-field diffraction pattern recorded as part of the ptychographic dataset (logarithmic scale).

A resolution test chart [cf. Fig. 1 (b)] was positioned at a distance of 0.5 mm behind the focus and was scanned through the focused beam in a two-dimensional grid perpendicular to the optical axis. At each scan position two far-field diffraction patterns [cf. Fig. 1 (c)] were recorded by a two-dimensional detector located 4.14 m behind the focus (see experimental details in the Methods). The XFEL beam was attenuated using polished single crystal silicon absorbers to the level that the diffraction patterns do not exceed the dynamic range of the detector. As a result, the beam intensity on the sample was well below its damage threshold. Based on this set of diffraction patterns the object and average illumination were reconstructed using the algorithm by Maiden and Rodenburg23 combined with a refinement of the scan positions (see position refinement in the Methods). The result of the reconstruction is depicted in Fig. 2, showing both the phase of the object [cf. Fig. 2 (a)] and the complex wave field in the plane of the object [cf. Fig. 2 (b)].

Figure 2. Numerically retrieved illumination and object function.

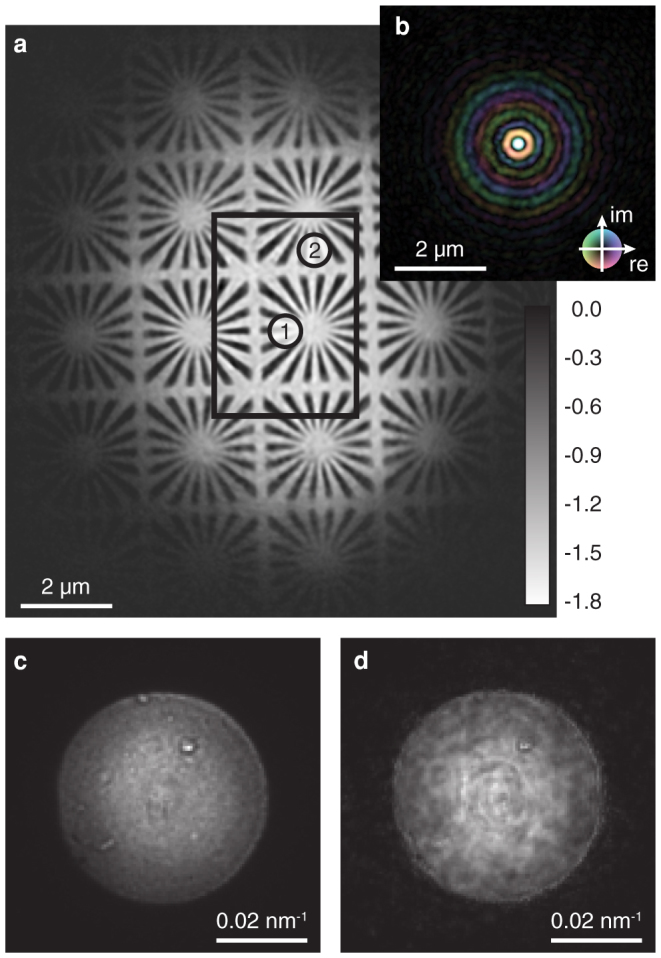
Figure 2

Open in a new tab

(a) Ptychographic reconstruction of the test object (phase shift in radian). All scan points lie within the black rectangle. Two specific diffraction patterns obtained from areas marked with numbers 1 and 2 are used to investigate pulse-to-pulse fluctuations of the nanofocused X-ray beam. (b) Reconstructed average illumination function is shown on the same length scale. The amplitude is encoded by brightness and the phase by hue. (c) Measured far-field image of the focused beam without any sample in the beam. (d) Far-field image calculated from the reconstructed wave field.

For the reconstruction, we assumed that the wave field in the focus was constant over the whole ptychographic scan, ignoring the pulse-to-pulse fluctuations of the XFEL beam. It was a priori not clear if this is a well justified assumption. However, the results show that the fluctuations in the wave field of the focused XFEL beam are small enough to allow for a meaningful average reconstruction. This is supported by the fact that the ptychographic reconstruction converged well, giving a detailed image of the object free of aberrations even far outside of the scanned area [cf. Fig. 2 (a)]. This is only possible if even the weak amplitudes of the illumination well away from the central focus are consistent and reconstructed faithfully. The maximum phase shift of approximately −1.8 rad is in good agreement with the theoretical value of −1.9 rad for a 1 μm thick tungsten layer.

Furthermore, one can check the consistency of the reconstructed wave field by numerically propagating it to the detector plane and comparing the resulting intensity distribution with that measured directly without sample and independently of the ptychogram. Fig. 2 (c) and (d) show the measured intensity and the corresponding one determined numerically from the reconstructed wave field, respectively. The reconstructed far-field intensity varies slightly more than the measured one. However, it contains all the characteristic features of the measured far-field intensity.

The reconstructed average wave field can now be used to fully characterize the nanobeam and understand the aberrations of the optic. Fig. 3 shows the complex wave field propagated along the optical axis using the Fresnel-Kirchhoff integral35. From Fig. 3 it is apparent, that paraxial rays are focused to a shorter focal length (arrow 1 in Fig. 3) than rays coming from larger angles (arrow 2 in Fig. 3). This spherical aberration is caused by deviations of the lens shape from a perfect rotational paraboloid and can occur, for example, when during fabrication of the lens the center of rotation is not perfectly aligned to the apex of the parabola. Therefore, the radius of curvature in the central area of the lens is typically increased as compared to the nominal parabolic shape. As a result, not all the intensity is focused to the central spot, giving rise to the side maxima [cf. Fig. 2 (b)]. Fig. 4 (d) shows a line profile through the focus that has a lateral extension of 125 nm FWHM, slightly larger than the expected size of 115 nm.

Figure 3. Complex wave field propagated ±15 mm along the optical axis.

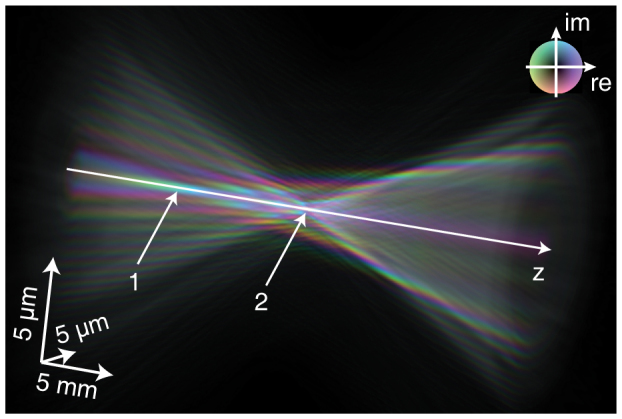
Figure 3

Open in a new tab

The colors indicate the local phase as illustrated in the inset. Amplitude is encoded by brightness.

Figure 4. Comparison of illumination functions retrieved from a single diffraction pattern (single pulse) and multiple diffraction patterns (average).

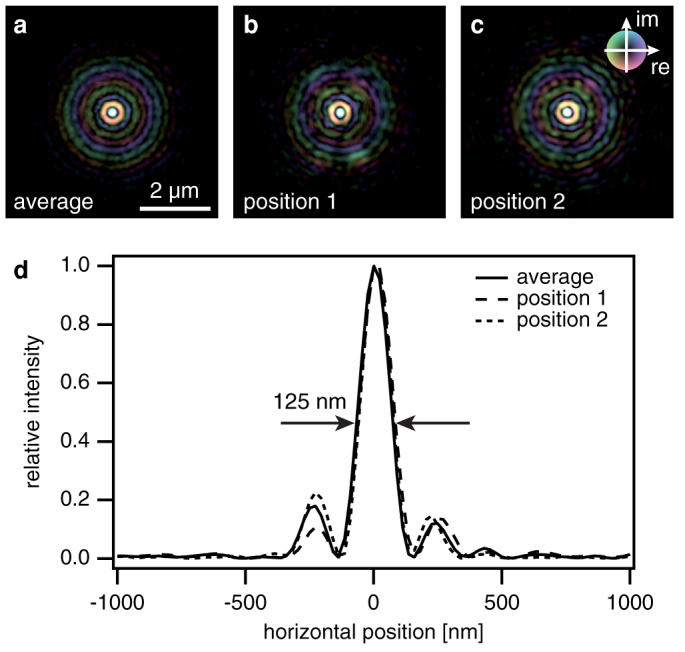
Figure 4

Open in a new tab

(a) Reconstructed average wave field in the sample plane. (b), (c) Wave fields obtained from a single diffraction pattern measured at position 1 and 2 as indicated in Fig. 2 (a). (d) Intensity profiles through the focus for the average and individual wave fields presented above, showing both the individuality of single pulses and the similarity to the reconstructed average wave field. The phase is coded according to the color wheel.

Finally, we can use the ptychographic data to reconstruct single pulse illumination functions for each pulse in the ptychographic data set and compare them to the average illumination. We do this by introducing an individual illumination to each ptychographic scan point and by refining them all with the ptychographic algorithm while keeping the (previously reconstructed) object function unchanged (see reconstruction of single-pulse illumination in the Methods). Fig. 4(b) and (c) show two single pulse reconstructions. They appear quantitatively similar to the average wave field [cf. Fig. 4 (a)] in the highest intensity part around the focus. The weaker amplitudes are slightly noisier, since there is only one diffraction pattern determining the single pulse illumination instead of several hundreds for the average illumination. Thus, the signal-to-noise ratio is reduced in these local reconstructions. The main features of the nanofocus, however, remain unchanged from pulse to pulse, despite pulse-to-pulse fluctuations of the XFEL beam. This in itself is an important result, showing that a focused XFEL beam is quite stable and reproducible in its spatial distribution.

Discussion

We have shown that ptychography is perfectly suited to characterize XFEL nanobeams with unprecedented spatial resolution, giving access to the spatial distribution of the complex amplitudes of XFEL pulses. Additionally, the method can be extended to characterize unattenuated XFEL pulses by scanning periodic test objects. In this way, the important prerequisite of ptychography, namely that adjacent scan points have to be recorded with a certain mutual overlap of the illumination21, could be virtually fulfilled by stepping to a new position on a similar object structure after each destructive pulse. We have successfully tested this approach by scanning the periodic test object in large steps with the attenuated beam.

Since most experiments rely at a minimum on the knowledge of the intensity distribution on the sample for their detailed modeling, the importance of the method for a fast and routine characterization of XFEL nanobeams is highlighted. The data presented here prove that a few tens of diffraction patterns are already sufficient to faithfully recover the illumination function.

Methods

Nanofocusing by beryllium CRL optics

The nanofocus was created by a set of 20 compound refractive X-ray lenses (CRLs) made of beryllium with a radius of curvature of R = 50 μm and geometric aperture of D = 300 μm. Due to absorption within the beryllium the aperture reduces to an effective aperture of Deff = 250 μm. At the photon energy of E = 8.2 keV a diffraction limited spot with a size of 115 nm is expected at a focal distance of f = 250 mm. The device yields a gain in fluence of 2 × 106 as compared to the flat XFEL beam.

Sample preparation

The resolution test chart contained a matrix of 40 by 40 identical Siemens stars with feature sizes from 200 nm down to 50 nm etched into a 1 μm thick tungsten layer. The sample was prepared in a trilayer process. First, a 1 μm thick tungsten layer was sputter deposited onto a 100 μm thick CVD diamond substrate. Then, a 30 nm thick chromium layer was electron-beam evaporated onto the tungsten. Finally, a 100 nm thick positive e-beam resist was spin-coated on top of the stack. Afterwards the resist was patterned with electron-beam lithography. The e-beam pattern was then transferred to the underlying chromium layer via a Cl2/O2-plasma-based reactive-ion-etch process. The chromium was finally used as hard mask for structuring the tungsten layer in a reactive-ion-etch step using a SF6/O2 mixture.

Experimental details

The resolution test chart was positioned 0.5 mm behind the focus and was scanned through the beam in a 20 by 20 grid with a step size of 100 nm. Since the XFEL intensity fluctuates from pulse to pulse, two single-pulse far-field diffraction patterns were recorded at each scan position with a two-dimensional position sensitive detector (Princeton Instruments, PIXIS-XF 2048B) located 4.14 m behind the focus [cf. Fig. 1 (c)]. This procedure increases the chance of recording a properly illuminated diffraction pattern. A 4 × 4-binning of the CCD reduced the pixel array to a size of 512 × 512 pixels with an effective pixel size of 54 × 54 μm2. The XFEL-beam was attenuated by polished single crystal silicon absorbers to 1% of the full beam intensity in order to prevent the saturation of the detector. At each position of the scan, the diffraction pattern with the highest integral intensity was selected for further processing. Of these, all those with an overall intensity of below 10% as compared to the diffraction pattern with maximum intensity were discarded. The remaining diffraction patterns served as input to the ptychographic reconstruction and were normalized to the pulse intensity.

Position refinement

The sample was positioned with a nano-positioning piezo stage (PhysikInstrumente P-615 NanoCube) providing a nominal repeatability lower than 10 nm. In practice, however, it turned out that, due to thermal drifts and instabilities of the setup, the dial values of the device were not sufficiently accurate for a successful ptychographic reconstruction of the object. For this reason, we developed an algorithm, which permits the numerical refinement of the position values based on the measured diffraction patterns alone. The algorithm is designed as follows.

The procedure starts with a standard ptychographic phase retrieval using the expected position values. Since these values often differ significantly from the real ones, the algorithm delivers the transmission function of the object with a low spatial resolution and some aberrations. The illumination function on the other hand is typically retrieved to a high degree of accuracy27. This first guess of illumination and object function is sufficient to pursue a local search for the correct position values.

Given an illumination and object function, we can calculate a modeled diffraction pattern for each position of the illumination on the object. By comparing these modeled diffraction patterns to the ones measured, we can find the positions that best match the measured data (minimal least square distance between the two diffraction patterns) and associate these new positions with the measured diffraction patterns. In practice, this is done in a neighborhood of 20 × 20 pixels around the nominal positions.

After such a positional refinement step, the ptychogram is reconstructed anew, yielding a much better reconstruction of the object function. The refinement procedure can be repeated until the positions reach stable values. Here, six iterations were performed to reach convergence.

Reconstruction of single-pulse illumination

The regular procedure for the ptychographic reconstruction relies on a constant common illumination for all points in the ptychographic scan22,23. For the XFEL source, we expect fluctuations in the illumination. In order to determine these fluctuations, we adopted the following procedure: for each scan point i we define an individual illumination Pi and initialize it with the average illumination given in Fig. 2 (b). The object O is initialized to the reconstruction shown in Fig. 2 (a). We then use the ptychographic engine23 to refine the local illumination while not updating the object. The illumination converges after a few hundred iterations. Two individual illuminations obtained in this way are shown in Fig. 4 (b) and (c).

Author Contributions

A.S., J.B.H. and C.G.S. conceived and coordinated the experiment. The setup was conceived and developed by A.S., C.G.S. and B.A. The beamline was set up and operated by H.J.L., B.N. and E.C.G. The experiment was carried out by A.S., R.H., V.M., J.P., F.S., H.J.L., B.N., E.C.G., U.Z., D.N., F.U., U.V., H.M.H. and C.G.S. The samples were provided by F.U., D.N., U.V. and H.M.H. The data were analyzed by A.S., R.H., V.M., J.P., F.S. and C.G.S.

Acknowledgments

Portions of this research were carried out at the Linac Coherent Light Source (LCLS) at the SLAC National Accelerator Laboratory. LCLS is funded by the U.S. Department of Energy's Office of Basic Energy Sciences. The MEC instrument was supported by U.S. Department of Energy, Office of Fusion Energy Sciences. This work was funded by Volkswagen Foundation, the DFG under grant SCHR 1137/1-1, the Swedish Research Council and the Göran Gustafsson Foundation. We would also like to thank the MEC team at SLAC, collaborating institutions, and Bruno Lengeler for fruitful discussions and providing the CRL optics.

References

  1. Koopmann R. et al. In vivo protein crystallization opens new routes in structural biology. Nature Methods 9, 259 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Johansson L. C. et al. Lipidic phase membrane protein serial femtosecond crystallography. Nature Methods 9, 263 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Chapman H. N. et al. Femtosecond x-ray protein nanocrystallography. Nature 470, 73–U81 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Vinko S. M. et al. Creation and diagnosis of a solid-density plasma with an x-ray free-electron laser. Nature 482, 59–62 (2012). [DOI] [PubMed] [Google Scholar]
  5. Glover T. E. et al. X-ray and optical wave mixing. Nature 488, 603–608 (2012). [DOI] [PubMed] [Google Scholar]
  6. Neutze R., Wouts R., van der Spoel D., Weckert E. & Hajdu J. Potential for biomolecular imaging with femtosecond X-ray pulses. Nature 406, 752–757 (2000). [DOI] [PubMed] [Google Scholar]
  7. Gaffney K. J. & Chapman H. N. Imaging atomic structure and dynamics with ultrafast x-ray scattering. Science 316, 1444 (2007). [DOI] [PubMed] [Google Scholar]
  8. Ziaja B. et al. Limitations of coherent diffractive imaging of single objects due to their damage by intense x-ray radiation. New Journal of Physics 14, 115015 (2012). [Google Scholar]
  9. Boutet S. et al. High-resolution protein structure determination by serial femtosecond crystallography. Science 337, 362–364 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Mimura H. et al. Focusing mirror for x-ray free-electron lasers. Review of Scientific Instruments 79, 083104 (2008). [DOI] [PubMed] [Google Scholar]
  11. David C. et al. Nanofocusing of hard X-ray free electron laser pulses using diamond based Fresnel zone plates. Scientific Reports 1, 57 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Schroer C. G. et al. Focusing hard x-ray FEL beams with parabolic refractive lenses. In Biedron, S. G., Eberhardt, W., Ishikawa, T. & Tatchyn, R. O. (eds.). Fourth Generation X-Ray Sources and Optics II, vol. 5534 of Proceedings of the SPIE, 116–124(2004). [Google Scholar]
  13. Miao J., Charalambous P., Kirz J. & Sayre D. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens. Nature 400, 342–344 (1999). [Google Scholar]
  14. Shapiro D. et al. Biological imaging by soft x-ray diffraction microscopy. P. Natl. Acad. Sci. USA 102, 15343–15346 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Seibert M. M. et al. Single mimivirus particles intercepted and imaged with an x-ray laser. Nature 469, 78–81 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Schropp A. & Schroer C. G. Dose requirements for resolving a given feature in an object by coherent x-ray diffraction imaging. New Journal of Physics 12, 035016 (2010). [Google Scholar]
  17. Doumy G. et al. Nonlinear atomic response to intense ultrashort x rays. Phys. Rev. Lett. 106, 083002 (2011). [DOI] [PubMed] [Google Scholar]
  18. Fratalocchi A. & Ruocco G. Single-molecule imaging with x-ray free-electron lasers: Dream or reality? Phys. Rev. Lett. 106, 105504 (2011). [DOI] [PubMed] [Google Scholar]
  19. Chalupsky J. et al. Spot size characterization of focused non-Gaussian X-ray laser beams. Optics Express 18, 27836–27845 (2010). [DOI] [PubMed] [Google Scholar]
  20. Quiney H. M., Peele A. G., Cai Z., Patterson D. & Nugent K. A. Diffractive imaging of highly focused X-ray fields. Nature Physics 2, 101–104 (2006). [Google Scholar]
  21. Rodenburg J. M. & Faulkner H. M. L. A phase retrieval algorithm for shifting illumination. Appl. Phys. Lett. 85, 4795–4797 (2004). [Google Scholar]
  22. Thibault P. et al. High-resolution scanning x-ray diffraction microscopy. Science 321, 379–382 (2008). [DOI] [PubMed] [Google Scholar]
  23. Maiden A. M. & Rodenburg J. M. An improved ptychographical phase retrieval algorithm for diffractive imaging. Ultramicroscopy 109, 1256–1262 (2009). [DOI] [PubMed] [Google Scholar]
  24. Schropp A. et al. Non-destructive and quantitative imaging of a nano-structured microchip by ptychographic hard x-ray scanning microscopy. J. Microscopy 241, 9–12 (2011). [DOI] [PubMed] [Google Scholar]
  25. Dierolf M. et al. Ptychographic x-ray computed tomography at the nanoscale. Nature 467, 436–440 (2010). [DOI] [PubMed] [Google Scholar]
  26. Schropp A. et al. Hard x-ray scanning microscopy with coherent radiation: Beyond the resolution of conventional x-ray microscopes. Appl. Phys. Lett. 100, 253112 (2012). [Google Scholar]
  27. Schropp A. et al. Hard x-ray nanobeam characterization by coherent diffraction microscopy. Appl. Phys. Lett. 96, 091102 (2010). [Google Scholar]
  28. Kewish C. M. et al. Reconstruction of an astigmatic hard x-ray beam alignment of K-B mirrors from ptychographic coherent diffraction data. Opt. Express 18, 23420–23427 (2010). [DOI] [PubMed] [Google Scholar]
  29. Kewish C. M. et al. Ptychographic characterization of the wavefield in the focus of reflective hard X-ray optics. Ultramicroscopy 110, 325–329 (2010). [DOI] [PubMed] [Google Scholar]
  30. Vila-Comamala J. et al. Characterization of high-resolution diffractive x-ray optics by ptychographic coherent diffractive imaging. Opt. Express 19, 21333–21344 (2011). [DOI] [PubMed] [Google Scholar]
  31. Hönig S. et al. Full optical characterization of coherent x-ray nanobeams by ptychographic imaging. Opt. Express 19, 16325–16329 (2011). [DOI] [PubMed] [Google Scholar]
  32. Emma P. et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nature Photonics 4, 641–647 (2010). [Google Scholar]
  33. Lengeler B. et al. Imaging by parabolic refractive lenses in the hard x-ray range. J. Synchrotron Rad. 6, 1153–1167 (1999). [Google Scholar]
  34. Lengeler B. et al. Refractive x-ray lenses. J. Phys. D: Appl. Phys. 38, A218–A222 (2005). [Google Scholar]
  35. Born M. & Wolf E. Principles of Optics (Cambridge University Press, Cambridge, 1999). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES