Modeling Cell Signaling Networks

Abstract

Cell signaling pathways interact with one another to form networks in mammalian systems. Such networks are complex in their organization and exhibit emergent properties such as bistability and ultrasensitivity. Analysis of signaling networks requires a combination of experimental and theoretical approaches including the development and analysis of models. This review focuses on theoretical approaches to understanding cell signaling networks. Using heterotrimeric G protein pathways an example, we demonstrate how interactions between two pathways can result in a network that contains a positive feedback loop and function as a switch. Different mathematical approaches that are currently used to model signaling networks are described, and future challenges including the need for databases as well as enhanced computing environments are discussed.

1. Introduction

Substantial progresses over the past three decades in biochemistry, molecular biology and cell physiology, coupled with emerging high throughput techniques for detecting protein-protein interaction, have ushered in a new era in signal transduction research. Studies of signaling pathways have traditionally focused on delineating immediate upstream and down stream interactions, and then organizing these interactions into linear cascades that relay and regulate information from cell surface receptors to cellular effectors such as metabolic enzymes, channels or transcription factors (Weng et al., 1999). However, recent analyses of signaling pathways in mammalian systems have revealed that cellular signals do not necessarily propagate in a linear fashion. Instead, cellular signaling networks are made up of highly connected modules that can be used to regulate multiple functions in a context dependent manner (Jordan et al., 2000). Because of their size and complexity, these networks are often too complicated for the human mind to organize and analyze. Therefore, it has become necessary to develop mathematical models to understand the system behavior of signaling networks, and to predict higher order functions that can be validated by experiments.

The use of mathematical models and computer simulation has had a rich history in modern biology. In the field of pharmacology and drug discovery, modeling has often used to study of receptor-ligand interactions and pharmacokinetics(Black et al., 1985; Furchgott, 1987). Cellular metabolic networks have also been long studied by use of sophisticated mathematical analysis to measure the flow of metabolites in large networks with many regulatory loops (Palsson et al 1987, Covert et al, 2001). More recently it has become feasible to simulate signaling networks with tens of components(Bhalla and Iyengar, 1999; Schuster et al., 2000). Like metabolic networks, signaling networks are characterized by modules with well-defined input and output, and by feedback loops and multi-step regulatory controls (Bruggeman et al., 2002). Mathematical analysis of how these modules interact should augment our understanding of signaling pathways in three ways. First, modeling yields insight into how individual pathways function within the context of other operational pathways. Second, modeling enables estimation of parameters that are not experimentally accessible with current technology, and often verifies whether if a proposed molecular mechanism is correct. Third, modeling identifies major regulatory hubs of signaling networks, and helps uncover possible targets for pharmacological intervention in diseases. Thus, the use of data-driven computer simulation empowers the biologist with a tool to quickly test and generate hypotheses about network structure and function, and to infer fundamental operating principles governing signal propagation.

The focus of this review is to develop a framework for thinking about the construction of a mathematical model for signaling networks, with focus on G protein pathways, and to summarize key concepts that have emerged from recent studies. First, we outline the steps one might take in constructing a mathematical model of signaling network. Next, we review mathematical formalisms for describing biochemical reactions. Finally, we discuss future challenges, which include modeling spatially restricted biochemical reactions and stochastic-continuous hybrid models of signaling networks.

2. Maps, and Modules

2.1. Defining Signaling Modules

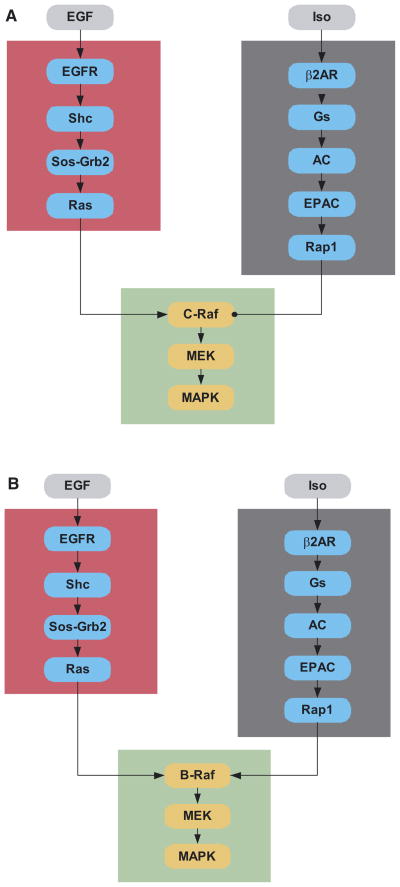
A key feature of any networks is its architecture. To understand network architecture and its biological implications from a bottom–up approach, the first step is to identify the “connection map,” and then to organize the connection into modules that can be constrained by experimental data and analyzed computationally. For instance, the modular organization of signaling network is illustrated here with a ubiquitous signaling pathway: the growth factor receptor Ras-MAP-kinase (MAPK) pathway. A typical growth factor that activates this receptor is the epidermal growth factor (EGF), and the canonical pathway involved in activation of MAPK by EGF is shown in Figure 1 (Schlessinger and Ullrich, 1992; Egan and Weinberg, 1993). One way to organize the signaling reactions might be to separate modules with clearly defined input and output based on pathway and cellular compartments. One module might be the MAPK cascade with Ras-GTP as an input and dually phosphorylated MAPK as an output. Another module might be defined for the reactions that take place at the plasma membrane, with EGF as an input and Ras-GTP as the output (Figure 1A). If one is interested in crosstalk between Ras and the small G-protein Rap1, another module could be defined for novel cAMP pathway that activates the Rap GEF Epac(Bos, 2003). Note that the relationship between the modules may depend on the biological state and cellular context. When c-Raf is the major isoform, activation of Rap1 leads to sequestration of c-Raf, resulting in antagonism of the signal flow from the EGF receptor to MAPK. (Figure 1A). Thus, c-Raf “subtracts” the signal from β2-adrenergic receptors from that of the EGF receptor. In contrast, B-Raf, which is present in many neuronal cell lines, can be activated by both Ras and Rap1 (Figure 1B)(Grewal et al., 2000; Schmitt and Stork, 2000). Here, B-Raf acts as an integrator that sums signals from the EGF and β-adrenergic receptors to activate MAPK.

Fig. 1. Modules and the their interactions in signaling sathways.

This figure shows the modules that could be used to describe interactions between the growth factor and β-adrenergic receptor pathways. The growth factor signaling pathway is divided into two modules (the red box and the green box). Such modularity divides this pathway by their location within different subcellular regions. All members of the red box are functional at the plasma membrane while the members of the green box are cytoplasmic. At a functional level, the reactions in the red box specify how EGF binding to its receptor regulates activation of Ras while the reactions in the green box specify how the activated Ras regulates MAPK phosphorylation. The gray box provides a counter point to the organizational logic of the red and green boxes. Here the module spans reactions from the membrane to the cytoplasm, from the β-adrenergic receptor agonist isoproternol to the small G protein Rap1 in the cytoplasm. This modular arrangement provides a facile way of understanding how β-adrenergic receptor stimulation could inhibit or augment EGF activation of MAP-kinase. Comparison of Figures 1A and 1B are crucial for understanding the necessity of specifying the isoforms of the components within the modules to understand regulatory behavior. When the major isoform is C-Raf, the interactions between the EGF receptor pathway and β-adrenergic receptor pathway are antagonistic since Rap1 sequesters but does not activate C-Raf (Figure 1A). In contrast, B-Raf is activated both by Ras and Rap1. Here, the two pathways are additive or synergistic in activating MAP-kinase (Figure 1B).

Although the process of defining signaling module is arbitrary and flexible, a module should have a dose-response curve and time course that can be manipulated and verified experimentally. In the system depicted in Figure 1, we have defined a module with a β2-adrenergic receptor agonist as the input, and activated Rap1 as the output. This input-output relationship can be experimentally constrained by measuring the time course of Rap1 activation at various isoproternol concentrations. Such constraints serve two purposes. First, they allow estimation of modeling parameters when the parameters do not exist in literature. Second, agreement between the predicted outcome and the experimental data acts as a valuable internal check for the model’s validity. This is particularly important in large networks, where parameters can be tuned to fit experimental results and many alternative mechanism can yield results that “look correct.”

2.2. Emergent Properties from Interacting Modules

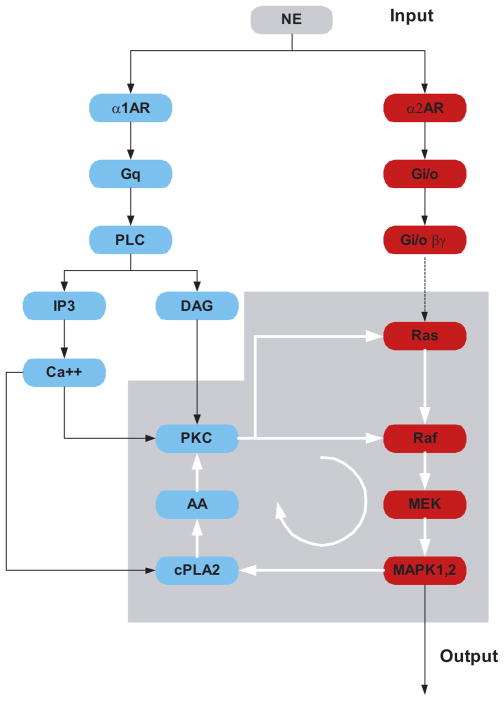
Because cellular regulation is achieved through dynamic interaction between many components and modules, the challenge is to develop ways of simplifying the description of these networks to provide qualitative insight. One mean of analyzing the network is to further organize components and modules into motifs, which describe the regulatory features of the network. A motif that is familiar to every biologist is the feedback loop. Negative feedback loop can give rise to adaptation and desensitization, while positive feedback loop can lead to emergent network properties such as ultrasensitivity and bistability (Bagowski and Ferrell, 2001; Bhalla et al., 2002; Ferrell, 2002). In many cases, regulatory motif arises from synergistic action of multiple pathways. For instance, the emergence of a positive feedback from interaction between two G protein coupled pathways is depicted in Figure 2. Here the presence of α1-adrenergic and α2- adrenergic receptors may result in activation of both the protein kinase C as well as the MAPK-pathways. These two pathways interact to form a positive feedback loop that can lead to the sustained activation of MAPK. Hence, the presence of multiple forms of G protein coupled receptor for the same extracellular hormone can lead to intracellular switching behavior due to the emergence of a key regulatory motif, the positive feedback loop.

Fig. 2.

Networking and activation of a positive feedback loop by norepi-nephrine acting through the α1- and α2- adrenergic receptor pathways.

When norepinephrine (NE) binds the α1 adrenergic receptor it activates the Gq pathway, leading to stimulation of the phospholipase C-β. This results in release of intracellular calcium and the activation of protein kinase C, which in turn can activate both Ras and Raf. When NE activates the α2-adrenergic receptor, which couples to the Gi/o pathway, release of Gβγ results in the activation of the Ras-MAPK pathway. Simultaneous activation of both pathways results in MAPK regulation of cytoplasmic phospholipase-A2 (cPLA2), which produces arachadonic acid (AA) that activates protein kinase C in the presence of basal levels of diacylglycerol (DAG). This sets up a positive feedback loop indicated by the circular arrow, resulting in sustained activation of MAP-kinase. Thus brief pulses of NE could lead to prolonged activation of MAP-kinase (MAPK) in cells where both α1 and α2 adrenergic receptors and other components of the network are present.

3. Modeling Methodology

Although the identification of modules and motifs can yield insight into the range of system behaviors that a network may demonstrate, it is impossible to predict the system-level dynamics without a mathematical model. The modeling methodology depends on the biology of the network and the phenomena that the modeler wants to capture. Here, we briefly describe the three most commonly used modeling frameworks. They are chemical kinetics models, compartmental models, and diffusion-reaction models.

3.1. Chemical Kinetics and Compartmental Modeling

Perhaps the most familiar, and certainly the simplest, modeling framework is the chemical kinetics approach. The fundamental assumption in this framework is that the cell is a well-stirred reactor. The governing equation that describes the dynamics of a signaling component has the form:

$$\frac{dC}{dt}=(\mathit{generation})-(\mathit{consumption})$$ (1)

The equation above, which is simply a formal mathematical statement of our intuition, states that the rate of change in concentration of any molecules is equal to the rate at which it is being generated and/or destroyed. The generation and consumption term can be a constant (e.g., synthesis), first order reactions (e.g., degradation), or nonlinear (e.g., second order reactions or Michelis-Menten kinetics for enzymes). Equation 1 is an example of Ordinary Differential Equations (ODEs). The term ODE refers to the fact that concentration is only a function of time, not space. The advantage of ODE-based models is that although analytical solutions are not guaranteed-- in most cases, it cannot be obtained-- numerical methods for solving a system with large number of coupled nonlinear ODEs are well developed (see Box 1). For networks such as those shown in Figures 1 or 2 with 10–20 components, a system of about 30–70 reactions would describe the network. Input–output relationships would then be computed for this set of coupled differential equations using numerical methods. The actual computation is often performed in software environments that provide graphical user interface (GUI) for front-end data entry as well display of computed data in graphical forms that are analogous to plots of empirical data (Bhalla and Iyengar, 1999; Bhalla et al., 2002). GEPASI(http://www.gepasi.org) and GENESIS with the Kinetikit interface (http://www.genesis-sim.org/GENESIS/) are some examples of software environments that can simulate ODE-based models. Curve fitting functions in program such as GEPASI also enable seamless determination of modeling parameters from experimental data. A major drawback of the chemical kinetics approach to model signaling networks is the inherent assumption that the cell is a well-stirred reactor. While this assumption is acceptable for some cases, it is not appropriate for modeling spatially restricted biochemical reactions. To understand the rich dynamics that arises from variation in both space and time, either a compartmental or a partial differential equation (PDE)-based model is needed.

Like chemical kinetics models, compartmental models are based on ODEs. However, instead of assuming that the same molecules in different compartments are regulated in similar manner, a compartmental model treats molecules in different compartment as separate species. Exchange of the molecules between compartments is modeled as a flux, which is determined from either a priori knowledge of the biology or from empirical observations. Because the same species in different cellular compartment is treated as different components, compartmental models capture the dynamics involved in spatially restricted biochemical reactions at the expense of increasing the numbers of independent variables and kinetic parameters. Compartmental modeling has been used extensively in modeling the network involved in protein secretion and trafficking, and developmental biology, and is appropriate for most networks where a “coarse-grained” description is sufficient to model the biological function (Hirschberg et al., 1998; Hirschberg and Lippincott-Schwartz, 1999; von Dassow et al., 2000). For the cases where explicit dependence on the spatial variables is needed (e.g., where micro-domain and/or chemical wave is an important feature or where one is interested in interaction between chemistry and geometry), a partial differential equation (PDE)-based model is needed (Fink et al., 1999; Fink et al., 2000; Smith et al., 2002).

3.2. Modeling Spatially Restricted Biochemical Reaction with Diffusion-reaction Equation

The spatiotemporal dynamics of any signaling component can be described by the diffusion-reaction equation:

$$\frac{\partial C}{\partial t}=D\frac{{\partial }^{2}C}{\partial x^2}-v\frac{\partial C}{\partial x}+R$$ (2)

where C is concentration, t is time, D is the diffusion coefficient, x is the spatial variable, v is the convective velocity, and R is the rate of generation and consumption. Since excellent derivations of Equation 2 exist elsewhere, here we focus only on the physical meaning and biological implications(Berg, 1993). Equation 2 is an example of a PDE because concentration depends on more than one independent variable, in this case, time and space. Physically, Equation 2 states that the rate of change of concentration of a component at any particular location depends on diffusion (e.g., the first term in Equation 2), active transport or convection (e.g., second term in Equation 2), and biochemical reactions (e.g., the last term in Equation 2). Equation 2 gives several insights. First, assuming that there is no convection or active transport, the diffusion coefficient determines the range of a diffusible signaling components. (In general, the range scales as the square root of the diffusion coefficient.) For example, the signaling network involved in pattern formation during development is thought to depend on local activation and global inhibition(Nagorcka and Mooney, 1992; Painter et al., 1999; Von Dassow and Odell, 2002). Those spatially restricted reactions can be modeled as small diffusion coefficients for components in the positive feedback loop, and large diffusion coefficients for components in the negative regulatory pathways. Another approach to modeling spatially restricted reaction is to allow the reaction terms to vary in space. As an extreme case, consider a reaction whereby an adaptor protein x binds to its receptor on the plasma membrane. Since the reaction only occurs at the boundary, the last term in Equation 2 disappears. Instead, the reaction kinetics is specified in the boundary condition, which states that the flux of component x into the membrane and is equal to the rate of reaction. Equation 2 thus enables fine-grained spatial variations in chemical kinetics to be modeled.

While modeling signaling network with reaction-diffusion equations affords a more realistic approach for the analysis of spatially restricted biochemical reactions, the mathematical challenges involved in solving a large system of coupled, nonlinear partial differential equations are nontrivial. PDE problems require many more parameters compared to ODE problems. In addition to the initial concentrations and kinetics parameters, PDE based model require diffusion coefficients, and mandate specification of concentration and/or flux at the boundary. Moreover, PDE problems require far greater computational skills, resources, and time than their ODE counterparts. Currently, most PDE problems are solved using custom- computing software that is tailored to a specific problem. These computer codes are generally only accessible to mathematicians and computational experts, and are usually not scaleable when modules are added or modified. Biologist-friendly software for solving PDEs are sparse; at the time of this writing, only the web-based program Virtual Cell (http://www.nrcam.uchc.edu/) has been specifically designed for solving biological problems in a user friendly manner(Moraru et al., 2002).

3.3. Model Testing

Because the modeling parameters are usually gathered from biochemical experiments on purified components while functional effects arise from cell physiological experiments, one does not aim for numerical agreement between the experimental data and modeling prediction. Instead, the modeler should aim for the correct “scaling relationship.” The gradual refinement of mathematical model based on experimental data is an iterative process. In our example of EGF-induced Ras activation, if the simulation predicts a dose response curve that is bell-shaped, the experimental data should support this conclusion even if the exact concentration does not match. If the dose-response curves match, the modeler can proceed by comparing the predicted time course of activation with experimental data. Once the time scale of activation and deactivation are correct, one can investigate the robustness of the model by systematic parameter variations. In general, most biological signaling networks are robust within an order of magnitude variation in kinetics parameters. That is, the model should not “blow up” (i.e., concentration of a reactant goes to infinity or zero) when the parameters are increased or decreased by less than ten-fold. If, on the other hand, the simulation predicts that some components are sensitive to small perturbations in biochemical parameters, this does not necessarily mean the model is incorrect. Instead, it suggests that the components might be susceptible to external perturbation, and experimental means to manipulate the biochemical activities of the molecule should be used to verify theoretical prediction. For example, in the MAP-kinase - cPLA2 - protein kinase C feedback loop studied in our laboratory, the switching behavior of the loop was sensitive to two-fold variations in protein kinase C concentrations (Bhalla and Iyengar, 1999). This is however entirely understandable in the context of the well known down regulation of protein kinase C upon persistent stimulation.

In summary, we have outlined the steps and considerations that go into the construction of a mathematical model. The first step is to generate a connection map and to identify regulatory features that may give rise to novel properties. After writing out the reaction schemes and collecting the necessary parameters, the modeler generates mathematical model using the appropriate frame work. Once the simulation has been performed, comparison between in silico and in vivo experiments is needed to validate the model. Often, this comparison is an iterative process that requires modification to the mathematical model and manipulations that alter the internal connectivities or the biochemical states of components within the network. Both positive and negative outcomes of the experimental verification are useful in challenging the accuracy and the underlying assumptions of the models. Such challenges often uncover novel features of cellular signaling networks.

4. Current Challenges and Future Directions

Although progresses have been made in modeling biological networks, many experimental and computational challenges remain unaddressed. One significant hurdle is the lack of quantitative experimental data (Weng et al., 1999). Mathematical modeling requires accurate estimation of both the concentration of signaling components inside the cells, and the kinetic parameters for each biochemical reaction. In many cases, it is difficult to accurate measure concentration of endogenous proteins in their natural environment. In addition, kinetics data have not yet been determined for many biochemical reactions. Even in cases where the rate constants are measured, the experiments are usually conducted in vitro with purified components. The interaction may have vastly different kinetics in vivo, because many biological reactions take place on scaffold, microdomains, or membrane that essentially increases the local concentration of the reactant. Addtionally issues related to molecular crowding have yet to be addressed. Thus far, techniques for measuring rates and concentration of reactants in their natural compartmentalized environment have not been well realized. The development of fluorescence probes for measuring reaction dynamics in situ will be instrumental in obtaining quantitative kinetics data (Dundr et al., 2002).

In addition to the experimental hurdles, computational challenges exist at multiple levels. Data on new protein-protein interactions and added details for signaling pathways are accumulating at an exponential rate due to new advances in high throughput technology. The biological context in which these interactions and connections play a meaningful role is not well understood. Hence, the potential value of networks constructed from these large data sets is uncertain. Guidelines for the inclusion and exclusion of such data sets need to be developed. Furthermore, the complexity of such data are far too complicated to be organized manually. What is needed is the development of a signaling database that generate “connection maps” which can be used to identify network architecture and the underlying regulatory motifs. Science’s STKE connection map (http://stke.sciencemag.org) represents a first attempt to develop qualitative connections maps from tables of components. A systematic “part list” of the components and their location, and kinetic properties, and tools to visualize the interaction will also greatly aid generation of new mathematical models. The Molecule Pages being developed by the Alliance for Cell Signaling (http://www.signaling-gateway.org/) should be useful in this regard. In addition, the construction of a model can be expedited by development of a database where all of the connection maps and the appropriate reactions are assembled into models that can be exported directly into computing environments. The SigPath database (www.SigPath.org) being developed as a joint effort between our laboratory and that of Weinstein and Campagne is an initial prototype of database that to catalog and annotate quantitative data in signaling networks.

Another crucial computational challenge is to design software packages that are easily accessible to the non-mathematicians, and to develop new modeling paradigms. While many “point-and-click” simulation platforms have been developed for chemical kinetics modeling, modeling spatially restricted biochemical reaction remains accessible only to scientists with computational skills and computational resources. In addition, new modeling algorithms have to be developed that deal with both the deterministic and stochastic nature of the signaling network. This is especially important when one considers that gene expression, the “output” of many network, is typically driven by only a few hundred molecules of transcription factors (Arkin et al., 1998; McAdams and Arkin, 1999). Simulation methodology that can integrate the deterministic regime of the signaling network with the stochastic reactions involved in gene expression will enable a better understanding of how signaling network suppresses (or exploits) biochemical noise.

Finally, a major long-term goal of biochemical simulations involves integrating signaling network output to functional outcomes. In many cases, the most relevant, and often the only measurable, output of signaling network is functional outcomes such as proliferation, polarization of cells, or migration. In studying Rac or Cdc42 signaling network, the modeler might be interested in modeling how the signal from extracellular matrices ultimately regulates the dynamics of the cytoskeleton and cell migration. Integrating models of signaling networks with the molecular machines such as those involved in the generation of mechanical force will give new insight into how cellular decision processes, which are digital in function can be decoded from biochemical signaling, which is analog in nature.

5. Example: Analytical and Numerical Solutions for Ordinary Different Equations

To illustrate how differential equations are solved, let us consider a simple model of protein degradation:

$$\frac{dC}{dt}=-kC$$ (B1)

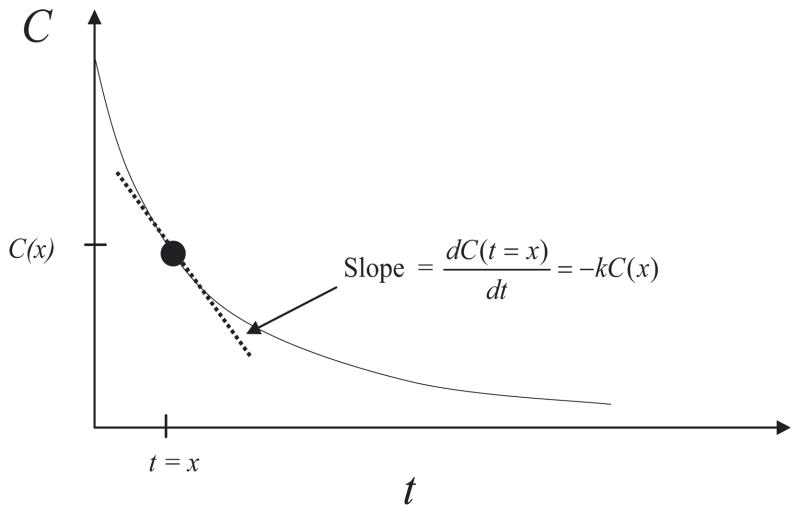
where C is the concentration and k is the rate of degradation. Equation B1 says that the rate of change in concentration at any time t is linearly proportional to the concentration at that particular moment. Our goal is now to find a function C(t) that has a special property: the value of the derivative of C at any time t is equal to the negative of the value of C multiplied by the constant k (see Figure B1).

Fig B1. Graphical Interpretation of Equation B1.

The solution to Equation B1 has the special property that its derivative (slope) at any given time is simply equal to the negative of its value multiplied by a proportional constant k

There are two ways of solving this problem. One method is to rearrange Equation B1 as follow:

$$\frac{dC}{C}=-\mathit{kdt}$$ (B2)

Since the left hand side of Equation B2 only depends on C and the right hand side only depends on t, Equation B2 can be integrated from t = 0 to t = t*

$$\underset{(t=0)}{\overset{(t=t^{\ast })}{\int }}\frac{dC}{C}=\underset{t=0}{\overset{t=t^{\ast }}{\int }}-\mathit{kdt}$$ (B3)

The result of the integration is

$$ln\frac{C(t)}{C(0)}=-kt$$ (B4)

Upon rearrangement, Equation B4 takes on a familiar form:

$$C(t)=C(0)exp(-kt)$$ (B5)

Most biologists are familiar with Equation B5. In a pulse-chase experiment, the concentration of the radiolabeled protein decays exponentially at a rate that is proportional to the rate of degradation.

Equation B5 is called an analytical solution, meaning that an exact mathematical expression of C as a function of t can be derived. Analytical solution is elegant because the relationship between C, the parameter k, and the independent variable t becomes immediately transparent. On the one hand, if the parameter k is doubled, we know that the characteristic time of decay (1/k) is half. On the other hand, if the initial concentration C(0) is doubled, the decay time is unchanged.

Unfortunately, it is not possible to arrive at analytical solutions for every ODE problem. Biological systems often involve large number of components, which usually leads to a large system of coupled, nonlinear ODEs. “Linear” refers to the order of the term that appears in the ODEs. For instance, Equation B1 is linear because it only depends on C. In contrast, the following equation is nonlinear:

$$\frac{dC}{dt}=-{kC}^2+\frac{V_{max}}{K_m+C}$$ (B6)

Equation B6 is nonlinear because the first term depends on C², and the second term depends on 1/C. Analytical solution is not guaranteed for nonlinear ODEs, and in general, it cannot be found. Instead, the ODEs are usually solved numerically. To illustrate how this is done, we revisit Equation B1:

$$\frac{dC}{dt}=\frac{C(t+\delta t)-C(t)}{(t+\delta t)-t}=-kC(t)$$ (B7)

where δt is an arbitrary, but small, time increment (“time step”). Suppose we know that the concentration at time t = 0 is C(0), the concentration at time just after t = 0 can be found:

$$\frac{C(0+\delta t)-C(0)}{(0+\delta t)-0}=\frac{C(\delta t)-C(0)}{\delta t}=-kC(0)\Rightarrow C(\delta t)=C(0)(1-k\delta t)$$ (B8)

Once C(δt) is found, the process is repeated to find C(2 δt). It is worth noting that the modeler only gets a series of data points from this iterative technique, and that the data point represents approximate, not exact solutions. (All computing software will allow the modeler to define the time-step δt. Smaller time steps generally take longer to solve, but also give more accurate numerical solutions.) In addition, the relationship between C and the parameter k is not immediately obvious. If k is doubled, the modeler will most likely have to repeat the procedure again to find that time scale of decay is half. Fortunately, numerical methods for solving ODEs are well developed, and modern desktop computers can easily handle the computational workload required to solve systems with hundreds of components.