Automated Liver Stiffness Measurements with Magnetic Resonance Elastography

Abstract

Purpose

To provide a fully-automated algorithm for obtaining stiffness measurements from hepatic MR Elastography images that are consistent with measurements performed by expert readers.

Materials and Methods

An initial liver contour was found using an adaptive threshold and expanded using an active contour to select a homogeneous area of the liver. The confidence map generated during the stiffness calculation was used to select a region of reliable wave propagation. The average stiffness within the automatically-generated ROI was compared to measurements by two trained readers in a set of 88 clinical test cases ranging from healthy to severely fibrotic.

Results

The stiffness measurements reported by the readers differed by −6.76% ± 22.8 % (95% confidence) and had an ICC of 0.972 (p<0.05).The algorithm and the more experienced reader differed by 4.32% ± 14.9 with an ICC of 0.987.

Conclusion

The automated algorithm performed reliably, even though MRE acquisitions often have motion artifacts present. The correlation between the automated measurements and those from the trained readers was superior to the correlation between the readers.

INTRODUCTION

Chronic liver disease is a significant world-wide health problem. The majority of complications associated with chronic liver disease stem from the development of hepatic fibrosis. Notably, fibrosis can be stabilized or even regress following therapy for underlying liver diseases (1–5). However, if left untreated, chronic liver disease can progress to cirrhosis and result in an increased risk for end-stage liver disease, hepatocellular carcinoma, an increased need for liver transplant, and death. Until recently, liver biopsy has been the standard method for detecting hepatic fibrosis. However, due to the invasiveness of the procedure and the risk of complications, plus concerns about the small sample size associated with biopsy and variability in the readings (6, 7), noninvasive techniques, such as Magnetic Resonance Elastography (MRE) and Transient Ultrasound Elastography, have been developed to assess liver fibrosis (8, 9). These techniques have shown high reliability and are being used with increasing frequency for clinical diagnosis.

MRE is an MRI-based technique that is capable of measuring tissue stiffness by observing the response of tissue to an intrinsic or extrinsic stress (10). In typical implementations of liver MRE, the liver is vibrated noninvasively at one or several frequencies by an external driver vibrating on the chest wall (11–13). The tissue motion is then imaged using phase-contrast MR techniques and gradient-echo, spin-echo, or echo-planar imaging sequences. Images of shear wave propagation (often called phase or wave images) can then be processed using appropriate equations of motion to produce quantitative images (or elastograms) describing the mechanical properties of the tissue, such as the effective stiffness, shear modulus, and shear viscosity (14, 15).

The final reading of MRE images to report a measurement of stiffness can be a time-consuming and subjective process. In our technique as clinically implemented, 4 2D slices in the liver are acquired, and planar wave propagation is assumed. Currently, a trained reader needs to examine the MR magnitude and phase images to define regions of interest (ROIs) within the liver that avoid blood vessels and boundary effects and have good wave quality in each 2D slice. The mean stiffness within the ROI is then calculated using the elastogram image. The elastogram is also reviewed for artifacts, such as hot/cold spots indicative of significant wave interference or oblique wave propagation, and such regions are excluded from the measurement. The procedure needs to be repeated for every slice of the exam. Depending on the technique and software used, the number, size and shape of ROIs can vary between readings, causing different readers to obtain different results for the same image and even individual readers to have a certain degree of variability.

This study presents a fully automated algorithm that defines an artifact-free ROI within the liver and takes the stiffness measurement. The hypothesis of this study was that this automated technique can assess liver stiffness as accurately as trained MRE readers. The potential benefits of this algorithm include decreased variability due to reader training and consistency of reading methods, as well as reduced time and cost for MRE exams.

MATERIALS AND METHODS

MRE Data

The algorithm described below was tested in a retrospective study designed in compliance with our institutional review board. The patients studied were affected by non-alcoholic fatty liver disease (NAFLD) and represent an at-risk population including cases of advanced fibrosis. MRE exams were performed on a 1.5T GE Signa Excite HDx scanner with a gradient-echo MRE sequence, an 8-channel receive-only torso coil array, and 60-Hz mechanical vibrations delivered by an active acoustic driver located outside of the scanner room to a passive plastic drum driver placed on the chest wall of the patient (11). Typical imaging parameters included a 44-cm FOV; 256x64 acquisition matrix (reconstructed to 256x256); parallel imaging acceleration factor of 2; TR/TE/flip angle/bandwidth = 50 ms/20 ms/30°/32 kHz; 4 contiguous axial 10-mm-thick slices acquired sequentially; right-left frequency-encoding direction; 1^st-moment gradient nulling of the imaging sequence; 4 time offsets; superior and inferior spatial saturation bands; and one 16.7-ms-duration, 3.2 G/cm, 1^st-moment-nulled motion-encoding gradient in the through-plane direction. Imaging was performed using four 14-second breath holds (1 breath hold for each slice). Ninety-six cases were analyzed by Reader 1 with over 6 years of experience, and these ROIs were used for designing and training the proposed algorithm. Eighty-eight more cases were analyzed by Reader 2, with 4 years of experience, as well as Reader 1 and were used to evaluate the performance of the algorithm with new data and to compare those results with multiple readers. The readers were blinded to each other’s results.

Each MRE exam included the MR magnitude images from the MRE acquisition (4 slices with 4 time offsets per slice), the phase/wave images used to calculate tissue stiffness, the stiffness images and a confidence map generated by the MRE inversion algorithm that reflects the quality of the wave data. The magnitude images from the four phase offsets were combined using a maximum intensity projection to compensate for phase offset dependent signal dropout due to intravoxel phase dispersion. These composite images are referred to in the rest of the paper as the “magnitude images.” Some examples containing different types of artifact are presented in Figure 1.

Figure 1.

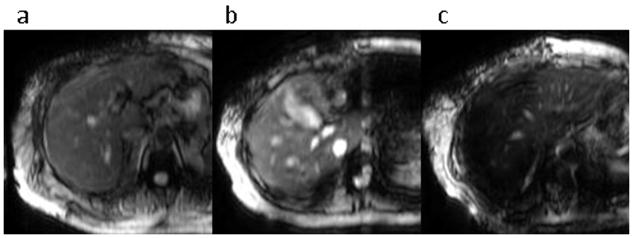
MRE magnitude images with different degrees of liver signal artifacts. The images have (a) no significant artifacts; (b) mild susceptibility-related signal loss, liver signal heterogeneity and some motion artifacts; and (c) severe susceptibility-related signal loss.

Initialization for Liver Segmentation

The initialization stage of the liver segmentation process was based on adaptive thresholding of the MR magnitude images. It was assumed that the liver was the largest organ in these images and would appear as a prominent peak in the intensity histogram. Furthermore, it was assumed that the liver was located on the right side of the body and the other half of the image was masked out for the purpose of initialization. The air around the patient was masked out with a fixed threshold of 10 and a function fitting multiple simultaneous Gaussian distributions was applied to the histogram to find the liver peak (Figure 2). In most cases the histogram was described well with two peaks – one corresponding to the liver and one accounting for the rest of the tissues. In the largest patients, however, a third Gaussian was necessary to describe the adipose tissue. In the GRE sequence used to acquire clinical MRE data, fat appears significantly brighter than the liver. Thus, if the mean intensity of the non-background image pixels was above 50, three peaks were fit to the histogram, otherwise, two were fit. This threshold is flexible and images with medium fat content are described well with either two or three Gaussians. The image was thresholded around the mean of the tallest Gaussian ± one standard deviation. This yielded an approximate mask that included most of the liver, but also regions in other organs (Figure 3-b). The mask was cleaned via morphological operations (Figure 3-c), including: 1) erosions to recede from liver edges, 2) opening of the mask and subsequent removal of all objects except the largest and 3) hole filling. This reduced mask was used for contour initialization.

Figure 2.

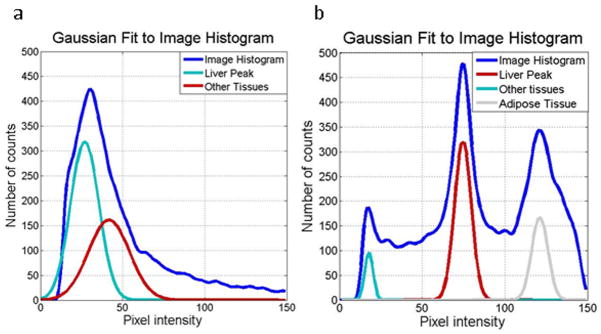
Gaussian fits to magnitude image histograms for a standard case (a) and a subject with a significant amount of adipose tissue (b).

Figure 3.

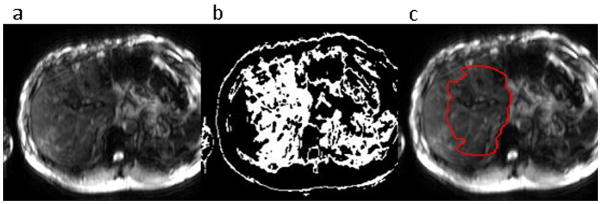
Stages of liver segmentation initialization - (a) original magnitude image, (b) image thresholded around the liver intensity peak, (c) initialization derived by morphologically eroding and hole-filling the initial threshold mask overlayed on the original image.

In cases with severe susceptibility effects, such as those due to iron overload or proximity of the lungs, a portion of the liver had low intensities and there was no prominent peak in the histogram causing a very small initialization region. If the threshold and morphological operations yielded a mask below 500 pixels in size, initialization was attempted using thresholds from adjacent slices. If this also resulted in a small mask, a default round initialization region, identical for all exams and located at the common liver position, was used. In the upper three slices of a 256x256 image, the default region is generated by placing a point at row 130, column 90 and dilating with a size 25 disk. In the inferior slice, the point is placed at row 150, column 75 and dilated with a size 20 disk, due to the more posterior and lateral position, as well as the smaller size, of the inferior lobe of the liver.

Segmentation

The segmentation of the liver in this application does not need to find the exact liver shape, which would be extremely challenging using clinical MRE images which contain motion artifact, signal dropouts and inhomogeneous intensity. Instead, the algorithm only needs to find a sample of liver tissue that is large enough and is far enough away from the liver edges and blood vessels to not be subject to partial volume effects from the processing that generates the elastograms. Additionally, regions that are shielded from the driver by dense blood vessels and narrow segments of the liver should be excluded as these areas commonly contain scattered, diffracted, and interfering waves which result in incorrect stiffness reconstruction.

A simple active contour model applied to the initialization region and controlled by the mean and standard deviation of the magnitude image was used as the basis for segmentation (16). Due to coil sensitivity profiles and susceptibility effects from iron in the liver and oxygen in the lungs, the magnitude images often had inhomogeneous intensity. Using the gradient of the image instead of the intensity itself to guide the active contour largely resolves the problem, but in images with low signal, the value of the gradient at the edges is also low and leakage occurs. Thus, gradient (G) normalized by intensity (I) was used to admit slowly varying areas while avoiding edges in images with different liver signal levels.

In regions where I is close to zero, such as the abdominal cavity, G is also small and the active contour will erratically admit or reject small regions depending on whether G/I is close to zero or infinity. Such behavior produces a jagged contour which is easily removed with morphologic erosion. Thus, leakage into low intensity areas is resolved. Beginning with the initialization shown in Figure 4-1, the result of running the active contour on G/I images is shown in Figure 4-2. The following equation was used to calculate the force that causes the contour expansion (defined as positive force) at every point:

$$F=-2\text{log}({\sigma }_u/{\sigma }_v)-{(G/I-u)}^2/{\sigma }_u^2+{(G/I-v)}^2/{\sigma }_v^2+c\kappa$$

where G/I is a vector of gradient normalized by intensity at every point along the contour, u and v are the means of the gradient normalized by intensity in the regions inside and outside the contour, σ_u and σ_v are the standard deviations of the internal and external regions, κ is the curvature of the contour, and c is a constant controlling the smoothness of the contour.

Figure 4.

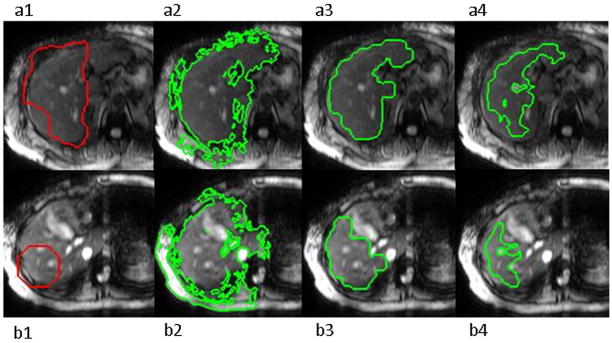
Stages of liver segmentation of images with no artifact (a) and medium artifact as well as difficult geometry (b). 1) Original images with automatically determined (a) and default (b) initialization regions. 2) Segmentation before morphological operations. 3) Segmentation mask after morphological operations and intensity thresholding, 4) Final contour representing the high confidence part of the segmentation mask with stiffness outliers excluded.

While the external surface of the liver is smooth, setting the value of c high to enforce smoothness results in the contour not being able to bypass blood vessels and reach distant areas. Additionally, when edge contrast is low and leakage occurs, a high c causes the leakage areas to be wider and harder to identify in postprocessing. Instead, the contour smoothness, c, was set to a low value of 0.1 and the contour was allowed to leak in predictably narrow tendrils. These were subsequently eroded with a size-3 disk.

An adaptive intensity threshold was then used to remove remaining leakage areas as well as blood vessels that may have been included in the mask. The intensity histogram of the pixels in the segmentation mask was thresholded at 20% of the intensity peak’s frequency. The small holes (under 100 pixels) generated in this way that were fully included in the mask correspond to blood vessels. They were temporarily filled, the mask eroded with size-7 elements, and all isolated regions, as well as the areas previously marked as “blood vessels” were removed. The morphologically opened mask, excluding vessels as well as very high and low intensities, was kept as the final liver tissue segmentation mask (Figure 4-3).

Confidence Map and Stiffness Measurement

The magnitude images from MRE acquisitions do not provide information about the quality of the shear waves in different regions of the liver. Small blood vessels, tumors, and narrow areas of the liver may disrupt wave propagation to varying degrees (17). When taking stiffness measurements, readers evaluate wave quality using the phase images and the reconstructed stiffness map. The inversion algorithm used to calculate stiffness from the wave images uses the MRE displacement data in sliding 11x11-pixel windows to perform a direct inversion of the differential equation modeling the wave propagation. Asecond-order or fourth-order polynomial is fit to the data depending on fit quality. The correlation coefficient (R²) for the fit is recorded for the center pixel of each window. This results in a confidence map with values between 0 and 1, the latter representing high confidence and good SNR. For the purpose of stiffness measurement, a confidence mask is created by keeping pixels with R² values greater than 0.95. Since the inversion algorithm is performed without knowledge of the anatomy, regions in organs other than the liver can be reported as having high confidence. Thus, the intersection of the segmentation mask and the confidence mask was used to determine the ROI to be analyzed (Figure 4--4).

Liver fibrosis is a diffuse disease and is expected to affect different parts of the liver to a similar degree. Local stiffness may be significantly different in regions in two important cases, however. Firstly, the presence of stiff tumors, regions with oblique wave propagation, and areas with phase unwrapping artifacts due to the high wave amplitude close to the driver can appear as regions of high stiffness (Figure 5-a). Secondly, small blood vessels that are hardly visible on the magnitude image will be blurred by the processing kernel and create larger regions of low stiffness. In stiff livers, this region around blood vessels has a significantly lower stiffness than the liver itself and is excluded by experienced readers (Figure 5-b). To reproduce this process and exclude artifactual hot/cold spots, a histogram of the stiffness values within the segmentation mask was calculated and the peak closest to the average stiffness of the mask was found. The stiffness image was then thresholded to remove stiffness values with less than 20% of the peak’s frequency. The final stiffness measurement was recorded as the mean of the high confidence region of the segmentation mask, excluding the outliers. Analysis without the removal of outliers was also performed for comparison. Although images with these “hot/cold spots” are infrequent, measurements taken with them caused significant deviations from the readers’reported stiffnesses during the training of this algorithm, particularly for stiff livers. Thus, only the results calculated with outlier removal are presented.

Figure 5.

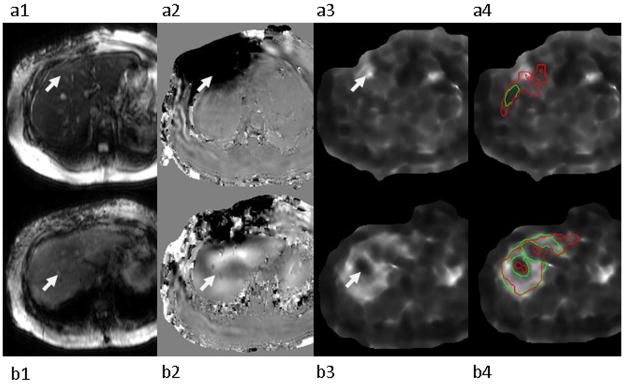
Examples of hot spot (a) and cold spot (b) artifacts (identified by the arrows). MRE magnitude image (1), MRE wave image (2), elastogram (3), and elastogram with reader-defined ROI in green and the automated ROI in red (4).

Data Analysis

First, the set of ninety-six cases and the corresponding expert ROIs were used to optimize the initialization and segmentation parameters. Stability across a large number of cases is of paramount importance, so the initialization was optimized to yield regions that were at least mostly within the liver in all cases. The segmentation was then optimized to acquire good quality tissue samples while avoiding the regions that the reader’s ROIs avoided, particularly focusing on cases where the measured stiffness difference was large. Subsequently, the algorithm was tested on the eighty-eight previously unseen cases that had been analyzed by Reader 1 and Reader 2 and the stiffness measurement was compared between the algorithm and each reader, as well as between the readers. The stability of initialization with respect to its parameters, namely the cutoff for using the third Gaussian in the histogram fits and the width of the threshold, was evaluated and the effects of varying them on the final result were tested.

To evaluate the confidence interval for the correspondence between the algorithm and each reader the Bland-Altman test (18) was used. The percent difference was calculated as (algorithm − reader)/mean(algorithm + reader) * 100. The results are reported as mean (percent difference) ±1.96* standard deviation (percent difference), which corresponds to the 95% confidence interval. Aprior study has also investigated the repeatability of stiffness measurements by an individual reader and between readers (19), reporting the intraclass correlation coefficient (ICC). To compare the current results with this earlier study, the ICC was also computed with the null hypothesis that the ICC = 0.8.

RESULTS

Initialization and Segmentation

The algorithm took an average of 138 seconds per case (4 slices) to run on a PC with an i5 processor and 4 GB of RAM running Windows 7 and Matlab 2011a (MathWorks, Natick, Massachusetts). Initialization based on the intensity histogram was successful in all slices of 84/88 exams. In images with severe artifact, however, the intensity peak was blurred and the default-region initialization was used.

Varying the threshold for choosing to fit two or three Gaussians by ± 10 intensity units from the original value of 50 caused an additional 2 cases to require default initialization, for a total of 6. In these 2 cases, the new ROI overlapped the original one by 50%. The initialization areas of the 82 cases that had successful automatic initializations had average overlaps with their original ROIs of over 97%. Changing the width of the Gaussian threshold by 20% did not affect the final ROI in 86/88 cases, but in the remaining two caused the resulting new ROI to overlap with the original one by 61%. The stiffness values, however, changed by less than 3% for all 88 cases when these parameters were modified.

Stiffness Measurements

The data contained cases ranging from healthy to severe fibrosis, with the training set having a range of 1.75 to 9.06 kPa and a mean of 2.68 kPa, and the test set having a range of 1.75 to 9.69 kPa and a mean of 3.14 kPa. Bland-Altman confidence intervals and ICC coefficients between Reader 1, Reader 2, and the algorithm are presented in Table 1 for the training and test sets. The corresponding Bland-Altman and ICC plots are shown in Figure 6 and Figure 7. Finally, Figure 8 shows examples of cases where the stiffness threshold excludes hot and cold spots improving the correspondence with the reader.

Table 1.

Correspondence between the algorithm and the reader

	Bland-Altman	ICC
Reader 1 – Algorithm (training set)	−3.4 ± 10.45 %	0.994
Reader 1 – Reader 2	−6.76% ± 22.8 %	0.972
Reader 1 - Algorithm	4.32% ± 14.9 %	0.987
Reader 2 - Algorithm	11% ± 22.4%	0.967

Figure 6.

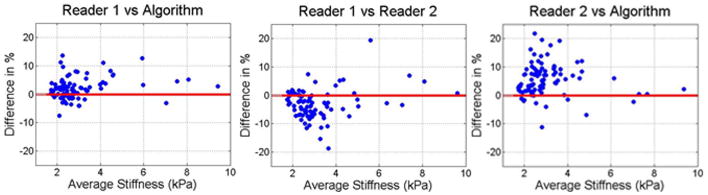
Bland-Altman plots comparing readers to each other and to the algorithm in ROIs based on liver segmentation, the wave field confidence map, and stiffness-outlier thresholding.

Figure 7.

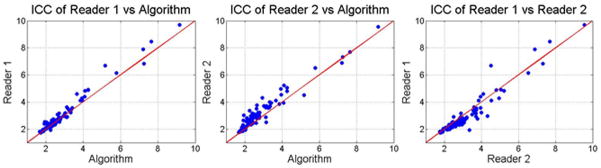
ICC plots comparing readers to each other and the algorithm in ROIs based on liver segmentation, the wave field confidence map, and outlier thresholding.

Figure 8.

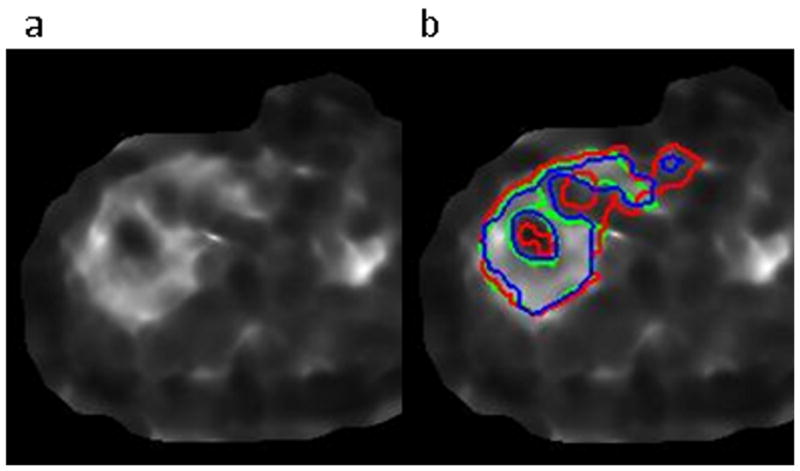
Improved algorithm-to-reader correspondence of the outlier-thresholded ROI (blue) versus the non-thresholded ROI (red) compared to the reader’s ROI (green) in the case of a stiff liver with a cold spot due to a blood vessel. The elastogram is shown in a) and the ROIs are shown in b).

DISCUSSION

The results of this study indicate that the proposed automatic stiffness measurement algorithm can provide results comparable to those obtained by trained readers of MRE data. In the test set, the difference between the measurements reported by the more experienced reader and the algorithm (4.32 ± 14.9%) was smaller than that between the two readers (−6.76% ± 22.8 %). Furthermore, a prior study by Shire et al. [19] reported the ICC between two readers as being greater than 0.9. The reader-algorithm ICC was 0.967–0.987 for the two readers in this study, which indicates very good agreement between the readers and the proposed algorithm. The use of automatic initialization makes the algorithm fully reproducible, unlike the subjective manual technique of a reader.

The correspondence between the algorithm and the reader with 6 years of experience (Reader 1) was significantly higher than that with the reader with 4 years of experience. Furthermore, the stiffness measurements from Reader 1 and the algorithm were both higher than those reported by Reader 2. This effect is attributed to differences in the techniques used by the two readers, including the degree to which blood vessels are avoided and the distance of the ROIs from the liver edges, and the algorithm had been tuned to mimic the technique of the more experienced reader. A bias due to differences in techniques between readers could be significant in practice, while the use of an automated technique can help to standardize these measurements, particularly between institutions.

A critical aspect of an automatic algorithm is its stability. The MRE magnitude images sometimes contained severe motion artifacts manifesting as low contrast of the liver edges, intensity dropout due to intravoxel phase dispersion and signal heterogeneity resulting in an unclear depiction of the anatomy. The poor anatomic clarity of many of the MRE magnitude images used in this study would pose a challenge for most standard segmentation techniques. However, since reporting MRE stiffness values does not require a full segmentation of the liver, but rather just a large region within the liver, our algorithm has resulted in a technique that is robust to patient-to-patient image variations and modest variations in parameter settings. The algorithm presented here yielded an accurate measurement in all 184 cases, 88 of which were previously unseen test cases. Changing parameters from the optimized settings within a 20% margin was also shown to have a negligible effect on the final results. Only the cases with the highest artifact content which failed, or nearly failed, the automatic initialization originally were affected by parameter variation. The effect of the segmentation on the final ROI is limited by the use of the confidence map threshold and stiffness thresholding, which provides additional stability. Should leakage occur into the abdominal cavity, it would be removed by the confidence threshold due to the low phase SNR. Leakage into other organs would at least partially be resolved by the stiffness threshold, as their stiffnesses are often different from that of the liver. The segmentation step is still important, however, as with too much leakage of the contour the liver itself may be considered an outlier.

Several steps and parameters, such as the size of elements in the morphological operations and the order of the erosion and hole-filling in the segmentation algorithm, can be changed to adapt the algorithm to mimic a reader’s ROI selection style. Since the size of the liver is large and the ROI’s are generally over 600 pixels per slice, readers are trained to exclude narrow and shielded regions even if the confidence map is high and no obvious interference is seen. The algorithm was configured to be likewise conservative to demonstrate that it is capable of reproducing that technique. If the algorithm becomes accepted by the community, further improvements upon the technique can be made over time.

The stiffness distribution within the liver does not usually appear homogeneous. This may be due to actual inhomogeneous fibrosis distribution as well as artifacts related to blood vessels, oblique wave propagation, and poor phase unwrapping. The readers analyze the wave and stiffness images attempting to remove artifacts from the ROI. Only the average stiffness of the liver is reported clinically due to uncertainty in differentiating real focally elevated stiffness from artifacts. The algorithm was designed to mimic this artifact removal step by thresholding the stiffness mask for outliers. A potential problem with this approach is that areas with actually differing fibrosis levels can be excluded. However, since fibrosis is a diffuse disease, it is not expected to produce focal regions of significantly different stiffness. The 20% of the mode frequency threshold is aimed at removing stiffness values which are sparse while preserving the main distribution, whether it is normal or multi-modal. If the distribution is broad or multi-modal, i.e. the stiffness distribution is complex, such a threshold will be conservative. If the distribution is narrow and nearly normal, the relative peak height will be large and the threshold will remove outliers more aggressively. Finding alternative methods for automatic artifact removal employing additional spatial information and measures of wave quality is a topic of active investigation.

The combination of magnitude images with a maximum intensity projection is intended to reduce signal dropout due to intravoxel phase dispersion, which is phase dependent, and does so with a good degree of success. Depending on the quality of the breath hold, this may result in decreased image contrast. Registering the phase offsets before combining them may improve the edge contrast but registration could be complicated by the phase dispersion and through-plane motion of the abdomen in different breath holds. The method for combining images from different phase offsets will need to be further investigated. In the current implementation, even if the segmentation included liver tissue with some partial volume edge effects due to low edge contrast, the erosion from the edges that is done should largely prevent the edges from being included in the final measurement.

Ascout acquisition or some other dedicated anatomic imaging sequence could be used to provide better visualization of the liver for initialization and, possibly, segmentation. For example, in-phase opposed-phase images can be acquired in a few seconds and provide good image contrast. Registration would be necessary between the anatomic and MRE images to deal with possible patient motion or changes in breath hold location, but the automatic initialization and segmentation would be more effective using the higher quality anatomic images.

The proposed algorithm was only applied to GRE-based images using a fixed imaging protocol which has been used for clinical hepatic imaging, but extending it to work with EPI and SE sequences is fairly straightforward. In many images where the liver is the largest structure, the algorithm may work without changes. To be applicable in the general case, a set of contrast-based criteria would need to be defined for each imaging sequence to guide initialization and thresholding. It should be noted that no patients with ascites were present in this study, so the effects of significant fluid content in the abdomen on the algorithm still need to be investigated. Extension to three dimensions should also be straightforward. One option would be to apply the current 2D algorithm to each slice of the 3D volume. A true 3D analysis would better account for out-of-plane effects of vessels and fissures and does not require any conceptual changes to the initialization or segmentation. Three-dimensional MRE processing may reduce the artifacts that arise due to through-plane wave propagation and wave scattering/diffraction that cause problems in 2D MRE analysis. This may remove the need for the stiffness outlier removal, though the amount and type of artifact present in 3D MRE needs to be further investigated. Three-dimensional MRE methods are actively being pursued for hepatic imaging and will one day likely become the standard, so this MRE image reading algorithm will need to be expanded to handle 3D volumes. The current clinical standard is 2D MRE, however, so we have focused on that for the current study.

An alternative approach to automating liver stiffness measurements in MRE has recently been presented (20). It uses level sets to simultaneously segment the magnitude image and calculate stiffness from the elastogram. This approach relies heavily on the assumption of stiffness being homogeneous within the liver and may have difficulty dealing with the hot and cold spots described here. Additionally, this study primarily dealt with phantoms experiments and did not compare the measurement to human readers in vivo.

A primary goal for the future improvement of this algorithm is the development of improved techniques for identifying and removing artifact-affected regions from the ROI. Additionally, the acquisition of a separate anatomical set of images with high edge contrast, or the modification of the MRE acquisition parameters to improve magnitude image quality, could be explored for the purpose of reducing artifacts in the images and improving segmentation.

In conclusion, the developed automated algorithm for reporting tissue stiffness from MRE data showed good correlation with trained readers, even in challenging cases with significant artifacts, across a large number of clinical images. The correspondence between the algorithm and the more experienced reader was better than the correspondence between the readers. Once optimized based on the image characteristics of GRE MRE images and the ROI selection of a trained reader, the algorithm performed well in an arbitrary test set of cases. This technique promises to offer significant advantages over current manual techniques for reading MRE cases both in terms of speed and reproducibility.