Artificial Lymphatic Drainage Systems for Vascularized Microfluidic Scaffolds

Abstract

The formation of a stably perfused microvasculature continues to be a major challenge in tissue engineering. Previous work has suggested the importance of a sufficiently large transmural pressure in maintaining vascular stability and perfusion. Here we show that a system of empty channels that provides a drainage function analogous to that of lymphatic microvasculature in vivo can stabilize vascular adhesion and maintain perfusion rate in dense, hydraulically resistive fibrin scaffolds in vitro. In the absence of drainage, endothelial delamination increased as scaffold density increased from 6 mg/mL to 30 mg/mL and scaffold hydraulic conductivity decreased by a factor of twenty. Single drainage channels exerted only localized vascular stabilization, the extent of which depended on the distance between vessel and drainage as well as scaffold density. Computational modeling of these experiments yielded an estimate of 0.40–1.36 cm H₂O for the minimum transmural pressure required for vascular stability. We further designed and constructed fibrin patches (0.8 by 0.9 cm²) that were perfused by a parallel array of vessels and drained by an orthogonal array of drainage channels; only with the drainage did the vessels display long-term stability and perfusion. This work underscores the importance of drainage in vascularization, especially when a dense, hydraulically resistive scaffold is used.

INTRODUCTION

Current strategies in vascularization focus on the self-organization of vascular cells and the release of growth factors in biologically-derived or synthetic matrices.¹ Before implantation, few of these self-organized vascular networks have been shown to sustain flow in vitro. In all cases, some (if not most) of the vascular supply is generated by the host upon implantation of a construct; the establishment of perfusion requires angiogenesis and vascular anastomosis, processes that take place over several days.^2–4 Given that clinical experience in microsurgical free tissue transfer has established the critical importance of immediate vascular anastomosis⁵, it is unclear to what extent thick, densely cellularized tissue grafts can withstand delays in perfusion.

Forming microfluidic networks within hydrogels has emerged as an attractive route to perfusion ^6–9 and vascularization.^10–13 By design, the patterned microfluidic channels inside such scaffolds allow instantaneous perfusion with culture media, thereby maintaining viability of embedded cells by the convection of fluid throughout the fluidic network and diffusion of solutes into and out of the surrounding tissue.^7–9 Vascularizing (i.e., endothelializing) these channels in extracellular matrix (ECM)-based scaffolds resulted in structures that exhibited microvascular functions such as endothelial barrier function ^10,14–18 and reactivity to inflammatory insult.^10,18 These perfused vessels should allow the culture and maturation of engineered tissues in vitro and possibly in vivo. We envision that microsurgical anastomoses—as is performed routinely in free flap transfers⁵—should enable the survival of thick and energetic tissues formed from microfluidic scaffolds after implantation in vivo.

An unresolved and largely overlooked issue in the design of such microfluidic scaffolds is the need for lymphatic drainage. In mammalian tissues, interstitial fluid is driven by hydrostatic pressure gradients into the leaky initial lymphatics, which then converge into collecting lymphatics that propel lymph downstream (i.e., toward the major lymphatic ducts) through muscular contraction.¹⁹ Clinically, compromised lymphatic drainage can lead to lymphedema which is characterized by excessive tissue swelling with serious complications that may require surgical removal of tissue.²⁰ Inspired by the biological example, we recently showed computationally that vascularized scaffolds also require drainage to maintain interstitial fluid homeostasis in vitro.²¹ In the absence of drainage, fluid filtration across the vascular endothelium was predicted to result in a build-up of interstitial pressure, leading to a decrease of transmural pressure (P_TM, defined as the intravascular pressure minus extravascular pressure)²¹; the P_TM may decrease below the threshold required to sustain an open vascular lumen for perfusion.^16,22,23 In addition, this study also predicted that the need for drainage will become more critical when the endothelial barrier is leaky or when the scaffold hydraulic conductivity is low.²¹ Experimental studies using undrained scaffolds have supported the first prediction by demonstrating a correlation between vascular delamination (i.e., detachment of the vessel from the scaffold) and a leaky barrier^14,16,17; we estimated that vascular leakage can decrease P_TM on the time-scale of minutes. ¹⁷

In this work, we determined how drainage affects vascular stability as a function of scaffold hydraulic conductivity. We chose to use microfluidic fibrin scaffolds because fibrin is a FDA-approved surgical sealant and thus an attractive scaffold for tissue engineering²⁴, and because it can be formed in high concentrations. We first tested whether concentrated, resistive scaffolds would favor vascular delamination and reduce perfusion rate. We then incorporated drainage channels and assessed their effects on vascular stability by varying vessel-to-drainage distances and scaffold densities. By coupling experimental data with numerical modeling of Darcy flow in the scaffold and Starling filtration across the endothelium, we estimated the minimum P_TM required for vascular stability. To demonstrate how this knowledge can aid in designing stably perfused tissues of a clinically relevant dimension, we constructed fibrin patches (0.8 cm × 0.9 cm) that contained a parallel array of perfusion vessels, computationally predicted the pressure profiles in the presence and absence of drainage channels, and experimentally studied vascular stability and perfusion over two weeks.

MATERIALS AND METHODS

Cell culture

We cultured endothelial cells derived from human dermal blood microvessels (lot 0040804.2 from PromoCell, and lot 5F1293 from Lonza) at 37°C in 5% CO₂. The standard culture media was MCDB 131 (Caisson Labs) with 10% fetal bovine serum (Atlanta Biologicals), 1% glutamine-penicillin-streptocymin (Invitrogen), 1 μg/mL hydrocortisone (Sigma), 80 μM dibutyryl cAMP (Sigma), 25 μg/mL endothelial cell growth supplement (Biomedical Technologies), 2 U/mL heparin (Sigma), and 0.2 mM ascorbic acid 2-phosphate (Sigma). Cells were routinely passaged at a 1:4 ratio onto gelatin-coated tissue culture plates and were discarded after passage 6.

Formation of undrained single microvessels in microfluidic fibrin scaffolds

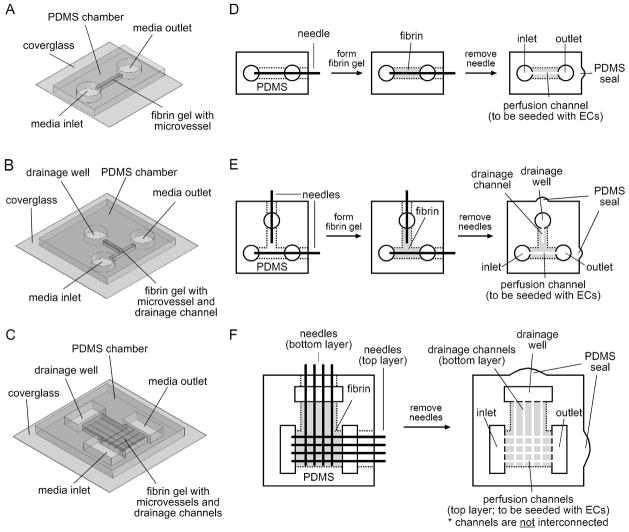
We constructed single microvessels in undrained fibrin gels (n = 67) as described previously^14,25, with fibrinogen concentrations of 6, 8, 10, 15, and 30 mg/mL. Figure 1A shows a three-dimensional (3D) drawing of the polydimethylsiloxane (PDMS) perfusion chamber, and Figure 1D illustrates the fabrication of microfluidic fibrin gels. Briefly, we mixed fibrin precursor solutions in an ice bath to obtain the desired final concentrations of human fibrinogen (Aniara) containing 2× PBS (Invitrogen), 2 mM CaCl₂ (Sigma), and 1 U/mL thrombin (Sigma). We then polymerized the solution around a stainless steel needle (120 μm; Seirin) inside the PDMS chamber at 21°C for 2 hours. Removal of the needle after gelling yielded an open cylindrical microchannel of ~8 mm in length (perfusion channel; Fig. 1D), which we seeded with a suspension of endothelial cells (density equivalent to 1 confluent 60-mm-dish in ~50 μL media). Cells adhered to the channels and to the sidewalls of the gel (the surfaces of the gel in contact with the media inlet and outlet), as diagrammed in Figure 2A.

Figure 1.

Three-dimensional drawings of the PDMS chambers that house the microfluidic fibrin scaffolds (A, undrained; B, T-junction drain; C, fibrin patch). Schematic diagrams (top view) for the fabrication of single perfusion channels in undrained (D) and drained (E) fibrin scaffolds, and arrays of perfusion and drainage channels in fibrin patches (F). Fabrication of channels in undrained scaffolds (D) was exactly the same as described in ref. ¹⁰. Needles for microchannel molding were 120 μm in diameter.

Figure 2.

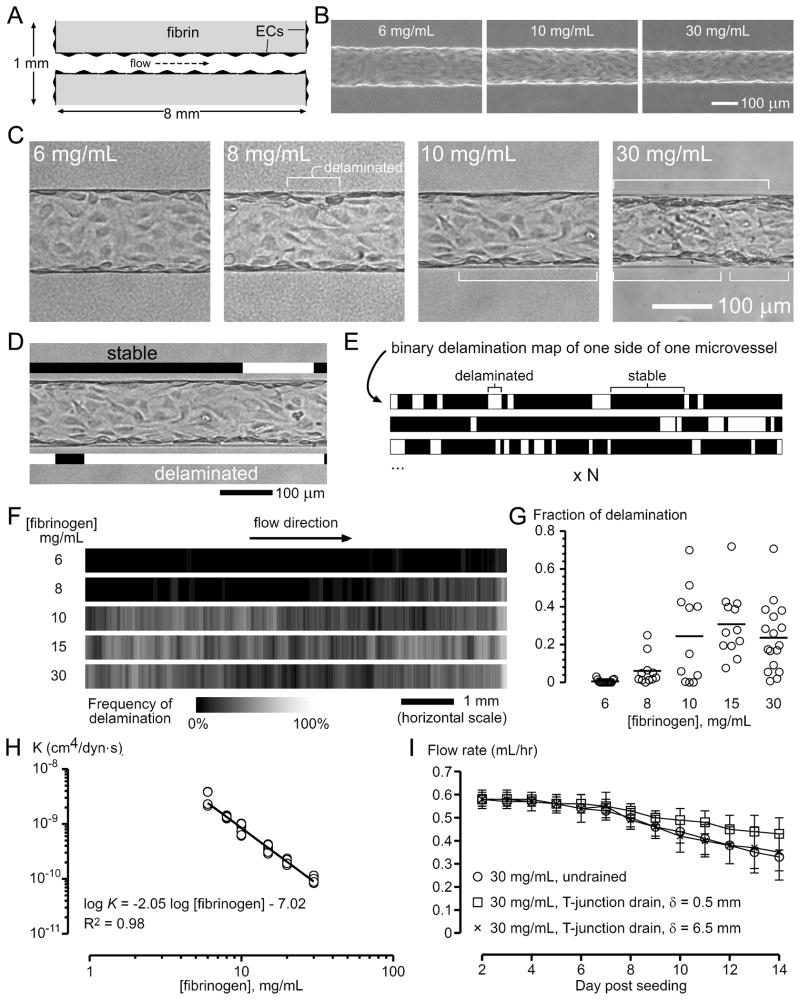
Endothelial delamination in the absence of drainage. (A) Relevant dimensions of the vascularized, undrained fibrin scaffold. Microvessels were constructed by growing blood microvessel-derived endothelial cells in microfluidic channels (120 μm diameter) inside fibrin gels. The length of microvessels was 8.1 ± 0.3 mm, and the thickness of the scaffold was 1.1 mm. (B) Phase-contrast images of microvessels that were perfused for 3 days in fibrin scaffolds of the indicated concentrations. (C) Brightfield images of microvessels that were perfused for 9 days; endothelial delamination is indicated. (D–E) Method for generating delamination frequency maps. (D) Black and white bars were used to highlight stable and delaminated regions, respectively, producing binary delamination maps along the entire length (as shown in (E)) on each side of the vessel; as such, two maps were obtained per vessel. (E) These binary maps were then stacked and their intensity averaged, to generate delamination frequency maps. (F) Frequency maps of delamination (6 mg/mL, 2n = 30; 8 mg/mL, 2n = 22; 10 mg/mL, 2n = 22; 15 mg/mL, 2n = 24; 30 mg/mL, 2n = 34). Brighter regions indicate higher delamination frequency. (G) Delaminated length expressed as a fraction of the total length. (H) Hydraulic conductivities of fibrin gels. (I) Flow rates of microvessels in 30 mg/mL scaffolds in the undrained and T-junction drainage conditions (δ = 0.5 mm and 6.5 mm).

We perfused microvessels by connecting the inlets and outlets of the PDMS chambers via PE-50 polyethylene tubing (Braintree Scientific) to separate media reservoirs and by gradually raising the pressure of the inlet reservoir to 5.7 cm H₂O over several hours while holding the outlet reservoir at 0 cm H₂O.^10,25 Pressure loss in the inlet and outlet connecting tubing accounted for ~0.35 cm H₂O each, as estimated from viscous flow in pipes. We supplemented the perfusion media with 3% dextran (70 kDa; Sigma) to promote vascular stability¹⁴, and with 2 mg/mL εACA (Sigma) to prevent fibrinolysis.²⁶ Flow rates were calculated daily by dividing the volume of media that had flowed into the outlet media reservoir by the time taken since the previous measurement. Shear stress τ was calculated based on viscous flow in pipes, τ = 4Qμ/πr³, where Q is flow rate, μ = 1.36 cP is media viscosity (measured as described previously^14,16), and r is vessel radius.

Formation of single microvessels that are adjacent to drainage channels

To form single drained microvessels (n = 71), we first fabricated PDMS perfusion chambers with an additional perpendicular gel compartment near the midpoint of the vessel (defined as the “T-junction”), and held the end of this compartment at atmospheric pressure for drainage (drainage well, Fig. 1B and E); this additional compartment was 1 mm wide and 6 mm long. To adjust the distance to drainage, we molded a blind-ended microchannel inside this T-junction so that it made a direct fluidic connection to atmospheric pressure on the drainage well while lying perpendicular but not in direct contact to the microvessel (Fig. 1E). Scaffolds without drainage microchannels were drained at ~6.5 mm from the centerline of the vessels. We seeded perfusion channels with endothelial cells, established perfusion, and measured flow rates exactly as we did in undrained scaffolds. During the course of the experiments, drainage wells were always hydrated with media, with fluid depths kept at <1 mm.

Formation of vascular arrays that are adjacent to arrays of drainage channels

To form arrays of microvessels and drainage channels (n = 20), we used PDMS chambers that housed a centimeter-scale fibrin “patch” (0.8 cm by 0.9 cm) (Fig. 1C). Figure 1F outlines the fabrication of a parallel array of four perfusion vessels and an orthogonal array of four drainage channels underneath. The thickness of this fibrin patch was 1.6 mm. We spaced needles 2 mm apart for both perfusion channel and drainage channel arrays, and placed drainage channels 0.4 mm below the microvessels. We seeded perfusion channels with endothelial cells as described in single vessels. In control experiments, we removed the drainage channels so that these scaffolds were drained only from the side drainage well at >7.5 mm from perfusion vessels.

Because these microvessels (~9 mm) were longer than single vessels (~8 mm) and the higher flow rate (from 4 vessels) resulted in higher pressure loss in the tubing (~1.7 cm H₂O), a pressure difference of 7.5 to 9.5 cm H₂O was used to maintain shear stresses in the same range of 10–15 dyn/cm². Flow rates were measured as described in single microvessels. We normalized the total flow rates through the four vessels in individual fibrin patches by their respective peak total flow rates, as the presence of four vessels in each scaffold led to greater variability of absolute flow rates. Shear stress in individual vessels was calculated assuming that flow was equally divided among the four vessels.

Quantification of delamination

To quantify delamination, we captured brightfield images of microvessels on day 9 of perfusion with an AxioCam HRm camera (1388 × 1034 resolution) using a Plan Neofluar 10× objective (NA 0.30, Zeiss). To analyze entire microvessels, we stitched images using the Panorama function in AxioVision 4.5 (Zeiss). We then manually outlined the delaminated and stable portions with white and black bars, respectively, and stacked these binary delamination maps using a customized code (Matlab ver. R2007a, MathWorks) to generate a frequency map of delamination for each experimental condition.

Measurement of scaffold hydraulic conductivity

We measured hydraulic conductivities of fibrin gels as described previously.¹⁷ We subjected rectangular fibrin gels to a pressure drop and measured the resulting flow of perfusion media at 37°C. Hydraulic conductivity K was calculated according to K = QL/AΔP, where Q is the measured flow rate, L is the length of the gel (1–5 mm), A is the cross-sectional area of the gel (1–1.5 mm²), and ΔP is the imposed pressure difference (5–12.5 cm H₂O). Multiple lengths, cross-sectional areas, and/or pressure differences were used for each fibrinogen concentration. Gel compression was negligible as the gel adhered strongly to the surrounding chamber during measurement.

Statistical analysis

Statistical analysis was performed with Prism 5 (GraphPad). Comparisons of grouped data used the Kruskal-Wallis test, followed by the Mann-Whitney U test for pairwise comparisons. Trends were analyzed by Spearman’s correlation. Comparisons of flow rates over time under different drainage conditions were tested with 2-way ANOVA. We considered a difference to be statistically significant if p < 0.05 divided by the number of comparisons. Data are presented as mean ± SD.

NUMERICAL MODELING

Governing equations

We modeled pressure profiles for the T-junction drainage configurations and the fibrin patches using finite-element modeling software (COMSOL Multiphysics ver. 3.5a). Fluid flow through the scaffold obeyed Darcy’s Law:

$$\nabla P_{\mathit{scaffold}}=-\frac{1}{K}{\mathbf{v}}_{\mathit{scaffold}}$$

where P_scaffold is the interstitial fluid pressure, v_scaffold is the interstitial velocity in the scaffold, and K is the hydraulic conductivity of the scaffold. Fluid flow through the microvessels and drainage channels obeyed steady-state Navier-Stokes equations:

$$\begin{array}{l}\rho ({\mathbf{v}}_{\mathit{vessel}}·\nabla ){\mathbf{v}}_{\mathit{vessel}}=-\nabla P_{\mathit{vessel}}+\mu {\nabla }^2{\mathbf{v}}_{\mathit{vessel}}\\ \rho ({\mathbf{v}}_{\mathit{drain}}·\nabla ){\mathbf{v}}_{\mathit{drain}}=-\nabla P_{\mathit{drain}}+\mu {\nabla }^2{\mathbf{v}}_{\mathit{drain}}\end{array}$$

where v_vessel and v_drain are the fluid velocities in vessels and drainage channels, P_vessel and P_drain are the pressures within vessels and drainage channels, μ = 1.36 cP is the measured viscosity of the perfusate at 37°C, and ρ = 1 g/cm³ is the assumed perfusate density. Fluid flux across the endothelium was modeled with Starling’s Law:

$$v_n=L_P(P_{\mathit{vessel}}-P_{\mathit{scaffold}})$$

where v_n is the fluid filtration velocity normal to the endothelium, and L_P is the effective hydraulic conductivity of the endothelium.

Boundary conditions

We imposed a no-flux boundary condition on scaffold-PDMS interfaces. For the non-vascularized interfaces between walls of drainage channels and the scaffold, we imposed a continuous velocity and pressure boundary condition.

Because the measurement of L_P was not possible in our hands, we used a range of values in the models. For the endothelium in vessels, we tested L_P values of 10⁻¹⁰, 3.2 × 10⁻¹⁰, 10⁻⁹ and 3.2 × 10⁻⁹ cm³/dyn·s, considering that vessels under steady shear should exhibit a reasonably strong barrier function.¹⁶ For the endothelium at the inlet sidewall of the fibrin scaffold (i.e., the vertical face of the scaffold that was in fluidic contact with the inlet media well), we assumed a higher L_P value of 10⁻⁸ cm³/dyn·s because the shear is very low and hence the endothelium should be more leaky.¹⁶ We imposed a continuous boundary condition at the outlet sidewall of the fibrin scaffold (i.e., the face of the scaffold in contact with the outlet media well), as this endothelium is under very low shear and negative transmural pressure, which are conditions that result in extremely weak barrier function.¹⁶ The fluid velocity between the scaffold and channels was constrained to be normal to the interface.

Mesh convergence

To demonstrate mesh independence, we doubled the degrees of freedom (DOF) of the computational mesh until the P_TM values (i.e., vessel pressure minus scaffold pressure on the vessel wall) of each vessel at the inlet, outlet, and the point(s) closest to the drainage channel(s) differed less than 0.05 cm H₂O between the finer and the coarser meshes. The converged T-junction models had 0.58–1 million DOF, whereas the models for undrained and drained fibrin patches had 0.86 and 1.5 million DOF, respectively.

Model validation

We tested the models at the limits of L_P → 0 and K → 0 in T-junction and patch configurations. As L_P → 0, the computed pressure profile matched that of Poiseuille flow, as expected from an impermeable endothelium. As K → 0, the computed drainage rate (i.e., the rate at which fluid accumulates in the drainage well) approached zero, as expected for an impermeable scaffold. We also compared the predicted drainage rate of vessels in 20 mg/mL T-junction gels with experimentally measured values.

Estimation of the minimal transmural pressure for vascular stabilization

We postulated that a minimal transmural pressure for vascular stability existed, and used the delamination heatmaps from T-junction drainage experiments to estimate this threshold value. Because the T-junction drain was positioned at the midpoint of the vessel, we defined the stable vascular region to be the largest contiguous middle region that showed a delamination frequency of less than 5%. We then took the computed P_TM values at the boundaries between stable and unstable regions to be the best estimates of the minimum P_TM required for stability.

RESULTS

Effect of scaffold density on vascular stability and perfusion rate in undrained microvessels

The longitudinal cross section drawing of the undrained scaffolds is shown in Figure 2A. Similar to seeding of endothelial cells in microfluidic collagen gels¹⁷, seeding in fibrin channels yielded confluent tubes by day 2 post-seeding. Measured on day 3, microvessels in scaffolds of lower fibrin concentrations (6–10 mg/mL) expanded (Fig. 2B); the concurrent increases in flow rate and diameter did not lead to statistically significant differences in wall shear stresses, which were 11.6 ± 1.6, 12.5 ± 1.6, 12.6 ± 1.1, 12.6 ± 0.5, and 12.1 ± 0.9 dyn/cm², for 6, 8, 10, 15, and 30 mg/mL scaffolds respectively (p = 0.47).

Endothelial delamination was visible under the microscope starting day 4 at the earliest for 30 mg/mL scaffolds. To quantify delamination, we outlined delamination along the entire length of microvessels on day 9 (Fig. 2C) to generate delamination frequency maps (Fig. 2D–F). High-density scaffolds (≥10 mg/mL) resulted in more delamination (Fig. 2F), expressed as a fraction of the total length of microvessels (Fig. 2G; p = 0.0025 for 6 mg/mL vs. 8 mg/mL, p = 0.0036 for 6 mg/mL vs. 10 mg/mL; p < 0.0001 for 6 mg/mL vs. 15 mg/mL and for 6 mg/mL vs. 30 mg/mL). Hydraulic conductivities (K) of concentrated fibrin scaffolds were lower (Fig. 2H): linear regression of a log-log plot yielded

$$logK=-2.05log[\mathit{fibrinogen}]-7.02$$

with R² = 0.98, where K is in cm⁴/dyn·s and [fibrinogen] is in mg/mL. Functionally, endothelial delamination caused lumenal constrictions that resulted in a 43% reduction in flow rate over two weeks in 30 mg/mL scaffolds (from 0.58 ± 0.03 mL/hr to 0.33± 0.10 mL/hr; Fig. 2I).

Effect of localized drainage on vascular stability

We chose to study drainage channels that were perpendicular—as opposed to parallel—to the vessels because 1) a perpendicular arrangement enables easy experimental alteration of vessel-to-drainage distances, and 2) arrays of perfusion and drainage channels that are perpendicular to each other are more easily scaled up and operated, for example in our fibrin patches (Fig. 1C and F) and layer-by-layer stacking of microfluidic hydrogels.

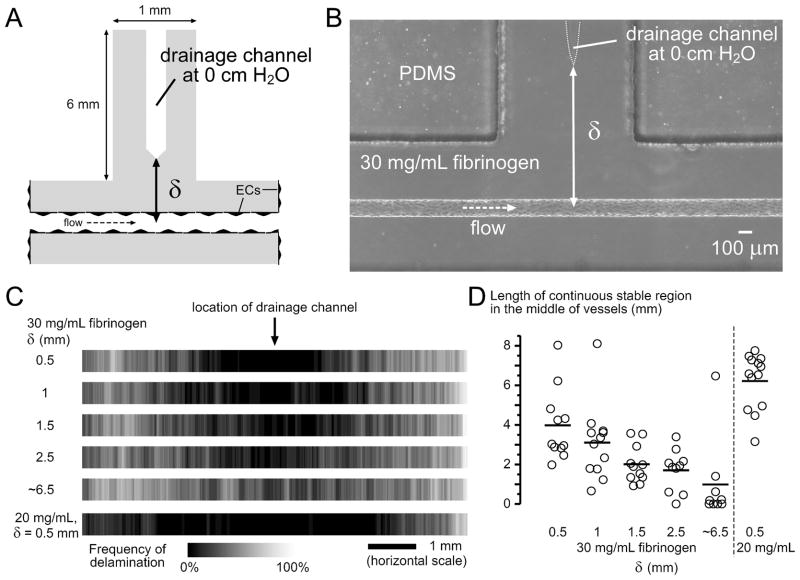
To incorporate drainage, we formed scaffolds with a perpendicular compartment that was exposed to atmospheric pressure to serve as a “sink” for interstitial fluid. A cell-free microfluidic channel that was molded inside the fibrin scaffold with the tip of the channel at a distance δ from the centerline of the vessel served as the drainage (Fig. 3A and B). Evidence of drainage came from the accumulation of media in the drainage well: in 20 mg/mL scaffolds with δ = 0.5 mm, the rate of fluid accumulation in the drainage well measured 4.2 ± 0.6 μL per day (n = 5).

Figure 3.

Drainage stabilized microvessels locally. (A) Addition of a T-junction gel compartment in the middle of the scaffold. The drainage channel was connected to a media reservoir at the end of this compartment, which was held at 0 cm H₂O (see Fig. 1C and D). The distance from the axis of the microvessel to the drainage channel is indicated by δ. The length of microvessels was 8.2 ± 0.3 mm, and the fibrin scaffold was 1.1 mm thick. (B) Phase-contrast image of the T-junction in a 30 mg/mL scaffold. (C) Delamination frequency maps of microvessels in 30 mg/mL scaffolds with different δ values, and 20 mg/mL scaffold with δ = 0.5 mm (0.52 ± 0.08 mm, 2n = 26). Conditions for 30 mg/mL scaffold are δ = 0.5 mm (0.47 ± 0.09 mm, 2n = 22), δ = 1 mm (1.02 ± 0.06 mm, 2n = 24), δ = 1.5 mm (1.48 ± 0.10 mm, 2n = 22), δ = 2.5 mm (2.45 ± 0.17 mm, 2n = 20), and δ ~ 6.5 mm (without drainage channel, 2n = 18). (D) Plot of the continuous stable lengths in the middle of vessels.

Since vessels formed within 30 mg/mL scaffolds are the most likely to delaminate, we used these scaffolds to test whether vessels in them can be stabilized, as a function of the different distance to drainage. Vessels that were constructed in these scaffolds were perfused with the same perfusion pressures as in undrained scaffolds, and resulted in the same shear stresses on day 3 (12.4 ± 0.7 dyn/cm²).

With drainage pressure set at 0 cm H₂O, drainage with δ = 0.5 mm (0.47± 0.09 mm) prevented delamination locally (Fig. 3C): measured from the midpoint of the vessel, no delamination was ever observed within 0.8 mm, both upstream and downstream, along the vessel. Perfusion through these vessels was significantly higher than through undrained vessels (p < 0.0001), but still decreased to 67% of the initial flow rate over two weeks (Fig. 2I). Drainage channels that were positioned further away exerted weaker stabilization (δ ranging from 0.5 to 2.5 mm; Fig. 3C), as quantified by the continuous delamination-free length in the middle of vessels (Fig. 3D; p = 0.0026). Without an explicit drainage microchannel, drainage occurred only at the fluid reservoir at ~6.5 mm from the microvessel, which did not result in any stabilization (δ = 6.5 mm; Fig. 3C); flow rate over two weeks decreased similarly as that of undrained vessels (Fig. 2I; p = 0.74 for δ = 6.5 mm vs. undrained) and to a greater extent than drained vessels with δ = 0.5 mm (Fig. 2I; p < 0.0001 for δ = 6.5 mm vs. δ = 0.5 mm).

Drainage in 20 mg/mL scaffolds (K ~ 2 times that of 30 mg/mL scaffolds) exerted much stronger stabilization effects than in 30 mg/mL scaffolds: δ = 0.5 mm (δ = 0.52± 0.08 mm) stabilized significantly longer regions in a 20 mg/mL scaffold than all other δ conditions in 30 mg/mL scaffolds (Fig. 3D; p = 0.0045, 0.001, < 0.0001, < 0.0001, and 0.0014, compared to 30 mg/mL with δ = 0.5, 1, 1.5, 2.5, and 6.5 mm, respectively).

Numerical modeling of pressure profiles

We wanted to estimate the minimum transmural pressure P_TM required for stable endothelial-scaffold adhesion, which may be useful to guide designs of engineered vascular systems.²¹ Direct measurement of interstitial pressure with fine spatial resolution, however, was not possible; we therefore inferred pressure profiles by numerical modeling, which had successfully predicted vascular phenotype in collagen gels.¹⁶

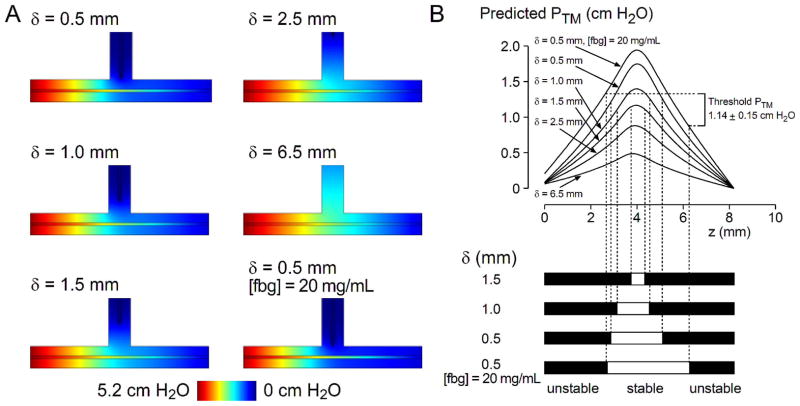
Figure 4A shows the predicted pressure profiles in T-junction drainage experiments for L_P = 3.2 × 10⁻¹⁰ cm³/dyn·s and various δ. Variation of P_TM along the microvessels under different drainage conditions are plotted in Figure 4B. As intended, the drainage channel lowered the interstitial pressure in its vicinity, resulting in higher P_TM around the middle of the vessel. Upon comparison with experimental delamination frequency maps (Fig. 4B), each estimated L_P value yielded a characteristic threshold P_TM across different δ conditions (Table 1). Across the range of estimated L_P values, the range of the minimal P_TM required for stable vascular adhesion to the scaffold was 0.40 to 1.36 cm H₂O. We note that for the 20 mg/mL, δ = 0.5 mm condition, the computed drainage rates of 2–4 μL/day were comparable to our experimentally measured rate of 4.2 μL/day.

Figure 4.

Numerical prediction of pressure profiles in T-junction drainage experiments. (A) Pressure distributions in the scaffold and vessels for L_P = 3.2 × 10⁻¹⁰ cm³/dyn·s and various δ. The displayed pressure map of the scaffold is a horizontal cross-section along the vessel axis, and that of the vessel is the intravascular pressure. Greater color contrast between the vessel and the scaffold indicate higher transmural pressure. (B) Predicted transmural pressure profiles along the length of the vessels. Z = 0 mm refers to the inlet. Experimental delamination frequency maps were thresholded, and the transmural pressure values at the boundaries between stable and unstable regions were extracted from the computed pressure distribution (see Materials and methods). The plot shown used a vessel L_P of 3.2 × 10⁻¹⁰ cm³/dyn·s.

Table 1.

Threshold transmural pressures obtained by comparing predicted pressure profiles to delamination frequency maps in T-junction drain experiments. See Materials and methods and Figure 4 for details.

Vessel LP (cm3/dyn·s)	PTM threshold (cm H2O)
	average	range
1 × 10−10	1.36 ± 0.18	0.95 – 1.49
3.2 × 10−10	1.14 ± 0.15	0.84 – 1.34
1 × 10−9	0.78 ± 0.12	0.69 – 0.87
3.2 × 10−9	0.40 ± 0.09	0.28 – 0.56

Drainage of vascular arrays in large-area fibrin patches

Engineering thick tissues will require perfusion via vascular networks or arrays that maximize transport efficiency.²⁷ Addition of perfusion vessels in a tissue construct will increase the demand for drainage²¹, and therefore it is important to also increase drainage capacity.

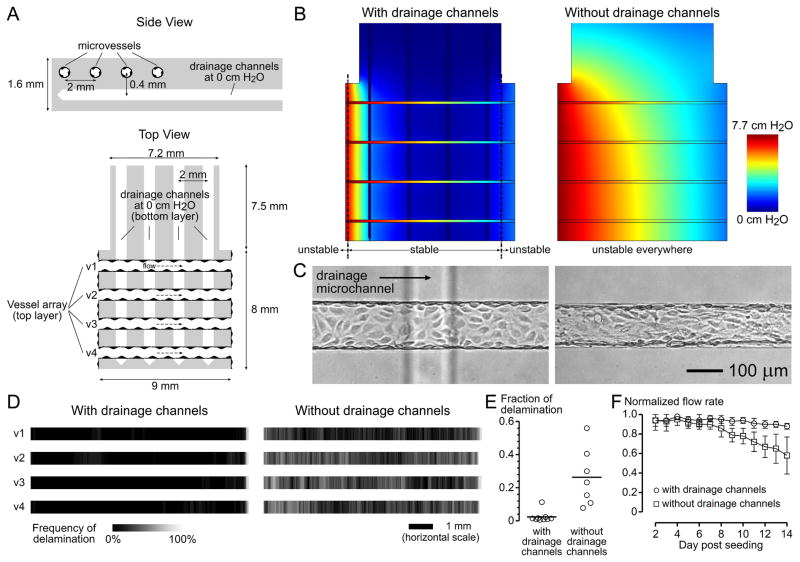
As T-junction experiments have shown, when the tip of a single drainage channel was within 0.5 mm from a single perfusion vessel in 30 mg/mL scaffolds, at least ~2 mm of endothelium could be stabilized (Fig. 3D). We hypothesized that parallel drainage channels spaced ~2 mm apart could provide sufficient drainage to an orthogonal array of perfusion vessels if these two arrays were separated vertically by <0.5 mm. We constructed scaffolds using 30 mg/mL fibrinogen with the vascular and drainage arrangements as shown in Figure 5A; the vertical distance between the vessel array and the underneath drainage array was 0.41 ± 0.12 mm. Shear stress on day 3 was 11.8 ± 1.2 dyn/cm².

Figure 5.

Perfusion and drainage of the centimeter-scale fibrin scaffolds (i.e., fibrin patches). (A) Dimensions of the fibrin patch. The average length of microvessels was 8.7 ± 0.2 mm, and the fibrin patch was 1.6 mm thick. (B) Numerical prediction of pressure profiles and vascular stability in the presence and absence of drainage microchannels, using a vessel L_P of 3.2 × 10⁻¹⁰ cm³/dyn·s and a corresponding threshold transmural pressure of 1.14 cm H₂O (Table 1). These models predicted that the presence of drainage channels maintained above-threshold transmural pressures in more than 89% of the lengths of vessels, whereas the absence of drainage channels would lead to sub-threshold transmural pressures everywhere. (C) Brightfield images on day 9 post-seeding. The drainage channel underneath the microvessel was not in focus. (D) Delamination frequency maps. Vessels v1 to v4 refer to the ones in (A) (with drainage channel, 2n = 18; without drainage channels, 2n = 14). (E) Delaminated length as a fraction of total vessel length. (F) Normalized flow rate of vascularized fibrin patches.

Numerical modeling in drained fibrin patches predicted that P_TM exceeded the threshold value for vascular stabilization everywhere, except near the very beginning and end of vessels (Fig. 5B). In control experiments, we removed the drainage channels such that these scaffolds were weakly drained at >7.5 mm from perfusion vessels, which is theoretically insufficient to sustain above-threshold transmural pressures (Fig. 5B). Experimentally, drainage channels effectively stabilized microvessels (Fig. 5C and D), as quantified by the fraction of delaminated endothelium (Fig. 5E; p = 0.0021), and preserved perfusion remarkably well (Fig. 5F; p < 0.0001) when compared to control samples; the average normalized flow rate on day 14 was 88 ± 3%, in contrast to 58 ± 19% in the absence of drainage channels (Fig. 5F).

DISCUSSION

Summary of findings

The current study shows that drainage is required to preserve vascular stability and perfusion rate in high-density fibrin scaffolds. Dense (≥10 mg/mL) fibrin scaffolds promoted vascular delamination and decreased perfusion. Localized drainage preserved vascular stability only locally and partially restored perfusion rate. The extent of stabilization depended on vessel-to-drainage distance and scaffold density. Computational modeling estimated the minimal P_TM (0.40–1.36 cm H₂O) required to prevent delamination, assisting in the design of vascular and drainage channels for long-term (14 days) perfusion in large-area fibrin scaffolds.

Transmural pressure is the predominant predictor of vascular stability

Recently, we showed experimentally that artificially holding P_TM near 0 cm H₂O can lead to endothelial delamination in vascularized collagen scaffolds.¹⁶ Although the minimum P_TM required for vascular stabilization was not known, we have used computational modeling to study the effect of drainage in maintaining P_TM.²¹ These models found that P_TM was largely determined by the relative hydraulic resistances across the endothelium and within the scaffold. An endothelial barrier that is relatively resistive to fluid flux when compared to the scaffold would favor the establishment of a high P_TM across the endothelium; in particular, the dimensionless parameter h·L_P/K should be much less than one, where h is the characteristic length of the interstitial hydraulic pathway, such as the vessel-to-drain distanceδ.²¹ A large body of our recent experimental work has confirmed that vessel leakiness (i.e., high L_P) correlates with endothelial delamination.^14,16,17 We note that delamination may be a unique mode of vascular failure in tissue engineering scaffolds; although microvessels in vivo narrow and eventually collapse when transmural pressure decreases, the mechanism does not appear to involve loss of endothelial-basement membrane adhesion.²²

The current experimental data strongly support the idea that a minimum P_TM is required for stable endothelial adhesion to the scaffold. First, scaffolds with a lower K (Fig. 2H) led to more vascular delamination in both the undrained (Fig. 2F and G) and drained scaffolds (Fig. 3C and D, 20 mg/mL vs. 30 mg/mL). Because undrained scaffolds contain impermeable boundaries at the PDMS-fibrin interfaces, it might appear that interstitial flow would be nearly zero everywhere and that P_TM should not depend on K. Because the endothelium at the outlet wall is extremely leaky, however, fluid that has leaked from the vessel lumen into the gel can escape via the low pressure end of the gel into the outlet media well. This flow causes P_TM to decrease from the inlet to the outlet of the vessel, with the magnitude of P_TM dependent on K.¹⁶

Second, in the presence of drainage channels, increasing the distance to drainage results in higher interstitial hydraulic resistance and thus a lower P_TM (Fig. 4A), which is associated with weaker vessel stabilization (Fig. 3C and D). In these experiments, δ·L_P/K ranged from 0.05 (δ = 0.5 mm) to 0.65 (δ = 6.5 mm) assuming L_P = 10⁻¹⁰ cm³/dyn·s. Third, flow driven by a hydrostatic pressure gradient leads to a lumenal pressure and thus a P_TM profile that decreases linearly along the vessel¹⁶, which may explain the transition from upstream stability to downstream delamination for the “intermediate” scaffold concentration of 8 mg/mL (Fig. 2B).

As with previous experimental studies^16,17, we employed finite element modeling to further understand the pressure profiles in these vascularized constructs. We relied on estimated endothelial hydraulic conductivity values since its direct measurement in our perfusion system was not possible; we based the estimates on our previous study that demonstrated a shear-dependent vascular barrier.¹⁶ For a given estimate of vascular L_P, these models and the experimentally determined delamination frequency maps predicted consistent threshold P_TM values. The minimal P_TM required for vascular stability ranged from 0.40 to 1.36 cm H₂O. Direct experimental measurement of pressure profiles and/or vascular L_P will be necessary to improve the precision of the predicted threshold P_TM. Along these lines, we recently proposed a force balance criterion for stable vascularization²⁸, in which the sum of stabilizing stresses—transmural pressure and endothelial adhesion—must be greater than the destabilizing cell contractile stress.

A limitation of our experiments is that we cannot exclude the effects of scaffold stiffness—which is changed concomitantly with scaffold density—on endothelial cell responses.^29,30 That P_TM profiles have strong predictive power for delamination frequency, and that drainage stabilized microvessels in scaffolds of the same concentration (and thus the same stiffness and K), suggest that changes in P_TM are sufficient to explain vascular stabilization. While scaffold conductivity may determine P_TM and the need for drainage, the stiffness of the scaffold may control other aspects of vascular function.³¹

Implications for the design of microfluidic scaffolds for tissue engineering

Scaffolds used in tissue engineering span a wide range of dimensions, concentrations, and physical properties tailored for the desired applications. For any given type of material, increasing the density of the scaffold will increase the mechanical strength, which is often desirable. Our data, however, suggest that this improvement may be obtained at the expense of vascular stability and perfusion. In particular, microfluidic hydrogels—designed primarily for perfusion—demand the use of mechanically robust gels^9,10,32 to withstand deformations involved in the fabrication processes and in perfusion. Typical concentrations range from 10 to 200 mg/mL in microfluidic scaffolds of alginate, polyethylene glycol (PEG), and agarose.^7–9 These scaffolds have hydraulic conductivities that are even lower than those in the present study: for 0.7% alginate gels, K ranges from 10⁻¹¹ to 10⁻¹⁰ cm⁴/dyn·s ³³; for 1 to 10% PEG gels, K ranges from 10⁻¹⁰ to 10⁻¹² cm⁴/dyn·s.³⁴ We propose that a drainage system be incorporated into these dense scaffolds to stabilize the vasculature without having to sacrifice mechanical integrity. We note that such low K values are physiologically relevant³⁵ and should not be considered a disadvantage per se.

CONCLUSIONS

We have placed drainage channels to stabilize perfusion microvessels in concentrated fibrin scaffolds, and estimated the minimum transmural pressure to aid in designing perfusion and drainage systems. Although these cell-free drainage channels lack the endothelial layer and active propulsion of real lymphatics, they could provide a useful drainage function. We note that maximizing scaffold porosity (while keeping the scaffold density above the percolation threshold) may increase vascular stability and minimize the need for densely packed drainage channels. The ability to stably perfuse large-area, high-density fibrin patches may accelerate the development of engineered tissues with clinically relevant dimensions.