Abstract
Introduction. The accuracy and clinical applicability of an improved model-based system for tracking hemodynamic changes is assessed in an animal study on septic shock. Methods. This study used cardiovascular measurements recorded during a porcine trial studying the efficacy of large-pore hemofiltration for treating septic shock. Four Pietrain pigs were instrumented and induced with septic shock. A subset of the measured data, representing clinically available measurements, was used to identify subject-specific cardiovascular models. These models were then validated against the remaining measurements. Results. The system accurately matched independent measures of left and right ventricle end diastolic volumes and maximum left and right ventricular pressures to percentage errors less than 20% (except for the 95th percentile error in maximum right ventricular pressure) and all R 2 > 0.76. An average decrease of 42% in systemic resistance, a main cardiovascular consequence of septic shock, was observed 120 minutes after the infusion of the endotoxin, consistent with experimentally measured trends. Moreover, modelled temporal trends in right ventricular end systolic elastance and afterload tracked changes in corresponding experimentally derived metrics. Conclusions. These results demonstrate that this model-based method can monitor disease-dependent changes in preload, afterload, and contractility in porcine study of septic shock.
1. Introduction
Cardiovascular management of the critically ill is often difficult due to the array of complex circulatory interactions that occur within hemodynamically compromised patients. The limited measurement set typically available in the intensive care unit (ICU) is sometimes insufficient to give a full picture of cardiovascular status. Hence, diagnosis and therapy are often based on the experience, skill, and intuition of the attending medical staff. However, difficulties in interpreting cardiac and circulatory measurements can result in misdiagnosis and suboptimal treatment, which may lead to inefficient use of resources, increased length of stay, and in some cases death [1–5].
To improve hemodynamic monitoring, model-based methods can be used to aggregate common ICU measurements into an easily understandable, physiological form. Other model-based methods have been used to estimate surrogate markers of cardiovascular performance from clinically available data. However, these approaches have only been used to identify a small number of hemodynamic parameters [6] or only describe localised behaviour [7, 8], normally to obtain estimates of CO [9–16]. To truly understand the effects of many common cardiovascular diseases in the ICU, one must consider the global effects these diseases have on a patient. Hence, a broader approach that describes the effects of disease on parameters of cardiac function, as well as parameters of systemic and pulmonary flows, is required. Patient-specific models, identified from clinical data, could be used to help paint a clearer physiological picture of the patient's global cardiovascular condition and assist medical staff with decision making [17, 18]. The goal of this research is to show that such an in silico system can accurately identify important disease and treatment dependent changes in the cardiovascular system (CVS).
A previously reported model-based method [19, 20] indicated that subject-specific disease induced hemodynamic changes due to pulmonary embolism could be tracked from common cardiovascular measurements. However, the method lacked clinical applicability because invasive measurements of left and right ventricular volumes waveforms were required, which are rarely available in the ICU. Thus, an enhanced method [21, 22] has been developed that only uses clinically available or easily inferred cardiovascular measurements, so the system can be used to monitor hemodynamics in a normal, clinical setting.
In the ICU, some of the most prevalent and deadly cardiovascular disorders are severe sepsis and septic shock [1, 2] which are caused by a whole body inflammatory response to an infection, resulting in systemic vasodilation. To further prove the monitoring ability of this new method, subject-specific CVS models are retrospectively identified and validated using measurements from a porcine study on septic shock and large-pore hemofiltration therapy [23]. Hence, in this study, the ability of subject-specific CVS models to monitor the signs of sepsis, including a decrease in systemic vascular resistance (R sys) [24–26], an increase in pulmonary vascular resistance (R pul) [26], and an increase right ventricle end diastolic elastances (RVEDV) [26], were analysed.
2. Materials and Methods
This study used cardiovascular measurements recorded during a porcine trial studying the efficacy of large-pore hemofiltration (LPHF) for treating septic shock [23]. Although the efficacy of LPHF is not of particular interest to this study, the induction of sepsis followed by LPHF provides a dynamic and clinically realistic background on which to test this model and methodology. Measurements taken from four pigs during this study provide a suitable dataset for identifying subject-specific CVS model parameters and safely validating the model-outputs. In this work, subject-specific CVS models were only identified from measurements commonly available in the ICU. Changes in the identified parameters in these models were analysed to track the effect of septic shock in the pigs. No prior assumptions were made or implemented regarding the trends in these identified parameters. The more invasive measurements recorded in the porcine study, which are not widely obtainable clinically, were used to validate the accuracy of the CVS models.
2.1. Subjects
Four pure Pietrain pigs weighing 20–30 kg were premedicated, anesthetized, and ventilated as described in [23, 27]. The animals received a 0.5-mg/kg endotoxin infusion (lipopolysaccharide from Escherichia coli serotype 0127:B8; Sigma Chemical, St. Louis, MO, U.S.A) over 30 minutes (from T0 to T30) to initiate sepsis. From T60 onwards the pigs underwent a zero balance continuous venovenous hemofiltration at a rate of 45 mL/kg/h with a 0.7 m2 large-pore (78 Å) membrane with a cut off of 80 kDa (Sureflux FH 70, Nipro, Osaka, Japan) and a BaxterBM 25-BM 14 hemofiltration device (Baxter Health Care, Munich, Germany). Each animal acted as its own control in this study with baseline measurements taken prior to the endotoxin infusions (T0), representing the undiseased state of the pig. All procedures and protocols used in the porcine experiments were reviewed and approved by the Ethics Committee of the Medical Faculty at the University of Liege (Belgium).
2.2. Measurements
The pulmonary trunk was accessed via medial sternotomy, and a micromanometer-tipped catheter (Sentron, Cordis, Miami, FL) was inserted into the main pulmonary artery through a stab wound in the RV outflow tract and positioned approximately 2 cm downstream of the pulmonary valve. Aortic pressure was measured using a micromanometer-tipped catheter inserted into the descending thoracic aorta through the right femoral artery. A 7F, 12 electrode conductance micromanometer-tipped catheter (CD Leycom, Zoetermeer, Holland), was positioned in each of the left and right ventricles, so that all electrodes were in their respective cavities. Further details on the trials can be found in [23].
These catheters provided measurements of the aortic and pulmonary pressure waveforms (P ao, P pa) and the left and right ventricular pressure and volume waveforms (P lv, V lv, P rv, and V rv). Continuous waveforms of P ao, P pa, P lv, V lv, P rv, and V rv (sampling frequency, f s = 200 Hz) were recorded from the four catheters at 30 minutes intervals (T0, T30, T60,…, T210, and T240) between initiation of anaesthesia (T0) and 4 hours subsequent (T240). At each 30 minute interval 6–12 heartbeats of these waveforms were recorded. For each set of waveforms one good heartbeat worth of data was selected. From this selected heartbeat discrete convergence set points for the parameter identification process were extracted. In this study, 34 sets of measurements were extracted from the raw data providing 34 sets of convergence set points from the four pigs. Two data sets were unusable as steady-state measurements could not be obtained.
2.3. Cardiovascular System Model
This study uses a previously validated cardiovascular system model [19, 28, 30–32] defined by a set of equations describing cardiac and circulatory flow. This model describes the “lumped” or global dynamics of major regions of the CVS, ignoring smaller localised behaviour. The lumped nature allows the model to be relatively light computationally, requiring a smaller number of parameters. However, it is complex enough to capture all the clinically important hemodynamics of the CVS.
The six chamber CVS model represents the left and right ventricles, aorta, pulmonary artery, vena cava, and pulmonary vein, as illustrated schematically in Figure 1. Pressures and volumes in the chambers (P, V) and flows between the chambers (Q) are defined using parameters of resistance to flow (R), blood inertia (L), and chamber elastance or stiffness (E). Cardiac muscle activation of the ventricles is represented using time varying elastances (driL and driR) which act as the driver functions for the CVS model. The ventricular chambers in the model are actively elastic meaning pressure changes nonlinearly with respect to volume, to model the effects of contraction and relaxation in these chambers. The noncardiac chambers are passively elastic. Thus, pressure is linearly related to volume in these chambers. Flow in and out of the ventricles is controlled via pressure-gated heart valves, and the parallel interaction between the ventricles is modelled through pericardial and septal dynamics. The combination of all these model features and parameters provides a means for accurately depicting ventricular, arterial, and venous blood pressures and volumes, and the blood flow rates through the heart valves, body, and lungs. The full model definition can be found in Hann et al. [33].
Figure 1.
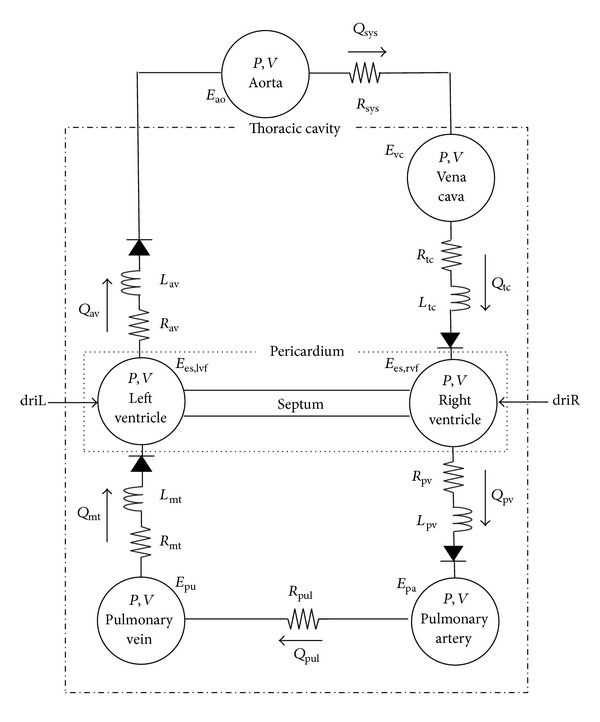
Overview of the six-chamber cardiovascular system model which relates the pressures (P), volumes (V), and flows (Q) in the cardiovascular system using parameters of elastance (E), resistance (R), and inertance (L); driL and driR represent cardiac muscle activation and act as the driver functions for the CVS model.
Please note that this model does not implicitly simulate any autonomic control mechanism. However, such mechanisms can be indirectly simulated through alteration of the model parameters. For example, sympathetic control of the blood pressure could be simulated by increasing the parameter R sys in the CVS model.
2.4. Parameter Identification Method: Pig-Specific Model
The parameter identification method used for this study was described by Revie et al. [21, 22]. The advantage of this method over the previously employed technique [19, 20] is that it only requires data from measurements typically available in an ICU environment. Table 1 shows the small set of measurements necessary to identify the patient-specific parameters required for the model.
Table 1.
List of identified parameters and corresponding measurements used to identify them for the simplified systemic, simplified pulmonary, and six-chamber models. Each line on the table represents a measurement/parameter pair, where the measurement on the line is used to directly identify the corresponding parameter. All the parameters in this table, except for the valve resistances, are uniquely identified for each set of measurements. The valve resistances are identified for each set of measurements and then averaged for a subject.
| Model | Measurement | Identified parameter | ||
|---|---|---|---|---|
| Name | Symbol | Name | Symbol | |
| Systemic | Global end diastolic volume | GEDV | Left ventricular elastance | E es,lvf |
| Stroke volume | SV | Mitral valve resistance | R mt | |
| Mean aortic pressure | MAP | Systemic vascular resistance | R sys | |
| Aortic pulse pressure | PPao | Aortic elastance | E ao | |
| Maximum ascending aortic gradient | dP ao,max/dt | Aortic valve resistance | R av | |
| Mitral valve closure time | t mt | Pulmonary vein pressure | P pu | |
|
| ||||
| Pulmonary | Global end diastolic volume | GEDV | Right ventricular elastance | E es,rvf |
| Stroke volume | SV | Tricuspid valve resistance | R tc | |
| Mean pulmonary artery pressure | MPAP | Pulmonary valve resistance | R pul | |
| Pulmonary artery pulse pressure | PPpa | Pulmonary artery elastance | E pa | |
| Maximum ascending pulmonary artery pressure | dP pa,max/dt | Pulmonary valve resistance | R pv | |
| Tricuspid valve closure time | t tc | Vena cava pressure | P vc | |
|
| ||||
| 6 chamber | Vena cava pressure (identified from systemic model) | P vc | Vena cava elastance | E vc |
| Pulmonary vein pressure (identified from pulmonary model) | P pu | Pulmonary vein elastance | E pu | |
The parameter identification process was performed in sequential stages to increase convergence stability. In this process the inertances in the CVS model were ignored (L mt = L av = L tc = L pv = 0), as they were found to have negligible effect on the modelled flow. To simplify parameter identification, the six-chamber CVS model was divided into two submodels of the systemic and pulmonary circulations, as shown in Figure 2. These models were decoupled by removing the ventricular interaction between the circulations. The submodels were independently simulated using left and right ventricular driver functions (driL and driR) and initial estimates for parameter values. The driver functions were identified using the method described in [34, 35] and help define the ventricular systolic and diastolic function in the identified models. These driver functions play an important role in defining pig and time dependent changes in diastolic ventricular function in the subject-specific CVS models, as the parameters of ventricular filling (as shown in ((A.4)) in the appendix) are held as constants (see Table 5) during the identification process.
Figure 2.

Simplified submodels of (a) the systemic and (b) pulmonary circulations with inertia and ventricular interaction removed. Note that for comparison the orientation of the pulmonary circulation has been reversed with respect to Figure 1.
Table 5.
| Symbol | Description | Value |
|---|---|---|
| P 0,lvf | Parameter of left ventricle EDPVR | 0 |
| λ lvf | Parameter of left ventricle EDPVR | 0.033 |
| V d,lvf | Parameter of left ventricle ESPVR | 23 |
| P 0,rvf | Parameter of right ventricle EDPVR | 0 |
| λ rvf | Parameter of right ventricle EDPVR | 0.023 |
| V d,rvf | Parameter of right ventricle ESPVR | 23 |
| V d,spt | Parameter of septal ESPVR | 2 |
| V 0,spt | Parameter of septal EDPVR | 2 |
| λ spt | Parameter of septal EDPVR | 0.435 |
| P 0,spt | Parameter of septal EDPVR | 1.1101 |
| E es,spt | Septum elastance | 48.7540 |
| P 0,pcd | Parameter of pericardium | 0.5003 |
| V 0,pcd | Parameter of pericardium | 200 |
| λ pcd | Parameter of pericardium | 0.03 |
| P th | Intrathoracic pressure | 0 |
| V d,ao | Aortic unstressed volume | 0 |
| V d,vc | Vena cava unstressed volume | 0 |
| V d,pa | Pulmonary artery unstressed volume | 0 |
| V d,pu | Pulmonary vein unstressed volume | 0 |
| L mt | Mitral valve inertance | 0 |
| L av | Aortic valve inertance | 0 |
| L tc | Tricuspid valve inertance | 0 |
| L pv | Pulmonary valve inertance | 0 |
An iterative proportional gain control method [22] was used to match the model outputs of Table 1 to the corresponding measurements, identifying the desired parameter set of Table 1. Each observable model output was used to identify one model parameter. Parameters (P) that were proportionally related to their corresponding model output were iteratively identified using the ratio of the true measurement to corresponding model output:
| (1) |
Parameters that were inversely related to their chosen model output were identified using
| (2) |
The parameters of the systemic submodels were identified first, followed by the pulmonary model. Once the both submodels were identified, they were joined together, with coupling between the models added in the form of septum and pericardium dynamics. The systemic and pulmonary models were then reidentified with the knowledge of this coupling, and the whole process was repeated until whole CVS model had converged. This process was repeated for each measurement set for that pig (i.e., T0, T30, T60,…, T240). From these identified models the valve resistances were averaged, and the remaining parameters were reidentified using these averaged valve resistances each measurement set from T0 to T240. Hence, for a given pig, nine unique sets of parameters were identified representing the hemodynamic state of the pig at the point in the experiment. A full description of the model identification process is provided by Revie et al. [22] and in the appendix for the interested reader. Figure 3 shows an example of the systemic model matching the mean, amplitude, and maximum ascending gradient of the aortic pressure waveform, through the identification of R sys, E ao, and R av, respectively (see ((A.21)), ((A.22)), and ((A.24)) in the appendix). It should be noted that the parameter identification method reported in [22] has been modified, so the dead space of volumes of the ventricles is assumed to be equal to 23 mL, as reported in [36], rather than 0 mL.
Figure 3.
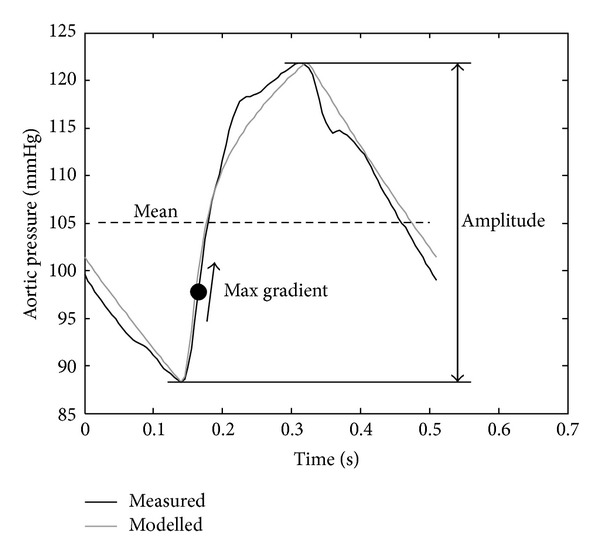
Example of the features from the aortic pressure waveform which are matched during the model identification process.
In this study, global end diastolic volume (GEDV) was assumed to be equal to the sum of the left and right ventricular end diastolic volumes (LVEDV + RVEDV). Stroke volume (SV) was calculated as the average of the amplitudes of the left and right ventricular volume waveforms. The mitral and tricuspid valve closure times (t mt, t tc) were estimated from the derived subject-specific left and right ventricular driver function, (time varying elastances). These driver functions were calculated using the method described by Hann et al. [37] from SV and features in the aortic and pulmonary artery pressure waveforms.
In this study, GEDV and SV were not directly measured but instead were inferred from the experimental measurements of V lv and V rv. However, clinically, GEDV and SV can be measured using minimally invasive thermodilution techniques [38–41]. The aortic pressure waveform can be estimated from radial artery pressure using one of the several transfer function methods [42–47]. Pulmonary artery indices can be determined using a pulmonary artery catheter (PAC). Vena cava pressure, P vc, can be identified from central venous pressure which is normally measured in the ICU, removing the need to measure t tc. Mitral valve closure time, t mt, can be estimated from ECG data. Hence, the data set required for model identification represents only measurements that are already measured or inferred in a typical ICU.
2.5. Analysis
Data sets were recorded every 30 minutes from T0 to T240 during the four trials. However, two sets of measurements for Pig 1 at T30 and T90 were unusable, as the pig's hemodynamics were unstable at these times. Thus, 34 data sets were available for analysis. For each data set, a subject-specific CVS model was retrospectively identified from a subset of available measurements. The model identification method was run on a 2.13 GHz dual core machine with 3 GB of ram. Since this research is still in the development stages it has only been fully tested using the development-orientated but relatively slow MATLAB software (MathWorks, Natwick, MA, USA). Using one processor the identification method took on average 6 minutes and 24 seconds to identify a subject-specific model of the CVS. Preliminary tests using C programming language, which is better suited for real time applications, have suggested that the identification process time can be reduced by a factor of 20–100, to approximately 4–19 seconds per identified model, which is an acceptable run time in a clinical environment.
During parameter identification, all the parameters listed in Table 1 were uniquely identified for each set of measurements (at T0, T30,…, T240), except for the valve resistances which were averaged over the duration of the trials (T0–T240) for each pig. The model outputs of the identified models were compared to the remaining recorded measurements to validate the accuracy of the identified models. Averaged data is presented as mean ± one standard deviation (1SD). A paired-sample t-test was used to check temporal variance over T0–T60 to analyse the effect of the endotoxin intervention. P < 0.05 was considered a statistically significant result. The relationship between the modelled and measured maximum left and right ventricular pressures and volumes was analysed statistically using correlation and linear regression analysis, including calculation of absolute percentage errors, and bias and precision analysis (Bland and Altman [48]). A percentage error less than 20% was regarded as an acceptable result as measurement of physiological variables often lack precision, with errors of ±10–20% not uncommon [49–51].
3. Results
The temporal variance in the measurements of the cohort was analysed between T0–T30, as well as T0–T60 and T30–T60 using paired sample t-tests. Temporal variance was analysed over T0–T60 and T30–T60 because sometimes the symptoms of septic shock do not manifest immediately after the endotoxin infusion at T30. Statistically significant changes (P < 0.05) were seen in the measured systolic and diastolic aortic and pulmonary artery pressures and right ventricular end diastolic volume over the first hour, showing the expected influence of the endotoxin infusion on the circulation. Figure 4 shows these main hemodynamic measurements across the four animals.
Figure 4.
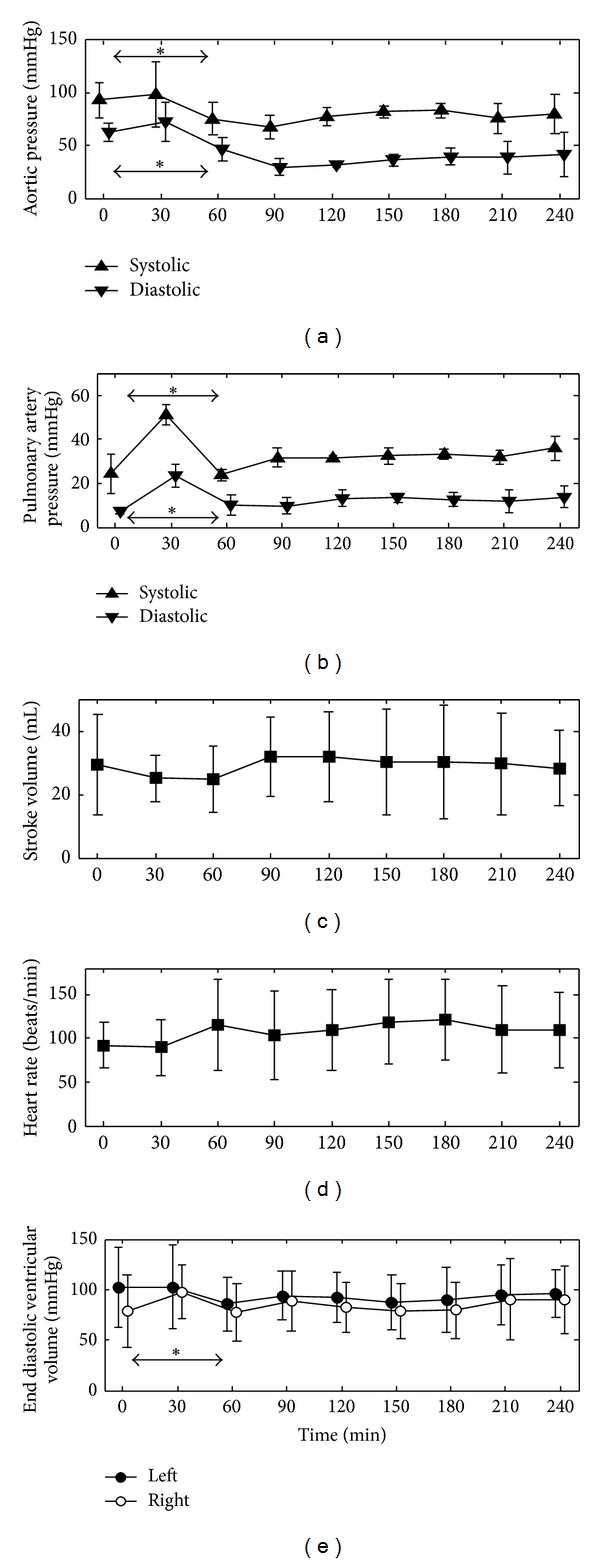
Evolution of the averaged hemodynamic measurements recorded during the trials. *indicates P < 0.05 for expected temporal changes over T0–T30, T0–T60, or T30–T60 due to the induction of septic shock. The data is presented as mean ± one standard deviation.
3.1. Subject-Specific Model Validation
For all the subject-specific models, the model outputs matched the measurements used in the identification process (mean aortic and pulmonary pressures, aortic and pulmonary artery pulse pressure, and stroke volume) to percentage errors of less than 0.5%. This result is expected and indicates the convergence of the identification process.
Validation was achieved by comparing model outputs of left and right ventricular end diastolic volumes (LVEDV, RVEDV) and maximum left and right ventricular pressures (P lv,max, P rv,max) to their corresponding measured value. These measurements were not used directly in the identification process, and thus, represent an independent validation of the method. Bias, precision, and correlation metrics were analysed for validation (Table 2 and Figures 5 and 6 for LVEDV and RVEDV). All four model outputs correlated well with the measured data (R 2 ≥ 0.76). Modelled left ventricular outputs (LVEDV, P lv,max) had a small negative bias (−3.4 mL, −1.6 mmHg), whereas right ventricular outputs (RVEDV, P rv,max) tended to slightly overestimate (3.8 mL, 4.5 mmHg) the true measurement. The precision (2 standard deviations) of the LVEDV and RVEDV predictions was 10.2 mL and 10.2 mL and 12.8 mmHg and 12.9 mmHg for P lv,max and P rv,max. All percentage errors were within and acceptable range (<20%), except for the 95th percentile error in the modelled maximum right ventricular pressure.
Table 2.
The median and range of the measured left and right end diastolic volumes (LVEDV, RVEDV) and maximum left and right ventricular pressures (P lv,max, P rv,max). Bias and precision metrics (2SD), median percentage errors with 5th and 95th percentile bounds, and correlation coefficients of the modelled LVEDV, RVEDV, P lv,max, and P rv,max.
| Median (range) | Bias ± 2SD | % Error (5th–95th percentile) | R 2 | |
|---|---|---|---|---|
| LVEDV | 97.7 mL (55.0–141.2) | −3.4 ± 10.2 mL | 3.5% (0.5–10.9) | 0.98 |
| RVEDV | 93.3 mL (44.8–138.2) | 3.8 ± 10.2 mL | 4.9% (0.4–16.3) | 0.96 |
| P lv,max | 86.1 mm Hg (63.2–121.8) | −1.6 ± 12.8 mm Hg | 3.8% (0.4–16.4) | 0.96 |
| P rv,max | 38.7 mm Hg (18.0–60.7) | 4.5 ± 12.9 mm Hg | 14.8% (2.6–29.9) | 0.76 |
Figure 5.
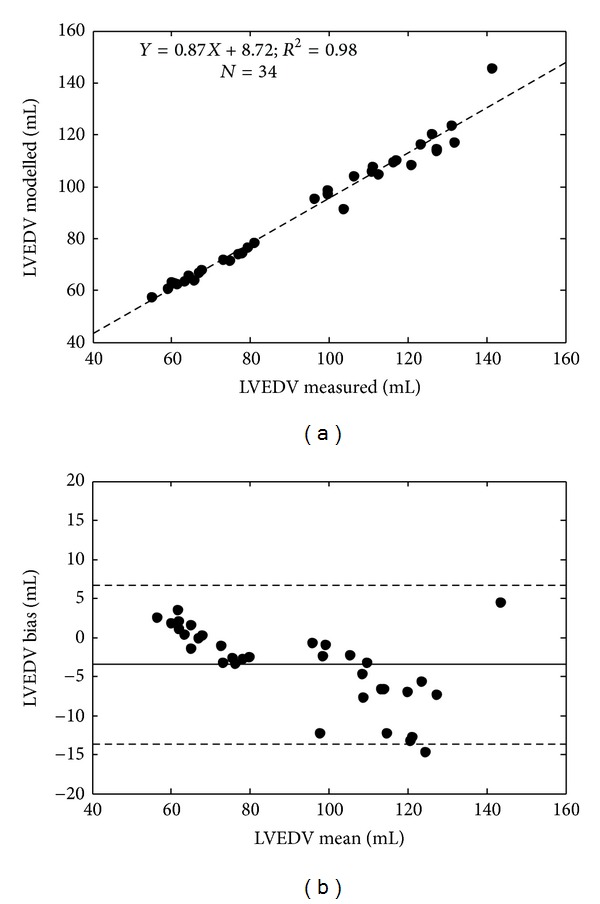
Regression (a) and Bland-Altman analysis showing 2 standard deviation limits (b) of the modelled and measured left ventricular end diastolic volume (LVEDV).
Figure 6.
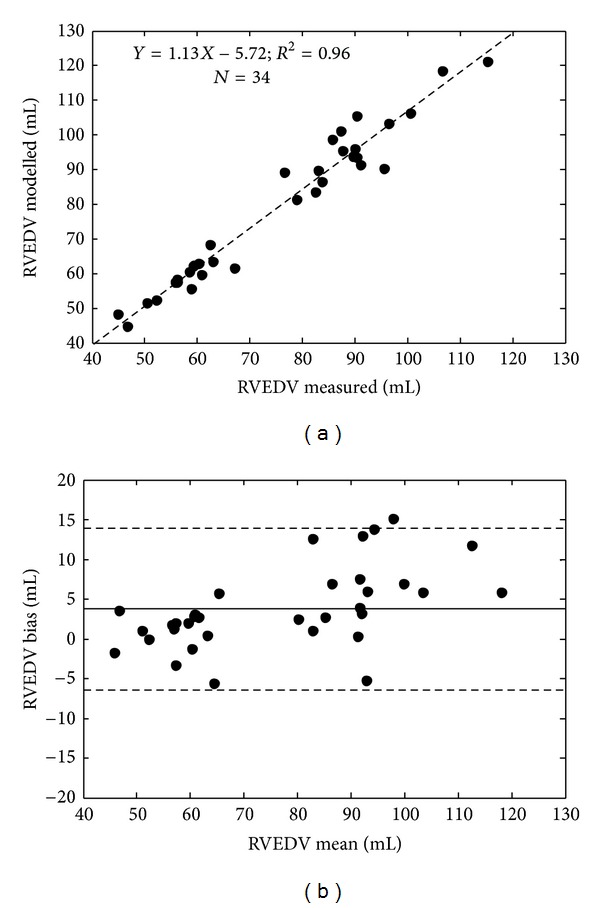
Regression (a) and Bland-Altman analysis showing 2 standard deviation limits (b) of the modelled and measured right ventricular end diastolic volume (RVEDV).
For further validation, the temporal trends of the identified right ventricular end systolic elastance, pulmonary afterload, and right ventricular arterial coupling (RVAC), from the model, were compared to corresponding metrics (E es,rvf, E a, and E es,rvf/E a). These metrics were determined experimentally in [23] using right ventricular pressure-volume analysis, for E es,rvf, and a windkessel model, for E a. The afterload on the right ventricle in the model is the sum of the resistance of the pulmonary valve and pulmonary vasculature divided by the period of one heartbeat (E a,model = [R pv + R pul]/T). From Figure 7 it is seen that the subject-specific models in most cases track the experimental trends in E es,rvf and E a. Weaker relationships are seen between the modelled and experimentally RVAC metrics (E es,rvf /E a). However, the model did capture all the averaged temporal trends for the cohort with R 2 = 0.62, 94, and 0.71 for E es,rvf, E a, and E es,rvf /E a. Note that experimental data was not available for Pig 1 at T0, T30, and T90, and Pig 2 at T150, due to difficulties performing the vena cava occlusion manoeuvre.
Figure 7.
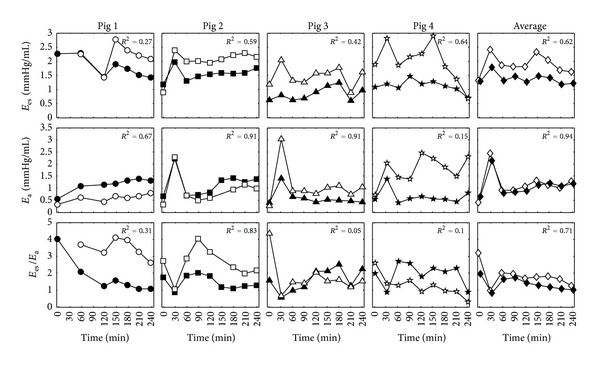
Comparison of subject-specific and averaged modelled right ventricle end systolic elastance (E es, rvf), pulmonary elastance (E a), and right ventricular arterial coupling (E es,rvf/E a), represented by the black symbols, against experimentally derived metrics from [23], represented by the white symbols.
3.2. Septic Shock Trends
Averaged model metrics were used to test whether the subject-specific CVS models could capture the general trends of septic shock across the cohort of pigs. These metrics include ventricular preload, afterload, and contractility, three of the main determinants of cardiac and circulatory function. The averaged temporal trends for the metrics used in this analysis are shown in Figure 8. Please note that the spike in some of these metrics at T30 due to initial reaction of the pigs to endotoxin insult is not discussed in the following sections. The analysis of preload, afterload, and contractility, as presented in the following, only focuses on overall trends seen in these parameters over the four-hour duration of the trials.
Figure 8.
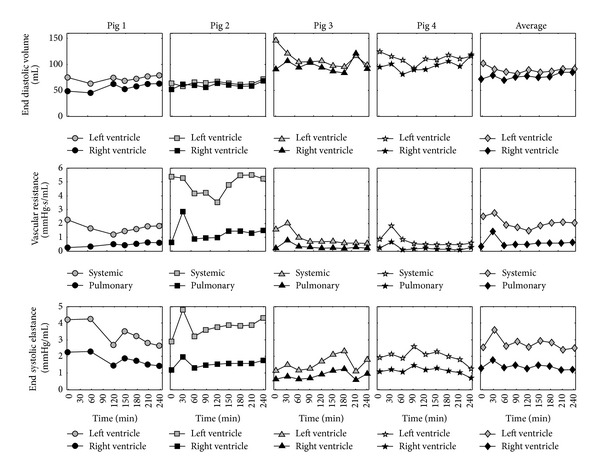
Modelled subject-specific indices of preload (end diastolic volume), afterload (vascular resistance), and contractility (end systolic elastance). The grey symbols represent the left ventricle or systemic metrics. The black symbols represent right ventricle or pulmonary metrics.
3.3. Preload
In the model, preload on the ventricles is represented by end diastolic volumes in the left and right ventricles (LVEDV, RVEDV). The average modelled LVEDV and RVEDV are shown in Figure 8. These results show the subject-specific models identified an increase in RVEDV during the study indicating the onset of right ventricle distension. In contrast, an initial decrease in LVEDV was observed, suggesting a decrease in venous return to the left heart immediately after the endotoxin infusion. However, LVEDV does start to increase during the second half of the trial indicating the activation of left ventricle compensatory mechanism which combats the effects of low venous return to the heart. Both these observations are known consequences of septic shock [25, 26].
3.4. Afterload
Another main hemodynamic consequence of septic shock is sudden decrease in left ventricle afterload due to a systemic inflammation [24–26]. In the model, the parameter systemic vascular resistance (R sys) represents the main component of the afterload on the left ventricle. The average trends for R sys, along with its pulmonary counterpart, pulmonary vascular resistance (R pul), can be seen in Figure 8. These identified trends show a significant decrease in R sys after T60, symptomatic of sepsis. Moreover, a steady increase in R pul after T60 was observed by the subject-specific CVS models, indicating an increase in right ventricle afterload due to the effects of the endotoxin. Again, both these findings are indicative of septic shock [24–26].
3.5. Contractility
In the subject-specific CVS models contractility is represented by parameters of left and right ventricular end systolic elastance (E es,lvf, E es,rvf), as shown in Figure 8. In septic shock a decrease in these parameters is expected due to myocardial depression [25, 26, 52, 53]. However, contrary to this expected trend, the averaged values for E es,lvf and E es,rvf stayed relatively constant over the trial. This unexpected outcome may be the consequence of the hemofiltration therapy, which has been shown to improve cardiac function during endotoxic shock in several experimental studies [23, 54, 55]. On the other hand, these results could be due to autonomous reflex responses, such as baroreflex control, attempting to maintain blood pressure by increasing contractility [56]. As a result, such mechanisms could be counteracting the effects of decreased myocardial state in the pigs. Since autonomous control mechanisms are not directly simulated in the CVS model it is impossible to fully distinguish if changes in the model parameters are due to the effects of these mechanisms or a result of the administered therapy.
3.6. Subject-Specific Response
Although the averaged results, seen previously, show that the model is capable of identifying the hemodynamic trends of the induced disease, it is also important to know how each subject responds to the disorder and corresponding treatment. Hence, it is essential to analyse the individual time varying trends for each pig, not just the averaged trends of the disease. Figure 8 illustrates the subject-specific response of R sys to the endotoxic shock and LPHF therapy. On average, systemic resistance drops by 20.3% across the four pigs over the duration of the trials. However, when analysing the individual response of each of the pigs, it is seen that the R sys returns to baseline for Pig 2, and a substantial improvement is observed in Pig 1 after LPHF treatment (T60 onwards). Whereas, there are large drops in R sys with no apparent improvement with treatment in Pigs 3 and 4, indicating the difference response to septic shock between the pigs.
4. Discussion
4.1. Modelling Errors
For validation the model was compared to independent measurements that were not used in the identification process, as well as pulmonary hemodynamic indices calculated using an independent method [23]. Almost all ventricular volumes (LVEDV and RVEDV) and maximum pressures (P lv,max and P rv,max) were identified to an error of less than 20% (except the 95th percentile error in the maximum right ventricular pressure), which is acceptable for this type of physiological monitoring. Furthermore, the time varying trends in these four measurements were identified to a high degree of accuracy, with calculated R 2 > 0.90, except for the maximum right ventricular pressure where R 2 = 0.76, which is still a very good result. These results suggest that subject-specific models of the CVS could be used to accurately monitor disease-dependent changes in ventricular preload in an intensive care environment.
In most cases, the temporal trends of right ventricular end systolic elastance and pulmonary afterload from the subject-specific CVS models correlated well to experimentally derived measurements of E es,rvf and E a from [23]. The modelled results tended to underestimate E es,rvf. The primary reason for this bias is because of the assumption in the model identification process that the dead space volume of the right ventricle (V d,rvf) is constant and equal to 23 mL, as reported in [36]. In reality, V d,rvf most likely changes as the contractile state of the pigs changes during the trials, but due to the lack of available measurements it cannot be identified. Hence, in the model the changes in contractile state are solely represented by E es,rvf. Poorer correlations were also noticed for RVAC. The reason for these poor relationships is most likely due to accumulation of errors in calculating this compound metric (E es,rvf/E a). These include the addition of error due to measurement noise in the experimental metrics and the addition of modelling errors in the identified parameters. However, a strong temporal relationship for RVAC could be seen of R 2 = 0.71 when the effects of measurement noise and modelling error were averaged over the cohort (as seen in Figure 7).
Noticeably, there were larger errors in the modelled E es,rvf and E a for Pig 4, as seen in Figure 7. This pig had a substantially higher heart rate than the other pigs, on average around 150 beats per minute compared to 122, 49, and 113 beats per minute for Pigs 1, 2, and 3. As a result, Pig 4 had a very high cardiac output up to seven times higher than the other pigs. In this extreme case, the CVS model was unable to capture the high flow dynamics of Pig 4. However, work is currently underway to improve the model for these types of cases.
A primary cause of some of the larger errors and difference in polarity of the mean errors between the left and right ventricle measurements, as seen in Table 2, is the inherent difficulty of measuring and calculating the right ventricular volume experimentally with a conductance catheter. Due to the complex shape of the right ventricle, the volume measurements were underestimated, especially for Pigs 3 and 4, where the left ventricular SV appeared to be more than double the right ventricular SV. The CVS is essentially a closed system and the ventricles pump in series. Hence, it is unsustainable for their SV of the ventricles to be a largely different for more than a couple of heartbeats, during a transient period, or else there would be a large buildup of volume somewhere in the circulation. However, the measurements were taken when the pigs were hemodynamically stable and should reflect steady state conditions. Hence, it is obvious that the measured right ventricular volume is underestimating the true volume in the right ventricle.
To overcome these measurement problems, the average value of the measured left and right ventricular stoke volumes was used in the model identification process for both ventricles. Thus, once converged, the identified models generally underestimated the measured left ventricular stoke volume and overestimated the measured right ventricular stroke volume. This issue caused the LVEDV and, consequentially, the left ventricular pressure in the model to be underestimated relatives to the measurements taken in the experiment, with the opposite occurring in the right ventricle. However, more importantly, these errors were generally systematic, so the trends associated with these measurements are still clearly identified and accurate.
4.2. Detecting Septic Shock
The subject-specific models of the CVS captured the main hemodynamic trends of septic shock. A drop in systemic vascular resistance and an increase in pulmonary vascular resistance were identified. As a result, an increase in RVEDV was also seen in the subject-specific CVS models. These changes are well-known consequences of the disease [24–26]. Hence, these results indicate that the identified models are able to accurately capture the expected trends of septic shock in the pigs.
4.3. Subject-Specific Modelling
The results show that personalised CVS models can be used to accurately match and predict important hemodynamic markers of afterload (R sys, R pul), preload (LVEDV, RVEDV), and contractility (E es,lvf, E es,rvf). Clinically, the contractile state and preload on the ventricles can be extremely difficult to continuously measure using traditional techniques. Generally, LVEDV and RVEDV can only be estimated intermittently using echocardiography, and there exists no widely accepted clinical measure of contractility. The model-based approach, used in this paper, provides a way to continuously estimate preload and contractility. These model-based metrics could be used to help guide therapy such as using fluids to increase LVEDV and the administering inotropes to control E es,lvf and E es,rvf. The accurate and continuous monitoring of preload is especially important in septic shock, as it has been shown that early goal-directed fluid resuscitation can increase patient outcomes [57]. Hence, metrics derived from identified subject-specific CVS models could help provide more meaningful targets for similar goal-directed therapies.
The subject-specific models were also able to track the main hemodynamic changes resulting from induced septic shock. These results show that the new model identification method utilised is capable of accurately identifying markers of cardiovascular health, like the previous integral-based method [19, 20] but requires a much smaller, more clinically available set of measurements including features (mean, amplitude, and maximum gradient) of the aortic and pulmonary artery pressures, SV, GEDV, and the mitral and tricuspid valve closure times. This measurement set is significantly smaller than the one used in the integral-based approach, in the sense that only discrete measurements are used instead of full pressure and volume waveforms. However, this new measurement set represents the most important features of these waveforms. For example, instead of fitting the integral of the aortic pressure the new method fits the mean, amplitude, and maximum gradient of aortic pressure in the CVS models, which are of more clinical importance. Hence, although less data is used to identify subject-specific CVS models, the models are actually matched to larger number of features within this data. Therefore, the smaller measurement set does not decrease the number of parameters that can be identified in these models, and its use increases the clinical applicability of the parameter identification method.
From the subject-specific CVS models, identified from this minimal set of measurements, the contrasting reaction of the pigs in response to the induced disease could be seen. Initially, R sys decreased in all the pigs, but in later stages of the trials R sys increased in Pigs 1 and 2, increasing aortic blood pressure in these pigs. These results tentatively suggest that the LPHF was responsible for increasing R sys through the removal inflammatory inducing molecules from the blood stream. However, this treatment appeared to have little effect on Pigs 3 and 4. Larger trials would be required before a more substantiated conclusion on this therapy could be made, which was not the goal of this research. However, it is clear that the identified CVS models were able to accurately segregate those subjects who did (and did not) respond positively to the endotoxin insult, due either to autonomous compensatory reflexes or because of the effects of this therapy.
The parameter identification method used in this study is a significant improvement on previous work [19, 20] especially with respect to clinical feasibility. Although the measurements in this study were only taken intermittently every 30 minutes, the system has the potential to provide continuous real-time information to medical staff. Accurate model identification can be achieved using low fidelity pressure measurements, as only the main features of the aortic and pulmonary artery pressure are required such as the mean, amplitude, and maximum gradient. In practice, the aortic pressure could be inferred from the radial artery pressure using several possible methods [42, 44, 46, 47]. The method could also be implemented in the ICU at little extra cost, as it only uses measurements already taken in the ICU. Thus, the approach could be applied without adding further invasive burden to the patient. In addition, the system can be easily automated, so that a full picture of a patient's hemodynamic state is available to clinicians with little extra effort required from medical staff.
4.4. Limitations
The number of parameters that can be identified in the CVS model is limited by the paucity of available measurements in the ICU, and thus, the amount of measurements that were used to identify pig-specific CVS models in this research. In this study only 14 out of a possible 37 parameters of the CVS model were identified. However, these 14 parameters control all the important dynamics in the model, including the contractility of the ventricles, vascular stiffness, and resistance to flow through parts of the CVS. In a clinical setting, these parameters can be controlled using common therapies including the administration of inotropes, vasoactive drugs, and/or fluid resuscitation. The other 23 parameters primarily have lesser effects, such as the inertia of blood through the heart valves, or are relatively constant over the population and are thus modelled as such, enabling accurate relative trend identification. The good validation and diagnostic results obtained in this study support the choice of model parameters to be identified.
A further limitation is the use of systemic and vascular resistance as the primary metric for ventricular afterload, although this approach is widely used [58–61]. A more complicated description of right ventricular afterload was utilised for validation, as shown earlier in Figure 7, so that the magnitude and units of the metric aligned with the experimentally derived value. However, clinically, systemic and pulmonary vascular resistances are still the most commonly used definitions of afterload [58]. Hence, the systemic and pulmonary vascular resistances were chosen for examination of afterload in this study.
5. Conclusion
This study presented a method for identifying pig-specific CVS models of endotoxic shock. These models were able to identify expected disease-dependent changes in ventricular preload, afterload, and contractility in the pigs, using typically available ICU measurements. These indices of cardiac function can be difficult, impossible, or impractical to monitor clinically but are extremely useful to know when guiding cardiovascular therapy. Hence, this model-based approach could potentially be used to help monitor these determinants of cardiac function and assist clinicians with diagnosis and treatment-based decisions.
Appendix
The CVS model is defined by (A.1)–(A.16). A full list of the model parameters, constants, and outputs is listed in Tables 3, 4, 5, and 6. Equation (A.1) describe the flow, Q, through the heart valves. These first-order differential equations state that the pressure (P) difference across a valve is proportional to the sum of the resistive (QR) and inertial effects on the flow as follows:
| (A.1) |
Nonvalvular flow is represented using Ohm's law (A.2). Hence, the flow through the vasculature is proportional to the pressure difference across the section divided by the resistance to flow as follows:
| (A.2) |
Pressure in the noncardiac chambers is proportional to the elastance (E) and stressed blood volume within the chamber. In these chambers the elastances are assumed to be constant over a heartbeat. The stressed blood volume in (A.3) is represented as the total blood volume (V) minus the unstressed volume (V d). Chambers within the thoracic cavity, as shown in Figure 1, are additionally influenced by the intrathoracic pressure (P th) in the thoracic cavity as follows:
| (A.3) |
The free wall pressure of the left and right ventricles (P lvf, P rvf) is calculated using (A.4). These equations ignore the effects of the intraventricular septum and pericardium which are taken into account later with (A.11)–(A.19), hence, the name free wall pressures. Myocardial activation of the left and right ventricles are represented using normalised time varying elastance curves (driL and driR) which vary in time between 0 and 1. The first term in both of these equations represent the percentage of the pressure generation in the ventricle due to dynamic contraction of the heart muscles. At maximum contraction, driL and driR equals 1, and the pressure volume relationship in the ventricles is represented by their end systolic pressure volume relationship (ESPVR). The second term represents the percentage of pressure generation due to the passive elastic recoil of the ventricular chambers. When driL and driR equal 0, the pressures in these chambers are bound by their end diastolic pressure volume relationship (EDPVR). In between end systole and end diastole the nonlinear ventricular pressure volume relationship is defined as a weighted sum of the ESPVR and EDPVR. In other words, (A.4) represents the percentage of dynamic and passive pressure generation that is occurring in the ventricles at any point in time, as defined by
| (A.4) |
The volume of blood in the noncardiac chambers varies at a rate proportional to the flow exiting and entering those chambers, as described by (A.5)–(A.8). Furthermore, (A.9) and (A.10), representing the volume in the left and right ventricles, take into consideration the nonlinear effects of valvular flow by using Heaviside functions. The use of Heaviside functions in these equations ensures that there is no backwards flow through the heart valves as follows:
| (A.5) |
| (A.6) |
| (A.7) |
| (A.8) |
| (A.9) |
| (A.10) |
Finally, ventricular interaction is modelled through considering the action of the intraventricular septum and the pericardium on cardiac dynamics. Equation (A.11) represents all the pressures acting on the intraventricular septum, where the muscle activation of the septum (driS) is assumed to be equal to the average of the left and right ventricular normalised time varying elastance curves (driL, driR). From (A.11) the blood volume displaced by the septum, V spt, can be evaluated and used to calculate the real left and right ventricular volumes (V lv, V rv), as shown by (A.13) and (A.14) as follows:
| (A.11) |
| (A.12) |
| (A.13) |
| (A.14) |
The pressure generated by the pericardium (P pcd), which encases the heart, is proportional to the sum of the left and right ventricular volumes (V pcd) as described by (A.15) and (A.16). The total external pressure acting on the cardiac chamber (P peri), as seen in (A.17)–(A.19), is therefore the sum of the pericardium and intrathoracic pressure, as the heart is located in the thoracic cavity. Please see [28, 30–32], for a more detailed description of the derivation of the CVS model equations. One has
| (A.15) |
| (A.16) |
| (A.17) |
| (A.18) |
| (A.19) |
Equations (A.17)–(A.34) make up the identification process. Table 3 lists all the parameters identified in the identification process and convergence set points used to identify them. Table 4 lists the driver functions, also known as time varying elastances used to simulate the effect of cardiac contraction in the left and right ventricles in the CVS model, and Tables 7 and 8 list the initial parameters estimates used to commence the parameter identification process.
Table 3.
Identified CVS model parameters and the measurements (convergence set points) used to identify them.
| Identified parameter | Measurement used to identify parameter | ||
|---|---|---|---|
| Symbol | Description | Symbol | Description |
| E es,lvf | Left ventricle end systolic elastance | GEDV | Global end diastolic volume |
| E ao | Aortic elastance | PPao | Amplitude of aortic pressure |
| E vc | Vena cava elastance | P vc | Modelled Vena cava pressure |
| E es,rvf | Right ventricle end systolic elastance | GEDV | Global end diastolic volume |
| E pa | Pulmonary artery elastance | PPao | Amplitude of pulmonary artery pressure |
| E pu | Pulmonary vein elastance | P vc | Modelled vena cava pressure |
| R mt | Mitral valve resistance | SV | Stroke volume |
| R av | Aortic valve resistance | dP ao,max/dt | Maximum ascending aortic pressure gradient |
| R sys | Systemic vascular resistance | P ao,mean | Mean aortic pressure |
| R tc | Tricuspid resistance | SV | Stroke volume |
| R pv | Pulmonary valve resistance | dP ao,max/dt | Maximum ascending pulmonary artery pressure gradient |
| R pul | Pulmonary vascular resistance | P po,mean | Mean pulmonary artery pressure |
| P vc | Vena cava pressure | t tc, SV | Tricuspid valve closure time and stroke volume |
| P pu | Pulmonary vein pressure | t mt, SV | Mitral valve closure time and stroke volume |
Table 4.
Identified cardiac driver functions (normalised time varying elastances) and the measurements used to calculate them.
| Identified cardiac activation | Measurement used to identify waveform | ||
|---|---|---|---|
| Symbol | Description | Symbol | Description |
| driL(t) | Left ventricle normalised time varying elastance | P ao, GEDV | Aortic pressure waveform and global end diastolic volume |
| driR(t) | Right ventricle normalised time varying elastance | P pa, GEDV | Pulmonary artery pressure and global end diastolic volume |
Table 6.
Full list of the CVS model outputs. Check marks indicate outputs that are also experimentally measured.
| Symbol | Description | Measured |
|---|---|---|
| V lv | Left ventricle volume | √ |
| V ao | Aorta volume | |
| V vc | Vena cava volume | |
| V rv | Right ventricle volume | √ |
| V pa | Pulmonary artery volume | |
| V pu | Pulmonary vein volume | |
| P lv | Left ventricle pressure | √ |
| P ao | Aorta pressure | √ |
| P vc | Vena cava pressure | |
| P rv | Right ventricle pressure | √ |
| P pa | Pulmonary artery pressure | √ |
| P pu | Pulmonary vein pressure | |
| Q mt | Mitral valve flow rate | |
| Q av | Aortic valve flow rate | |
| Q sys | Systemic flow rate | |
| Q tc | Tricuspid valve flow rate | |
| Q pv | Pulmonary valve flow rate | |
| Q pul | Pulmonary flow rate | |
| V spt | Septum volume | |
| P pcd | Pericardium pressure |
Table 7.
Initial systemic model parameter inputs.
| Parameter | P pu | R mt | E es,lvf | R av | E ao | R sys | P vc |
|---|---|---|---|---|---|---|---|
| Initial value | 5 | 0.05 | 2 | 0.04 | 2.5 | 2.5 | 5 |
Table 8.
Initial pulmonary model parameter inputs.
| Parameter | P vc | R tc | E es,rvf | R pv | E pa | R pul | P pu |
|---|---|---|---|---|---|---|---|
| Initial value | 5 | 0.04 | 0.8 | 0.03 | 2.1 | 0.4 | 5 |
Initially, the driver functions for the left and right ventricles are estimated using GEDV and features from the aortic pressure waveform (for driL) and pulmonary artery pressure waveform (for driR) using the method described in [34, 35]. The systemic model is identified first. The model is initially simulated using the parameters values given in Table 7. A method is then used to iteratively simulate and improve the estimates of R mt, E ao, and R sys in the systemic submodel by matching the modelled SV, PPao and P ao,mean to their measured value as follows:
| (A.20) |
where SVlv,approx = max(V lv) − min(V lv),
| (A.21) |
where PPao = max(P ao) − min(P ao),
| (A.22) |
where P ao,mean = (max(P ao) + min(P ao))/2.
Once the modelled SV, PPao, and P ao,mean have converged, new estimates of P pu and R av are identified. R mt, E ao, and R sys are then reidentified with the new estimates of P pu and R av, and the whole process is repeated until P pu does not change between iterations, and dP ao,max/dt converges to its measured value. In this process, P pu and R av are identified independently of R mt, E ao, and R sys, as they interact and are dependent on the correct convergence of these parameters as follows:
| (A.23) |
| (A.24) |
During this process E es,lvf is left as its constant value to be identified later in the identification process.
The same approach is used to identify the pulmonary sub-model, as the pulmonary model essentially mirrors the systemic model. R tc, E pa, and R pul are identified first. Then P vc and R pv are updated, these values are used to reidentify R tc, E pa, and R pul, and the process is repeated until SV, PP, P ao,mean, P vc, and dP ao,max/dt have converged. During this process E es,rvf is held as its original value to be identified later. Consider
| (A.25) |
where SVrv,approx = max(V rv) − min(V rv),
| (A.26) |
where PPpa = max(P pa) − min(P pa),
| (A.27) |
where P pa,mean = (max(P pa) + min(P pa))/2
| (A.28) |
| (A.29) |
Once, the systemic and pulmonary submodelss have converged, E es,lvf and E es,rvf are updated. First, the sum of the end systolic elastances (E es,sum) is updated by matching GEDV as follows:
| (A.30) |
where GEDVapprox = max(Vlv) + max(Vrv ).
Then a relationship, derived from the afterloads on the left and right ventricles, is used to calculate the relative contribution of E es,lvf from this sum. The derivation of this relationship is shown in [22] as follows:
| (A.31) |
| (A.32) |
Finally, E es,rvf can also be found using
| (A.33) |
During this step in the identification process, ventricular interaction, in the form of septal and pericardial dynamics (V spt and P pcd) are calculated and added to the systemic and pulmonary submodelss to couple the systems. Once E es,lvf and E es,rvf have been updated, and V spt and P pcd have been calculated, the systemic and pulmonary models are reidentified using the new values for these parameters and interactions. This overall process, for identifying E es,lvf and E es,rvf, is repeated until GEDV converges, thus completing the identification of the systemic and pulmonary models.
The systemic and pulmonary models are then identified for the remaining measurement sets, T0–T240 for that pig. The valve resistance are averaged across these models with these averaged valve resistance used to reidentify the systemic and pulmonary models. Hence, (A.20), (A.24), (A.25), and (A.29) are no longer required, and (A.23) and (A.28) are replaced by (A.34) and (A.35) for identifying P pa and P vc as follows:
| (A.34) |
| (A.35) |
Once the systemic and pulmonary models have been identified with the averaged valve resistances, the final parameters of the six-chamber model, E vc and E pu, can be identified. This is done by using the parameters of systemic and pulmonary to simulate the six-chamber CVS model. The six-chamber model is iteratively simulated, and (A.36) and (A.37) are used to identify E vc and E pu. The parameter identification process is concluded when the mean of the six-chamber P vc,6 and P pu,6 matches their corresponding identified values from the simplified submodels (P vc,simple, P pu,simple), producing a full six-chamber subject-specific model of the CVS as follows:
| (A.36) |
| (A.37) |
Figure 9 outlines the steps used to identify the parameters of the six-chamber CVS model.
Figure 9.

Step-by-step overview of the parameter identification used to create subject-specific CVS models.
References
- 1.Angus DC, Linde-Zwirble WT, Lidicker J, Clermont G, Carcillo J, Pinsky MR. Epidemiology of severe sepsis in the United States: analysis of incidence, outcome, and associated costs of care. Critical Care Medicine. 2001;29(7):1303–1310. doi: 10.1097/00003246-200107000-00002. [DOI] [PubMed] [Google Scholar]
- 2.Brun-Buisson C. The epidemiology of the systemic inflammatory response. Intensive Care Medicine. 2000;26(supplement 1):S64–S74. doi: 10.1007/s001340051121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Franklin C, Mathew J. Developing strategies to prevent inhospital cardiac arrest: analyzing responses of physicians and nurses in the hours before the event. Critical Care Medicine. 1994;22(2):244–247. [PubMed] [Google Scholar]
- 4.Perkins GD, McAuley DF, Davies S, Gao F. Discrepancies between clinical and postmortem diagnoses in critically ill patients: an observational study. Critical Care. 2003;7(6):R129–R132. doi: 10.1186/cc2359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Smith WR, Poses RM, McClish DK, et al. Prognostic judgments and triage decisions for patients with acute congestive heart failure. Chest. 2002;121(5):1610–1617. doi: 10.1378/chest.121.5.1610. [DOI] [PubMed] [Google Scholar]
- 6.Samar Z, Heldt T, Verghese GC, Mark RG. Model-based cardiovascular parameter estimation in the intensive care unit. Proceedings of the IEEE Computers in Cardiology; September 2005; pp. 635–638. [Google Scholar]
- 7.Wang JJ, O’Brien AB, Shrive NG, Parker KH, Tyberg JV. Time-domain representation of ventricular-arterial coupling as a windkessel and wave system. American Journal of Physiology. 2003;284(4):H1358–H1368. doi: 10.1152/ajpheart.00175.2002. [DOI] [PubMed] [Google Scholar]
- 8.Davies JE, Baksi J, Francis DP, et al. The arterial reservoir pressure increases with aging and is the major determinant of the aortic augmentation index. American Journal of Physiology. 2010;298(2):H580–H586. doi: 10.1152/ajpheart.00875.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Parlikar TA, Heldt T, Ranade GV, Verghese GC. Model-based estimation of cardiac output and total peripheral resistance. Proceedings of the IEEE Computers in Cardiology; October 2007; pp. 379–382. [Google Scholar]
- 10.Wesseling KH, Jansen JRC, Settels JJ, Schreuder JJ. Computation of aortic flow from pressure in humans using a nonlinear, three-element model. Journal of Applied Physiology. 1993;74(5):2566–2573. doi: 10.1152/jappl.1993.74.5.2566. [DOI] [PubMed] [Google Scholar]
- 11.Schuerholz T, Meyer MC, Friedrich L, Przemeck M, Sümpelmann R, Marx G. Reliability of continuous cardiac output determination by pulse-contour analysis in porcine septic shock. Acta Anaesthesiologica Scandinavica. 2006;50(4):407–413. doi: 10.1111/j.1399-6576.2006.00982.x. [DOI] [PubMed] [Google Scholar]
- 12.Mukkamala R, Xu D. Continuous and less invasive central hemodynamic monitoring by blood pressure waveform analysis. American Journal of Physiology. 2010;299(3):H584–H599. doi: 10.1152/ajpheart.00303.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Johansson A, Chew M. Reliability of continuous pulse contour cardiac output measurement during hemodynamic instability. Journal of Clinical Monitoring and Computing. 2007;21(4):237–242. doi: 10.1007/s10877-007-9079-7. [DOI] [PubMed] [Google Scholar]
- 14.Jeong YB, Kim TH, Roh YJ, Choi IC, Suh JH. Comparison of uncalibrated arterial pressure waveform analysis with continuous thermodilution cardiac output measurements in patients undergoing elective off-pump coronary artery bypass surgery. Journal of Cardiothoracic and Vascular Anesthesia. 2010;24(5):767–771. doi: 10.1053/j.jvca.2010.02.006. [DOI] [PubMed] [Google Scholar]
- 15.Hamm JB, Nguyen BV, Kiss G, et al. Assessment of a cardiac output device using arterial pulse waveform analysis, Vigileo in cardiac surgery compared to pulmonary arterial thermodilution. Anaesthesia and Intensive Care. 2010;38(2):295–301. doi: 10.1177/0310057X1003800211. [DOI] [PubMed] [Google Scholar]
- 16.Cooper ES, Muir WW. Continuous cardiac output monitoring via arterial pressure waveform analysis following severe hemorrhagic shock in dogs. Critical Care Medicine. 2007;35(7):1724–1729. doi: 10.1097/01.CCM.0000266590.25109.F2. [DOI] [PubMed] [Google Scholar]
- 17.Chase J, Le Compte A, Preiser JC, Shaw G, Penning S, Desaive T. Physiological modelling, tight glycemic control, and the ICU clinician: what are models and how can they affect practice? Annals of Intensive Care. 2011;1(1):p. 11. doi: 10.1186/2110-5820-1-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shaw GM, Chase JG, Starfinger C, et al. Modelling the cardiovascular system. Critical Care and Resuscitation. 2007;9(3):264–269. [PubMed] [Google Scholar]
- 19.Starfinger C, Hann CE, Chase JG, Desaive T, Ghuysen A, Shaw GM. Model-based cardiac diagnosis of pulmonary embolism. Computer Methods and Programs in Biomedicine. 2007;87(1):46–60. doi: 10.1016/j.cmpb.2007.03.010. [DOI] [PubMed] [Google Scholar]
- 20.Starfinger C, Chase JG, Hann CE, et al. Model-based identification and diagnosis of a porcine model of induced endotoxic shock with hemofiltration. Mathematical Biosciences. 2008;216(2):132–139. doi: 10.1016/j.mbs.2008.08.014. [DOI] [PubMed] [Google Scholar]
- 21.Revie JA, Stevenson DJ, Chase JG, et al. Clinical detection and monitoring of acute pulmonary embolism: proof of concept of a computer-based method. Annals of Intensive Care. 2011;1(1):p. 33. doi: 10.1186/2110-5820-1-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Revie JA, Stevenson DJ, Chase JG, et al. Validation of subject-specific cardiovascular system models from porcine measurements. Computer Methods and Programs in Biomedicine. 2013;109(2):197–210. doi: 10.1016/j.cmpb.2011.10.013. [DOI] [PubMed] [Google Scholar]
- 23.Lambermont B, Delanaye P, Dogné JM, et al. Large-pore membrane hemofiltration increases cytokine clearance and improves right ventricular-vascular coupling during endotoxic shock in pigs. Artificial Organs. 2006;30(7):560–564. doi: 10.1111/j.1525-1594.2006.00260.x. [DOI] [PubMed] [Google Scholar]
- 24.Parrillo JE, Parker MM, Natanson C, et al. Septic shock in humans. Advances in the understanding of pathogenesis, cardiovascular dysfunction, and therapy. Annals of Internal Medicine. 1990;113(3):227–242. doi: 10.7326/0003-4819-113-3-227. [DOI] [PubMed] [Google Scholar]
- 25.Dellinger RP. Cardiovascular management of septic shock. Critical Care Medicine. 2003;31(3):946–955. doi: 10.1097/01.CCM.0000057403.73299.A6. [DOI] [PubMed] [Google Scholar]
- 26.Chan CM, Klinger JR. The right ventricle in sepsis. Clinics in Chest Medicine. 2008;29(4):661–676. doi: 10.1016/j.ccm.2008.07.002. [DOI] [PubMed] [Google Scholar]
- 27.Lambermont B, Ghuysen A, Kolh P, et al. Effects of endotoxic shock on right ventricular systolic function and mechanical efficiency. Cardiovascular Research. 2003;59(2):412–418. doi: 10.1016/s0008-6363(03)00368-7. [DOI] [PubMed] [Google Scholar]
- 28.Smith BW, Chase JG, Nokes RI, Shaw GM, Wake G. Minimal haemodynamic system model including ventricular interaction and valve dynamics. Medical Engineering and Physics. 2004;26(2):131–139. doi: 10.1016/j.medengphy.2003.10.001. [DOI] [PubMed] [Google Scholar]
- 29.Hann CE, Chase JG, Desaive T, et al. Unique parameter identification for cardiac diagnosis in critical care using minimal data sets. Computer Methods and Programs in Biomedicine. 2010;99(1):75–87. doi: 10.1016/j.cmpb.2010.01.002. [DOI] [PubMed] [Google Scholar]
- 30.Smith BW, Andreassen S, Shaw GM, Jensen PL, Rees SE, Chase JG. Simulation of cardiovascular system diseases by including the autonomic nervous system into a minimal model. Computer Methods and Programs in Biomedicine. 2007;86(2):153–160. doi: 10.1016/j.cmpb.2007.02.001. [DOI] [PubMed] [Google Scholar]
- 31.Smith BW, Chase JG, Shaw GM, Nokes RI. Experimentally verified minimal cardiovascular system model for rapid diagnostic assistance. Control Engineering Practice. 2005;13(9):1183–1193. [Google Scholar]
- 32.Smith BW, Chase JG, Shaw GM, Nokes RI. Simulating transient ventricular interaction using a minimal cardiovascular system model. Physiological Measurement. 2006;27(2):165–179. doi: 10.1088/0967-3334/27/2/007. [DOI] [PubMed] [Google Scholar]
- 33.Hann CE, Chase JG, Desaive T, et al. Unique parameter identification for cardiac diagnosis in critical care using minimal data sets. Computer Methods and Programs in Biomedicine. 2010;99(1):75–87. doi: 10.1016/j.cmpb.2010.01.002. [DOI] [PubMed] [Google Scholar]
- 34.Stevenson D, Revie J, Chase JG, et al. Beat-to-beat estimation of the continuous left and right cardiac elastance from metrics commonly available in clinical settings. Biomedical Engineering Online. 2012;11:p. 73. doi: 10.1186/1475-925X-11-73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Stevenson D, Revie J, Chase JG, et al. Algorithmic processing of pressure waveforms to facilitate estimation of cardiac elastance. Biomedical Engineering Online. 2012;11(1):p. 28. doi: 10.1186/1475-925X-11-28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Desaive T, Lambermont B, Ghuysen A, et al. Cardiovascular modelling and identification in septic shock—experimental validation. Proceedings of the 17th IFAC World Congress; 2008; Seoul, Republic of Korea. pp. 2976–2979. [Google Scholar]
- 37.Hann CE, Revie J, Stevenson D, et al. Patient specific identification of the cardiac driver function in a cardiovascular system model. Computer Methods and Programs in Biomedicine. 2011;101(2):201–207. doi: 10.1016/j.cmpb.2010.06.005. [DOI] [PubMed] [Google Scholar]
- 38.Michard F, Alaya S, Zarka V, Bahloul M, Richard C, Teboul JL. Global end-diastolic volume as an indicator of cardiac preload in patients with septic shock. Chest. 2003;124(5):1900–1908. doi: 10.1378/chest.124.5.1900. [DOI] [PubMed] [Google Scholar]
- 39.Sakka SG, Rühl CC, Pfeiffer UJ, et al. Assessment of cardiac preload and extravascular lung water by single transpulmonary thermodilution. Intensive Care Medicine. 2000;26(2):180–187. doi: 10.1007/s001340050043. [DOI] [PubMed] [Google Scholar]
- 40.Stetz CW, Miller RG, Kelly GE, Raffin TA. Reliability of the thermodilution method in the determination of cardiac output in clinical practice. The American Review of Respiratory Disease. 1982;126(6):1001–1004. doi: 10.1164/arrd.1982.126.6.1001. [DOI] [PubMed] [Google Scholar]
- 41.Ganz W, Donoso R, Marcus HS, Forrester JS, Swan HJC. A new technique for measurement of cardiac output by thermodilution in man. The American Journal of Cardiology. 1971;27(4):392–396. doi: 10.1016/0002-9149(71)90436-x. [DOI] [PubMed] [Google Scholar]
- 42.Westerhof BE, Guelen I, Stok WJ, et al. Individualization of transfer function in estimation of central aortic pressure from the peripheral pulse is not required in patients at rest. Journal of Applied Physiology. 2008;105(6):1858–1863. doi: 10.1152/japplphysiol.91052.2008. [DOI] [PubMed] [Google Scholar]
- 43.O’Rourke MF. Estimation of central aortic pressure by SphygmoCor requires accurate peripheral pressure measurement. Clinical Science. 2004;106(4):434–435. doi: 10.1042/CS20030320. [DOI] [PubMed] [Google Scholar]
- 44.Hope SA, Tay DB, Meredith IT, Cameron JD. Use of arterial transfer functions for the derivation of central aortic waveform characteristics in subjects with type 2 diabetes and cardiovascular disease. Diabetes Care. 2004;27(3):746–751. doi: 10.2337/diacare.27.3.746. [DOI] [PubMed] [Google Scholar]
- 45.Cloud GC, Rajkumar C, Kooner J, Cooke J, Bulpitt CJ. Estimation of central aortic pressure by SphygmoCor requires intra-arterial peripheral pressures. Clinical Science. 2003;105(2):219–225. doi: 10.1042/CS20030012. [DOI] [PubMed] [Google Scholar]
- 46.Pauca AL, O’Rourke MF, Kon ND. Prospective evaluation of a method for estimating ascending aortic pressure from the radial artery pressure waveform. Hypertension. 2001;38(4):932–937. doi: 10.1161/hy1001.096106. [DOI] [PubMed] [Google Scholar]
- 47.Chen CH, Nevo E, Fetics B, et al. Estimation of central aortic pressure waveform by mathematical transformation of radial tonometry pressure: validation of generalized transfer function. Circulation. 1997;95(7):1827–1836. doi: 10.1161/01.cir.95.7.1827. [DOI] [PubMed] [Google Scholar]
- 48.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. The Lancet. 1986;1(8476):307–310. [PubMed] [Google Scholar]
- 49.Clancy TV, Norman K, Reynolds R, Covington D, Maxwell JG. Cardiac output measurement in critical care patients: thoracic electrical bioimpedance versus thermodilution. The Journal of Trauma. 1991;31(8):1116–1121. [PubMed] [Google Scholar]
- 50.Critchley LAH, Critchley JAJH. A meta-analysis of studies using bias and precision statistics to compare cardiac output measurement techniques. Journal of Clinical Monitoring and Computing. 1999;15(2):85–91. doi: 10.1023/a:1009982611386. [DOI] [PubMed] [Google Scholar]
- 51.Salandin V, Zussa C, Risica G, et al. Comparison of cardiac output estimation by thoracic electrical bioimpedance, thermodilution, and Fick methods. Critical Care Medicine. 1988;16(11):1157–1158. doi: 10.1097/00003246-198811000-00015. [DOI] [PubMed] [Google Scholar]
- 52.Merx MW, Weber C. Sepsis and the heart. Circulation. 2007;116(7):793–802. doi: 10.1161/CIRCULATIONAHA.106.678359. [DOI] [PubMed] [Google Scholar]
- 53.Vincent JL, Gris P, Coffernils M, et al. Myocardial depression characterizes the fatal course of septic shock. Surgery. 1992;111(6):660–667. [PubMed] [Google Scholar]
- 54.Grootendorst AF, van Bommel EF, van Leengoed LA, Nabuurs M, Bouman CS, Groeneveld AB. High volume hemofiltration improves hemodynamics and survival of pigs exposed to gut ischemia and reperfusion. Shock. 1994;2(1):72–78. doi: 10.1097/00024382-199407000-00014. [DOI] [PubMed] [Google Scholar]
- 55.Grootendorst AF, van Bommel EFH, van Leengoed LAMG, van Zanten ARH, Huipen HJC, Groeneveld ABJ. Infusion of ultrafiltrate from endotoxemic pigs depresses myocardial performance in normal pigs. Journal of Critical Care. 1993;8(3):161–169. doi: 10.1016/0883-9441(93)90022-d. [DOI] [PubMed] [Google Scholar]
- 56.Aylward PE, McRitchie RJ, Chalmers JP, West MJ. Baroreflex control of myocardial contractility in conscious normotensive and renal hypertensive rabbits. Hypertension. 1983;5(6):916–926. doi: 10.1161/01.hyp.5.6.916. [DOI] [PubMed] [Google Scholar]
- 57.Rivers E, Nguyen B, Havstad S, et al. Early goal-directed therapy in the treatment of severe sepsis and septic shock. The New England Journal of Medicine. 2001;345(19):1368–1377. doi: 10.1056/NEJMoa010307. [DOI] [PubMed] [Google Scholar]
- 58.Tibby SM, Murdoch IA. Monitoring cardiac function in intensive care. Archives of Disease in Childhood. 2003;88(1):46–52. doi: 10.1136/adc.88.1.46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lang RM, Borow KM, Neumann A, Janzen D. Systemic vascular resistance: an unreliable index of left ventricular afterload. Circulation. 1986;74(5):1114–1123. doi: 10.1161/01.cir.74.5.1114. [DOI] [PubMed] [Google Scholar]
- 60.Naeije R. Pulmonary vascular resistance: a meaningless variable? Intensive Care Medicine. 2003;29(4):526–529. doi: 10.1007/s00134-003-1693-3. [DOI] [PubMed] [Google Scholar]
- 61.Hunter KS, Lee PF, Lanning CJ, et al. Pulmonary vascular input impedance is a combined measure of pulmonary vascular resistance and stiffness and predicts clinical outcomes better than pulmonary vascular resistance alone in pediatric patients with pulmonary hypertension. American Heart Journal. 2008;155(1):166–174. doi: 10.1016/j.ahj.2007.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]


