Skip to main content
PMC home page
Brain Connectivity logoLink to Brain Connectivity
. 2012 Oct;2(5):284–290. doi: 10.1089/brain.2012.0096

Automated Determination of Axonal Orientation in the Deep White Matter of the Human Brain

Hauke Bartsch 1, Paul Maechler 1, Jacopo Annese 1,✉
PMCID: PMC3621296  PMID: 23030312

Abstract

The wide-spread utilization of diffusion-weighted imaging in the clinical neurosciences to assess white-matter (WM) integrity and architecture calls for robust validation strategies applied to the data that are acquired with noninvasive imaging. However, the pathology and detailed fiber architecture of WM tissue can only be observed postmortem. With these considerations in mind, we designed an automated method for the determination of axonal orientation in high-resolution microscope images. The algorithm was tested on tissue that was stained using a silver impregnation technique that was optimized to resolve axonal fibers against very low levels of background. The orientation of individual nerve fibers was detected using spatial filtering and a template-matching algorithm, and the results are displayed as color-coded overlays. Quantitative models of WM fiber architecture at the microscopic level can lead to improved interpretation of low-resolution neuroimaging data and to more accurate mapping of fiber pathways in the human brain.

Key words: anatomical connectivity, axonal fiber, Fourier transform, human brain connectivity, white matter

Introduction

Increasing importance has been given in recent years to the anatomy of the deep white matter ([WM]; Kleinfeld et al., 2011; Sporns et al., 2005), and specifically to the geometry and topography of fiber tracts, which define effective connectivity (Horowitz, 2003) between different parcels of gray matter. Effective connectivity is currently perceived as the blueprint for behavior, the latter being dependent on the temporal and spatial dynamics of distributed functional networks (van Essen et al., 2012). In addition, diffusion-weighted imaging (DWI), a relatively recent magnetic resonance imaging (MRI) technique that provides measures of WM integrity (Chan et al., 2003), indicates that pathological and age-related WM changes not only affect the density of myelination but also create changes in fiber architecture. In spite of the significance of the WM anatomy in studies of the brain function and disease, very little is known about the detailed arrangement of axonal fiber pathways in the human brain. Improved sensitivity is offered by specialized imaging techniques such as diffusion tensor imaging (DTI) and diffusion spectrum imaging (Wedeen et al., 2012); however, axonal architecture at the microstructural level can only be directly observed postmortem on stained histological sections. Furthermore, to study detailed axonal geometric properties, the examination has to be conducted at a relatively high magnification, ideally equal to or higher than 10× (this optical magnification corresponds to a resolution of 1 μm/pixel using a common 2-megapixel scientific digital camera). The higher the magnification, the smaller the field of view (FOV); accordingly, considerable time would be required to examine even small areas of tissue without the utilization of digital microscopy techniques. The latter facilitate large-scale analyses of the histological material and comparisons with MRI data at the system level, that is, for the whole brain (Annese, 2012). Stereological protocols based on systematic sampling (West, 2002) also offer practical means to quantify tissue parameters; the method produces reliable estimates from the examination of only a limited sample, but these results can be generalized across whole specimens, and in some cases, they may provide useful validation information in respect to MRI (Bürgel et al., 2005, Hsu et al., 1998, Kielar et al., 2012, Leergaard et al., 2010). In these studies, inter-rater variability and error coefficients need to be tested accurately to guarantee the validity and reproducibility of results (Scollan et al. 1998).

Automated image analysis has several advantages over the techniques above mentioned. First, it eliminates the concerns of observer-dependent bias. Secondly, it does not require lengthy operator training. Finally, it allows for processing large batches of image files consecutively without supervision. This is important, as future systematic comparisons between MRI data and tissue-level features will require efficient large-scale methods of histological analysis and quantification that are not typically used in the context of classic neuropathological examinations (Annese, 2012).

To date, very little has been done to survey the WM with automated image analysis protocols; in fact, most algorithms for image analysis are geared toward measuring the density or size of cellular features based on texture information, using intensity measures and pattern recognition (Armstrong, 2010; Budde et al., 2011; Wedeen et al., 2012). Because the study of detailed fiber distribution and orientation in the WM will become increasingly relevant for studies of brain connectivity and disease, we have designed a method for the automated detection of axonal fiber architecture in digital histological images of the deep WM acquired via computer-assisted microscopy. Image analysis is based on a template-matching algorithm that classifies parcels of the WM contained in FOVs based on the orientation of axonal segments relative to a discrete array of templates.

Methods

Data

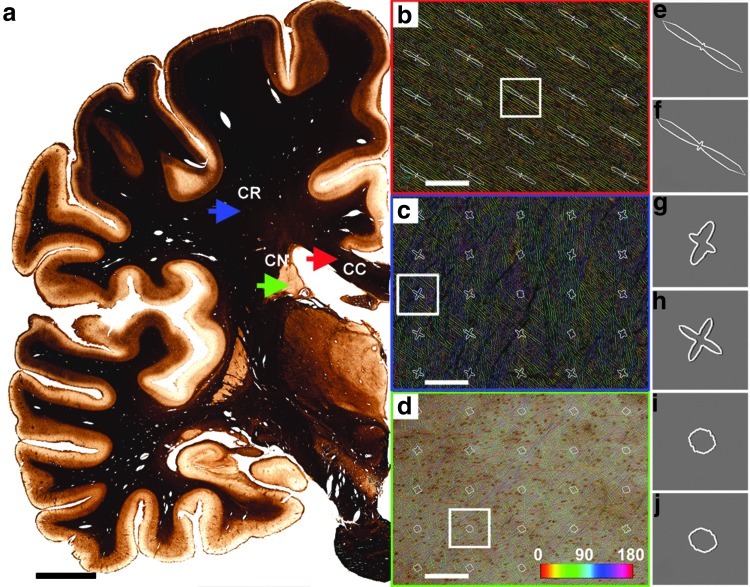
The algorithm was tested on five sample images acquired from frozen sections (70-μm thickness) that were stained using a modified Bielschowsky silver impregnation method (Bielschowsky, 1902) that reveals axons and, to a lesser extent, neuroglia. The contrast between stained features and the background is improved by treating the sections with a potassium ferricyanide (K3[Fe(CN)6]) solution to remove excess silver from the parenchima (Merker and Hess, 1983). The brain belonged to a 50-year-old man with no history of mental illness or neurological disease. It was fixed by immersion in a phosphate-buffered formaldehyde solution, cryoprotected in increasing solutions of sucrose (10%–30%), and cut on a large-format motorized microtome (Leica Microsystems, Buffalo Grove, IL). Images were acquired at 20× magnification using a Retiga R4000 digital camera (Q imaging, Surrey, Canada) mounted on an Olympus BX51WI upright microscope (Olympus America, Center Valley, PA), equipped with a grid-encoded motorized stage (Ludl Electronic Products, Hawthorne, NY). Microlucida software (MBF Biosciences, Williston, VT) was used to acquire multiple image tiles systematically (single tile size: 1486×1238 pixels, resolution: 0.37 μm/pixel; FOV in terms of tissue area: 550×458 μm). Multiple tiles were stitched into a whole-slice montage (Fig. 2a; made of ∼40,000 tiles) that was the basis for the selection of sample images for local analyses. Silver impregnation and subsequent development produced excellent image contrast, revealing single axonal fibers very sharply.

FIG. 2.

FIG. 2.

Open in a new tab

(a) Stained histological section at the level of the pons with the regions of interest indicated by arrows; red, blue, and green, in the area of the corpus callosum (CC), corona radiata CR), and caudate nucleus (CN), respectively. Scale bar=2 cm. (b, c, d) Sample images at 20× magnification (field of view=550×458 μm), framed by colored boxes corresponding to the regions indicated by arrows in (a). Scale bars=100 μm. (e–j) Glyphs representing summed orientation histograms for tissue areas 100×92-μm wide; with (f, h, j) and without (e, g, i) Rayleigh threshold (0.8). The exclusion of cross-over pixels has a noticeable effect on the geometry of the glyphs for regions populated by crossing fibers predominantly (c), while having little-to-no effect on regions containing axons with single preferred orientations (b), or regions with no preferred orientation (d).

Image processing

Image analysis was designed to assign a value representing orientation to pixels that included segments of nerve fibers. The axonal location was determined and orientated within a discrete area surrounding each pixel, as described below.

Image normalization

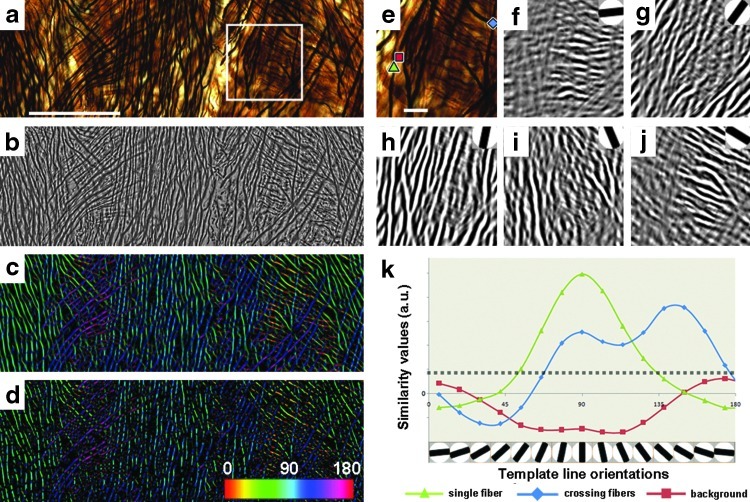
Preprocessing steps included adjusting for large intensity changes caused by uneven histological staining or illumination, as well as enhancing contrast where the tissue was not completely in focus. Specifically, we used spatial filtering to calculate the local mean intensity and variance values for a predefined area surrounding each pixel (neighborhood area: 10×10 pixels). Images were normalized by calculating the local mean intensity and the local image contrast to obtain a measure of intensity variance, then subtracting the mean intensity from the image, and dividing the result by the variance. Normalization of intensities in the raw image (Fig. 1a) produced a gray-scale image x with uniform intensity and image contrast (Fig. 1b).

FIG. 1.

FIG. 1.

Open in a new tab

Preprocessing and template-matching process applied to a sample image acquired in the deep white matter. (a) Raw image illustrating crossing fibers from the corticospinal tract in a section stained with a modified Bielschowsky silver impregnation technique; scale bar=100 μm. (b) The same image after spatial filtering and normalization. (c) A color map of the mean orientation at each pixel overlaid on the raw image data. (d) By applying the Rayleigh threshold, color coding of the mean orientation at each pixel is restricted to pixels that have a single preferred orientation. (e) Magnified image selection from white box in (a). The colored geometrical markers represent three pixels that contain either a single fiber (green triangle), two crossing fibers (blue diamond), or background (red square); scale bar=25 μm. (f–j) Similarity maps in respect to discrete templates (upper right corner). Higher similarity values are visible as areas of enhanced contrast and brightness. (k) Graph showing similarity values plotted against template line orientations for each of the three selected pixel regions in (e). The masking threshold level is displayed as a dotted horizontal line (β=0.0024). The color bar indicates detected fiber orientations from 0 to 180°.

Feature detection

A template-matching algorithm was used to calculate a similarity measure that compared fiber segments within the neighborhood area surrounding each pixel (Fig. 1e) to a dictionary of orientation templates (Fig. 1k). The latter were constructed as line segments rotated at different angles (i.e., representing discrete orientations; Fig. 1f–j). The templates were designed to match the range of thickness values d that matched the characteristics of the population of fibers in the tissue. A complete range of orientation angles θ (θ=0–180) was considered. For the neighborhood area of each pixel in the image x, we defined a similarity measure based on thickness and orientation sd,θ(x); the latter was described by the cross-covariance in respect to the templates. To improve performance, template matching was implemented in Fourier space as a convolution with a complex conjugate using the Fastest Fourier Transform in the West (FFTW) library (Frigo and Johnson, 1998) and a custom code written in C++.

In the presence of a fiber at a specific pixel location xi, if the orientation and thickness of the axonal fiber matched the orientation and thickness of a specific template, then the value of sd;θ(xi) was positive. Conversely, when local axonal orientation did not match the orientation of the template or the pixel represented an area dominated by noise, the cross-covariance value was lower. The value of sd;θ(xi) was negative when the contrast was reversed, for instance, when the pixel occurred in a background region between two darkly stained fibers (the opposite of the template images). In short, the cross-covariance s is equivalent to a similarity value describing how well the fiber matches the template in thickness and orientation. Specific template angles (possible orientations) as well as the number of templates (angular resolution) are user defined. In the context of this study, we used 15 templates ranging 180°. The angular resolution for 15 templates is ∼6° based on the Nyquist–Shannon theorem: (180−(180/15))/14/2.

To obtain a distribution function that was better suited for statistical analysis (i.e., to remove negative values), we mapped the similarity values to a normalized range of 0–1 using the logistic function

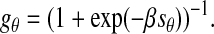graphic file with name M1.gif

The variable β was used to match the logistic function to the overall distribution of similarity values. In practice, within the range of fiber densities contained in our sample images, the actual value of β was not a determining factor for obtaining correct orientation maps. The formula

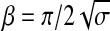graphic file with name M2.gif

was used to set β relative to the variance σ of the distribution of similarity values in the image of the histological slice and provided sufficient normalization across a wide range of morphological conditions (Fig. 2b–d).

Thresholding

We applied a fiber detection threshold based on the maximum value of g for all orientations to exclude areas that contained high noise levels or just background. Based on the g function, fibers were likely to be detected if the maximum value of g across all orientations for a given pixel was above a value of 0.5. Therefore, in this study, pixels within an image were considered to contain fibers if maxθ (gθ) >0.9.

A problem with this thresholding rationale is that it does not exclude complex fiber orientation distributions such as regions with two or more crossing or kissing (juxtaposed) fibers. Such distinction would require higher thresholding values resulting in a degradation of performance in areas containing higher noise levels. However, it was possible to account for these regions by examining the shape of the distribution function gθ. In fact, while for regions with a single preferred fiber orientation, the distribution g was condensed around a single peak representing the major orientation, and regions of fiber crossing with multiple detected orientations were characterized by several peaks (see blue curve in Fig. 1k).

Fiber classification

To classify pixels belonging to areas with multiple fiber orientations, we introduced an analysis based on a circular version of the distribution g. Subsequently, we applied Rayleigh's test for uniformity (Mardia and Jupp, 2000b) based on the assumption that it is possible to reject uniformity (no single peak) if the mean resultant length 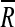Inline graphic defined as

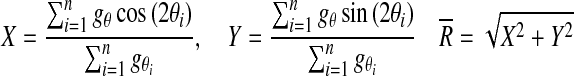graphic file with name M4.gif

is large. We rejected the null hypothesis that no single orientation existed for a Rayleigh threshold of

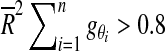graphic file with name M5.gif

Because lines contained in the templates have an inherent rotational (antipodal) symmetry, the values of s and g are the same for θ and θ+180°. Therefore, we only considered the range of 0°−180° for sampling orientations to increase processing speed. However, because the statistical classification based on the Rayleigh's test requires a circular distribution (θ=0°−360°), the latter was restored by using antipodal values over 180°.

Detecting fiber orientation

The final fiber orientation was calculated as the mean orientation of the circularly distributed values of gθ using the method of doubling the angles (Mardia and Jupp, 2000a). According to this method, we calculated the mean orientation 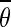Inline graphic as

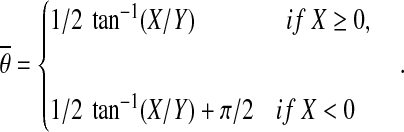graphic file with name M7.gif

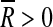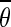given Inline graphic as a measure of confidence relative to the obtained mean orientation Inline graphic.

The detection of fiber orientation was repeated as multiple iterations of the same process, but for different thickness (fiber diameter), values d and eventually combined into a final orientation map for the population of fibers in the sample area of tissue. For each pixel, we selected the mean orientation that produced the largest value of g. In this study, three different line thicknesses were used; specifically, d was 2-, 4-, and 8-pixel wide, respectively. These values corresponded to fiber diameters ranging from 0.7 to 3 μm.

Results

The filtering operation removed large-to-intermediate intensity differences from the input as shown in Figure 1b. The locations of detected fibers are displayed in Figure 1c as color overlays (same section as in Fig. 1a). After the Rayleigh's test for uniformity was applied, the pixels containing multiple crossing fibers were removed from the image (Fig. 1d). The algorithm correctly classified fibers against the noisy background and identified regions with unspecific orientations. Specifically, the feature detection operation distinguished between regions containing single, crossing, or no fibers at all. The distribution of orientations outputted by the template-matching algorithm was in accordance with the actual distribution of axonal fibers in the sample images, as evaluated by an expert anatomist (author J.A.). Although this retrospective evaluation does not prove that the algorithm would perform consistently in all situations, it is a good indication of the validity of the analysis in terms of underlying anatomy.

To demonstrate the reliability of the algorithm, we sampled three regions of the WM containing qualitatively different fiber populations. Figure 2 shows the results of the processing pipeline applied to these regions. The template-matching algorithm was applied to areas sampled from the corpus callosum (containing a single predominant fiber tract), corona radiata (where the tissue is populated by multiple crossing fibers), and the caudate nucleus (constituting predominantly the gray matter). The algorithm was successful in identifying regions with uniform fiber orientations, as well as regions populated by crossing fibers; thus, it was possible to resolve complex architectural patterns occurring even in very different conditions, reflecting WM geometry underlying specific anatomical regions of the brain (Fig. 2c).

Orientation glyphs were generated by drawing a histogram of orientation values (0–360) as a polar plot. The orientation values were collected from the proportion of pixels that show a single preferred orientation in the image sample (Fig. 2e–j). For each location, histograms were created using two different Rayleigh threshold values (0 and 0.8). A non-zero value of the Rayleigh threshold sharpened the orientation peak by rejecting spurious orientation values. In regions of crossing fibers (i.e., in the region of the corona radiata), the effect of this thresholding operation was especially pronounced (Fig. 2g, h). The resulting peaks in the orientation profiles were tight enough to allow the simultaneous detection of multiple fiber orientations for regions approaching the size of the templates.

The proposed algorithm provides the basis for quantitative analysis of a simple property, that is, axonal orientation. More complex properties, such as fiber crossing and kissing (juxtaposition), are complex architectonic features that can be detected based on the collection of multiple measurements provided by the algorithm. The threshold chooses pixels that are characterized by complex orientation profiles. The glyph representations can be used to detect crossing fibers either by examining the ratio of eigenvalues or by computing statistically independent components in the orientation density. Regions where the components of the glyphs that are orthogonal to the main detected orientation are also consistent are likely to be populated by parallel fibers; the smaller (shorter) these orthogonal components are, the closer the fibers, approaching juxtaposition (overlap) when the orthogonal component approaches zero. By creating orientation-dependent histograms over increasingly larger areas of tissue, it is possible to extrapolate the orientation structure at different levels of magnification; in other words, the analysis can be done at different scales (microscopically and macroscopically).

Discussion

We described an observer-independent method to measure nerve fiber distribution in stained histological sections of the brain. In this study, three consecutive iterations of the template-matching algorithm were employed using template sizes of 2, 4, and 8 pixels, respectively. Because the resolution of our images was 0.37 μm/pixel, these templates are valid for a range of fibers between 0.7 and 3 μm in diameter. We determined that this was the optimal range for detecting fibers in the WM regions selected for this study. Because the size of axonal fibers in the human WM ranges from 0.5 to 20 μm, the range of template thickness used in our image analysis protocol should be increased to capture the WM morphology exhaustively.

Because the analysis was conducted on stained tissue samples, potential artifacts that occur as a consequence of histological processing should be considered. These include staining inhomogeneity within the same section and differences in staining across different batches of sections that are processed separately. It is possible to control for these factors using specific equipment and protocols that afford high levels of consistency and reproducibility. In our case, the thickness of frozen tissue sections (which is the main parameter affecting observed staining density) is controlled by maintaining narrow ranges of temperature during the cutting process. Furthermore, when conducting analyses across multiple sections, that is, when examining the three-dimensional (3-D) course of specific fiber bundles or when comparing different subjects, all sections should be stained as a part of the same batch. These relatively straightforward solutions are the basis for reliable, large-scale bran mapping at the microscopic level.

The study was focused on demonstrating the ability to detect local differences in axonal architecture; however, an important issue to consider is how well the algorithm performs in classifying similar patterns in the same slice and in multiple sections. Repeatability is guaranteed by the fact that the method is automated, once the necessary parameters are established. Therefore, any eventual discrepancy in the results would be due to qualitative issues related to histological staining. Consistency of the results of the analysis is directly related to the quality of the histological material; it can therefore be increased by applying appropriate methods to maximize uniformity in the level of staining.

We performed image analysis on two-dimensional (2-D) images acquired from the histological samples. This poses two main limitations. First, the slides contain tissue slices that have a tangible thickness, even taking into consideration the shrinkage effect of staining and dehydration. Specifically, our histological material underwent significant thinning (from 70 to 15–20 μm) after treatment with alcohols and solvents. To obtain clear images of the tissue throughout the depth of the slice, microscope imaging was performed using an objective with relatively a low numerical aperture (NA) (and large depth of field). Therefore, most of the elements contained in the raster images were in focus. Nevertheless, the tissue sample may contain fibers that do not run parallel to the image plane, and further work is required to resolve the inclination (relative to the z-axis) of this population of fibers and to reconstruct axonal architecture within the thickness of the tissue. An obvious solution is to use higher magnification oil-immersion objectives (60× to 100×) as the latter also have higher NA ranges and narrow depth of field. In these conditions, it is possible to acquire registered stacks of images reproducing narrow optical layers through the tissue section where it is possible to trace the course of vertically oriented fibers running across multiple layers. In turn, this process potentially allows for reconstructing a 3-D orientation map from the results of 2-D analyses conducted with the same parameters at multiple levels, although in practice, this has yet to be demonstrated. Naturally, using higher-magnification and higher NA objectives also means minimizing the FOV considerably; this increases not only the time necessary for acquiring data, but also the computational demands and overall processing times. Ideally, the study would benefit from novel optical hardware that can afford macroscopic imaging with very high NA.

Secondly, depending on the plane of section applied to the brain specimen, there will be anatomical regions where the majority of the fibers run toward (normal to) the optical plane. Our method is not intended to resolve inclination angles. Nevertheless, a substantial length of moderately inclined fibers is detectable after the preprocessing step (image normalization) is completed. The orientation computed from these fibers represents only the 2-D component of the inclined fiber. It is difficult to provide the actual angular resolution with respect to the z-plane of our method, because this feature depends largely on the thickness and staining intensity of each individual fiber, the overall density of fibers in the sample region, and the level of background staining.

Filtering was used as a preprocessing step in our method to normalize the data with respect to local differences in image intensity and contrast. Interestingly, such decorrelating spatial filtering mimics the illumination-invariant response properties of simple cells in the primary visual cortex (Olshausen and Field, 1996). Even though the goal of the analysis was the detection and measurement of axons and fiber orientation, intensity and contrast values represent important parameters in determining the state of WM tissue in stained histological material (indeed, the intensity of staining after treatment with dyes such as Luxol Fast Blue is one of the major features examined in routine WM neuropathology). The method that we described also provides information on staining density, as this parameter can be extracted from the initial image normalization process. In any case, fiber orientation analysis should be combined with quantitative techniques that provide maps of complementary histological features that are relevant to WM anatomy and disease, such as myelination levels and the density of glia (Budde et al., 2011).

Knowledge of WM anatomy is necessary to calibrate the algorithm correctly. User input is necessary to set appropriate threshold levels and to define the number of iterations applied to different axonal diameters (fiber thickness). The analysis is practically user-independent beyond these initial calibration steps.

The range of threshold values is obtained using cross-covariance calculations, followed by a logistic function and the introduction of scaling parameter β. It could be argued that cross-correlation, applied directly to the templates and the real fibers, would be more efficient because cross-correlation values are naturally bounded between −1 and +1. However, our goal was to perform operations that could eventually be extended to very large areas of tissue; therefore, our emphasis was placed on high processing speed. Unlike cross-covariance, cross-correlation cannot easily be computed in Fourier space; therefore, it is a much slower operation overall.

We have not attempted to time the performance of the algorithm on very large samples, including the whole cross-sectional area of the brain. It should be noted that different CPU architectures and processing speed would affect the overall speed of analysis. Each giant histological section can be represented at 20× magnification by ∼40,000 image tiles. These tiles could potentially be batch-processed using the same parameters, assuming staining is homogeneous throughout the whole surface of the slice. The process could be repeated on multiple stacked sections, to sample orientations across the whole brain. While this is certainly an exciting prospect, a more immediate and practical application of the algorithm would be at the level of selected sample regions where it would be possible to demonstrate disease-related changes of the well-known WM regions and fiber tracts.

The application of the template-matching algorithm to biological samples from clinical cases with a known WM pathology might be useful to provide detailed characterizations of disease-related WM changes and could help the interpretation of noninvasive diagnostic data (Pierpaoli et al., 2001). MRI- and DTI-detectable lesions in the deep WM are significant biomarkers for several debilitating neurological conditions, such as multiple sclerosis (van Waesberghe et al., 1999) and HIV-related dementia (Ernst et al., 1999; Gongvatana et al., 2009); they also occur as a consequence of the normal process of aging (Fjell and Walhovd, 2010; Wahlund et al., 2001). DTI provides two main parameters as indicators of WM integrity. Mean diffusivity is expressed as the average of the three eigenvalues of the diffusion tensor, and it reflects the magnitude of water molecule diffusion in the tissue. Fractional anisotropy is the degree of directionality of water diffusion; this index is defined as a coefficient of variation of the eigenvalues (Basser et al., 1994; Pierpaoli et al., 1996). However, when considered separately, the eigenvalues reflect different microscopic phenomena. The main eigenvalue is called axial diffusivity (AD) and describes diffusion that occurs parallel to the axon fibers. The average of the second and third eigenvalues is referred to as radial diffusivity (RD); this is an indicator of diffusion perpendicular to the axonal fibers. A decrease in RD is associated with WM damage due to demyelination; conversely, changes in AD are likely to occur when axons are damaged because of secondary degeneration (such as in Wallerian degeneration). In view of these considerations, AD would be the parameter that would more closely correlate with the results of our analysis based on template matching. Areas of high AD would likely contain a high degree of fibers sharing the same orientation. More importantly, the structure of the glyphs obtained with our algorithm could help differentiate instances of low AD due to axonal disaggregation from low AD due simply to regions having a high degree of crossing fibers.

Robust (and scalable) measurement methods that can elucidate WM architecture at the microscopic level will play an increasingly important role in understanding brain maturation and neuropathogenetic phenomena underlying known MRI (and DWI) biomarkers of neurological disease.

Acknowledgments

The work was supported by two research grants from the National Eye Institute, R01 EY01835902 and ARRA R01 EY01835902S1 (Jacopo Annese, Principal Investigator), and a research grant from the National Institute for Mental Health R01MH084756 (Jacopo Annese, Principal Investigator). The template-matching algorithm was developed by Dr. Hauke Bartsch as a part of a comprehensive program conducted at The Brain Observatory that is aimed at providing formal computational descriptors for morphological and histological features in the human brain. The authors would like to thank the research staff of The Brain Observatory for the generation and maintenance of the histological archive from which the samples used in this study were acquired.

Author Disclosure Statement

No competing financial interest exists.

References

  1. Annese J. The importance of combining MRI and large-scale histology in neuroimaging studies of brain connectivity and disease. Front Neuroinform. 2012;6 doi: 10.3389/fninf.00013. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Armstrong RA. Quantitative methods in neuropathology. Folia Neuropathol. 2010;48:217–230. [PubMed] [Google Scholar]
  3. Basser PJ. Mattiello J. leBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson. 1994;103:247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
  4. Bielschowsky M. Die Silberimprägnation der Achsencylinder. Neurologisches Zentralblatt. 1902;13:579–584. [Google Scholar]
  5. Budde MD. Janes L. Gold E. Turtzo LC. Frank JA. The contribution of gliosis to diffusion tensor anisotropy and tractography following traumatic brain injury: validation in the rat using fourier analysis of stained tissue sections. Brain. 2011;134:2248–2260. doi: 10.1093/brain/awr161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bürgel U. Amunts K. Hoemke L. Mohlberg H. Gilsbach JM. Zilles K. White matter fiber tracts of the human brain: three-dimensional mapping at microscopic resolution, topography and intersubject variability. NeuroImage. 2005;29:1092–1105. doi: 10.1016/j.neuroimage.2005.08.040. [DOI] [PubMed] [Google Scholar]
  7. Chan J. Tsui E. Peh W. Fong D. Fok K. Leung K, et al. Diffuse axonal injury: detection of changes in anisotropy of water diffusion by diffusion-weighted imaging. Neuroradiology. 2003;45:34–38. doi: 10.1007/s00234-002-0891-y. [DOI] [PubMed] [Google Scholar]
  8. Ernst T. Chang L. Witt M. Walot I. Aronow H. Leonido-Yee M, et al. Progressive multifocal leukoencephalopathy and human immunodeficiency virus-associated white matter lesions in AIDS: magnetization transfer MR imaging. Radiology. 1999;210:539–543. doi: 10.1148/radiology.210.2.r99fe19539. [DOI] [PubMed] [Google Scholar]
  9. Fjell AM. Walhovd KB. Structural brain changes in aging: courses, causes and cognitive consequences. Rev Neurosci. 2010;21:187–221. doi: 10.1515/revneuro.2010.21.3.187. [DOI] [PubMed] [Google Scholar]
  10. Frigo M. Johnson SG. FFTW: An adaptive software architecture for the FFT. In Proceedings of the 1998 IEEE International Conference Acoustics Speech and Signal Processing; Seattle, WA, USA. 1998. pp. 1381–1384. [Google Scholar]
  11. Gongvatana A. Schweinsburg BC. Taylor MJ. Theilmann RJ. Letendre SL. Alhassoon OM, et al. White matter tract injury and cognitive impairment in human immunodeficiency virus infected individuals. J Neurovirol. 2009;15:187–195. doi: 10.1080/13550280902769756. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Horowitz B. The elusive concept of brain connectivity. NeuroImage. 2003;19:466–470. doi: 10.1016/s1053-8119(03)00112-5. [DOI] [PubMed] [Google Scholar]
  13. Hsu EW. Muzikant AL. Matulevicius SA. Penland RC. Henriquez CS. Magnetic resonance myocardial fiber-orientation mapping with direct histological correlation. Am J Physiol Heart Circ Physiol. 1998;274:H1627–H1634. doi: 10.1152/ajpheart.1998.274.5.H1627. [DOI] [PubMed] [Google Scholar]
  14. Kielar C. Sawiak SJ. Navarro Negredo P. Tse DHY. Morton AJ. Tensor-based morphometry and stereology reveal brain pathology in the complexin1 knockout mouse. PLoS One. 2012;7:e32636. doi: 10.1371/journal.pone.0032636. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kleinfeld D. Bharioke A. Blinder P. Bock DD. Briggman KL. Chklovskii DB, et al. Large-scale automated histology in the pursuit of connectomes. J Neurosci. 2011;31:16125–16138. doi: 10.1523/JNEUROSCI.4077-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Leergaard TB. White NS. de Crespigny A. Bolstad I. D'Arceuil H. Bjaalie JG, et al. Quantitative histological validation of diffusion MRI fiber orientation distributions in the rat brain. PLoS One. 2010;5:e8595. doi: 10.1371/journal.pone.0008595. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Mardia KV. Jupp PE. Directional Statistics. West Sussex, England: John Wiley and Sons, Ltd; 2000a. pp. 15–17. 52–53. [Google Scholar]
  18. Mardia KV. Jupp PE. Directional Statistics. West Sussex, England: John Wiley and Sons, Ltd; 2000b. pp. 94–99. [Google Scholar]
  19. Merker BH. Hess DT. Technical modifications of Gallyas' stain for myelin. J Neurosci Methods. 1983;8:95–97. doi: 10.1016/0165-0270(83)90055-9. [DOI] [PubMed] [Google Scholar]
  20. Olshausen BA. Field DJ. Emergence of simple cell receptive field properties by learning a sparse code for natural images. Nature. 1996;381:607–609. doi: 10.1038/381607a0. [DOI] [PubMed] [Google Scholar]
  21. Pierpaoli C. Barnett A. Pajevic S. Chen R. Penix LR. Virta A. Basser P. Water diffusion changes in Wallerian degeneration and their dependence on white matter architecture. Neuroimage. 2001;13:1174–1185. doi: 10.1006/nimg.2001.0765. [DOI] [PubMed] [Google Scholar]
  22. Pierpaoli C. Jezzard P. Basser PJ. Barnett A. Di Chiro G. Diffusion tensor MR imaging of the human brain. Radiology. 1996;201:637–648. doi: 10.1148/radiology.201.3.8939209. [DOI] [PubMed] [Google Scholar]
  23. Scollan DF. Holmes A. Winslow R. Forder J. Histological validataion of myocardial microstructure obtained from diffusion tensor magnetic resonance imaging. Am J Physiol. 1998;275:H2308–H2318. doi: 10.1152/ajpheart.1998.275.6.H2308. [DOI] [PubMed] [Google Scholar]
  24. Sporns O. Tononi G. Kötter R. The human connectome: a structural description of the human brain. PLoS Comput Biol. 2005;1:e42. doi: 10.1371/journal.pcbi.0010042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. van Essen DC. Ugurbil K. Auerbach E. Barch D. Behrens TE. Bucholz R, et al. The human connectome project: a data acquisition perspective. NeuroImage. 2012;62:2222–2231. doi: 10.1016/j.neuroimage.2012.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. van Waesberghe JH. Kamphorst W. De Groot CJ. van Walderveen MA. Castelijns JA. Ravid R, et al. Mapping of fiber orientation in human internal capsule by means of polarized light and confocal scanning laser microscopy. Ann Neurol. 1999;46:747–754. [Google Scholar]
  27. Wahlund LO. Barkhof F. Fazekas F. Bronge L. Augustin M. Sjögren M, et al. A new rating scale for age-related white matter changes applicable to MRI and CT. Stroke. 2001;32:1318–1322. doi: 10.1161/01.str.32.6.1318. [DOI] [PubMed] [Google Scholar]
  28. Wedeen VJ. Rosene DL. Wang R. Dai G. Mortazavi F. Hagmann P, et al. The geometric structure of the brain fiber pathways. Science. 2012;335:1628–1633. doi: 10.1126/science.1215280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. West MJ. Design-based stereological methods for counting neurons. Prog Brain Res. 2002;135:43–51. doi: 10.1016/S0079-6123(02)35006-4. [DOI] [PubMed] [Google Scholar]

Articles from Brain Connectivity are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES