Investigating Effective Brain Connectivity from fMRI Data: Past Findings and Current Issues with Reference to Granger Causality Analysis

Abstract

Interactions between brain regions have been recognized as a critical ingredient required to understand brain function. Two modes of interactions have held prominence—synchronization and causal influence. Efforts to ascertain causal influence from functional magnetic resonance imaging (fMRI) data have relied primarily on confirmatory model-driven approaches, such as dynamic causal modeling and structural equation modeling, and exploratory data-driven approaches such as Granger causality analysis. A slew of recent articles have focused on the relative merits and caveats of these approaches. The relevant studies can be classified into simulations, theoretical developments, and experimental results. In the first part of this review, we will consider each of these themes and critically evaluate their arguments, with regard to Granger causality analysis. Specifically, we argue that simulations are bounded by the assumptions and simplifications made by the simulator, and hence must be regarded only as a guide to experimental design and should not be viewed as the final word. On the theoretical front, we reason that each of the improvements to existing, yet disparate, methods brings them closer to each other with the hope of eventually leading to a unified framework specifically designed for fMRI. We then review latest experimental results that demonstrate the utility and validity of Granger causality analysis under certain experimental conditions. In the second part, we will consider current issues in causal connectivity analysis—hemodynamic variability, sampling, instantaneous versus causal relationship, and task versus resting states. We highlight some of our own work regarding these issues showing the effect of hemodynamic variability and sampling on Granger causality. Further, we discuss recent techniques such as the cubature Kalman filtering, which can perform blind deconvolution of the hemodynamic response robustly well, and hence enabling wider application of Granger causality analysis. Finally, we discuss our previous work on the less-appreciated interactions between instantaneous and causal relationships and the utility and interpretation of Granger causality results obtained from task versus resting state (e.g., ability of causal relationships to provide a mode of connectivity between regions that are instantaneously dissociated in resting state). We conclude by discussing future directions in this area.

Introduction

The major goal of functional magnetic resonance imaging (fMRI) studies is to understand brain function. Since its inception in the early nineties, fMRI has primarily focused on the spatial localization of brain function (Friston et al., 1994). Accordingly, distinct brain regions are assumed to be specialized for distinct functions. Although this model has provided tremendous insights into the workings of the brain, higher-level functions that require coordinated action of many brain areas have not been sufficiently well explained by this model. For example, a flashing checkerboard will activate the primary visual area, implying that this area encodes basic intensity information in the input image. However, an ecologically valid, complex natural scene that contains people and their associated motions and emotions may activate a swathe of regions such as primary/secondary visual area, fusiform, middle temporal, and amygdala. Where exactly are all these aspects of the brain activity bound together to form a unified experience? This question has necessitated an alternate model of brain function based on distributed information processing. This model does not exclude the spatial localization model. Rather, it hypothesizes that spatially localized activated regions do encode basic properties of internally or externally generated inputs, and that the interactions between these regions contribute to the encoding of more complex properties, giving rise to a repertoire of experiences.

Interactions between regions can be of two types. First, information flow (monosynaptic, polysynaptic, or otherwise) leads to a causal relationship between activities in different regions. For example, it is well documented that visual stimuli (e.g., human faces) from the retina travel through the optic nerve to the lateral geniculate nucleus, primary visual area V1, higher-order visual area V5, and fusiform area, in that order (Kandel et al., 2000). The evoked potentials measured through electroencephalography (EEG) source localization seem to have a larger latency in the downstream areas as compared to the upstream ones (Russo et al., 2001; Sadeh et al., 2008). This suggests a causal relationship between activities in these brain areas. Second, general network level synchronization may lead to simultaneous and coherent activity in many brain regions. For example, EEG synchronization in the alpha-, beta-, theta-, and-gamma bands has been associated with memory, sensory integration, attention, and consciousness, respectively (Sauseng and Klimesch, 2008).

Friston referred to the causal and synchronous relationships derived from fMRI data as effective connectivity (EC) and functional connectivity (FC) (Friston, 1995), respectively. FC has been extensively studied, primarily using the correlation coefficient, in resting state (Biswal et al., 1995) and also in task-based analyses using the concept of psychophysiological interactions (O'Reilly et al., 2012). On the other hand, EC has been extensively applied to task-based studies (Deshpande et al., 2009; Friston et al., 2003; McIntosh and Gozales-Lima, 1994; Roebroeck et al., 2005) and to a lesser degree to resting-state data (Deshpande et al., 2011; Liao et al., 2010; Sridharan et al., 2008). Methodologically speaking, most, if not all, FC analyses employ the correlation coefficient or independent component analysis while wide variability exists in EC analyses. Specifically, EC studies have employed probabilistic/Bayesian methods (Patel et al., 2006; Zheng and Rajapakse, 2006), dynamic causal modeling (DCM) (Friston et al., 2003), structural equation modeling (SEM) (Zhuang et al., 2005), and autoregressive modeling/Granger causality analysis (Abler et al., 2006; Deshpande et al., 2008, 2009; Roebroeck et al., 2005; Sathian et al., 2011). The variability in the methodology used to investigate EC stems from the fact that causal influence is a diverse concept with multiple interpretations (as opposed to the comparatively straightforward notion of synchronization in FC).

Many previous studies, including some of our group, have weighed in on the relative merits and caveats of these methods (Bressler and Seth, 2011; Roebroeck et al., 2009; Valdes-Sosa et al., 2011) for fMRI. Most of these studies address issues unique to fMRI. For example, an fMRI time series is modeled as a coarse sampling of the byproduct of the convolution of a hidden neuronal variable with the hemodynamic response function (HRF). Consequently, what could be the effect of non-neuronal spatial variability of the shape of HRF and slow sampling rate on our ability to infer causal relationships between hidden neuronal variables (defined as neuronal causality) from corresponding fMRI time series? It is evident that loss of neuronal timing information in fMRI is detrimental to EC analysis, but the bounds of fMRI acquisition parameters and postprocessing methodologies that might overcome the apparent fallacies of fMRI for inferring neuronal causality are still an open matter of debate in these studies. These studies can be classified into simulations, theoretical developments, and experimental investigations. In the first part of this review, we will consider each of these themes and critically evaluate their arguments, with specific emphasis on Granger causality analysis. In the second part, we will consider additional major current issues in connectivity analysis—hemodynamic variability across brain regions and subjects, sampling, instantaneous versus causal relationship, and task versus resting states—and highlight some of our own previous work and discuss future directions.

Background Information

Granger causality basics

Granger causality is based on the principle that directional causal influence from time series A to time series B can be inferred if past values of time series A help predict the present and future values of the time series B (Granger, 1969). Given k time series X(t)=[x₁(t)×₂(t)…x_k(t)], the multivariate vector autoregressive (MVAR) of order p is

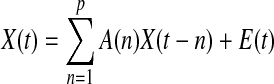(1)

where A(n) is the coefficient of the model as shown in Eq. (2), and E(t) is the model error.

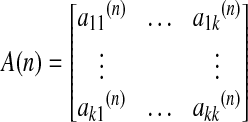(2)

Multivariate Granger causality between the time series can be inferred from the model coefficients (Kaminski et al., 2001). The estimation of the coefficients can also be achieved in the frequency domain that gives rise to several metrics, including directed transfer function and partial directed coherence (Kus et al., 2004). Bivariate and conditional Granger causality between time series can also be obtained using Geweke's formulation. Accordingly, the total linear dependence between time series can be split into an instantaneous part and a causal part, which can be estimated using the error variances of the restricted and unrestricted VAR models, rather than model coefficients (Geweke, 1982). These two types of approaches, that is, based on model coefficients or error variances, have been shown to be equivalent (Deshpande et al., 2010b; Kaminski et al., 2001).

Hemodynamic variability basics

When fMRI time series are used in the MVAR model of Eq.1 to infer neuronal causality, the characteristics of the HRF, which defines the relationship between neuronal activity and observed fMRI signal, become an important consideration. It has been demonstrated that the shape and magnitude of the HRF vary across brain regions and individuals (Aguirre et al., 1998; Handwerker et al., 2004; Silva and Koretsky, 2002). Only a part of this variance is attributable to neuronal activity while various other factors such as vasculature differences, baseline cerebral blood flow, hematocrit, alcohol/caffeine/lipid ingestion, partial volume imaging of veins, global magnetic susceptibilities, slice timing differences, and pulse or respiration differences (Buxton, 2002; Handwerker et al., 2004; Levin et al., 1998, 2001; Noseworthy et al., 2003) are responsible for the spatial variability of the HRF. A large portion of HRF variability is attributable to vasculature differences, which are structural, and hence the variability is also spatial. This spatial variability can be expressed in terms of differences in time to onset, time to peak, and peak width. Handwerker and associates (2004) found that the time to peak had a spatial variability of about 2 s under normal physiological conditions. On the other hand, others have found larger spatial differences when dealing with pathological populations (David et al., 2008). When referring to HRF variability in this article, we are almost always referring to its spatial variability as it can be of vascular, non-neuronal origin. This can potentially confound Granger causality obtained from fMRI data, because it assumes that any lag in fMRI time series is neuronal in origin (Deshpande et al., 2010c). According to the Balloon model, temporal variability of HRF, unlike its spatial variability, is mostly driven by underlying neuronal processes (Buxton, 2002). Later on, we make a reference to HRF's temporal variability in the context of using its neuronal origin to infer neuronal causality from fMRI.

A Critical Look at Previous Work

Simulations

It is difficult to establish the ground truth in an experimental setup; for example, suppose we want to know whether visual stimulation causes V1 to influence V3 using fMRI. The ground truth is whether stimulus-induced action potentials in V1 neurons actually travel down to V3 neurons, causing depolarization of their soma, opening voltage-gated channels in them, and triggering an action potential. How do we measure this ground truth? One could use simultaneous EEG or MEG and fMRI, since the former is a marker of electrical activity (but then, it suffers from poor spatial resolution). A more reliable way would be to perform invasive electrical recordings in animals simultaneously with fMRI. Due to the technical challenges involved in doing such an experiment, many researchers have taken recourse to simulations.

Friston et al. have used simulated systems to illustrate the efficacy of DCM and its variants in their various reports (Friston et al., 2003; Li et al., 2011). Similarly, whenever a new method is proposed, it is invariably evaluated by simulations. Examples include Granger causality analysis and its variants (Deshpande et al., 2010b; Kus et al., 2004; Roebroeck et al., 2005), multivariate dynamical system (MDS) model (Ryali et al., 2011), and Bayes net (Ramsey et al., 2010; Zheng and Rajapakse, 2006). Others have used a single simulation to test different models (Smith et al., 2011; Witt and Meyerand, 2009).

Our contention is that there are subtle (and sometimes gross) differences in the way synthetic data are simulated, and these differences can lead to vastly discrepant results. We present two examples of specific cases of differing evaluations and then discuss a general approach for resolving such differences in results. In the first example, Smith et al. used a generative biophysical model without an explicit delay and found that Patel's τ (Patel et al., 2006) performed the best, and Granger causality analysis performed worst. This is not surprising because the former is not based on a delay assumption while the latter is. On the other hand, Roebroeck and colleagues (2005) had explicit delays in the synthetic data and found excellent results with Granger causality analysis. Also, in a recent simulation study, Wen and colleagues showed a monotonic relationship between neural-level Granger causality and fMRI-level Granger causality (Wen et al., 2012), thus contradicting the findings of Smith and colleagues.

In the second example, we discuss how seemingly reasonable assumptions made in simulations are challenged. In the face of experimental data showing that the shape of the hemodynamic response varied in a random manner across different brain regions and subjects (Aguirre et al., 1998; Handwerker et al., 2004), we investigated the effect of spatial hemodynamic variability on Granger causality analysis in single subjects and found that causality results were indeed affected by hemodynamic variability under certain conditions (Deshpande et al., 2010c). Schippers and colleagues (2011) showed that such effects were minimized in multisubject group inference obtained from Granger causality analysis. This follows from the observation that if the variability of the hemodynamic response was indeed random (or at least pseudorandom) while the underlying neuronal lag was systematic, the effect of neuronal causality should rise above that of vascular-driven variability of the HRF in group-level inference. This follows from the simple fact that averaging enhances a systematic effect while decreasing a random (or pseudorandom) effect. Thus, group-level Granger causality inference, in the vast majority of cases, is likely to be driven by underlying neuronal causality rather than hemodynamic variability. The Schippers' study was criticized in a follow-up article where the authors speculated that hemodynamic variability could be systematic (Smith et al., 2012).

The instances of divergence of opinion from different simulations and the ensuing circular arguments indicate that simulations are bounded by assumptions and simplifications made by the simulator. The researchers themselves will defend that their simulation methodology best represents reality, but when we have multiple studies claiming the same, it is an exercise in futility. For example, earlier simulations based their conclusions upon synthetic fMRI data with TR=2s, which was common then. However, with new acquisition techniques such as multiband echo-planar imaging (EPI), subsecond TRs are likely to become routine in future (Feinberg et al., 2010). Therefore, it is not possible to generalize the conclusions of such simulations. Given these considerations, it is unfortunate that conclusions drawn from simulation studies are being viewed by the community as definitive verdicts for whether a method works or not. Our intention is not to criticize simulations per se, but to underscore the point that they ought to be interpreted with their limitations in mind. Further, simulations can guide us toward improvements in the data acquisition methodology that we need to strive for, to make these methods work better.

Theoretical developments

Most of the theoretical arguments have called for a grand unified model for assessing directional brain connectivity from fMRI data. This prospect is not implausible. Barnett and colleagues (2009) have demonstrated the equivalence of causal models based on prediction and resolution of uncertainty, for Gaussian variables. For example, Granger causality modeling is based on the predictability of the future of time series Y from the past/present of time series X for inferring that X causes Y. Causality can also be framed in probabilistic terms, that is, whether Y disambiguates X, which is captured by transfer entropy. Barnett et al. mathematically demonstrated that Granger causality and transfer entropy are equivalent for Gaussian variables. Chen and colleagues (2011) have shown that there are advantages in using a unified model that incorporates both SEM and autoregressive models as opposed to using either of them individually. We have recently demonstrated a synthesis of Granger causality analysis and Patel's τ (Patel et al., 2006), wherein a large number of activated regions were initially considered in the model, and the network was reduced to a smaller size based on concurrent evidence from both the methods (Sathian et al., 2011). Recent implementations of Granger causality analysis have formulated the problem as a state-space model, while simultaneously incorporating hemodynamic deconvolution using Kalman filters or variational Bayes (as in MDS) (Ryali et al., 2011). These efforts bring Granger causality modeling closer to DCM.

Likewise, notwithstanding the recent criticism of DCM for combinatorial explosion (Lohmann et al., 2012), improvements to DCM have made the method better than what was initially proposed. Most notable advances are stochastic DCM (Li et al., 2011) and more efficient ways of searching for larger model spaces (Friston et al., 2011), that make DCM more exploratory than was initially proposed, while simultaneously recognizing the fact that completely deterministic models are likely too simplistic to model a system as complex as the brain. The hope is that this cross-fertilization of ideas will ultimately lead to a method most suitable for fMRI, and that such an end product is likely to be substantially different from any of the models initially proposed.

Experimental studies

Contrary to popular opinion, efforts to recover neuronal timing from fMRI did not start with Granger causality analysis. Menon and coworkers showed way back in 1998 that by fitting a linear function to the early rise of the blood oxygenation level dependent (BOLD) response, timing differences of the order of 125 ms can be recovered (Menon et al., 1998). Subsequently, different techniques such as magnetic resonance inverse imaging (Lin et al., 2008), Fourier-based methods, time to half-peak, mental chronometry, and temporal derivative of the canonical HRF have been employed for detecting neuronal timing differences of the order of 100–300 ms from fMRI [for a review see (Menon, 2012)]. A validation study by David and associates (2008) showed that in an animal model with a pathologically deviant hemodynamic response, Granger causality analysis was able to infer the correct direction of neuronal causality when the hemodynamic response was deconvolved, and those results agreed with that of DCM. Most recently, Rogers and associates showed in a visual stimulus-onset asynchrony experiment performed at high field (7T) that Granger causality analysis can detect neuronal timing differences down to 112 ms with TRs of 250 and 1000 ms (Katwal et al., 2009; Rogers et al., 2010). In a follow-up study, using a fast TR of 250 ms and voxel size of 1×1×2 mm³, they have shown that using data-driven selection of activated voxels using self-organizing maps, as opposed to GLM, neuronal timing difference as low as 28 ms can be resolved with fMRI even without hemodynamic deconvolution (Katwal et al., 2011).

In the face of mounting experimental evidence that it is possible to infer neuronal timing differences from Granger causality analysis under certain experimental conditions, it is surprising and indeed baffling that a sweeping, generalized negative judgment is being rendered against Granger causality modeling solely based on simulations [e.g., Smith and associates (2011) claim that lag-based methods do not work in fMRI based on their simulations]. Such sweeping and generalized judgments are misleading many fMRI researchers. Our intention here is to express a more balanced view of Granger causality modeling to inform the community that using a well-designed experiment and properly performed analysis, Granger causality modeling can infer neuronal causality in a data-driven way. Of course, further methodological development and validation are needed to make EC analysis (either using Granger causality analysis or other confirmatory models such as SEM/DCM or some combination of both) as reliable as activation analysis. However, given the experimental evidence to date, it is worth pursuing this goal further rather than abandon it based on one set of simulations.

Interplay between theory, simulation, and experiment

Before concluding this section, we provide a general comment on theory, simulation, and experiment, and the interplay between them. A mathematical theory based only on axiomatic truths is usually sought, but is often not available when modeling reality. Therefore, theoretical models of reality often have underlying assumptions that are only approximately valid. Furthermore, even if such a theory is available, analytical solutions are not readily available, and simulations are often conducted. Simulations are used to test specific realizations of the theoretical model and make predictions on what one might observe in reality. Finally, experiments play out those specific realizations in reality and provide feedback on whether the underlying assumptions are realistic in the first place. If not, the cycle continues to refine the theory and simulation framework to match experimental results. An example of this cycle in neuroimaging is the investigation into the basis of the hemodynamic response. Initial models of the HRF were based on gamma-functions (Friston et al., 1994), which was then refined into a more biophysical Balloon model (Friston et al., 2000), which simulated the BOLD response well and was confirmed by experimental data. However, recent experimental evidence shows that different aspects of neural activity can drive oxygen metabolism and blood flow in parallel, which necessitates some modifications to the Balloon model (Buxton, 2012).

Current Issues in EC Analysis

Hemodynamic variability

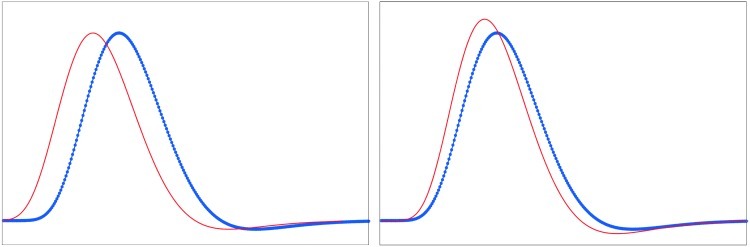
In their initial demonstration of the application of Granger causality analysis to fMRI data, Roebroeck and colleagues (2005) cautioned that spatial variability of the hemodynamic response had the potential to confound Granger causality estimates obtained from fMRI and hence proposed a solution that if connectivity varied as a function of experimental context, then it cannot be because of spatial hemodynamic variability. This follows from the fact that spatial hemodynamic variability is an outcome of structure, and hence HRF characteristics must be stationary across time. This point has been less appreciated in the subsequent discussion on spatial HRF variability (Friston, 2009; Smith et al., 2011; Valdes-Sosa et al., 2011). In our single-subject simulations, we demonstrated that when the spatial variability in the HRF is due to different rise times and time-to-peaks (Fig. 1), it alters the shape of the HRF rather than introduces a simple time shift (Fig. 1). In this case, the neuronal timing is not totally lost in the fMRI signal by the HRF convolution. Consequently, given fast sampling and spatial hemodynamic variability within the range reported in previous experimental studies (Handwerker et al., 2004), neuronal causality of the order of hundreds of milliseconds could be detected using Granger causality analysis of fMRI (Deshpande et al., 2010c). Subsequently, Schippers and associates (2011) showed that if the spatial variability of the hemodynamic response was indeed random (or at least pseudorandom) while the underlying neuronal lag was systematic, then the effect of neuronal causality as inferred from Granger causality analysis must dominate that of vascular-driven spatial variability of the HRF in a group-level inference. In spite of these observations, pathological conditions can create extreme variations in hemodynamic response that is outside the normal range of spatial variability (David et al., 2008).

FIG. 1.

Examples of HRF variability: The red and blue curves represent two different HRFs. Left: the blue HRF is time shifted from the red HRF which preserves the shapes of the HRFs; Right: the blue HRF is having a different rise time which alters its shape, but there is no time shift with respect to the red HRF

There are many strategies available to deal with spatial hemodynamic variability. The first set of methods exploits one property of spatial hemodynamic variability, namely that it arises from structural differences, and hence is invariant across time. Based on this property, Roebroeck and colleagues pointed out that when Granger causality is modulated by different experimental conditions, it cannot be confounded by spatial hemodynamic variability. We have applied this concept in a novel way in our recent work, wherein we obtained dynamic Granger causality (Sato et al., 2006) as a function of time and investigated whether the dynamic variations in causality correlated with the exogenous input (Lacey et al., 2011). Such correlation cannot be the result of spatial hemodynamic variability as argued below.

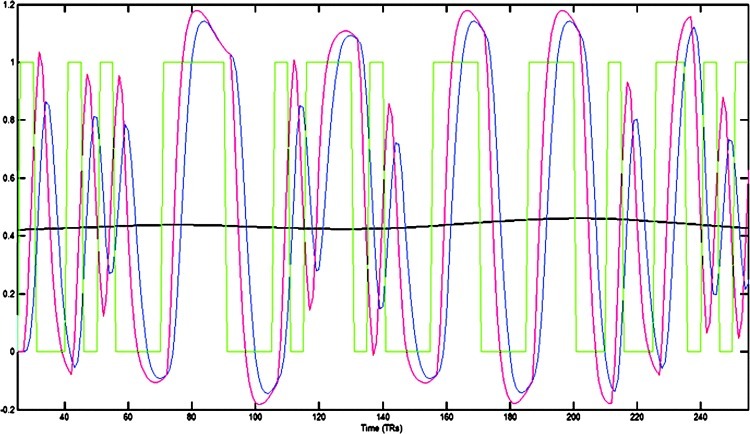
Consider the stimulus paradigm in a subject shown in Figure 2 (green line) and the product of the convolution of two different HRFs (red and blue lines) and the stimulus paradigm, with timing difference of 2.5 s between the HRF functions. It can be seen that, given the temporally constant timing difference, dynamic Granger causality measured using an adaptive MVAR model (Lacey et al., 2011; Sato et al., 2006) remains relatively constant around 0.4 (black line). We also verified using the Wald test that dynamic causality between the red and blue time series in Figure 2 did not significantly vary across time (p>0.05). This indicates that dynamic Granger causality can covary with the external stimulus only if it is driven by underlying neuronal modulation. Therefore, stimulus-dependent temporal variability of causality cannot be a spurious consequence of vascular-driven spatial variability of the hemodynamic response.

FIG. 2.

Example of task paradigm with different HRF convolutions (see text for details). Green line: the stimulus paradigm in a subject; red line: the product of the convolution of a HRF1 with the stimulus paradigm; blue line: the product of the convolution of a different HRF2 and the stimulus paradigm, with HRF2 lagging HRF1 by 2.5s; black line: dynamic Granger causality between red and blue lines.

The second set of methods relies on the blind deconvolution of the hemodynamic response from the observed fMRI signal. Examples include dynamic expectation maximization (Friston et al., 2008), variational Bayes (Ryali et al., 2011), and cubature Kalman filter (Havlicek et al., 2011). All of these methods rely on probabilistic estimation of the HRF based on priors obtained from the biological plausibility of the parameters in the model. These methods, particularly the cubature Kalman filter approach (Havlicek et al., 2011), seem to give excellent estimates of the underlying neuronal variables in simulated systems. Briefly, this method uses a forward-pass Kalman filter and a backward-pass Rauch–Tung–Striebel smoother for estimating the HRF parameters, hidden states, and the underlying neuronal input. Given that the HRF parameters in this method are derived from the Friston-Buxton model, BOLD nonlinearities are not present in the deconvolved time series (Friston et al., 2000). The implementation of Havlicek and colleagues (2011) is an efficient square-root formulation of the cubature Kalman filter algorithm (Arasaratnam and Haykin, 2008) in the context of blind deconvolution of the hemodynamic response. Although experimental validation of these methods using simultaneous electrophysiological data is yet to be carried out, they provide a way of deconvolving the HRF and obtaining underlying neuronal variables that can be subsequently subjected to Granger causality analysis.

Sampling

Problems arising from slow sampling in fMRI are not limited to connectivity analysis. Rather, the poor temporal resolution of fMRI makes it harder to accurately capture the time course of activation even in traditional fMRI experiments. However, slow sampling exacerbates the difficulties in estimating relationships between time series that are nonsynchronous in nature. We will revisit this issue from a theoretical perspective in the next section while discussing instantaneous-versus-causal relationships.

On the experimental side, the advent of fast imaging techniques will go a long way in increasing the validity of fMRI-based EC methods. Notable data acquisition strategies with increased temporal resolution include multiband EPI (Feinberg et al., 2010), echo–volume imaging (Posse et al., 2012), magnetic resonance inverse imaging (Lin et al., 2008), and MR-encephalography (Zahneisen et al., 2011). Among these, multiband EPI seems to be most exciting as it imposes relatively little collateral cost (unlike other methods where spatial resolution and/or coverage is compromised), and yet is able to achieve subsecond TRs (as low as 200–400 ms with whole-brain coverage for 3-mm isotropic voxels). Such sampling periods may capture neuronal timing differences, which also happen to occur in the hundreds of millisecond range. For example, EEG studies have shown that visual evoked potentials are seen in the primary visual cortex around 100 ms poststimulus (Foxe and Simpson, 2002; Sadeh et al., 2008). Other event-related potential (ERP) signals such as the P300 have neuronal latencies that are 100s of milliseconds. We showed in our simulations that increasing temporal resolution of fMRI, such as shortening the TR to that comparable to neuronal latency, significantly improves the accuracy of Granger causality analysis (Deshpande et al., 2010c). With multiband EPI, we will be able to use Granger causality analysis to capture the EC underlying many neuronal signals on the scale of 100 ms, such as the P300, using fMRI.

It is noteworthy that fast sampling alone cannot capture neuronal causality of 100s of milliseconds. Rather, the smoothing of the neuronal response by the HRF imposes an inherent constraint on EC analysis of raw fMRI data. Therefore, to infer neuronal causalities of 100s of milliseconds, it is desirable to perform hemodynamic deconvolution in addition to fast sampling.

Some researchers have suggested that neuronal latencies are governed by axonal conduction delays, which are of the order of 10s of milliseconds, making them hard to infer from fMRI (Smith et al., 2011). We would like to argue otherwise. First, it takes more than axonal conduction for activity in one neuron to induce activity in another. Most neurons have chemical synapses (exceptions are gap junctions, which are very rare in the human brain), which act much slower compared to electrical activities such as action potentials. Also, ionic transport across dendrites, which eventually give rise to the depolarizing voltage in the soma of neurons, is also much slower than action potentials. Second, most of the connectivity investigations involve distributed networks containing regions that are connected by polysynaptic pathways. Taking these factors into account, it is likely that many sensory neuronal processes have latencies around 75–200 ms (Russo et al., 2001; Sadeh et al., 2008) and cognitive processes around 100–500 ms (Kutas et al., 1977). Of course, certain slow neuronal processes such as the slow cortical potential could have latencies up to 1000 ms (He and Raichle, 2009). Therefore, subsecond TRs achievable using fast imaging techniques are sufficient to capture a large class of neuronal latencies.

Smith and colleagues argue against using ERP latencies as a marker of neuronal latencies as follows–“Event-related potentials are often reported as being a few hundred milliseconds, but this is generally the delay between external stimulation and the response generated by a higher cognitive area; hence, this period will typically have involved communication between several distinct functional units, and is unlikely to reflect a single network ‘connection’ that is of interest for investigation with imaging-based network modeling.” Their argument is subject to question for the following reasons. For instance, consider a syntactic ERP experiment wherein the potential in V1 was observed at 100 ms poststimulus and in the parietal cortex around 500–600 ms (Gouvea et al., 2010). In this case, a network connection from V1 to the parietal cortex has an underlying neuronal delay of around 400–500 ms and is amenable to being investigated using Granger causality analysis of fMRI. This does not mean that monosynaptic connections with latencies <100 ms do not exist in the brain. They do, and it will take a carefully designed experiment, including strategies such as faster sampling and/or high field/SNR, to detect them using any EC method employing fMRI data without deconvolution, including the ones promoted by Smith and colleagues. Therefore, targeted criticism of Granger causality modeling in this context is not fully justified.

Instantaneous versus causal relationship

In the EEG literature, instantaneous and causal relationships have specific neurobiological correlates. For example, instantaneous relationships are referred to as synchronization, which is purported to support certain neural processes (such as seizures, event-related synchronization in specific frequency bands, and long-term potentiation) (Cantero and Atienza, 2005; Pfurtscheller and Lopes da Silva, 1999). On the other hand, causal relationships are supposed to model the underlying neuronal delay and to characterize information transfer. For example, the visual-evoked potential for a visual stimulus-based language experiment in V1 occurs around 100 ms, while syntactic ERP over parietal electrodes occurs around 500–600 ms, which is commonly referred to as the P600. This reflects a causal inference from the visual to the parietal area that underlies the propagation of low-level visual activity to a higher-level multimodal area required for language comprehension (Gouvea et al., 2010).

In fMRI literature, the underlying meaning of instantaneous and causal relationship has been a matter of debate. The effect of temporal aggregation and sampling of time series on instantaneous and causal relationships between them was systematically investigated by Wei way back in 1982 (Wei, 1982). Accordingly, let x and y be the time series that have a unidirectional causal relationship between them (x→y). Let X_m(t)=x(mt) and Y_m(t)=y(mt) be the down-sampled versions of x(t) and y(t). It can be shown that the relationship X_m→Y_m is preserved, although with a reduced magnitude. On the other hand, let us define temporally aggregated time series X(T) and Y(T) such that

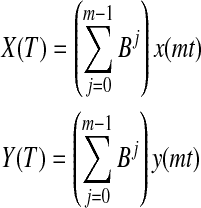where the operator B shifts the operand by j, and T=mt is the amount of aggregation. In this case, Wei demonstrated that not only the causal influence between X(T) and Y(T) becomes bidirectional, but also the instantaneous relationship between them became nonzero (which is zero in the unaggregated time series). The transformation from neuronal activity to fMRI could be modeled as a sequence of aggregation (hemodynamic convolution) and sampling (MR readout) operations. Therefore, not all synchronous relationships between fMRI time series can be attributed to neuronal synchronicity alone. Therefore, for instantaneous relationships between fMRI time series to be attributed to neuronal synchronicity, hemodynamic deconvolution, that is, removing temporal aggregation, is imperative. It is very surprising that this aspect has not been appreciated or debated in the fMRI community, because instantaneous relationships between fMRI time series seem to be robust, reproducible, and of clinical and scientific value.

From Wei's model, it is evident that hemodynamic deconvolution is highly desirable when inferring neuronal causality from fMRI time series. In addition, his model also reaffirms the fact that the detrimental effect of slow sampling in Granger causality analysis of fMRI can be significantly lessened through deconvolution. With new fast imaging techniques such as multiband EPI (Feinberg et al., 2010) allowing whole-brain coverage with subsecond TRs, it would be interesting to experimentally test the effect of sampling on Granger causality analysis of fMRI to verify Wei's predictions.

In a series of simulations (Deshpande et al., 2010b) and experiments (Deshpande et al., 2010a, 2010b), we demonstrated that a purely instantaneous relationship at the neuronal level can manifest as both an instantaneous and causal relationship at the fMRI level. Combining the results of this study with Wei's demonstration (above), it is apparent that a causal relationship at the neuronal level could manifest as both an instantaneous and causal relationship at the fMRI level. This ambiguity is introduced primarily due to the aggregation of phase relationships at the fMRI level, which we term leakage.

We proposed to model both instantaneous and causal relationships simultaneously in a single model of fMRI time series and termed the resulting causality as correlation-purged Granger causality (Deshpande et al., 2010b). Others such as Kim and associates (2007) have used a unified SEM-AR model to separate contemporaneous and causal influences. Although their contemporaneous influence obtained from SEM is not the same as the instantaneous zero-lag relationship we obtained, their model falls within the spirit of our recommendation. Unified models of correlation and causality on neuronal latent variables obtained from hemodynamic deconvolution (instead of raw fMRI time series) seem to be the best available option for inferring neuronal synchronicity versus causal influence from fMRI data.

Task versus resting state

The discussion in the previous section was generic, but is also very relevant to the consideration of task versus resting state. EC methods have been primarily applied to task data (Deshpande et al., 2008; Hampstead et al., 2011; Krueger et al., 2011; Pruesse et al., 2011; Stilla et al., 2007, 2008; Strenziok et al., 2011) and FC to resting state (Biswal et al., 1995; Buckner et al., 2008; Grecius et al., 2003; Raichle et al., 2001). In task fMRI, the external input introduces synchronicity in fMRI data (as many regions are driven by a common input), making it difficult to assess instantaneous relationships. Also, EC is more appealing in task fMRI, since the external input represents a starting point to which information flow can be traced back. For example, in a visual-event related experiment, if one could show effective causal connectivity from lateral geniculate nucleus→primary visual (V1)→higher-order visual (V5 or fusiform)→frontal areas, the directional flow of information could be traced back to the visual input. On the other hand, very few studies have examined EC in resting-state fMRI, because the results are difficult to interpret. This stems from the fact that ambiguity exists in the neurophysiological origin of resting-state fMRI and the spatial distribution of the correlated spontaneous brain activity. Nevertheless, resting-state FC is accepted because of its robustness, reproducibility, and scientific and possibly clinical utility (Buckner et al., 2008). Studies are yet to demonstrate the same regarding resting-state EC. Also, an EC result from resting-state fMRI cannot be traced back to an initial cause such as a known external input. No such difficulties exist with interpreting FC results. Therefore, previous reports of resting-state EC have only tried to interpret their results as a corroboration of task-based EC results (Sridharan et al., 2008) or what is already known from FC. For example, resting-state EC studies have shown that the default-mode network and dorsal attention network have complementary connectivity patterns (Liao et al., 2010). This is not unexpected from the fact that those two networks are anticorrelated.

In 2011, we reported a study in which we performed functional and effective resting-state connectivity analysis of 33 brain regions belonging to default-mode, dorsal attention, hippocampal cortical memory, and fronto-parietal control networks using a unified multivariate model that we had previously used for correlation-purged Granger causality analysis (Deshpande et al., 2011). We presented instantaneous connectivity on a force-directed layout (Ebbels et al., 2006) and overlaid the causal interactions on it, allowing simultaneous visualization of instantaneous and causal relationships between the ROIs. We found that two regions, posterior cingulate and inferior parietal regions, exhibited connections, mostly bidirectional, with all other ROIs in the four networks. This result established the two regions as information-transit hubs. Additionally, most unidirectional inputs ended in the hippocampal formation, indicating memory encoding and the anterior prefrontal cortex, which is at the apex of the cognitive hierarchy, indicating cognitive integration. Most unidirectional outputs came from the insula, probably carrying information about cognitive, homeostatic, and emotional salience to other regions, specifically to hippocampus, posterior cingulate, and anterior prefrontal regions. Interestingly, a causal relationship between hippocampus and medial prefrontal cortex was observed. This seems to explain the paradox that even though these regions are uncorrelated, it is imperative that a signal about past associations and analogies from the hippocampus reach the medial frontal cortex, where mental simulations with reference to self, constrained by past associations and analogies, are carried out (Bar, 2007). It is worth noting that the most significant causal relationships in our data did not overlap with the most significant instantaneous relationships. Therefore, we suggested that resting-state causal connectivity provides an alternate mode of communication between brain regions that are instantaneously dissociated. In this context, it is interesting to note that a recent study found that resting-state Granger causalities were significantly stronger between regions connected by a white-matter fiber as compared to those that were not, providing a strong structural underpinning to the causal mode of interactions between brain regions in resting state (Li et al., 2011).

Notwithstanding our encouraging resting-state EC results in terms of neuroscientific relevance, it is to be stressed that temporal band-pass filtering of fMRI data in the frequency range between 0.01 Hz and 0.1 Hz (which is an essential preprocessing step in all resting-state fMRI analysis, including ours) introduces additional temporal aggregation over and above what is already present in fMRI data. This is likely to make attribution of instantaneous and causal relationships from filtered resting-state fMRI to either synchronous or time-lagged neuronal activity even more difficult.

There are certain reasons why temporal band-pass filtering is popular. First, it removes some obvious sources of thermal and physiological noise. Second, if instantaneous relationship at the fMRI level is caused by a neuronal causal relationship as shown by the Wei model, then the detectability of instantaneous relationship from fMRI will increase with more temporal aggregation (Wei, 1982). However, the downside is that it makes it harder to separate the contribution of neuronal synchronicity from that of causal influences to fMRI-based instantaneous connectivity. Due to these considerations, temporal band-pass filtering of resting-state fMRI improves the sensitivity and is thereby a popular preprocessing choice. However, if we have to distinguish between the contribution from causality and that from synchronicity, band-pass filtering is not a desirable preprocessing method. With the advent of blind deconvolution techniques such as the cubature Kalman filter, which is potentially capable of deconvolving resting-state fMRI data to recover the underlying neuronal latent variables (Havlicek et al., 2011), it is preferable to estimate both resting-state functional and EC from the recovered neuronal latent variables without performing temporal band-pass filtering as a preprocessing step. The performance and clinical/scientific utility of such an approach are yet to be investigated.

Conclusions and Future Directions

In this article, we have critically evaluated previous work related to EC methods for fMRI, especially Granger causality analysis, and discussed current issues in fMRI EC analysis with references to our previous work regarding Granger causality analysis. Regarding existing literature, we have argued that simulations are bounded by the assumptions and simplifications made by the simulator, and hence should not be viewed as conclusive. On the theoretical front, we are optimistic about the converging of different methods, and future research must concentrate on a unified framework specifically designed for fMRI. Recent experimental evidence has shown strong evidence supporting the use of Granger causality analysis, and future experiments must be designed to replicate those findings using Granger causality analysis as well as other methods. We have discussed some major current issues in EC analysis of fMRI—hemodynamic variability, sampling, instantaneous versus causal relationship, and task versus resting states. Accordingly, our opinion is that performing hemodynamic deconvolution or if that is not possible, designing experiments that aim at only examining the change of connectivity with experimental context is a very important caveat to keep in mind while designing fMRI experiments with GCA. Also, we think that sampling is less of a problem than the hemodynamic variability and hope that recent fast imaging techniques will alleviate the matter. Finally, we have discussed instantaneous versus causal relationships between brain regions in task and resting-state fMRI, an aspect of connectivity analysis that we think has not been sufficiently addressed. We expect this aspect to develop as we gain more understanding into the neurobiological basis of resting-state FC. Specifically, we think that there is a need for future studies to address the relationship between synchronous and causal relationships at the neuronal level to that in the fMRI level in resting-state. This has major consequences for our understanding of resting-state networks, especially if nonsynchronous causal relationships at the neuronal level appear synchronous in fMRI.

Author Disclosure Statement

No competing financial interests exist.