Potential assessment of genome-wide association study and genomic selection in Japanese pear Pyrus pyrifolia

Abstract

Although the potential of marker-assisted selection (MAS) in fruit tree breeding has been reported, bi-parental QTL mapping before MAS has hindered the introduction of MAS to fruit tree breeding programs. Genome-wide association studies (GWAS) are an alternative to bi-parental QTL mapping in long-lived perennials. Selection based on genomic predictions of breeding values (genomic selection: GS) is another alternative for MAS. This study examined the potential of GWAS and GS in pear breeding with 76 Japanese pear cultivars to detect significant associations of 162 markers with nine agronomic traits. We applied multilocus Bayesian models accounting for ordinal categorical phenotypes for GWAS and GS model training. Significant associations were detected at harvest time, black spot resistance and the number of spurs and two of the associations were closely linked to known loci. Genome-wide predictions for GS were accurate at the highest level (0.75) in harvest time, at medium levels (0.38–0.61) in resistance to black spot, firmness of flesh, fruit shape in longitudinal section, fruit size, acid content and number of spurs and at low levels (<0.2) in all soluble solid content and vigor of tree. Results suggest the potential of GWAS and GS for use in future breeding programs in Japanese pear.

Introduction

Genetic improvement of fruit trees is strongly hindered by their long lifespan, large plant size, an extended juvenile phase for seedlings and a marketable product that cannot be assessed until a seedling is physiologically mature (Luby and Shaw 2001, Rikkerink et al. 2007). Multiple biotic and abiotic factors that affect both quality and quantity of products during preharvest and postharvest periods also add complications to the genetic improvement (Rikkerink et al. 2007). Marker-assisted selection (MAS) is one candidate technology to surmount fruit tree breeding problems because it enables selection without field testing and can accelerate the selection process and reduce the progeny sizes and the costs of carrying individuals to maturity in the fields (Luby and Shaw 2001). Attempts to use MAS in fruit tree breeding programs, however, are just beginning and remain limited to the selection of a few simply inherited traits because marker development for MAS via bi-parental QTL mapping is also hindered by the same complications as described above.

High-throughput genotyping technologies such as DNA chips (Gupta et al. 2008) and genotyping using the next generation sequencing (Davey et al. 2011) have enabled new genomic-based strategies such as genome-wide association study (GWAS), which is a method for detecting causal genes or QTL based on the association between genome-wide markers and phenotypes caused by linkage disequilibrium (LD) between markers on one hand and causal genes or QTL on the other. Initially developed for detection of human disease genes, GWAS has emerged as a powerful tool also in plant species (Hamblin et al. 2011, Yu and Buckler 2006). GWAS, which requires line-crossing experiments, is suitable for QTL detection especially in long-lived perennials (Oraguzie et al. 2007). However, it is just beginning to be applied to fruit tree species and only in a few species (Myles et al. 2011).

Novel genotyping technologies also lead the way for genomic-based breeding strategies such as genomic selection (GS, Meuwissen et al. 2001). Similarly to GWAS, GS uses LD between markers on one hand and causal genes and QTL on the other. Unlike GWAS, however, it is designed to detect genes and QTL, GS aims to predict the genetic potential (e.g. breeding values) of breeding lines without locating genes and QTL. GS has been put to practical use in animal breeding (Hayes et al. 2009) and is gathering attention also in plant breeding (Grattapaglia et al. 2010, Heffner et al. 2009, Iwata et al. 2011, Jannink et al. 2010, Kumar et al. 2012, Lorenz et al. 2011). GS can avoid issues of uncertainty in QTL identification and effect estimation, which can be problematic in MAS, by estimating the effects of all marker loci simultaneously. The simultaneous estimation of genomic effects provides the further benefit that even effects that might be too small to be declared “statistically significant” can be captured by markers. Because of these characteristics, GS is expected to be efficient even for a low-heritability polygenic trait (Heffner et al. 2009, Jannink et al. 2010, Lorenz et al. 2011), whereas MAS is unsuitable for the improvement of such a trait.

Pear (Pyrus spp.), which belongs to the subfamily Spiraeoideae in the family Rosaceae, is an important fruit tree grown in Asia, Europe and all other temperate regions around the world. Approx. 22 million tons of pear fruit, accounting for 4% of all fruit production (FAOSTAT, http://faostat.fao.org/), are produced worldwide. Four major species (Japanese pear, Pyrus pyrifolia Nakai; European pear, P. communis L.; Chinese pear, P. bretschneideri Rehd. and P. ussuriensis Maxim.) are grown commercially in temperate regions (Bell 1990). In pear breeding, as in other fruit tree breeding, a long time is required. Japanese pear takes about 15–20 years from the crossing of parental lines to the release and registration of new cultivars. For example, ‘Hosui’ (syn. ‘Housui’) took 18 years (Kajiura et al. 1974) and ‘Shuurei’ 21 years (Kotobuki et al. 2004). During the long breeding process, large areas of land are necessary for plant maintenance and fruit evaluation. At the National Institute of Fruit Tree Science (NIFTS, Ibaraki, Japan), the first stage of selection programs of Japanese pear required 0.4 ha to test 1,000 trees in a field trial. The last stage required ca. 0.33 ha to test 100 trees. Intensive labor is also necessary for plant maintenance and fruit evaluation. At the end of the breeding process, however, a high proportion of inferior seedlings are destined for culling, as generally required for most fruit breeding programs (Rikkerink et al. 2007). In Japanese pear breeding, the current most important breeding targets are disease resistance and the rate of fruit set, in the short term and the restoration of vigor that has been reduced during unintentional inbreeding, in the long term. To investigate the inheritance of these economically important complex traits, numerous high-throughput SNP markers are currently under development in addition to hundreds of SSR markers that have been developed to date (Fernandez-Fernandez et al. 2006, Inoue et al. 2007, Nishitani et al. 2009, Sawamura et al. 2004, Yamamoto et al. 2002a, 2002b, 2002c, 2007). To improve the complex target traits described above while maintaining the high-quality characteristics of current modern cultivars, it is necessary first to develop genomic-breeding approaches based on genomic studies and tools that have been conducted and developed. Pear is a long-lived perennial. Therefore, GWAS and GS will play a central role in the development and implementation of genomic-breeding approaches.

The object of this study is to evaluate the potential of GWAS and GS in future Japanese pear breeding. We conducted GWAS and validated the accuracy of GS with a dataset consisted of 162 markers and 76 Japanese pear cultivars. GWAS and GS are both LD-based approaches possibly affected by population stratification. Therefore, we evaluate the extent of LD and population structure in a population of the Japanese pear cultivars. For both GWAS and GS, we investigated nine agronomic traits that are important in Japanese pear production: harvest time, resistance to black spot, firmness of flesh, fruit size (fruit weight), fruit shape in longitudinal section, acid content, total soluble solid content (sugar content), number of spurs and tree vigor. In GWAS and GS model training, we applied multi-loci Bayesian models that were able to treat multi-allelic marker data and ordinal categorical trait data. Although the scale (i.e., the number of markers and cultivars) of this study might be small to evaluate the full potential of GWAS and GS, the study was undertaken to collect basic information about LD and population structure in a population of Japanese pear cultivars and to evaluate the future potential of GWAS and GS in pear breeding.

Materials and Methods

Plant materials

For this study, we used 76 Japanese pear varieties including 31 modern elite cultivars, 19 old cultivars, 17 indigenous cultivars, and 9 breeding lines (Table 1). Among them, 17 cultivars were bred and released by the National Institute of Fruit Tree Science (NIFTS, Ibaraki, Japan). All plant materials were maintained and collected at NIFTS. Genomic DNA was isolated from young leaves using a Genomic-tip 20/G (Qiagen Inc., Germany) as described by Yamamoto et al. (2006).

Table 1.

List of pear cultivars and breeding lines analyzed in this study. Asterisks after release years represent modern elite cultivars bred by the National Institute of Fruit Tree Science (NIFTS, Ibaraki, Japan)

Name	Type	Release year	Name	Type	Release year
Akiakari	Modern	2003*	Doitsu	Indigenous
Akizuki	Modern	2001*	Natsuhikari	Modern	1995
Akibae	Modern	1997	Nangetsu	Modern	1997
Akemizu	Modern	1997	Niitaka	Old
Asahi	Old		Nijisseiki	Indigenous
Atago	Old		Nikkori	Modern	1996
Amanogawa	Indigenous		Hatsuaki	Old
Ishii Wase	Indigenous		Hakko	Modern	1972*
Ichihara Wase	Indigenous		Hattatsu	Old
Inagi	Old		Hayatama	Modern	1968*
Imamuraaki	Indigenous		Touno	Old
Oushuu	Modern	2003*	Hiratsuka-10	Modern
Okusankichi	Indigenous		Heiwa	Old
Natsushizuku	Modern	2005*	Hougetsu	Modern	1994*
Gion	Old		Hosui	Modern	1972*
Kikusui	Old		Hokushin	Modern	1997
Kisui	Modern	1990	Mishirazu	Indigenous
Kimitsuka Wase	Old		Meigetsu	Indigenous
Kunitomi	Old		Yali	Indigenous
Kumoi	Modern	1955*	Yasato	Modern	1990*
Kogetsu	Old		Yachiyo	Old
Kosui	Modern	1959*	Yanaga	Old
Sagami	Old		Laiyangcili	Indigenous
Shuugyoku	Modern	1988*	Ri-14	Breeding line
Shuurei	Modern	2003*	Wakahikari	Modern	1992
Shinkou	Old	1941	Waseaka	Indigenous
Shinsui	Modern	1965*	Wase Kouzou	Indigenous
Shinsei	Modern	1984*	162-29	Breeding line
Shinseiki	Old		42-6	Breeding line
Shinsetsu	Modern	1949	C2	Breeding line
Suisei	Modern	1955*	266-27	Breeding line
Seigyoku	Old		48-96	Breeding line
Seiryuu	Indigenous		I-33	Breeding line
Taihaku	Indigenous		O-9	Breeding line
Tama	Modern	1971	Shinchuu	Indigenous
Chikusui	Modern	1989*	92-7	Breeding line
Choju	Modern	1973	Tsukuba52	Modern
Chojuro	Indigenous		Tsukuba53	Modern

Genetic markers

The 76 varieties were genotyped for 162 DNA markers, including 155 simple sequence repeats (SSRs) from pear and apple, four RAPD-STS, two ACC synthase genes and one locus encoding S-RNase gene, which are listed in the Appendix (Guilford et al. 1997, Ishimizu et al. 1999, Itai et al. 2003, Liebhard et al. 2002, Sawamura et al. 2004, Silfverberg-Dilworth et al. 2006, Terakami et al. 2006, Yamamoto et al. 2002b). Then SSR-PCR amplification was performed in a 10 μl reaction solution containing 10 mM Tris-HCl (pH 8.3), 50 mM KCl, 1.5 mM MgCl2, 0.001% gelatin, 0.2 mM each of dNTPs, 5 pmol of each forward primer labeled with fluorescent chemical (Fam/Vic/Ned) and unlabelled reverse primer, 5 ng of genomic DNA and 0.25 unit of Taq polymerase (Invitrogen Corp., USA). Amplification was performed as follows: 35 cycles at 94°C for 1 min, 50–55°C for 1 min and 72°C for 2 min, for denaturation, annealing and primer extension, respectively. The PCR products were separated and detected using a DNA sequencer (Genetic Analyzer 3100, Applied Biosystems, USA). The amplified band size was determined based on an internal standard DNA (400HD-Rox, Applied Biosystems, USA) using GeneScan software (Applied Biosystems, USA).

Appendix.

List of markers used in the present study. Linkage groups and positions of DNA markers were identified by three genetic linkage maps of pears (Nishitani et al. 2009, Terakami et al. 2009, Yamamoto et al. 2007)

Marker name	LGa	Pos.b	Origin	ID nos. or references
NH013a	1	6.6	pear SSR	AB061367
STS-OPW02	1	20.0	RAPD-STS	Terakami et al. (2006)
STS-OPAW13	1	24.8	RAPD-STS	Terakami et al. (2006)
STS-OPO09	1	26.0	RAPD-STS	Terakami et al. (2006)
KA4b	1	55.9	pear SSR	AB219793
TsuENH003	1	61.5	pear EST-SSR	AB450691
CN581493SSR	2	0.1	apple SSR	Silfverberg-Dilworth et al. (2006)
Hi22d06	2	0.1	apple SSR	Silfverberg-Dilworth et al. (2006)
TsuENH017	2	6.6	pear EST-SSR	AB450702
KU10	2	15.0	pear SSR	AB219798
TsuENH001	2	16.5	pear EST-SSR	AB450689
TsuENH062	2	21.5	pear EST-SSR	AB450733
CN444636SSR	2	21.5	apple SSR	Silfverberg-Dilworth et al. (2006)
BGT23b	2	28.1	pear SSR	AB219800
TsuENH045	2	30.0	pear EST-SSR	AB450721
CH03d10	2	36.5	apple SSR	Liebhard et al. (2002)
CH02b10	2	41.5	apple SSR	Liebhard et al. (2002)
CH02a04	2	42.0	apple SSR	Liebhard et al. (2002)
TsuENH087	2	50.0	pear EST-SSR	AB450752
NH002b	2	56.5	pear SSR	AB061359
NH023a	3	24.3	pear SSR	Yamamoto et al. (2002b)
NB113a	3	48.1	pear SSR	Yamamoto et al. (2002b)
NH203a	3	49.7	pear SSR	Sawamura et al. (2004)
TsuENH074	3	50.0	pear EST-SSR	AB450742
TsuENH023	3	51.0	pear EST-SSR	AB450706
BGA35	3	70.0	pear SSR	AB219799
NB109a	3	70.1	pear SSR	Yamamoto et al. (2002b)
MS14h03	3	73.0	apple SSR	Liebhard et al. (2002)
HGA8b	3	85.0	pear SSR	AB219801
NH209a	4	5.0	pear SSR	Sawamura et al. (2004)
NH011b	4	5.3	pear SSR	AB061365
TsuENH063	4	10.0	pear EST-SSR	AB450734
CH01d03	4	13.0	apple SSR	Liebhard et al. (2002)
TsuENH019	4	15.5	pear EST-SSR	AB450704
Hi23g08	4	16.0	apple SSR	Silfverberg-Dilworth et al. (2006)
CH02h11a	4	25.0	apple SSR	Liebhard et al. (2002)
NB141b	4	39.8	pear SSR	AB302443
TsuENH014	4	45.1	pear EST-SSR	AB450700
CH02c02b	4	50.7	apple SSR	Liebhard et al. (2002)
NB131a	4	55.0	pear SSR	AB302437
CH03a09	5	10.0	apple SSR	Liebhard et al. (2002)
EMPc106	5	16.7	pear SSR	AM182391
TsuENH086	5	25.0	pear EST-SSR	AB450751
NB103a	5	37.6	pear SSR	Yamamoto et al. (2002b)
CH02b12	5	52.3	apple SSR	Liebhard et al. (2002)
CH01b11	6	32.8	apple SSR	Liebhard et al. (2002)
TsuENH046	6	34.1	pear EST-SSR	AB450722
CH03d12	6	39.8	apple SSR	Liebhard et al. (2002)
TsuENH006	7	5.0	pear EST-SSR	AB450694
CH04e05	7	20.7	apple SSR	Liebhard et al. (2002)
NH019b	7	30.0	pear SSR	Yamamoto et al. (2002b)
EMPc117	7	41.3	pear SSR	AM182398
EMPc111	7	47.9	pear SSR	AM182394
NH036b	8	1.6	pear SSR	Sawamura et al. (2004)
EMPc116	8	5.0	pear SSR	AM182397
NB114a	8	10.0	pear SSR	AB302423
Hi20b03	8	22.0	apple SSR	Silfverberg-Dilworth et al. (2006)
OPH-19	8	25.0	RAPD-STS	Terakami et al. (2006)
TsuENH034	8	30.0	pear EST-SSR	AB450714
NH005b	8	33.0	pear SSR	AB061361
IPPN19	8	36.4	pear SSR	AB250799
CH01h10	8	50.0	apple SSR	Liebhard et al. (2002)
NH201a	8	60.0	pear SSR	Sawamura et al. (2004)
IPPN13	9	0.0	pear SSR	AB250792
NH029a	9	6.7	pear SSR	Yamamoto et al. (2002b)
TsuENH008	9	19.7	pear EST-SSR	AB450696
NB134a	9	36.7	pear SSR	AB302440
Hi04a05	9	40.0	apple SSR	Silfverberg-Dilworth et al. (2006)
CH05a03	9	51.5	apple SSR	Liebhard et al. (2002)
NH206a	10	22.0	pear SSR	Sawamura et al. (2004)
NH039a	10	24.1	pear SSR	Sawamura et al. (2004)
NH017a	10	25.0	pear SSR	AB061370
EMPc114	10	31.2	pear SSR	AM182395
Hi03f06	10	31.2	apple SSR	Silfverberg-Dilworth et al. (2006)
CH01f12	10	31.5	apple SSR	Liebhard et al. (2002)
NH045a	10	32.8	pear SSR	AB302421
EMPc105	10	34.4	pear SSR	AM182390
CH02b03b	10	50.0	apple SSR	Liebhard et al. (2002)
TsuENH029	10	56.2	pear EST-SSR	AB450710
TsuENH009	10	56.2	pear EST-SSR	AB450697
CH01f07a	10	56.2	apple SSR	Liebhard et al. (2002)
MS06g03	10	56.2	apple SSR	Liebhard et al. (2002)
CH04h02	11	0.0	apple SSR	Liebhard et al. (2002)
TsuENH083	11	9.0	pear EST-SSR	AB450749
CH03d02	11	12.6	apple SSR	Liebhard et al. (2002)
TsuENH044	11	25.5	pear EST-SSR	AB450720
IPPN14	11	30.1	pear SSR	AB250793
NB135a	11	60.0	pear SSR	AB302441
NB118a	11	64.0	pear SSR	AB302426
NB105a	11	64.8	pear SSR	Yamamoto et al. (2002b)
CH04g07	11	64.8	apple SSR	Liebhard et al. (2002)
CH04d08	11	65.0	apple SSR	Liebhard et al. (2002)
NH207a	12	7.0	pear SSR	Sawamura et al. (2004)
CH04g04	12	10.0	apple SSR	Liebhard et al. (2002)
CH05d11	12	12.7	apple SSR	Liebhard et al. (2002)
KA16	12	14.5	pear SSR	AB219796
NZ28f4	12	14.8	apple SSR	Guilford et al. (1997)
NB104a	12	30.0	pear SSR	Sawamura et al. (2004)
CH04d02	12	41.6	apple SSR	Liebhard et al. (2002)
CH02g01	13	10.0	apple SSR	Liebhard et al. (2002)
TsuENH025	13	16.6	pear EST-SSR	AB450707
NH009b	13	19.9	pear SSR	AB061364
NB120a	13	43.9	pear SSR	AB302428
TsuENH058	14	0.0	pear EST-SSR	AB450730
IPPN01	14	3.0	pear SSR	AB250786
NH004a	14	5.0	pear SSR	AB061360
CH01a09	14	20.1	apple SSR	Liebhard et al. (2002)
CH01g05	14	32.0	apple SSR	Liebhard et al. (2002)
CH04f06	14	32.0	apple SSR	Liebhard et al. (2002)
NH001c	14	38.5	pear SSR	AB061358
Hi02d11	14	40.1	apple SSR	Silfverberg-Dilworth et al. (2006)
CH04c07	14	41.7	apple SSR	Liebhard et al. (2002)
TsuENH032	14	44.0	pear EST-SSR	AB450712
NH035a	14	44.9	pear SSR	Sawamura et al. (2004)
TsuENH031	14	44.9	pear EST-SSR	AB450711
CH05d03	14	44.9	apple SSR	Liebhard et al. (2002)
CH03g06	14	48.4	apple SSR	Liebhard et al. (2002)
TsuENH093	15	0.0	pear EST-SSR	AB450757
NH027a	15	0.0	pear SSR	Yamamoto et al. (2002b)
CH02e12	15	1.0	apple SSR	Liebhard et al. (2002)
CH02d10b	15	1.6	apple SSR	Liebhard et al. (2002)
CH03b06	15	2.0	apple SSR	Liebhard et al. (2002)
Hi03g06	15	3.0	apple SSR	Silfverberg-Dilworth et al. (2006)
NH204a	15	5.0	pear SSR	Sawamura et al. (2004)
IPPN17	15	10.0	pear SSR	AB250796
NH025a	15	11.2	pear SSR	Yamamoto et al. (2002b)
IPPN08	15	12.8	pear SSR	AB250789
Hi02d02	15	12.8	apple SSR	Silfverberg-Dilworth et al. (2006)
PPACS2	15	13	ACC synthase	Itai et al. (2003)
Hi11a01	15	56.8	apple SSR	Silfverberg-Dilworth et al. (2006)
Hi09f01	15	56.8	apple SSR	Silfverberg-Dilworth et al. (2006)
TsuENH040	15	68.3	pear EST-SSR	AB450717
CH02c09	15	68.4	apple SSR	Liebhard et al. (2002)
TsuENH007	15	70.0	pear EST-SSR	AB450695
TsuENH035	15	70.1	pear EST-SSR	AB450715
TsuENH016	15	70.1	pear EST-SSR	AB450701
PPACS1	15	unknown	ACC synthase	Itai et al. (2003)
TsuENH079	16	0.0	pear EST-SSR	AB450745
TsuENH022	16	3.5	pear EST-SSR	AB450705
TsuENH036	16	3.5	pear EST-SSR	AB450716
NH026a	16	6.0	pear SSR	Yamamoto et al. (2002b)
KA14	16	10.0	pear SSR	AB219795
NH007b	16	15.0	pear SSR	AB061362
CH01f03a	16	15.0	apple SSR	Liebhard et al. (2002)
Hi04e04	16	17.0	apple SSR	Silfverberg-Dilworth et al. (2006)
AU301431SSR	16	20.0	apple SSR	Silfverberg-Dilworth et al. (2006)
CH05a04	16	30.0	apple SSR	Liebhard et al. (2002)
NB123a	16	65.0	pear SSR	AB302430
NB116b	16	65.0	pear SSR	AB302425
NH015a	17	0.0	pear SSR	AB061369
TsuENH026	17	1.2	pear EST-SSR	AB450708
AF527800SSR	17	1.2	apple SSR	Silfverberg-Dilworth et al. (2006)
AT000174SSR	17	1.2	apple SSR	Silfverberg-Dilworth et al. (2006)
CH01h01	17	3.8	apple SSR	Liebhard et al. (2002)
TsuENH033	17	4.2	pear EST-SSR	AB450713
NB125a	17	4.2	pear SSR	AB302432
CH05g03	17	10.0	apple SSR	Liebhard et al. (2002)
TsuENH071	17	38.0	pear EST-SSR	AB450740
NH014a	17	40.9	pear SSR	AB061368
NH008b	17	45.0	pear SSR	AB061363
Slocus	17	54.2	S-Rnase	Ishimizu et al. (1999)
CH01b12	unknown	unknown	pear SSR	Liebhard et al. (2002)

^aLinkage group

^bPosition (cM)

Identification of S1–S7 alleles was performed according to the protocol described by Ishimizu et al. (1999). A procedure for detecting the S8 allele was reported by Castillo et al. (2001). Allele-specific PCR for detection of the S9 allele was conducted by DNA sequencing, as described by Sawamura et al. (2002). Four RAPD-STS markers were analyzed according to the method described in Terakami et al. (2006). Two ACC synthase genes, which were involved in the ethylene synthesis pathway, were genotyped using the method reported by Itai et al. (2003). Linkage groups and roughly estimated map positions of DNA markers in this study were identified using three genetic linkage maps of a Japanese pear variety ‘Hosui’ and European pear varieties ‘Bartlett’ and ‘La France’ (Nishitani et al. 2009, Terakami et al. 2009, Yamamoto et al. 2007). We combined the information of three linkage maps using ‘Bartlett’ map as a framework and locating markers that were specific to ‘Hosui’ and ‘La France’ maps at their relative positions to common markers. Correspondence between the pear maps to the saturated reference map of apple suggests that the combined information covered almost the entire genome, which consists of the 17 pairs of chromosomes of Japanese pear (Yamamoto et al. 2007).

Phenotypic records

Nine phenotypic traits were characterized for 76 cultivars based on the plant genetic resource criteria (Kotobuki 1999), including harvest time, resistance to black spot, firmness of flesh, fruit size (fruit weight), fruit shape in longitudinal section, acid content, total soluble solid content (sugar content), number of spurs and vigor of tree. The abbreviations, the number of rating scale categories and the number of observations in each category of traits analyzed in this study are presented in Table 2.

Table 2.

Summary of traits evaluated in this study

Trait	Abbr.	Number of levels	Rank or measurement unit	Number of observations in each category
Harvest time	HarT	4	very early, early, intermediate, late (observation)	10, 16, 32, 18
Resistance to black spot	BSR	2	resistance, susceptibility (observation)	11, 65
Firmness of flesh	FruH	3	soft (<4.9 lb), intermediate (5.0–6.9 lb), firm (>7.0 lb) (measurement using Magness-Taylor pressure tester)	45, 23, 6
Fruit size (fruit weight)	FruW	3	small (25–199 g), intermediate (200–399 g), large (≥400 g) (measurement of average weight of mature fruit)	3, 43, 28
Fruit shape in longitudinal section	FruS	5	oblate, round, broad elliptical, spindle, obovate (observation)	43, 19, 5, 3, 4
Acid content	Aci	3	low (<4.3), intermediate (4.4–4.6), high (>4.7) (measurement of pH of juice)	48, 18, 8
Total soluble solid content (sugar content)	SugC	3	low (<10.4%), intermediate (10.5–12.4%), high (>12.5%) (measurement of Brix of juice)	3, 52, 19
Number of spurs	SpuN	3	few, intermediate, many (observation)	14, 37, 25
Vigor of tree	TreV	3	weak, intermediate, strong (observation)	4, 57, 15

LD and population structure analysis

LD between pairs of markers was evaluated using the R package “genetics”. The function “LD” in the “genetics” package estimated unknown linkage phase using maximum likelihood and calculated LD statistics. In this study, we calculated the squared allele-frequency correlation (r²) between the most common alleles at both of markers located on the same chromosomes. The r² values were shown against marker distance in cM. The relation between the r² values and linkage map distance between the corresponding markers was further modeled by fitting local polynomials with the function “locpoly” in the R package “KernSmooth”.

The population structure of the 76 pear cultivars was estimated via hierarchical clustering and Bayesian model-based clustering. The hierarchical clustering was conducted based on the Ward method (Ward 1963) using the R function “hclust”. Simple allele-sharing distances (Bowcock et al. 1994) between the 76 cultivars were calculated based on the genotypes of the 162 markers and used in the clustering. Bayesian mode-based clustering (Pritchard et al. 2000) was conducted using the program Structure. Eighty markers were selected from the 162 markers so that each pair of adjacent markers was more than 5 cM apart. Markov chain Monte Carlo (MCMC) cycles were repeated 1 × 10⁶ times after 1 × 10⁵ cycles of a burn-in period. In the analyses, we tested the admixture models with 1–7 populations. Because the posterior probability of a model almost reached a plateau when the number of population (K) was four, we chose K = 4 and obtained estimates for the proportion of variety i’s genome that originated from population k, q_ik. The Q matrix whose (i, k)-th element was q_ik was further incorporated into the Bayesian regression model for GWAS.

Bayesian regression in GWAS and GS prediction

In GWAS, we fit a linear model that includes the effects of population stratification as well as effects of multiple QTL (Iwata et al. 2007, 2009). The phenotypic records analyzed in this study were scored in several ordered categories. Therefore, we modeled observed ordinal data via an ordinal probit model (Iwata et al. 2009). The model presumed a latent (i.e., unobservable or unrecorded) continuous variable y_i* that underlies the observable (or recorded) ordinal response y_i for the ith sample. When the phenotypic records were scored in M ordinal categories, the value of each y_i* falls into one of M contiguous bins on the real line demarcated by the cut-points κ₀, κ₁, ..., κ_M and the observed values of y_i are determined using the following relation:

$$y_i=m\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\text{if\hspace{0.28em}}{\kappa }_{m-1}<{y_i}^{*}\le {\kappa }_m\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }(m=1,2,\dots ,M).$$

Because the cut-points are also unobservable, the values of κ_m were also estimated, but the first, second and last cut-points were fixed as κ₀ = −∞, κ₁ = 0 and κ_M = ∞. The latent continuous variable y_i* was then described as

$${y_i}^{*}=\sum _k^K{q}_{ik}{\alpha }_k+\sum _j^J\sum _l^{L_j}{\gamma }_j(x_{ijl}+{x^{\prime }}_{ijl}){\beta }_{jl}+e_i.$$ (Eq. 1)

In that equation, q_ik represents the estimated share of variety i’s genome that originated from population k. α_k stands for the population effect associated with population k (k = 1, 2, ..., K). L_j represents the number of alleles of marker j (j = 1, 2, ..., J). x_ijl (x′_ijl) denotes the maternal (paternal) allele of marker j for variety i and equals 1 if the maternal (paternal) allele is the lth allele (l = 1, ..., L_j) and 0 otherwise. γ_j signifies the indicator variable and γ_j = 1 corresponds to the case in which marker j is included in the model as a QTL representative and γ_j = 0 implies exclusion. β_jl denotes the genetic effect associated with the allele l for marker j, which is assumed to follow N(0, σ_βj²). e_i the residual error, which is assumed to follow N(0, σ_e²). The genetic variance of marker j, σ_{β j}² and the error variance, i.e., σ_e², were assumed to follow scaled inverted chi-square distributions Inv-χ² (ν_β, S_β) and Inv-χ² (ν_e, S_e) as described in Iwata et al. (2009). A prior probability for γ_j is assumed to follow the Bernoulli distribution with probability $\pi =\frac{\lambda }{J}$, as described in Iwata et al. (2010).

In GS prediction, we used two different models for building prediction models. The first model is the same as that used in GWAS (i.e. Eq. 1), except that it did not involve the effects of population structure. We removed the effects of population structure from the GS prediction model, as is usually done, because spurious associations are not an important cause of loss of predictive ability (Lorenz et al. 2011). The second model assumed that all markers always have nonzero effects, aiming to capture polygenic effects and is a special case of the first, in which γ_j were fixed to 1. The model fixing γ_j to 1 corresponded to the model known as BayesA (Meuwissen et al. 2001) and Bayesian shrinkage regression (Xu 2003), whereas the model with variable γ_j corresponds to the model known as BayesB (Lorenz et al. 2011, Meuwissen et al. 2001) and stochastic search variable selection (George and McCulloch 1993, Kuo and Mallick 1998).

Bayesian estimation of parameters in the models was conducted as described in Iwata et al. (2009). MCMC sampling was used for Bayesian inference for each of the parameters. For each dataset, MCMC cycles were repeated 13 × 10⁴ times. The first 3 × 10⁴ (burn-in) cycles were not used for estimation of the parameter values. The sampling conducted every ten cycles to reduce serial correlation, so that the total number of samples we retained was 1 × 10⁴. The hyperparameters of the models were set as ν_β = 4, S_β² = 0.04, ν_e = −2, S_e² = 0 and π = 0.06 (λ = 10) for BayesB. For BayesA, we set S_β² = 0.004 instead to incorporate consideration of the fact that most markers have small genetic effects. This sampling scheme was based on the previously described evaluation of the convergence of MCMC cycles (Iwata et al. 2007, 2009).

In GWAS, we identified markers showing significant association with phenotype via the posterior mean of γ_j. Larger posterior mean of γ_j indicated that the kth marker was associated with phenotype more significantly. We used the phenotype permutation method (Churchill and Doerge 1994) to ascertain an appropriate threshold for the posterior mean of γ_j. We permuted the phenotypes randomly to eliminate the association between phenotypes and marker genotypes and fitted the Bayesian model to each of the permuted datasets in the same way as the original dataset. For each dataset, we monitored the largest posterior mean of γ_j, which was largest among all the markers, as a test statistic. An empirical distribution of the test statistic was obtained by repeating the permutation analysis 100 times. Finally, we chose the significance threshold based on the empirical distribution at the 90% percentile.

In GS prediction, we measured the accuracy of prediction via leave-one-out cross-validation (LOOCV). Using the Bayesian regression described above, we were able to predict the values (ŷ_i*) of latent continuous variable y_i* for a left-out sample as

$${{\widehat{y}}_i}^{*}={\tilde{\alpha }}_1+\sum _j^J\sum _l^{L_j}{\tilde{\gamma }}_j(x_{ijl}+{x^{\prime }}_{ijl}){\tilde{\beta }}_{jl}$$

where α̃₁, β̃_jk and γ̃_j are the posterior means of the parameters estimated with non-left-out samples (i.e., samples for “training” a model). As described above, we removed the effects of population structure from the GS prediction model by setting q_il = 1 and thus α̃₁ became the constant term. In BayesA, γ̃_j was always fixed to 1 as described above. We calculated a Pearson’s product moment correlation coefficient between y_i and y_i* as an index of the accuracy of GS prediction.

To see the prediction accuracy based on markers that were significant in GWAS, we built GS prediction models that involved only the significant markers: the reduced model had the identical form as Eq. 1 except that it involved the effect of marker j only when the marker j was significant in GWAS. For the reduced model, the accuracy of the predictions was measured via LOOCV as for the full model (i.e., the model involving all markers).

Results

LD and population stratification

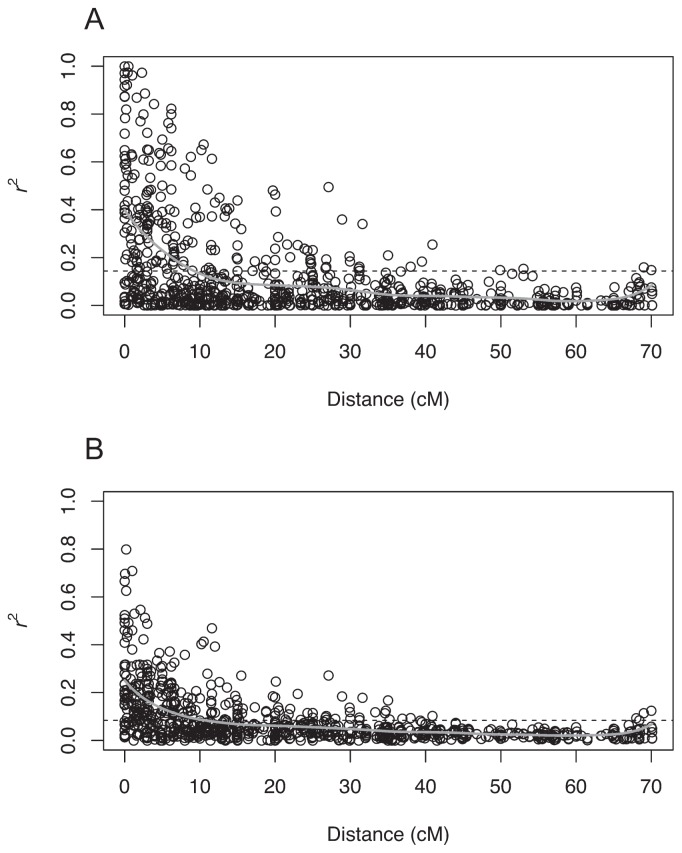
Seventy-six pear cultivars were used in this study (Table 1). The 76 cultivars were genotyped with 155 SSRs, four RAPD-STS, two ACC synthase genes and the self-incompatibility (S-) locus. The LD statistics of two types were measured between pairs of markers linked on the same chromosome (Fig. 1). The r² values based on the most major alleles were larger than those based on all allele combinations. Based on the intersections between the curves fitted to the relations between r² values and map distance on one hand and the horizontal lines corresponding to the 95^th percentile of the distribution of unlinked r² values on the other, the short range of LD extended around 10 cM in a population of the 76 pear cultivars in both LD statistics. For the r² values based on the most major alleles, averages were, respectively 0.35, 0.28 and 0.16 for markers <2, 2–5 and 5–10 cM apart. For the r² values based on all allele combinations, average were, respectively 0.22, 0.16 and 0.10 for markers <2, 2–5 and 5–10 cM apart. Long range LD, i.e., LD between markers more than 10 cM apart, also existed between some marker combinations.

Fig. 1.

Plots of linkage disequilibrium (LD) values (r²) against linkage map distance (cM) between pairs of markers linked on the same chromosome. The r² values were calculated in two ways: calculated between the most major alleles at both markers (A), or calculated among all combinations of alleles at both markers and summed up with weight of allele frequencies (B). Gray curves show local polynomial fits using kernel smoothing regression. The horizontal dashed lines represent the baseline r² values based on the 95^th percentile of the distribution of r² values between pairs of unlinked markers.

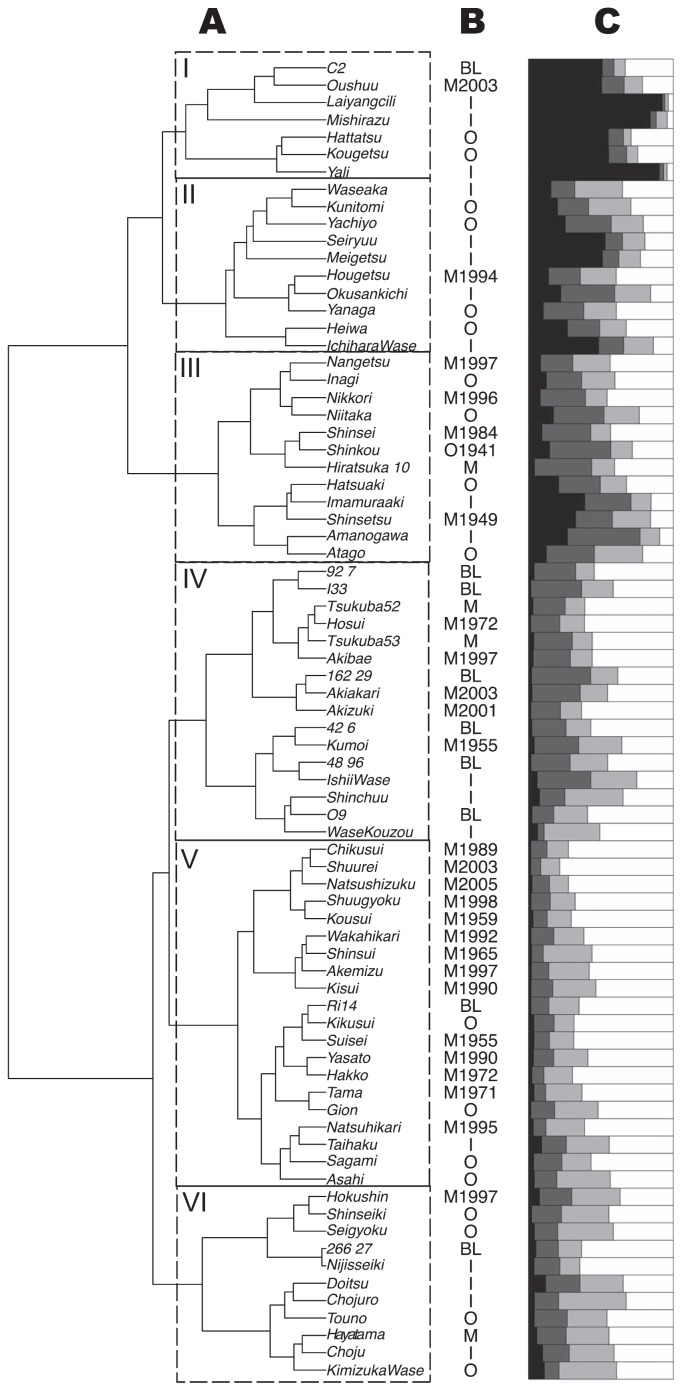
The population structure of the 76 pear cultivars was estimated via hierarchical clustering and Bayesian clustering analyses (Fig. 2). In hierarchical clustering, clusters I and II mainly involved old and indigenous cultivars and the cluster III old and modern cultivars (Fig. 2A and Table 1). The cluster IV mainly involved recent modern cultivars and current breeding lines. The cluster V mainly involved modern and old cultivars and the cluster VI old and indigenous cultivars (Fig. 2A, 2B). Correspondence between hierarchical clustering and Bayesian clustering analysis was not so clear (Fig. 2A, 2C). Varieties in cluster I had larger membership coefficients for group 1, whereas the varieties in the cluster V had larger membership coefficients for group 4. The difference in the membership coefficients between clusters II and III and also among the clusters IV, V and VI was not discrete but continuous.

Fig. 2.

Estimated genetic structure among 76 pear varieties. The genetic structure was estimated using Ward clustering based on simple allele sharing distance (A) and by Bayesian clustering (C). Types and release years of the varieties are listed in B. The indices of variety types (O, old; I, indigenous; M, modern; BL, breeding line) are followed by the release years with four digits. In the Bayesian clustering, each cultivar is divided into four hypothetical sub-populations based on the population membership coefficients totaling 1 for the four sub-populations. Each subgroup is represented by a different color as listed: black (group 1), dark gray (group 2), light gray (group 3) and white (group 4).

GWAS

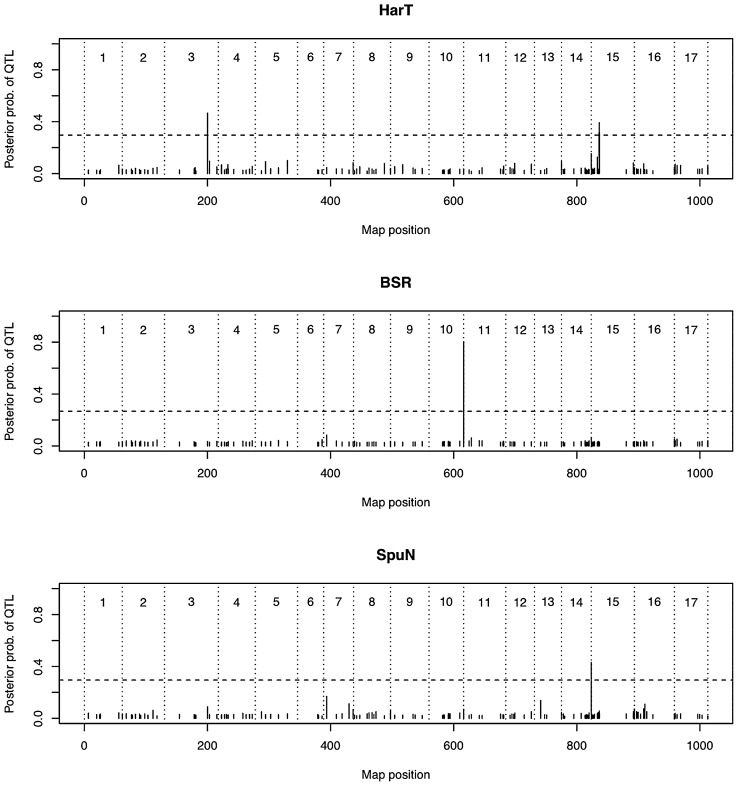
We conducted GWAS to detect significant associations between the 162 markers (Table 2) and the nine agronomic traits (Table 3). Markers showing significant associations were detected in three traits (harvest time, resistance to black spot and number of spurs, Fig. 3 and Table 3), suggesting that these markers are linked to major QTL controlling these traits.

Table 3.

Markers showing significant association with traits evaluated in GWAS. Linkage groups and positions of DNA markers were identified using three genetic linkage maps of pears (Nishitani et al. 2009, Terakami et al. 2009, Yamamoto et al. 2007)

Trait	Marker	LGa	Pos.b	Posterior average of γj	Allele size	Estimated effects
HarT	BGA35	3	70	0.47	129-bp	0.247
					130-bp	−0.030
					132-bp	−0.048
					134-bp	−0.026
					136-bp	−0.144
	PPACS2	15	13	0.39	245-bp	0.192
					253-bp	−0.068
					255-bp	−0.035
					263-bp	−0.089
BSR	CH04h02	11	0	0.80	154-bp	4.845
					170-bp	1.251
					172-bp	−2.204
					182-bp	0.434
					184-bp	−4.360
					200-bp	0.034
SpuN	CH03g06	14	48.4	0.43	137-bp	0.228
					139-bp	−0.040
					144-bp	0.001
					146-bp	−0.026
					148-bp	−0.029
					155-bp	−0.055
					165-bp	−0.078

^aLinkage group

^bPosition (cM)

Fig. 3.

Posterior probability of having a QTL (posterior average of γ_j) at 162 marker positions, estimated for four agronomic traits for which significant associations were detected. Each marker position j (j = 1, 2, ..., J) has its own indicator variable γ_j, where the value one (γ_j = 1) corresponds to the case in which the marker is included in the model as a QTL representative; the value zero (γ_j = 0) implies exclusion. Horizontal broken lines correspond to the threshold obtained from the random permutation procedure.

Two markers showed significant association with harvest time and one marker, BGA35, was located at the 70 cM position on the third chromosome. The other, PPACS2, was located at the 13 cM position on the fifteenth chromosome (Table 3). The 129-bp allele of BGA35 had a positive effect, which made harvest time later, while the remainder alleles of BGA35 had negative effects, which made harvest time earlier. The 245-bp allele of PPACS2 had a positive effect, whereas the other allele of PPACS2 had negative effects.

Regarding resistance to black spots, one marker, CH04h02, was located at the 0 cM position on the eleventh chromosome, showed significant association (Table 3). The 184-bp and 172-bp alleles of CH04h02 had negative effects, suggesting that these two alleles linked to the susceptible alleles of a black spots gene.

In the number of spurs, one marker, CH03g06, which was located at the 48.4 cM position on the fourteenth chromosome, showed significant association (Table 3). The 137-bp allele of the CH03g06 had a positive effect, suggesting that this allele associated with a QTL allele increasing the number of spurs.

Accuracy of GS predictions

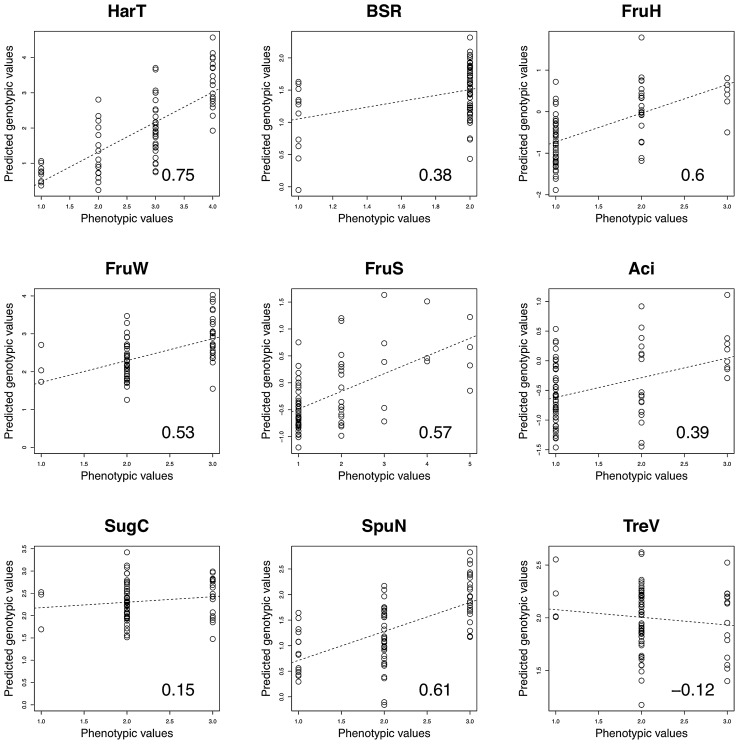
The accuracy of GS predictions was evaluated through leave-one-out cross-validation of phenotype and marker genotype data of the 76 pear cultivars (Fig. 4 and Table 4). In the prediction, we applied two different models: BayesB, i.e., the model including the effects of a part of markers, while BayesA, i.e., the model including the effects of all markers. BayesB is the same as one used in the GWAS except that it did not have the effects of population structure. The accuracy of GS predictions was greater in BayesA than BayesB except for two traits, black spot resistance and fruit shape in longitudinal section (Table 4). With BayesA, the accuracy was highest (0.75) in harvest time, medium (0.38–0.61) in fruit size, firmness of flesh, number of spurs, fruit shape in longitudinal section, resistance to black spot, acid content and low (0.15, −0.12) in all soluble solid content and vigor of tree (Table 4).

Fig. 4.

Correlations between phenotypic values and predicted genotypic values in nine agronomic traits. Predicted genotypic values were calculated via leave-one-out cross-validation. Each point corresponds to one cultivar. Dashed lines through the graphs are fitted regression lines of y and x.

Table 4.

Accuracy of genomic estimated breeding values (GEBVs) in traits evaluated in this study. Accuracy was evaluated as a Pearson’s product-moment correlation coefficient between GEBVs and phenotypic values. Full models involved genotypes of all markers as explanatory variables, whereas reduced models involved genotypes of markers that were significant in GWAS as explanatory variables. Reduced models were built only for traits in which significant association(s) was (were) detected in GWAS.

	Full model		Reduced model
	BayesA	BayesB	BayesA	BayesB
HarT	0.75	0.71	0.56	0.59
BSR	0.38	0.41	0.30	0.39
FruH	0.60	0.57	–	–
FruW	0.53	0.42	–	–
FruS	0.57	0.58	–	–
Aci	0.39	0.35	–	–
SugC	0.15	0.01	–	–
SpuN	0.61	0.43	0.15	0.04
TreV	−0.12	−0.45	–	–

The prediction accuracy described above was based on full prediction models, in which genotypes of all markers were included as explanatory variables. For traits in which significant association was detected in GWAS, we also built reduced prediction models, in which genotypes of markers found to be significant in GWAS were included as explanatory variables, to ascertain whether the accuracy of predictions based only on markers showing significant association with a target trait. In GWAS, significant associations were detected in harvest time, resistance to black spot and the number of spurs. The relative accuracy of the reduced model to the full model showed different patterns for different traits. In resistance to black spot, the reduced prediction model based on one significant marker showed a similar level of accuracy with the full prediction model based on all 162 markers. However, for harvest time and the number of spurs, the accuracy of the reduced prediction models was lower than the accuracy of the full prediction models. Especially for the number of spurs, the accuracy was markedly lower when we used only one significant marker for predictions.

Discussion

The pattern of LD in Japanese pear cultivars

Detailed knowledge related to the extent of LD in a population of breeding lines and cultivars is basic information to consider the future potential of GWAS and GS in a target crop species because different levels of LD are expected in different species because the extent of LD and genetic stratification depend largely on their reproductive characteristics and their history and evolution as cultivated species (Gupta et al. 2005, Oraguzie et al. 2007). In the present study, we evaluated the extent of LD in 76 Japanese pear cultivars using 162 genome-wide markers. The extent of LD in the population of the 76 Japanese pear cultivars was higher than that expected from their cross-pollinating nature because of self-incompatibility, given that allogamous species have a low level of LD conservation in general (Gupta et al. 2005, Oraguzie et al. 2007). The high LD in the Japanese pear cultivars is regarded as the result of genetic bottlenecks during domestication and breeding of Japanese pear because a genetic bottleneck increases the extent of LD by eliminating recombinant lineages. Even when loci remain polymorphic during bottlenecks, the number of allelic combinations across loci can be much reduced, thereby leading to extensive haplotype structure (Hamblin et al. 2011). Vegetative reproduction, which is the most common way to propagate pear trees, conserves the LD caused by the bottlenecks because the genotype of each cultivar is fixed and the number of generations after the bottlenecks might be far fewer than in species with annual sexual reproduction (Rikkerrink et al. 2007). The common strategy in Japanese pear breeding, in which future cultivars are selected directly from F₁ progenies (i.e., are not selected from progenies in a later generation) derived from crosses between commercial cultivars, also makes the number of generations after the bottleneck small.

In Rosaceae crop species, the extent of LD has been reported in peach via genetic analysis with 50 SSR polymorphisms in 224 peach cultivars (Aranzana et al. 2010). In peach, LD was high and decreased with distance in all three cultivar groups: melting peaches, melting nectarines and non-melting peaches. In all groups, LD decayed at 13–15 cM with the threshold at the 5% level significant level. The extent of LD observed in the present study in pear cultivars is similar to that observed in the three groups in peach cultivars, despite their different reproductive characteristics: peach is self-fertile, whereas pear is self-incompatible because of its functional gametophytic self-compatibility. The extent of LD is influenced by various biological and historical factors of the species (Gupta et al. 2005, Oraguzie et al. 2007). Therefore, a careful comparison of the extent of LD among various Rosaceae species will be necessary to elucidate the relation between the extent of LD and biological behavior of Rosaceae species.

Population structure in Japanese pear cultivars

Knowledge about genetic structure among breeding lines and cultivars is necessary for selecting promising parental lines for crossing and using efficiently genetic resources available for breeding. The population structure can also result in nonfunctional spurious associations in association studies (Lander and Schork 1994) and its information is expected to be involved in the statistical model of GWAS as a factor affecting phenotypic variations (e.g., Iwata et al. 2007, Thornsberry et al. 2001, Yu et al. 2006). In this study, we evaluated the population structure among the 76 Japanese pear cultivars. In hierarchical clustering, five major clusters included cultivars of different types. For example, two clusters mainly involved old and indigenous cultivars, whereas three clusters mainly involved modern cultivars and breeding lines. Some exceptions (e.g., indigenous cultivars were also involved in the later type of clusters) were also observed. Bayesian clustering analysis revealed that the model dividing cultivars into four sub-populations was best. The correspondence between the hierarchical clustering and Bayesian clustering analysis, however, was not clear but rather continuous. These results indicated that the population structure of Japanese pear cultivars is not distinct.

In Rosaceae crop species, the genetic structure was investigated in peach via analysis with 50 SSR polymorphisms in 224 peach cultivars (Aranzana et al. 2010). The 224 peach cultivars were divided into three main groups based mainly on major common commercial fruit characteristics: melting flesh peaches, melting flesh nectarines and non-melting varieties. The three main groups were obvious both in hierarchical clustering and Bayesian clustering analyses. Compared to the peach cultivars, Japanese pear cultivars had a weak and rather continuous population structure, except for the cluster I and group 1 (Fig. 2). This weakness might exist because a population of Japanese pear cultivars has no clear subdivision that is closely related to varietal characteristics. Self-compatibility in peach might also be a cause of a strong genetic structure in peach cultivars.

GWAS in Japanese pear cultivars

GWAS using the 76 Japanese pear cultivars detected four markers showing significant associations with three traits: resistance to black spot, harvest time and the number of spurs.

Black spot disease, caused by the Japanese pear pathotype of Alternaria alternata (Fr.) Keissler (previously A. kikutiana Tanaka), is a severe disease in Japanese pear cultivation. Susceptibility to the disease has been regarded as a simple trait, i.e., a trait controlled by a single dominant gene (Kozaki 1973). Map positions of genes controlling susceptibility have been estimated in linkage analyses with segregating families (Terakami et al. 2007). The marker CH04h02, which showed significant association with black spot resistance in the present study, was located at the top of linkage group (LG) 11 and was linked closely to the disease susceptibility genes Ani and Ana, which had been detected respectively in cultivars ‘Nijisseiki’ and ‘Nansui’ (Terakami et al. 2007). The 184-bp allele of CH04h02, which had the most negative estimated effects on the black spot resistance (Table 3), is known to be coupled with the susceptible allele Ana (Terakami et al. 2007). The 184-bp allele was harbored by 8 out of 11 susceptible cultivars and 3 out of 65 resistance cultivars in the present study. The 172-bp allele of CH04h02, which showed the second largest negative effects on the resistance (Table 3), is known to be coupled with the susceptible allele Ani.

Harvest time is a quantitative trait and an important characteristic of pear varieties because it differentiates varieties from other varieties and makes them competitive in the market. Two markers showed significant association with harvest time. One marker, PPACS2, was the marker for ACC synthase (1-aminocyclopropane-1-carboxylate synthase) gene. In Japanese pear, ripening and fruit storage potential are related to the amount of ethylene produced. Harvest time is related to the maximum ethylene production during fruit ripening (Itai et al. 2003). ACC synthase (1-aminocyclopropane-1-carboxylate synthase) converts S-adenosyl methionine (SAM) to ACC. Then, ACC oxidase catalyzes the oxidative fragmentation of ACC to form ethylene. Itai et al. (2003) found that PPACS2 is associated with moderate ethylene production, suggesting that the association of PPACS2 observed in the present study is related to the ethylene production ability of Japanese pear cultivars. Although Itai et al. (2003) also found that another marker, PPACS1, was strongly associated with ethylene production, we found no significant association between PPACS1 and harvest time in the present analysis. This is probably because PPACS1 did not have causal alleles in the population of the 76 Japanese pear cultivars. Because PPACS1 is related to strong ethylene production, we speculate that the causal alleles of PPACS1 have been removed from a Japanese pear population via selection against extremely high ethylene production. In this study, we found significant association in the marker BGA35. This marker, probably unrelated to ethylene production, is a good candidate as a marker enabling us to select harvest time independently from ethylene production. Additional studies are expected to fruitful for use of this marker effectively in Japanese pear breeding.

Spur number, a quantitative trait, has not been investigated for its mode of inheritance and QTL. Significant markers detected in this study might serve as clues for the concise genetic analysis of this trait, and be useful also for MAS of this trait in a pear breeding program.

In this study, significant associations were detected despite the few markers and few samples used for GWAS. In human GWAS, even when numerous samples and high-density markers are used, it is sometimes difficult to detect causal genes, and most genetic variation remains unexplained (e.g., Aulchenko et al. 2009). Recent research related to crop GWAS, however, has yielded results contrasting to human GWAS and are obtaining greater success with fewer markers and fewer samples (Hamblin et al. 2011). As Hamblin et al. (2011) suggested, genetic bottlenecks occurring during the histories of crop domestication and modern crop breeding have increased LD between markers and QTL and have also increased the minor allele frequency in both markers and QTL. A population of Japanese pear cultivars is thought to present similar circumstances to those of other crop species.

GS prediction in Japanese pear cultivars

Results of this study suggest that predictions based on genome-wide marker had high (0.75) or medium levels (0.38–0.61) of accuracy in seven out of nine traits. Even in traits for which no significant association was detected, GS predictions showed some levels of accuracy. Specifically, in fruit characteristics, i.e., firmness of flesh, fruit shape in longitudinal section, fruit size, acid content, total soluble solid content, which are important varietal characteristics in Japanese pear breeding, no significant association was detected in GWAS, but GS prediction showed medium levels of accuracy except in all soluble solid content. In addition, in traits in which significant association was found in GWAS, GS predictions were more accurate than predictions based on significant markers. Specifically, in harvest time and the number of spurs, two and one significant markers were detected in GWAS, respectively, but the predictions based on significant markers was much less accurate than GS predictions, suggesting that the traits are determined by several minor and medium QTL as well as major QTL detected in GWAS. In resistance to black spot, predictions based on a significant marker detected in GWAS had comparable accuracy with GS prediction, indicating that the trait is controlled by a major gene and the significant marker closely linked to the major gene. Even in resistance to black spot, however, GS predictions were slightly better than predictions based on the significant marker, suggesting that some minor QTL might also be related to resistance to black spot.

For this study, we compared two Bayesian models—BayesA and BayesB—to determine the accuracy of GS predictions. BayesA, in which all marker effects are always included as explanatory variables, assumes that the trait is controlled by many loci, while BayesB, in which only markers selected via MCMC sampling process are included in the model, assumes that the trait is controlled by few loci (Lorenz et al. 2011). Results of the present study show that BayesA provides higher accuracy than BayesB in seven out of nine traits, suggesting that the assumption of BayesA is more plausible than the assumption of BayesB in these seven traits. At harvest time and the number of spurs, significant associations detected in GWAS suggest the existence of major QTL, but BayesA still showed higher accuracy than BayesB, which suggests that these traits are controlled by several minor and medium QTL as well as major QTL. In resistance to black spot, BayesB was more accurate than BayesA, which agrees with the result that predictions based on the significant marker had comparable accuracy with GS prediction. It is noteworthy that the advantage of BayesA over BayesB might depend not only on the number and size of QTL but also on LD between markers and QTL because genetic variation explained by each marker is determined by the level of LD between the marker and QTL linked to the markers as well as the size of the QTL (Jannink et al. 2010). Additional studies will be necessary to determine the relative advantage of the Bayesian models when the number of markers that is useful for genome-wide predictions is greatly increased in the future.

Potential for GWAS and GS in Japanese pear breeding

The results of this study suggest that GWAS and GS will be useful to accelerate genetic improvement of Japanese pear. Markers detected in GWAS are regarded as linked closely to causal genes and major QTL controlling important agronomic traits. Therefore, they will be useful for MAS. Even for traits for which no significant marker was detected via GWAS, we can predict their phenotypic values with GS prediction models at some level of accuracy, suggesting the future potential of GS in the genetic improvement of complex traits controlled using a number of QTL, e.g., traits related to fruit quality and quantity. GS prediction models will be useful not only for selecting favorable seedlings but also for designing cross breeding and for selecting pairs of parental lines for crossing.

Neither the number of markers nor genotypes (i.e. cultivars) used in this study were sufficient to conduct full-scale GWAS and to train a prediction model for future GS. The power of GWAS and the accuracy of GS prediction can be enhanced by increasing the number of markers and genotypes. Recent advances in genotyping technology have made scoring genome-wide marker polymorphisms cost effective (Davey et al. 2011, Syvänen 2005). Therefore, the number of markers available for analyses can be increased considerably in the near future. A draft genome sequence of the domesticated apple has been published (Velasco et al. 2010). Approximately 2.1 million SNPs for the domesticated apple are now available on Genome Database for Rosaceae (GDR; http://www.rosaceae.org/). Given high collinearity of genomes and high transferability of genetic markers between Malus and Pyrus (Celton et al. 2009a, 2009b, Yamamoto et al. 2007), SNP information for domesticated apple will be useful for SNP marker development in Pyrus species. Genotyping using the next generation sequencer (Davey et al. 2011) will be useful to score a massive number of SNP markers for numerous genotypes. The number of genotypes can be increased by the inclusion of breeding lines that have been evaluated in local adaptability tests but which did not pass the tests. The phenotypes of these lines have been accumulated usually as breeding records. They are useful for GWAS and also for the training of GS prediction models.

A key advantage of the long-lived perennial trees might be the lasting presence of genotypes across years or centuries (Wilcox et al. 2007). The capability of asexual propagation is another advantage of most fruit trees that enables repeated measurements of trait phenotypes with clonally replicated genotypes. Actually, in Japanese pear, a promising breeding line is cloned and cloned genotypes are further tested for their local adaptability over multiple locations and multiple years. The long life and the ability of asexual propagation also enable us to use genotypes almost permanently as parental lines in cross-breeding programs. These advantages, however, might not be so prominent if we were forced to test every new genotype generated in a breeding program with cost-intensive field-testing. If we were able to build good prediction models using the field-test data over multiple locations and multiple years, then GS could reap a great harvest from the data and make the best use of the advantages of long-lived perennial trees.

In a breeding program, field test data are often collected as ordinal categorical scores rather than as continuous values to save labor for measuring traits. As demonstrated in this study, our Bayesian approach can accommodate ordinal categorical scores with modeling latent continuous variations behind the ordinal categorical scores both in GWAS and GS prediction. The Bayesian approach is so flexible that it can be extended further to model genetic variations behind the data of various types (e.g., non-ordinal categorical data and count data). Flexibility will be necessary to use field-test data collected in breeding programs for conducting GWAS and building a GS prediction model. Even though the Bayesian modeling allows us to use ordinal categorical data, we should heed that ordinal categorical scoring might loose some information required for GWAS and GS. By simulation analysis, Iwata et al. (2009) suggested that GWAS in an ordinal trait could miss a large proportion of intermediate to minor QTL. Ordinal categorical scoring might also reduce the accuracy GS prediction. It will be necessary to seek a balance between the benefits (e.g., increase in the power of GWAS and the accuracy of GS prediction) and costs (e.g., increase in time and labor, decrease in the number of measurable samples) from accurate phenotyping.