Intrinsic Functional-Connectivity Networks for Diagnosis: Just Beautiful Pictures?

Abstract

Resting-state functional connectivity has become a topic of enormous interest in the Neuroscience community in the last decade. Because resting-state data (1) harbor important information that often is diagnostically relevant and (2) are easy to acquire, there has been a rapid increase in the development of a variety of network analytic techniques for diagnostic applications, stimulating methodological research in general. While we are among those who welcome the increased interest in the resting state and multivariate analytic tools, we would like to draw attention to some entrenched practices that undermine the scientific quality of diagnostic functional-connectivity research, but whose correction is relatively easy to accomplish. With the current commentary we also hope to benefit the field at large and contribute to a healthy debate about research goals and best practices.

Introduction

Studies of resting blood oxygen level-dependent functional magnetic resonance imaging functional connectivity (FC) have seen an impressive upsurge in the last decade. Beside research questions concerning the interaction of different brain areas that have been pursued in cognitive neuroscience for the last 2 decades, there has been an increase in the number of studies showing altered FC in a host of neurodegenerative and psychiatric disorders. We believe that this new research stems from the realization that resting-state data (1) harbor important information that often is diagnostically relevant [for instance, see Greicius et al., 2004; Uddin et al., 2008; Weng et al., 2009)] and (2) are easy to acquire. The result has been a rapid increase in the development of a variety of network analytic techniques (e.g., Bullmore and Sporns, 2009; Wang et al., 2010) stimulating methodological research in general. While we are among those who welcome the increased interest in the resting state and multivariate analytic tools, we would like to draw attention to some entrenched practices that undermine the scientific quality of the diagnostic FC enterprise whose correction would benefit the field and lead to a discussion and formulation of research goals and best practices. Our intent is to provide a common-sense commentary that a broad audience might appreciate, where our main concerns are cast in terms that do not require readers to be experts in mathematics. It is our hope that some of our points are compelling enough to be adapted as standards for good practice in research and reporting.

Network Derivation and Taxonomy

Identification and attribution of different networks in functional-connectivity research is often performed either (1) via seed-correlation techniques or (2) unsupervised multivariate decomposition routines, such as independent component analysis (ICA)/principal component analysis (PCA), that is, decomposition routines that purely utilize neural data, with subsequent visual topographic inspection of the resulting components and interpretations of these components as networks. Face validity is oftentimes bestowed on a network-based, in large part, on a story line that is developed post-hoc. Data containing an independent validation are oftentimes absent or minimal; further, the citation of previously published research may not include some cogent information. Also, evidence in the form of behavioral or diagnostic correlates of the network activity is too frequently absent. The most disappointing scenario is that in which networks are derived and interpreted purely by virtue of their mutual statistical independence (ICA), or orthogonality (PCA), in which post-hoc functional interpretations are simply based on the brain areas involved.

Such practices are problematic on several counts. Blind decomposition techniques like PCA or ICA, or other techniques, are useful tools for data reduction. This means that they achieve a parsimonious representation of a data array by reducing it to its main components. Here “main” is a quantitative criterion that a priori has no neuroscientific meaning. For instance, in an application of group-level PCA for a brain imaging study one might find that five Principal Components capture 95% of the aggregate variance in the data, for a data array with 40 observations. Disregarding all other components apart from these five would result in a data reduction that would be quite impressive: instead of keeping track of 40 different brain images, we now only have 5 component images and their brain scores. Overall, the data reduction would thus be almost eightfold.

Now even with this impressive data reduction, or compression, it cannot be assumed from the outset that the individual components represent intrinsic features of functional brain architecture. PCA, for example, simply renders an ordering of components in terms of variance contribution; further, the components are mutually orthogonal. Both variance ordering and orthogonality though are true by design, and thus would also be found in completely meaningless statistical noise. The same applies to ICA: here the components are spatially independent (for spatial ICA) in a more general sense than PCA (which just postulates independence up to the second-order moment), but whether the components have intrinsic meaning cannot be answered just from the mathematical principles of ICA itself. It is possible—we would say likely—that brain networks underlying a cognitive process do not neatly break out into mutually orthogonal or independent components, and testing any construct validity would necessitate additional information.

It is our impression that, despite these well-known facts, researchers have found it difficult to resist over-interpreting the topographic composition of the spatial components (either from PCA or ICA). A typical characterization might be offered with a phrase like “ventromedioprefrontal network,” etc., but this is a topographic account that can only screen for artifacts located in implausible areas like ventricles or white matter; without replication in independent data or an assessment of robustness in the training data set at hand, and without an association with a behavioral or clinical subject variable, we have no way of telling whether the components resulting from the PCA/ICA really occupy any privileged position concerning neuroscientific meaning. As such they are purely mathematical dimensions of the data and could really be mixtures of different effects; one should take care and be mindful in the proliferation of such constructs.

Sometimes, additional evidence is offered and component expression across subjects correlates with a behavioral or demographic subject variable. This is superior to the purely phenomenological approach and gives some converging evidence that the identified component has some meaning that transcends its role as a mathematical dimension. It is our impression though that such additional evidence is presented rarely. In summary, while we encourage the use of PCA/ICA-based methods, we would also caution investigators to be mindful that intrinsic features of functional brain architecture may not be separable into individual PCA/ICA components. Indeed, it might be good practice to entertain two distinct interpretations of each PCA or ICA component, where both make sense in terms of experimental design.

Our Take-Home Message

ICA, PCA, and other multivariate decomposition routines are useful for data reduction and compression. But do not assume that the resulting components are intrinsically meaningful. For this assessment, additional information is needed.

Lack of True Network Assessment with Mass-Univariate Techniques

We offer this next point not as a criticism, but rather further elaboration and clarification. Despite network metaphors, analyses presented in functional-connectivity studies are often univariate. Notably, seed-correlation is a univariate approach and utilizes voxel-wise mass-univariate associations with a single reference location only. We are not arguing against the use of seed-correlations and believe it to be a valuable tool that has its place in functional-connectivity research. However, a clarification as to what seed-correlation does not do is in order.

Because seed-correlation is a univariate approach it is possible that the identified areas resulting from it (1) do not show a level of pairwise inter-correlation that would suggest direct functional connectivity (FC) between them, or (2) are linked to a common node other than the seed voxel that, for a of a variety of reasons, does not show up in the seed-correlation map.

Both these possible scenarios follow simply from the nature of high-dimensional data. For a timeseries of at least 5 min, we have at least 150 data points if a repetition time of 2 sec is adopted in the MRI scan. For this fairly standard number of data points it is relatively easy for the activation at two different brain regions to display no relationship to one another, while both displaying a significant correlation with a third region. When there are many observations, high correlations R(A,B) and R(A,C) do not imply a high correlation R(B,C).

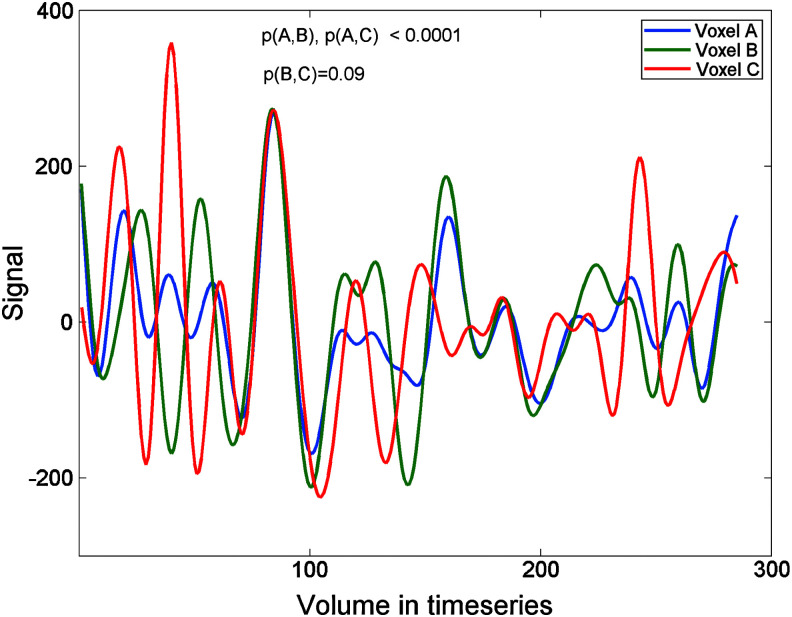
Figure 1 shows some actual timeseries in three locations in a resting scan that was acquired over 9.5 min at TR=2 sec. While voxel A is correlating significantly in its timeseries with voxel B and C, voxel B and C are not significantly correlated. Thus, while the identified voxel locations might share significant connections with one another, they cannot be guaranteed to do so. In the most extreme scenario, a hub-and-spokes structure might be uncovered, with the seed voxel in the center, manifesting only outward connections to the discovered voxels, whereas the discovered voxels share no connections among one another. This might still qualify as a network in a sense, but it might not be exactly what most people assume when viewing the results of seed-correlation approaches.

FIG. 1.

Illustration of nontransitivity of correlational associations. Voxel A shows significant correlation in its timeseries with voxels B and C (p<0.0001). B and C, however, do not show a significant correlation, p=0.09.

This point has a broader message too: the community would do well to define clearly in either analytical or operational terms what exactly constitutes a network, and how it can be tested and replicated. As it stands, the term “network” seems to encompass a large variety of phenomena exhibiting varying degrees of association or even just co-activation. Some fine-tuning would help and increase mutual understanding.

Our Take-Home Message

Be careful to infer direct FC between two brain areas only because they both manifest significant activation in a seed-correlation map with a third location. The converse is true too: two brain areas can show high mutual correlation even though they are not both identified in a seed-correlation map with a third brain area.

Lack of Comparative Assessment and “Anti Occam's Razor” in FC-Based Biomarker Construction

This point is the most important one of our critique: FC has been used extensively for diagnostic purposes, with derived biomarkers that show a difference between patients suffering from a neurodegenerative or psychiatric disorder and healthy control subjects. In practice, this means that innovative, but complex, network measures (based on graph theory, seed-maps, ICA, etc.) are shown to hold diagnostic promise in the subject sample they are derived from, but often might not have the same high levels of sensitivity and specificity compared to extant biomarkers, although the latter biomarkers are likely to be based on earlier technologies (e.g., FDG-PET) and are more likely to be based on simpler first-order statistics (e.g., time averaged signals). Along these lines, there have been few studies comparing FC-based measures obtained from resting-functional magnetic resonance imaging (fMRI) and FDG-PET/SPECT/PET perfusion to check whether FC-based measures provide additional information above and beyond traditional imaging biomarkers, particularly concerning out-of-sample prediction and diagnosis. Rather, FC-based measures for the most part remain untested novel proof of concepts. When independent data for the validation of FC-measures are lacking, a minimum requirement should be a thorough assessment of the replication of the derived FC-measures in the training sample via cross-validation, yet often even such a test is missing too.

This goal would be relatively straightforward to accomplish. For example, when constructing diagnostic biomarkers using FC methods, the fMRI data likely came from a study designed to investigate regional interactions. The timeseries data of each participant thus offer computation of the FC-based disease marker of interest with a variety of simple time-averaged first-order statistics for reference, like the mean time-averaged activation at critical locations, or the grand mean. Cross-validation can be performed to determine whether the FC-biomarkers perform better in the left-out data folds than the simple first-order reference measures. Further cross-validation comparisons can also be performed using data from other imaging modalities, for example, FDG-PET, SPECT, or PET perfusion data, if these are available.

Some skepticism when looking at FC-biomarkers is justified given the fact that functional-connectivity is based on correlations and other measures of association that are 2nd-order measures, which are less robust than 1st-order measures (e.g., time averaged measures). Any diagnostic information afforded by these biomarkers therefore needs to compensate for a potentially higher amount of statistical noise. This consideration applies of course to any biomarker: the more processing steps are involved in the construction of a marker, the more variance is introduced too. A typical graph-theory application, for instance, might choose a set of ROIs, an association measure, and a threshold to apply to obtain an adjacency matrix, from which to compute measures like local or global efficiency (Wang et al., 2010). These indicators might constitute mechanistically justified biomarkers, but on account of their complex and derived nature they could be quite noisy and need to be compared to simpler but equally plausible biomarkers.

We illustrate these points on a small data set of resting-state fMRI in which we use a variety of simple markers with only one marker based on FC, to predict subjects' age status (young/old) out of sample. We admit that this example is somewhat contrived: chronological age status is usually not a variable that has to be inferred from neural data, given that it is perfectly known a priori. However, the example gives a flavor of the comparative assessment that could be readily performed in clinical neuroimaging research, but so far is often lacking.

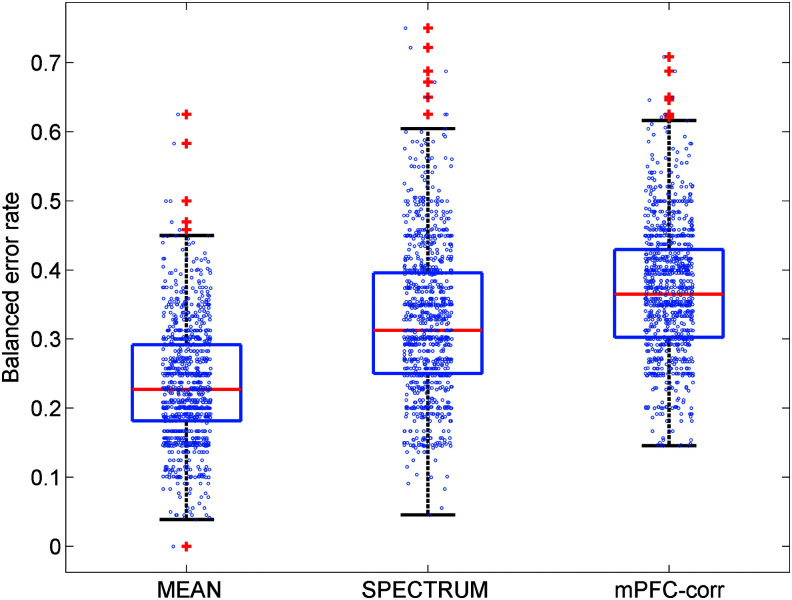
We acquired 9.5 min of resting fMRI data from 24 young (age 22–30) and 21 aged (age 62–69) subjects, at a repetition time of TR=2 sec (=285 volumes). Details of the acquisition and preprocessing, including a correction for white-matter and ventricular nuisance regressors, can be found elsewhere (Habeck et al. under review) and are not of crucial importance for the comparative assessment. From the corrected timeseries data, we computed three types of input data: (1) mean signal maps, that is, every voxel's timeseries was averaged across the 285 volumes in the timeseries, leading to one map per subject; (2) power spectra for the mean-voxel timeseries, that is, every time point was averaged across all voxels and the resulting timeseries submitted to a Fourier decomposition, leading to one power spectrum of 143 frequencies; and (3), seed-correlation Fisher-Z maps for which a medioprefrontal reference seed was used (TAL=[1 40 16] from [Andrews-Hanna et al., 2007]). These three types of input data were used to predict subjects' age status in a split-sample simulation. For every iteration in this simulation, the pool of 45 subjects was randomly divided into a training set of 25 subjects, with a test set of the remaining 20 subjects, for a total of 1000 iterations. A support vector classifier (SVM) (Hastie et al., 2009) was derived from the training data set for all three data types, and tested in the test data set. Test performance was recorded with the balanced error rate, that is, the average of type-I and type-II error for classifying a subject as old. The result of the simulation can be seen below.

One can see that the mean signal maps (“MEAN”) performed the best, whereas performance of the mean-timeseries spectra (“SPECTRUM”) was worse, and the seed-correlation maps (“mPFC-corr”) performed even worse (Fig. 2).

FIG. 2.

Out-of-sample prediction of age in a test sample of 20 subjects, based on support vector classifiers constructed in a training sample of 25 subjects, averaged over 1000 iterations of a split-sample simulation. The mean maps (MEAN) give the best prediction of age status; the seed-correlation maps (mPFC-corr) give the worst prediction.

There are of course many ways in which this comparison could be optimized: adaptive subspace selection techniques could be used to make all maps less noisy before they enter the SVM classification; different machine-learning tools could be used altogether; different ratios in the strength of training and test data sets could be used; and different reference-seed voxel locations could be used. We have varied some of these parameters, but essentially found the same relative results: the seed-correlation maps [also when using other default-mode network seeds as outlined in (Andrews-Hanna et al., 2007)] have the worst test performance in the age status classification. As we stated before, our sample size was quite small and age status prediction as a goal is rather didactic. Methodological optimization of our different classifiers is not the point of this commentary, so we kept the methods rather simple. It could thus be that seed-correlation or other functional-connectivity measures are indeed the most powerful predictors for out-of-sample diagnosis of disease (rather than chronological age), but in the existing literature the empirical proofs for this assertion are often lacking. As we tried to show here, this need not be the case.

We can further illustrate the larger variability of correlational measures: they involve 2nd-order moments and are thus more influenced by statistical noise than measures constructed from 1st-order moments. We performed PCA on all three types of data, that is, mean maps, power spectra, and seed-correlation maps, and inspected the relative eigenvalues. Further, we also performed a bootstrap resampling procedure (Efron and Tibshirani, 1993) for which we resampled the data with replacement and computed first principal components for all three types of data 80 times. This yielded 80 versions of the resampled first PC for each data set. We computed the subtending angles of all 3160 possible pairs of first PCs (within each data set) that can be formed from the 80 bootstrap samples to get an idea about the variability of the PC under the resampling procedure, which approximates the population variability.

From the Table 1 one can appreciate that the seed-correlation maps possess a flatter and more degenerate eigenvalue distribution, hinting at larger noise contributions. The first 10 Principal Components account for 71%, 97%, and 50% variance in the aggregate for mean, spectral, and seed-correlation maps, respectively. For the bootstrap samples, one can see that the seed maps have larger subtending angles, that is, sampling variability influences the first PC to a greater extent, than for the other two data types.

Table 1.

Seed-Correlation Maps Have a Flatter, More Degenerate Eigenvalue Distribution and Show Larger Bootstrap Variability

	Mean maps	Spectra	Seed maps
First eigenvalue	0.45	0.54	0.16
Sum of first 5 eigenvalues	0.62	0.83	0.35
Sum of first 10 eigenvalues	0.71	0.97	0.50
Median between-PC angle (degree)	14	12	33

Eigenvalues and bootstrap simulations are not designed to address the aims of prediction or classification: they simply illustrate that seed-correlation maps, due to their more derivative nature, are more variable and less robust. This will influence the derivation of biomarkers though and necessitate larger data sets.

Our Take-Home Message

The fact that FC-derived biomarkers show significant differences as a function of disease in a training sample does not guarantee (1) that they will also show a significant difference in an independent test data-set or (2) that they are the best biomarkers available. Both assertions would have to be proved empirically and researchers should routinely include performance comparisons with other biomarkers in their studies, using replication in independent data sets, or at least cross-validation in the training sample.

Low Data-Ink and “Anti Occam's Razor” in Article Figures

The relevance of this last observation is not onlt limited to the analysis of resting-state FC research, but also applies to brain-imaging neuroscience in general. Here also, existing practices could easily be changed and re-focused. We refer to the Principles of Graphical Excellence, outlined in the landmark book The Visual Display of Quantitative Information by E. Tufte (Tufte, 2001). The first principle spells out the need above all else to show the data and maximize data ink. This tenet can be loosely translated as, “Make sure to only display things that are relevant to the message you want to convey to the audience based on the results of your study.” In our opinion, violations of this principle can be observed rather frequently in article figures that sometimes show little to do with the data and results of the study under consideration, but instead appear to driven by the need to provide visually aesthetic background. Unfortunately, this background often takes such prominence that the foreground can easily get lost. We have two concrete examples in mind: (1) brain templates on which functional-imaging results are displayed, and (2) colorful high-dimensional correlation matrices. For (2) we can blame the software package Matlab: plotting a visually appealing correlation-matrix with color coding is very easy and literally can be accomplished with one short command in the Matlab console—it thus offers itself to any high-dimensional data array, whether the display is useful or not. To make the correlation-matrix display useful, a clear understanding of the row and column ordering is essential, lest the main insight that can come out of a correlation matrix computation, the presence and location of off-diagonal elements, is not easily understandable. Instead, the purpose for the visual display becomes purely incidental: a visually appealing display with an attractive symmetry as an end in and of itself. We might add, somewhat more controversially, that figures of graphs (with nodes and edges) based on thresholded measures of functional association are in our opinion even less useful: since they are critically dependent on a threshold, one would usually do better to display the unthresholded association matrix and thus suffer no loss of any information. Further, graphs for functional data are too suggestive of structural connectivity and might confuse the readers more than enlighten them, particularly if the location of the nodes in the graph has no meaningful equivalent in 3D space. For instance, a graph that shows temporal correlation between components from an ICA thresholded at R>0.4 might make a visually pleasing display that evokes impressions of a structural wiring diagram—although with an arbitrary placement of the nodes in the graph and a correspondingly large variety of edge constellations that all express the same underlying adjacency matrix. Less distracting and ambiguous would be a listing of all pairwise correlations in a table, or a display in a correlation matrix.

Brain templates are different in that they are necessary for conveying information of spatial location (where?), before providing detailed quantification (how much?) of the results at the specific locations. However, state-of-the-art software packages often allow one to go further and can add much information not relevant to the results of the study, distracting the audience from the research at hand and often offering visually compelling information that only minimally supports the primary hypotheses. We offer one easy suggestion: try to write the article as if no figures were allowed by inclusion of tables and coordinate listings first; next, think about what information you want to add to a figure that is not explicitly presented in the tables. This simple exercise is very effective in uncovering redundancy and nondata ink. Ideally, your figure should show more than that can be conveyed by table listings or verbal descriptions, but should not include things that could safely be left out without hindering the presentation of the results.

Our Take-Home Message

Figures should convey important information pertaining to the results of your research that cannot easily be captured with words or tables. Visually pleasing displays of nonessential information have no place in such figures.

Conclusion

We believe that our criticisms have easy remedies that do not require a large amount of extra work or a high degree of mathematical sophistication. Point 1 calls for a higher evidentiary standard in the attribution of a special role to multivariate activation patterns. Point 2 is mainly a clarification as to what seed-correlation approaches actually do. Point 3 calls for a substantial increase in comparative out-of-sample validation of FC-based biomarkers. Point 4 calls for tighter graphics that make data and results in their displays more prominent while refraining from purposeless, but beautiful, displays of colorful brain templates or correlation matrices. We stress that our commentary is based on observations from attending a recent resting-state conference and can, of course, not be exhaustive: other researchers may have a different list of shortcomings that they consider equally relevant, or may disagree with us entirely. Our intent is to contribute to a dialog that eventually leads to a roster of best practices for FC research and fosters a better style of science, leading to clinically useful and replicable insights from this exciting field of research.

Acknowledgments

We thank Yunglin Gazes for a careful reading of the article and helpful suggestions. Discussions of C. Habeck with Anette Fasang in the context of Sequence Analysis gave helpful inspiration for this commentary.

Author Disclosure Statement

No competing financial interests exist.