Measurement of Single Cell Refractive Index, Dry Mass, Volume, and Density Using a Transillumination Microscope

Abstract

Phase contrast microscopy has become ubiquitous in the field of biology, particularly in qualitative investigations of cellular morphology. However, the use of quantitative phase retrieval methods and their connection to cellular refractive index and dry mass density remain under utilized. This is due in part to the restriction of phase and cellular mass determination to custom built instruments, involved mathematical analysis, and prohibitive sample perturbations. We introduce tomographic bright field imaging, an accessible optical imaging technique enabling the three dimensional measurement of cellular refractive index and dry mass density using a standard transillumination optical microscope. The validity of the technique is demonstrated on polystyrene spheres. The technique is then applied to the measurement of the refractive index, dry mass, volume, and density of red blood cells. This optical technique enables a simple and robust means to perform quantitative investigations of engineered and biological specimens in three dimensions using standard optical microscopes.

The use of high magnification optical microscopy has become an indispensable resource in the investigation of cellular organisms. Owing to their low endogenous absorbance and weak scattering properties over the visible optical spectrum, cells primarily affect the phase of optical waves traveling through them and thus appear semitransparent when imaged with standard bright field microscopes. This fact has inspired the utilization of phase to enhance contrast in cellular imaging (e.g., phase contrast and differential interference contrast microscopy) and quantify cellular structure [1-3]. While the use of phase contrast and differential interference contrast microscopy in qualitative investigations of cellular morphology has become widespread, the use of quantitative phase retrieval methods and their connection to cellular refractive index and dry mass density [4] remain confined to a handful of laboratories. This is a result of the restriction of phase and cellular mass determination to custom built instruments [3,5,6], involved mathematical analysis [7], and prohibitive sample perturbations [4]. In this Letter, we introduce tomographic bright field imaging (TBFI), an optical imaging technique enabling the measurement of cellular refractive index and dry mass density using a standard transillumination optical microscope.

TBFI is an extension of quantitative noninterferometric propagation-based phase determination methods based on the transport of intensity equation (TIE) [8,9]. Posed under the paraxial approximation to the full wave dynamics, TBFI relates intensity disturbances along the optical axis in the wave field to transverse (perpendicular to the optical axis) refractive index variations of the medium. The method is thus applicable only to specimens with transverse index gradients. The appropriateness of the paraxial approximation is ensured by the weak index contrast of biological specimens and the illumination of the object with collimated unidirectional monochromatic plane waves. These waves are easily produced on standard microscope setups employing low numerical aperture (NA = 0:2) condenser lenses in a Köhler configuration with a narrow band color filter (λ = 540 ± 20 nm) placed in the illumination arm of the instrument.

Experimentally, the TBFI technique consists of an image acquisition step and post-processing procedure: through-focus bright field images, acquired with a charge coupled device (CCD) camera mounted on a standard microscope, serve as the input to the TBFI model from which the specimen refractive index and mass density are determined using a fast Fourier transform based numerical method.

To develop the TBFI formalism we define three dimensional coordinates (r_⊥, z) where z denotes the position along the optical axis and r_⊥ the position within a plane normal to the optical axis. ∇_⊥ is the gradient and Δ_⊥ the Laplacian in r_⊥ coördinates. Defining the wave field traversing the specimen by $U(r_{\perp },z)=\sqrt{I(r_{\perp },z)}\exp \left(i\varphi \right(r_{\perp },z\left)\right)$, where I is the intensity and φ the phase, the TIE is obtained by substituting U into the paraxial wave equation and taking the imaginary part of the resulting expression; the eikonal equation arises from the real terms. Letting k = 2π/λ, the TIE is given by [9,10]

$$-k\frac{\partial }{\partial z}I(r_{\perp },z)={\nabla }_{\perp }\cdot \left[I\right(r_{\perp },z\left){\nabla }_{\perp }\varphi \right(r_{\perp },z\left)\right],$$ (1)

with boundary conditions I(r_⊥, z) ≥ 0 in L × D and I(r_⊥, z) = 0 on ∂L × ∂D.

Denoting the trajectory of waves through the sample by the parametric curve $\overrightarrow{p}\left(s\right)$, s ∈ [0, l], phase distortions induced in the wave field as the wave propagates from point $\overrightarrow{p}\left(0\right)=(r_0,z_0)$ to $\overrightarrow{p}\left(l\right)=(r_{\perp },z)$ can be related to the refractive index, n(r_⊥, z), of the specimen through solutions to the eikonal equation [11] for phase

$$\varphi \left(\overrightarrow{p}\right(l\left)\right)-\varphi \left(\overrightarrow{p}\right(0\left)\right)=k{\int }_0^{l}n\left(\overrightarrow{p}\right(s\left)\right)\mid {\overrightarrow{p}}^{\prime }\left(s\right)\mid ds.$$ (2)

The objective lens of the microscope images spherical waves emanating from the sample plane onto the CCD camera while plane waves are out of focus due to the Köhler illumination conditions. As a result, waves contributing to image formation are not propagating solely along the optical (z) axis; their deviation is slight enough however, as detailed by Mie theory and the Born approximation for weak index contrast systems, to satisfy the constraints of the PA. The optical sectioning of the sample, due to spatial frequency space filtration by the objective lens under the Bragg condition [12], ensures that phase contributions to the spherical waves leaving the sample plane are specific to that plane when imaged onto the CCD camera. Moreover, the waves contributing to image formation, ignoring out-of-focus contributions, can be considered as plane waves up to their interaction inside the focal volume of the objective lens. This is justified by the first order Born approximation in which weak index systems do not give rise to appreciable multiple scattering. Together, these properties enable the restriction of Eq. (2) to straight-line trajectories of wave energy along the optical axis through the sample: $\overrightarrow{p}\left(s\right)\approx s\widehat{k}$.

Letting (r₀, z₀) be the origin, swapping dummy variable s with z′, and taking the specimen to be located directly above the origin, hence φ(r₀, z₀) = 0, for points inside the specimen we find $\varphi (r_{\perp },z)=k{\int }_0^{z}n(r_{\perp },z^{\prime })d{z}^{\prime }$. Substitution of this integral expression for phase into the TIE, followed by a subsequent differentiation in z yields the TBFI imaging model: an equation relating the measurable axial intensity variations to the refractive index of the sample

$$-\frac{{\partial }^{2}I}{\partial z^2}+{\nabla }_{\perp }\cdot \left\{\frac{\partial I}{\partial z}\left\{I^{-1}{\nabla }_{\perp }\left[{\nabla }_{\perp }^{-2}\frac{\partial I}{\partial z}\right]\right\}\right\}={\nabla }_{\perp }\left[I{\nabla }_{\perp }n\right].$$ (3)

In the development of this expression we have used the identity [10] ${\nabla }_{\perp }\varphi =-(k∕I){\nabla }_{\perp }[{\nabla }_{\perp }^{-2}\partial I∕\partial z]$.

Following the techniques presented in [9,10] we develop a solution for the refractive index. Letting G denote the Green function of the Laplacian in ${\mathbb{R}}^2$, the refractive index has the formal representation

$$n(r_{\perp },z)=-{\int }_{{\mathbb{R}}^2}\frac{\partial }{\partial z}\left\{\right[I{(r_{\perp }^{\prime },z)}^{-1}{\int }_{{\mathbb{R}}^2}\left(\frac{\partial }{\partial z}I\left(r_{\perp }^{″},z\right)\right)\cdot {\nabla }_{{\perp }^{″}}G(r_{\perp }^{\prime },r_{\perp }^{″})d{r}_{\perp }^{″}]\cdot {\nabla }_{{\perp }^{\prime }}G(r_{\perp },r_{\perp }^{\prime }\left)\right\}d{r}_{\perp }^{\prime }.$$ (4)

The numerical implementation of this formula can be carried out in a practical manner, via the convolution theorem, as the application of several two dimensional Fourier transforms, denoted by $\mathcal{F}$:

$$\begin{array}{cc}\hfill n(r_{\perp },z)=& -{\mathcal{F}}^{-1}\left\{\frac{k_x}{k_x^2+k_y^2}\mathcal{F}\left\{I^{-2}\frac{\partial I}{\partial z}{\mathcal{F}}^{-1}\left\{\frac{k_x}{k_x^2+k_y^2}\mathcal{F}\left(\frac{\partial I}{\partial z}\right)\right\}\right\}\right\}+{\mathcal{F}}^{-1}\left\{\frac{k_x}{k_x^2+k_y^2}\mathcal{F}\left\{I^{-1}{\mathcal{F}}^{-1}\left\{\frac{k_x}{k_x^2+k_y^2}\mathcal{F}\left(\frac{{\partial }^{2}I}{\partial z^2}\right)\right\}\right\}\right\}\hfill \\ \hfill & -{\mathcal{F}}^{-1}\left\{\frac{k_y}{k_x^2+k_y^2}\mathcal{F}\left\{I^{-2}\frac{\partial I}{\partial z}{\mathcal{F}}^{-1}\left\{\frac{k_y}{k_x^2+k_y^2}\mathcal{F}\left(\frac{\partial I}{\partial z}\right)\right\}\right\}\right\}+{\mathcal{F}}^{-1}\left\{\frac{k_y}{k_x^2+k_y^2}\mathcal{F}\left\{I^{-1}{\mathcal{F}}^{-1}\left\{\frac{k_y}{k_x^2+k_y^2}\mathcal{F}\left(\frac{{\partial }^{2}I}{\partial z^2}\right)\right\}\right\}\right\}.\hfill \end{array}$$ (5)

Through-focus intensity images are used to approximate the axial intensity derivatives appearing in Eq. (5) using finite differences. Here k_x and k_y denote the spatial frequency variables corresponding to the coordinates x and y, respectively. Low frequency noise contributions are eliminated by taking $k_{x,y}∕k_x^2+k_y^2=0$ for k_x,y = 0. With the elimination of these “dc” frequency components, a knowledge of the ambient refractive index is required to set the absolute scale for the refractive index.

The TBFI model was validated on four engineered samples: 0.1, 2.8 and 4.8 μm diameter polystyrene spheres (n = 1.597) imaged with a ×63 oil-coupled objective lens, NA₀ = 1.4; as well as a water (n = 1.333) filled fused silica glass (n = 1.460) microfluidic channel (Translume, Ann Arbor, MI) of width 100 μm and depth 100 μm imaged with a ×10 air-coupled objective lens, NA₀ = 0.25. Through-focus bright field images at an illumination wavelength λ = 540 ± 20 nm (Chroma Technology Corp, Bellows Falls, VT) were acquired in 0.1 μm axial increments using a Zeiss Axio Imager 2 microscope (Carl Zeiss MicroImaging GmbH, Germany) outfitted with a condenser lens, NA_c = 0:2, with the microscope under software control by SlideBook (Intelligent Imaging Innovations, Denver, CO).

In Fig. 1 we demonstrate three dimensional TBFI refractive index reconstructions of 0.1 μm diameter spheres, Figs. 1(a)-1(d), suspended in fluoromount G (SouthernBiotech, Birmingham, AL) (n = 1.4) and 2.8 μm spheres, Figs. 1(e)-1(h), suspended in glycerol (n = 1.474). TBFI reconstructions of the 0.1 μm spheres demonstrated an enhancement of the theoretical transverse diffraction limit of the system (= 1.22λ/(NA₀ + NA_c) = 0.41 μm) with a measured transverse resolution of 0.26 μm, Fig. 1(b). The axial resolution was measured to be 0.35 μm, Fig. 1(d). Reconstructions on 0.1 μm diameter spheres were subject to higher noise during image acquisition which translated to artifacts in the reconstructions; Fig. 1(d). Reconstruction of the 2.8 μm diameter spheres enjoyed higher signal to noise ratios during image acquisition and were successful in capturing the cross sectional geometry of the sphere; Fig. 1(h).

FIG. 1.

(color online). Three dimensional TBFI refractive index reconstructions of polystyrene spheres. (a) Enface bright field image of 0.1 μm polystyrene sphere (n = 1.597, imaging wavelength λ = 540 nm), suspended in fluoromount G (n = 1.4) (b) corresponding refractive index map. (c) Cross sectional image of 0.1 μm sphere, (d) corresponding refractive index map. (e) Enface bright field image of 2.8 μm polystyrene sphere suspended in glycerol (n = 1.474), (f) corresponding refractive index map, (g) cross sectional bright field image of 2.8 μm sphere, (h) cross sectional refractive index map.

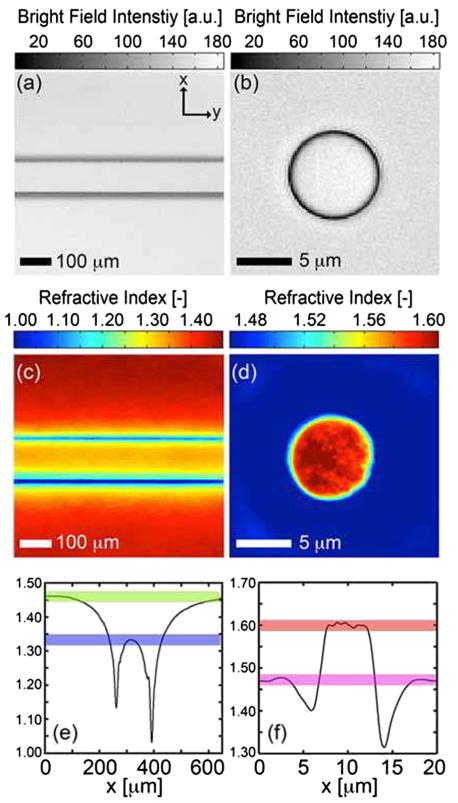
Polystyrene spheres larger than 2.8 μm diameter are problematic to reconstruct as diffraction effects nullify the paraxial TBFI model assumptions. However, in the central plane of larger objects, where diffraction effects are minimized, the refractive index can be reconstructed. In Fig. 2(a) we demonstrate an example bright field image of water in a 100 μm deep by 100 μm wide microfluidic channel and in Fig. 2(c) we report the corresponding refractive index map. Figure 2(b) and 2(d) demonstrate a bright field image and corresponding refractive index map for a 4.8 μm diameter polystyrene sphere suspended in glycerol. In both experiments, the recovered refractive indices were found to fluctuate within a 1% range around the accepted values, Figs. 2(e) and 2(f), shaded bars denote a 1% range.

FIG. 2.

(color online). TBFI refractive index reconstructions of the central focal plane in thicker specimens. (a) Bright field image of water in a 100 μm wide fused silica microfluidic channel, air-coupled ×10 lens with NA = 0.25 and (b) 4.8 μm diameter polystyrene sphere suspended in glycerol, oil-coupled lens with NA = 1.4. (c) Refractive index map of water, n = 1.333, in glass microfluidic, n = 1.460, (d) index map of polystyrene sphere, n = 1.597 in glycerol n = 1.474. (e) Average refractive index profile versus the x direction of the channel, (f ) refractive index along the diagonal of (d). Shaded bars in (e), (f) denote ±1%.

For biological applications on cellular specimens, the dry mass density, C [g/dL], can be inferred from the refractive index through a linear calibration model [4,13]

$$n(r_{\perp },z)=n_{{\mathrm{H}}_2\mathrm{O}}\left[\alpha \right(\lambda \left)C\right(r_{\perp },z)+1].$$ (6)

α(λ) [dL/g] is the specific refractive increment of the cell solids: for nucleated cells α = 0.002/nH₂O [4] independent of λ, while for hemoglobin (Hb) rich red blood cells α(λ) = 0.001981 at λ = 540 nm [13].

To demonstrate the ability of TBFI to recover properties of biological specimens, we applied the technique, with the optimized axial increments from the sphere calibration, to the measurement of the mass, volume, and density of 20 red blood cells (RBCs) at ×63 magnification. Peripheral blood was obtained from a healthy volunteer, dispersed onto a glass microscope slide and fixed with paraformaldehyde. A coverslip was mounted over the RBCs using fluoromount G.

Figure 3(a) demonstrates the bright field image of RBCs, Fig. 3(b) the in-plane refractive index, and Fig. 3(c) the inplane mass density at the central focus position. To demonstrate the optical sectioning capabilities of TBFI we report the recovered refractive index and mass density in planes ±0.4 μm about the central focal position of a single RBC, Figs. 3(e) and 3(f), respectively, along with the xz projection average of these quantities over the axial extent of the RBC, Figs. 3(h) and 3(i). The Cartesian product of the xz, yz, and enface projection averages of the RBCs was used to generate a three dimensional characteristic function, χ, for the extent of the cell: letting D denote the spatial collection of voxels comprising the cell, χ(r_⊥, z) = 1 if (r_⊥, z) ∈ D, χ(r_⊥, z) = 0 if (r⊥, z)D. The mass and volume were then computed according to $M={\int }_{D}C(r_{\perp },z)\chi (r_{\perp },z)d{r}_{\perp }dz,V={\int }_D\chi (r_{\perp },z)d{r}_{\perp }dz$.

FIG. 3.

(color online). TBFI reconstruction of refractive index and dry mass density of red blood cells. (a) Bright field intensity image of RBCs, (b) refractive index map of RBCs computed using TBFI, (c) mass density map of RBCs using the Hb calibration reported in [13]. (d) Bright field intensity images at 0 and ±0.4 μm of the boxed RBC in (a) about the focus, (e) corresponding refractive index maps, and (f) corresponding mass density maps. xz projection averages of (g) bright field intensity, (h) refractive index, (i) mass density.

As measured by TBFI, red blood cells were found to have an average refractive index of 1.402 ± 0.008, (all quantities mean ± standard deviation), in keeping with Hb associated refractive index values at λ = 540 nm reported in [13], an average dry mass of 27.2 ± 5.3 [pg], volume 100.7 ± 17.9 [fL], and density 27.1 ± 3.1 [pg/fL] (or [g/mL]); all within physiological norms [14].

In summary, TBFI is a technologically accessible label-free imaging modality capable of quantifying cellular refractive index, mass, volume, and density of multiple biological specimens simultaneously. TBFI is readily extended to live cell imaging to monitor growth dynamics over time, subcellular architecture, studies of sample dispersion properties [15] through the use of multiple color filters, e.g., liquid crystal tunable filters, and is readily utilized in parallel with phase contrast enhancement techniques [16], and fluorescence microscopy on standard optical microscopes.